Improved analytical methods for microarray-based genome-composition analysis

Short abstract

Genome-composition analysis using microarrays can be used to categorize genes into 'present' and 'divergent' categories. This involves selecting a signal value that is used as a cutoff to discriminate present and divergent genes, but this can result in the misclassification of many genes. A method is described that depends on the shape of the signal-ratio distribution and does not require empirical determination of a cutoff. Many genes previously classified as present using static methods are in fact divergent on the basis of microarray signal; this is corrected by our algorithm.

Abstract

Background

Whereas genome sequencing has given us high-resolution pictures of many different species of bacteria, microarrays provide a means of obtaining information on genome composition for many strains of a given species. Genome-composition analysis using microarrays, or 'genomotyping', can be used to categorize genes into 'present' and 'divergent' categories based on the level of hybridization signal. This typically involves selecting a signal value that is used as a cutoff to discriminate present (high signal) and divergent (low signal) genes. Current methodology uses empirical determination of cutoffs for classification into these categories, but this methodology is subject to several problems that can result in the misclassification of many genes.

Results

We describe a method that depends on the shape of the signal-ratio distribution and does not require empirical determination of a cutoff. Moreover, the cutoff is determined on an array-to-array basis, accounting for variation in strain composition and hybridization quality. The algorithm also provides an estimate of the probability that any given gene is present, which provides a measure of confidence in the categorical assignments.

Conclusions

Many genes previously classified as present using static methods are in fact divergent on the basis of microarray signal; this is corrected by our algorithm. We have reassigned hundreds of genes from previous genomotyping studies of Helicobacter pylori and Campylobacter jejuni strains, and expect that the algorithm should be widely applicable to genomotyping data.

Background

Categorization of bacteria on the basis of their genotypic characteristics is supplanting classification based on phenotypic markers. Genotypic information surpasses the resolution achievable with phenotypic markers, giving deeper insights into evolutionary relationships between species that are indistinguishable on the basis of phenotypic traits. We are particularly interested in the use of genome-composition information to identify factors that distinguish pathogenic bacteria from their non-pathogenic counterparts.

Although more than 86 prokaryotes have been sequenced since the first completed genome in 1995 [1], the vast majority of the sequenced genomes represent different species. Use of this information is therefore generally limited to mapping relationships on the genus and species levels. However, much of the interesting genome information that determines phenotypic traits, such as degree of virulence, is encoded in small differences between strains and serovars, rather than species. Although considerable time will elapse before enough strain-specific sequence information becomes available through genome sequencing projects to identify such traits, microarrays provide us with a tool to gain insight into genome composition at present.

A number of studies have investigated genome composition using spotted DNA microarrays [2,3,4,5,6,7,8,9,10,11,12,13], a technique that has been referred to as genomotyping [14]. The basic methodology is to hybridize the fluorescently labeled genomic DNA of the strain of interest to the microarray along with the fluorescently labeled genomic DNA of a reference strain, typically the strain whose genome sequence the array was based on. By comparing the ratios of the signals obtained from the spots on the microarray, one can predict whether a given gene is present or divergent (the latter referring to either an absent gene or a gene that is divergent to the point of having poor hybridization properties) in the strain of interest. Current data-analysis methods typically use a constant ratio value as a cutoff for assignment into either the divergent or present categories. This cutoff is typically empirically determined from a comparison of the reference strain to a similar strain that is known to be missing certain genetic elements. However, a strain with known deletions is not always available for every organism, hindering empirical determination of a constant cutoff. This has led some researchers to adopt published cutoff values without empirical determination. This approach may be inappropriate, however, as variability in appropriate cutoffs will be inherent in the many variations of microarray technology and analysis methods, as well as in the strains being analyzed.

In addition to these limitations, we have observed that use of a constant cutoff leads to erroneous assignment of gene presence in many cases. First, using a constant cutoff demands that the microarrays exhibit high reproducibility. Each dataset must exhibit an almost identical distribution of ratio values in order for the chosen value to fall in the same relative location along the distribution. Variation in the width of the ratio distribution, which occurs as a result of variable array and hybridization quality, results in anomalous categorization of genes. More problematically, strains which are highly divergent from the reference strain cannot be compared to the reference because of strain-specific inconsistencies in established normalization procedures (described in more detail below). For these reasons, we have developed a method for dynamic assignment of genes, where an independent cutoff is calculated for each hybridization dataset. Array-specific cutoff determination provides more flexibility in the hybridizations and strains that can be compared. The method is more accurate than using a constant-ratio cutoff for identification of divergent genes, and also allows extraction of data from lower-quality hybridizations which would otherwise be discarded. We have implemented these methods in the genomotyping analysis program GACK.

Results

Constant cutoffs are not appropriate for varying distributions

One might expect that in comparing the genome composition of a strain of interest to a reference (usually a sequenced) strain, the genes would either be present or absent. In examining such a strain on a microarray, the spots would either exhibit signal (corresponding to present genes) or be missing signal (corresponding to absent genes). This would manifest itself in a distribution of signal intensity ratios as a bimodal distribution representing present and absent genes. In practice, we observe a major peak (present genes) with a left-hand tail for every distribution we have examined, including several published datasets (see, for example, Figures 1, 2). We presume that the manifestation of the non-present genes as a left-side tail rather than a peak is due to a combination of divergence on the nucleotide-sequence level (see below), cross-hybridization and variability inherent in the calculation of ratios for small signal-intensity values. We refer to these genes as divergent rather than absent, as they may be present but too divergent in nucleotide sequence to show a good hybridization signal. Owing to the continuous nature of the ratio distribution representing both present and divergent genes (Figure 3), the selection of a cutoff ratio value to assign the genes into these classes is not straightforward.

Figure 1.

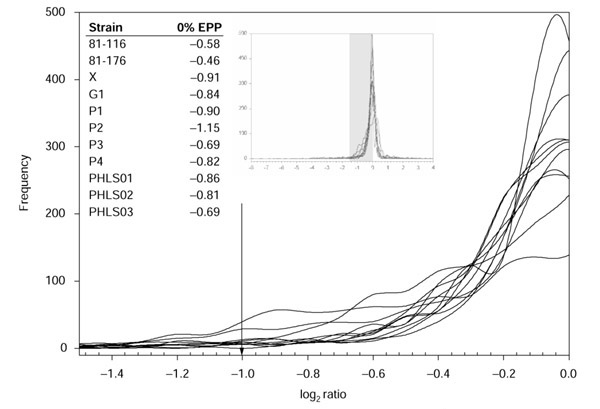
Magnified portion of the ratio distributions of all previously published C. jejuni strains. The arrow indicates the published constant cutoff. Inset graph: the full ratio distributions of C. jejuni. The shaded region indicates the region taken for magnification. Inset table: log ratio values of the 0% EPP transition points chosen by GACK in a strict analysis of divergent genes.

Figure 2.

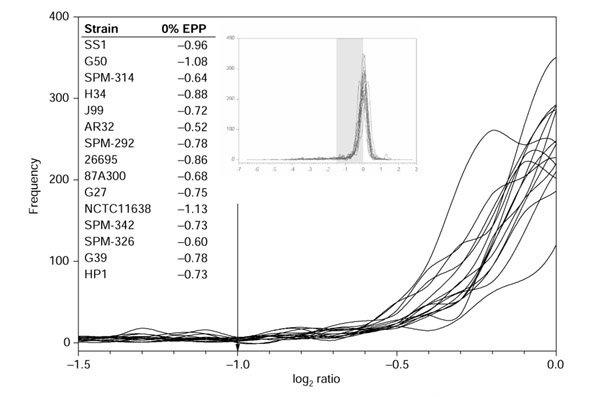
Magnified image of the ratio distributions of all previously published H. pylori strains. The arrow indicates the published constant cutoff. Inset chart: the full ratio distributions of H. pylori. The shaded region indicates the magnified region. Inset table: the log ratio values of the 0% EPP transition points chosen by GACK in a strict analysis of divergent genes.

Figure 3.

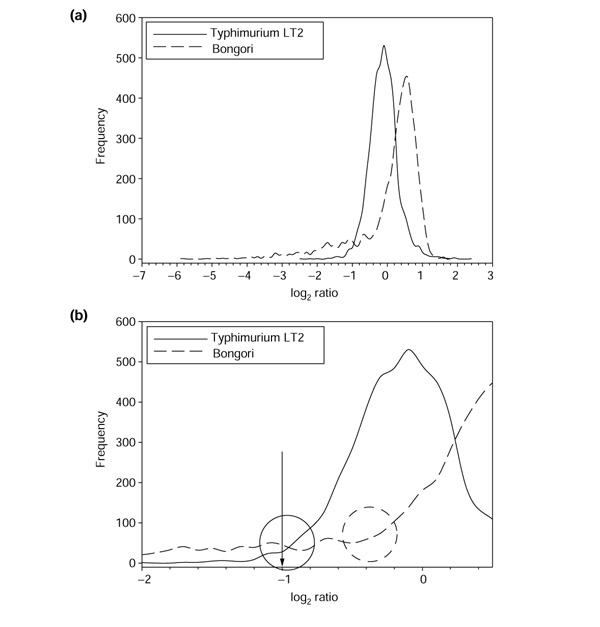
Hybridizations of S. enterica serovar Typhimurium and S. bongori, each to a serovar Typhimurium reference on a Typhimurium LT2 array. (a) Distribution of log ratios for serovar Typhimurium and S. bongori. Serovar Typhimurium is expected to hybridize to all spots, whereas S. bongori is expected to have divergent genes. Note the left tail in the S. bongori distribution, which is absent in the serovar Typhimurium distribution (skewness = 0.322 for Typhimurium; skewness = -2.094 for Bongori). (b) Magnification of the region between -2.0 and 0.5. The circles represent the transition regions, where the main peak meets the left tail for each distribution. The arrow represents the constant cutoff which previous publications have used to distinguish present and divergent genes.

Previously published work has empirically determined a cutoff value utilizing a strain known to be missing certain genetic elements [8,10,11]. The raw ratios are normalized to represent a linear ratio of 1, which assumes that most genes are present in both the comparison and reference strains. The constant-ratio cutoff is an arbitrarily chosen value that divides the known present and divergent genes (based on genome sequence) into their respective categories. However, small differences in selection of a constant-ratio cutoff can lead to improper assignment of hundreds of genes (Tables 1,2,3). We desired a more robust method of cutoff assignment that would address this problem. Furthermore, whereas the constant cutoff method may be reasonably accurate for strain comparisons in which closely related strains are compared, we discovered during the comparison of several Salmonella enterica serovars using our serovar Typhimurium microarray that this procedure is inaccurate for relatively divergent strains.

Table 1.

Divergent genes of Campylobacter jejuni strains

Strain	Number of divergent genes found in the original publication [7]	Number of divergent genes found by our constant-cutoff reanalysis	Number of divergent genes found by GACK trinary analysis	Difference between GACK and [7]
81-116	133	135	178	45
81-176	74	61	117	43
X	20	28	28	8
G1	17	17	37	20
P1	32	59	72	40
P2	63	68	38	-25
P3	91	108	140	49
P4	57	74	83	26
PHLS01	58	63	104	46
PHLS02	36	47	59	23
PHLS03	8	42	66	58
Mean	54	64	84	30

The reanalysis column in this and the other tables is our attempt to reproduce the published analysis.

Table 2.

Divergent genes of Helicobacter pylori strains

Strain	Number of divergent genes found in the original publication [11]	Number of divergent genes found by our constant-cutoff reanalysis	Number of divergent genes found by GACK trinary analysis	Difference between GACK and [11]
SS1	175	171	174	-1
G50	143	141	136	-7
SPM-314	117	114	161	44
H34	193	192	202	9
J99	130	130	161	31
AR32	122	122	158	36
SPM-292	190	188	208	18
26695	87	86	88	1
87A300	156	153	225	69
G27	147	148	164	17
NCTC11638	136	135	127	-9
SPM-342	164	166	185	21
SPM-326	129	130	190	61
G39	151	142	162	11
HP1	137	135	188	51
Mean	145	144	169	23

Table 3.

Present genes of H. pylori strains

Strain	Number of present genes found in the original publication [11]	Number of present genes found by our constant-cutoff reanalysis	Number of present genes found by GACK trinary analysis	Difference between GACK and [11]
SS1	1,463	1,467	1,256	-207
G50	1,499	1,501	1,371	-128
SPM-314	1,526	1,529	1,289	-237
H34	1,449	1,450	1,249	-200
J99	1,511	1,511	1,309	-202
AR32	1,510	1,513	1,251	-259
SPM-292	1,453	1,455	1,242	-211
26695	1,556	1,557	1,398	-158
87A300	1,487	1,490	1,185	-302
G27	1,476	1,478	1,288	-188
NCTC11638	1,502	1,503	1,445	-57
SPM-342	1,477	1,475	1,302	-175
SPM-326	1,514	1,513	1,241	-273
G39	1,488	1,499	1,345	-143
HP1	1,506	1,508	1,284	-222
Mean	1,494	1,497	1,297	-197

The first facet of the problem exists within the normalization procedure. In a typical normalization of a microarray dataset, the ratio values are converted to a log scale, and each data point is normalized by subtraction of the mean or median log-ratio value of the dataset in order to center the distribution around zero. This procedure was primarily developed for the analysis of RNA expression data, in which the shape of the distribution of ratios is often consistent from hybridization to hybridization regardless of the conditions. In genomic DNA comparisons, however, the distributions display more variation in their shape as a result of different numbers of divergent genes (Figures 1, 2, 3a). The distribution of ratios is generally skewed to the left, but the size of the left tail, as represented by the area under the tail, varies depending on the number of divergent genes (Figure 3). A larger tail results in the main peak being shifted further to the right during this type of normalization, as the main peak must balance the values of the tail. As the divergent genes presumably fall primarily within the left tail of the distribution and the main peak primarily consists of present genes, the ideal cutoff value to distinguish present and divergent genes is located near the base of the left side of the main peak.

As different types of analysis will require slightly different cutoffs (see below), we refer to the region near the left base of the main peak as the 'transition region', and to the precise cutoff value selected for a given analysis as the 'transition point' (Figure 3b). Owing to different proportions of divergent genes, the boundary values of the transition region change depending on the strain being analyzed, which results in different degrees of shifting of the main peak. In addition, variability in hybridization quality will influence the boundary values, as the main peaks of the distributions will vary in width and position. Using a constant-ratio cutoff for the transition point leads to the cutoff having a variable location along different distributions, rather than intersecting each distribution at an identical point. Ideally, the transition point should fall at the same location along the distribution of ratios for every hybridization; that is, the transition point should always be located near the base of the left side of the main peak. Visual inspection of the intersection of a constant cutoff ratio with a distribution with many divergent genes demonstrates first, that the constant transition point intersects different distributions at different locations along the curve (Figure 3b; see also Figures 1, 2), and second, that there are divergent genes in some hybridizations which would be inappropriately deemed present instead of divergent because the constant transition point falls far to the left of the transition region (Figure 3b, Bongori hybridization).

Dynamic cutoff determination

One solution to the above problems is to choose a different cutoff for each hybridization dataset, which we refer to as dynamic cutoff determination. By calculating independent cutoff ratio values for each dataset, we can eliminate the problems of variability in the ratio distributions. Manual selection of cutoffs for each dataset is both tedious and inaccurate, so we desired an algorithm that would perform reproducible and consistent analyses. In order to select a cutoff dynamically, we first require an algorithm for identifying the transition region. This algorithm can either describe the left tail or the main peak; identification of one allows identification of the other by subtraction from the overall distribution. We initially employed what we refer to as positive-side mirroring to describe the peak. In this algorithm, the highest point of the main peak is identified, and the right half of the main peak of the distribution is mirrored over the maximum. This creates a symmetrical distribution in which the right half of the main peak is mirrored to the left side, creating a distribution which approximately resembles the distribution we would expect if all of the genes were present (for example, the reference strain hybridized to the reference strain). However, we found this algorithm was not very accurate for peaks that deviated from perfect symmetry around their maxima (data not shown). We subsequently turned to an algorithm that estimates the main peak using the normal probability density function, which we found to be more accurate in describing the shape of the main peak for datasets deviating from symmetry.

The first step of the normal curve-mapping algorithm is to find the location and height of the maximum of the major peak. The sides of the distribution are then determined on the basis of the ratio values at half of the peak's maximum height. A normal probability density function is fitted to the main peak on the basis of these three parameters (height of peak + coordinates of two side points) (Figure 4a). This normal curve is used as an estimate of the peak representing the present genes. We observe a left tail in the actual ratio distribution, which deviates from the normal curve and represents the population of putatively divergent genes (shaded region, Figure 4a). We have thus established a mathematical description of the main peak of the distribution, allowing us to identify the transition region, that is, the region at the left base of the mapped normal curve. This is the first step in allowing us to distinguish between present and divergent genes.

Figure 4.

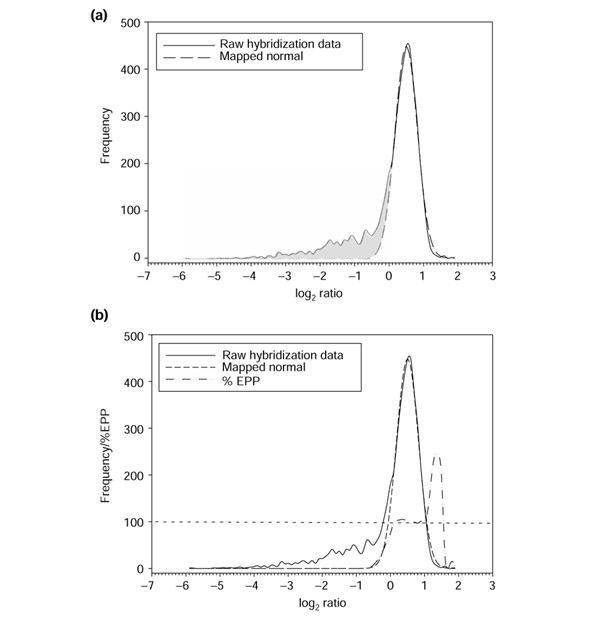
Distribution for S. bongori. (a) Distribution of log ratios for an S. bongori hybridization with a serovar Typhimurium reference. The mapped normal curve estimates the general shape of the main peak; the difference between this idealized curve and the observed data is indicated by the shaded region. (b) The EPP distribution is negligible in the left tail, but increases quickly to 100% as the estimated proportion of present genes increases in the transition region.

Estimated probability of presence

Most published genomotyping analyses have been limited to identification of divergent genes. However, this is only one type of analysis that can be accomplished with microarray data. One can also determine core sets of genes that are common to multiple strains, as in the case of Helicobacter pylori [11]. With the first step of describing the distributions complete, the challenge becomes to select a precise transition point. Our genomotyping program GACK allows the user to carry out different types of analyses that require different transition-point cutoff values. For example, determination of the set of genes that are divergent in a strain with a 0% false-discovery rate will require a different cutoff compared to determination of the set of core conserved genes within a set of strains with a 0% false-discovery rate. In other words, depending on the type of analysis and the confidence desired in the predictions, the cutoffs will need to be assigned either very close to or farther away from the base of the main peak. We have observed that the empirical determination of cutoff values generally tends to be conservative in the assignment of divergent genes (Figures 1, 2); that is, genes that fall to the left of a cutoff of -1.0 are likely to be truly divergent. However, assigning all genes with signals larger than this cutoff value to the present category is not accurate, as many genes that are actually divergent will be assigned as present. A cutoff that is conservative for determination of divergent genes inappropriately overestimates the number of present genes, and vice versa. To make these assignments more accurately, we invoke a simple method for estimating the probability that a gene with a given ratio value is present.

Estimated probability of presence (EPP) is calculated by dividing the mapped normal curve value, which is the expected value for a distribution in which all spots have signal present on the hybridized microarray, by the actual observed data distribution value for any given ratio.

%EPP = 100 × (expected normal value/observed value)

By comparing the expected distribution for a hybridization with no absent genes (estimated by the mapped normal curve) to the actual observed distribution, it is possible to estimate the degree of divergence of the genome compositions based on the divergence of the distributions.

EPP values are calculated across the distribution in order to assess the probability of presence for any given ratio value (Figure 4b). In the left-hand tail of the observed data distribution, the normal distribution approaches zero. This reflects the fact that in this region genes have a very low (close to 0%) chance of being present. As the EPP distribution approaches the main peak, it rapidly increases as the mapped normal distribution becomes substantial in relation to the observed hybridization data distribution, which reflects the increasing proportion of present genes. Eventually, the EPP crosses 100%, at which point all genes with that particular ratio or higher are expected to be present.

After the point at which it crosses 100%, the shape of the EPP distribution for different hybridizations is variable and unpredictable. As a result, we only consider the left portion before the curve reaches 100% for the determination of EPP. Once the EPP distribution reaches 100%, all genes to the right are considered to be present. We therefore have a measure of the probability that a gene is present for every data point in the hybridization.

Categorical assignment based on EPP

The final problem is assignment into categories. The EPP gives us an estimate of how likely a gene is to be present. Genes with 0% or 100% EPP are easily assigned into the divergent and present categories, respectively. However, a significant number of genes have EPP values between 0% and 100%. These genes fall into the transition region, which is defined by the 0% and 100% EPP boundaries.

Typically, divergent and present are the primary categories of interest. However, if a gene is predicted to have a 50% chance of being present, the question arises as to how it should be assigned. Moreover, in a strict analysis of divergent genes, one would want to exclude even genes with a 10% chance of being present from the divergent category. It is clear that selection of a transition point within the transition region is also a variable that should be specified by the user depending on the type of analysis. To provide flexibility in the types of analysis that can be carried out, we provide three categorization tools in the GACK software for assignment into various categories as well as parameters for controlling the stringency with which the genes are assigned to the categories.

The categorization options that are offered to the user are binary assignment (present and divergent), trinary assignment (present, slightly divergent, highly divergent), and an assignment scale that reflects the EPP for every data point (graded assignment). To date, most publications have used a binary assignment scale [3,5,7,8,11], whereas others have circumvented the problem of representation by reporting raw values [10] or only identifying divergent genes [4,9]. As noted above, the transition region contains the transition point, but the precise point must be user-specified depending on the type of analysis. In binary assignment, a transition point is selected on the basis of the percent EPP. In a strict divergent genes analysis, the user would specify 0% EPP as the cutoff, which would result in approximately 0% falsely assigned divergent genes. In contrast, a strict analysis of present genes should use a 100% EPP to minimize falsely assigned genes.

Although binary assignment is desirable in some cases as it gives an orderly appearance, this sort of assignment discards probability information that can serve as an indicator of confidence in the category assignments. Trinary assignment is identical to binary assignment, except that in addition to the divergent and present categories, a third category is added for data values that fall in the uncertain transition region. Two transition points are specified, resulting in three categories. Only the genes with the most confident predictions are included in the absolute present and highly divergent categories, whereas a third category contains the genes that could not be assigned with high certainty. These uncertain genes represent the class of genes that are slightly divergent (see "Assessment of divergence" below). The precise EPP values to use as the cutoffs for trinary assignment are user-specified in the software, but we recommend using the most stringent values, 0% and 100%, for most analyses. Using these values, there is high confidence that genes assigned into the three categories are accurate.

The graded assignment categorization option is used to preserve the most information regarding the probability that a gene is present. A gene with a 100% chance of being divergent is assigned a value of -0.5; a gene with a 50% chance of being divergent or present is assigned a value of 0; a gene with a 100% chance of being present is assigned 0.5. Genes with intermediate EPP values are assigned values in between -0.5 and 0.5 on a linear scale on the basis of the likelihood of their being present. This graded scale will ultimately give the most accurate assessment of the data, as it preserves information about the location along the distribution for each gene.

Analysis of published results

Only two published spotted microarray genomotyping analysis studies have made their raw datasets publicly available [7,11]. We reanalyzed these datasets to evaluate the performance of GACK.

Dorrell et al. [7] analyzed human isolates of Campylobacter jejuni using a microarray constructed from the library of clones used for genome sequencing of C. jejuni NCTC 11168. Using other published analyses as a basis, these researchers chose a linear constant cutoff of 0.5 (-1.0 in log₂ space) to identify divergent genes. We conducted our own constant-cutoff analysis using the same parameters on the published raw data, and our results generally agree with the published analysis (Table 1, and Additional data files). However, we note that even following the methods of the original authors, we were unable to reproduce the analysis with 100% precision.

We next analyzed the original raw dataset with our algorithm coded in the program GACK and used trinary categorization for the output. Visual inspection of the frequency distributions of their hybridization data reveals that the cutoff was generally conservative (Figure 1). This was reflected in the EPP values; all except one of the 0% EPP values is greater than a log₂ ratio of -1.0 (Figure 1). The less conservative cutoff resulted in the larger number of highly divergent genes predicted by GACK (Table 1; median of 40 more highly divergent genes per strain). We conclude that as a result of GACK's dynamic cutoff determination, less conservative transition points, which are still appropriate as judged by visual inspection of the ratio distributions, can be used for gene categorization.

The overall genome compositions look fairly similar across the analyses (Figure 5), even though many additional divergent genes are predicted by GACK. Closer analysis of the loci analyzed in the original publication (restriction modification, lipo-oligosaccharide, and capsule biosynthesis) show that on the gene level, the analytical methods yield similar results (Figures 6,7,8). GACK, however, predicts additional divergent genes in these previously identified variable loci, suggesting that the level of divergence may be even greater than determined by the original authors. Some of these additional loci are readily explainable: in the original publication, a single present locus is sometimes flanked by two regions of deleted genes. Our analysis finds that such loci often fall into the divergent category or into the transition region, indicating a low signal ratio. These genes are presumably divergent, but did not meet the constant-cutoff analysis criterion for a divergent gene because of a slightly higher signal. Using the combination of a less conservative cutoff and trinary output shows that such loci are not very likely to be highly conserved. Furthermore, sequencing of these loci has confirmed that many genes previously assigned to be present are in fact divergent, and that GACK is more accurate than constant-cutoff approaches in identifying these divergent loci (B. Wren, personal communication). A complete list of divergent genes is available from our website [15] and as additional data files.

Figure 5.

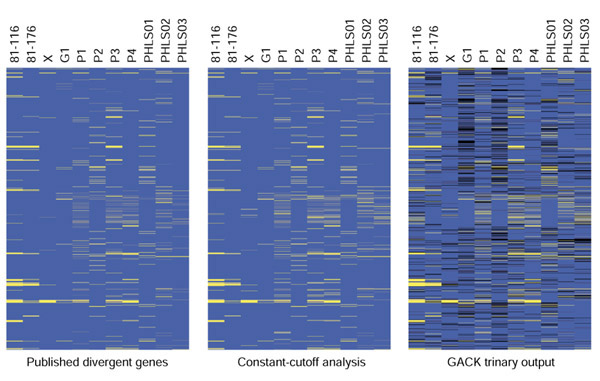
Whole-genome depiction of present and divergent genes for C. jejuni. Blue denotes present genes, black denotes slightly divergent genes, and yellow denotes highly divergent genes.

Figure 6.

GACK trinary analysis of restriction/modification loci of C. jejuni. Blue denotes present genes, black denotes slightly divergent genes, yellow denotes highly divergent genes, and grey denotes missing data. The analysis corresponds to Table 2 of [7].

Figure 7.

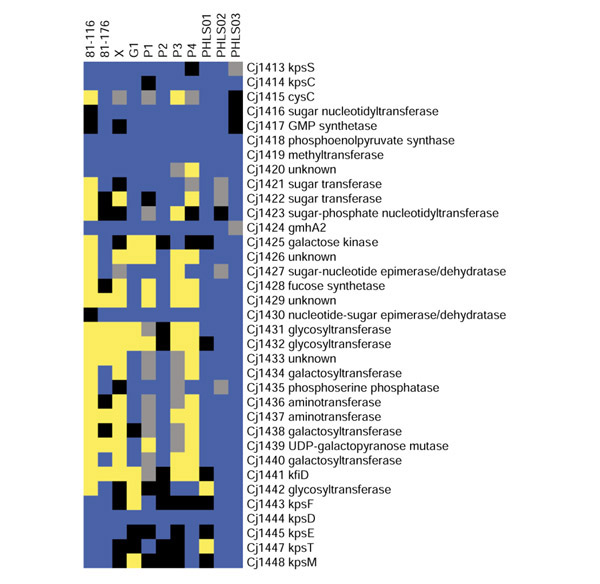
GACK trinary analysis of the capsule biosynthetic locus of C. jejuni. Blue denotes present genes, black denotes slightly divergent genes, yellow denotes highly divergent genes, and grey denotes missing data. The analysis corresponds to Table 3 of [7].

Figure 8.

GACK trinary analysis of the lipo-oligosaccharide biosynthetic locus of C. jejuni. Blue denotes present genes, black denotes slightly divergent genes, yellow denotes highly divergent genes, and grey denotes missing data. The analysis corresponds to Table 4 of [7].

Salama et al. [11] analyzed strains of Helicobacter pylori using a spotted microarray based primarily on the strain 26695 genome sequence, with additional spots representing strain J99-specific genes. The array therefore contains sequences that are unique to J99 and others that are unique to 26695, which proved useful for empirically choosing a log₂ cutoff of -1.0. As observed for the C. jejuni analysis, we observed that a log₂ cutoff of -1.0 was generally conservative (Figure 2), and that many divergent genes were falsely assigned to the present category. We compared the trinary GACK output to published analyses of divergent and present genes. In some strains, more highly divergent genes are predicted by GACK, but in other strains, fewer highly divergent genes are predicted (Table 2). In the case of present genes, fewer present genes are predicted by GACK for all strains (Table 3), which is due to the assignment of many of the genes to the slightly divergent category. In conclusion, whereas GACK analysis coupled with trinary output is generally less conservative in predicting highly divergent genes, the predictions for present genes are more conservative (that is, they predict fewer present genes) as a result of assignment of some of these genes to the slightly divergent category. From visual inspection of the position of the cutoff values along the ratio distributions we expect that these assignments more accurately reflect the true genome compositions.

Viewing the whole genomes indicated that the major variable loci predicted in the original publication are preserved in the GACK analysis. No additional major contiguous regions of divergence are predicted. A full list of divergent loci predicted by GACK is available [15]. Analysis of the cag pathogenicity island reveals that whereas the major differences are conserved, some loci also display consistent weak signal across a portion of the strains (black regions, Figure 9). Examples of these loci are orf7, cag4, cag22 and cag25. Intriguingly, multiple alleles of orf7 are apparent across the strains (N. Salama, personal communication). The microarray contains the 26695 allele of orf7, which is confirmed to be present in strains G27, NCTC11638 and SPM-342 by PCR and sequencing, in agreement with GACK analysis. The locus is absent in strains SS1, G50, SPM-314, H34 and SPM-292, also in agreement with GACK analysis. In J99 and 87A300, orf7 contains an insertion in the coding sequence. These two strains exhibit weak hybridization signal, resulting in assignment of orf7 to the slightly divergent category, presumably due to the presence of the insertion. The orf7 alleles present in AR32, SPM-326, G39, and HP1 are uncharacterized, but our results would predict that these strains also contain the J99 allele or another allele that is divergent from the 26695 allele. This finding suggests that the preservation of ratio-intensity information in the trinary or graded output may be useful in identifying allelic differences in some genes.

Figure 9.

The cag pathogenicity island of H. pylori. Trinary GACK output was directly visualized in Treeview [22]. Blue denotes present genes, black slightly divergent genes, and yellow highly divergent genes.

Assessment of divergence detection for H. pylori microarrays

The complete sequencing of a second H. pylori strain, J99 [16,17], provides a convenient means for assessing how divergence in sequence identity affects microarray signal, and therefore categorization. As the design of the microarray was based on the 26695 sequence, the J99 hybridization products represent a spectrum of sequence identities between target and probe. We examined the correlation between signal intensities and percent sequence identity for a J99 hybridization dataset in order to assess the degree of sequence divergence that could be detected on the H. pylori microarray. As expected, the hybridization signal decreases with increasing sequence divergence (Figure 10a). For a constant-cutoff analysis using a log₂ cutoff of -1.0, the identity level for categorization as divergent is approximately 88%. For the trinary GACK analysis, the transition points were at -0.2 and -0.7, corresponding to approximately 92% and 89% sequence identity. These trends are reflected in Figure 10b; approximately 50% of the genes with 88% sequence identity are categorized as present, and the other 50% are divergent for the constant-cutoff analysis. Similarly, the GACK analysis assigns approximately 50% of the genes with 89% identity to divergent, and close to 100% of the genes with greater than 92% identity as present. This suggests that the detection limit of the H. pylori microarray is approximately 88% sequence identity, and that this detection limit results in classification of certain genes as divergent in spite of the fact that sequence identity may be relatively high (80-85%).

Figure 10.

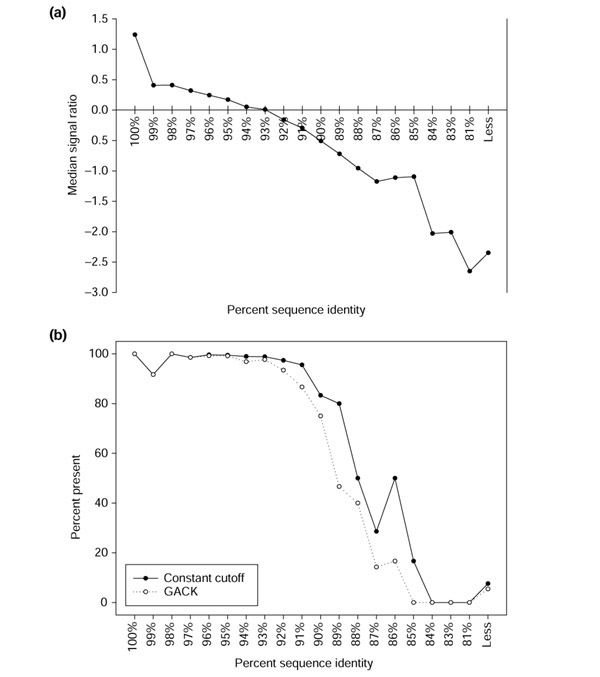
Microarray results as a function of sequence identity for H. pylori J99. (a) H. pylori J99 sequences show varying degrees of divergence from the 26695 sequences present on the microarray, which is reflected in the microarray signal. Median signal ratios were calculated from J99 spots grouped by predicted degree of local sequence identity greater than 50 nucleotides in length with 26695. (b) The proportion of present genes for J99 spots grouped by sequence identity with 26695 was tabulated for constant cutoff and GACK analyses.

We observe, however, that the majority of PCR products on the array are approximately 93-97% identical to J99 (Figure 11a), and that the distribution of percent sequence identity bears a striking resemblance to the shape of the distribution of the array data (Figure 11b). This implies that the shape of the array data distribution may largely be a function of the genome content, in addition to the hybridization quality and parameters, and that the limits of detection for the H. pylori microarray may be considerably lower than the apparent value. The consequence for interpretation of genomotyping data is that divergence is always relative to the main peak of present genes. This main peak will represent differing degrees of sequence identity for different organisms and strains, limiting our ability to make precise predictions about the absolute degree of divergence for any given gene. Furthermore, the predictions are likely to be affected by the hybridization conditions. Nevertheless, it is evident that the microarray data contain a fairly high level of sequence identity resolution, and that binary representation unnecessarily overlooks this information.

Figure 11.

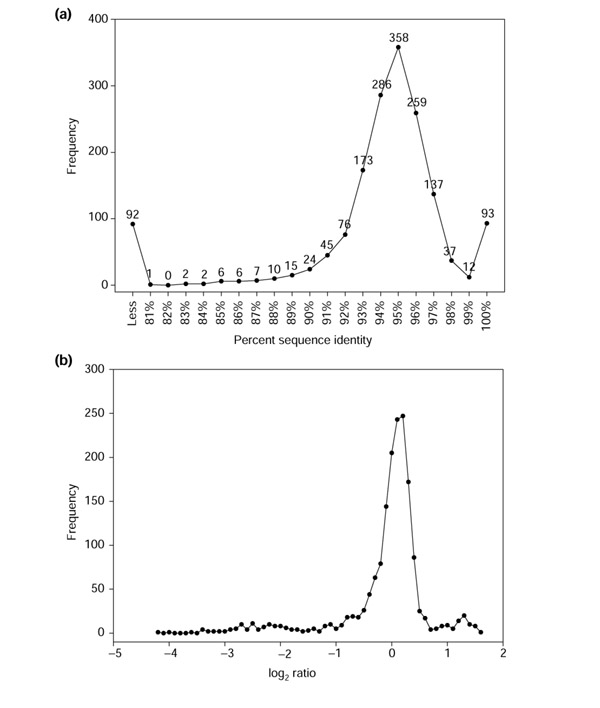
Comparison of sequence identity and microarray hybridization distributions for J99. (a) Percent local sequence identity shared between the amplicons present on the H. pylori microarray and J99. The majority of J99 genes share 93-97% identity with the array sequences, which are based on 26695. A peak of 93 genes with 100% identity is mostly comprised of J99-specific sequences that were added to the array. (b) J99 hybridization distribution. Note the presence of a small peak to the right of the main peak, similar to above.

Validation of GACK predictions

Sequencing of the C. jejuni capsule biosynthetic locus from several strains has indicated that some regions which were incorrectly predicted to be present by constant-cutoff methods are correctly predicted to be divergent by GACK (B. Wren, personal communication). To further validate the algorithm, we attempted to PCR-amplify and sequence 40 genes representing a spectrum of array intensities from the H. pylori strain G27. We successfully amplified 21 regions for subsequent sequencing. Many of the genes predicted to be highly divergent by GACK did not amplify, presumably because of their divergence. However, in the cases where amplification and sequencing were successful for the highly divergent genes, we observed approximately 90% sequence identity between G27 and the amplified sequence present on the array (26695 or J99) (Table 4). All genes that were predicted to be slightly divergent by GACK (array ratio of -0.6 to -0.2) were 91-96% identical with sequences on the H. pylori array, with a median of 94%. Genes with stronger array intensities were predicted to be present by GACK, and, not surprisingly, corresponded to higher sequence identities. On the basis of a linear regression of the sequencing results, we predict that the majority of genes of G27 share approximately 96% identity with the sequences on the array (primarily 26695). These data, taken together with our analyses of the J99 hybridizations, indicate that microarrays do not just predict presence or divergence, but can resolve variation in sequence identity between target and probe. Furthermore, GACK is able to correctly categorize these genes.

Table 4.

Sequencing summary

Range of array signals	Attempted PCRs	Successful PCRs	Median percent sequence identity
-4.2 to -1.0	9	1	90.2
-1.0 to -0.5	8	1	90.5
-0.5 to -0.3	9	7	94.3
-0.3 to -0.1	9	8	95.2
-0.1 to 1.1	5	4	97.5

Discussion

Microarrays are increasingly used as a tool for genome-composition analysis, or genomotyping [14,18]. Current methods of microarray data analysis are primarily designed for expression (mRNA) studies, in which the distribution of signals is assumed to remain relatively similar across conditions. For microarray-based comparative genome analyses, the signal distributions may show significant variation between species or strains. Furthermore, normalization procedures in which distributions are centered to zero on a log₂ scale are not appropriate for strain comparisons, as the majority of the distributions are skewed. This skew manifests itself as the main peak of the ratio distribution, representing the present genes, being shifted to different degrees for different strains. The peak's position is also dependent on the length of, and number of genes present in, the left tail (area under the left tail). Because of the varying position of the ratio distributions, a constant-cutoff analysis results in selection of a different location on each distribution as the transition point for category assignment. Other normalization procedures can be used that will not be subject to such problems, but are more complicated to implement and require some prior knowledge of genome composition [19]. We hypothesized that a more accurate approach to creating these assignments is to select a mathematically identical point on each distribution being analyzed as the transition point. We subsequently developed an algorithm to reproducibly identify such a point.

The algorithm assumes that a hybridization in which all spots have signal present are distributed normally. This assumption proves to be fairly accurate, as is observed in the mapping of normal curves to the hybridization distributions (for example, Figure 4). Slight deviations are seen in the tails of the distributions, suggesting that better estimates of the distributions may exist. The observation that percent sequence identity is at least crudely resolved on the microarrays suggests that a multinormal model maybe more accurate. Nonetheless, the normal curve mapping consistently gives good overlap with the main peak of the ratio distributions in our analyses. Furthermore, normalization of the dataset does not impact on analysis with GACK because the algorithm depends on the shape of the distribution. The genes are determined to be present or divergent on the basis of their relative position in the distribution, rather than an absolute signal intensity ratio. We observed that the algorithm works as well on un-normalized datasets as it does on normalized datasets (data not shown), circumventing the need to implement more complex normalization procedures for genomotyping data. However, while GACK is able to account for minor variations in a set of replicate hybridizations, we emphasize that hybridizations of poor quality yield irreproducible results regardless of the analysis method.

We originally considered using the left side of the normal curve map as a transition point for binary analysis. This point effectively represents a 0% EPP cutoff, which we believe is appropriate and accurate for a strict divergent genes analysis. However, we realized that genomotyping data embodies information that can be analyzed in many other ways, and therefore chose to implement multiple flexible assignment systems in the software. The choice of the transition point(s) and the output format depend closely on one another; regardless of this, the algorithm selects points that are consistent in their location on each distribution for any given analysis. This method, coupled with our estimates of probability that a gene is present (EPP values), should give more accurate assignments across hybridizations and strains.

We developed GACK to improve analysis of genomotyping data generated in our laboratory. In an effort to both determine if the algorithm would be broadly applicable to other genomotyping datasets generated from different microarrays and by other laboratories, we tested all of the publicly available datasets with GACK. It should be noted that at present only two datasets are available, both of which were generated using spotted DNA microarrays, and therefore the applicability of GACK to data generated from oligo-based arrays remains to be tested. Nonetheless, our analyses generally correspond well with the published analyses of C. jejuni and H. pylori strains. Categorical assignments were based on a constant log₂ cutoff of -1.0 in these publications, which, from visual inspection of the distributions, appear to be conservative for divergent gene identification. Accordingly, GACK predicted transition-point values that were generally higher than -1.0. As these publications primarily focused on divergent genes, conservatism in the predictions was appropriate, but resulted in lower sensitivity of detection. Our analyses have recategorized several hundred genes based on 0% and 100% EPP values. Although many genes have been reclassified as highly divergent, many also fall into the slightly divergent category. In creating this additional category, we make a relatively conservative prediction of both highly divergent and present genes, which results in more confidence in our assignments.

We found that the published analyses of H. pylori strains were also conservative in their predictions of divergent genes, although less so than the C. jejuni analysis. In contrast, the published predictions for present genes were less conservative, as genes that lie within the tail of the ratio distribution but have a ratio of greater than -1.0 were classified as present (Figure 2). This is a limitation of binary representation of the information. This limitation, coupled with our observations that sequence-identity information is present in the array data, indicate to us that more sophisticated and detailed representation systems are necessary. We believe that at present, trinary and graded output are the best options, as they preserve more information than binary output, but more work is needed in this area.

Closer analysis of the cag pathogenicity island revealed that the predictions were for the most part identical to the previously published predictions. Intriguingly, some loci, such as orf7, consistently show hybridization, but with relatively low strength. This is particularly interesting because there are multiple allelic forms of orf7 in different H. pylori strains (N. Salama, personal communication). This indicates that preservation of ratio information, such as in the output of trinary or graded analyses, can result in detection of relevant biological differences and should be done for most analyses.

Analysis of the degree of sequence identity required for detection on the H. pylori microarray revealed that sequences with less than 88% identity resulted in dramatically reduced signal on the microarray. Genes with this degree of identity or lower were typically classified as highly divergent, regardless of the method of analysis. In contrast to the hybridization results, loci with greater than 80% sequence identity are generally considered to be likely homologs by in silico comparison. This is a limitation of the microarray technology that should be considered when referring to a particular locus as divergent.

We attempted to validate the GACK predictions by PCR amplifying and sequencing loci of the different classes. Not surprisingly, many of the highly divergent genes did not amplify, limiting our ability to draw any conclusions about the precise degree of sequence identity that results in a gene being classified as divergent. Nevertheless, the observed PCR success/failure rate and percent sequence identities are consistent with the GACK predictions. True validation of this analysis method, and of microarray genomic comparison and analysis methods in general, will be achieved through a combination of more strain comparison work and accompanying sequence information in the form of genome sequencing projects and the sequencing of particular loci by individual laboratories. Multiple strain and species genomes are available, or will be soon, for a number of organisms, providing a wealth of information for direct comparative genomic analysis and the groundwork for further establishing microarray-based genomic comparisons as a viable means of assessing genetic differences in strains of interest.

Our findings offer improved methods for analysis of microarray-based genome-composition data. Analysis of genomotyping datasets of S. enterica serovars has demonstrated that dynamic cutoff selection is more reliable and reproducible than constant cutoffs [20]. We have also described two additional systems for representation, which preserve more of the raw information than a binary analysis. Most importantly, we have identified shortcomings in currently available analytical methods. Most of the tools for microarray data analysis have been developed for use with expression data, but even simple manipulations such as normalization of the datasets are not necessarily appropriate in the case of genomic comparisons. We hope and anticipate that identification of these problems will facilitate that development of even more sophisticated analysis methods.

Materials and methods

GACK programming

GACK was written in Perl. Testing was conducted on a Windows 2000 system with ActivePerl 5.6.1 build 631. The script requires Perl/Tk for the user interface. A stand-alone executable for Windows was created using Perlapp (Activestate Perl Developer's Kit 4.0).

Reconstruction of datasets

We found that we could not precisely reproduce the results of two previously published works [7,11]. We therefore detail here the reconstruction of the raw datasets that we generated for our analyses, as well as make available our datasets [15].

C. jejuni dataset

Raw hybridization values were downloaded for triplicate hybridizations of the 11 C. jejuni strains [7]. The linear data was converted to log₂, although the linear data contained negative values (median 0.8% per strain, or 14 spots out of 1,730), which could not be converted to log₂ and were subsequently discarded from the dataset. The triplicates were averaged, and these data served as the raw dataset for our analyses. The published present/divergent genes category sizes were tabulated from the lists of divergent genes available at [15].

H. pylori dataset

Raw values were downloaded from the Stanford Microarray Database [21]. The data for the AR32 and H34 strains were absent in the Published Data section, and were obtained directly from the authors. The data were filtered to include the same genes as the previously published dataset [11]. Numbers describing the size of the present and divergent genes categories were obtained directly from the publication.

PCRs and sequencing

Genes were selected for sequencing using various criteria, including array signal intensity, variance in the replicates and amplicon length. Primers were selected that were identical to those used to construct the H. pylori array. Sequencing was from both ends of the PCR products and was carried out by Sequetech (Mountain View, CA). H. pylori G27 genomic DNA was a gift from Douglas Scott Merrell.

Additional data files

The Perl source code for GACK, a Windows-executable version of the program, and a manual in PDF format are freely available here and at our website [15]. A complete list of divergent genes, raw ratio values and trinary outputs are also available for C. jejuni as well as lists of divergent genes, raw ratio values and trinary outputs for H. pylori. A tool for constant-cutoff analysis, CCACK, can also be downloaded at our website [15].

Supplementary Material

Additional data file 1

Perl source code for GACK

Additional data file 2

Windows-executable version of the program

Additional data file 3

A manual in PDF format

Additional data file 4

A complete list of divergent genes for C. jejuni

Additional data file 5

A complete list of raw ratio values for C. jejuni

Additional data file 6

A complete list of trinary outputs for C. jejuni

Additional data file 7

A complete list of divergent genes for H. pylori.

Additional data file 8

A complete list of raw ratio values for H. pylori.

Additional data file 9

A complete list of trinary outputs for H. pylori.