Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 1976 Jan;16(1):13–26. doi: 10.1016/S0006-3495(76)85659-7

Membrane viscoplastic flow.

E A Evans, R M Hochmuth
PMCID: PMC1334810  PMID: 1244887

Abstract

In this paper, a theory of viscoplasticity formulated by Prager and Hohenemser is developed for a two-dimensional membrane surface and applied to the analysis of the flow of "microtethers" pulled from red blood cells attached to glass substrates. The viscoplastic flow involves two intrinsic material constants: yield shear and surface viscosity. The intrinsic viscosity for plastic flow of membrane is calculated to be 1 X 10(-2) dyn-s/cm from microtether flow experiments, three orders of magnitude greater than surface viscosities of lipid membrane components. The fluid dissipation is dominated by the flow of a structural matrix which has exceeded its yield shear. The yield shear is the maximum shear resultant that the membrane can sustain before it begins to deform irreversibly. The yield shear is found to be in the range 2-8 X 10(-2) dyn/cm, two or three orders of magnitude smaller than the isotropic tension required to lyse red cells.

Full text

PDF
13

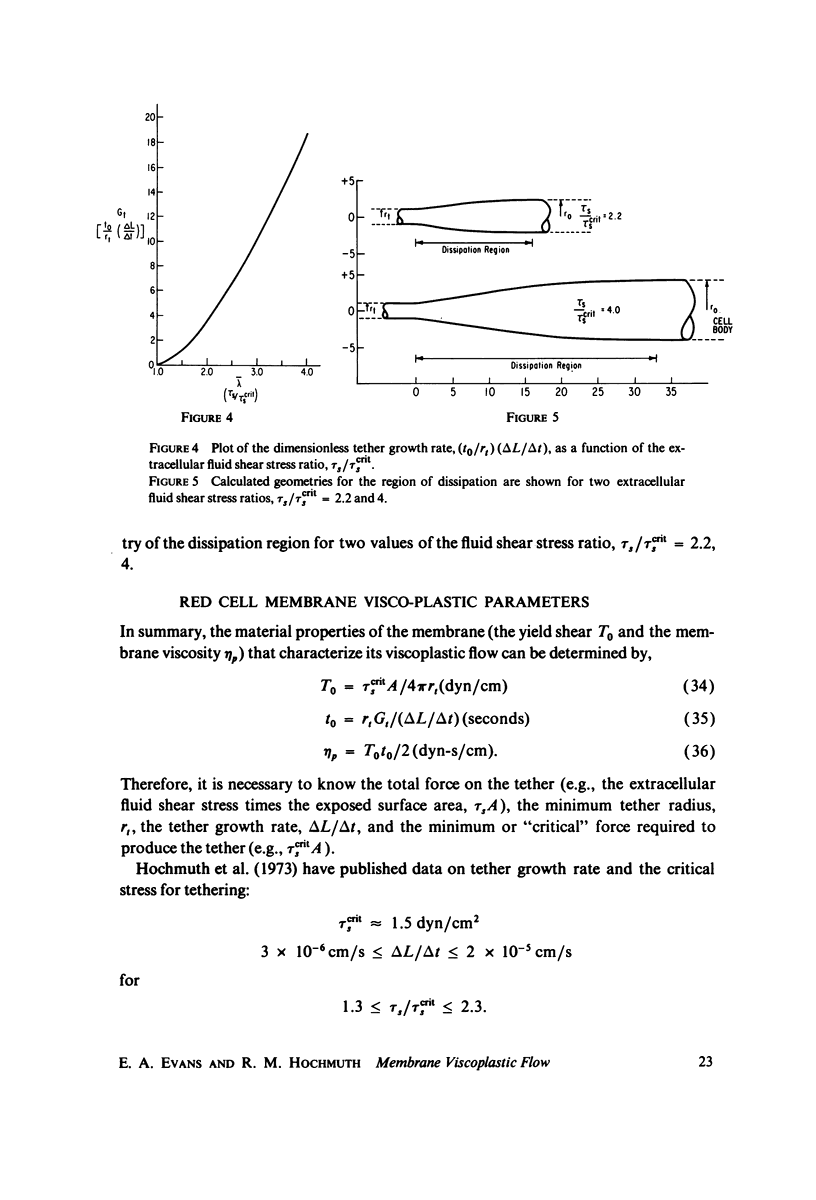
Images in this article

18FIGURE 2
on p.18

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Bull B. S., Kuhn I. N. The production of schistocytes by fibrin strands (a scanning electron microscope study). Blood. 1970 Jan;35(1):104–111. [PubMed] [Google Scholar]
  2. Bull B. S., Rubenberg M. L., Dacie J. V., Brain M. C. Microangiopathic haemolytic anaemia: mechanisms of red-cell fragmentation: in vitro studies. Br J Haematol. 1968 Jun;14(6):643–652. doi: 10.1111/j.1365-2141.1968.tb00370.x. [DOI] [PubMed] [Google Scholar]
  3. Edidin M. Rotational and translational diffusion in membranes. Annu Rev Biophys Bioeng. 1974;3(0):179–201. doi: 10.1146/annurev.bb.03.060174.001143. [DOI] [PubMed] [Google Scholar]
  4. Evans E. A., Hochmuth R. M. Membrane viscoelasticity. Biophys J. 1976 Jan;16(1):1–11. doi: 10.1016/S0006-3495(76)85658-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Evans E. A., La Celle P. L. Intrinsic material properties of the erythrocyte membrane indicated by mechanical analysis of deformation. Blood. 1975 Jan;45(1):29–43. [PubMed] [Google Scholar]
  6. Evans E. A. New membrane concept applied to the analysis of fluid shear- and micropipette-deformed red blood cells. Biophys J. 1973 Sep;13(9):941–954. doi: 10.1016/S0006-3495(73)86036-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Hochmuth R. M., Mohandas N., Blackshear P. L., Jr Measurement of the elastic modulus for red cell membrane using a fluid mechanical technique. Biophys J. 1973 Aug;13(8):747–762. doi: 10.1016/S0006-3495(73)86021-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hochmuth R. M., Mohandas N. Uniaxial loading of the red-cell membrane. J Biomech. 1972 Sep;5(5):501–509. doi: 10.1016/0021-9290(72)90007-3. [DOI] [PubMed] [Google Scholar]
  9. LaCelle P. L. Alteration of membrane deformability in hemolytic anemias. Semin Hematol. 1970 Oct;7(4):355–371. [PubMed] [Google Scholar]
  10. RAND R. P. MECHANICAL PROPERTIES OF THE RED CELL MEMBRANE. II. VISCOELASTIC BREAKDOWN OF THE MEMBRANE. Biophys J. 1964 Jul;4:303–316. doi: 10.1016/s0006-3495(64)86784-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Singer S. J., Nicolson G. L. The fluid mosaic model of the structure of cell membranes. Science. 1972 Feb 18;175(4023):720–731. doi: 10.1126/science.175.4023.720. [DOI] [PubMed] [Google Scholar]
  12. Skalak R., Tozeren A., Zarda R. P., Chien S. Strain energy function of red blood cell membranes. Biophys J. 1973 Mar;13(3):245–264. doi: 10.1016/S0006-3495(73)85983-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES