Abstract
DNA replication initiates at discrete origins along eukaryotic chromosomes. However, in most organisms, origin firing is not efficient; a specific origin will fire in some but not all cell cycles. This observation raises the question of how individual origins are selected to fire and whether origin firing is globally coordinated to ensure an even distribution of replication initiation across the genome. We have addressed these questions by determining the location of firing origins on individual fission yeast DNA molecules using DNA combing. We show that the firing of replication origins is stochastic, leading to a random distribution of replication initiation. Furthermore, origin firing is independent between cell cycles; there is no epigenetic mechanism causing an origin that fires in one cell cycle to preferentially fire in the next. Thus, the fission yeast strategy for the initiation of replication is different from models of eukaryotic replication that propose coordinated origin firing.
INTRODUCTION
Eukaryotic DNA replication begins at discrete origins distributed along chromosomes. Although much progress has been made in understanding the mechanisms that establish and activate individual origins, the manner in which origin firing is coordinately regulated spatially along the chromosomes and temporally throughout S phase remains unclear (Kelly and Brown, 2000; Gilbert, 2001; Schwob, 2004). These questions are of particular interest because in most cases origin firing is not efficient; that is, a particular origin will fire in only a fraction of cell cycles. The observation that origins do not fire in every cell cycle raises the question of how individual origins are selected to fire and if that selection is distributed in a coordinated manner. In the absence of such coordination, origin firing would be randomly distributed, leading to the random gap problem; some cells would have large gaps between origin firing that would take a long time to replicate (Lucas et al., 2000; Herrick et al., 2002; Hyrien et al., 2003; Jun et al., 2004). Simple models of replication kinetics predict that if replication origins are randomly distributed, ∼5% of the cells will have such large gaps between active origins that they will take four times longer than average to replicate (see Materials and Methods for calculations). Alternatively, cells could have a mechanism that evenly distributes origin firing across the genome; they would thus avoid the random gap problem, and replication would be efficient. Models for such mechanisms have been proposed; for instance, origins within specific clusters could be selected to fire, or active origins could suppress their neighbors by lateral inhibition (Mesner et al., 2003; Shechter and Gautier, 2005). However, little direct evidence exists to either support or refute these models.
Origin structure and function has been well characterized in the budding yeast Saccharomyces cerevisiae (Kelly and Brown, 2000; Gilbert, 2001). Budding yeast have small (∼100 base pairs) origins characterized by a 17-base pair autonomously replicating sequence (ARS) consensus. This consensus sequence comprises the recognition site for the six-protein origin recognition complex (ORC), which in turn serves as the site of assembly for the replication complex (Gilbert, 2001).
Origins have been more difficult to identify in other eukaryotes, and sequence-specific ORC binding sites have not been identified outside of budding yeast (Burhans and Huberman, 1994; Gilbert, 2001; Schwob, 2004). Nonetheless, there are defined replication origins in other eukaryotes, and distinct initiation sites have been mapped at several metazoan origins (Bielinsky and Gerbi, 1999; Abdurashidova et al., 2000; Gilbert, 2001). However, these origins are not efficient. In the well-studied example of the origins at the hamster DHFR locus, the most efficient origins fire in only 20% of S phases (Dijkwel et al., 2002).
Fission yeast origins share important characteristics with those of metazoans; both are genomically complex—composed of cooperative and redundant elements, lacking origin-specific sequences—and both are inefficient, firing in only a subset of cell cycles (Shinomiya and Ina, 1994; Clyne and Kelly, 1995; Dubey et al., 1996; Gilbert, 2001; Dijkwel et al., 2002; Norio and Schildkraut, 2004). Fission yeast origins are about one kilobase in length and display no particular sequence bias, except for the presence of A-rich tracts (Clyne and Kelly, 1995; Dubey et al., 1996; Segurado et al., 2003; Dai et al., 2005). Although fission yeast origins are not strictly sequence specific, replication does originate at defined sites in the genome, and many of these origins have been mapped (Dubey et al., 1994; Gomez and Antequera, 1999). However, none of the identified origins are efficient. In the one case in which origin efficiency has been directly quantitated, ORI19 fires in 40% of S phases and ORI22 fires in 30% (Segurado et al., 2002). In other examples, one of the most efficient fission yeast origins, ars2-1, appears to fire in no more than 50% of S phases; others appear to fire in <30% of S phases (Dubey et al., 1994; Gomez and Antequera, 1999; Kim and Huberman, 2001).
Two very different examples of how origin firing can be organized are provided by budding yeast, in which firing is relatively well organized (Raghuraman et al., 2001; Yabuki et al., 2002) and frog embryos extracts, in which it is random (Herrick et al., 2000; Lucas et al., 2000; Blow et al., 2001; Marheineke and Hyrien, 2001; Herrick et al., 2002). The efficiency of budding yeast origins ranges from those that almost never fire to those that fire in almost every cell cycle. The efficient origins are spaced fairly evenly, with one about every 50 kb along the genome (Lengronne et al., 2001; Raghuraman et al., 2001; Yabuki et al., 2002). The relatively even distribution of efficient origins in budding yeast ensures the even distribution of origin firing across the genome. This strategy avoids the random gap problem and ensures efficient replication.
In contrast, in Xenopus laevis frog embryo extracts the distribution of origin firing is random (Herrick et al., 2000; Lucas et al., 2000; Blow et al., 2001; Marheineke and Hyrien, 2001; Herrick et al., 2002). Replication in frog embryos is unusual, in that replication initiation is not limited to specific origin sequences; any DNA sequence seems to be capable of acting as an origin (Harland and Laskey, 1980). This situation leads to a truly random distribution of origin firing (although there has been a report of nonrandom firing of origin clusters; Blow et al., 2001) and raises the random gap problem (Herrick et al., 2000; Lucas et al., 2000; Hyrien et al., 2003). However, frogs have somehow solved the random gap problem because frog embryonic replication is extremely efficient, lasting only 20 min. One model that reconciles random origin firing with efficient replication posits that origins in unreplicated regions will fire with increasing probability as S phase proceeds (Lucas et al., 2000; Herrick et al., 2002). Thus, early large gaps have an increasing chance of an origin firing within them, making it unlikely for large gaps to persist.
Neither the budding yeast nor the frog embryo example serves as a good model for general eukaryotic replication, because most eukaryotes have inefficient origin, unlike budding yeast, and defined origins, unlike frog embryos. Thus it is an open question how origin firing is spatially distributed in most eukaryotes. In particular, it is unclear if origin firing is coordinated to give an even spacing as in budding yeast or if it is uncoordinated, resulting in stochastic origin firing.
In addition to being spatially distributed, origin firing is temporally distributed throughout S phase. Budding yeast origins fire at reproducible times, with some generally firing early and others generally firing later (Raghuraman et al., 2001; Yabuki et al., 2002). The same is true of fly and mammalian origins (MacAlpine et al., 2004; Woodfine et al., 2004; Jeon et al., 2005). The distribution of origin firing time in budding yeast forms a continuum, with no clear demarcation between early and late firing (Raghuraman et al., 2001). However, an operational distinction between early and late origins has been made based on the ability of an origin to fire when the cell is starved of deoxynucleotides (dNTPs; Santocanale and Diffley, 1998). The drug hydroxyurea (HU) inhibits ribonucleotide reductase, preventing dNTP synthesis and causing replication to deplete dNTPs, thus stalling replication forks. The HU-induced replication block activates the DNA replication checkpoint, which stabilizes the stalled forks and inhibits or greatly delays the subsequent firing of origins (Santocanale and Diffley, 1998; Lopes et al., 2001; Yabuki et al., 2002). Origins that fire in the presence of HU tend to be those that fire early in a normal S phase, presumably because they fire before dNTP pools are depleted and the checkpoint is activated and are thus defined as early-firing origins (Yabuki et al., 2002). Other origins are prevented from firing in HU by the DNA replication checkpoint; they are generally considered to be late-firing origins.
To directly test if there is a mechanism that coordinates the firing of neighboring origins in fission yeast, we have measured the distribution of origin firing using a single molecule technique called DNA combing. This technique involves stretching long, individual, protein-free DNA molecules on a glass surface and visualizing the DNA by fluorescence microscopy (Bensimon et al., 1994; Michalet et al., 1997; Herrick and Bensimon, 1999). Pulse-labeling of DNA with thymidine analogs such as bromodeoxyuridine (BrdU) allows visualization of the regions around replication origins (Herrick and Bensimon, 1999). The technique can be combined with in situ hybridization to identify specific loci in the genome and to investigate the behavior of specific origins (Norio and Schildkraut, 2001; Pasero et al., 2002; Anglana et al., 2003). We find that the firing is randomly distributed among fission yeast origins. These results suggest that origins fire stochastically, without regard to their neighbors, and raise important questions about how fission yeast reconcile random origin firing with efficient replication.
MATERIALS AND METHODS
General Methods
The fission yeast strain yFS240 (h- leu1-32 ura4-D18 ade6-210 his7-366 leu1::pFS181(leu1 adh1:hENT1) pJL218 (his7 adh1:tk)) was grown in YES medium at 25°C (Moreno et al., 1991; Sivakumar et al., 2004). Synchronized early G2 cultures at OD600 0.2 were prepared from asynchronous log phase cultures (OD600 = 1.5) by centrifugal elutriation.
Labeling of the DNA
HU Block. G2 synchronized yFS240 cultures were grown in YES with 12 mM HU and 500 nM BrdU for 4 h to allow cells to complete their first G2, M, and G1 phases and arrest in S phase. Cells were harvested and stored at -80°C.
Pulse Labeling. G2 synchronized yFS240 cultures were grown in YES with 500 nM BrdU. Cell cycle progression was monitored by septation index and subsequently confirmed by flow cytometry (Supplementary Figure S1). Ten ODs of cells were harvested every 4 min throughout S phase and stored at -80°C. The stage of replication at each time point was subsequently determined by the extent of replication evident on molecules from cells harvested at that point. Early S phase was found to be at time points around 142 min after synchronization at 25°C; mid-S phase was around 8 min later.
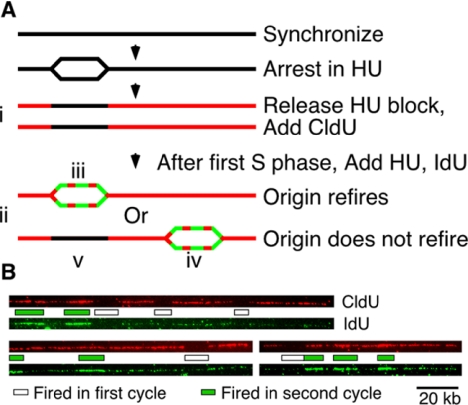
Sequential Origin Labeling. The origin refiring experiment presented in Figure 3 is complicated by the fact that thymidine analogs cannot be washed out once they have been added to cells, presumably because after the nucleoside analog enters the cell through the nucleoside transporter, it is phosphorylated and can no longer leave (Sivakumar et al., 2004). To avoid this problem, elutriation synchronized cells were treated with 12 mM HU for 4 h to allow cells to arrest in early S phase, washed, and grown for 2 h in presence of 500 nM chlorodeoxyuridine (CldU) to allow them to complete replication. This step resulted in unlabeled patches where origins fired early in the first cycle on otherwise CldU-labeled molecules. After the first S phase, the cells were washed and incubated for 3 h in 500 nM iododeoxyuridine (IdU) and 12 mM HU to allow them to arrest in their second S phase, resulting in IdU-labeled patches where origins fired early in the second cycle on the same molecules. The cells were then harvested and DNA was prepared for combing (Figure 3A). Because the analogs cannot be washed out, origins that fired in the second cycle are labeled with both CldU and IdU, making it impossible to distinguish origins that fired in both cycles for those that only fired in the second. Thus, we compared the origins that only fired in the first S phase and not in the second (patches unlabeled with CldU) with those that fire in the second S phase and may or may not have fired in the first (patches labeled with IdU).
Figure 3.
The ability of an origin to fire is not epigenetically inherited. (A) The experimental strategy, as described in the text. (B) Representative molecules. The upper, red images are visualized with anti-CldU antibodies; the gaps in the CldU signal, indicating origins that fired only in the first cell cycle, are marked below by white rectangles. The lower, green images are the same molecules visualized with anti-IdU antibodies; the IdU-labeled patches, indicating origins that fired in the second cell cycle, are marked above by green rectangles.
DNA Preparation for Combing
Yeast genomic DNA was prepared as described previously (Michalet et al., 1997), with some modifications. Agarose plugs were made by mixing 10 ODs of yeast cells in 200 μl SB (20 mM citrate phosphate, 50 mM EDTA, 900 mM sorbitol) with 100 μl 1.5% low-melting agarose in SB buffer, all at 37°C. The plugs were incubated with 1 ml of SB buffer containing with 2 mg/ml Zymolase-20T (United States Biological, Swampscott, MA) and 2 mg/ml lysing enzyme (Sigma, St. Louis, MO; L1412) and incubated at 37°C for 4 h. These plugs were then transferred into DB buffer (50 mM EDTA, pH 8.0, 1% SDS, 0.5 mg/ml protease-K) and incubated at 50°C for at least 16 h with a minimum three changes of the same buffer. They were then washed in 1× TE buffer (10 mM Tris, 1 mM EDTA, pH 8.0) with a minimum three changes, 2 h each. The plugs were soaked in 200 μl 1 μM YOYO-1 (Molecular Probes, Eugene, OR) in TE for 1 h and washed with fresh TE to remove excess stain. An equal volume of 1× TE was added to each plug and melted by incubating at 68°C for 20 min, cooled to 43°C, and digested with β-agarase (NEB). To the solution, 200 μl of TE was added and the concentration of DNA was approximated by agarose gel electrophoresis and EtBr staining, using λ DNA standards. The solution for combing was prepared by adding 20 ng genomic DNA, 240 μl of 0.5 M MES, pH 5.4, 960 μl H2O, and adjusting the volume to 1.4 ml with 1× TE.
DNA Combing and Visualization
The DNA combing was performed as described (Michalet et al., 1997), with some modifications. A specially silanized glass coverslip was dipped into a solution of high-molecular-weight genomic DNA and was slowly withdrawn, drawing out DNA molecules that had bound nonspecifically to the glass by an end, and laying the stretched DNA flat against the surface. The parameters of dipping and withdrawal were controlled by an automated combing apparatus. The combed molecules were fixed by drying at 60°C for 2 h. The coverslips were then mounted on glass slides for subsequent handling and washed in succession with 70, 90, and 100% alcohol, each for 5 min. After air drying, they were washed with 2 M NaOH for 30 min, followed by three washing with 1× phosphate-buffered saline (PBS), pH 7.4, each for 5 min. Simultaneous detection of CldU and IdU was performed as described with some modification (Solovei et al., 2001). This protocol has five serial incubations: 1) 1% block solution (Roche, Indianapolis, IN), 2) rat anti-BrdU (1:50; AbCam, Cambridge, United Kingdom; BU1/75(ICR1) recognizes BrdU and CldU, but not IdU), 3) Alexa-594-coupled goat anti-rat (1:200; Molecular Probes), 4) mouse anti-BrdU (1:20; Becton-Dickinson, Mountain View, CA; B44 recognizes BrdU and IdU, but not CldU), and 5) Alexa-488-coupled goat anti-mouse (1:200; Molecular Probes). All solutions were diluted in 1× PBST (1× PBS + 0.05% Tween-20) and incubations were performed with 50 μl under a plain glass coverslip, for 20 min at 37°C in a humid chamber. For DNA molecules labeled with BrdU, a modified series was used: 1) 1% block solution, 2) rat anti-BrdU (1:50), 3) Alexa-488-coupled goat anti-rat (1:200; Molecular Probes), 4) mouse anti-ssDNA (1:10 Argene, North Massapequa, NY), and 5) Alexa-594-coupled goat anti-mouse (1:200; Molecular Probes). In both protocols, after each step, slides were rinsed twice with PBST for 3 min. Slides were mounted in Vectasheild antifade (Vector Laboratories, Burlingame, CA) under a plain glass coverslip, sealed with nail polish, and stored at 4°C.
Fluorescent In Situ Hybridization
The cosmids C330, C1235, C1884 (close to ura4 locus), and C1223 (close to nmt1 locus) were obtained from the pombe Genome Project at the Sanger Center (www.sanger.ac.uk/Projects/S_pombe). These cosmids were digested with BsiWI, SpeI, XhoI, and XhoI, respectively. They were religated to create truncated cosmids with 10-20-kb base pairs missing in the middle and asymmetric lengths at both ends. These truncated cosmids were used as probes for selectively detecting and orienting molecules from the ura4 or nmt1 loci. Five hundred micrograms of probe were labeled with biotin using Bioprime (Invitrogen, Carlsbad, CA). The labeled probe was resuspended at 60 μl hybridization buffer (5× SSPE, 1% blocking solution, 1% BSA, 1% Tween 20). Hybridization was carried out by the protocols described previously with minor changes (Anglana et al., 2003). Hybridization was carried out in a humid chamber at 37°C for 8 h to overnight. The slides were washed with 5× SSPE for 5 min, followed by 1× PBST for 5 min, twice. Signals were sequential developed as above with the following combinations of antibodies: 1) rat anti-BrdU (1:100), streptavidin-594 (1:100; Vector Laboratories), 2) chicken anti-rat Alexa-488 (1:100; Molecular Probes), anti-streptavidin (1:200; Vector Laboratories); 3) rat anti-BrdU (1:200), mouse anti-guanosine (1:10; Argene), streptavidin-594 (1:200); 4) chicken anti-rat Alexa-488 (1:200), rabbit anti-mouse Alexa-350 (1:200; Molecular Probes), anti-streptavidin (1:200); 5) goat anti-chicken Alexa-488 (1:200; Molecular Probes), goat anti-rabbit Alexa-350 (1:200; Molecular Probes), and streptavidin-594 (1:200). Slides were mounted and stored as above.
Image Acquisition and Analysis
The signals were visualized using a Zeiss Axioskop 2 epifluorescence microscope (Thornwood, NY); images were captured on a SPOT monochrome cooled-CCD camera (Diagnostic Instruments, Sterling Heights, MI), and manipulated for color, contrast, brightness, and pixel input range using Photoshop (Adobe Systems, San Jose, CA) or Canvas (Deneba Systems, Saanichton, British Columbia, Canada). Each image was uniformly manipulated. Molecule lengths, bubble length, and interbubble distances were measured using ImageJ (NIH), and analyzed using Excel (Microsoft, Redmond, WA). Because of the noise in our data, signals are scored as real incorporation patches only if they are longer than 3 kb (∼30 pixels in the original micrographs); smaller signals are assumed to be background. Likewise, because of discontinuities in signals, gaps between signals are scored as real gaps only if they are longer than 3 kb and show clear continuity of DNA with the anti-guanosine anti-body. To determine the distribution of origin firing, we analyzed interbubble distances, that is, the distances between the edges of neighboring bubbles, instead of interorigin distances, which involves assuming that there is a origin at the center of every bubble and measuring the center-to-center distances. The disadvantage of measuring interorigin distances is that as bubbles fuse, the center of the fused bubbles is incorrectly assumed to be an origin and the location of the actual origins is obscured (Herrick et al., 2002). The advantage of measuring interbubble distances is that it avoids the fusion problem and, if origins are randomly distributed, the fusion of bubbles does not affect the exponential character of the distribution of the remaining gaps (Jun et al., 2005). The exponential and Gaussian fits of interbubble distances in the whole genome experiments and the reanalysis of the published budding yeast data were performed using KaleidaGraph (Synergy Software, Reading, PA). For the data in Figure 1, D, G, and J, we also calculated best Gaussian fits; when constrained to positive values (fits that extend into negative values indicate negative distances between origins and are thus meaningless) none of the fits had R2 > 0.6. For the fluorescence in situ hybridization (FISH) experiments, each molecule was scored by four people; bubbles were included in the analysis if scored at least three people. The efficiency of firing for each origin was calculated as the percentage of fibers that contained a bubble that overlapped the origin. The efficiency with which an origin fired in the same S phase as one of its neighboring origins was calculated as the percentage of an origin firing on a fiber on which that neighbor also fired; fibers that contained only one of the other were excluded from the calculation. Correlation between the firing of neighboring origins was evaluated by stepwise logistic regression using p values from likelihood ratio tests of improvement to rank candidate predictors (Hosmer and Lemeshow, 1989). Kappa statistics were calculated as a measure of agreement and their associated p values reported (Fleiss, 1981). Statistical significance was defined as p ≤ 0.05. Computations were performed using the SAS (SAS Institute, Cary, NC), SPSS (Chicago, IL) and StatXact (Cytel, Cambridge, MA) statistical software packages.
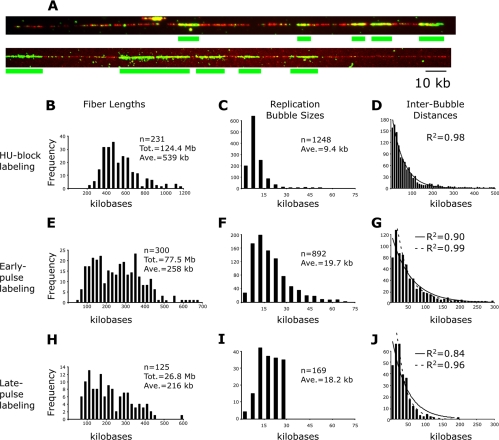
Figure 1.
Origin firing is randomly distributed across the genome. (A) Representative combed DNA molecules. Nascent replication bubbles are labeled green with anti-BrdU. The DNA molecule is labeled red with anti-guanosine. The positions of the nascent bubbles are indicated below the image with a green line. Signals are scored as real incorporation patches if they are longer than 3 kb; smaller signals are assumed to be background. The top molecule is from the HU-block data set; the bottom is from the early-pulse data set. (B-J) Histograms of the combing data. (C, F, and I) The distribution of bubble lengths. The HU-blocked bubbles stall after 9.4 ± 5.7 kb, consistent with replication forks stalling after ∼5 kb. The early-pulse-labeled bubbles show a more heterogeneous distribution, averaging 19.7 ± 13.1 kb. The late-pulse labeled bubbles were selected to be <30 kb (see Materials and Methods). (D, G, and J) The distribution of interbubble distances. Best-fit exponential curves and associated R2 values are shown. The dashed curves represent the best fit excluding the first data point. For all three histograms, the best Gaussian fit has R2 < 0.6 (unpublished data).
Calculations
The calculation for percentage of cells that will have large gaps due to a random distribution of origin firing is based on the fact that if origin firing is distributed randomly and the average distance between firing is n, then the interorigin distances have an exponential distribution with cumulative distribution function of D(L) = e-L/n, where L is a specific length. Thus, the number of gaps greater than c times the average length (i.e., c*n) is e-c*n/n = e-c. If we assume that there are on the order of 200 interorigin distances during a yeast S phase (there are ∼120 early interorigin-distances in fission yeast [Supplementary Figure S2] and estimates of between ∼250 and 300 in budding yeast [Raghuraman et al., 2001; Yabuki et al., 2002]) and the average gap size takes half of S phase to replicate (the average gap size in budding yeast of ∼50 kb would take 10 min for replicate at 2.5 kb/min and S phase takes ∼20 min; Raghuraman et al., 2001), then the probability of taking four times as long to replicate is 200*e-(4*2) = 6.7%. Likewise, the probability of taking five times as long (or 100 min as in the example in the discussion) is 200*e-(5*2) = 0.9%.
The calculation of 33% for the average early-firing efficiency of origins at the ura4 and nmt1 loci is based on the efficiencies of all loci that fire on at least 8% of fibers. This group includes all of the predicted origins in the regions (those listed in Figure 2, B and C), as well as three other loci in the ura4 region (those labeled 3002.2, 3003.3, and 3003.5 in Figure 2A) and three other loci in the nmt1 region; these loci account for 96% of observed origin firings. For this calculation, we count the closely spaced origins at 3004/5 and 3008/9 as single loci, because we would not be able the resolve the distance between them in the refiring assay. The estimate from the FISH data are in good agreement with a independent estimate made from dividing the estimated numbers of origins that fire in each cell in HU, 120 (Supplementary Figure S2), by the estimated number of origins in the genome, 384 (Segurado et al., 2003): 120/384 = 31%.
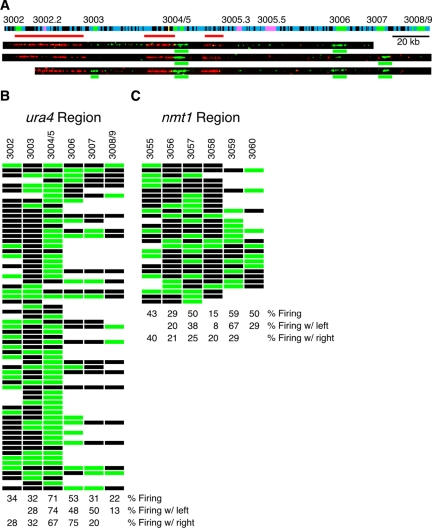
Figure 2.
Origins in the ura4 region fire stochastically. (A) The ura4 region of chromosome III and representative molecules. The graphic represents the left end of chromosome III from nucleotides 29423-254496. Blue represents coding sequences, black noncoding sequences, green noncoding sequences predicted to be origins by AT richness (Segurado et al., 2003) and yellow ura4. Predicted origins are labeled above with the systematic nomenclature of Segurado et al. (2003). Three additional loci, labeled 3002.2, 3005.3, and 3005.5 and shown in pink, are just below the AT-threshold used for origin prediction. Origin pairs 3004/3005 and 3008/3009 are too close together to be reliably distinguished by combing, and each pair is treated as one origin. The red bars represent the FISH probes used to identify molecules from this region. Three representative molecules labeled with BrdU and identified with the FISH probes are shown. The BrdU signals scored as replication bubbles are indicated by green lines below the images. The length and continuity of all molecules was determined with anti-guanosine antibodies, which label DNA (unpublished data). (B) A graphic table of origin use in the ura4 region. Each row represents a DNA molecule; each column represents an origin in the region. A green box indicates the origin fired on that molecule; a black box indicates it did not; no box indicates that the fiber did not extend to include that origin. Only the 82% of replication bubbles that overlapped predicted origins are included. Below the table is the quantitation of the origin efficiencies, and the efficiencies when either the right or left neighbor fired. The high efficiency of 3004/5 is due to the fact that it actually represents three origins: 3004 (also known as ars3003) and two closely spaced origins in 3005 (ars3002 and ars3004; Dubey et al., 1994). The 71% efficiency of the three is consistent with an efficiency of ∼35% for each individual origin, consistent with 2D-gel analyses of the origins (Dubey et al., 1994). (C) A graphic table of origin use in the nmt1 region.
RESULTS
To determine if origin firing is coordinated, we measured the distances between the replication bubbles on individual fission yeast DNA molecules. If origin firing is uncoordinated, the distribution of interbubble distances should be exponential, with many bubbles clustered close together and occasional large gaps between bubbles. This prediction follows from the fact that elements randomly distributed on a line are characterized by an exponential distribution of interelement distances (Birnbaum, 1954). If, on the other hand, there is a mechanism that evenly distributes origin firing, the distribution of interbubble distances should be Gaussian, with a mean equal to the average distance between active origins. A third possibility, that clusters of origins are coordinately regulated and could lead to more complicated distributions, but would not be expected to produce an exponential distribution.
Whole-genome Analysis
We labeled the DNA in nascent replication bubbles by in vivo pulse-labeling synchronized cells with the thymidine analog BrdU. Wild-type fission yeast do not use exogenous thymidine analogs; to facilitate BrdU labeling, we used a strain that expresses the human equilibrative nucleoside transporter 1 (hENT1) and herpes thymidine kinase (tk), allowing BrdU uptake and phosphorylation (Sivakumar et al., 2004). We used two complementary approaches to label replication bubbles: HU-block labeling and pulse labeling. In both cases, synchronous cells enter S phase in the presence of BrdU, and origins that fire are identified by the incorporation of BrdU into the newly replicated DNA flanking the origin. HU-block labeling takes advantage of the fact that HU prevents deoxynucleotide synthesis, so as cells begin replication they run out of deoxynucleotides, replication forks stall after ∼5 kb, and subsequent origin firing is inhibited by the replication checkpoint (Santocanale and Diffley, 1998; Kim and Huberman, 2001). Thus HU-block labeling specifically labels origins that fire early. In the pulse labeling strategy, cells can be harvested at any time during S phase, so pulse labeling can be used to label origins throughout S phase. After labeling, the DNA is isolated, combed onto a glass surface, and visualized by fluorescence microscopy, using anti-guanosine antibodies to visualize the DNA molecules and anti-BrdU antibodies to localize the labeled replication bubbles (Figure 1A). Because the combed molecules are uniformly stretched to a length of ∼2 kb/μm (Michalet et al., 1997), we can measure the location of active replication origins with ∼1-kb resolution (Figures 1A and 2A).
We initially measured interbubble distances using the HU-block labeling strategy, which has the advantage of giving uniform bubble sizes and reducing the number of bubble fusions. We measured 1137 interbubble distances on 231 molecules constituting 124.4 Mb of DNA (Figure 1B). Because the fission yeast genome is only 14 Mb, this data set provides ninefold statistical coverage of the genome. The length of the HU-blocked bubbles show a tight distribution around 9.4 kb, consistent with a uniform arrest of earlyfiring origins, with a slight shoulder on the right likely due to the fusion of closely neighboring origins (Figure 1C). The distribution of interbubbles distances is clearly uneven, with many origins firing close together and occasional large gaps of up to 500 kb between fired origins (Figure 1D). The distribution is well fit by the calculated exponential curve shown (Figure 1D, R2 = 0.98). The exponential nature of this distribution indicates that the ability to fire is randomly distributed among fission yeast origins (Birnbaum, 1954). Thus, it appears that no mechanism distributes the early firing of origins evenly across the genome, rather origins fire stochastically, with no influence from neighboring origins.
As a complementary approach, we measured interbubble distances using an early-pulse-labeling strategy. Synchronous cells entered S phase in the presence of BrdU and were harvested in early S phase. Because of the imperfect synchrony of our cultures, early pulse labeling gives a less homogeneous distribution of bubble sizes than HU-block labeling, indicating that some of the bubbles are from slightly later firing origins and that others are fused bubbles from closely neighboring origins (Figure 1F). Nonetheless, the early-pulse-labeling strategy does not perturb replication and thus is free of any potential HU-induced artifacts. The distribution of 677 interbubble distances on 300 molecules covering 77.5 Mb of DNA also approximates an exponential curve (Figure 1G, R2 = 0.90). The data deviates significantly from an exponential distribution only at the first point, 0-10 kb. Because the BrdU signals are imperfectly continuous, we only score gaps that are at least 3 kb and have clear continuity of the DNA signal spanning them. Thus, we undercount the smallest gaps, leading to a low estimate of the first data point. If the first data point is removed from the early-pulse-labeled data set, the rest of the data are well fit by an exponential curve (Figure 1G, R2 = 0.99). Thus, in early S phase, the ability to fire is distributed randomly among fission yeast origins.
The HU-block and early-pulse-label experiments specifically examine origins that fire early in S phase. To test if origin firing is also randomly distributed later in S phase, we used a pulse-labeling strategy with longer pulses of BrdU. To identify origins firing in later in S phase, we scored replication bubbles of <30 kb (indicative of recent firing) on molecules that were more than 40% replicated (indicative of cells in mid-S phase). We measured 303 distances between such later-firing origins and neighboring replication forks (Figure 1J), and as for early-firing origins, they approximate an exponential distribution (R2 = 0.84) and are well fit by an exponential distribution if the first data point is excluded (R2 = 0.96). These results suggest that the ability to an origin to fire is distributed randomly throughout S phase. It should be noted that although this approach identifies later-firing origins, it excludes late-S-phase fibers with large gaps, because they are <40% replicated. Therefore, the data in Figure 1J is skewed toward shorter gaps. The conclusion that origins firing in late S phase are randomly distributed is based on the assumption that origins that fire late in moderate gaps (50-200 kb), which are included in our analysis, behaves the same as origins that fire late in large gaps (>200 kb), which are excluded.
Specific-locus Analysis
The whole-genome data in Figure 1 examines the distribution of origin firing with out identifying specific origins. To determine if specific, individual origins fire stochastically, as predicted by the whole-genome data, we examined the firing of specific origins in the ura4 and nmt1 regions. We chose these regions because the predicted origins in the regions are well spaced, and because each region contains verified replication origins (Dubey et al., 1994; Segurado et al., 2003). We first examined eight origins that span 217 kb on the left end of chromosome III and include the well-studied origins at the ura4 locus (Dubey et al., 1994). In addition to the ura4 origins, six other loci in the region have been predicted to act as origins based on their high AT content (Segurado et al., 2003; Figure 2A). HU-block labeled DNA molecules were combed, hybridized with ura4-specific FISH probes, and probed with anti-guanosine and anti-BrdU antibodies.
We scored a total of 135 labeled bubbles on 65 molecules. Labeled replication bubbles correlated well with the origins predicted based on high AT content; 82% of BrdU incorporation patches overlapped with predicted origins and all predicted origins fired in on least 22% of fibers. Of the 18% of bubbles that did not overlap with predicted origins, most overlapped with three AT-rich regions, labeled 3002.2, 3005.3, and 3005.5 in Figure 2A, which fall just below the AT threshold used; these origins fired on 14, 8, and 19% of fibers, respectively. The remaining 5% of bubbles were scattered. These results confirm that, although fission yeast origins are not defined by strict sequence motifs, replication does initiate at specific chromosomal loci. To determine if any of the origins in this region are coordinately regulated, we asked if the frequency at which an origin fires is influenced by the firing of a neighboring origin (Figure 2B). We compared the total firing efficiency of each origin with its efficiency on fibers where its neighbor also fired. Using Fisher's Exact Test, we found no significant positive or negative correlation between firing of any neighboring origins (Figure 2B, p > 0.05 for each pairwise correlation).
We also examined the firing of the six origins that span 212 kb in the nmt1 region of the right arm of chromosome III. Using the HU-block strategy, we observed 58 labeled origins on 28 molecules. We found that the five of the six predicted origins (3055-3060) fired early on between 29 and 59% of fibers; 3058 appears to be less efficient than the other origins we have examined, firing on just 15% of fibers. As for the ura4 region, there was no significant correlation between the firing of neighboring origins (Figure 2C, p > 0.1 for each pairwise correlation). Thus, as predicted by our whole-genome results, the origins surrounding ura4 and nmt1 fire stochastically. In particular, these results are inconsistent with coordinated regulation of origin clusters.
Sequential S-phase Analysis
The random distribution of origin firing within each S phase prompted us to ask if the distribution is stochastic between S phases; is an origin that fires in one S phase epigenetically programmed to be more likely to fire in the next S phase? To label origins that fired in sequential S phases, we double-labeled cells, labeling in the first cell cycle with CldU and the second with IdU (Figure 3). The experiment is complicated by the fact that thymidine analogs cannot be washed out once they have been added to cells, presumably because after the nucleoside analog enters the cell through the nucleoside transporter, it is phosphorylated, and can no longer leave. To avoid this problem, synchronized cells were arrested with HU in early S phase and released into CldU to allow them to complete replication. This step allows origins that fired early in the first cycle to be recognized as unlabeled patches on otherwise CldU-labeled molecules (Figure 3Ai). After the first S phase, the cells were grown in IdU and HU to arrest them early in their second S phase. This step allows origins that fired early in the second cycle to be recognized as IdU-labeled patches on the same molecules (Figure 3Aii). Because the analogs cannot be washed out, origins that fired in the second cycle are labeled with both CldU and IdU, making it impossible to distinguish origins that fired in both cycles (Figure 3Aiii) from those that only fired in the second (Figure 3Aiv). Thus, we compared the origins that only fired in the first S phase and not in the second (patches unlabeled with CldU, Figure 3Av) with those that fire in the second S phase and may or may not have fired in the first (patches labeled with IdU, Figure 3A, iii and iv).
If origins that fire in one cycle are significantly more likely to fire in the subsequent cycle, we would expect a high frequency of doubly labeled origins and a low frequency of singly labeled origins. However, if there is no correlation between origins firing in sequential S phases, we would expect the ratio of origins labeled only in the first cycle to those labeled in the second to be 0.70, because 30% of those that fire in the first cycle will randomly fire in the second, whereas 70% will not. (This calculation assumes an average firing probability of 30%; the average efficiency of all the origins identified by FISH in the ura4 and nmt1 region, including those below the published AT threshold, is ∼33%. See Materials and Methods for the derivation of this estimate.) In fact, among 436 labeled origins on 109 molecules spanning 23 Mb, we see a ratio of 0.72, consistent with random refiring in each cycle and inconsistent with any significant epigenetic regulation of origin firing from one cycle to the next.
DISCUSSION
We have tested whether the firing of fission yeast replication origins is coordinated to ensure an even distribution of replication bubbles across the genome. We found no evidence for such coordination. On the contrary, we found that origins fire stochastically and that this stochastic firing leads to a random distribution of replication bubbles during S phase.
The Random Distribution of Origin Firing in Fission Yeast
To examine the distribution of origin firing in fission yeast, we used the single molecule analysis technique of DNA combing. We labeled nascent replication bubbles in vivo and visualized those bubbles on isolated, combed DNA molecules. We used two approaches to determine if origin firing is globally coordinated or if origins fire independently of each other. First, we used a whole genome approach to measure the distances between neighboring replication bubbles. We measured interbubble distances on almost 230 Mb of DNA, ensuring good statistical coverage of the 14-Mb fission yeast genome. Any mechanism that coordinates an even distribution of origin firing would result in a Gaussian distribution of interbubble distances. On the contrary, bubbles are very unevenly distributed, with many bubbles close together and occasional large gaps of hundreds of kilobases between replication bubbles (Figure 1, D, G, and J). Elements randomly placed on a line display an exponential distribution of interelement distances (Birnbaum, 1954); thus, the exponential character of the interbubble distances in Figures 1, D, G, and J, indicate that origin firing is randomly distributed across the fission yeast genome. Second, we looked directly at the coordination of origin firing around ura4 and nmt1, using FISH to identify combed molecules from these regions. In total, we examined 14 origins that span over 400 kb, ∼3% of the genome. We found that these origins also fire stochastically; there is no significant positive or negative correlation between the firing of any neighboring origins in either region.
DNA combing provides an excellent means of identifying in vivo replication origins. In our experiment examining origin firing in the ura4 and nmt1 regions, we identified origins in an unbiased manner by visualizing all nascent replication bubbles. However, 82% of the bubbles around ura4 overlapped with loci that had been predicted to be origins of replication by their AT-rich character (Segurado et al., 2003; Dai et al., 2005). Furthermore, all of the predicted origins were found to overlap with replication bubbles on at least 15% of molecules. These results are consistent with the previous analysis of the firing of predicted origins, and corroborate the accuracy of the predictions (Segurado et al., 2003; Dai et al., 2005). In addition, the average distance between active origins of ∼110 kb (Supplementary Figure S2) is about three times the average distance of 35 kb between predicted origins (Segurado et al., 2003), consistent with an average origin efficiency of 30%.
Origins have been proposed to fire at specific times during S phase, some exclusively early and some exclusively late (Fangman and Brewer, 1992). We find no evidence for exclusively late-firing origins in fission yeast. Early-firing can be defined as the ability of an origin to fire in HU (Santocanale and Diffley, 1998; Kim and Huberman, 2001). By this definition, none of the 14 origins in the ura4 or nmt1 regions are restricted from firing early in S phase. Thus, if there are euchromatic origins in fission yeast that specifically fire late in S phase, they must be infrequent (less than ∼7% of origins, because we see none in the 14 origins we have examined), unevenly distributed (absent from large regions around ura4 and nmt1) or different in sequence structure from all known fission yeast origins (so that we would not recognize them in the ura4 and nmt1 regions). These conclusions are consistent with work showing that of 16 fission yeast origins that are active on plasmids, 14 fire early at their chromosomal loci and 2 do not seem to fire at all at their chromosomal loci (Kim and Huberman, 2001).
The Distribution of Origin Firing in Other Organisms
Our results suggest that the distribution of origin firing in fission yeast is dramatically different from that in budding yeast. The distribution of origin firing in budding yeast has been examined using two distinct microarray techniques (Raghuraman et al., 2001; Yabuki et al., 2002). In both cases, if distance between origins is plotted versus frequency, they give an approximately Gaussian distribution of interorigin distances (Supplementary Figure S3, A and B, R2 > 0.85). In neither case is the distribution close to exponential (R2 < 0.33). These results are consistent with budding yeast whole-genome, HU-block combing experiments, and older fiber autoradiography studies, which both show an approximately Gaussian distribution of interorigin distances (Newlon and Burke, 1980; Rivin and Fangman, 1980; Lengronne et al., 2001, Supplementary Figure S3C). Thus, budding yeast appear to rely on evenly distributed efficient origin firing to ensure efficient replication. Although budding yeast have inefficient as well as efficient origins, the fact that the inefficient origins fire less often means that they contribute little to overall replication (Raghuraman et al., 2001; Yabuki et al., 2002). Because origin firing in most eukaryotes does not seem to be efficient (Shinomiya and Ina, 1994; Clyne and Kelly, 1995; Dubey et al., 1996; Gilbert, 2001; Dijkwel et al., 2002; Norio and Schildkraut, 2004), the budding yeast strategy of evenly distributed efficient origins is unlikely to be generally conserved.
The distribution of origin firing has also been examined in frog embryo extracts, and, in general, has been found to be random (Herrick et al., 2000, 2002; Lucas et al., 2000; Blow et al., 2001; Marheineke and Hyrien, 2001). (One group concluded that origin firing is clustered (Blow et al., 2001), but that conclusion has been questioned (Hyrien et al., 2003).) The random distribution of origin firing is presumably due to the fact that replication initiates at random sites (Harland and Laskey, 1980). Drosophila embryos also initiate replication in a sequence-independent manner, suggesting that they too may have randomly distributed origin firing (Shinomiya and Ina, 1991). The random distribution of origin firing raises the random gap problem; a random distribution will lead to occasional large gaps that should take a long time to replicate, yet frog embryos replicate extremely efficiently (Hyrien et al., 2003). A potential solution to this paradox is discussed below.
The distribution of origin firing in metazoans is unknown. Large regions of metazoan genomes replicate at specific times during S phase. Recent microarray studies in humans and flies confirm these domains of early and late replication timing at even higher resolution (MacAlpine et al., 2004; Woodfine et al., 2004; Jeon et al., 2005). However, these techniques are not sufficiently high resolution to pinpoint specific origins, nor do they measure the efficiency with which these domains replicate early. Therefore, it is still unclear how many origins are involved in replicating these domains and whether these origins are coordinately regulated or if they could be replicated by stochastic origin firing (Berezney et al., 2000; Hyrien et al., 2003).
Mechanisms of Random Origin Firing
The simplest explanation for the random distribution of origin firing is that origins fire stochastically, independent of the firing of their neighbors. Such stochastic origin firing could arise from the random interaction of a rate-limiting factor with the origins. For instance, if the number of ORC in the cell was less than the number of origin sequences, random association of ORC with origins would lead to a random distribution of origin firing (Dai et al., 2005). However, in both budding and fission yeast, origins that normally do not fire can be made to fire by preventing them from being passively replicated, suggesting that origins that do not fire can have assembled, functional prereplication complexes (Dubey et al., 1994; Santocanale et al., 1999; Vujcic et al., 1999; Kim and Huberman, 2001). Other plausible rate-limiting candidates include the Cdc6/Cdc18 origin licensing protein, the Cdc45 replication initiation protein, and the CDK and DDK replication kinases.
Consequences of Random Origin Firing
A random distribution of origin firing raises the random gap problem; in a significant percentage of cells, occasional large gaps should disrupt efficient replication. A trivial solution to this problem in fission yeast is offered by the fact that they have a relatively long G2. Perhaps, if 1% of cells take 100 min, instead of the usual 20 min, they would not suffer, because G2 lasts 80 min. Thus the 100 min of S plus G2 would be long enough for 99% of the cell to finish replication.
Alternatively, fission yeast may have a mechanism to complete replication in a timely manner despite random origin firing. Replication in frog embryo extracts provides a precedent in which replication origins are distributed randomly, but replication is completed efficiently (Herrick et al., 2000, 2002; Lucas et al., 2000). This observation demonstrates that a random distribution of origin firing does not necessarily imply inefficient replication. One model that reconciles random firing and efficient replication posits that origins fire with increasing probability as S phase proceeds (Lucas et al., 2000; Herrick et al., 2002; Hyrien et al., 2003). Thus, initial gaps have an increasing chance of an origin firing within them, making it unlikely for large gaps to persist.
However fission yeast deals with stochastic origin firing, its replication strategy is clearly different from traditional models of how replication would be coordinated across a eukaryotic genome. In particular, it uses no fixed replication program and requires no communication between neighboring or distant origins. Although the fission yeast replication strategy cannot account for the differences in replication timing seen in large domains of metazoan genomes, it may account for the behavior of origin firing and replication within domains of similar replication timing.
Supplementary Material
Acknowledgments
We thank John Woodward at the Sanger Center for pombe genomic cosmids. We are grateful Tony Carruthers for help with curve fitting; to the members of the Bensimon, Arcangioli, and Rhind laboratories for helpful suggestions, in particular Catherine Schurra, Chiara Conti, and Sandrine Caburet for combing advice; to Mary Munson and Bill Kobertz for helping to score the FISH experiments; and to John Bechhoefer, Audrey Huang, Sean Ryder, and Mary Munson for critical reading of the manuscript. This study was supported by the University of Massachusetts Medical School, the Worcester Foundation for Biomedical Research, and a Leukemia and Lymphoma Special Fellowship and Short Term Scientific Exchange Award to N.R.
This article was published online ahead of print in MBC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E05-07-0657) on October 26, 2005.
The online version of this article contains supplemental material at MBC Online (http://www.molbiolcell.org).
References
- Abdurashidova, G., Deganuto, M., Klima, R., Riva, S., Biamonti, G., Giacca, M., and Falaschi, A. (2000). Start sites of bidirectional DNA synthesis at the human lamin B2 origin. Science 287, 2023-2026. [DOI] [PubMed] [Google Scholar]
- Anglana, M., Apiou, F., Bensimon, A., and Debatisse, M. (2003). Dynamics of DNA replication in mammalian somatic cells: nucleotide pool modulates origin choice and interorigin spacing. Cell 114, 385-394. [DOI] [PubMed] [Google Scholar]
- Bensimon, A., Simon, A., Chiffaudel, A., Croquette, V., Heslot, F., and Bensimon, D. (1994). Alignment and sensitive detection of DNA by a moving interface. Science 265, 2096-2098. [DOI] [PubMed] [Google Scholar]
- Berezney, R., Dubey, D. D., and Huberman, J. A. (2000). Heterogeneity of eukaryotic replicons, replicon clusters, and replication foci. Chromosoma 108, 471-484. [DOI] [PubMed] [Google Scholar]
- Bielinsky, A. K., and Gerbi, S. A. (1999). Chromosomal ARS1 has a single leading strand start site. Mol. Cell 3, 477-486. [DOI] [PubMed] [Google Scholar]
- Birnbaum, A. (1954). Statistical methods for Poisson processes and exponential populations. J. Am. Stat. Assoc. 49, 254-266. [Google Scholar]
- Blow, J. J., Gillespie, P. J., Francis, D., and Jackson, D. A. (2001). Replication origins in Xenopus egg extract are 5-15 kilobases apart and are activated in clusters that fire at different times. J. Cell Biol. 152, 15-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burhans, W. C., and Huberman, J. A. (1994). DNA replication origins in animal cells: a question of context? Science 263, 639-640. [DOI] [PubMed] [Google Scholar]
- Carlson, C. R., Grallert, B., Bernander, R., Stokke, T., and Boye, E. (1997). Measurement of nuclear DNA content in fission yeast by flow cytometry. Yeast 13, 1329-1335. [DOI] [PubMed] [Google Scholar]
- Clyne, R. K., and Kelly, T. J. (1995). Genetic analysis of an ARS element from the fission yeast Schizosaccharomyces pombe. EMBO J. 14, 6348-6357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai, J., Chuang, R. Y., and Kelly, T. J. (2005). DNA replication origins in the Schizosaccharomyces pombe genome. Proc. Natl. Acad. Sci. USA 102, 337-342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dijkwel, P. A., Wang, S., and Hamlin, J. L. (2002). Initiation sites are distributed at frequent intervals in the Chinese hamster dihydrofolate reductase origin of replication but are used with very different efficiencies. Mol. Cell. Biol. 22, 3053-3065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubey, D. D., Kim, S. M., Todorov, I. T., and Huberman, J. A. (1996). Large, complex modular structure of a fission yeast DNA replication origin. Curr. Biol. 6, 467-473. [DOI] [PubMed] [Google Scholar]
- Dubey, D. D., Zhu, J., Carlson, D. L., Sharma, K., and Huberman, J. A. (1994). Three ARS elements contribute to the ura4 replication origin region in the fission yeast, Schizosaccharomyces pombe. EMBO J. 13, 3638-3647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fangman, W. L., and Brewer, B. J. (1992). A question of time: replication origins of eukaryotic chromosomes. Cell 71, 363-366. [DOI] [PubMed] [Google Scholar]
- Fleiss, J. L. (1981). Statistical Methods for Rates and Proportions, New York: John Wiley and Sons.
- Gilbert, D. M. (2001). Making sense of eukaryotic DNA replication origins. Science 294, 96-100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomez, M., and Antequera, F. (1999). Organization of DNA replication origins in the fission yeast genome. EMBO J. 18, 5683-5690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harland, R. M., and Laskey, R. A. (1980). Regulated replication of DNA microinjected into eggs of Xenopus laevis. Cell 21, 761-771. [DOI] [PubMed] [Google Scholar]
- Herrick, J., and Bensimon, A. (1999). Single molecule analysis of DNA replication. Biochimie 81, 859-871. [DOI] [PubMed] [Google Scholar]
- Herrick, J., Jun, S., Bechhoefer, J., and Bensimon, A. (2002). Kinetic model of DNA replication in eukaryotic organisms. J. Mol. Biol. 320, 741-750. [DOI] [PubMed] [Google Scholar]
- Herrick, J., Stanislawski, P., Hyrien, O., and Bensimon, A. (2000). Replication fork density increases during DNA synthesis in X. laevis egg extracts. J. Mol. Biol. 300, 1133-1142. [DOI] [PubMed] [Google Scholar]
- Hosmer, D. W. and Lemeshow, S. (1989). Applied Logistic Regression, New York: John Wiley and Sons.
- Hyrien, O., Marheineke, K., and Goldar, A. (2003). Paradoxes of eukaryotic DNA replication: MCM proteins and the random completion problem. Bio-Essays 25, 116-125. [DOI] [PubMed] [Google Scholar]
- Jeon, Y., Bekiranov, S., Karnani, N., Kapranov, P., Ghosh, S., MacAlpine, D., Lee, C., Hwang, D. S., Gingeras, T. R., and Dutta, A. (2005). Temporal profile of replication of human chromosomes. Proc. Natl. Acad. Sci. USA 102, 6419-6424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jun, S., Herrick, J., Bensimon, A., and Bechhoefer, J. (2004). Persistence length of chromatin determines origin spacing in Xenopus early-embryo DNA replication: quantitative comparisons between theory and experiment. Cell Cycle 3, 223-229. [PubMed] [Google Scholar]
- Jun, S., Zhang, H., and Bechhoefer, J. (2005). Nucleation and growth in one dimension. I. The generalized Kolmogorov-Johnson-Mehl-Avrami model. Phys. Rev. E. Stat. Nonlin Soft. Matter Phys. 71, 011908. [DOI] [PubMed] [Google Scholar]
- Kelly, T. J., and Brown, G. W. (2000). Regulation of chromosome replication. Annu. Rev. Biochem. 69, 829-880. [DOI] [PubMed] [Google Scholar]
- Kim, S. M., and Huberman, J. A. (2001). Regulation of replication timing in fission yeast. EMBO J. 20, 6115-6126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lengronne, A., Pasero, P., Bensimon, A., and Schwob, E. (2001). Monitoring S phase progression globally and locally using BrdU incorporation in TK(+) yeast strains. Nucleic Acids Res. 29, 1433-1442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopes, M., Cotta-Ramusino, C., Pellicioli, A., Liberi, G., Plevani, P., Muzi-Falconi, M., Newlon, C. S., and Foiani, M. (2001). The DNA replication checkpoint response stabilizes stalled replication forks. Nature 412, 557-561. [DOI] [PubMed] [Google Scholar]
- Lucas, I., Chevrier-Miller, M., Sogo, J. M., and Hyrien, O. (2000). Mechanisms ensuring rapid and complete DNA replication despite random initiation in Xenopus early embryos. J. Mol. Biol. 296, 769-786. [DOI] [PubMed] [Google Scholar]
- MacAlpine, D. M., Rodriguez, H. K., and Bell, S. P. (2004). Coordination of replication and transcription along a Drosophila chromosome. Genes Dev. 18, 3094-3105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marheineke, K., and Hyrien, O. (2001). Aphidicolin triggers a block to replication origin firing in Xenopus egg extracts. J. Biol. Chem. 276, 17092-17100. [DOI] [PubMed] [Google Scholar]
- Mesner, L. D., Li, X., Dijkwel, P. A., and Hamlin, J. L. (2003). The dihydrofolate reductase origin of replication does not contain any nonredundant genetic elements required for origin activity. Mol. Cell. Biol. 23, 804-814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michalet, X. et al. (1997). Dynamic molecular combing: stretching the whole human genome for high-resolution studies. Science 277, 1518-1523. [DOI] [PubMed] [Google Scholar]
- Moreno, S., Klar, A., and Nurse, P. (1991). Molecular genetic analysis of fission yeast Schizosaccharomyces pombe. In: Guide to Yeast Genetics and Molecular Biology: Methods in Enzymology, Vol. 194, ed. C. Guthrie and G. R. Fink. New York: Academic Press, 795-823. [DOI] [PubMed] [Google Scholar]
- Newlon, C. S., and Burke, W. G. (1980). Replication of small chromosomal DNAs in yeast. In: Mechanistic Studies of DNA Replication and Recombination 19, ed. B. Alberts and C. F. Fox, New York: Academic Press, 339-409.
- Norio, P., and Schildkraut, C. L. (2001). Visualization of DNA replication on individual Epstein-Barr virus episomes. Science 294, 2361-2364. [DOI] [PubMed] [Google Scholar]
- Norio, P., and Schildkraut, C. L. (2004). Plasticity of DNA replication initiation in Epstein-Barr virus episomes. PloS. Biol. 2, 816-833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasero, P., Bensimon, A., and Schwob, E. (2002). Single-molecule analysis reveals clustering and epigenetic regulation of replication origins at the yeast rDNA locus. Genes Dev. 16, 2479-2484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raghuraman, M. K., Winzeler, E. A., Collingwood, D., Hunt, S., Wodicka, L., Conway, A., Lockhart, D. J., Davis, R. W., Brewer, B. J., and Fangman, W. L. (2001). Replication dynamics of the yeast genome. Science 294, 115-121. [DOI] [PubMed] [Google Scholar]
- Rivin, C. J., and Fangman, W. L. (1980). Replication fork rate and origin activation during the S phase of Saccharomyces cerevisiae. J. Cell Biol. 85, 108-115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santocanale, C., and Diffley, J. F. (1998). A Mec1- and Rad53-dependent checkpoint controls late-firing origins of DNA replication. Nature 395, 615-618. [DOI] [PubMed] [Google Scholar]
- Santocanale, C., Sharma, K., and Diffley, J. F. (1999). Activation of dormant origins of DNA replication in budding yeast. Genes Dev. 13, 2360-2364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwob, E. (2004). Flexibility and governance in eukaryotic DNA replication. Curr. Opin. Microbiol. 7, 680-690. [DOI] [PubMed] [Google Scholar]
- Segurado, M., de Luis, A., and Antequera, F. (2003). Genome-wide distribution of DNA replication origins at A+T-rich islands in Schizosaccharomyces pombe. EMBO. Rep. 4, 1048-1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segurado, M., Gomez, M., and Antequera, F. (2002). Increased recombination intermediates and homologous integration hot spots at DNA replication origins. Mol. Cell 10, 907-916. [DOI] [PubMed] [Google Scholar]
- Shechter, D., and Gautier, J. (2005). ATM and ATR check in on origins: a dynamic model for origin selection and activation. Cell Cycle 4, 235-238. [PubMed] [Google Scholar]
- Shinomiya, T., and Ina, S. (1991). Analysis of chromosomal replicons in early embryos of Drosophila melanogaster by two-dimensional gel electrophoresis. Nucleic Acids Res. 19, 3935-3941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinomiya, T., and Ina, S. (1994). Mapping an initiation region of DNA replication at a single-copy chromosomal locus in Drosophila melanogaster cells by two-dimensional gel methods and PCR-mediated nascent-strand analysis: multiple replication origins in a broad zone. Mol. Cell. Biol. 14, 7394-7403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivakumar, S., Porter-Goff, M., Patel, P. K., Benoit, K., and Rhind, N. (2004). In vivo labeling of fission yeast DNA with thymidine and thymidine analogs. Methods 33, 213-219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solovei, I., Walter, J., Cremer, M., Habermann, F., Schermelleh, L., and Cremer, T. (2001). FISH on three-dimensional nuclei. In: FISH: A Practical Approach, ed. B. Beatty, S. Mai, and J. Squire, Oxford, UK: Oxford University Press. 119-157.
- Vujcic, M., Miller, C. A., and Kowalski, D. (1999). Activation of silent replication origins at autonomously replicating sequence elements near the HML locus in budding yeast. Mol. Cell. Biol. 19, 6098-6109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodfine, K., Fiegler, H., Beare, D. M., Collins, J. E., McCann, O. T., Young, B. D., Debernardi, S., Mott, R., Dunham, I., and Carter, N. P. (2004). Replication timing of the human genome. Hum. Mol. Genet. 13, 191-202. [DOI] [PubMed] [Google Scholar]
- Yabuki, N., Terashima, H., and Kitada, K. (2002). Mapping of early firing origins on a replication profile of budding yeast. Genes Cells 7, 781-789. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.