Selective sweep mapping of genes with large phenotypic effects

Abstract

Many domestic dog breeds have originated through fixation of discrete mutations by intense artificial selection. As a result of this process, markers in the proximity of genes influencing breed-defining traits will have reduced variation (a selective sweep) and will show divergence in allele frequency. Consequently, low-resolution genomic scans can potentially be used to identify regions containing genes that have a major influence on breed-defining traits. We model the process of breed formation and show that the probability of two or three adjacent marker loci showing a spurious signal of selection within at least one breed (i.e., Type I error or false-positive rate) is low if highly variable and moderately spaced markers are utilized. We also use simulations with selection to demonstrate that even a moderately spaced set of highly polymorphic markers (e.g., one every 0.8 cM) has high power to detect regions targeted by strong artificial selection in dogs. Further, we show that a gene responsible for black coat color in the Large Munsterlander has a 40-Mb region surrounding the gene that is very low in heterozygosity for microsatellite markers. Similarly, we survey 302 microsatellite markers in the Dachshund and find three linked monomorphic microsatellite markers all within a 10-Mb region on chromosome 3. This region contains the FGFR3 gene, which is responsible for achondroplasia in humans, but not in dogs. Consequently, our results suggest that the causative mutation is a gene or regulatory region closely linked to FGFR3.

Dogs are the most diverse domestic animal species known. The origin of this diversity may reflect unique developmental patterns (Wayne 1986a,b; Morey 1992; Wayne and Ostrander 1999), non-classical genetic mechanisms (Fondon and Garner 2004), high levels of genetic variation (Vilà et al. 1997; Wayne and Ostrander 1999; Parker et al. 2004), and strong divergent selection (e.g., Darwin 1859). Despite considerable interest, genes influencing the striking morphological differences among breeds have yet to be identified. The extensive cross-breeding design required for marker association studies is a potential impediment in dogs because of their long gestation time, the expense and logistical problems associated with housing and feeding, and animal welfare reasons. However, the intense selection for specific phenotypic traits that occurs at the founding of a dog breed, and thereafter, may leave a genetic signal in the underlying genome that allows the genetic basis of the trait to be determined without an extensive breeding design. Specifically, intense selection on single discrete phenotypic traits is predicted to result in reduced levels of variability in the region surrounding the gene or genes that influence the phenotypic trait.

The theory of selective sweeps has been developed to predict the scope of the initial reduction in variation as well as its decay with time (Smith and Haigh 1974; Fay and Wu 2000; Kim and Stephan 2002; Przeworski 2002, 2003; Kim and Nielsen 2004). Selectively swept regions in the genome can potentially be identified by a genome scan, and the low-variation interval surrounding the gene under selection narrowly circumscribed by fine-scale mapping. For example, a marker-based survey of chromosome 1 in rats from warfarin-resistant populations found a 0.5-centimorgan (cM) region in a moderately resistant population that was the likely locus of the warfarin resistance gene (Kohn et al. 2000, 2003). This information was later used to identify the gene through more traditional candidate gene approaches and association mapping techniques (Rost et al. 2004). Similarly, selective sweeps have been identified in domestic and wild populations, suggesting a general approach for finding genes under selection (Berry et al. 1991; Begun and Aquadro 1992; Kohn et al. 2000; Matsuoka et al. 2002; Schloetterer 2002; Luikart et al. 2003; Akey et al. 2004; Storz 2005; Wright et al. 2005).

Dog breeds are generally founded by a relatively small number of related individuals who express a particular trait of interest. As remarked by Darwin, breeds may originate as discrete mutations or “sports” that are rapidly fixed through selection (Darwin 1859; Wilcox and Walkowicz 1995). Examples include skeletal mutations such as achondroplasia or brachycephally. Alternatively, crossing between breeds followed by selection of individuals segregating specific traits in the F2 generation can be used to identify segregating mutations that are then fixed in the incipient breed (e.g., Stockard 1941). Finally, multigenerational selection for desirable traits could also be practiced on large populations (Ash 1927; Epstein 1971; Hutt 1979; American Kennel Club 1997). Remarkably, the majority of dog breeds have been created since the mid-19th century (Ash 1927; Epstein 1971; American Kennel Club 1997), and hence a vast phenotypic diversification has occurred in <200 yr, or ∼100 generations. The recent and rapid genesis of breeds from a limited number of individuals suggests that, in many cases, a small number of genes of large effect are responsible for breed characteristics. For example, recent genetic studies of the Portuguese water dog showed skeletal differences were primarily due to a limited number of genes of major effect, one of which appears to regulate growth factor IGF-1 (Chase 2000). Similarly, studies of quantitative trait loci (QTLs) in domesticated cereal crops (rice, wheat, millet, and sorghum) have shown that a small number of loci are responsible for much of the observed evolution in several traits under strong artificial selection, such as increased seed mass (e.g., Paterson et al. 1995; Matsuoka et al. 2002).

A second unique feature of dog breeds is that breed phenotypes often have evolved in parallel in many lineages, such as toy, miniature, and standard forms; brachycephalic breeds; and breeds with foreshortened limbs (Supplemental Table S1). These breeds may share mutations in the same gene(s) or regulatory region and consequently may have selective sweeps in the same area of the genome. However, the scope of selective sweeps may differ among breeds sharing mutations in the same genes because of differences in breed history, effective population size, and mutation rate. Consequently, these observations suggest a general approach to finding genes of large phenotypic effect in dogs. First, breed groups are chosen that express similar phenotypic traits (e.g., Supplemental Table S1). Then, assuming that at least one breed in each phenotypic group has a sweep region of 5-10 Mb in genomic extent, a moderate scan of ∼500 markers (for a spacing of one marker every 5 Mb, given a genome size of 2.5 gigabases; Guyon et al. 2003) should reveal areas of low variability due to a selective sweep. Importantly, if breeds within a phenotypic group experience mutations in the same genes, comparison of the sweep region among them may narrow considerably the putative interval containing the genes under selection. Thereafter, fine-scale mapping and candidate gene approaches using information gleaned from the complete dog genome sequence as well as comparative haplotype analysis might allow a precise localization of the causative genes and the mutations that cause breed-specific phenotypes.

In this study, we test the assumptions of the selective sweep approach in dogs by using simulations and empirical marker surveys. First, we simulate the process of breed formation and assess the probability that in a moderate-density genomic scan, a single marker or two or three adjacent markers would have reduced or no heterozygosity. We show that under a wide variety of demographic scenarios the probability that a single breed or two or more breeds would have two or three adjacent monomorphic markers is small. We test these predictions using a marker survey of Large Munsterlanders. This breed was known to have been formed at the turn of the last century through exclusive breeding of black dogs amongst a population that included both black and brown dogs. The causative mutations for these coat colors have been found in the TYRP1 (tyrosinase-related protein) gene located on chromosome 11. We show that the selective sweep region near the mutation in Large Munsterlanders is considerable and spans a 40-Mb region. Further, intense artificial selection has caused divergence in marker frequency between Large Munsterlanders and control breeds. Finally, we utilize selective sweep mapping to identify a genetic interval containing putative genes causing foreshortened limbs in Dachshunds. Although this breed has an achondroplasia-like phenotype, thus far the causative mutation has not been identified in the FGRF3 (fibroblast growth factor receptor) gene in dogs, although it has in humans (Martinez et al. 2000). We find a large sweep region in the vicinity of the FGRF3 gene, suggesting that the mutation in dogs is in a gene or regulatory region closely linked to FGRF3. Our results demonstrate the utility of selective sweep mapping in dogs and suggest a novel approach to finding genes of large phenotypic effect in dogs and other domestic species.

Results

Simulations

We used coalescent simulations with population splitting, bottlenecks, and growth to assess the Type I (false-positive) error rates of genomic scans for identifying selective sweeps using microsatellites or other hypervariable markers. The rationale is that if linked markers are commonly homozygous by chance alone, then their discovery in a genomic scan for a selective sweep may represent a false positive. Our first goal was to assess the frequency that linked markers are homozygous in a breed by chance given the density and variability of markers and the time since breed origin (Figs. 1, 2; Supplemental Figs. S1-S3). We compared four homozygosity statistics: 1) Z₁, the proportion of markers that are homozygous in at least one breed; 2) Z₂, the proportion of adjacent markers that are homozygous in at least one breed; 3) Z₃, the proportion of adjacent triplets of markers that are homozygous in at least one breed; and 4) Z_2/3, the proportion of triplets in which two markers are homozygous and separated by one that is variable. Although a run of invariant markers may appear to be an ad hoc choice of statistic, its usefulness comes from being an efficient summary of the local spatial pattern of heterozygosity. Similarly, strong divergent selection on a phenotypic trait in one breed will result in allele frequency differentiation in the markers linked to the gene under selection (Hartl and Clark 1997). In our coalescent simulations, we assess genetic differentiation based on F_ST as a function of time since breed origination (τ) and marker variability (θ). If F_ST is commonly much larger than the mean value in single or adjacent markers, then the Type I error rate may be unacceptable for genomic scans to search for selective sweeps. We consider here six statistics: the probability that one marker (Y₁) or two (Y₂) and three (Y₃) adjacent markers have F_ST >25% and 50% of the mean value (denoted by subscripts in Fig. 2 and Supplemental Fig. S3). In order to assess the effects of bottleneck size, growth rate after a bottleneck, number of surveyed populations, marker density, and number of individuals per breed sampled, we undertook 500,000 coalescent simulations with parameters chosen at random as described in the Methods section. All of our simulations also take into account the ascertainment bias of using only markers that are found to be variable in at least one surveyed subpopulation.

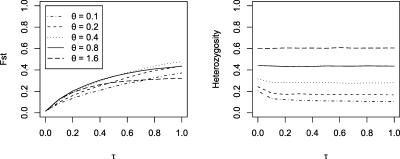
Figure 1.

Effects of time since breed formation on F_ST and observed marker heterozygosity. Expected levels of marker heterozygosity under the infinite-alleles model (E(H) = θ/(1 + θ)); (gray lines). Observed heterozygosity after conditioning on markers showing variability among breeds (black lines).

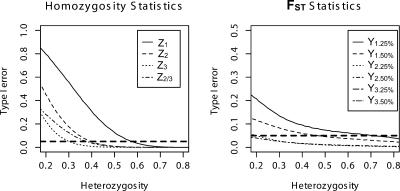
Figure 2.

Effect of heterozygosity on Type I error of all statistics considered in this study across 500,000 simulated replicate data sets. Simulations simultaneously varied time since breed formation, number of breeds compared, number of chromosomes sampled per breed, extent of bottleneck, duration of bottleneck, marker variability and density, and size of ancestral population.

Supplemental Figure S1 depicts nine typical patterns of genomic variation for the case of 50 markers per chromosome spaced at a density of 1 cM/marker, infinite-alleles mutation at each marker locus (with mutation rate varying among panels in the figure from θ = 0.2 to θ = 0.8 per marker), and breed formation times ranging from t = 0.1 to t = 1 (in units of 4N_e generations where N_e is the effective population size). The nine panels are arranged from left to right such that marker variability is decreasing, and from top to bottom such that time since breed formation is decreasing. In this figure, K represents the average number of alleles for the mutation/divergence combination, black dots are homozygous markers in at least one breed, and red squares are pairs of homozygous markers. These results suggest that the variance in heterozygosity across a chromosome depends weakly on time since splitting, and very strongly on marker mutation rate. The reason for the strong dependence on mutation rate is that decreasing marker variability leads to an increase in the rate of correlated homozygosity along the chromosome.

This result is most clearly seen in Figure 1, where we report the relationship between time since breed formation and mutation rate on heterozygosity and F_ST of typed markers. Expected heterozygosity under the infinite-alleles model in a panmictic population is also reported in dashed lines for different mutation rates. As expected, F_ST and K (results not shown) increase monotonically with time since breed formation, but at different rates depending on marker mutation rate. Likewise, we note that time since breed formation affects the variability of typed markers, but only for markers with low mutation rate. The reason for this result is that we condition our simulations on using only markers that are found to be variable among breeds, as in a typical empirical survey. Therefore, marker loci that are invariant in our sample of typed individuals are excluded in the analysis in Figure 1. Clearly, the rate of marker exclusion decreases with time since breed formation for low mutation rate markers, but not for high mutation rate markers. These results highlight the importance of choosing highly variable markers for selective sweep mapping, even if these markers are less densely spaced along the chromosome. For highly variable markers, even substantial population differentiation does not lead to a preponderance of double homozygous markers along the chromosome.

In Supplemental Figure S2, we present the Type I error rate as a function of t for Z₁, Z₂, Z₃, and Z_2/3 under an approximate 1 cM per marker spacing density, a scaled growth rate of 1, a sample of 50 chromosomes per breed, four breeds in the analysis, and varying mutation rate. This figure shows that the fraction of two or three adjacent markers that are homozygous is <5% as long as the scaled mutation rate (θ) is greater than 0.8 per marker (corresponding to an average heterozygosity of 44.4% and K = 5.01 alleles per marker locus, via the Ewens sampling formula [Hartl and Clark 1997]). Our simulations also show that the values of Z₁, Z₂, Z₃, and Z_2/3 are most strongly affected by the marker mutation rate (Supplemental Fig. S2). Except in the case of very little population differentiation and high marker variability, Z₁ has a Type I error rate >5%. In the case of high differentiation (t = 1.0) and low variability (θ < 0.1 per marker locus), the Type I error rate for Z₁ can reach as high as 95%. However, the error rates of Z₂, Z₃, and Z_2/3 are much lower and generally <5% as long as θ is >0.4 per marker. Only in the case of high differentiation and low variability are adjacent markers invariant with >5% frequency (Supplemental Fig. S2).

The simulation results also suggest that differentiation, as measured by F_ST, is rarely >25% or 50% above the mean value for the case of two or three adjacent markers as long as the markers are hypervariable (Supplemental Fig. S3). The probability that adjacent highly variable markers have high F_ST relative to the mean does not seem to vary greatly with time (except to increase slightly for low variability markers and decrease slightly for high variability markers). Similarly, the magnitude and variance of F_ST along a chromosome clearly increases with time since breed formation as expected given drift and recombination (Fig. 1). Average F_ST in dogs is ∼30% (Parker et al. 2004); this corresponds roughly to a time between t = 0.4 and t = 0.8 generations in our model. This indicates that the few pairs (<5%) of adjacent markers should exhibit F_ST values >45% (corresponding to the Y_2.50% statistic in Supplemental Fig. S3). Likewise, very few triplets of adjacent markers (<1%) should have F_ST >45%.

In order to assess the relative robustness of these analyses, we simulated 500,000 random coalescent data sets with 50 markers per chromosome under a model of population splitting, bottleneck of daughter populations, and recovery (growth) to population size some fraction f smaller than the original parental population. We varied many parameters simultaneously: number of breeds compared (m = 2-7, uniformly); chromosomes sampled per breed (10-60 uniformly in steps of 10); mutation rate per marker (θ = 0.08 to 1.8 on a transformed log scale); recombination rate between simulated (not necessarily typed) markers (ρ = 0 to 50 between markers, uniformly); time of breed formation (t_breed = 0.2 to 1.1 before the present in units of generations divided by four times the present-day effective population size); length of the bottleneck to form a breed (t_bott = 0.01 to 0.2); extent of bottlenecking (0.1 to 0.6 of present-day size); and size of ancestral population (one to three times bigger than present-day size, uniformly). We found that the single parameter governing the Type I error of our statistics was average heterozygosity at typed markers (Fig. 2). None of the other parameters had predictive power on Type I error once their effect on heterozygosity was regressed out (results not shown). As seen in Figure 2, all three homozygosity statistics and four F_ST statistics that compare at least two outlier markers have <5% Type I error across a 50-marker data set as long as the average heterozygosity of typed markers is >40%. This result is largely independent of the time since breed formation, extent of bottleneck size, rate of recovery, etc. Of course, these demographic parameters all affect the relative probability of typing markers that are ≥40% variable in the surveyed breeds, but conditional on having typed markers with at least this level of variability, the Type I error rates seem to be relatively well controlled. In conclusion, if highly variable markers are used, than either homozygosity or a large deviation in F_ST are reliable statistics for identifying selective sweeps in the canine genome. It should be noted that our simulations were carried out at a higher density than those used in the empirical studies below, indicating that our estimates of the Type I error rates are conservative (since tighter linkage in the simulations will increase the correlation among markers).

Selection and power

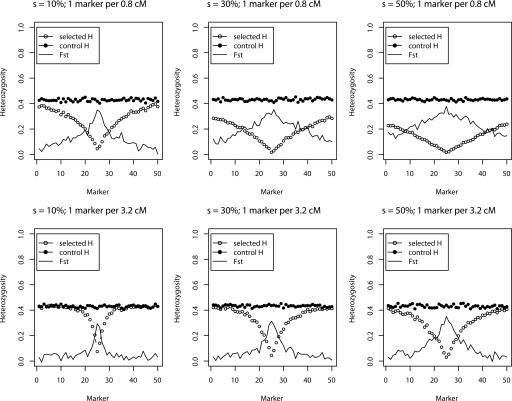
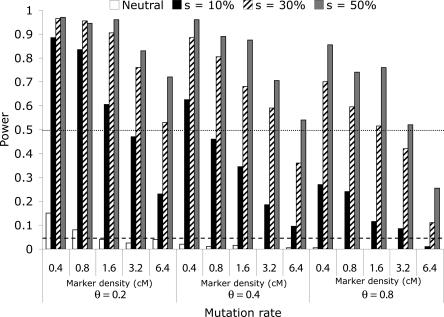
In order to address the power of our statistics to identify regions that have been targets of artificial selection, we undertook simulations with a single selected site embedded among a set of 50 markers, varying marker mutation rate, density, and strength of selection. Simulations were carried out using the program SelSIM, assuming a complete sweep in one dog breed that recently split from another (control) breed that did not contain the mutation, as well as equal sampling (n = 20) from each breed (details in Methods section). Patterns of heterozygosity were then compared between the control and selected breed. Figure 3 summarizes average heterozygosity and F_ST among 200 replicate data sets per parameter combination (selection ranging from 10%-50% for marker density of 0.8 cM and 3.2 cM between markers, assuming an effective population size of 100 for each breed). This figure shows that the result of a selective sweep is to greatly reduce variation at markers linked to the target of selection, and that the extent of the reduction depends on the strength of selection, original marker variability, and marker density. Likewise, expected F_ST is highest at the target of selection. In Figure 4, we summarize the power of the homozygosity statistics with varying recombination, selection, and mutation parameters. A data set was coded as successfully recovering the signal of a sweep if at least two invariant markers were adjacent to or contained the selected site (which was assumed not to have been typed). This design corresponds to using the Z₂ statistic (or better). We note that we have excellent power to identify the presence of artificial selection using this approach. In the control breed, none of the parameter combinations presented had a Type I error of >5% (i.e., <10 data sets per parameter combination in the control breed elicited a signal of a sweep based on at least two homozygous markers adjacent to or containing the known target of selection). Also note that a “neutral” sweep (i.e., a site that is invariant in one breed but not the other) does not leave a characteristic pattern that could be confused with a sweep except in the case of the highest marker density for the least variable markers. Even then, the vast majority of rejections of the “no-sweep” model are due to actual rather than false sweeps.

Figure 3.

Simulation results summarizing the effect of selection on the average heterozygosity and F_ST among 200 replicate data sets per parameter combination (selection ranging from 10%-50% for marker density of 0.8 cM and 3.2 cM spacing between markers).

Figure 4.

Summary of the power of the homozygosity statistics with varying values of recombination, selection, and mutation.

We note that our use of a partial selective sweep in a panmictic population to model selection in one breed and not in the control breed is only an approximation to the actual situation. Because most breeds share very recent common ancestry, this approximation should be reasonable. For more divergent populations (for example at the species level), this approach is likely inappropriate.

Size of the selective sweep in Large Munsterlanders

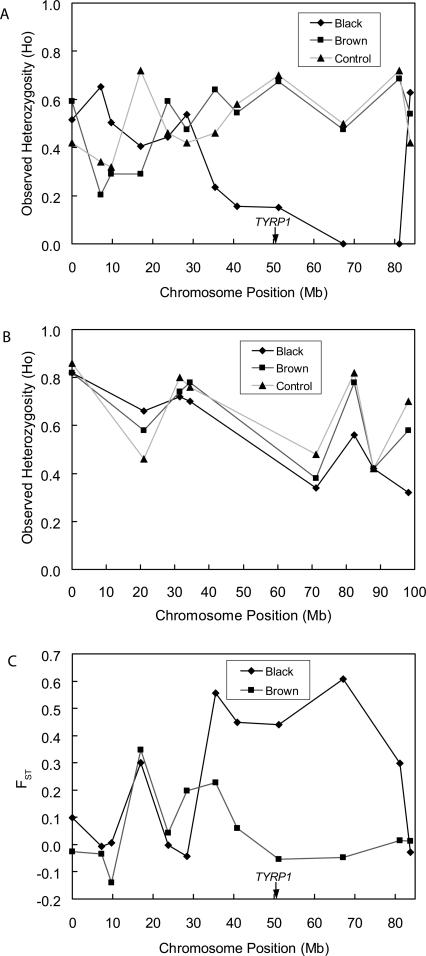
Large Munsterlanders are a recently formed dog breed, originating about 1910 from a pool of black and brown dogs (Schmutz 1992). This pool was selectively bred as two distinct breeds: the Large Munsterlander (black coat color) and the German Longhair (brown coat color). A recent study by Schmutz et al. (2002) examined TYRP1 and MC1R (melanocortin 1 receptor) gene sequence variations and their correlation with coat color in brown (including brown and white) and black (including tricolor, black and tan, and black and white) coat color dogs. They observed that wild-type alleles at both TYRP1 and MC1R correlated with black coat color. In contrast, brown coat color dogs demonstrated one of three mutations: a homozygote or compound heterozygote premature stop codon, amino acid deletion, or amino acid change in TYRP1 (Supplemental Table S2). Consequently, because a single allele at the TYRP1 locus is responsible for the black phenotype, evidence of a selective sweep is expected at TYRP1 for Large Munsterlanders. The TYRP1 gene has been mapped to chromosome 11 by linkage (Schmutz et al. 2002) and by RH mapping by Lorentzen and Ostrander (pers. comm.; chromosomal position shown in Guyon et al. [2003]). We surveyed 12 markers spanning ∼70 Mb on chromosome 11 and, as a control, eight markers on chromosome 5 in a panel of black, brown, and control (no black or brown) dogs, consisting of dogs from the Schmutz et al. (2002) study and additional pedigreed Large Munsterlanders and German Longhairs. As shown in Figure 5A, we observed a region of low heterozygosity (H_o = 0 to 0.14) spanning 40 Mb in Large Munsterlanders as defined by five microsatellite loci. In contrast, heterozygosity outside this region was high in both Large Munsterlanders and the German Longhairs (H = 0.4 to 0.7) despite their recent history of selective breeding. Overall heterozygosity was similar to that observed in the control breeds and on chromosome 5 (Fig. 5B). None of the other surveyed loci had heterozygosity levels <0.3, whereas two of five loci in the sweep region have no heterozygosity, and three have heterozygosity values of 0.2. The low-heterozygosity region is approximately centered on the TYRP1 gene location. In our simulation we find that the average Type I error for all data sets with average heterozygosity in the range of H = 0.4 to 0.7 is <0.009 for the Z₂ statistic and 0.001 for the Z₃ statistic irrespective of time since breed formation. Consequently, these results support the predictions from our simulations and the use of selective sweep mapping even in recently originated breeds.

Figure 5.

Microsatellite marker heterozygosity (A,B) and F_ST (C) values for the Large Munsterlander (Black), German Longhair (Brown), and control breeds. (A) Heterozygosity for markers on chromosome 11, the location of the TYRP1 gene, (B) heterozygosity for markers on control chromosome 5, (C) F_ST values for markers on chromosome 11.

Theory predicts that divergent selection should lead to allele frequency differentiation in the region bounding the gene under selection (e.g., Lewontin and Krakauer 1975; Robertson 1975; McDonald 1994; Taylor et al. 1995; Kohn et al. 2000; 2003). Therefore, we measured allele frequency differentiation between Large Munsterlanders, German Longhairs, and the control breed (Fig. 5C). We found relatively strong allelic differentiation as measured by F_ST between Large Munsterlanders and control breeds compared with F_ST values between brown and control breeds. The differentiation is due to the high frequency of otherwise rare alleles in Large Munsterlanders and reflects the limited haplotype diversity associated with the origin mutation. For example, marker REN89J24 has allele A at frequency 0.9 in Large Munsterlanders, whereas it has frequency 0.2 and 0.1 in the brown breed and the control breeds, respectively. Similarly, marker REN245N06 has allele F at frequency 0.9 in Large Munsterlanders, whereas it has frequency 0.1 and 0.3 in the brown breed and the control breeds, respectively. The region defined by the high F_ST is the same as that defined by low heterozygosity, suggesting F_ST analysis may provide an effective tool for locating genes under selection. This result is consistent with other studies finding that divergent selection leads to divergent allele frequencies in markers associated with genes under selection (e.g., Kohn et al. 2003; Aguilar et al. 2004).

The genetic locus for achondroplasia in Dachshunds

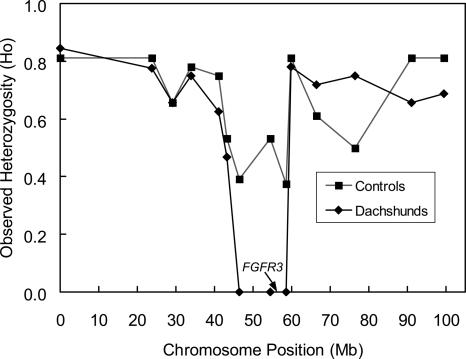
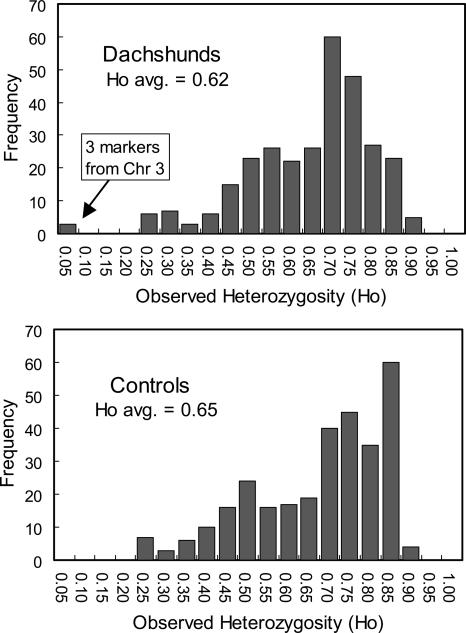
To identify the gene for foreshortened limbs in dogs, we typed 302 microsatellite markers in a panel of eight to 12 Dachshunds and four to 12 control non-afflicted dogs. The panel of Dachshunds was composed of four different lineages representing distinct outcrossing events to maximize background heterozygosity. The panel of framework markers was chosen from the 1-Mb RH map of 1596 microsatellite markers (Guyon et al. 2003), selected principally from the minimum marker set MSS-2, to represent all dog chromosomes with an average of spacing of about 10 Mb. In the entire set, we found only three microsatellite loci with a 15-Mb region on chromosome 3 to be monomorphic for our panel of Dachshunds and polymorphic for the non-afflicted dogs (Figs. 6, 7; Supplemental Fig. S4). The “sweep” region observed on chromosome 3 contained the FGFR3 gene (see Fig. 6). These results are consistent with the simulation given that the modern Dachshund breeds are of moderate age (origin <100 generations ago; American Kennel Club 1997) and were likely initiated with a small number of founders. Consequently, the fraction of homozygous triplets is predicted to be <5% (Supplemental Fig. S2). Pending confirmation with larger samples of dogs, these results implicate a gene or regulatory element closely associated with the FGFR3 gene as the cause of foreshortened limbs in Dachshunds. This finding mirrors the result of a recent Japanese study involving considerably more effort and using RH mapping to identify the locus responsible for achondroplasy in Japanese brown cattle. In this study, the FGFR3 gene did not cause achondroplasy; however, the causative gene was QTL mapped to the same chromosomal region as FGFR3 (Takami et al. 2002). In conclusion, these results clearly demonstrate that false positives (regions of very low heterozygosity due to chance) appear to be rare in the dog genome, at least in breeds of moderate heterozygosity whose phenotypes likely originated from a discrete mutation.

Figure 6.

Heterozygosity for markers on chromosome 3 for Dachshunds and control breeds. A low heterozygosity sweep region unique to Dachshunds and including the FGFR3 gene is found.

Figure 7.

Heterozygosity frequency distribution for 302 microsatellite markers in Dachshunds (top) and control breeds (bottom).

Discussion

Selective sweep mapping

A rich genomic toolkit has been developed for many domestic species, including dense genetic maps specifying the location of genetic markers such as microsatellite loci and single nucleotide polymorphisms (SNPs), as well as expressed genes (Waterston et al. 2002; Gibbs et al. 2004; Lindblad-Toh 2004; Murphy et al. 2004; Ostrander and Comstock 2004). However, the information is of limited use in identifying the specific genes that are under selection unless markers and genes can be associated with specific phenotypes. Similarly, in natural populations, the critical missing element in evolutionary studies is an understanding of the dynamics of genes that affect fitness. In model species that have been the object of genomic sequencing efforts, the search for genes under selection is advancing (e.g., Gilad et al. 2000; Bustamante et al. 2002; Fay et al. 2002; Harr et al. 2002; Sabeti et al. 2002; Clark et al. 2003; Bustamente et al. 2005). However, for the majority of plant and animals species for which little genomic or comparative mapping information is available, few tools are available to study adaptation at the molecular level and find genes under selection.

The approach widely used in model organisms is association mapping, in which a genomic scan of hundreds of marker loci is done for a large pedigree of afflicted and unaffiliated individuals (Lynch and Walsh 1998). Often little is known about the genomic location or number of loci involved in the trait. Alleles that are consistently associated with the phenotype of afflicted individuals, such as those associated with susceptibility to certain kinds of cancer (Jonasdottir et al. 2000), are presumed to be genetically linked to genes influencing the traits. These marker loci are most often chosen because they are highly polymorphic and their chromosomal location is known; thus, their identification can begin the process of localizing and mapping the genes underlying the studied traits. However, this approach generally requires extensive pedigrees and a well defined genetic map, is time-intensive, and cannot easily be applied to non-model organisms. Alternatively, candidate genes of known function can be identified that might be predicted to influence specific traits, such as hemoglobin proteins in Antarctic fish (Bargelloni et al. 1998), heat shock proteins in Drosophilia (Michalak et al. 2001), or fat deposit tendencies in cattle (Buchanan et al. 2002). However, candidate gene studies often represent educated guesses and may not be successful.

We suggest an additional approach applicable in any population experiencing divergent selection for specific traits (such as domestic plant and animal varieties). This approach involves searching for genomic regions of reduced variation and that are divergent in allele frequency. Areas of the genome under selection may have reduced levels of variation through the process of a selective sweep and hence be detected either as a reduction in the heterozygosity of linked sites or as an increase in the allele frequency variation of linked sites among populations experiencing divergent selection (e.g., Przeworski 2002; Schlotterer 2002; Fay and Wu 2003; Luikart et al. 2003; Clark et al. 2004; Storz 2005). The distortion in allele frequency spectrum will depend on the strength of selection, the recombination rate, time since the selection occurred, and gene flow (e.g., Stephan 1994; Charlesworth et al. 1997; Slatkin and Wiehe 1998; Barton 2000).

In this study, we determined the feasibility of the selective sweep approach for finding genes of large phenotypic effect in the dog. Our approach was to use simulations of breed formation and empirical data to test the power of a low-resolution genomic scan to identify genomic regions under selection, given the possibility of markers being homozygous by chance. We show across a myriad of demographic scenarios that simple heterozygosity and F_ST-based statistics across at least two adjacent markers have low experiment-wide Type I error when markers of high allelic variation are used. Consequently, the probability that two or three adjacent markers are homozygous by chance is generally low if breeds and markers are chosen with these characteristics. These random demographic simulations are obviously a simplification of actual histories. However, in all cases, we found that there was only a single reliable predictor of the Type I error of our statistics: the observed level of heterozygosity at the typed markers. We are cautiously optimistic that other demographic models should behave in a similar fashion with the observed heterozygosity as a determinant of the false-positive error rate.

Conversely, our analysis suggests that for ancient breeds a selective sweep approach may not be feasible, especially if markers of low mutation rate (such as SNPs) are used. However, despite this caveat, we find evidence for a 40-Mb selective sweep in the Large Munsterlander, a breed initiated only in 1910. This sweep is demonstrated by reduced levels of heterozygosity in the genomic neighborhood of the TYRP1 gene known to be responsible for black color, as well as high values of allele frequency divergence (F_ST). Background levels of variation appear to be high in the Large Munsterlander, as shown by marker analysis of another chromosome. However, our genomic survey of the Large Munsterlander was limited, and presumably other chromosomes may show areas of reduced variation that might confound identification of putative sweep regions in cases in which the chromosome location is not known. Consequently, we conduced a more extensive genomic scan using 302 microsatellite framework markers to identify a selective sweep caused by selection for foreshortened limbs in the Dachshund. We found a single region of reduced variation, and this locus contained promising candidate genes, including the gene causing achondroplasia in humans. Consequently, these simulations and preliminary empirical results support the notion that selective sweep mapping can be an effective tool to locate genes under selection.

The utility of the selective sweep approach can potentially be greatly enhanced by two additional elements to the study design. First, because some breeds share a similar phenotype, but have dramatically different breed histories, genomic scans of such breed groups (e.g., Supplemental Table S1) will reveal selective sweeps of differing genomic extent (assuming mutations in the same gene are responsible for the phenotype). For example, at least two other breeds share a similar phenotype with the Dachshund: the corgi and the basset hound. Further, there are different varieties of Dachshunds, such as the longhair and wirehaired varieties, which have different origination times, breeding histories, and effective population sizes. Consequently, if the same genes are responsible for the foreshortened limbs in all these forms, then a selective sweep of various sizes should be found in each variety and breed. Alignment of these sweep regions potentially will reveal an area of much narrower scope containing the gene under selection and facilitating fine-scale mapping and testing of specific candidate genes. Secondly, haplotype analysis of these different breeds in the area of the selective sweep may allow the exact location of the causative mutation to be found.

The genetic locus for achondroplasia

The condition of foreshortened limbs caused by the premature cessation of cell division in the cartilaginous growth plates of endochrondral bone is commonly designated as achondroplasia (Passos-Bueno et al. 1999). The spontaneous achondroplasia phenotype has been observed in a wide variety of domestic and wild vertebrates in addition to humans (Moritomo et al. 1989; Bugalia et al. 1990; Martinez et al. 2000). In humans, this condition is caused by any one of four missense mutations in the FGFR3 (fibroblast growth factor receptor) gene (Passos-Bueno et al. 1999). The severity of the disease differs for each of the missense mutations (Naski et al. 1996). The disease has one of the highest mutation rates observed in humans, as one in 20,000 humans is afflicted. FGFR3 is a negative regulator of endochondral ossification, and thus achondroplasia mutations activate tyrosine kinase activity, causing the suppression of long bone growth. A recent study by Beever et al. (2006, Accession no. AY737276) of sheep has identified a single base change in FGFR3 that correlates with hereditary chondrodysplasia. However, extensive studies examining FGFR3 in dogs and cattle (Usha et al. 1997; Martinez et al. 2000; Takami et al. 2002) have not found missense mutations in the coding region of FGFR3, suggesting the action of a regulatory region or another gene. For example, recent research on Japanese Brown Cattle exhibiting achondroplastic phenotypes (Takami et al. 2002) showed an absence of missense mutations in FGFR3, but linkage mapping indicated that the achondroplasy locus was near FGFR3. Our results likewise found that the mutation responsible for achondroplasia in dogs likely resides in a 10-Mb region centered near the FGRF3 gene. This suggests that in domestic mammals either the genes or regulatory elements causing achondroplasia are distinct from those causing the condition in humans.

To further identify the causative mutation for achondroplasia and verify our preliminary results, we currently are utilizing additional microsatellite loci and SNPs to narrow the sweep region, as well as examining candidate genes in afflicted and non-afflicted breeds. For example, examination of the human and mouse syntenic regions encompassing FGFR3 provides a possible candidate gene, FGFRL1, that we are currently attempting to sequence to identify potential causative mutations. Finally, fine-scale mapping of the sweep region in other breeds with foreshortened limbs (e.g., full-size vs. miniature, longhair, wirehair, red-hair Dachshunds) as well as other achondroplasic breeds (e.g., corgi and basset hound), may allow us to identify the causative mutation(s) through association and haplotype analysis.

Conclusions

We show through simulation of dog breed origin and expansion that the rate of false positives is generally low if highly variable markers are used to scan dog breeds, irrespective of breed age, as long as the target breeds show marker variability >40%. In general, the fraction of two or three adjacent markers that is homozygous or >50% above the mean value of F_ST is <5% in the simulations, suggesting that regions of low heterozygosity will only rarely be due to chance. Our empirical results support the predictions of these simulations. The TYRP1 gene responsible for black color in Large Munsterlanders has two linked and adjacent monomorphic microsatellite markers as well as three others having variation below background. Similarly, a more extensive scan of the Dachshund showed a single 10-Mb region of low heterozygosity near the FGRF3 gene, a genomic locus implicated in human and cattle achondroplasia. Analysis of this region in other achondroplasic dog breeds will potentially further reduce the genomic scope of the region containing the causative mutation. Our approach does not require extensive pedigree construction and takes advantage of the unique breed structure of dogs, in which discrete phenotypes are segregated into distinct lines that likely originated from a limited subset of founders. However, the selective mapping approach might apply to any domestic and wild population experiencing divergent natural selection in the absence of substantial gene flow (Berry et al. 1991; Begun and Aquadro 1992; Kohn et al. 2000; Schlotterer 2002; Vigouroux et al. 2002; Luikart et al. 2003; Storz 2005).

Methods

Simulations

In order to assess the Type I error of selection mapping in dogs, we performed extensive coalescent simulations with recombination and population substructure using the computer program ms (Hudson 2002). The model we investigated was a fusion with growth model such that at some point in time t in the past (scaled in units of 4N_e generations), m breeds are formed from a large population of constant size through a bottleneck of varying severity, and then each breed is allowed to grow to its current size without exchanging migrants with other breeds. We also considered a model in which breeds are created by the admixture of two previously separated populations and then allowed to grow exponentially. Surprisingly, patterns of F_ST and homozygosity along the chromosome did not differ dramatically between the two models. We present only results from the former model.

The parameters we varied among simulations included the density of markers; variability of markers; time, severity, and duration of the bottleneck, as well as of the split time (t); number of individuals sampled for each breed; number of breeds used to define variable markers; and size of the ancestral population relative to the current population. For all results presented here, we simulated a chromosome with 50 recombining regions (i.e., markers) that each evolve according to an infinite-alleles model. The population rate of recombination across the entire chromosome was ρ = 4N_er, and we considered values of 200, 400, and 800, corresponding roughly to marker densities of 1, 2, and 4 cM (assuming N_e = 100) between markers with 500 replicates per parameter combination. We considered two major sampling schemes of n = 25 and n = 50 individuals per breed. We used these values because we felt they represented typical sample sizes for a genomic scan, although the sample sizes used in our empirical studies are slightly smaller. Simulations were carried out holding the total number of mutations across the region constant among replicates and among demographic parameters, as well as holding the mutation rate constant. The reason for the former simulation was to keep the number of alleles roughly constant for a given mutation rate level as t was varied. We considered 100, 200, 400, and 800 mutations per chromosomal region for the entire coalescent history. In order to assess the unconditional Type I error rates, we also simulated data holding the mutation rate constant and allowing the number of segregating sites to vary with mutation rate θ. We considered five mutation rate levels (5, 10, 20, 40, and 80) for the entire genomic region that consisted only of marker DNA (Fig. 1, Supplemental Figs. S1-S3). In general, we were interested in comparing patterns of variation within and among m = 4 simulated breeds. Further, for Figure 2, we simultaneously varied a dozen parameters to insure the robustness of our simulations, as detailed in the Results section.

Summary statistics of interest included number of alleles per marker, average heterozygosity, and F_ST. We also studied the behavior of homozygosity along the chromosome via four statistics: Z₁, the fraction of markers that are homozygous in at least one breed; Z₂, the fraction of adjacent markers that are homozygous in at least one breed; Z₃, the fraction of adjacent triplets of markers that are homozygous in at least one breed; and Z_2/3, the fraction of triplets of markers where two markers found to be homozygous in one population are separated by a variable marker (Fig. 1). Similarly, for F_ST, we compute the average heterozygosity among the four breeds for each marker and the frequency of one marker, two adjacent markers, and three adjacent markers that are 25% and 50% greater than the mean F_ST.

To assess the power of the proposed homozygosity statistics, we simulated data under a partial selective sweep model with stochastic trajectory of the selected allele as implemented in SelSIM (Spencer and Coop 2005) that uses the algorithm of Coop and Griffiths (2004). The sampling scheme was 20 alleles that carry the selected mutation and 20 alleles that do not. If one breed was recently formed by selection of a mutation that arose in an ancestral population, the partial selective sweep ought to be a good approximation of the true process. The main assumption we are making is that the majority of neutral variation arose before the selected mutation, so that the family of alleles that carries the selected mutation contains a subsample of the neutral variation in the ancestral population. Additionally, the selective sweep model we employ assumes that the initial mutation is rare. If selection occurs on mutations that have reached appreciable frequencies in both control and selected breeds, our model will overestimate the signal of differentiation. We believe this problem is not substantial because most dog breeds were formed by the selective breeding of small numbers of individuals who shared a particular phenotype of interest to the exclusion of other potential founders.

In our simulations, recombination was allowed to occur across 200 points, 50 of which contain microsatellite markers. The rate of recombination (ρ = 4N_er) for the region was varied along the progression: 80, 160, 320, 640, and 1280. Assuming N_e = 100, this corresponds to a marker density ranging from 0.4 to 6.4 cM between markers. We considered mutations with selective effects of 0 (neutral), 10%, 30%, and 50% and marker variability in the ancestral population ranging from 0.2 to 0.8 with 200 replicates per combination of parameters. For these simulations, a step-wise mutation model was utilized for the evolution of the microsatellite markers. In Figure 3, we summarized average heterozygosity along the chromosome for the selected and control breeds typed at 50 markers under marker spacings of 0.8 cM and 3.2 cM between markers. In Figure 4, we summarize the power of the homozygosity statistics. A data set was considered to have positively identified the region of the sweep if at least two markers were invariant and either adjacent to or containing the selected mutation. Data simulated under the neutral scenario can be considered a conservative gauge of the Type I error of the method (that is, a mutation that is fixed but having taken a neutral trajectory in the history of the two breeds).

Size of the selective sweep in Large Munsterlanders

Our test panel consisted of five Large Munsterlanders from the Schmutz et al. (2002) study with seven additional pedigreed Large Munsterlanders for the black coat color panel, one German Longhair from Schmutz et al. (2002), four additional pedigreed German Longhairs for the brown coat color panel, and five control breed samples (not black or brown coat color), also from Schmutz et al. (2002). The TYRP1 gene position was linkage mapped to chromosome 11 (Schmutz et al. 2002) and RH mapped on chromosome 11 by Lorentzen and Ostrander (pers. comm.), and its position (50.1 Mb) is included in the 1-Mb map (Guyon et al. 2003). We scanned the chromosome with 12 microsatellite markers selected from the 1800 marker map (Breen et al. 2001) and the 1-Mb RH map (Guyon et al. 2003). The markers/chromosome 11 positions are: LE001—1.5 Mb, REN182P10— 15.0 Mb, REN174P22—20.1 Mb, REN245N06—27.2 Mb, CO2712—36.0 Mb, REN89J24—41.3 Mb, REN242K04—46.9 Mb, REN286P10—51.0 Mb, REN207M19—57.8 Mb, REN181F15— 63.1 Mb, REN161P13—65.1 Mb, and REN164B05—70.7Mb. We also scanned chromosome 5 with eight microsatellite markers selected from Breen et al. (2001): CPH14—0.5 Mb, REN68H12— 0.3 Mb, REN213E01—15.6 Mb, CPH18—26.4 Mb, REN192M20— 29.9 Mb, ZUBECA6—52.3 Mb, GLUT4—60.0 Mb, REN51I08— 65.2 Mb, and FH2594—80.2 Mb. The marker maps, specific location information, and primer sequences for the markers on each chromosome are available at the NHGRI Dog Genome Web site for the 1-Mb dog RH map http://research.nhgri.nih.gov/dog_genome/guyon2003/ (Guyon et al. 2003).

PCR reactions utilized either a fluorescent dye-labeled forward primer or a hybrid combination of forward primers consisting of the published forward primer with the M13F (–20) sequence (16 bp) added to the 5′ end and a fluorescent dye-labeled M13F (–20) primer (Boutin-Ganache et al. 2001). The unlabeled reverse primer was used in both cases. We used the PCR conditions for the hybrid combination primer (a two-step cycle). Primer dye labeling utilized ABI Prism fluorescent dyes, and PCR products were sized on an ABI 3700 capillary sequencer.

The genetic locus for achondroplasia in Dachshunds

To determine if selective sweeps in the dog genome would be obscured by false positives of low heterozygosity generated through chance events and to further test the general validity of the selective sweep approach, we selected 302 microsatellite loci to provide an average spacing of ∼10-Mb resolution and covering all 38 canid autosomes, largely based on the Minimum Marker Set 2 (MMS-2, Guyon et al. [2003]). This marker set and their positions are summarized on our Web site (http://www.eeb.ucla.edu/dogmarkerset/). We used a panel of Dachshunds and non-afflicted dogs for each marker. The Dachshund samples consisted of four to 10 individuals representing the shorthair, longhair, wirehair, and miniature shorthair breed varieties. These different varieties represent unique breeding histories, and were used to maximize background heterozygosity within the Dachshund sample set. The control sample set of dogs consisted of four breeds that were not afflicted with achondroplasy (Boxer, Golden Retriever, Beagle, Sheltie). PCR primer dye labeling, PCR reactions, and PCR product size determination utilized the same methods as described above.

Observed heterozygosity H_o for each marker was calculated according to Nei (1987). Pairwise F_ST values were calculated using FSTAT (http://www2.unil.ch/popgen/softwares/fstat.htm).