Abstract
This article considers the precision positioning problem associated with high-speed operation of the Atomic Force Microscope (AFM), and presents an inversion-based control approach to achieve precision positioning. Although AFMs have high (nanoscale) spatial resolution, a problem with current AFM systems is that they have low temporal resolution, i.e., AFM imaging is slow. In particular, current AFM imaging cannot be used to provide three-dimensional, time-lapse images of fast processes when imaging relatively-large, soft samples. For instance, current AFM imaging of living cells takes 1-2 minutes (per image frame) — such imaging speeds are too slow to study rapid biological processes that occur in seconds, e.g., to investigate the rapid movement of cells or the fast dehydration and denaturation of collagen. This inability, to rapidly image fast biological processes, motivates our current research to increase the operating speed of the AFM. We apply an inversion-based feedback/feedforward control approach to overcome positioning problems that limit the operating speed of current AFM systems. The efficacy of the method, to achieve high-speed AFM operation, is experimentally evaluated by applying it to image collagen samples.
1 Introduction
In this paper, we consider the precision positioning problem associated with high-speed operation of the Atomic Force Microscope (AFM) and present an inversion-based control approach to achieve precision positioning. It is noted that the nanoscale resolution of the AFM has made the AFM an attractive tool to image as well as to manipulate biological phenomena at the cellular and sub-cellular level (e.g., [1, 2, 3]). For example, AFM imaging can be used to investigate cellular function such as the migration of cells, and to study the mechanical properties of sub-cellular components such as collagen. Although AFM systems can image biological samples with high (nanoscale) spatial resolution, a problem with current AFM systems is that they have low temporal resolution. In particular, current AFM systems cannot provide three-dimensional, time-lapse images of fast processes when imaging relatively-large, soft samples. For instance, AFM imaging of living cells takes 1-2 minutes (per image frame) [4]. The resulting AFM images have substantial distortions if the sample properties change rapidly in time because the initial pixel of the image and the final pixel of the image are acquired at very different time instants (due to the low operating speed [1]). Therefore, current AFMs are too slow to study biological processes that occur in seconds such as the rapid movement of cells [4] or the fast dehydration and denaturation of collagen [5, 6]. This inability, to image fast biological processes, motivates our current research to increase the operating speed of the AFM. We apply an inversion-based control approach to overcome current positioning problems that limit the operating speed of AFM systems. The efficacy of the method, to achieve high-speed AFM operation, is experimentally evaluated by applying it to image collagen samples.
Precision positioning of the AFM-probe is critical to the investigation of biological samples using AFMs. For example, precision control of the distance between the AFM probe and the sample surface is needed to maintain the probe-sample force at very small values (e.g., less than 1nN [7, 8]) to prevent damage and distortion of soft biological samples such as cells [9, 10]. (The probe-sample force changes if the distance between the AFM probe and the sample surface changes.) Therefore, precision AFM-probe positioning is needed to control the applied forces during imaging of soft biological samples. Precision positioning is also needed to apply external perturbations (forces) at a specified location on a biological sample, e.g., to investigate the transmission of surface forces to the substrate during cell locomotion [3]. Moreover, the AFM-probe needs to be precisely positioned at specified locations over the sample when investigating spatial and temporal changes in a sample’s visco-elastic properties. Thus, precision positioning of the AFM-probe at a desired location over the sample surface is important when investigating and manipulating biological samples.
Precisely positioning the AFM-probe is challenging during high-speed operation due to movement-induced vibrations in the positioning system. Currently, AFM positioning systems use piezo-scanners to position the AFM-probe over the sample surface; both parallel to the sample surface (along the x and y axes) and perpendicular to the sample surface (z axis). Therefore, precision positioning of the AFM-probe over the sample surface requires precision positioning of the piezo-scanner. As a result, one of the main challenges, in precision positioning of the AFM-probe over the sample surface, is to compensate for positioning errors due to vibrations induced by the movement of the piezo-scanner. (Such movement-induced positioning errors are different from those caused by vibrations transmitted to the AFM from external sources; external-vibration-caused problems are relatively easy to address using vibration-isolation schemes [1].) In particular, the scanning movement of the piezo-scanner in the x axis tends to induce vibrations and cause positioning errors in the x, y and z axes. Errors in the x and y axes (parallel to the sample surface) results in image distortion and prevent manipulation of biological samples at the desired location. The image distortion can be corrected using post-processing of the image, such as re-plotting the image against the measured x and y positions; however, such an approach is not acceptable if the goal is to manipulate a sample at pre-specified locations. Positioning errors are also not acceptable in the z axis (perpendicular to the sample surface) because such errors cause a change in the tip-sample force — excessive forces cause sample damage. These adverse positioning errors caused by movement-induced vibrations become more significant during high-speed AFM operation [11] and limit the maximum operating speed of the AFM [12, 13]. In practice, the achievable AFM operating speed (scan frequency) in biological applications is substantially smaller (100 times smaller) than the smallest, resonant-vibrational frequency of the AFM’s piezo-scanner. Consequently, techniques are needed to reduce these movement-induced vibrations for achieving precision positioning of the AFM-probe during high-speed imaging and manipulation of biological samples.
High-bandwidth positioning in AFM can be achieved by using miniaturized or stiffened (plate-type) piezoactuators [14, 15]. The high bandwidth of the piezos implies that the piezo-scanner’s smallest, resonant-vibrational frequency is much higher than the desired scan frequencies. Therefore, the relatively-low-frequency scanning movement does not significantly excite the resonant vibrational modes of the scanner, and does not induce large vibrations in the AFM-probe’s position. Thus, piezo-scanners with substantially high bandwidth can achieve precision positioning during high-speed AFM operation; however, this approach requires the use of smaller (or stiffer) piezos that tend to have smaller positioning range. For example, high-bandwidth piezo-scanners has been used in Ref. [16] to enable AFM imaging at a high scan frequency of 1.25KHz, which resulted in an imaging time of 80 milliseconds per frame. However, the high-speed (80ms per frame) AFM imaging in Ref. [16] had a relatively small scan-area of 0.24μm × 0.24μm. This small scan area is not sufficient to image relatively-large features; for example, imaging of cell protrusions such as lamellipodia can require scan sizes in the order of 20μm (see, e.g., Refs. [17, 18]). Therefore, increasing the operating speed by using smaller (or stiffer) high-bandwidth piezos results in smaller scan size, which prevents AFM imaging of biological samples with relatively-large features — in this article, we attempt to increase the operating speed of the piezo without reducing the scan size of the piezo-scanner.
An alternate to using smaller piezos (for increasing operating speed) is to compensate for the adverse movement-induced vibrations by using control techniques. In this area, our research efforts have focused on the use of an inversion-based control approach to achieve high-speed scanning [12, 19, 20, 21]. In this approach, we model the positioning dynamics of the piezo-scanner and then invert it to find an input that achieves precise positioning of the AFM-probe; this inverse input is applied to the piezo-scanner as a feedforward input. The feedforward input can be used to account for positioning errors caused by predictable disturbances such as the scanning movement of the AFM-probe across the sample. Additionally, positioning errors due to unknown (unmodeled) disturbances can be accounted-for by integrating feedback controllers with the feedforward input [22, 23]. It is noted that the addition of the inverse input as feedforward can improve the tracking performance of any feedback controller — even in the presence of computational errors in the inverse input due to modeling uncertainties (the size of acceptable uncertainties has been quantified in Ref. [24]). The use of inverse feedforward to increase the bandwidth of piezo-scanners has been experimentally verified in, e.g., Refs. [12, 19, 20, 21].
An important issue in implementing the inversion-based approach is the computational complexity of modeling and inverting the nonlinear hysteresis behavior of the piezo-scanner. Positioning errors due to hysteresis effects become significant when the piezo-scanner is used to position the AFM probe over relatively-large areas, for example, when imaging biological samples with large features (such as cells). Previous works have used inversion-type approaches to account for such hysteresis effects (e.g., [12, 25, 26, 27]). For example, in Ref. [27], the inverse of the nonlinear hysteresis was modeled using polynomials. However, the polynomial-based model does not account for variations in the amplitude of the applied input; therefore, this approach cannot correct-for the hysteresis effects when the amplitude of the input is not constant. (Variations in the input amplitude are needed to precisely track a general output trajectory). These errors caused by variations in the input amplitude can be corrected by using more detailed Preisach models of the nonlinear input-to-output hysteresis in the piezo dynamics [25]; the inverse input is found in Ref. [25] by using an iterative method. Rather than first model the input-to-output hysteresis model and then second use an iterative method to find the inverse-hysteresis model [25], the inverse hysteresis was directly modeled using the Preisach approach in Ref. [12]. Experimental results in Ref. [12] show that the inverse input can effectively compensate for creep, hysteresis, and vibration effects in piezos, and thereby enable high-speed AFM operation. However, implementing such model-based inversion technique can be challenging because modeling the nonlinear hysteresis is time intensive, requires the identification of a large number of parameters, and might need to be repeated if the system parameters change due to piezo aging. Therefore, while the use of inverse feedforward leads to increased precision in piezo-scanner positioning, techniques are needed to reduce the complexity of computing the inverse feedforward input.
In this article, we account for hysteresis and vibrations in the AFM’s piezo-scanner by using a recently-developed decoupled approach that reduces the complexity of computing the inverse feedforward input [23]. In particular, (a) a high-gain feedback controller is used to compensate for hysteresis, and (b) the inverse feedforward input is used to compensate for vibrations. It is noted that the use of higher feedback-gain makes the closed-loop input-to-output gain (at any frequency) closer to one, i.e., the output of the system matches the desired-position waveform (that is applied as a reference input to the system). Therefore, high-gain feedback can improve the piezo-scanner’s ability to track a desired output (position) — provided the system is stable. However, there are limits to the maximum feedback gains that can be used in the AFM’s positioning system because piezo-scanners tend to have low gain margins, i.e., high-gain feedback tends to destabilize the piezo-scanner [28, 29]. The tendency to become unstable at high gains has limited the success of traditional AFM feedback techniques such as proportional, integral and derivative (PID) controllers. We enable the use of high-gain feedback by increasing the gain margin of the system using a notch-filter-based approach [30]). The resulting high-gain controller is used to correct for nonlinear hysteresis effects. The use of feedback to control hysteresis (and creep in the piezo [23]) implies that the inverse input only needs to account for vibrational effects, which can be done by modeling and inverting the system using linear models. Inversion of linear models is less computationally challenging than the inversion of nonlinear piezo-dynamics models (studied in [12]). Thus, the use of high-gain feedback (to correct for hysteresis effects) reduces the complexity of implementing the inversion-based approach. In this article, we show that the integration of inverse feedforward with high-gain feedback leads to substantial improvements in piezo-scanner positioning with the use of PID controllers (that are commonly used in current AFM systems). Although we show substantial improvement with a PID feedback controller, it is noted that the proposed inverse feedforward can be integrated with any feedback controller. Therefore, the performance of the inversion-based approach can be further improved if the inverse feedforward is integrated with more advanced feedback controllers such as the robust controllers developed in, e.g., [11, 31, 32, 33, 34]. The improvement in the positioning performance with the inversion-based approach and the resulting increase in AFM operating speed are verified using experimental results when imaging collagen samples.
2 System Description and Modeling
2.1 AFM Operation
A critical component of the AFM is the piezo-scanner which is used to spatially position and scan the AFM-probe relative to the sample surface as shown in Fig. 1(a). The piezo-scanner enables sample-relative positioning of the AFM probe both parallel to the sample surface (along the x and y-axis) and perpendicular to the sample surface (z-axis). The scanning motion of the piezo-scanner is depicted schematically in Fig. 1(b). The imaging process is initiated by gradually moving the sample close to the probe until a desired (nominal) probe-sample force (force between the AFM-probe and the sample) is reached and then scanning the AFM-probe across the sample. During AFM imaging, the effects of the probe-sample force is measured as the probe is scanned across the sample’s surface. In particular, the displacement of the AFM-probe (cantilever) is measured using an optical system — this displacement is proportional to the probe-sample force and is used to form an image of the sample topography, e.g., [35].
Figure 1.
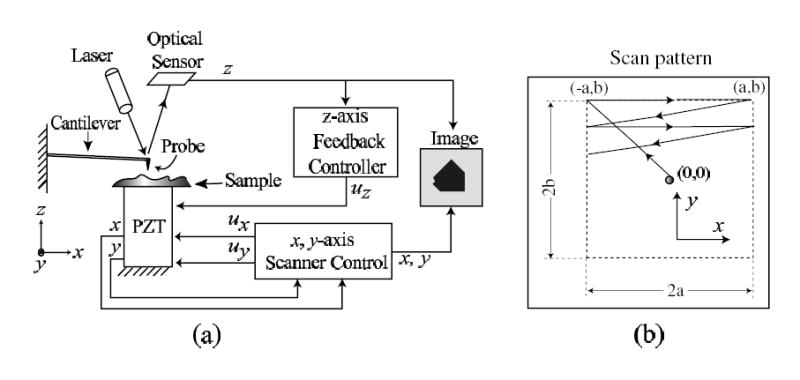
(a) Schematic of Atomic Force Microscope (AFM) and (b) scan trajectory.
In our experiments we first move the scanner from its nominal location (centered at (0, 0)) to the top-left position of the imaging area (−a, b) (as shown in Fig. 1b). Next, the sample is scanned through a rastering (back and forth) movement of the sample relative to the AFM-probe tip in the x-direction. This periodic scan pattern is divided into two portions: (a) the forward scan (from left-to-right) and (b) the return scan (from right-to-left). During the forward scan portion, the cantilever deflection is measured at a constant sampling rate and the y-position is held constant. Then the y-position is increased during the return scan while the cantilever deflection is not measured. This process of rastering along the x-direction and incrementing along the y-direction is repeated until the desired area is imaged. Finally, an image of the surface topology is obtained by plotting the measured cantilever displacement versus the desired x and y-position of the AFM probe — this mode of operation is called the constant-height contact mode (for other AFM modes of operation, see, e.g., [36]).
2.2 Positioning Problem Investigated in this Article
The inversion-based approach can be used to reduce the positioning errors caused by the movement of the piezo-scanner as it moves the sample relative to the AFM-probe. In general, movement along an axis of the piezo-scanner induces vibration-caused positioning errors in all three axis. For example, the scanning movement of the piezo-scanner in the x axis induces positioning errors in the same (x) axis ; additionally, coupling effects result in positioning errors in the other two axes (y and z). The proposed inversion-based approach is a general method that can be used to achieve precision control in multiple-input multiple-output systems (e.g., see Ref. [37]), and can therefore be used to account for positioning errors in all three axes (and to account for coupling effects). However, to illustrate the application of inversion-based approach to achieve precision high-speed positioning, we focus this article on the correction of vibration-caused positioning errors in the x axis.
In this article, we show that the inversion-based approach can be used to compensate for the main cause of movement-induced vibrations in the x axis — the scanning movement in the x axis. Coupling effects, such as vibration in the x axis due to the scanning movement in the y axis, tend to be less prominent. This is because the scan frequency in the y axis is Nl times smaller than the scan frequency in the x axis, where Nl × Nl is the number pixels in each image. Since the number of pixels along any row of the image, Nl, tends be 100 or more, the scan frequency in the y direction tends to be at least 100 times slower than the scan frequency in the x direction. This implies that the slower y axis movements do not cause significant positioning errors in the x axis. Similarly, induced vibrations in the x axis due to coupling effects from the z axis are not pronounced because the movement in the z axis tend to be small in magnitude (typically at least ten times smaller than the x movements). Therefore, the most prominent movement-induced vibration in AFM is caused in the x axis due to the scanning movement in the x direction. Although the inversion-based approach can be used to correct for movement-induced vibrations in all three axes, we focus this article on the reduction of the x axis positioning errors to illustrate the technique.
2.3 Modeling the AFM-scanner Dynamics
The linear dynamics model for the piezo-scanner on an AFM (Burleigh Metris 2000NC) was obtained by curve fitting the piezo-scanner’s measured frequency response that was measured using a dynamic signal analyzer (DSA, Stanford Research Systems Model SR785). A sinusoidal input voltage, u(t), generated by the DSA was applied to the piezo-scanner and the resulting lateral displacement of the scanner (in the x-direction) was measured by an optical sensor (which has a static gain of 18.9 μm/V). The resulting input-output frequency response is shown in Fig. 2.
Figure 2.
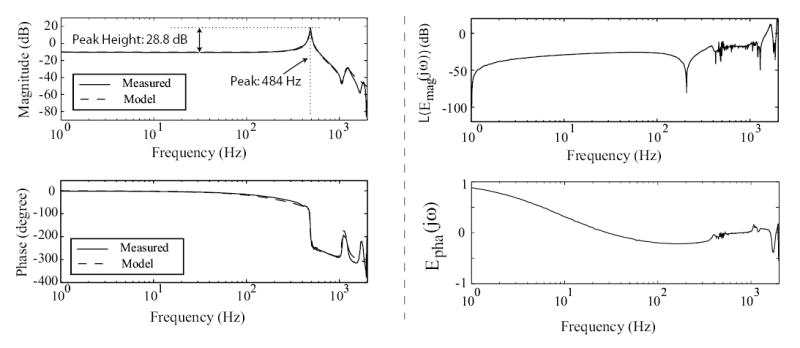
Bode plots of AFM system. The left column shows the measured frequency response Gmea;(jω) (solid line), along with the linear model obtained using curve fitting (dashed line). The right column shows the relative-magnitude error, with Emag(jω) given by Eq. (2), and the relative-phase error, Epha(jω) (Eq. (3)), between the measured frequency response and the model.
A linear dynamics model, represented as a transfer function in the Laplace domain, relating the input, u (in volts), to the sensor output, (in volts), was curve-fitted to the measured frequency response. The linear single-input single-output (SISO) model was found to be
| (1) |
where = 6.4056 × 1013, the zeros, z1, z2, are {−25 ± 1059j} Hz, and the poles, pn, are {−411, −5 ± 486j, −70 ± 1200j, −1200} Hz. The frequency response of the linear SISO model is compared with the measured frequency response in Fig. 2 (left column plots). To quantify the modeling error, we plot the relative modeling error in Fig. 2 (right column plots), where
| (2) |
| (3) |
The logarithm of the relative-magnitude error, L(Emag(jω)) = 20 * log10(Emag(jω)), is shown in the upper right plot of Fig. 2, and the relative-phase error, Epha(jω), is shown in the lower right plot of Fig. 2. It can be seen from Fig. 2 that the model is a good fit of the measured frequency response — for example, the magnitude error is less than 27% (L(Emag(jω)) = −11.4 dB) up to 1 kHz. Therefore, adding the model-based inverse input as a feedforward can improve the tracking performance of a feedback controller for positioning trajectories with frequency components up to 1 kHz, because the modeling error is less than the size of the model [24]. Finally, the dynamics model Gx(jω) relating the input voltage, u (in volts), to the actual piezo-scanner displacement x (in microns, μm) is
| (4) |
Remark 1
The frequency response reveals a sharp resonant peak (peak height equals to 28.8 dB, see Fig. 2) at 486 Hz which limits AFM-probe scanning to very low frequencies — typically 10 – 100 times lower than the first resonance frequency during high-precision applications. Therefore, open-loop scanning is limited to around 5 Hz for avoiding adverse vibration effects.
3 High-speed Scanning: Precision Control
High-speed positioning of the piezo-scanner is achieved by integrating feedback and feedforward control as shown in Fig. 3. Specifically, a high-gain feedback controller is used to reduce creep and hysteresis effects in the piezo-scanner. Additionally, feedback control provides robustness to modeling errors, and enables disturbance rejection. The feedback control is augmented with an inversion-based feedforward input to improve tracking performance during high-speed operations. In the following, we describe the design of the feedback and feedforward components in the controller.
Figure 3.
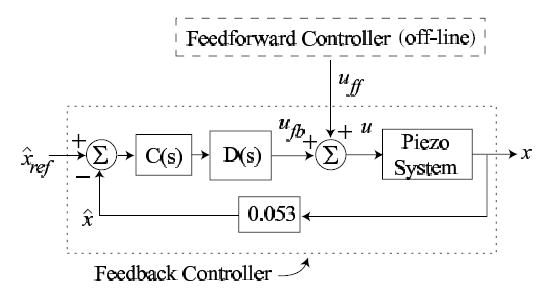
The control scheme for the piezo-scanner in the x-direction, where uff and ufb are the feedforward and feedback inputs, respectively; C(s) is the feedback controller; D(s) is the notch filter used to improve the gain margin; is the desired scan trajectory (scaled by the gain, 0.053, of the optical sensor); x is the actual piezo-scanner displacement in the x-direction; and is the output of the optical sensor.
3.1 High-gain Feedback Control
Low Gain-Margin of Piezo-Scanner System
Feedback control can substantially reduce positioning errors in piezo-scanners provided the feedback gain is sufficiently high. However, piezo-scanners have low structural damping, and as a result these systems have a sharp resonant peak in the frequency response where the magnitude response increases dramatically. For the piezo-scanner studied in this article, the magnitude response increases by 28 dB while the phase plummets by 180° (at the first vibrational resonance, see Fig. 2). Such sharp resonance peaks with rapid drop in phase results in low gain margins — the open loop gain margin of our piezo-scanner system is only −17.05 dB. This low gain margin implies that the feedback gain has to be small to ensure stability; low-gain feedback controllers do not yield sufficient precision when tracking a specified output (position) trajectory.
Use of Notch-Filter to Increase the Gain Margin
The gain margin of the system was increased by cascading a notch filter with the piezo-scanner system to remove the sharp resonant peak in open-loop frequency response. The notch filter was chosen as [23]:
| (5) |
where the gain is kD = 2.22, the zeros are z1,2 = −5 ± 475j (Hz), and the poles are p1 = −100(Hz), p2 = −5000 (Hz). The open-loop frequency response of the composite system, i.e, the notch filter D(s) cascaded with the piezo x-dynamics , shows a significant increase in the gain margin from −17.05 dB to 30.86 dB [23].
The PID Feedback Controller
A proportional-integral-derivative (PID) controller, which is traditionally used in AFM systems, was chosen as:
| (6) |
where the proportional gain is Kp = 20, the gain for the integral term is Ki = 1000, the (filter) pole for the integral term is pi = 0.1 (Hz), the gain for the derivative term is Kd = 6.56 × 10−3, the (filter) pole for the derivative term is σ = 5000 (Hz), and KC is the controller gain.
Tracking Performance Improvement with the High-gain Feedback
High-gain feedback can be used if the open-loop system has sufficient gain margin. The use of the notch-filter D(s) increases the gain margin of the composite system from −43.22 dB (without the notch filter, i.e., to 8.62 dB (with the notch filter, i.e., as shown in Fig. 4. Therefore, the allowable feedback gain (KC ≤ 2.70 ) with the notch filter is much higher than the allowable feedback gain (KC ≤ 0.0069) without the notch filter. The bode plots of the closed-loop system with the notch filter and feedback gain KC = 1 is compared with the closed-loop system without the notch filter and a relatively low feedback gain of KC = 0.00685 in Figure 4.
Figure 4.
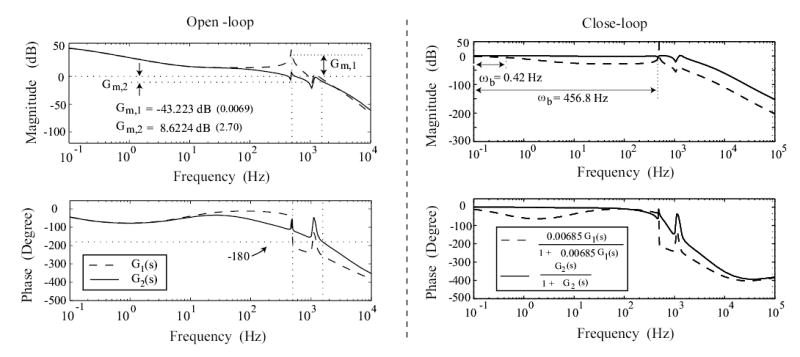
Bode-Plots: left column shows the open-loop bode-plots of the system without the notch filter (dashed line), and with the notch filter (solid line), where Gm,1 and Gm,2 are the gain-margin of these two cases respectively. Right column shows the closed-loop bode plot of the system without the notch filter (dashed line, KC = 0.00685), and with the notch filter (solid line, KC = 1), where ωb denotes the bandwidth of the corresponding system.
The use of high-gain feedback (KC = 1, with the notch filter) substantially improves the system’s tracking performance when compared with the low-gain-feedback case (KC = 0.00685, without the notch filter). In particular, use of high gain feedback moves the system’s DC gain closer to one (increases from 0.773 to 0.998) as shown in Figure 4, which implies that the desired position will be tracked more precisely. Moreover, the bandwidth (at which the closed-loop gain changes by 3 dB from the DC gain) increases from 0.46 Hz to 456.8 Hz, as shown in Figure 4, which implies that the higher-gain (KC = 1) feedback controller can track higher-frequency output trajectories. Additionally, such high-gain feedback controllers can also be used to compensate for positioning errors due to creep and hysteresis effects [23].
3.2 Inversion-based feedforward control
The inversion-based feedforward approach exploits the known dynamics of the AFM’s piezo-scanner to find inputs that reduce movement-induced positioning errors during high-speed operation. An input that achieves exact positioning without vibration-caused errors can be computed by inverting a model of the piezo-scanner dynamics as [38]:
| (7) |
where xd(jω) is the Fourier transform of the desired x-position trajectory (in time), Gx−1(jω) is the inverse of the piezo-scanner dynamics Gx(jω) in Eq. (4).
Optimal Inversion Scheme
Although the exact inversion-based approach (in Eq. (7)) compensates for movement-induced vibrations, a major drawback with the exact inversion approach is that the model needs to be known exactly to compute the inverse correctly. Additionally, the desired output (position) trajectory might require inputs that violate actuator limits such as bandwidth or available energy. To account for modeling uncertainties and actuator limitations, we use the optimal inversion approach, which minimizes the following cost functional [39]:
| (8) |
The resulting optimal inverse input uopt(jω) is given by
| (9) |
In Eqs. (8) and (9), ‘*’ denotes complex conjugate transpose, x(jω) − xd(jω) is the Fourier transform of the tracking error, and R(jω) and Q(jω) are frequency dependent weights on the input energy and tracking error, respectively. The weights R(jω) and Q(jω) are chosen to be nonnegative functions of jω, such that [R(jω) + G*(jω)Q(jω)G(jω)] > 0 for all ω ∈ ℝ. The corresponding optimal output trajectory xopt, is given by
| (10) |
which is applied to the control system (see Fig. 3) as the reference trajectory, i.e., .
Remark 2
The frequency-dependent weights R(jω) and Q(jω) can be used to account for modeling errors and input constraints. The optimal inversion technique gives a designer the ability to only invert the model in the frequency range where the dynamics is known accurately — the acceptable size of model uncertainty has been quantified in Ref. [24]. For example, choosing the input-energy weight R(jω) = 0 and the tracking-error weight Q(jω) = I for all ω ∈ ℝ, we obtain uopt(jω) = Gx −1(jω)xd(jω) = uinv(jω), i.e., the optimal inverse input becomes the exact inverse input. At frequencies where the uncertainty is large, the inversion-based feedforward input can be set to zero by choosing R(jω) = I and Q(jω) = 0 leading to uopt(jω) = 0. The above optimal inverse can be used to trade off the exact-output tracking requirement to achieve other goals like reduction of input and vibration control or to meet actuator bandwidth limitations as in Ref. [39]. Furthermore, the approach can be used to design output-tracking controllers for non-square systems [40].
Comparison with Input-Shaping
Another approach to reduce movement-induced vibrations is to use the input shaping technique [41, 42]. This approach requires prior knowledge of the input to the system; however, this method cannot be applied if the output trajectory is specified (and if the input is not known a-priori). In particular, for flexible structures such as AFM piezo-scanners, finding the system input for a desired output requires inversion of the system dynamics. The input has to be found before it can be redesigned. Thus, if an output-maneuver is being designed, then input-modification based approaches (like input-shaping) are not directly applicable. A resolution to this problem of unknown input is to: (a) choose a feedback-based tracking controller – the desired trajectory is now a known reference input to the closed-loop system; and then (b) redesign this reference input to the closed-loop system. However, such redesign depends on the choice of the feedback controller [43] because the controller optimization and trajectory redesign problems become coupled — this coupled optimization is still an open problem. In contrast, the problem of unknown input does not arise in the inversion-based approach, because the optimal-inversion technique allows the user to directly re-design the desired output trajectory. As part of the process, the method also finds the optimal inverse input uopt that exactly tracks the optimal output trajectory xopt.
4 Experiment: High-speed Imaging of Collagen
The optimal-inversion technique was applied to image a collagen (type I) sample. Imaging and tracking results, with and without the movement-induced-vibration compensation, are compared to quantify the efficacy of the proposed approach.
4.1 The need for high-speed imaging of collagen samples
High-speed AFM can be used to image rapid changes of structural and chemical properties of cellular components such as collagen. For example, high-speed AFM can enable the real-time investigation of collagen proteolysis [44], which is important in many physiological and pathological processes [45] because collagen is the main structural component of the extracellular matrix (ECM). Although current AFMs can be used to observe collagen proteolysis, the low temporal resolution of current AFMs limit these studies to relatively slow proteolysis reactions — the study of faster reactions requires an increase in AFM imaging speed [44]. Another application of the high-speed AFM is in the study of rapid dehydration of dentin collagen exposed by acid treatment [5]. The dehydration process plays a crucial role in dental clinical applications because surface structural changes (caused by water-loss) can significantly affect dentin bonding (e.g., [46]). Current AFMs enable the imaging of structural changes in dentin collagen before and after dehydration, however, at current imaging speeds, the AFM cannot be used to study the rapid dehydration process [5]. This interest in high-speed AFM imaging of collagen motivates the use of collagen samples in the following experiments.
4.2 Experimental Methods
Sample Preparation and Imaging Method
Glass chamber slides were coated with 50mg/ml of rat tail collagen I (BD Biosciences), incubated for at least 20 minutes at 37°C, blocked with 1% bovine serum albumin (BSA) for one hour, and then washed with phosphate-buffered saline (PBS). Images acquired with the AFM are presented for samples that were air dried for more than three days. Previous results indicate that low-stiffness AFM-probes can be used to image soft samples such as cells with sufficiently small probe-sample forces to avoid sample damage [7]). Such a low-stiffness AFM probe, with nominal stiffness of 0.03N/m (MikroMasch Inc), was used in our experiments to keep probe-sample forces small. Additionally, the smallest nominal AFM-probe deflection (which corresponds to the smallest nominal probe-sample force) that enables successful imaging without distortions was used — the smallest nominal AFM-probe deflection was found experimentally by comparatively evaluating the visual quality of images acquired at different nominal value of the AFM-probe deflection when operating in the constant-height, contact mode. Imaging was performed at different scan rates, with and without the inversion-based control approach, during which the actual x axis position of the piezo-scanner and the AFM-probe displacement were measured.
Positioning With and Without Dynamics Compensation
Two methods were applied to control the scanning of AFM in the x-direction: (a) control without compensating for the AFM scanner dynamics, and (b) control with dynamics compensation. The experimental output tracking and imaging results acquired with these two methods are used to illustrate (a) that dynamics affects both the AFM-probe positioning and imaging results as the scan frequency increases, and (b) that the proposed inversion-based feedback/feedforward technique can be applied to significantly increase the scanning speed. Next, the two methods are summarized.
-
Control without compensation of the piezo-dynamics (DC-Gain approach) In this approach, which is prevalent in current industrial AFM systems, the input u is chosen as the output of the system scaled by the DC-gain of the system, i.e.,
(11) where xopt(t) is the desired scanning trajectory and k is the DC-gain of the system. The DC-gain can be measured as the ratio of the output’s amplitude to the input’s amplitude (when the scan size and scan frequency are small). We note that the DC-gain of the system changes due to operating conditions and piezo aging effects. To account for such effects, we calibrate the DC-gain of the system at the start of each experiment and accordingly adjust the gain of the system ( in Eq. 1).
-
Inversion-based control that accounts for the piezo-scanner dynamics High scan frequencies can be achieved if the scanner dynamics is accounted for by using the inversion-based feedback/feedforward approach, where the control input applied to the piezo scanner is:
(12) as shown in Fig. 3.
Controller Implementation
The feedback input ufb(t) was obtained using an analog circuit (using operational amplifiers). The (optimal-inverse) feedforward input uff (t) was computed o²ine. To compute the optimal inverse, the desired output was tracked perfectly at low frequencies, i.e., the input energy weight was chosen as R(jω) = 0 and tracking error weight was chosen as Q(jω) = 1 for ω ≤ 650 * 2π rad/sec. At higher frequencies, we did not invert the system — we chose R(jω) = 1 and Q(jω) = 0. This frequency-dependent choice of weights R and Q enabled us to smooth the triangular output trajectory and thereby to avoid unwanted high-frequency components in the inverse input. The optimal input was computed offline using MATLAB 3 because the desired scan trajectory was known. It is noted that even when the desired trajectory is unknown, information from a previous scan line can be used to approximate the desired trajectory when finding the feedforward input [31]. Moreover, the optimal inverse can be implemented online if preview-information of the desired output is available [21].
4.3 Experimental Results and Discussion
4.3.1 Inversion-based Approach Enables High-speed AFM Imaging
The collagen images acquired in the experiments are shown in Figs. 5 and 6, where the images are presented by plotting the normalized AFM-probe deflection, at each sampled location (x, y). The normalized AFM-probe deflection is defined as
Figure 5.
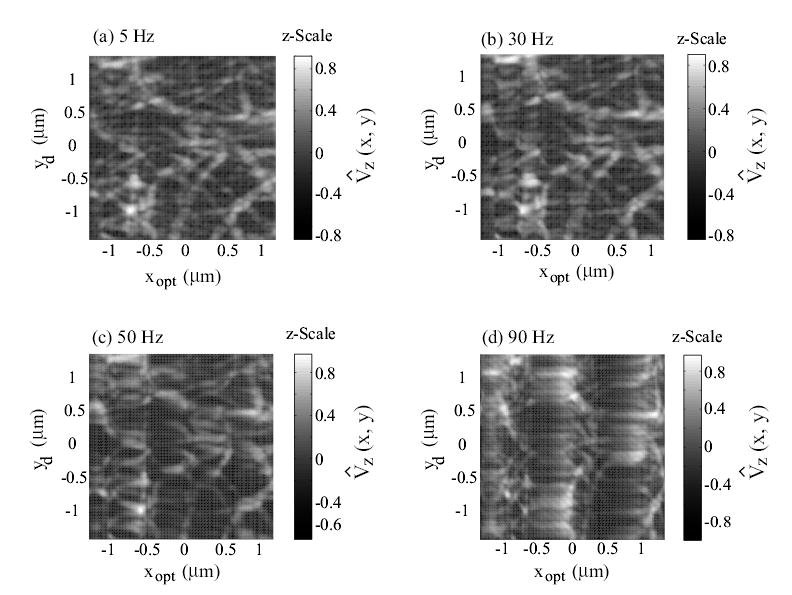
Experimental AFM images of collagen (type I) obtained when using the DC-Gain approach at scan frequencies of: (a) 5 Hz; (b) 30 Hz; (c) 50 Hz; and (d) 90 Hz. The scan size is 2.4 μm × 2.4 μm, and the z-Scale represents the normalized AFM-probe deflection, given by Eq. (13).
Figure 6.
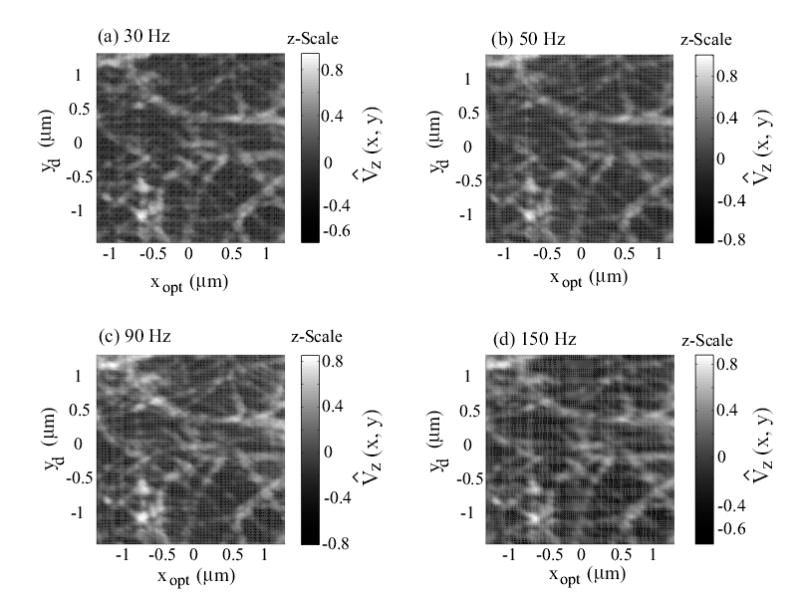
Experimental AFM images of collagen (type I) obtained when using the inversion-based feedback/feedforward approach at scan frequencies of: (a) 30 Hz; (b) 50 Hz; (c) 90 Hz; and (d) 150 Hz. The scan size is 2.4 μm × 2.4 μm, and the z-Scale represents the normalized AFM-probe deflection, given by Eq. (13).
| (13) |
where Vz(x, y) is the optical-sensor voltage output, which is proportional to the AFM-probe deflection and represents the topography of the collagen sample. In the above Eq. (13), the mean value and the absolute-maximum value maxx,y|Vz(x, y)| are computed across all the images in Figs. 5 and 6. As shown in plot (a) in Fig. 5, collagen fibrils can be clearly seen in the images obtained at slow scan frequency of 5 Hz. However, significant image distortions occur if the piezo-dynamics is not compensated for. For example, images acquired with the DC-Gain approach show increasing distortions as the scan frequency is increased; the collagen fibrils are twisted and elongated in the fast x-scanning direction, as shown in Fig. 5 (plots (b), (c), (d)). Such distortions, while relatively small at the lower scan frequency of 30Hz, become significant at 50Hz scan frequency. On the contrary, these image distortions do not appear when the collagen images are obtained with the inversion-based approach that accounts for the piezo-dynamics (Fig. 6). Note that the image acquired with the inversion-based approach even at 150Hz scan frequency (Fig. 6(d)) is similar to the image acquired with the DC-Gain method at the relatively low scan frequency of 5 Hz shown in Fig. 5(a). Therefore, the experimental images show that compensating for the piezo-dynamics enables high-speed AFM imaging. This increase in AFM operating speed is due to precision positioning of the AFM-probe at high scan frequencies. Next, we quantify the improvement in positioning precision and bandwidth with the inversion-based approach.
4.3.2 Inversion-based Approach Reduces Positioning Errors During High-speed Scanning
Quantifying Tracking Performance
To quantify the improvement in positioning precision and bandwidth with the inversion-based approach, we comparatively evaluated the experimental positioning results obtained at different scan frequencies (ωs equal to 5, 30, 90 and 150 Hz). The experimentally measured output (x) and the computed tracking error (ex)
are shown in Figs. 7 and 8 for the DC-Gain method and the inversion-based approach, respectively. The positioning performance was quantified in terms of the maximum tracking error emax(%) and the root-mean-square (RMS) error erms(%),
Figure 7.
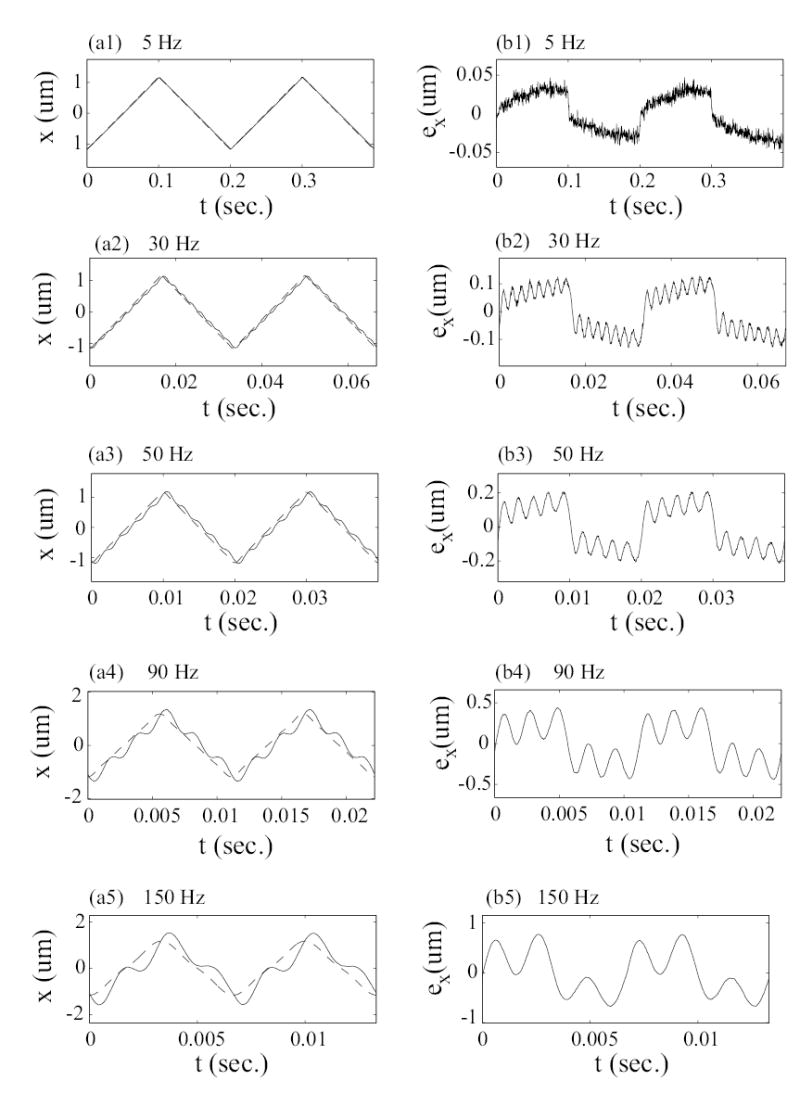
Experimental Results: Tracking performance with the DC-Gain approach. The x-axis position is shown in the left column and the positioning error is in the right column. In the left column plots, the solid line is the measured position x(t), and the dashed line is the optimal desired trajectory xopt(t).
Figure 8.
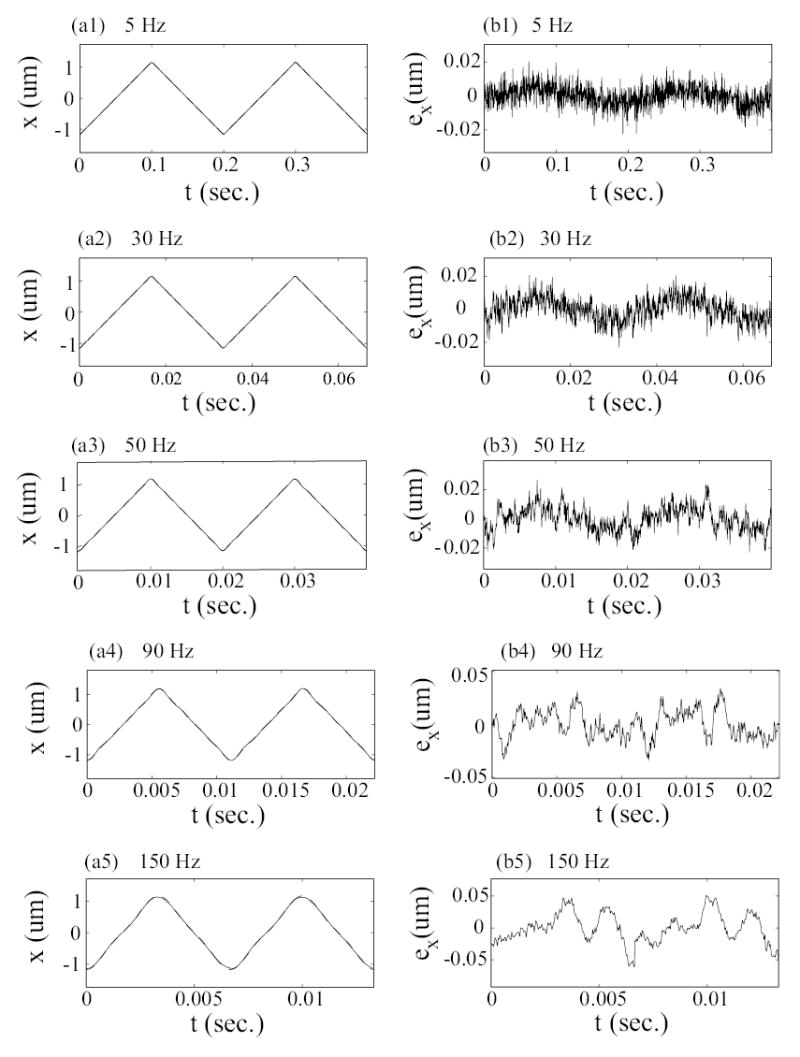
Experimental results: Tracking performance with the inversion-based approach. The x-axis position is shown in the left column and the positioning error is in the right column. In the left column plots, the solid line is the measured position x(t), and the dashed line is the optimal desired trajectory xopt(t).
| (14) |
| (15) |
where Ts = 1/[ωs(Hz)] denotes the scan period and Ax,opt denotes the peak-to-peak amplitude of the optimal desired trajectory. These tracking errors were computed for different scan frequencies and are presented in Table 1. Additionally, the positioning errors caused by exciting the piezo-scanner resonance was quantified by first expanding the tracking error ex(t) using the Fourier series as
Table 1.
Tracking Performance: ‘DC’ denotes the DC-Gain approach, ‘INV’ denotes the inversion-based feedback/feedforward approach. The error is quantified in terms of emax(%) and erms(%) defined in Eqs. (14, 15). Ex[ωs] and Ex[ωn] are tracking-error components at ωs and ωn, respectively (see Eq. (16)).
| emax (%) | erms (%) | Ex[ωs] (dB) | Ex[ωn] (dB) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Scan Rate ωs (Hz) | DC | INV | DC | INV | DC | INV | ωn(Hz) | DC | INV |
| 5 | 2.01 | 0.95 | 1.07 | 0.26 | −29.66 | −48.17 | 485 | −66.44 | −83.8 |
| 30 | 5.65 | 1.00 | 3.41 | 0.31 | −20.12 | −43.92 | 450 | −33.42 | −57.91 |
| 50 | 9.20 | 1.14 | 5.60 | 0.35 | −15.96 | −42.79 | 450 | −24.40 | −52.52 |
| 90 | 18.7 | 1.45 | 11.2 | 0.56 | −10.94 | −39.64 | 450 | −13.28 | −40.38 |
| 150 | 33.0 | 2.64 | 18.7 | 0.98 | −6.76 | −33.41 | 450 | −7.74 | −35.77 |
| (16) |
Second, the amplitude of the tracking error component Ex[ωn] for the frequency ωn closest to the resonance frequency (484 Hz) of the piezo-scanner was computed, and used as a measure to quantify the excitation of the piezo-scanner resonance. The results are presented in Table 1 along with the amplitude of the error-component Ex[ω1 = ωs] at the scan frequency (ωs).
Piezo-scanner Dynamics Causes Significant Positioning Errors During High-speed Scanning
Positioning errors become significant as the scan frequency increases with the use of the DC-gain approach (compare plots (b1) and (b5) in Fig. 7), In particular, the maximum positioning error emax increases from 2.01% to 33% as the scan frequency is increased from 5Hz to 150Hz (see Table 1). It is noted that the DC-gain approach does not account for piezo-scanner dynamics effects such as changes in amplitude gain and phase shift between the input and the output. These gain-change and phase-shift effects become large near the resonance frequency of the piezo-scanner dynamics and cause substantial tracking errors if the input has significant components near the resonance frequency. In particular, substantial tracking errors can be expected at the most significant frequency component of the triangular input that is closest to the piezo-scanner’s resonance frequency (484Hz). For example, the frequency component of the input that is close to the resonance frequency is 450Hz when the scan frequency is 30Hz or higher. (For a triangular scan trajectory, this is the odd harmonic of the scan frequency, ωs, that is closest to the resonance frequency.) As the scan frequency increases, the magnitude of the high-frequency component (at 450Hz) also increases, resulting in increased tracking errors as seen in Fig. 7, plots (b1)-(b5). It is noted that the frequency of the large oscillatory part of the tracking error (Fig. 7, plots (b2)-(b5)) is 450Hz and this component increases by more than 19 times from −33.42 dB to −7.74 dB as the scan frequency increases from 30 Hz to 150 Hz (see Table 1). Thus, the frequency-dependent amplitude gain and phase shift between the input and the output (due to piezo-scanner dynamics) cause substantial positioning errors, if they are not accounted for. These positioning errors can be as large as 33% of the desired scan size (see Table 1).
Inversion-based Approach Increases Positioning Precision and Bandwidth
Dynamics-caused positioning errors are substantially reduced by using the inversion-based approach, which accounts for the piezo-scanner dynamics. Note that at the relatively slow scan frequency of 5Hz, the amplitude of the output matches the amplitude of the desired optimal scan trajectory (because we calibrate the system’s DC gain). However, the error with the inversion-based approach (Fig. 8, plot (b1)) is still smaller (about 2 times smaller) than the error with the DC-gain approach (compare Fig. 8, plot (b1) with Fig. 7, plot (b1)). The error with the DC-gain approach is caused by a small phase shift between the input and output due to the piezo-scanner dynamics. While the error caused by the piezo-scanner dynamics is small at low frequencies, the errors become significant at high frequencies. For example, as the scan frequency was increased from 30 Hz to 150 Hz, the tracking-error’s component at the scan frequency, Ex[ωs], increased about 4.6-times (from −20.12 dB to −6.76 dB). In contrast the the tracking-error’s component at 450Hz increased much more — over 19 times, from −33.42 dB to −7.74 dB (see the 6th and 9th columns of Table 1). The inversion-based approach compensates for the high-frequency tracking errors; the error components at the lower scan frequency and at the higher 450 Hz are both substantially reduced. For example, at the scan frequency of 150 Hz, components of the tracking error (at both the scan frequency and at 450 Hz) are reduced by more than 20 times when compared with the results from the DC-gain approach (compare 6th and 7th columns with 9th, 10th columns in Table 1). Thus, the dynamics-caused positioning errors are substantially reduced with the use of inversion-based control approach; the maximum positioning errors are reduced by more than 16 times, from 33.0% (without dynamics compensation) to 2.64% at scan frequency of 150 Hz. Additionally, the inversion-based approach enables high-speed imaging (for the same acceptable precision in output tracking) because the positioning error (0.062 μm) at the high-scan frequency of 150Hz with the inversion-based approach is similar to the positioning error (0.077 μm) at the relatively lower 5Hz without dynamics compensation.
4.3.3 Hysteresis compensation for large scan size
The hysteresis-caused positioning errors, which become dominant for large scan size, can also be substantially reduced by using the inversion-based feedback/feedforward approach. To evaluate the reduction in hysteresis-caused positioning errors, we comparatively evaluated experimental positioning results for a large scan size of 32 μm, which is over 13-times larger than the scan size of 2.4 μm used to image the collagen. The experimental tracking results are shown in Fig. 9 and Table 2. Note that there are significant tracking errors even at the low scan frequency of 5Hz. This error is not caused by an error in the output amplitude; such error was removed by calibrating the DC-gain of the system and as seen in plot (a1) of Fig. 9, the tracking errors at the turn-arounds of the triangle scan signal are small. However, large tracking errors can be seen in the middle of two successive turn-arounds (in the desired output position). These large errors are caused by hysteresis in the piezo-scanner. By using the proposed inversion-based control method, such hysteresis-caused positioning errors are reduced by about 6-times (compare plot (b1) with plot (b2) in Fig. 9 and also see the 2th and 3rd columns of Table 2). As the scan frequency increases, the vibration caused errors are also added to the hysteresis-caused errors (see Fig. 9, plot (b3)).
Figure 9.
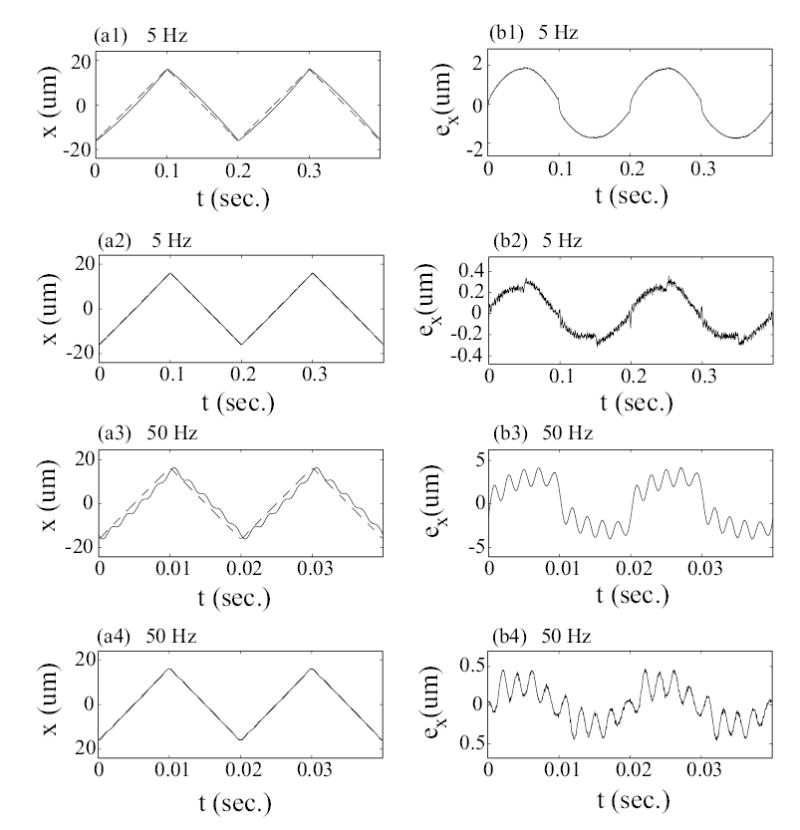
Experimental results for large-range scanning (32 μm). Left column compares the tracking by using the DC-Gain method at scan frequency of 5 Hz (plot (a1)) and 50 Hz (plot (a3)) with the tracking by using the inversion-based approach at scan frequency of 5 Hz (plot (a2)) and 50 Hz (plot (a4)) respectively, where the solid lines is the measured tracking results x(t) and the dashed lines are the optimal desired trajectories xopt(t). Right column shows the corresponding tracking errors.
Table 2.
Comparison of the tracking error for large-range scanning (32μm). DC denotes the DC-Gain method, INV denotes the proposed inversion-based approach, and emax(%) and erms are the maximum tracking error and RMS tracking error, respectively (see Eq. (15)).
| emax (%) | erms (%) | |||
|---|---|---|---|---|
| Scan Rate (Hz) | DC | INV | DC | INV |
| 5 | 5.9 | 1.12 | 4.25 | 0.60 |
| 30 | 9.0 | 1.14 | 6.20 | 0.64 |
| 50 | 13.1 | 1.46 | 8.30 | 0.73 |
| 90 | 25.5 | 3.51 | 15.2 | 1.73 |
| 150 | 43.1 | 3.36 | 23.8 | 1.67 |
The inversion-based feedback/feedforward method compensates for both hysteresis and vibration effects; in particular, the feedforward input compensates for the vibrational effects, while the modeling errors (including the unmodeled hysteresis effects) are compensated by the high-gain PID feedback controller. For example, the inversion-based feedback/feedforward method reduces the overall positioning errors to 1.46% for tracking a triangular desired output at 50Hz scan frequency and 32 μm scan size (see Table 2). This improvement in tracking precision (using the high-gain PID controller) compares well with the tracking performance achieved by using more advanced feedback controllers such as robust feedback control in [33], which achieved tracking with 1.6% error for a sinusoidal desired output at a scan frequency of 50 Hz and scan size of 19 μm. Thus, the experimental results show that the inversion-based feedback/feedforward method effectively compensates for both the linear vibrational dynamics and nonlinear-hysteresis effects of the piezo-scanner. Moreover, the inversion-based feedback/feedforward approach can be used to achieve high-speed high-precision positioning of AFM-probe when imaging relatively large features. This ability to image faster without reducing the scan size is important when imaging and manipulating biological samples such as living cell with large features [7].
5 Conclusion
This article addressed a critical need in the development of high-speed AFMs for imaging biological samples — the need to achieve precision AFM-probe positioning during high-speed operations. High-precision positioning was achieved by using an inversion-based feedback/feedforward technique to compensate for movement-induced errors in the piezo-scanner that is used to position the AFM probe. The method was applied for precision AFM-probe positioning when imaging collagen samples. The experimental results demonstrate the following three points: (a) substantial positioning errors are caused by piezo-scanner dynamics at high scan-frequencies; (b) piezo-scanner dynamics can be compensated for by using the inversion-based feedback/feedforward approach; (c) the feedback/feedforward approach can be used to reduce positioning errors when scanning at high scan frequencies without sacrificing the achievable scan size. The ability to increase positioning speed without reduction in scan size makes the approach suitable for fast AFM imaging of biological samples such as cells that have relatively large features. Our current efforts are aimed at extending this method to achieve precision high-speed positioning in all three axes of the AFM for enabling high-speed imaging of soft biological samples.
Footnotes
Support from NIH Grant GM68103 is gratefully acknowledged.
A MATLAB code for optimal inversion can be obtained by e-mail todevasia@u.washington.edu.
References
- 1.Shao Z, Mou J, Czajkowsky DM, Yang J, Yuan J-Y. Biological atomic force microscopy: What is achieved and what is needed. Advances in Physics. 1996;45(1):1–86. [Google Scholar]
- 2.Lal R, John SA. Biological applicaitions of atomic force microscopy. American Journal of Physiology. 1994;266:C1–C21. doi: 10.1152/ajpcell.1994.266.1.C1. [DOI] [PubMed] [Google Scholar]
- 3.Mathur AB, Truskey GA, Reichert WM. Atomic force and total internal reflection fluorescence microscopy for the study of force transmission in endothelial cells. Biophysical Journal. April 2000;78:1725–1735. doi: 10.1016/s0006-3495(00)76724-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rotsch C, Jacobson K, Radmacher M. Dimensional and mechanical dynamics of active and stable edges in motile fibroblasts investigated by using atomic force microscopy. Cell Biology. Proc Natl Acad Sci USA. Feb 1999;96:921–926. doi: 10.1073/pnas.96.3.921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.El Feninat F, Ellis TH, Sacher E, Stangel I. A tapping mode afm study of collapse and denaturation in dentinal collagen. Dental Materials. 2001;17:284–288. doi: 10.1016/s0109-5641(00)00083-x. [DOI] [PubMed] [Google Scholar]
- 6.Marshall GW, Wu-Magidi IC, Watanabe LG, Inai N, Balooch M, Kinney JH, Marshall SJ. Effect of citric acid concentration on dentin demineralization, dehydration, and rehydration: Atomic force microscopy study. Journal of Biomedical Material Research. 1998;42:500–507. doi: 10.1002/(sici)1097-4636(19981215)42:4<500::aid-jbm4>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 7.Le Grimellec C, Lesniewska E, Giocondi MC, Finot E, Vie V, Goudonnet JP. Imaging of the surface of living cells by low-force contact-mode atomic force microscopy. Biophysical Journal. Aug 1998;75:695–703. doi: 10.1016/S0006-3495(98)77559-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Viani MB, Schaffer TE, Chand Ami, Rief M, Gaub HE, Hansma PK. Small cantilever for force spectroscopy of single molecules. Journal of Applied Physics. 1999;86(4):2258–2262. [Google Scholar]
- 9.Radmacher M, Fritz M, Hansma PK. Imaging soft samples with atomic force microscope: Gelatin in water and propanol. Biophysical J. 1995;69:264–270. doi: 10.1016/S0006-3495(95)79897-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.You HX, Lau JM, Zhang S, Yu L. Atomic force microscopy imaging of living cells: a preliminary study of the disruptive effect of cantilever tip on cell morphology. Ultramicroscopy. 2000;82:297–305. doi: 10.1016/s0304-3991(99)00139-4. [DOI] [PubMed] [Google Scholar]
- 11.A. Daniele, S. Salapaka, M.V. Salapaka, and M. Dahleh. Piezoelectric scanners for atomic force microscopes: Design of lateral sensors, indentification and control. In Proceedings of the American Control Conference, pages 253–257, San Diego, CA, June 1999.
- 12.Croft D, Shedd G, Devasia S. Creep, hysteresis, and vibration compensation for piezoactuators: Atomic force microscopy application. ASME Journal of Dynamic Systems, Measurement and Control. March 2001;123(35):35–43. [Google Scholar]
- 13.N. Tamer and M. A. Dahleh. Feedback control of piezoelectric tube scanners. Proceedings of Control and Decision Conference, Lake Buena Vista, Florida, pages 1826–1831, 1994.
- 14.Koops R, Sawatzky GA. New scanning device for scanning tunneling microscope applications. Rev Sci Instrum. August 1992;63(8):4008–4009. [Google Scholar]
- 15.Sulchek T, Hsieh R, Adams JD, Minne SC, Quate CF, Adderton DM. High-speed atomic force microscopy in liquid. Rev of Scientific Instruments. May 2000;71(5):2097–2099. [Google Scholar]
- 16.Ando T, Kodera N, Takai E, Maruyama D, Saito K, Toda A. A high-speed atomic force microscope for studying biological macromolecules. Proceedings of the National Academy of Sciences of the USA. Oct 2001;98(22):12468–12472. doi: 10.1073/pnas.211400898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lehenkari PP, Charras GT, Nykanen A, Horton MA. Adapting atomic force microscopy for cell biology. Ultramicroscopy. 2000;82:289–295. doi: 10.1016/s0304-3991(99)00138-2. [DOI] [PubMed] [Google Scholar]
- 18.Abraham VC, Krishnamurthi V, Taylor DL, Lanni F. The actin-based nanomachine at the leading edge of migrating cells. Biophysical Journal. Sept 1999;77(3):1721–1732. doi: 10.1016/S0006-3495(99)77018-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Croft D, Devasia S. Vibration compensation for high speed scanning tunneling microscopy. Review of Scientific Instruments. Dec 1999;70(12):4600–4605. [Google Scholar]
- 20.Perez H, Zou Q, Devasia S. Design and control of optimal feedforward trajectories for scanners: Stm example. Proceedings of American Control Conference. 2002;3:2305–2312. [Google Scholar]
- 21.Q. Zou and S. Devasia. Preview-based optimal inversion for output tracking: Application to scanning tunneling microscopy. IEEE Trans. on Control Systems Technology. accepted.
- 22.Croft D, Devasia S. Hysteresis and vibration compensation for piezo actuators. AIAA Journal of Guidance, Control and Dynamics. SeptemberOctober 1998;21(5):710–717. [Google Scholar]
- 23.Leang KK, Devasia S. Hysteresis, creep, and vibration compensation for piezoactuators: Feedback and feedforward control. The 2nd IFAC Conference on Mechatronic Systems. 2002:283–289. [Google Scholar]
- 24.Devasia S. Should model-based inverse input be used as feedforward under plant uncertainty? IEEE Trans on Automatic Control. Nov 2002;47(11):1865–1871. [Google Scholar]
- 25.Ge P, Jouaneh M. Tracking control of a piezoceramic acuator. IEEE Trans on Control Systems Technology. May 1996;4(3):209–216. [Google Scholar]
- 26.Coleman BD, Hodgdon ML. A constitutive relation for rate-independent hysteresis in ferromagnetically soft material. Int J Eng Sci. 1986;24(6):897–919. [Google Scholar]
- 27.Holman AE, Scholte PMLO, Heerens Chr, Tunistra F. Analysis of piezo actuators in translation constructions. Review of Scientific Instruments. May 1995;66(5):3208–3215. [Google Scholar]
- 28.Barrett RC, Quate CF. Optical scan-correction system applied to atomatic force micropscopy. Review of Scientific Instruments. 1991;62:1393–1399. [Google Scholar]
- 29.Main JA, Garcia E. Piezoelectric stack actuators and control system design: Strategies and pitfalls. Journal of Guidance, Control, and Dynamics. MayJune 1997;20(3):479–485. [Google Scholar]
- 30.H. Numasato and M. Tomizuka. Setting control and performance of dual-actuator systems for hard disk drives. American Control Conference, pages 2779–2785, June 2001. Arlington, VA.
- 31.Schitter G, Stemmer A, Allgwer F. Robust 2d of-control of a piezoelectric tube scanner for high speed atomic force microscopy. American Control Conference, Denver, CO. 2003:3720–3725. [Google Scholar]
- 32.Salapaka S, Sebastian A, Cleveland JP, Salapaka MV. High bandwidth nano-positioner: A robust control approach. Review of Scientific Instruments. Sept 2002;73(9):3232–3241. [Google Scholar]
- 33.Tsai MS, Chen JS. Robust tracking control of a piezoacuator using a new approximate hysteresis model. ASME Journal of Dynamics Systems, Measurement and Control. March 2003;125:96–102. [Google Scholar]
- 34.Chang T, Sun X. Analysis and control of monolithic piezoelectric nano-actuator. IEEE Trans on Control Systems Technology. 2001;9(1):69–75. [Google Scholar]
- 35.Rugar D, Hansma P. Atomic force microscopy. Physics Today, October. 1990;43(10):23–30. [Google Scholar]
- 36.R. Wiesendanger, editor. Scanning Probe Microscopy and Spectroscopy. Cambridge University Press, 1994.
- 37.Devasia S, Chen D, Paden B. Nonlinear inversion-based output tracking. IEEE Trans on Automatic Control. 1996;41(7):930–942. [Google Scholar]
- 38.Bayo E. A finite-element approach to control the end-point motion of a single-link flexible robot. Journal of Robotic Systems. 1987;4(1):63–75. [Google Scholar]
- 39.Dewey JS, Leang KK, Devasia S. Experimental and theoretical results in output-trajectory redesign for flexible structures. ASME Journal of Dynamics Systems, Measurement and Control. Dec 1998;120:456–461. [Google Scholar]
- 40.Brinkerhoff R, Devasia S. Output tracking for actuator deficient/redundant systems: Multiple piezoactuator example. Journal of Guidance, Control, and Dynamics. 2000;23(2):370–373. [Google Scholar]
- 41.Singer NC, Seering WP. Preshaping command inputs to reduce system vibration. ASME Journal of Dynamics Systems, Measurement and Control. Mar 1990;112:76–82. [Google Scholar]
- 42.Singhose WE, Banerjee AK, Seering WP. Slewing flexible spacecraft with deflection-limiting input shaping. Journal of Guidance, Control, and Dynamics. 1997;20(2):291–297. [Google Scholar]
- 43.Cook G. Discussion: Preshaping command inputs to reduce system vibration. ASME Journal of Dynamics Systems, Measurement and Control. June 1993;115:309–310. [Google Scholar]
- 44.Lin H, Clegg DO, Lal R. Imaging real-time proteolysis of single collagen i molecules with an atomic force microscope. Biochemistry. 1999;38:9956–9963. doi: 10.1021/bi990800q. [DOI] [PubMed] [Google Scholar]
- 45.Gomez DE, Alonso DF, Yoshiji H, Thorgeirsson UP. Tissue inhibitors of metalloproteinases: Structure, regulation and biological functions. European Journal of Cell Biology. 1997;74:111–122. [PubMed] [Google Scholar]
- 46.Kanca J. Improving bond strength through acid etching of dentin and bonding to wet dentin-surface. Journal of American Dental Association. 1992;123:35–43. doi: 10.14219/jada.archive.1992.0248. [DOI] [PubMed] [Google Scholar]


