Molecular Dynamics Simulation of Sperm Whale Myoglobin: Effects of Mutations and Trapped CO on the Structure and Dynamics of Cavities

Abstract

The results of extended (80-ns) molecular dynamics simulations of wild-type and YQR triple mutant of sperm whale deoxy myoglobin in water are reported and compared with the results of the simulation of the intermediate(s) obtained by photodissociation of CO in the wild-type protein. The opening/closure of pathways between preexistent cavities is different in the three systems. For the photodissociated state, we previously reported a clear-cut correlation between the opening probability and the presence of the photolyzed CO in the proximity of the passage; here we show that in wild-type deoxy myoglobin, opening is almost random. In wild-type deoxy myoglobin, the passage between the distal pocket and the solvent is strictly correlated to the presence/absence of a water molecule that simultaneously interacts with the distal histidine side chain and the heme iron; conversely, in the photodissociated myoglobin, the connection with the bulk solvent is always open when CO is in the vicinity of the A pyrrole ring. In YQR deoxy myoglobin, the mutated Gln(E7)64 is stably H-bonded with the mutated Tyr(B10)29. The essential dynamics analysis unveils a different behavior for the three systems. The motion amplitude is progressively restricted in going from wild-type to YQR deoxy myoglobin and to wild-type myoglobin photoproduct. In all cases, the principal motions involve mainly the same regions, but their directions are different. Analysis of the dynamics of the preexisting cavities indicates large fluctuations and frequent connections with the solvent, in agreement with the earlier hypothesis that some of the ligand may escape from the protein through these pathways.

INTRODUCTION

For more than 40 years, myoglobin (Mb), the oxygen carrier of red muscles, has played the role of a model system in the investigation of the relationships between structure, dynamics, and function in proteins. Sperm-whale Mb is a small globular heme protein (153 amino acids long) that reversibly combines with small ligands such as O₂, CO, and NO. Immediately after the seminal discovery of Mb's three-dimensional structure (1), it was recognized that there is no open passageway between the heme iron and the bulk solution. When Perutz and Matthews (2) proposed the so-called “histidine gate hypothesis”, they hypothesized that the distal histidine (His64, E7) acts as a gate allowing access of the ligand to the heme iron. Later it was argued that the His-gate may not be the only pathway (3,4), and it became apparent that ligand binding has to rely on more extended structural fluctuations that provide transient channels for the ligand to enter and exit the protein. In 1984, Tilton et al. (5) solved the structure of met-Mb equilibrated with xenon gas (at 7 atm), and observed the presence of four preexistent cavities occupied by xenon atoms (named Xe1–Xe4 (Fig. 1)). .

FIGURE 1.

Crystal structure of the sperm whale Mb and of the distal pocket, Xe1, Xe2, Xe3, Xe4, Ph1, and Ph2 cavities

The functional role of these “xenon cavities” emerged initially from kinetic studies carried out by Scott and Gibson (6) on wild-type (WT) and mutant Mbs and was confirmed by several other investigations (7). More recently, new hypotheses assigning multiple functional roles to Mb cavities have been published (8–10). Employing time-resolved x-ray crystallography of photoproducts (11–14, and references therein), time-resolved spectroscopy (15, and references therein) and molecular dynamics (MD) simulations (3,16,17), it has been shown that, after photolysis, CO migrates from the distal heme pocket (DP) to the Xe1 cavity on the proximal side of the heme, via a pathway involving the whole web of internal cavities. Thus, the xenon cavities appeared as hosting stations for the ligand migrating away from the active site. Nevertheless, in the crystallographic structure, passageways between the cavities are not obvious; therefore, conformational fluctuations have been invoked as a mechanism that could transiently establish connectivity between cavities and form channels, eventually either leading back to the active site or out to the solvent phase. Computational techniques based on MD simulations have provided important insight for the understanding of diffusion pathways through the protein (3,16–19) and for the functional significance of large-scale motions in Mb (9,20, and references therein). The recent article by Bossa et al. (17) reported the results of an extended (90-ns) MD simulation of the migration of photodissociated CO in WT sperm whale Mb photoproduct (indicated herein as WT-Mb··CO simulation). The results allowed us to follow one possible ligand migration from the distal pocket to the Xe1 cavity via a pathway involving the other xenon-binding cavities and two additional packing defects along the pathway (called phantom1 (Ph1) and phantom2 (Ph2)) (Fig. 1). In that study, the dynamical behavior of the cavities in the interior of the protein, their volume fluctuations, and their interconnecting channels were investigated in the presence of the photodissociated CO migrating in the matrix. It emerged that protein fluctuations are affected by the ligand in such a way that the opening/closure of passages between adjacent cavities are correlated to the presence of CO in the proximity of the “gate”. It was concluded that the photodissociated ligand (momentarily trapped in the matrix) behaves as a perturbation of the protein equilibrium dynamics at large and of the cavities in particular. This view of a ligand as a perturbant opens the way to investigations of other kinds of perturbation causes, and primarily point mutations, in view of their significance for mechanistic studies and pathophysiological effects.

In this article, the results of extended (80-ns) MD simulations of wild-type (WT-Mb) and YQR triple mutant (YQR-Mb) sperm whale deoxy-Mb in water, are reported and compared with the results obtained on the photoproduct WT-Mb··CO. The long timescale of the simulations allowed us to characterize the equilibrated protein dynamics of deoxy WT-Mb and thereby compare them with the protein perturbed either by mutations or by a gaseous ligand. The triple mutant of sperm whale Mb (YQR-Mb), carrying the L29(B10)Y, H64(E7)Q, and T67(E10)R substitutions and originally designed to mimic the distal pocket structure of Ascaris suum hemoglobin (21), seemed particularly suitable as a model system in view of its interesting and almost unique properties. It displays peculiar ligand binding properties such as absent geminate rebinding and a reduced bimolecular rate constant of CO and O₂ binding (7); moreover, it proved very informative to investigate structural dynamics by time-resolved Laue crystallography (11).

The results reported below confirm the hypothesis that these perturbations have a role in modulating the protein dynamics and controlling internal pathways in the protein matrix. Moreover, we observe that the presence in the distal pocket of water molecule(s) or CO affects the opening/closure of the His-gate in a specific manner.

METHODS

Starting coordinates

The starting structures of the simulations were taken for the WT-Mbs from the 1.15-Å resolution refined crystal structures of the sperm whale deoxy Mb (Protein Data Bank (pdb) entry 1bzp) and carbon monoxide-ligated Mb (pdb entry 1bzr, in which we cut the CO-iron bond) (22), whereas for the deoxy YQR-Mb mutant starting structures were taken from the 1.8-Å resolution refined crystal structure (pdb entry 1dxd) (7). The crystal structure of deoxy WT-Mb contains a water molecule in the DP, near the sixth coordination site of the heme iron (22), whereas the structures of carbon monoxide-ligated Mb and deoxy YQR-Mb do not contain any water in the DP. Following previous theoretical and experimental studies (22,23), His(E7)64 in WT-Mb and WT-Mb··CO was modeled as the neutral tautomer, with hydrogen at the δ position. It must be pointed out, however, that recently published articles (24,25) suggest that in Mb··CO His(E7)64 has the hydrogen in the ɛ position and the authors hypothesize that this tautomer does not change upon photolysis. The overall WT systems were neutral; conversely, the total charge of the deoxy YQR-Mb system was +2e.

Molecular dynamics simulations

Each protein was solvated in a rectangular periodic box with explicit simple point charge water molecules (26), large enough to contain the protein and 0.8 nm of solvent on all sides. In the deoxy YQR-Mb system, two Cl⁻ counterions were added by replacing water molecules at the most positive electrical potential to provide a neutral simulation cell. The total number of atoms for the systems was ∼20,000. MD simulations were performed with the Gromacs software package (27), using Gromos96 force-field (28). The CO molecule was modeled with the three-site “quadrupolar” CO model of Straub and Karplus (29).

Simulations were carried out at a constant temperature of 300 K within the fixed-volume rectangular box using periodic boundary conditions. The Lincs algorithm (30) to constrain bond lengths, and the rototranslational constraint algorithm (31) were used. The initial velocities were taken randomly from a Maxwellian distribution at 300 K and the temperature was held constant by the Berendsen algorithm (32). By using dummy hydrogen atoms (33), a time-step of 4 fs could be chosen. To improve the stability of the simulations, the water oxygen mass was redistributed on the hydrogen atoms, as suggested by Feenstra et al. (33).

The particle mesh Ewald (PME) method (34) was used for the calculation of the long-range interactions with a grid spacing of 0.12 nm combined with a fourth-order B-spline interpolation to compute the potential and forces between grid points. A nonbond pair-list cutoff of 9.0 Å was used and the pair-list was updated every four time steps.

For all systems, the solvent was relaxed by energy minimization followed by 100 ps of MD at 300 K, restraining protein atomic positions with a harmonic potential. The systems were then minimized without restraints and their temperature brought to 300 K in a stepwise manner: 30-ps MD runs were carried out at 50, 100, 200, 250, and 300 K, before starting the production runs at 300 K.

The package SURFNET (35) was used for detecting the cavities and calculating their volume. In this program gap regions are defined by filling the empty regions in the interior of the molecule with gap spheres of variable radius (r_min = 1.0 Å and r_max = 3.0 Å, in our case). These spheres are then used to compute a three-dimensional density map which, when contoured, defines the surface of the gap region. Cavity volumes were evaluated without taking into account the presence of either CO or water. A cavity is considered “exposed” if the SURFNET program shows a continuity between the cavity and the solvent (thus in the range between r_min and r_max).

Essential dynamics analysis

Quantitative characterization of the dynamical properties relied on principal component analysis of the covariance matrix of the positional fluctuations of the C_α atoms, as described elsewhere (36,37). This matrix was built from the equilibrated portion of the trajectories (beyond 5 ns), and its diagonalization yielded the principal directions of the large-amplitude concerted motions (essential eigenvectors) that characterize the essential subspace of a protein's internal dynamics. The root-mean square inner product (RMSIP) between the essential subspaces of different simulated systems has been used to assess their dynamical similarity (38). In our analysis, we used the RMSIP value between the first 10 eigenvectors of two different sets, defined as:

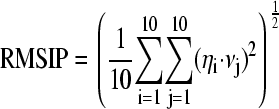where η_i and ν_j are ith and jth eigenvectors, respectively, of the two different sets.

RESULTS AND DISCUSSION

Structural behavior

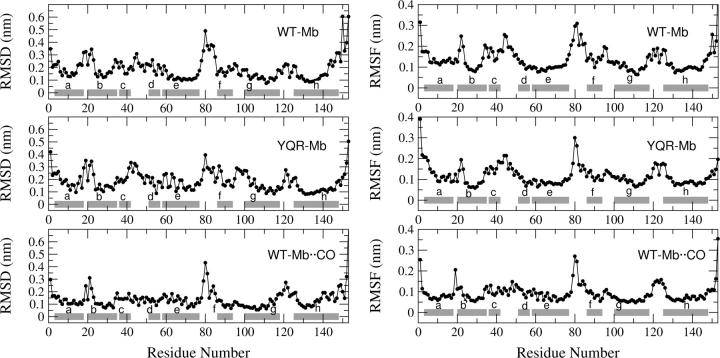
To investigate the structural behavior of the protein and test the stability of the simulations, we calculated the root-mean square deviation (RMSD) of the C_α atoms from the crystal structure. In Fig. 2, the RMSD distribution histograms are reported. It is evident that deoxy WT-Mb explores different conformers with the largest peak located at ∼0.22 nm (Fig. 2 a), whereas deoxy YQR-Mb has a more restricted range of deviation from the crystal structure, with an average value of 0.2 nm and a bimodal distribution (Fig. 2 b). Finally the photoproduct WT-Mb··CO has an even more homogeneous and narrower distribution peaked at the value of 0.16 nm (Fig. 2 c). Comparing the residue-based RMSD and root-mean square fluctuation (RMSF) plots (Fig. 3), it may be noted that in the three systems the largest deviations occur in the terminal and the loop regions, that are known experimentally to be the most flexible ones (39). In particular the EF loop is the most flexible unit, as in the normal-mode analysis study by Seno and Go (40), and the pattern is very similar to that found in conformational flooding simulations by Schulze et al. (20); the CD loop in the WT-Mb··CO is less flexible than in the deoxy Mbs. It should be stressed here that the triple mutation in deoxy YQR-Mb, or the presence of the ligand trapped in the protein matrix in WT-Mb··CO, seem not to perturb the average structural behavior observed in deoxy WT-Mb.

FIGURE 2.

Histograms of the Cα RMSD values from the crystal structure during the simulation of deoxy WT-Mb (a), deoxy YQR-Mb (b), and WT-Mb··CO (c).

FIGURE 3.

(Left) Cα RMSD from the crystal structure on the equilibrated trajectory of deoxy WT-Mb, deoxy YQR-Mb, and WT-Mb··CO. (Right) Cα RMSF on the equilibrated (t > 5 ns) trajectory of deoxy WT-Mb, deoxy YQR-Mb, and WT-Mb··CO. The horizontal bars indicate the crystal boundaries of the α-helices.

Other structural parameters that were monitored during the time-course of the simulation (Table 1) are comparable with the values calculated from the crystal structure, and confirmed the stability of the trajectory in time. In particular, analysis of the percentage of helicity of each residue as a function of time (data not shown) shows that all α-helices are well conserved during the whole simulation for the three systems. Furthermore, the unstructured loop region between helices C and D adopts α-helical conformation for >30% of time in the simulations without the ligand (deoxy WT-Mb and deoxy YQR-Mb), in agreement with previous calculations (20).

TABLE 1.

Comparison of the RMSD, radius of gyration and α-helical content in the crystal structure and in the MD simulations

Mb	RMSD (nm)	Radius of gyration (nm)	α-Helical content (%)
WT-Mb (MD)	0.21 ± 0.03	1.50 ± 0.01	73.0 ± 2.2
WT-Mb (crystal)	—	1.5	75.0
YQR-Mb (MD)	0.20 ± 0.03	1.50 ± 0.01	74.2 ± 2.5
YQR-Mb (crystal)	—	1.5	75.0
WT-Mb··CO (MD)	0.16 ± 0.02	1.48 ± 0.01	72.0 ± 2.7
WT-Mb··CO (crystal)	—	1.5	74.5

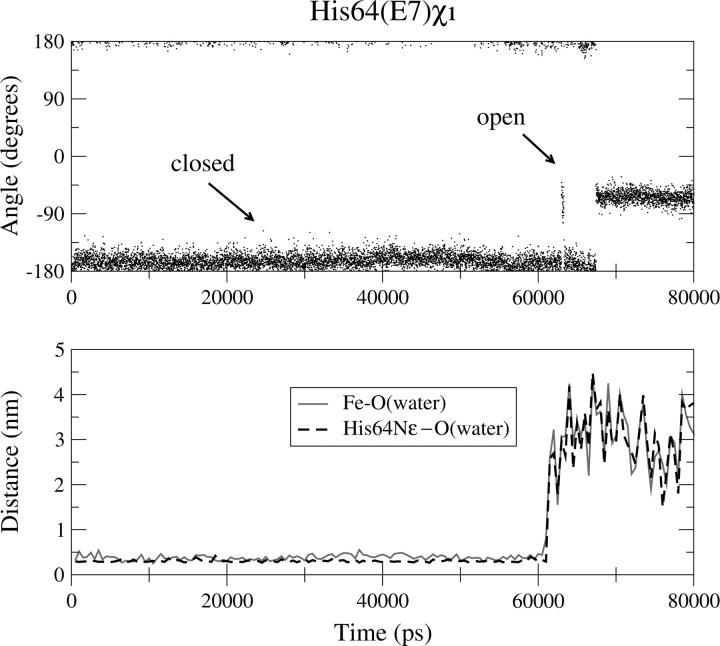
We have monitored the opening of the His-gate in deoxy WT-Mb and its correlation with the presence of the distal pocket water observed in the crystal structure (22). In Fig. 4, the trajectory of the χ₁ torsion angle of the His(E7)64 side chain is reported (upper panel), together with the trajectory of the distance of the oxygen water molecule from the His Nɛ atom and from the heme iron (lower panel). Fig. 4 shows that up to 60 ns His(E7)64 is in the closed conformation due to the H-bond with a water molecule that is close to the sixth coordination site of the iron over the same time interval. It should be pointed out that although three different water molecules at this position are in exchange during the simulation, the distances reported in Fig. 4 refer only to the nearby one. After 60 ns, all the water molecules escape from the DP and the His-gate opens.

FIGURE 4.

Deoxy WT-Mb: trajectory of the His(E7)64 χ₁ torsion angle (upper panel) and trajectory of the distance of the water oxygen from the His Nε atom and from the heme iron (lower panel).

These findings indicate that the water molecule plays an important role in the opening/closure of the His-gate.

We have also analyzed in detail the opening of the His-gate in the simulation of the WT-Mb··CO (see Bossa et al. (17)), in particular its correlation with the presence of CO in the vicinity of pyrrole ring A or in the primary docking site (i.e., between the B and C pyrrole rings). It must be pointed out that the CO cannot play the role of the water molecule in bridging the histidine ring to the iron, differently from what is seen for deoxy WT-Mb. The results of this analysis show that when the ligand is close to the pyrrole ring A the His-gate is open, indicating a strong correlation between gate opening and presence of CO in its vicinity; conversely, no correlation is observed when the ligand is in the primary docking site or in the other cavities, as the His-gate flips randomly between the open and closed conformations. It should be pointed out that in the previously reported study by Bossa et al. (17), the free energy gradient of the ligand in the distal pocket avoids free diffusion toward the solvent.

In the deoxy YQR-Mb simulation, Gln(E7)64 and Tyr(B10)29 interact steadily during the whole simulation. The hydroxyl group of Tyr(B10)29 forms an H-bond with the amide group of Gln(E7)64 side chain. Due to the the Gln(E7)64 χ₃ torsion angle rotation, this H-bond is formed by Tyr(B10)29 either as an acceptor (∼63% of the time, with the amide Nɛ of Gln(E7)64 as a donor) or as a donor (∼27% of the time, with the amide Oɛ of Gln(E7)64 as an acceptor).

Dynamical analysis

Essential dynamics analysis on the α-carbon atoms was used as a tool to analyze and visualize the overall motions in the three simulations.

In Table 2, we report the RMSIP between the first 10 eigenvectors in the three simulations. The diagonal values represent the RMSIP between the first 10 eigenvectors extracted from the first and the second half of the trajectory. According to Amadei et al. (43), the values obtained (>0.7), show a good convergence of the essential subspace. It should be pointed out that the essential subspace is expected to change in the presence of molecular motions of time constant longer than the present simulation length. Therefore, only large conformational transitions occurring with a relaxation time much longer than 70–80 ns and involving a significant essential subspace rotation, may be missed in our essential dynamics analysis, a possibility that we consider unlikely. The low values of the RMSIP show that there is a low similarity of the overall motions in deoxy YQR-Mb with respect to the other two simulations.

TABLE 2.

RMSIP between the first ten eigenvectors in the three simulations

	WT-Mb	YQR-Mb	WT-Mb··CO
WT-Mb	0.71	0.47	0.62
YQR-Mb	—	0.76	0.45
WT-Mb··CO	—	—	0.71

The diagonal values represent the RMSIP between the first 10 eigenvectors extracted from the first and second half of the trajectory.

Although in all simulations the principal directions of the collective motions involve almost the same regions (helix A, CD loop, EF-F-FG region, GH loop, and N- and C-terminal regions; data not shown), their directions are quite different in the deoxy YQR-Mb simulation. In particular, the most significant conformational changes of deoxy WT-Mb (Fig. 5, left side) are represented by a motion of the EF loop in the plane defined by helices E and F (i.e., in the plane of Fig. 5), together with a displacement of the terminal region of helix F out of the plane of Fig. 5. Furthermore, a large motion along the first eigenvector is observed for loop CD and helix A. Conversely, in deoxy YQR-Mb (Fig. 5, right side) the motion of EF loop is in a direction orthogonal with respect to the plane defined by helices E and F, and helix F moves as a rigid body in the plane of Fig. 5. The CD loop movement is similar to that seen in deoxy WT-Mb, whereas helix A motion is more restricted.

FIGURE 5.

Superposition of 10 configurations obtained by considering Cα motions due to the first eigenvector for deoxy WT-Mb (left) and deoxy YQR-Mb (right). Letters from A to H indicate Mb α-helices. For the sake of clarity, the heme crystallographic position is also depicted.

The traces of the covariance matrix, which account for the overall amount of motion, are 3.0, 2.2, and 1.4 nm for deoxy WT-Mb, deoxy YQR-Mb, and WT-Mb··CO simulations, respectively. This indicates that the overall motions are increasingly restricted in going from deoxy WT-Mb to deoxy YQR-Mb and WT-Mb··CO.

The crystal structure of deoxy YQR-Mb was determined in the P6 space group whereas that of deoxy WT-Mb was determined in the P2₁ group; it could be argued, therefore, that differences in their dynamics may be ascribed to the different starting conditions (41). The trajectories of the RMSD and RMSF, and the analysis of the convergence of the principal directions of motion in different time intervals, show that the equilibration of the structural and dynamic properties occurs in a time range of 5 ns, and therefore it can be concluded that the length of the simulation should overcome the initial bias, if any.

The projections of the trajectory structures onto the first two eigenvectors, reported for deoxy WT-Mb, deoxy YQR-Mb and WT-Mb··CO (Fig. 6), show that in the deoxy WT-Mb simulation, the structure underwent a number of conformational changes. The protein entered sequentially four energetically favorable conformational regions. Analysis of these regions shows that structural differences occurred almost exclusively in the loops, in agreement with the early findings by Elber and Karplus (3) that motions in loop regions initiate conformational transitions, whereas α-helices are quite stable and remain largely unaffected. In particular, the four regions are characterized by a progressive rearrangement of EF and CD loops along the directions previously described in the text (see also Fig. 5).

FIGURE 6.

Projection of the equilibrated trajectory onto the first essential plane for the three systems.

On the other hand, the deoxy YQR-Mb triple mutant uniformly samples the conformational subspace. Finally the WT-Mb··CO simulation seems to be a case of its own. In the latter case, the projection of the trajectory onto the first two eigenvectors shows that a number of discrete conformational substates are sampled (Fig. 6), although the amplitude of the principal motions is now reduced with respect to the equilibrium deoxygenated systems, as already shown by the trace of the covariance matrix. It is important to notice that for WT-Mb··CO the different substates of Fig. 6 correspond to the presence of CO in different cavities: region A when CO is in the distal cavities, i.e., distal pocket, Xe4 and Ph1; region B when CO is in the Xe1 cavity and region C when CO is in the Xe2 cavity. The values of the RMSIP between the first 10 eigenvectors calculated on these three regions of the essential space are significantly high (RMSIP_A–B = 0.70, RMSIP_B–C = 0.69, RMSIP_A–C = 0.68), showing that the motions are similar in direction; furthermore, from the trace of the covariance matrix (TCM) it can be seen that they are also similar in amplitude (TCM_A = 1.0, TCM_B = 1.1, and TCM_C = 1.1). Thus it seems clear that the ligand during its internal migration selects different regions of the overall essential subspace.

Taken together, these results show that, by reference to deoxy WT-Mb, deoxy YQR-Mb exhibits different directions of motions but with similar amplitude; on the other hand WT-Mb··CO shows similar directions of motions but with restricted amplitude; more importantly, in the latter case the regions involved in the motions are correlated with the presence of CO in a specific cavity.

Cavities fluctuation

According to the results so far reported, the three systems show similar structures, but overall motions are different either in direction or in amplitude. This affects the fluctuations of the cavities in the interior of the molecule. We focused on the four Xe binding cavities, the distal pocket, and the two so-called phantom cavities (Ph1 and Ph2) that were important in the CO migration through the protein matrix (17) (Fig. 1). In Table 3, we report the crystallographic value of the volume of the cavities (as calculated by program SURFNET (35)), the persistence of each cavity during the entire simulation and the mean volume estimated from the simulation (when isolated and not in contact with the solvent).

TABLE 3.

Cavity volume in the crystal and mean volume estimated from the MD simulations

	DP	Xe1	Xe2	Xe3	Xe4	Ph1	Ph2
WT-Mb	Crystal	47	65	47	93	71	52	24
	MD	45 (85.6)	47 (88.8)	105 (98.7)	28 (17.2)	24 (45.4)	43 (56.8)	27 (23.2)
YQR-Mb	Crystal	139*	57	40	81	139*	42	0
	MD	22 (58.7)	49 (93.5)	111 (96.5)	52 (1.4)	54 (38.0)	46 (60.7)	44 (20.8)
WT-Mb··CO	Crystal	67	76	45	95	68	60	18
	MD†	58 (92.7)	71 (98.6)	41 (70.0)	25 (62.9)	35 (26.6)	62 (98.0)	20 (33.5)

Cavity- and mean-volume values are given in ų. Numbers in parentheses indicate the occurrence of each cavity during the simulations as a percentage of time.

^*Sum of the DP and Xe4 volumes that are connected in the crystal.

^†Data for WT-Mb··CO MD simulations was taken from Bossa et al. (17).

In most cases, the values calculated from the MD simulations differ significantly from one system to the other. It can be noticed that the mean volume of DP in deoxy YQR-Mb has a slightly lower value with respect to deoxy WT-Mb and WT-Mb··CO (22 ų vs. 45 ų of deoxy WT-Mb and 58 ų of WT-Mb··CO), mainly due to the presence in the distal pocket of the mutation Leu(29)Tyr, its side-chain fluctuations modulating this volume during the entire simulation.

The volume of each cavity fluctuates during the simulation and assumes values ranging from zero (i.e., the cavity momentarily occluded) to almost twice the crystal volume. During these variations, transiently formed hydrophobic channels may connect two or more cavities and/or eventually lead to the solvent phase. In Fig. 7, the occurrences of each cavity, and of the connectivity between cavities and with the solvent are reported for the three systems. It can be noticed that the patterns are quite different. In particular, the connection Xe4-DP, present in deoxy WT-Mb (involving also the Xe2 cavity, label Xe2-Xe4-DP) and in WT-Mb··CO (label Xe4-DP), is almost absent in deoxy YQR-Mb due to the fluctuations of Tyr(B10)29 introduced in the mutant (vide infra). The Xe1-Xe2 connection occurs for a comparable amount of time in the three systems. In every simulation, DP, Xe1, Xe2, Xe3, and Ph1 cavities are connected with the solvent for a nonnegligible amount of time, suggesting that the ligand migration to and from the solvent occurs through these pathways as well as the His-gate, in agreement with Elber and Karplus (3). This information must be confronted with the results reported by Scott et al. (15), who estimated from an extensive analysis of the geminate kinetics of many mutants of sperm-whale Mb that ∼80% of the ligand may escape through the His-gate.

FIGURE 7.

Occurrence of each cavity, of the connection between cavities, and of the connection with the solvent for deoxy WT-Mb, deoxy YQR-Mb, and photoproduct WT-Mb··CO systems.

It is important to note that the time dependence of the opening/closure of the passage between cavities is different in the three simulations. In deoxy WT-Mb and deoxy YQR-Mb, the opening/closure is randomly distributed along the trajectory; conversely, in WT-Mb··CO it is strictly correlated with the presence of the ligand in the proximity of the gate, as indicated by Bossa et al. (17). In particular, in that work, connection between cavities was found to involve fluctuations of a few key residues. The connectivity DP-Xe4 involved a hydrophobic cluster formed by Ile(B9)28, Leu(B10)29, and Ile(G8)107, the rotation of the χ₁ torsion angle of Ile(B9)28 acting as a gate for the opening/closure of the DP-Xe4 connection. On the other hand, the migration from Xe1 to Xe2 cavity was accomplished by the rotation of the χ₁ torsion angle of Phe(H14)138 side chain, which opened the channel connecting the two cavities, at the same time occluding the Xe3 cavity. In Fig. 8, we report the trajectories of the Ile(B9)28 and Phe(H14)138 χ₁ torsion angles during the three simulations. For what concerns the connectivity DP-Xe4, the configuration of the torsion angle that corresponds to the opening of the channel is randomly populated over the whole trajectory in deoxy WT-Mb (see Fig. 3, left side, upper panel). Conversely, in the case of WT-Mb··CO the passageway is open only when the ligand is in the proximity (Fig. 8 left side, bottom panel). In deoxy YQR-Mb, the flip/flop between the two configurations of the χ₁ torsion angle is random and frequent (Fig. 8, left side, center panel); nevertheless, the occurrence of the connectivity is reduced by the mutation Leu(B10)29 Tyr that affects the DP-Xe4 gating mechanism. In fact, the essential dynamics analysis (over the whole trajectory) of the three residues involved (Ile(B9)28, Tyr(B10)29, and Ile(G8)107) shows that the rotation of the Ile(B9)28 χ₁ torsion angle is accomplished by a rigid movement toward the heme of Tyr(B10)29 in such a way that opening of the channel partially closes the DP. Furthermore, rotation of Tyr(B10)29 χ₂ torsion angle reduces accessibility to the Xe4 cavity. The connection between DP and Xe4, found in the crystal, only persists in the very initial picoseconds of the trajectory. Experimental results (11,42), which identified photolyzed CO in Xe4 cavity immediately after photodissociation, are consistent with an active role of the ligand in “pushing” side chains and forcing its passage inside the protein.

FIGURE 8.

Ile(B9)28 χ₁ (left) and Phe(H14)138 χ₁ trajectory (right) in the three simulations.

On the right hand side of Fig. 8, the trajectory of the Phe(H14)138 χ₁ torsion angle, involved in the mechanism of opening/closure of the passageway between Xe1 and Xe2, is shown for the three simulations. The configuration that in WT-Mb··CO corresponded to an opening of the channel, in deoxy WT-Mb and deoxy YQR-Mb is populated early on; however, only rarely (in deoxy WT-Mb) or never (in deoxy YQR-Mb) goes back to the closed state (Fig. 8, right side). In summary, the Xe1-Xe2 connectivity is high in deoxy YQR-Mb (Fig. 7), whereas in deoxy WT-Mb the intrusion of Ile(H18)142 side chain in between reduces the frequency of this connection. On the other hand, in WT-Mb··CO the Xe1-Xe2 connectivity is open only in the last part of the simulation, when the CO molecule is hopping in between the Xe1 and Xe2 cavities.

CONCLUSIONS

Since the main issue of this article is the comparison of structural and dynamic properties of the three molecular systems, it is important to discuss how the convergence of these properties can be established. The dynamic properties have been analyzed by the essential dynamics method, which is based on the covariance matrix of the atomic positional fluctuations, obtained from MD simulations of finite length. This sampled covariance matrix, is an estimate of the covariance matrix that could be obtained with an “infinite” time-length simulation of the folded protein (the expectation covariance matrix). The accuracy of this estimate depends on the statistical relevance of the configurational subspace sampled within the simulation. It has already been reported (43) that using simulations of a few hundred picoseconds, the eigenvectors converge in time toward a “stable” set, at least up to the nanoseconds time range, and that such a convergence is statistically significant. In this case, the convergence was checked with simulations close to 100 ns and, in agreement with Amadei et al. (43), it is reasonable that such a convergence of the eigenvectors can be valid over a time range of at least one order of magnitude greater. Whether this stable set is really stable beyond this 100-ns time range, and coincides with the expectation set, is still an open question.

It is important to note that convergence for the essential and near constraints subspaces does not imply a good sampling of the configurational space. This is a crucial issue when large conformational rearrangements are expected, as in studies of protein folding, misfolding, and aggregation. In the case described here, the conformations of deoxy WT-Mb, deoxy YQR-Mb, and WT-Mb··CO are in good agreement with the crystal structures, as shown by the RMSD plots (Fig. 2). In addition, the analysis of the projections of the trajectory structures onto the first essential subspace (Fig. 6) shows for deoxy YQR-Mb and WT-Mb··CO several forward and backward transitions between different regions of the plane (data not reported), thus suggesting a complete sampling of the space accessible in the time interval of the simulations. The same analysis for deoxy WT-Mb shows that the allowed space is sampled sequentially, so that no backward transitions between the different regions of the first essential plane are observed. However, it should be noted that, different from this first essential plane, accounting mainly for the motions of loops EF and CD, the other essential planes in this system are sampled more densely. Whether the structural properties obtained remain stable beyond the time range of the simulation is again an open question.

The results reported above show that the overall structural features of the protein in the three cases are similar and comparable with the crystal structures. Our results clarify the mechanics of the opening/closure of the His-gate. In deoxy WT-Mb the closure of the gate is due to a water molecule that simultaneously interacts with the distal histidine side chain and the heme iron; the loss of this interaction corresponds to the opening of the gate. In WT-Mb··CO the ligand impedes this interaction and the His-gate is always open when CO is in the vicinity of pyrrole ring A. On the other hand, when the ligand is in the primary docking site or in the other cavities, the gate flips almost randomly. In the deoxy YQR-Mb a stable H-bond between Gln(E7)64 and Tyr(B10)29 is observed.

The essential dynamics analysis shows significant dynamical differences between the three systems. Although the overall motions of deoxy WT-Mb and photoproduct WT-Mb··CO are comparable in direction, the latter displays a large restriction in amplitude. In contrast, the overall dynamics of the triple mutant deoxy YQR-Mb is different in the directions of motion, with amplitude comparable to that of deoxy WT-Mb. In addition the WT protein (whether deoxy or photolyzed) samples different conformational subspaces in the simulation, whereas deoxy YQR-Mb samples a unique subspace.

Analysis of the occurrence of each cavity and of the connectivities between adjacent cavities also shows a difference in behavior in the three simulations. In all cases there is evidence that each cavity is in contact with the solvent for a nonnegligible fraction of time, which supports the hypothesis that pathways for diffusion of the ligand to the bulk solvent different from the His-gate are present (3,4,15). Conversely, the connections between adjacent cavities are different in the three systems examined. These results show that the presence of a perturbation (either a mutation or a ligand) strongly affects the cavity fluctuations. One of the most interesting results comes from the analysis of the time dependence of these fluctuations. In deoxy WT-Mb and deoxy YQR-Mb these fluctuations occur randomly over the whole trajectory; in contrast, a clear correlation between cavity fluctuations and the trajectory of the ligand migration inside the protein can be observed in WT-Mb··CO, as already reported (17). This strengthens the hypothesis that the overall motion of the protein is somehow tuned by the ligand trapped within the matrix.