Abstract
We report a detailed study of the behavior (shapes, experienced forces, velocities) of giant lipid vesicles subjected to a shear flow close to a wall. Vesicle buoyancy, size, and reduced volume were separately varied. We show that vesicles are deformed by the flow and exhibit a tank-treading motion with steady orientation. Their shapes are characterized by two nondimensional parameters: the reduced volume and the ratio of the shear stress with the hydrostatic pressure. We confirm the existence of a force, able to lift away nonspherical buoyant vesicles from the substrate. We give the functional variation and the value of this lift force (up to 150 pN in our experimental conditions) as a function of the relevant physical parameters: vesicle-substrate distance, wall shear rate, viscosity of the solution, vesicle size, and reduced volume. Circulating deformable cells disclosing a nonspherical shape also experience this force of viscous origin, which contributes to take them away from the endothelium and should be taken into account in studies on cell adhesion in flow chambers, where cells membrane and the adhesive substrate are in relative motion. Finally, the kinematics of vesicles along the flow direction can be described in a first approximation with a model of rigid spheres.
INTRODUCTION
The behavior of individual blood cells subjected to a flow close to a vessel or a tube wall has generated a great number of experimental and theoretical studies. Indeed, the quantitative description of the motions of isolated single red and white blood cells (translation, rotation, and deformation in a flow) is a prerequisite to better understanding the blood microrheology. In addition, the dynamics of individual cells is important for understanding the early inflammatory response where flowing leukocytes leave the blood flow to adhere, roll, and stop onto the endothelium (1–4).
For instance, the motion of red blood cells is known to present two regimes. In the first one, at low shear rates and low external fluid viscosity the cell rotates as a rigid disk. As the shear rate increases there is a gradual transition to a tank-treading motion where the cell maintains a steady tilt with respect to the flow (5–7). In this regime, migration of the cell away from the vessel wall has been shown experimentally and has long been believed by physiologists to occur in vivo (8,9,6). Flexible rouleaux of red blood cells also exhibit inward migration away from the vessel wall. This inward migration phenomenon, known for asymmetric deformable particles in laminar viscous creeping flow since the 1960s (10,11) is due to a viscous lift force. It has been explained for liquid drops in terms of modifications of the flow field induced by the asymmetric deformation of a liquid drop and the presence of the wall (12) or, in other terms, as originating from the fore-aft asymmetric pressure field existing in the space between the tilted tank-treading particle and the wall (13).
However, the exact description of this lift force is nontrivial, not only for the case of liquid droplets, whose area can increase and whose shape is governed by the surface tension, but also for the important class of deformable systems that present a fixed volume and area (nonextensibility of the membrane) like cells. For instance, the shape of red blood cells starts from a biconcave shape at rest and changes to a prolate ellipsoid shape at higher shear rates without an increase of the surface area of the membrane (5). In general, the determination of the shapes of deformable particles is complex, because they are governed by hydrodynamic forces, the internal fluid viscosity, the bending elasticity, and the constraints of fixed volume and area. Recently, nevertheless, several theoretical (13–17) and experimental approaches (18,19) have considered the dynamics in a wall-bounded shear flow of deformable vesicles, which are closed fluid membranes of constant surface area and volume, and which are filled by an aqueous solution. These studies have demonstrated the existence of a lift force that acts on nonspherical vesicles and tends to unbind them from the wall. This force is due to the asymmetry of the particles and has a purely viscous origin because it applies in the absence of inertia of the fluid. This lift force, therefore, is not related to the Magnus force (20). Despite the above-listed theoretical works, the quantitative description for the variation of the lift force with its driving parameters has not been established up to now.
This hydrodynamic lift force may also play a role in the behavior of leukocytes close to the vessel walls by keeping away from the endothelium nonspherical leukocytes or by counterbalancing adhesion forces during the rolling stage, when leukocytes are deformed (2,21,22). Indeed, recent three-dimensional biomechanics simulations have pointed out the importance of deformation on the capture and the rolling of leukocytes onto the endothelium (23,24), although the rolling phenomenon was theoretically predicted without accounting for cell deformability by Hammer and co-workers (25,26) and observed in vitro for undeformed spherical beads (26–28).
It therefore turns out to be important to refine the description of this force. This article is dedicated to a detailed experimental study of the lift force exerted on soft artificial shells. It includes the determination of the functional variation of the force with the shape of the objects, the distance to the substrate, and the characteristics of the flow. The artificial soft shells studied here are giant unilamellar vesicles, which are closed inextensible fluid membranes composed of a bilayer of phospholipids separating the inner aqueous solution from the outer solution. The shells are deformable objects and present a constant surface area and volume.
The article is organized as follows. In the next section we briefly recall the main results reported in the literature on deformable vesicles under flow, which are relevant for our study. The Materials and Methods section describes the material and the experimental methods. Then we describe in the next section after that the behavior of vesicles and beads under a shear flow close to a substrate. In “Tilt and shape of deformable vesicles”, we analyze shapes and orientations of tank-treading deformed vesicles followed in the “Lift Force” section by the study of the lift force acting on the vesicles. We finish in the “Kinematics and deformation: translation and tank-treading” section with a study of the effect of deformability and the presence of the wall on the kinematics of vesicles. The “Discussion and conclusion” section is dedicated to a general discussion of the results and a general conclusion of the study.
THEORETICAL BACKGROUND
The theoretical approaches treating the dynamics of a deformable shell whose shape is free to adapt to the surrounding flow enter the class of problems that are nonlocal, even nonlinear, and therefore not trivial to solve analytically. We briefly summarize the main theoretical and experimental results already reported on the motion of rigid and/or soft shells under a shear flow.
Unbounded shear flow
The motion under an unbounded shear flow of ellipsoidal particles of given shape, volume and area, consisting of an incompressible viscous fluid surrounded by a fluid membrane was modeled analytically by Keller and Skalak (8), with the aim of describing the motion of red blood cells. Under suitable conditions of aspect ratio (the ratio of the minor/major axis) and viscosity ratio (the ratio of internal/external fluid viscosities), the particles exhibit a tank-treading motion, where their membrane rotates around their center of mass in a tank-tread-like motion. The rotating motion of the membrane transfers the tangential stresses of the shear flow to the inner fluid, which rotates and dissipates the work done by external flow, allowing the particles to maintain a steady stationary orientation, characterized by a constant angle of inclination with respect to the flow direction.
Both the inclination angle and the tank-treading frequency decrease when the aspect ratio decreases. The constraint of fixed ellipsoidal shape has been relaxed in numerical approaches in three dimensions (29) and two dimensions (16). The simulations show that when the external viscosity is equal to that within the particle, as is the case for a vesicle, the object undergoes a tank-treading motion of its membrane and its angle of inclination is correctly predicted by the model of Keller and Skalak. In particular, the inclination angle decreases with the reduced volume and is independent of the shear rate. In experimental studies of lipid vesicles under shear flow, de Hass et al. (30,31) confirmed this prediction: the vesicles tank-tread and their shape rapidly reaches a stationary prolate shape whose angle of inclination is independent of the shear rate.
Effect of a wall: shapes and lift
The effect of a wall on the motion under shear flow of deformable vesicles has generated several recent theoretical studies (13–17) and experimental investigations on giant lipid vesicles. Two features observed in the absence of a wall were recovered: vesicles tank-tread and present a steady tilt. Vesicle shapes and tilt were numerically computed by Sukumaran and Seifert (17). The steady tilt of the vesicle was found to induce a fore-aft asymmetric pressure field beneath the vesicle, giving rise to a net lift force of viscous origin. The effects of this lift force were indeed experimentally observed on buoyant vesicles, which have the capacity to unbind from the wall at high wall shear rate (18,32,19). By balancing this lift force with vesicle buoyancy, we proposed a first characterization of this force (19). Nonbuoyant and nonadhesive vesicles were predicted to progressively drift away from the wall with a velocity calculated by Olla (15).
Effect of a wall: translational and rotational velocity
The velocity of soft shells flowing close to and parallel to a wall was not detailed in the recent theoretical works on deformable particles (13,15,17). It has been determined for rigid spheres of radius R as a function of their distance h to a wall by Goldman and co-workers (33). Because the sphere is torque-free, it rotates as a consequence of the presence of the wall. Both translational V and rotational ω velocities were calculated as a function of the applied wall shear rate  in both limits h ≪ R and h ≫ R. The hydrodynamic description yields for V:
in both limits h ≪ R and h ≫ R. The hydrodynamic description yields for V:
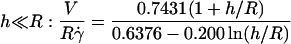 |
(a) |
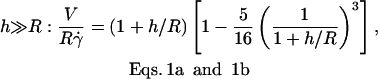 |
(b) |
and for 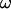 :
:
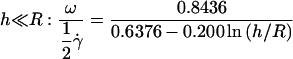 |
(a) |
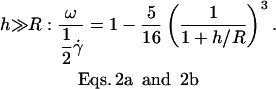 |
(b) |
MATERIALS AND METHODS
Vesicle preparation
Giant unilamellar vesicles were prepared by the standard electroformation method (34) by hydrating a lipid film under an AC field. 1,2-Dioleoyl-sn-glycero-3-phosphocholine, purchased from Sigma (St Louis, MO) (powder, P 6354), was first dissolved in chloroform and methanol solutions (9:1 volume ratio) at 1.5 mg/ml and the solution was then spread on the conductive faces of two transparent glass plates coated with a film of indium tin oxide (ITO). After drying (2 h under primary vacuum), a sucrose solution was injected in a chamber formed by the ITO plates facing each other, separated by a Teflon spacer and connected to an AC generator (frequency 10 Hz). The potential was progressively increased from 0.2 to 1.5 V and kept constant for 3 h. The frequency was finally decreased to 4 Hz to detach vesicles from the ITO plates. Various concentrations of sucrose solution of 50, 100, 200, and 250 mM were used of densities, respectively, equal to 100.5, 101.1, 102.4, and 103.1 g/l (40). Vesicles were then diluted in glucose solution of higher osmolality from 50 to 290 mM but lower buoyancy for at least 1 h. All solutions were prepared at pH = 7.4 in Hepes buffer (0.5 mM). As vesicle membranes are permeable to water and not to sucrose and glucose, the difference between the inner and the outer osmotic pressures resulted in partial water diffusion out of the vesicles, which produces partially deflated flaccid deformable objects. It should be noted that over the timescale of the flow experiments described below, the vesicle membranes can be considered as impermeable. Finally, due to the difference of molar weights between the sucrose and the glucose, vesicles settled on the substrate and their buoyancy was controlled and varied over a large range. The precision of the densities of the sucrose and glucose solutions were 0.13 and 0.07 g/l, respectively, and is due to the experimental uncertainty of the concentration of the solutions (1 mM). The difference of density Δρ obtained for all the vesicles are reported in Table 1. These values have an estimated precision of 0.2 g/L. Consequently, the equivalent precision of the weights of the vesicles are of the order of 0.01 pN for vesicles of 10 μm in radius and 3 pN for bigger vesicles of 70 μm in radius. To model the motion of the vesicles we also used spherical rigid polystyrene beads of radii equal to 5, 12.3, 21, 42.5, 45, and 45.6 μm, purchased from Polysciences Europe (Eppleheim, Baden-Würtemberg, Germany).
TABLE 1.
Experimental parameters for 33 vesicles named by their rank, used in the determination of the lift force
| No | R(μm) | P = Fl (pN) | Δρg (Pa/m) |  |
1 − ν |
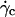 (s−1) (s−1) |
θL(rad) |
|---|---|---|---|---|---|---|---|
| 1 | 8.7 | 0.2 | 68.7 | 1.052 | 0.036 | 0.45 | 0.687 |
| 2 | 13.4 | 1.6 | 162.8 | 1.147 | 0.024 | 1.62 | 0.654 |
| 3 | 14.7 | 0.9 | 68.7 | 1.052 | 0.138 | 0.44 | 0.475 |
| 4 | 15.5 | 1.1 | 68.7 | 1.052 | 0.060 | 0.45 | 0.525 |
| 5 | 15.6 | 2.4 | 149.1 | 1.131 | 0.017 | 1.45 | – |
| 6 | 17.3 | 0.2 | 9.8 | 1.016 | 0.015 | 0.45 | 0.641 |
| 7 | 18.1 | 4.2 | 168.4 | 1.153 | 0.045 | 1.07 | – |
| 8 | 18.7 | 1.9 | 68.7 | 1.052 | 0.065 | 0.44 | – |
| 9 | 19.5 | 5.2 | 168.4 | 1.153 | 0.053 | 1.00 | – |
| 10 | 19.6 | 5.3 | 168.4 | 1.153 | 0.072 | 0.88 | – |
| 11 | 20.5 | 4.7 | 131.9 | 1.115 | 0.045 | 0.94 | – |
| 12 | 20.5 | 5.1 | 140.5 | 1.122 | 0.056 | 0.88 | – |
| 13 | 20.9 | 2.6 | 68.7 | 1.052 | 0.077 | 0.44 | – |
| 14 | 21.3 | 6.6 | 162.8 | 1.147 | 0.010 | 6.59 | – |
| 15 | 21.3 | 5.3 | 131.9 | 1.115 | 0.071 | 0.82 | – |
| 16 | 23.3 | 3.6 | 68.7 | 1.052 | 0.031 | 0.56 | – |
| 17 | 23.7 | 6.8 | 121.9 | 1.082 | 0.023 | 1.44 | – |
| 18 | 23.9 | 3.9 | 68.7 | 1.052 | 0.023 | 0.75 | – |
| 19 | 24.1 | 9.6 | 162.8 | 1.147 | 0.025 | 1.66 | 0.587 |
| 20 | 25.3 | 9.6 | 140.5 | 1.122 | 0.042 | 1.00 | – |
| 21 | 25.9 | 2.9 | 39.6 | 1.021 | 0.054 | 0.31 | 0.540 |
| 22 | 26.2 | 0.7 | 9.8 | 1.016 | 0.015 | 0.35 | 0.655 |
| 23 | 26.5 | 5.4 | 68.7 | 1.052 | 0.020 | 0.63 | – |
| 24 | 27.3 | 13.4 | 157.9 | 1.141 | 0.033 | 1.14 | 0.562 |
| 25 | 28.4 | 11.7 | 121.9 | 1.082 | 0.026 | 1.13 | – |
| 26 | 31.2 | 15.5 | 121.9 | 1.082 | 0.057 | 0.88 | – |
| 27 | 32.5 | 5.7 | 39.6 | 1.021 | 0.029 | 0.31 | 0.576 |
| 28 | 35.3 | 29.9 | 162.8 | 1.147 | 0.012 | 1.76 | 0.663 |
| 29 | 36.9 | 2.1 | 9.8 | 1.016 | 0.020 | 0.25 | – |
| 30 | 39.0 | 40.5 | 162.8 | 1.147 | 0.026 | 1.21 | 0.632 |
| 31 | 42.8 | 22.5 | 68.7 | 1.052 | 0.021 | 2.80 | – |
| 32 | 50.9 | 87.1 | 157.9 | 1.141 | 0.022 | 1.28 | 0.560 |
| 33 | 67 | 153.6 | 121.9 | 1.082 | 0.010 | 2.20 | – |
P is the weight of the vesicles, Δρ is the difference of density between the inner and the outer fluid, g is the acceleration of gravity, η is the viscosity of the outer fluid given relatively to the viscosity of water ηwater, R is the radius of the vesicles, ν their reduced volume, 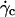 the critical wall shear rate of detachment measured visually, and θL is the limit angle of inclination of the major axis of inertia of the vesicle relative to the direction of the flow.
the critical wall shear rate of detachment measured visually, and θL is the limit angle of inclination of the major axis of inertia of the vesicle relative to the direction of the flow.
Flow chamber
The flow chamber was a parallelepiped-plate chamber (spectrophotometric circulation chamber from Hellma (Müllheim, Germany), height d = 1 mm, width a = 10 mm, length = 45 mm) with four optical faces. No significant adhesion between vesicles and the glass substrate was observed. The flow was applied using a syringe pump. The laminar wall shear rate 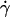 was calibrated using suspensions of 2-μm diameter latex beads. Bead velocities were measured at given flow rates as a function of their distance to the substrate. The velocities were found to vary linearly with the distance to the substrate (up to a distance of 150 μm from the wall where the parabolic character of the flow appears) and the slopes of the obtained linear curves yielded the wall shear rates. Also, we verified that we obtained a linear relationship between the wall shear rate
was calibrated using suspensions of 2-μm diameter latex beads. Bead velocities were measured at given flow rates as a function of their distance to the substrate. The velocities were found to vary linearly with the distance to the substrate (up to a distance of 150 μm from the wall where the parabolic character of the flow appears) and the slopes of the obtained linear curves yielded the wall shear rates. Also, we verified that we obtained a linear relationship between the wall shear rate 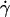 and the flow rate Q produced in the chamber according to the relation:
and the flow rate Q produced in the chamber according to the relation: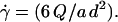
Side-view observation
We oriented a phase contrast inverted microscope (Leica DM IRB, Wetzlar, Germany) horizontally. The flow chamber was mounted on a homemade stainless steel holder keeping the chamber horizontal with the 10- × 45-mm faces orthogonal to gravity. The observation of the motion of the vesicles was done through the 1- × 45-mm cross-section faces. The flow was produced in the chamber parallel to the 10- × 45-mm faces, along the 45-mm side. Tipping the microscope horizontally and working at low-angle incidence allowed us to observe well-defined side-view images of both vesicles and their reflections on the substrate. The angle of observation relative to the 10- × 45-mm face was fixed by the holder to a small constant value (φ ≤ 1°) throughout all the experiments. The vesicles were hence flowing and observed at low-angle incidence orthogonally to gravity and in the plane of shear. The measured value h of the distance between the membrane of the vesicle and the substrate is a projection of the real distance hreal. The relation between hreal and h is simply h = cos(φ)hreal ≈ 0.9998 hreal. We see that the low value of the observational angle was not the main source of error on the measurement of hreal and in the following h = hreal. Indeed, most observations were performed with a 20× phase contrast objective allowing the observation of the vesicles deep in the chamber (long working distance). Hence, the main source of error originates from the optical resolution of the objective giving a resolution of 0.8 μm/pixel on the images and restricting the precision of the measurement of h to 1 μm. Pictures were captured with a charge-coupled device camera (COHU 4910) and image analysis was performed using the image software (National Institutes of Health, 1.62c). All vesicles studied were at a minimal distance of 1 mm from the nearest 1- × 45-mm face of the chamber, so that velocity field and wall shear rate values were not disturbed by the presence of the side walls.
Protocol of measurement
Vesicles are slowly injected in the chamber and allowed to settle. One well-contrasted axisymmetric vesicle is chosen at rest. A flow is then applied. The wall shear rate applied to the vesicle is then increased gradually from 0.1 to 10 s−1, by increasing step by step the flow rate in the chamber. The vesicle reaches a constant velocity for each flow rate or wall shear rate. Its motion is observed over a traveling distance varying from 600 to 1200 μm. The flow is finally stopped to check that the vesicle recovers its initial shape at rest.
Determination of vesicle shape and position
The projection of the beads (Fig. 1 a) and the vesicles (Fig. 1, b and c) onto their meridian plane is directly observed with side-view microscopy. The analysis of the images allows the determination of beads radii Rb and the geometrical characteristics of the vesicles. The enclosed volume V and surface area S of each vesicle are deduced from azimuthal integration over the vesicle contour at rest by applying the Papus-Guldin theorem (assuming an axisymmetric shape) (35). V and S are then given, respectively, by 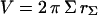 and
and 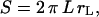 where Σ and L are the surface area and the contour length of half of the vesicle projection onto its meridian plane, respectively, rΣ and rL are the distances of the centers of mass of the surface and the contour from the vertical symmetry axis (Fig. 1 c). Each vesicle is also characterized by its effective radius R = (3V/4π)1/3 defined as the radius of the sphere with the same volume. The state of deswelling of the vesicles is characterized by their reduced volume,
where Σ and L are the surface area and the contour length of half of the vesicle projection onto its meridian plane, respectively, rΣ and rL are the distances of the centers of mass of the surface and the contour from the vertical symmetry axis (Fig. 1 c). Each vesicle is also characterized by its effective radius R = (3V/4π)1/3 defined as the radius of the sphere with the same volume. The state of deswelling of the vesicles is characterized by their reduced volume, 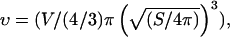 defined as the ratio of the volume of the vesicle relative to the volume of the sphere with the same surface (ν ≤ 1, ν = 1 for a sphere). The observation plane intercepts the meridian plane of the vesicle yielding the direction of two of its three principal axes of inertia. Indeed, one axis of inertia is given by the direction of observation and the two other axes of inertia belong to the plane of observation that is actually a plane of symmetry for the vesicle in motion. Therefore, the two axes of inertia can be determined by image analysis of the cross section of the vesicle, along with the angle θ between the major principal axis of inertia and the flow direction, and the position of the center of mass of the vesicle during the motion. The distance of the vesicle from the substrate h is also directly determined from the side-view observation. The measurement of h is performed by measuring the closest distance between the membrane of the vesicle and its reflection on the substrate; h is hence half this distance. The precision reached by this measurement is optically estimated to 1 μm.
defined as the ratio of the volume of the vesicle relative to the volume of the sphere with the same surface (ν ≤ 1, ν = 1 for a sphere). The observation plane intercepts the meridian plane of the vesicle yielding the direction of two of its three principal axes of inertia. Indeed, one axis of inertia is given by the direction of observation and the two other axes of inertia belong to the plane of observation that is actually a plane of symmetry for the vesicle in motion. Therefore, the two axes of inertia can be determined by image analysis of the cross section of the vesicle, along with the angle θ between the major principal axis of inertia and the flow direction, and the position of the center of mass of the vesicle during the motion. The distance of the vesicle from the substrate h is also directly determined from the side-view observation. The measurement of h is performed by measuring the closest distance between the membrane of the vesicle and its reflection on the substrate; h is hence half this distance. The precision reached by this measurement is optically estimated to 1 μm.
FIGURE 1.
Side views of a (a) polystyrene bead of radius Rb = 45 μm, (b) vesicle of radius R = 67 μm, (c) vesicle of radius R = 22 μm. On the figure (c), Σ and L are the surface area and the contour length of half of the vesicle projection onto its meridian plane respectively, rΣ and rL are the distances of the centers of mass of the surface and the contour from the vertical symmetry axis.
The moment of inertia of an object relative to a given axis is by definition the sum of the square of the distances between the points in the object and the axis, and the principal axes of inertia of the object represent the axes for which the moments of inertia are minimal. We developed a simple edge recognition program to detect the cross section of the vesicle and analyzed the image to find the direction of the two axes of inertia by giving a virtual weight to the pixels of the cross section corresponding to their gray level. When the vesicle is at rest the axis of symmetry is one of the axes of inertia.
BEHAVIOR OF VESICLES AND BEADS UNDER SHEAR FLOW
Typical images obtained during a flow experiment are given in Figs. 2 and 3. Vesicles and beads as well as their lower reflection on the substrate are well contrasted. When a given wall shear rate  is applied, vesicles and beads slowly move along the flow direction at constant velocity. They rotate, which is clearly seen from the motion of defects within the beads or bound to vesicle membranes (Fig. 2).
is applied, vesicles and beads slowly move along the flow direction at constant velocity. They rotate, which is clearly seen from the motion of defects within the beads or bound to vesicle membranes (Fig. 2).
FIGURE 2.
Tank-treading motion of a vesicle at 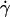 = 0.5 s−1 disclosed by the presence of a marker (invaginated vesicle). The time between each picture is 6 s.
= 0.5 s−1 disclosed by the presence of a marker (invaginated vesicle). The time between each picture is 6 s.
FIGURE 3.
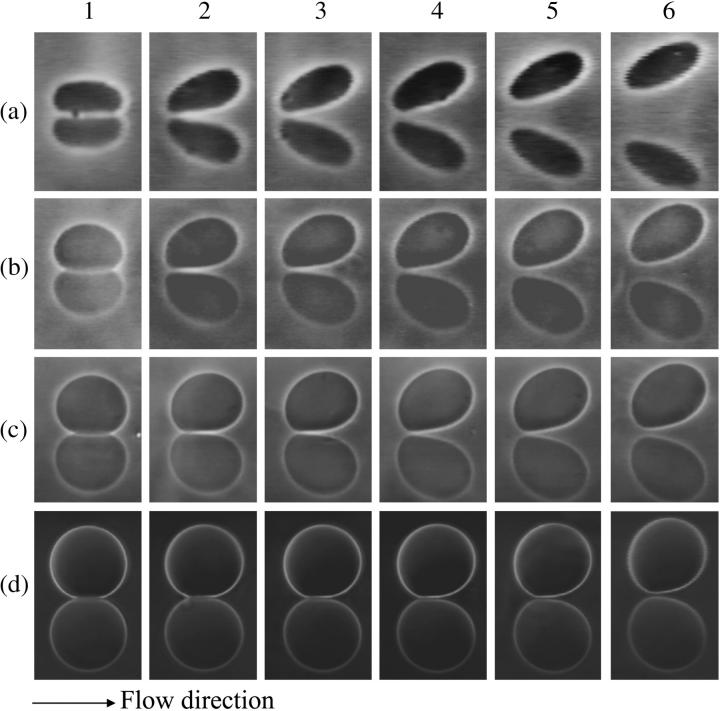
Shape diagram of vesicles under flow. Each row of pictures represents the deformation of one vesicle for different flow rate indexed from 1 to 6. Vesicle properties are listed in Table 1 by vesicle number. (a) Vesicle No. 3: (a,1) 0 s−1, (a,2) 0.25 s−1, (a,3) 0.38 s−1, (a,4) 0.50 s−1, (a,5) 1.00 s−1, (a,6) 2.1 s−1. (b) No. 21: (b,1) 0 s−1, (b,2) 0.11 s−1, (b,3) 0.17 s−1, (b,4) 0.28 s−1, (b,5) 0.45 s−1, (b,6) 0.79 s−1. (c) No. 29: (c,1) 0 s−1, (c,2) 0.09 s−1, (c,3) 0.14 s−1, (c,4) 0.23 s−1, (c,5) 0.32 s−1, (c,6) 0.36 s−1. (d) No. 33: (d,1) 0 s−1, (d,2) 0.38 s−1, (d,3) 0.63 s−1, (d,4) 1.25 s−1, (d,5) 1.9 s−1, (d,6) 3.77 s−1.
Initially deflated vesicles undergo a shape change when 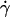 is applied: they exhibit stationary tilted shapes (characterized by the angle θ between their major axis of inertia and the flow direction). Vesicle tank-treading motion, i.e., fixed vesicle orientation associated with rotational motion of the membrane, is clearly observed from the motion of membrane-bound defects as illustrated in Fig. 2.
is applied: they exhibit stationary tilted shapes (characterized by the angle θ between their major axis of inertia and the flow direction). Vesicle tank-treading motion, i.e., fixed vesicle orientation associated with rotational motion of the membrane, is clearly observed from the motion of membrane-bound defects as illustrated in Fig. 2.
When the wall shear rate is progressively increased, shapes of flaccid vesicles go on changing and the angle θ increases, while the vesicles remain in the vicinity of the substrate. The vesicle-substrate distance is then too small to be directly determined from microscope imaging. Above a critical wall shear rate 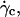 which depends on characteristics of the vesicles, their shapes change less and tend to be a prolate ellipsoid, and their tilt reaches a steady value. Concomitantly, the distance h between these quasiellipsoidal vesicles and the substrate strongly increases (several microns) and is directly observed on the images as illustrated in Fig. 3. When the wall shear rate is increased above
which depends on characteristics of the vesicles, their shapes change less and tend to be a prolate ellipsoid, and their tilt reaches a steady value. Concomitantly, the distance h between these quasiellipsoidal vesicles and the substrate strongly increases (several microns) and is directly observed on the images as illustrated in Fig. 3. When the wall shear rate is increased above 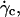 ellipsoidal vesicles move farther away from the substrate. This behavior is not observed for quasispherical vesicles and beads that are not deformed by the flow and remain settled on the substrate even under large wall shear rates (up to
ellipsoidal vesicles move farther away from the substrate. This behavior is not observed for quasispherical vesicles and beads that are not deformed by the flow and remain settled on the substrate even under large wall shear rates (up to 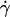 = 10 s−1).
= 10 s−1).
TILT AND SHAPE OF DEFORMABLE VESICLES
The evolution of the vesicle shapes under an increasing wall shear rate is represented in Fig. 3. It is clearly seen that the front of the vesicle moves upward progressively. One can notice also the region under the vesicle where the membrane is flat. Such profiles are very similar to those computed by Sukumaran and Seifert (17) or by Cantat and Misbah (13) for two-dimensional buoyant vesicles in adhesion, both subjected to a shear flow close to a substrate. In both cases of adhesion or buoyancy, a force is pulling the vesicles down.
Orientation far from the wall
When the wall shear rate 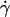 increases, the angle θ between the vesicles major axis of inertia and the flow direction increases up to a characteristic wall shear rate
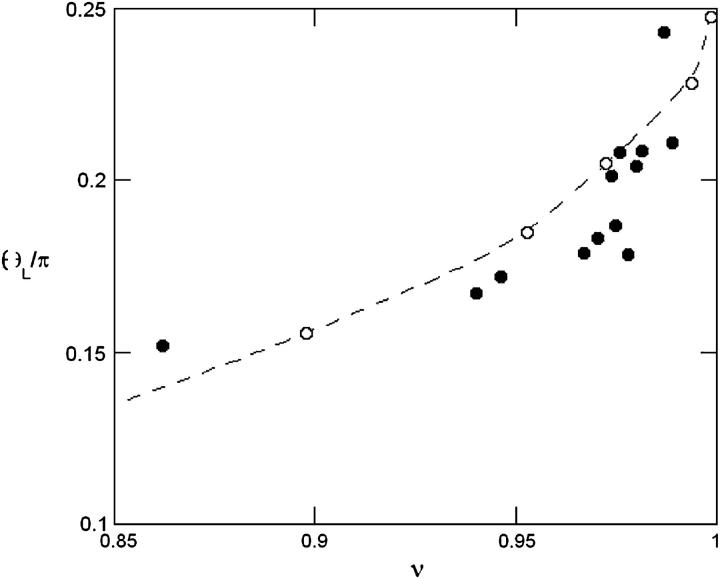
increases, the angle θ between the vesicles major axis of inertia and the flow direction increases up to a characteristic wall shear rate 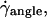 where θ reaches a limiting value θL. This limiting angle is independent of the wall shear rate and increases with the reduced volume ν of the vesicles as shown in Fig. 4. The maximum value of θL is π/4 for a quasispherical vesicle (ν ≈ 1). θL is reached when the wall-vesicle distance is of the order of magnitude of the vesicle radius. The “bulk” behavior of our vesicles is compared with the bulk predictions from Kraus et al. (29) in Fig. 4. We find a good agreement between the calculations of Kraus et al. and our experiments. Nevertheless, one can notice a slight difference of curvature between the numerical plot and the experimental data. The origin of this difference is likely due to the presence of the wall, which may change the value of θL.
where θ reaches a limiting value θL. This limiting angle is independent of the wall shear rate and increases with the reduced volume ν of the vesicles as shown in Fig. 4. The maximum value of θL is π/4 for a quasispherical vesicle (ν ≈ 1). θL is reached when the wall-vesicle distance is of the order of magnitude of the vesicle radius. The “bulk” behavior of our vesicles is compared with the bulk predictions from Kraus et al. (29) in Fig. 4. We find a good agreement between the calculations of Kraus et al. and our experiments. Nevertheless, one can notice a slight difference of curvature between the numerical plot and the experimental data. The origin of this difference is likely due to the presence of the wall, which may change the value of θL.
FIGURE 4.
Limit angle θL as a function of the reduced volume ν. The dashed line and the open circles represent the numerical simulations of Kraus et al. (29).
Orientation close to the wall
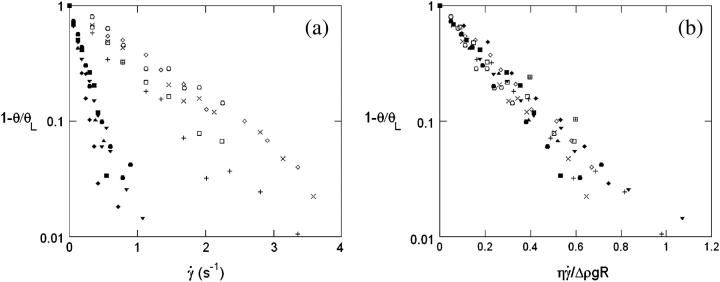
When the wall shear rate 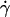 increases, the angle θ increases sharply. Variations of 1 − θ/θL with
increases, the angle θ increases sharply. Variations of 1 − θ/θL with 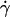 are plotted in Fig. 5 a with a logarithmic scale. An exponential decay is observed and yields the characteristic wall shear rate
are plotted in Fig. 5 a with a logarithmic scale. An exponential decay is observed and yields the characteristic wall shear rate 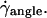 This characteristic wall shear rate depends on the viscosity
This characteristic wall shear rate depends on the viscosity 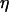 of the suspending fluid, the buoyancy of the vesicle (determined by the difference of density Δρ between the inner and the outer fluids), and its radius R. The normalized angle 1 − θ/θL is plotted as a function of a reduced parameter
of the suspending fluid, the buoyancy of the vesicle (determined by the difference of density Δρ between the inner and the outer fluids), and its radius R. The normalized angle 1 − θ/θL is plotted as a function of a reduced parameter 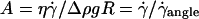 in Fig. 5 b, where g is the acceleration of gravity. A good superposition of the experimental curves is observed with only a slight dispersion. The parameter A is defined as the ratio of the viscous stresses produced by the shear flow to the hydrostatic pressure coming from the buoyancy of the internal fluid relative to the outer fluid. It describes the competition between the shear flow, which tends to produce a tilt of the vesicle, and gravity, which causes the sedimentation of the vesicle.
in Fig. 5 b, where g is the acceleration of gravity. A good superposition of the experimental curves is observed with only a slight dispersion. The parameter A is defined as the ratio of the viscous stresses produced by the shear flow to the hydrostatic pressure coming from the buoyancy of the internal fluid relative to the outer fluid. It describes the competition between the shear flow, which tends to produce a tilt of the vesicle, and gravity, which causes the sedimentation of the vesicle.
FIGURE 5.
(a) 1 − θ/θL in function of the wall shear rate 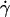 for 10 vesicles. The properties of the vesicles are reported in Table 1: (♦) No. 1; (▴) No. 3; (▪) No. 4; (+) No. 19; (▾) No. 21; (□) No. 24; (•) No. 27; (⋄) No. 28; (×) No. 30; (○) No. 32. (b) 1 − θ/θL in function of the
for 10 vesicles. The properties of the vesicles are reported in Table 1: (♦) No. 1; (▴) No. 3; (▪) No. 4; (+) No. 19; (▾) No. 21; (□) No. 24; (•) No. 27; (⋄) No. 28; (×) No. 30; (○) No. 32. (b) 1 − θ/θL in function of the 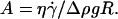 Symbols are the same as in panel a. (⊞) Angle of the two shapes extracted from Sukumaran and Seifert (18) and plotted in Fig. 6, e and f.
Symbols are the same as in panel a. (⊞) Angle of the two shapes extracted from Sukumaran and Seifert (18) and plotted in Fig. 6, e and f.
The parameter A can be rewritten as the ratio of a capillary number Ca and a bond number Bo that one can define for vesicles, by replacing the usual surface tension term by a bending term κ:  and
and 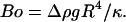 We then understand that the parameter A describes the systematical coupling that occurs between the elastic deformation (bending) of the vesicles induced by the shear flow and that produces the tilt, the presence of the gravity trying to orient the vesicle's major axis of inertia, and also the presence of the substrate that produces a counter force to the sedimentation. It is interesting to notice that the bending modulus cancels out and does not appear in the definition of A.
We then understand that the parameter A describes the systematical coupling that occurs between the elastic deformation (bending) of the vesicles induced by the shear flow and that produces the tilt, the presence of the gravity trying to orient the vesicle's major axis of inertia, and also the presence of the substrate that produces a counter force to the sedimentation. It is interesting to notice that the bending modulus cancels out and does not appear in the definition of A.
Shape of the vesicles under bounded shear flow
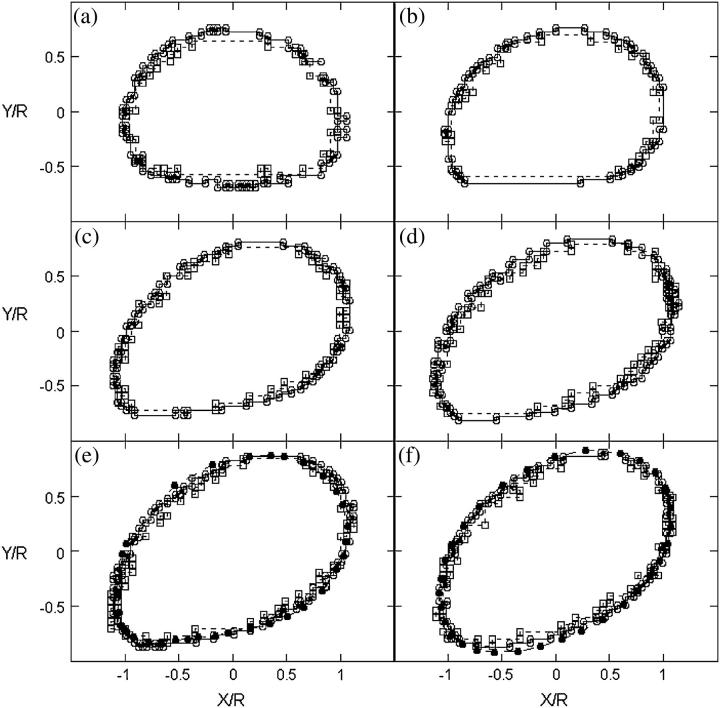
The global shape of the vesicles changes when the wall shear rate increases. The fore-aft symmetry is rapidly lost. The front of the vesicle moves upward whereas the rear stays close to the substrate and has a higher curvature than the front. The flat region beneath the vesicles close to the substrate seems to be reduced when A and/or the reduced volume increases (Fig. 3). The sequences of deformation shown in Fig. 3 for different vesicles depend on the reduced volume of the vesicles and the wall shear rate, but all shapes can be compared and superimposed by renormalizing the distances by R and the wall shear rate by 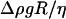 as is shown on Fig. 6 for two vesicles with the same reduced volume ν = 0.95. This observation confirms the role played by the dimensionless parameter A and shows that A and the reduced volume ν are the relevant parameters to describe the shape of vesicles subjected to a bounded shear flow without adhesion. Finally, we note that these shapes are well fit by the shape calculated by Sukumaran and Seifert (17) for the same value of the parameter A. Two of these shapes are shown in Fig. 6, e and f. The angles of inclination of the shapes calculated by Sukumaran and Seifert are also represented on Fig. 5 b and are in agreement with the experimental measurement obtained for all the vesicles. Nevertheless, we had to multiply the coordinates X/R and Y/R of the shape of the vesicles presented by the authors by a constant factor of 0.71 that we do not understand the origin. The shapes of buoyant vesicles presented by Sukumaran and Seifert (18) disclose a volume V that seems to be bigger than the sphere with the same surface S. We think that the authors have a numerical error on their XY scale explaining why we needed to rescale their shape by a constant value of 0.71.
as is shown on Fig. 6 for two vesicles with the same reduced volume ν = 0.95. This observation confirms the role played by the dimensionless parameter A and shows that A and the reduced volume ν are the relevant parameters to describe the shape of vesicles subjected to a bounded shear flow without adhesion. Finally, we note that these shapes are well fit by the shape calculated by Sukumaran and Seifert (17) for the same value of the parameter A. Two of these shapes are shown in Fig. 6, e and f. The angles of inclination of the shapes calculated by Sukumaran and Seifert are also represented on Fig. 5 b and are in agreement with the experimental measurement obtained for all the vesicles. Nevertheless, we had to multiply the coordinates X/R and Y/R of the shape of the vesicles presented by the authors by a constant factor of 0.71 that we do not understand the origin. The shapes of buoyant vesicles presented by Sukumaran and Seifert (18) disclose a volume V that seems to be bigger than the sphere with the same surface S. We think that the authors have a numerical error on their XY scale explaining why we needed to rescale their shape by a constant value of 0.71.
FIGURE 6.
Shapes of two vesicles with approximately the same ν = 0.95 at different wall shear rate 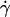 or A. The two vesicles are represented with two symbols and their properties are reported in Table 1. (○) Vesicle No. 21 and (□) vesicle No. 4. Each image from panels a to f represents the normalized shapes for the two vesicles having the closest parameter A. (a) (○), A = 0; (□), A = 0; (b) (○), A = 0.042; (□), A = 0.059; (c) (○), A = 0.168; (□), A = 0.177; (d) (○), A = 0.280; (□), A = 0.295; (e) (○), A = 0.391; (□), A = 0.413; (f) (○), A = 0.502; (□), A = 0.531. (•) Rescaled shapes of Sukumaran and Seifert (18) for a vesicle of a reduced volume of 0.95 and with panel e A = 0.398; (f) A = 0.597.
or A. The two vesicles are represented with two symbols and their properties are reported in Table 1. (○) Vesicle No. 21 and (□) vesicle No. 4. Each image from panels a to f represents the normalized shapes for the two vesicles having the closest parameter A. (a) (○), A = 0; (□), A = 0; (b) (○), A = 0.042; (□), A = 0.059; (c) (○), A = 0.168; (□), A = 0.177; (d) (○), A = 0.280; (□), A = 0.295; (e) (○), A = 0.391; (□), A = 0.413; (f) (○), A = 0.502; (□), A = 0.531. (•) Rescaled shapes of Sukumaran and Seifert (18) for a vesicle of a reduced volume of 0.95 and with panel e A = 0.398; (f) A = 0.597.
LIFT FORCE
In this section, we show that nonspherical vesicles are able to unbind from the substrate under sufficiently high wall shear rates. From the study of 33 vesicles prepared of various sizes, buoyancies, and reduced volumes, we deduce the typical values of this lift force and its functional dependence with the relevant parameters.
Observations
As it was shown in Fig. 3, the deflated vesicles lift off from the substrate when the wall shear rate is higher than a typical value 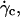 which depends on the viscosity
which depends on the viscosity 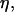 the difference of density Δρ of the vesicles, and their radius R. It is significant that at
the difference of density Δρ of the vesicles, and their radius R. It is significant that at 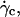 the vesicle shapes barely change and reach the asymptotic shapes observed far from the substrate, which reveals the weaker influence of the substrate. From a first group of 33 vesicles, we estimated visually the characteristic wall shear rate
the vesicle shapes barely change and reach the asymptotic shapes observed far from the substrate, which reveals the weaker influence of the substrate. From a first group of 33 vesicles, we estimated visually the characteristic wall shear rate 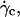 and for a second group of 11 vesicles, we studied the complete lift off by measuring the increase in height h as a function of the wall shear rate. Experimental quantities related to each vesicle are listed in Table 1.
and for a second group of 11 vesicles, we studied the complete lift off by measuring the increase in height h as a function of the wall shear rate. Experimental quantities related to each vesicle are listed in Table 1.
Measurement and characterization of the lift force
In the regime where the vesicles have clearly unbound from the substrate, they hover at a distance h from the wall, which increases upon increasing the wall shear rate. The distance h self-adjusts so that the sum of the forces applied to each vesicle is equal to zero, disclosing therefore the existence of a hydrodynamic lift force Fl, which counterbalances exactly the vesicle weight 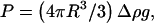 corrected by the buoyancy of the fluid. The value of this lift force, which acts on nonspherical vesicles, is therefore known for each lifted vesicle. It ranges in our experiment over three decades from 0.2 to 150 pN (Table 1).
corrected by the buoyancy of the fluid. The value of this lift force, which acts on nonspherical vesicles, is therefore known for each lifted vesicle. It ranges in our experiment over three decades from 0.2 to 150 pN (Table 1).
Dimensional analysis of the lift force
By dimensional analysis, the lift force Fl can be expressed as: 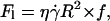 where f is a dimensionless function that depends on geometrical parameters, as the normalized geographical position of the vesicle from the substrate, expressed through the variable R/h, and on the shape of the vesicle that depends itself on the wall shear rate
where f is a dimensionless function that depends on geometrical parameters, as the normalized geographical position of the vesicle from the substrate, expressed through the variable R/h, and on the shape of the vesicle that depends itself on the wall shear rate 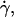 the reduced volume ν, and the bending module κ of the membrane. As proposed before (1), it is possible to characterize these features by using the global parameter ν only, because the vesicle shape is
the reduced volume ν, and the bending module κ of the membrane. As proposed before (1), it is possible to characterize these features by using the global parameter ν only, because the vesicle shape is 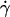 -independent at the unbinding, allowing us to drop the dependence with the bending modulus κ. The functional form of the lift force is then expected to be:
-independent at the unbinding, allowing us to drop the dependence with the bending modulus κ. The functional form of the lift force is then expected to be:
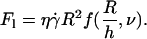 |
(3) |
We explored the R and h dependence of the hovering regime. We can already notice that the variations in R and h must be intimately related because they appear as a ratio and allow us in the following part to deduce the law of variation of Fl with the physical parameters.
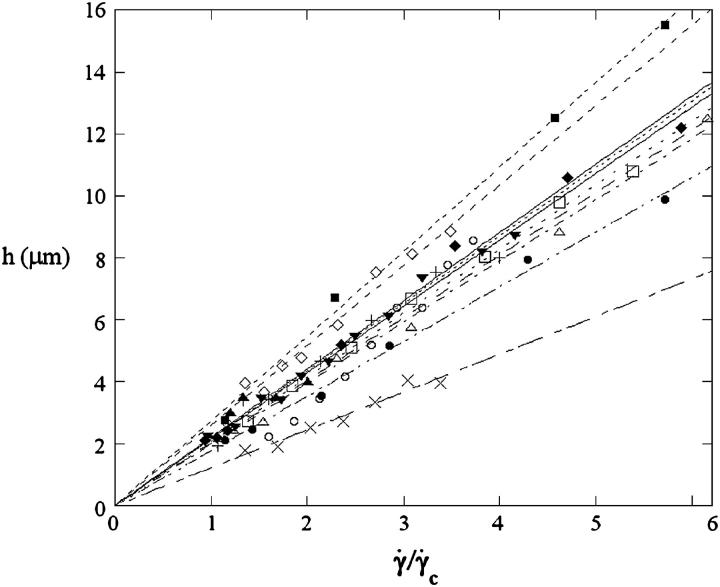
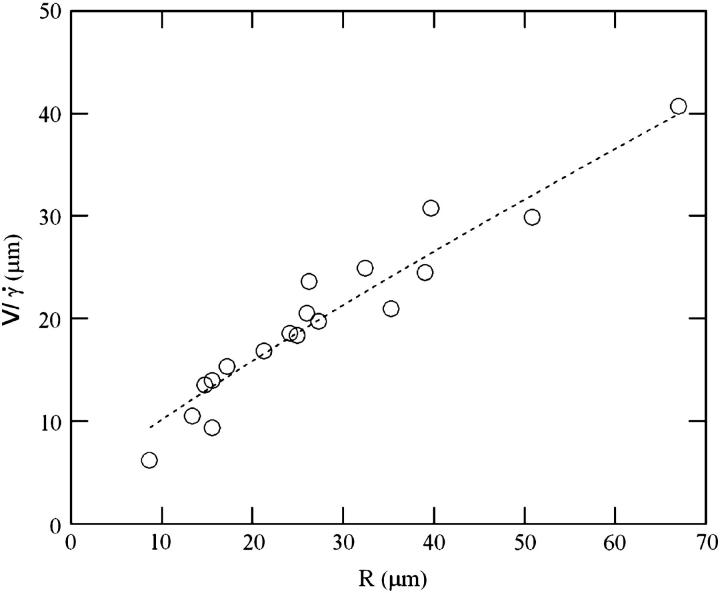
The h dependence of the lift measured visually: distance to the substrate at γ̇c
We report the variation of h with 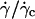 for the 11 vesicles in Fig. 7. A linear behavior is clearly observed. In this hovering regime, the lift force Fl is constant and equal to the vesicle weight P. For a given wall shear rate, the vesicle-substrate distance self-adjusts so that Fl = P. A linear variation of h with
for the 11 vesicles in Fig. 7. A linear behavior is clearly observed. In this hovering regime, the lift force Fl is constant and equal to the vesicle weight P. For a given wall shear rate, the vesicle-substrate distance self-adjusts so that Fl = P. A linear variation of h with 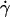 therefore implies a R3/h variation of the lift force. Indeed, if Fl = P, then
therefore implies a R3/h variation of the lift force. Indeed, if Fl = P, then 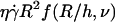 is a constant, implying that
is a constant, implying that 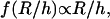 so that h varies linearly with
so that h varies linearly with 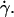 Therefore Fl should be written as:
Therefore Fl should be written as:
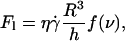 |
(4) |
which can be expressed at unbinding as:
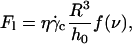 |
(5) |
where h0 is the distance of the vesicle when it notably lifts off under the typical wall shear rate 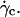 The equality between Eqs. 4 and 5 imposes a linear relation between the height of the vesicle and the applied wall shear rate given by the following equation:
The equality between Eqs. 4 and 5 imposes a linear relation between the height of the vesicle and the applied wall shear rate given by the following equation:
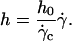 |
(6) |
FIGURE 7.
Height h of 11 vesicles in function of 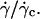 The linear fits give an estimation of the distance h0 at the unbinding from Eq. 7. Vesicles properties are reported in Table 1. (+) Vesicle No. 1: h0 = 2.1 μm; (▾) No. 2: 2.1; (▪) No. 3: 2.7; (□) No. 4: 2.1; (○) No. 6: 2.0; (♦) No. 7: 2.2; (▵) No. 15: 2.0; (⋄) No. 21: 2.6; (×) No. 22: 1.2; (•) No. 27: 1.8; (▴) No. 33: 2.2.
The linear fits give an estimation of the distance h0 at the unbinding from Eq. 7. Vesicles properties are reported in Table 1. (+) Vesicle No. 1: h0 = 2.1 μm; (▾) No. 2: 2.1; (▪) No. 3: 2.7; (□) No. 4: 2.1; (○) No. 6: 2.0; (♦) No. 7: 2.2; (▵) No. 15: 2.0; (⋄) No. 21: 2.6; (×) No. 22: 1.2; (•) No. 27: 1.8; (▴) No. 33: 2.2.
We note that, for the 11 studied vesicles in Fig. 7, h0 > 1 μm and most h0 values range in a narrow interval (1.2–2.7 μm), with a mean value equal to 2.2 ± 0.4 μm.
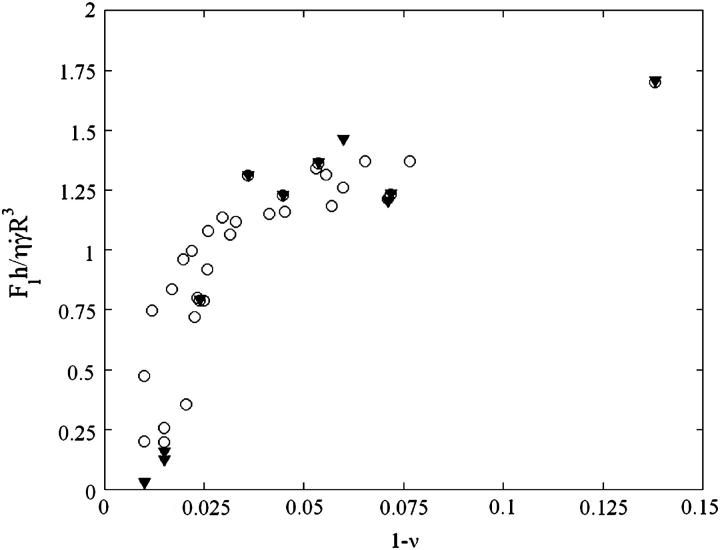
To probe the proposed functional dependence for the lift force and to experimentally determine the function f(ν), we plotted in Fig. 8 the force Fl normalized by 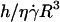 as a function of the parameter 1 − v for the 11 fully unbound vesicles for which Fl is known and equal to the weight, 4πΔρgR3/3. This normalized force writes as 4πΔρgh/3η
as a function of the parameter 1 − v for the 11 fully unbound vesicles for which Fl is known and equal to the weight, 4πΔρgR3/3. This normalized force writes as 4πΔρgh/3η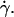 Moreover, we added on the curve the data obtained for the 33 vesicles, for which we did not experimentally determine the full h vs.
Moreover, we added on the curve the data obtained for the 33 vesicles, for which we did not experimentally determine the full h vs.  curve. Note that
curve. Note that 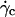 was determined visually. In this case, h0 was not known and we used the average value found from Fig. 7, which was equal to 2.2 μm. The curve obtained is unique for all the studied vesicles. The curve allows us to estimate the lift force close to a substrate experienced by an object whose mass, size, and aspect ratio are known.
was determined visually. In this case, h0 was not known and we used the average value found from Fig. 7, which was equal to 2.2 μm. The curve obtained is unique for all the studied vesicles. The curve allows us to estimate the lift force close to a substrate experienced by an object whose mass, size, and aspect ratio are known.
FIGURE 8.
Variation of the normalized lift force Fl in function of 1 − ν (○) at the unbinding when Fl = P, 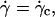 and h = h0:
and h = h0: 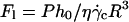 ; (▾) after unbinding where Fl = P and
; (▾) after unbinding where Fl = P and 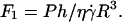
KINEMATICS AND DEFORMATION: TRANSLATION AND TANK-TREADING
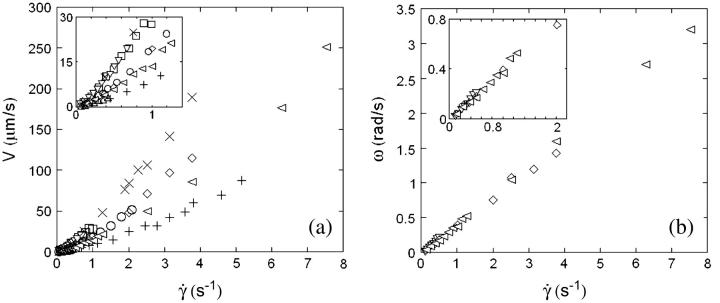
In this section, we describe the kinematics of the motion of vesicles both far from and close to the wall. From the coordinates of the center of mass of each vesicle, we calculate the translational velocity V as a function of the wall shear rate. Moreover, for three vesicles, we have extracted the rotational velocity of the membrane 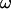 as a function of
as a function of 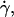 by following the position of a defect attached to the membrane (Fig. 2) relative to the center of mass of the vesicle. The plots obtained for both V and
by following the position of a defect attached to the membrane (Fig. 2) relative to the center of mass of the vesicle. The plots obtained for both V and 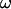 are represented respectively on Fig. 9 a for eight vesicles and Fig. 9 b for the three vesicles whose tank-treading frequency was measured.
are represented respectively on Fig. 9 a for eight vesicles and Fig. 9 b for the three vesicles whose tank-treading frequency was measured.
FIGURE 9.
(a) Translational velocities V of the vesicles in function of the wall shear rate 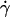 for eight vesicles. Their properties are reported in Table 1. (+) Vesicle No. 2; (▿) No. 21; (□) No. 22; (○) No. 4; (▵) No. 1; (⋄) No. 3; (×) No. 33; (◃) No. 7. (b) Tank-treading velocities for three vesicles. Same symbols as in panel a.
for eight vesicles. Their properties are reported in Table 1. (+) Vesicle No. 2; (▿) No. 21; (□) No. 22; (○) No. 4; (▵) No. 1; (⋄) No. 3; (×) No. 33; (◃) No. 7. (b) Tank-treading velocities for three vesicles. Same symbols as in panel a.
We observe a nonlinear behavior of the translational velocity V with the wall shear rate 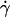 as the vesicles deform and unbind from the substrate, whereas the rotational velocity
as the vesicles deform and unbind from the substrate, whereas the rotational velocity 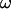 remains linear within the whole range of wall shear rates explored and is the same for the three vesicles.
remains linear within the whole range of wall shear rates explored and is the same for the three vesicles.
We next study the kinematics of the vesicles through the framework of the Goldman et al. model (33) for rigid spheres subjected to a linear shear flow far from and close to a wall.
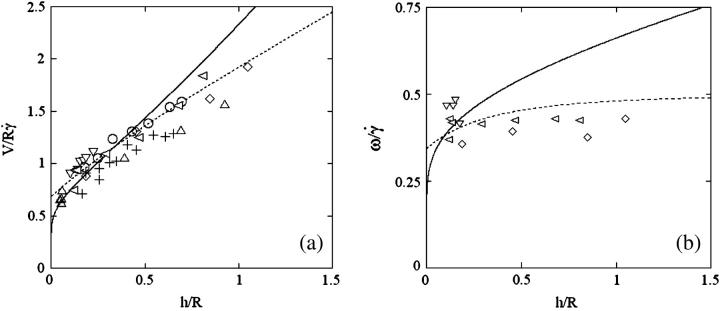
Kinematics far from the wall and the Goldman et al. approximation
We measured the translational and the rotational velocities of the vesicles far from the wall (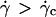 ), where the vesicles are detached from the substrate, their shape is almost stationary, and their distance h is measurable. In Fig. 10 a, we have plotted the variation of
), where the vesicles are detached from the substrate, their shape is almost stationary, and their distance h is measurable. In Fig. 10 a, we have plotted the variation of 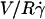 with h/R for the eight vesicles reported in Fig. 9 a, whose both translational velocities V and height h were determined experimentally. In Fig. 10 b, we have represented the variations of
with h/R for the eight vesicles reported in Fig. 9 a, whose both translational velocities V and height h were determined experimentally. In Fig. 10 b, we have represented the variations of 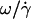 as a function of h/R for the three vesicles presented in Fig. 9 b. The data in Fig. 10 show a single trend that is well approximated by the two regimes given for rigid spheres far from (dashed lines; h/R ≫ 1) and close to (solid lines; h/R ≪ 1) the substrate (see Eqs. 1 and 2). They strongly suggest that the model of Goldman et al. for rigid spheres correctly describes the kinematics of moderately deflated vesicles close to a wall. The observed dispersion in the data may come from the nonspherical shape of the vesicles.
as a function of h/R for the three vesicles presented in Fig. 9 b. The data in Fig. 10 show a single trend that is well approximated by the two regimes given for rigid spheres far from (dashed lines; h/R ≫ 1) and close to (solid lines; h/R ≪ 1) the substrate (see Eqs. 1 and 2). They strongly suggest that the model of Goldman et al. for rigid spheres correctly describes the kinematics of moderately deflated vesicles close to a wall. The observed dispersion in the data may come from the nonspherical shape of the vesicles.
FIGURE 10.
(a) Translational velocities of the eight vesicles of Fig. 9 a normalized by the wall shear rate and the radius in function of the distance h of the vesicles divided by their radius R. (b) Tank-treading velocities of the three vesicles reported in Fig. 9 b in function of h/R. The symbols used are the same as in Fig. 9. In both cases, the fit lines represent the Goldman et al. laws without any adjustable parameter. The dashed lines represent the limit h/R ≫ 1 and the solid lines the case h/R ≪ 1.
Translation and kinematics: discussion on the distance h0 to the substrate at γ̇c
At 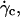 the distance to the substrate cannot be determined optically. We plotted the variations of
the distance to the substrate cannot be determined optically. We plotted the variations of 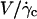 for all studied vesicles at the detachment as a function of R. The data fairly fall on a single curve independent of the reduced volume. The data of the translational velocity were fitted using Eq. 2 a with h = h0 as one adjustable parameter (Fig. 11). The fit yields h0 = 2.4 ± 0.3 μm. This value is in very good agreement with the value independently measured from the slopes of the linear curve of Fig. 7 for vesicles far from the substrate. It confirms that the substrate-membrane distance is similar for all vesicles at
for all studied vesicles at the detachment as a function of R. The data fairly fall on a single curve independent of the reduced volume. The data of the translational velocity were fitted using Eq. 2 a with h = h0 as one adjustable parameter (Fig. 11). The fit yields h0 = 2.4 ± 0.3 μm. This value is in very good agreement with the value independently measured from the slopes of the linear curve of Fig. 7 for vesicles far from the substrate. It confirms that the substrate-membrane distance is similar for all vesicles at 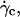 when they reach the shape they have far from the substrate, just before notably lifting off.
when they reach the shape they have far from the substrate, just before notably lifting off.
FIGURE 11.
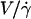 for (○) vesicles at
for (○) vesicles at 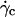 and (•) polystyrene beads. The dashed line represents the fit realized with Eq. 3a with the single adjustable parameter h0, found to be equal to 2.4 μm for all the vesicles.
and (•) polystyrene beads. The dashed line represents the fit realized with Eq. 3a with the single adjustable parameter h0, found to be equal to 2.4 μm for all the vesicles.
This distance differs from that reported on quasispherical vesicles either at rest (36) or moving in a quiescent fluid without unbinding (37), where the authors estimate that the substrate/membrane separation is of the order of 50 nm.
Translation and kinematics: discussion on the distance to the substrate below γ̇c
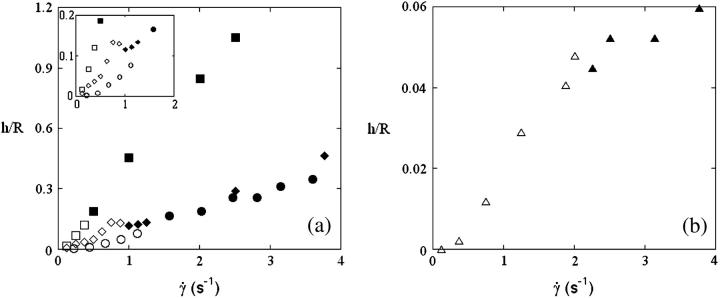
The question arises of the substrate-membrane separation distance at wall shear rates smaller than 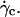 In absence of direct experimental measurements, we calculated the distance h between the vesicles and the substrate by injecting in Eq. 1 the experimental data (radius, translational velocity). The normalized heights h/R are reported for four vesicles in Fig. 12, a and b, for different reduced volume. We observe a crossover between the calculated value of h and the values measured optically just above
In absence of direct experimental measurements, we calculated the distance h between the vesicles and the substrate by injecting in Eq. 1 the experimental data (radius, translational velocity). The normalized heights h/R are reported for four vesicles in Fig. 12, a and b, for different reduced volume. We observe a crossover between the calculated value of h and the values measured optically just above 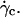 This result suggests that the vesicles continuously lift off from an equilibrium distance at rest around 50 nm to a distance of the order of 1 μm at
This result suggests that the vesicles continuously lift off from an equilibrium distance at rest around 50 nm to a distance of the order of 1 μm at 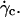 Nevertheless, the nonsphericity of vesicles may induce small changes in Goldman et al. equations that we did not account for. These effects may be significant because below
Nevertheless, the nonsphericity of vesicles may induce small changes in Goldman et al. equations that we did not account for. These effects may be significant because below 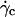 vesicle shapes change with
vesicle shapes change with 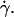 It is therefore impossible here to definitively discriminate if the increase of the separation distance with
It is therefore impossible here to definitively discriminate if the increase of the separation distance with 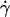 obtained from Eq. 1 is a real effect or if it is an artifact due to the variation of the shape of the vesicles. Indeed, the calculus of Goldman et al. considers a fixed spherical shape moving at a constant height h that is an external parameter of the problem not fixed by the hydrodynamics. In our case, below
obtained from Eq. 1 is a real effect or if it is an artifact due to the variation of the shape of the vesicles. Indeed, the calculus of Goldman et al. considers a fixed spherical shape moving at a constant height h that is an external parameter of the problem not fixed by the hydrodynamics. In our case, below 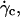 both the shape and the height are changing and coupled by the lift force pushing away the vesicle with an intensity dependent of the shape. We still do not know how to separate the effect of the shape from the effect of the changing distance to the wall on the kinematics of the vesicles.
both the shape and the height are changing and coupled by the lift force pushing away the vesicle with an intensity dependent of the shape. We still do not know how to separate the effect of the shape from the effect of the changing distance to the wall on the kinematics of the vesicles.
FIGURE 12.
The open symbols are the calculated heights h of the vesicles normalized by their radius R in function of 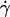 using the Goldman et al. equations (Eq. 3a); the solid symbols represent the actual measurements of the height. (a) Vesicle (▪ and □) No. 3; (• and ○) No. 2; (♦ and ◊) No. 7; and (b) (▴ and ▵) No. 33 a quasispherical vesicle. The properties of the vesicles are all reported in Table 1.
using the Goldman et al. equations (Eq. 3a); the solid symbols represent the actual measurements of the height. (a) Vesicle (▪ and □) No. 3; (• and ○) No. 2; (♦ and ◊) No. 7; and (b) (▴ and ▵) No. 33 a quasispherical vesicle. The properties of the vesicles are all reported in Table 1.
DISCUSSION AND CONCLUSION
In this article, we presented a thorough experimental study of the effect of the deformability on the shape and the kinematics of vesicles under wall-bounded shear flow. We showed how giant buoyant vesicles deform and incline relative to the direction of the flow. Far from the substrate, the angle of inclination between the major axis of inertia of the vesicles is found to follow the calculations of Kraus et al. (29). The inclination angle at the vicinity of the substrate deviates from that predicted by the simulation of Kraus et al.. This deviation decays exponentially with a reduced parameter A, which is the ratio of the viscous stresses and the hydrostatic pressure that act on the vesicles. We find that the observed detailed shapes of vesicles are well described by the simulation of Sukumaran and Seifert (17) and are fully characterized by two dimensionless parameters: their reduced volume 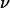 and the parameter
and the parameter 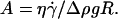
We confirmed in this article the existence of a viscous lift force pushing away the vesicles from the wall for increasing wall shear rates. We determined the functional variation of the lift force Fl above 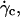 when the vesicle shape is stationary and we propose an empirical law for which there is at yet no theoretical explanation. The curve plotted in Fig. 9 permits the estimation of the lift force acting on a tank-treading object of known shape in a shear flow close to a wall. This force has to be accounted for when one tries to describe cell and vesicle behavior in a wall-bounded shear flow. Adhesion of the most deflated deformable objects may be significantly disturbed because such objects experience the strongest lift force. Nevertheless, the formula for Fl gives an order of magnitude of the repulsive forces pushing away from the endothelial walls cells like red blood cells or leukocytes during their flow. If we consider the flow in the postcapillary venules, the shear stresses range from 0.2 to 1 Pa. If we consider a typical distance h of 350 nm between the vascular wall and the cell membrane (typical size of a microvilli (38)), the lift force can be estimated from 31 to 155 pN for red blood cells (with
when the vesicle shape is stationary and we propose an empirical law for which there is at yet no theoretical explanation. The curve plotted in Fig. 9 permits the estimation of the lift force acting on a tank-treading object of known shape in a shear flow close to a wall. This force has to be accounted for when one tries to describe cell and vesicle behavior in a wall-bounded shear flow. Adhesion of the most deflated deformable objects may be significantly disturbed because such objects experience the strongest lift force. Nevertheless, the formula for Fl gives an order of magnitude of the repulsive forces pushing away from the endothelial walls cells like red blood cells or leukocytes during their flow. If we consider the flow in the postcapillary venules, the shear stresses range from 0.2 to 1 Pa. If we consider a typical distance h of 350 nm between the vascular wall and the cell membrane (typical size of a microvilli (38)), the lift force can be estimated from 31 to 155 pN for red blood cells (with 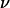 = 0.7, f(1 − 0.7) ∼ 2 by extrapolation in Fig. 9, and R = 3 μm) and from 46 to 230 pN for leukocytes (with
= 0.7, f(1 − 0.7) ∼ 2 by extrapolation in Fig. 9, and R = 3 μm) and from 46 to 230 pN for leukocytes (with 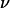 = 0.95, f(1 − 0.95) ∼ 1.25 in Fig. 9, and R = 4 μm). This estimation of Fl shows how hydrodynamic forces can be important at cellular scales. On one hand, the discoid shape of red blood cells together with the fluidity of both their membrane and their interior can induce a strong lift force, which helps to maintain the cells away from the endothelial walls producing a cell-free layer. On the other hand, the preservation of the spherical shape of leukocytes flowing close to a wall ensures that the lift force is weak and permits their capture onto the endothelium and the formation of adhesive links. Indeed, a little deformability (
= 0.95, f(1 − 0.95) ∼ 1.25 in Fig. 9, and R = 4 μm). This estimation of Fl shows how hydrodynamic forces can be important at cellular scales. On one hand, the discoid shape of red blood cells together with the fluidity of both their membrane and their interior can induce a strong lift force, which helps to maintain the cells away from the endothelial walls producing a cell-free layer. On the other hand, the preservation of the spherical shape of leukocytes flowing close to a wall ensures that the lift force is weak and permits their capture onto the endothelium and the formation of adhesive links. Indeed, a little deformability (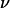 = 0.95) produces large hydrodynamic forces, which can be of the order of the adhesive forces (10–100 pN scale) (39). Moreover, we believe that this viscous lift force has to be taken into account in experiments using laminar flow chambers to study the interactions between a cell membrane and an adhesive wall in relative motion.
= 0.95) produces large hydrodynamic forces, which can be of the order of the adhesive forces (10–100 pN scale) (39). Moreover, we believe that this viscous lift force has to be taken into account in experiments using laminar flow chambers to study the interactions between a cell membrane and an adhesive wall in relative motion.
Finally, we showed that the kinematics of moderately deflated vesicles of fixed shapes at a distance of a few microns from the substrate can be described in a first approximation with a model of rigid spheres given by Goldman et al. (33). The expected deviation to these analytical results due to the nonsphericity of the vesicles is small; values of calculated vesicle-substrate distances h are within the (large) error bars of measured values. Very close to the substrate, the variation of the vesicle-substrate distance with the wall shear rate, estimated from the theoretical predictions of Goldman et al. (33), must be taken with caution because of the constant variation of the vesicle shape for increasing wall shear rates. The dynamical measurement of the distance h of the vesicles to the substrate during their motion below 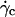 remains an experimental challenge but is a key parameter to better understand the continuous lifting phenomena.
remains an experimental challenge but is a key parameter to better understand the continuous lifting phenomena.
Acknowledgments
We thank Professor H. A. Stone for the reading of the manuscript and for fruitful discussions.
References
- 1.Godin, C., A. Caprani, J. Dufaux, and P. Flaud. 1993. Interactions between neutrophils and endothelial cells. J. Cell Sci. 106:441–448. [DOI] [PubMed] [Google Scholar]
- 2.Damiano, E. R., J. Westheider, A. Tozeren, and K. Ley. 1996. Variation in the velocity, deformation, and adhesion energy density of leukocytes rolling within venules. Circ. Res. 79:1122–1130. [DOI] [PubMed] [Google Scholar]
- 3.Chen, S. Q., R. Alon, R. C. Fuhlbrigge, and T. A. Springer. 1997. Rolling and transient tethering of leukocytes on antibodies reveal specializations of selectins. Proc. Natl. Acad. Sci. USA. 94:3172–3177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chen, S. Q., and T. A. Springer. 2001. Selectin receptor-ligand bonds: formation limited by shear rate and dissociation governed by the Bell model. Proc. Natl. Acad. Sci. USA. 98:950–955 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fischer, T. M., M. Stohrliesen, and H. Schmidschonbein. 1978. Red-cell as a fluid droplet—tank tread like motion of human erythrocyte membrane in shear flow. Science. 202:894–896. [DOI] [PubMed] [Google Scholar]
- 6.Goldsmith, H., and J. Marlow. 1972. Flow behavior of erythrocytes. I. Rotation and deformation in dilute suspensions. Proc. R. Soc. Lond. B Biol. Sci. 182:351–384. [Google Scholar]
- 7.Keller, S., and R. Skalak. 1982. A tank treading ellipsoidal particle in shear flow. J. Fluid Mech. 120:27–47. [Google Scholar]
- 8.Goldsmith, H. L. 1971. Red cell motions and wall interactions in tube flow. Fed. Proc. 30:1578–1588. [PubMed] [Google Scholar]
- 9.Goldsmith, H. L. 1967. Microscopic flow properties of red cells. Fed. Proc. 26:1813–1820. [PubMed] [Google Scholar]
- 10.Goldsmith, H. L., and S. G. Mason. 1962. Flow of suspensions through tubes. 1. Single spheres, rods, and discs. J. Colloid Sci. 17:448–476. [Google Scholar]
- 11.Karnis, A., H. L. Goldsmith, and S. G. Mason. 1963. Axial migration of particles in Poiseuille flow. Nature. 200:159–160. [Google Scholar]
- 12.Chaffey, C. E., H. Brenner, and S. G. Mason. 1965. Particle motions in sheared suspensions. VIII. Wall migration (theoretical). Rheol. Acta. 4:64. (Corrections. 1967. Rheol. Acta. 6:100). [Google Scholar]
- 13.Cantat, I., and C. Misbah. 1999. Lift force and dynamical unbinding of adhering vesicles under shear flow. Phys. Rev. Lett. 83:880–884. [Google Scholar]
- 14.Seifert, U. 1999. Hydrodynamics lift on bound vesicle. Phys. Rev. Lett. 83:876–879. [Google Scholar]
- 15.Olla, P. 2000. The behavior of closed inextensible membranes in linear and quadratic shear flows. Physica A. 278:87–106. [Google Scholar]
- 16.Beaucourt, J., F. Rioual, T. Seon, T. Biben, and C. Misbah. 2004. Steady to unsteady dynamics of a vesicle in a flow. Phys. Rev. E. 69:011906. [DOI] [PubMed] [Google Scholar]
- 17.Sukumaran, S., and U. Seifert. 1916. 2001. Influence of shear flow on vesicles near a wall: a numerical study. Phys. Rev. E. 64:1–11. [DOI] [PubMed] [Google Scholar]
- 18.Lorz, B., R. Simson, J. Nardi, and E. Sackmann. 2000. Weakly adhering vesicles in shear flow: tanktreading and anomalous lift force. Europhys. Lett. 51:468–474. [Google Scholar]
- 19.Abkarian, M., C. Lartigue, and A. Viallat. 2002. Tanktreading and unbinding of deformable vesicles in shear flow: determination of the lift force. Phys. Rev. Lett. 88:8103–8107. [DOI] [PubMed] [Google Scholar]
- 20.White, F. M. 2003. Fluid Mechanics, 5th ed. McGraw-Hill, New York, NY.
- 21.Dong, C., and X. X. Lei. 2000. Biomechanics of cell rolling: shear flow, cell-surface adhesion, and cell deformability. J. Biomech. 33:35–43. [DOI] [PubMed] [Google Scholar]
- 22.Ramachandran, V., M. Williams, T. Yago, D. W. Schmidtke, and R. P. McEver. 2004. Dynamic alterations of membrane tethers stabilize leukocyte rolling on P-selectin. Proc. Natl. Acad. Sci. USA. 101:13519–13524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jadhav, S., C. D. Eggleton, and K. Konstantopoulos. 2005. A 3-D computational model predicts that cell deformation affects selectin-mediated leukocyte rolling. Biophys. J. 88:96–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Khismatullin, D. B., and G. A. Truskey. 2004. A 3D numerical study of the effect of channel height on leukocyte deformation and adhesion in parallel-plate flow chambers. Microvasc. Res. 68:188–202. [DOI] [PubMed] [Google Scholar]
- 25.Chang, K. C., D. F. J. Tees, and D. A. Hammer. 2000. The state diagram for cell adhesion under flow: leukocyte rolling and firm adhesion. Proc. Natl. Acad. Sci. USA. 97:11262–11267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.King, M. R., and D. A. Hammer. 2001. Multiparticle adhesive dynamics: hydrodynamic recruitment of rolling leukocytes. Proc. Natl. Acad. Sci. USA. 98:14919–14924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Park, E. Y., M. J. Smith, E. S. Stropp, K. R. Snapp, J. A. DiVietro, W. F. Walker, D. W. Schmidtke, S. L. Diamond, and M. B. Lawrence. 2002. Comparison of PSGL-1 microbead and neutrophil rolling: microvillus elongation stabilizes P-selectin bond clusters. Biophys. J. 82:1835–1847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yago, T., A. Leppanen, H. Qiu, W. D. Marcus, M. U. Nolbert, C. Zhu, R. D. Cummings, and R. P. McEver. 2002. Distinct molecular and cellular contributions to stabilizing selectin-mediated rolling under flow. J. Cell Biol. 158:787–799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kraus, M., W. Wintz, U. Seifert, and R. Lipowsky. 1996. Fluid vesicles in shear flow. Phys. Rev. Lett. 77:3685–3689. [DOI] [PubMed] [Google Scholar]
- 30.de Hass, K. H., C. Blom, D. van den Ende, M. G. H. Duits, and J. Mellema. 1997. Deformation of giant lipid bilayer vesicles in shear flow. Phys. Rev. E. 56:7132–7137. [Google Scholar]
- 31.de Hass, K. H., D. van den Ende, C. Blom, E. Altena, and G. Beukema. 1998. A counter-rotating Couette apparatus to study deformation of a sub-millimeter sized particle in shear flow. Rev. Sci. Instrum. 69:1391–1397. [Google Scholar]
- 32.Razpet, A., G. Gomišč, V. Arrigler, S. Svetina, and B. Žekš. 2000. Rotation of giant phospholipid vesicles in uniform shear flow. Eur. J. Physiol. 439(Suppl):R141–R142. [PubMed] [Google Scholar]
- 33.Goldman, A. J., R. G. Cox, and H. Brenner. 1967. Slow viscous motion of a sphere parallel to a plane. Chem. Eng. Sci. 22:637–660. [Google Scholar]
- 34.Angelova, M. I., S. Soléau, P. Méléard, J. Faucon, and P. Bothorel. 1992. Preparation of giant vesicles by external AC electric fields. Prog. Colloid Polym. Sci. 89:127–133. [Google Scholar]
- 35.Kern, W. F., and J. R. Bland. 1948. Theorem of Pappus. In Solid Mensuration with Proofs, 2nd Ed. Wiley, New York, NY. 110–115.
- 36.Braun, D., and P. Fromherz. 1998. Fluorescence interferometry of neuronal cell adhesion on microstructured silicon. Phys. Rev. Lett. 81:5241–5244. [Google Scholar]
- 37.Abkarian, M., C. Lartigue, and A. Viallat. 2001. Motion of phospholipidic vesicles along an inclined plane: sliding and rolling. Phys. Rev. E. 63:1–7. [DOI] [PubMed] [Google Scholar]
- 38.Shao, J. O., H. P. Ting-Beall, and R. M. Hochmuth. 1998. Static and dynamics lengths of neutrophil microvilli. Proc. Natl. Acad. Sci. USA. 95:6797–6802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bongrand, P. 1999. Ligand-receptor interactions. Rep. Prog. Phys. 62:921–968. [Google Scholar]
- 40.Weast, R., M. Astle, and W. Beyer. 1989. CRC Handbook of Chemistry and Physics, 69th Ed. CRC Press, Boca Raton, FL.