Measurement of Single Macromolecule Orientation by Total Internal Reflection Fluorescence Polarization Microscopy

Abstract

A new approach is presented for measuring the three-dimensional orientation of individual macromolecules using single molecule fluorescence polarization (SMFP) microscopy. The technique uses the unique polarizations of evanescent waves generated by total internal reflection to excite the dipole moment of individual fluorophores. To evaluate the new SMFP technique, single molecule orientation measurements from sparsely labeled F-actin are compared to ensemble-averaged orientation data from similarly prepared densely labeled F-actin. Standard deviations of the SMFP measurements taken at 40 ms time intervals indicate that the uncertainty for individual measurements of axial and azimuthal angles is ∼10° at 40 ms time resolution. Comparison with ensemble data shows there are no substantial systematic errors associated with the single molecule measurements. In addition to evaluating the technique, the data also provide a new measurement of the torsional rigidity of F-actin. These measurements support the smaller of two values of the torsional rigidity of F-actin previously reported.

INTRODUCTION

High-resolution structures of proteins trapped in distinct static configurations have shown that rotational motions of compact domains are a common feature of their enzymatic and energy transducing mechanisms (1–11). In all of these systems, plausible relationships have been proposed between the observed rotational motions and the functional output, but testing the structurally derived hypotheses requires detection of the timing and extent of the rotations during activity.

Fluorescence polarization on bulk biological samples, such as suspensions of macromolecules or lipid vesicles, is a commonly used method to detect rotational motions (12,13). The signals are typically sensitive to the time course and extent of motions of the probe molecules. The method is well suited to detect time-resolved structural changes in organized systems, such as proteins embedded in lipid membranes (14) or muscle fibers (15). In these samples having a symmetry axis, the absolute distribution of probe orientations relative to that axis becomes available (16). With the recent availability of probes having known local orientation within the domain of interest (17,18), the information can be directly converted into distributions and motions of the local molecular domain. Among techniques available for detecting protein rotational motions, fluorescence polarization has the advantages of good sensitivity and time resolution and being relatively straightforward to set up and interpret.

In bulk experiments, however, relating the information about protein distributions to the orientation and dynamics of individual protein molecules is difficult because of averaging over an unsynchronized population. Abrupt perturbations of a molecular ensemble, such as temperature or pressure jumps, or rapid addition of substrate, can partially synchronize the population, but some important characteristics, such as fast or backward reaction steps and rare states, are usually not accessible.

Single molecule fluorescence measurements have been used to avoid the complications caused by the ensemble averaging in measurements on molecular distributions. Whereas most single molecule experiments have been focused on detecting the temporally resolved location of individual molecules, some have used fluorescence polarization to also determine structural information (e.g., 19–22). Single molecule fluorescence polarization has the potential to bridge the gap between techniques with atomic spatial resolution but poor time resolution (e.g., x-ray crystallography) and those capable of resolving kinetics but giving somewhat ambiguous structural information (e.g., fluorescence energy transfer).

Here, we present single molecule fluorescence polarization instrumentation that utilizes total internal reflection (TIR) microscopy. The TIR excitation offers an advantage over epifluorescence and confocal microscopy of a strong polarization component along the z axis (optical axis of the microscope) as well as along the x and y axes, making it possible to determine the three-dimensional (3D) orientation (22,23). Analytical techniques are described to determine, with a temporal resolution of ∼1–40 ms, the full 3D orientation of individual fluorescent probes and the extent of their wobbling motions on the microsecond and subnanosecond timescales. Comparison of single molecule and ensemble measurements of rhodamine bound to actin filaments are used to evaluate the accuracy and limits of the technique. Large rotational motions of the rhodamine probes (40° half-width of the wobble cone) on the microsecond timescale confirm other measurements of the dynamics of actin monomers in filaments that have been hypothesized to be crucial for actomyosin-based motility (24).

METHODS

Protein purification

Fast skeletal muscle myosin II was purified from New Zealand white rabbit back muscle as described by Margossian and Lowey (25) with minor modifications. Myosin was stored in 0.3 M KCl, 5 mM Hepes, pH 7.0, 5 mM NaN₃ and 50% glycerol at −20°C for up to 6 months. Actin was also purified from rabbit muscle according to a protocol similar to Spudich and Watt (26) as modified by Murray et al. (27). G-actin was stored on ice in G-buffer (2 mM Tris, pH 8.0, 0.2 mM CaCl₂, 0.2 mM ATP, 0.5 mM DTT) for 3–4 weeks or frozen in liquid N₂ and stored at −80°C for up to a year.

Protein labeling

G-actin was labeled at Cys³⁷⁴ with either 1,5-I-AEDANS (N-(iodoacetyl-N′(5-sulfo-1-napthyl)ethylenediamine, Sigma, St. Louis, MO, No. I8879) or 5-IATR (5-iodoacetamidotetramethylrhodamine, a gift from J. E. T. Corrie, National Institute for Medical Research, Mill Hill, London) following the protocol for labeling with pyrenyl-iodoacetamide (28) with minor modifications. Actin concentration and extent of labeling were determined using ɛ₂₉₀ = 2.66 × 10⁴ M⁻¹ cm⁻¹ for actin (29), ɛ₅₄₉ = 9.69 × 10⁴ M⁻¹ cm⁻¹ and ɛ₂₉₀/ɛ₅₄₉ = 0.21 for ATR (30,31), and ɛ₃₃₇ = 6.0 × 10³ M⁻¹ cm⁻¹ and ɛ₂₉₀/ɛ₃₃₇ = 0.21 for AEDANS (32). Labeled G-actin was aliquoted, rapidly frozen in liquid nitrogen, and stored at −80°C for up to 1 year. F-actin with various ratios of AEDANS-labeled, ATR-labeled, and unlabeled actin was made at a total actin concentration of 1 μM in F-buffer (10 mM Hepes, pH 7.0, 75 mM KCl, 2.5 mM MgCl₂) and stabilized with 5 μM phalloidin (Molecular Probes, Eugene, OR). Sparsely labeled F-actin was polymerized with 0.1% ATR-actin, 86% AEDANS-actin, and 14% unlabeled actin, whereas densely labeled F-actin had 10% ATR-actin, 10% AEDANS-actin, and 80% unlabeled actin. F-actin was stored on ice and used for up to 1 month.

Slide preparation

Labeled actin was held close to the microscope slide surface by binding to adhered myosin in the absence of ATP. A 10–20 μl flow cell was prepared using a 25 mm × 76 mm × 1 mm thick fused silica slide (Quartz Scientific, Fairport Harbor, OH), a 22 mm × 30 mm No.1 glass coverslip (Fisher Scientific, Hampton, NH), and two pieces of double-sided adhesive tape (Scotch, ∼80 μm thick). All buffers were passed through the flow cell by capillary action driven by wicking into filter paper; 30 μl of 225 nM full-length skeletal muscle myosin in high salt buffer (20 mM Hepes, pH 7.0, 5 mM MgCl₂, 600 mM KCl, 20 mM DTT) was added first and allowed to stand for 2–5 min. Next, 30 μl of 100 nM F-actin in F-buffer plus 20 mM DTT and 1 mM ATP was flowed in and allowed to stand for 5 min. Finally, 120 μl of F-buffer with 20 mM DTT was flowed through. Introducing the F-actin first in the presence of ATP, and then removing the ATP, aided in aligning filaments with the flow direction.

Experimental apparatus

The experimental apparatus (Fig. 1) was built around a Nikon TE-300 inverted epifluorescence microscope equipped with a computer-controlled piezoelectric x-y stage (Polytec PI (Auburn, MA) P-731.20). The excitation source was a 532 nm frequency doubled Nd:YAG laser (Lightwave Electronics (Mountain View, CA), Series 142, 220 mW). A rotatable half-wave plate (Meadowlark Optics, Frederick, CO) and linear polarizer were used to adjust the laser power. An electro-optical modulator (Conoptics (Danbury, CT), Pockel cell M370) rapidly switched the beam's polarization between vertical and horizontal polarizations, and then a polarizing beam splitter (PBS; Karl Lambrecht (Chicago, IL) BBPC-12-550nm) directed the beam alternatively along one of two directions (path 1 and path 2 in Fig. 1). Extinction ratios better than 1000:1 in this beam path alternation were necessary to reduce intensity variations at the sample due to interference. This was accomplished using a feedback system described in the Supplementary Material.

FIGURE 1.

Experimental apparatus. The input laser beam was alternately directed along path 1 and path 2. For each path, the beam passed through a linear polarizer (P), and then a Pockel cell (PC) to generate alternating linear polarizations parallel to (p) and perpendicular to (s) the relevant reflection plane. The beam was coupled into the quartz microscope slide by passing through the coupling prism (CP) and through index matching liquid. At the quartz/water interface, total internal reflection occurred, sending the beam back out through the coupling prism to a beam dump (not shown). The quartz slide was mounted on a piezoelectric stage (PS). Fluorescence was collected by a microscope objective lens (OL), passed through a barrier filter (BF), and imaged by a lens (L). Depending on the position of a removable mirror (RM), the fluorescence was imaged either onto an intensified CCD camera (ICCD) or through a Thompson beam splitting prism (BSP), onto two avalanche photodiodes (APDs).

Along each path, the laser beam passed through a “cleanup” Glan-Thompson polarizer (Newport Corp. (Irvine, CA) 10GT04AR.14) and then through another Pockel cell that rapidly rotated the polarization back and forth between vertical and horizontal. The beam was directed toward the sample flow cell by mirrors carefully aligned to reflect in the vertical and horizontal planes. Each beam passed through a 200 mm focal length lens, a custom built BK7 glass octagonal prism (ESCO Products, Oak Ridge, NJ), optical immersion liquid (Cargille (Cedar Grove, NJ) No. 50350, n = 1.458), and finally, into a 1 mm thick quartz slide. Each of the focused beams intersected the quartz-water interface, at the bottom of the slide, at an angle of ∼69° relative to the slide normal, an angle greater than the critical angle for total internal reflection (23,33). The incident laser beam was thus totally reflected and only an evanescent wave with a 1/e intensity decay constant of ∼140 nm was present in the flow cell at the surface of the quartz slide.

The path 1 laser beam is reflected at the quartz-water interface in the x-z plane, and path 2 in the y-z plane. By time multiplexing the two input paths at 50 Hz, and the two input beam polarizations for each path at 100 Hz, four excitation polarizations, labeled s1, p1, s2 and p2, were generated sequentially. The dwell time at each path and polarization was 9.9 ms, and 0.1 ms was allotted for switching between them.

Fluorescence was collected by a 100×, 1.2 numerical aperture water immersion objective lens (Leica (Heerbrugg, Switzerland) PL Fluotar) and passed through two emission filters (Chroma (Rockingham, VT) HQ575/90M and HQ545LP) to remove background light. The emitted light was imaged onto an intensified charge-coupled device camera (CCD; Roper Scientific Princeton Instruments (Trenton, NJ) V/ICCD). Images were captured and digitized by a frame grabber (Data Translation (Marlboro, MA), DT3152), displayed on a computer monitor and used to manually select a location for further data collection. Alternately, the emitted light was redirected by a mirror (RM; Fig. 1), collimated by a 125 mm focal length lens, passed through a beam-splitting Thompson polarizer (Karl Lambrecht, SMTA-12-45) where it was separated into its component polarizations along projections of the stage x and y axes, and refocused by 125 mm focal length lenses onto two avalanche photodiodes (APDs; PerkinElmer (Freemont, CA), SPCM-AQR-16). A piezoelectric stage, under computer control, was used to align a spot selected from the camera images, with the APDs.

Custom built electronics and a counting board (National Instruments (Austin, TX), PCI-MIO-16E-4) were used to bin individual photon pulses into 9.9 ms gates synchronized with the polarization switching. The counts per gate gave intensities for each combination of excitation and detection polarization. With the four excitation modes, s1, p1, s2, p2, and the two detection polarizations, x and y, eight raw polarized intensities, were measured during each 40 ms cycle of data collection. For each 40 ms cycle, an estimate of the total intensity was calculated using the equation The factor 0.885 was determined empirically using the expressions in Appendix A of the Supplementary Material (Eq. A.3) to cause this total intensity to be relatively insensitive to probe orientation. includes probe fluorescence plus background intensities.

For visualization of the AEDANS-actin, a 1 mW ultraviolet laser (355 nm, Uniphase (San Jose, CA), NV-10110-100) was also directed into the coupling prism and quartz slide at a glancing angle to generate an evanescent wave. Fluorescence from the AEDANS-actin was passed through a 400 nm long-pass filter (Corning GG400) and imaged onto the intensified CCD camera. Computer-controlled shutters blocked both the 532 nm and 355 nm lasers except during data collection.

Experimental procedure

For each data spot, images of a single field of view were acquired, first exciting the AEDANS with the 355 nm laser and then exciting the rhodamine with the 532 nm laser switching quickly (at 10 kHz) between the four input polarizations to generate nearly unpolarized excitation. These images were digitized and overlaid on a computer screen. For each single molecule measurement on a sparsely labeled filament, a rhodamine spot was selected based on colocalization with an actin filament aligned along the x axis. The spot was then shifted in the x-y plane into the point conjugate with the APDs. The excitation was adjusted to ∼20 mW at the sample for experiments on sparsely labeled filaments, and to 3–30 mW for densely labeled filaments. Sparsely labeled filaments were interrogated for 250 cycles of the 8 polarized intensities, thereby accumulating 10 s of data. For densely labeled filaments, a spot near the middle of a horizontal or vertical filament was selected and interrogated for 50 cycles. Data were collected on each slide for up to 30 min after preparation. Background intensities were recorded from nearby filament-free regions.

After data collection on a sparsely or densely labeled F-actin slide, calibration data, used to calculate the correction factors C_d, X₁, X₂, and X₁₂ (defined below), were obtained as described in the Supplementary Material (Appendix B).

Definition of calibration factors

The four calibration factors X₁, X₂, X₁₂, and C_d take into account the nonideal optical properties of the apparatus and are defined as follows. X₁ is the ratio of excitation intensities at the sample for s1 and p1 polarizations, divided by the ratio expected from the optical arrangement (see the Supplementary Material, Appendix A—Eqs. A.1). X₂ is the corresponding factor for the s2 and p2 intensities. X₁₂ is the ratio of excitation intensities along path 1 and path 2. C_d is the ratio of sensitivities of the x-polarized and y-polarized detection paths (including the relative sensitivities of the two detectors). With these definitions, the raw observed intensities, 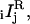were readily converted into corrected intensities, 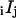(see the Supplementary Material, Appendix B—Eqs. B.1).

For the experiments reported in this article, the values of X₁, X₂, X₁₂, and C_d were all within ∼10% of 1.0. That these values are close to unity indicates that the alignment of the microscope is close to ideal and that the optics do not introduce substantial polarization dichroism.

Data analysis for densely labeled F-actin

For each spot measured on a horizontal (parallel to the x axis) or vertical (parallel to the y axis) densely labeled filament, polarized intensities with background subtracted were corrected by multiplying or dividing by the appropriate correction factors (Supplementary Material, Appendix B, Eqs. B.1), and averaged over 2 s to give eight average polarized intensities, 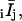per spot. These were used to calculate the following absorption and emission polarization ratios:

(1)

Data from the densely labeled F-actin were also analyzed to obtain order parameters, and (16) which describe the axial orientation and motion of the rhodamine probes. The eight raw polarized fluorescence intensities, including the effects of the high numerical aperture objective, were transformed into nine low-aperture corrected intensities, 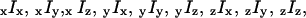on the assumption that the densely labeled filaments were cylindrically symmetrical. Here, the first (second) index indicates excitation (detection) polarization. For a filament oriented along the x direction, cylindrical symmetry implies 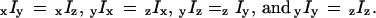For a filament oriented along the y direction, analogous symmetries hold, with each x replaced by y and vice versa. The nine low-aperture intensities for each spot on a densely labeled filament were obtained by fitting the measured raw polarized intensities, with background subtracted, to Eqs. C.1 in Appendix C (Supplementary Material). The expressions used for calculating order parameters 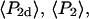and 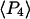from the low-aperture polarized fluorescence intensities are listed in Appendix C (Supplementary Material).

The assumption of cylindrical symmetry of the filaments was tested by relaxing that constraint using one further intensity factor (C₀), which expresses the extent of azimuthal asymmetry around the filament axis between the otherwise symmetrically related low-aperture intensities. For example, when the filaments are aligned along the x axis, 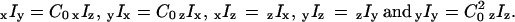Values of C₀ found using these relaxed constraints averaged 0.87 ± 0.04, indicating that the filaments were nearly cylindrically symmetric.

Data analysis for single fluorophores in sparsely labeled F-actin

Traces from individual rhodamine molecules in sparsely labeled actin filaments were selected for further analysis if they had total intensity, I_Tot, typical of single molecules (500–1500 detector counts per 40 ms recording cycle) and all eight of their raw polarized intensities bleached to background levels simultaneously in a single step. For traces that exhibited two or more steps to background, only the steady intensity levels immediately preceding the final step were analyzed. For each molecule analyzed, the raw polarized intensities were corrected as shown in the Supplementary Material, Appendix B, Eqs. B.1, and averaged over the steady interval before photobleaching. For each molecule, intensity levels measured after photobleaching were temporally averaged to obtain eight background intensities. In some cases (11 out of 160 analyzed molecules), when a sudden photochemically induced intensity transition was observed before photobleaching (see the accompanying article (34)), averages were taken preceding the photochemical event.

For each molecule analyzed, Eqs. A.3 in the Supplementary Material were fitted to the eight traces of the corrected intensity signals and background levels to yield angular parameters, θ, φ, and δ, and intensity factor, K, for that molecule. θ and φ correspond to the polar angles in the microscope coordinate system (Fig. 2 a); θ is the axial angle relative to the z axis (normal to the slide surface); φ is the azimuthal angle around the z axis; and δ is the half-angle of a cone describing the amplitude of the restricted diffusion of the fluorophore on a timescale much longer than the 4 ns fluorescence lifetime and much shorter than the 10 ms data collection time. A Levenberg-Marquardt algorithm adjusted trial values of θ, φ, δ, and K to maximize the likelihood that the recorded data, with its Poisson-distributed uncertainties, described the data (35). A 3 × 3 × 3 matrix of 27 provisional values for θ, φ, and δ, each of which was set independently to 15°, 45°, or 75°, was used as starting values. For each of the 27 starting values, a χ² value was calculated by summing the squared differences between measured and best-fit polarized intensities for all of the input/output polarizations and at each time point. When the best fit had any of the three angles within 3° of 0° or 90°, the next best fit was retained, provided its χ² value was not significantly larger. If the χ² value of the next best fit was significantly larger, or if all 27 provisional values resulted in fits with at least one of the angles within 3° of 0° or 90°, then the best fit was retained. After fitting, the data were filtered to remove from further analysis any molecules that, using the criteria above, resulted in fitted angles within 0.5° of 0° or 90°. Using these criteria, 12 out of 160 data points were removed from further analysis. Further details of the fitting algorithm are available by request to Y.E.G.

FIGURE 2.

Coordinate systems. (a) Laboratory (or microscope) coordinate system (see Fig. 1). The positive z axis lies along the optical axis of the microscope and points from the surface of the slide toward the objective. The x and y axes lie in the reflection planes of beam paths 1 and 2, respectively, with the positive directions determined by the projections of the beam propagation directions onto the slide surface. θ and φ are the axial and azimuthal angles, respectively, of the rhodamine dipole moment relative to the laboratory coordinate system. δ is the half-cone angle that describes the motion of the flourophore on a timescale ≫4 ns and ≪10 ms. (b) Actin coordinate system. β and α are the axial and azimuthal angles, respectively, relative to the axis of the actin filament.

The parameter expressing the extent of subnanosecond probe wobble, δ_f, (Appendix A, Supplementary Material), was fixed for the analysis at its value (25°) determined from the densely labeled filament experiments. When δ_f was also made adjustable in fitting data from individual molecules, its value was similar (see Results). Values for β and α, corresponding to the axial and azimuthal angles, respectively, relative to the F-actin axis (see Fig. 2 b), were determined from θ and φ using a standard Euler rotation matrix (36).

Order parameters for the static axisymmetric distribution of single molecules, 〈P_2s〉 and 〈P_4s〉, were calculated from the measured β-angles using the equations

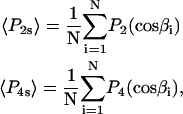(2)

where 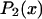and 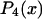are the second and fourth-order Legendre polynomials, respectively (16,37). Order parameters describing the “slow wobble” were calculated using the equations

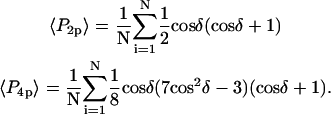(3)

The order parameters 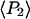and determined from the densely labeled F-actin data (see above) do not distinguish between the static and slow wobble distributions, but instead are sensitive to the combined distribution. The corresponding order parameters were determined from the single molecule data using the relations (16,38)

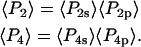(4)

The single molecule data were also combined and analyzed as a virtual densely labeled filament. For each molecule, eight average intensities were determined from the data traces after background subtraction and correction. For each combination of excitation/detection polarizations, the average intensities from all of the analyzed single molecules were summed to give the corresponding polarized intensity level expected from a more densely labeled filament. 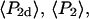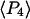Absorption and emission polarization ratios as well as and values were calculated for these summed intensities following the procedures described above for analyzing intensities from actual densely labeled filaments.

RESULTS

Measurement of single molecule 3D orientation at 40 ms time resolution

Sparsely labeled actin filaments, containing 0.1% ATR-labeled and 86% AEDANS-labeled actin monomers, were bound to a myosin coated, fused silica slide and preferentially aligned with the flow direction in the sample chamber as described in Methods. Fig. 1 of the accompanying article (34), shows flow alignment of actin similar to that typically achieved here. Slides were placed on the microscope stage with the flow direction, and most F-actin filaments, aligned with the x axis of the microscope coordinate frame (Fig. 2). Video camera images of the AEDANS and of the rhodamine fluorescence were used to locate individual rhodamine fluorophores on single filaments. At this low density of labeling, single fluorophores were typically separated by several micrometers, allowing individual spots to be readily identified. Once a particular fluorophore was selected, sets of eight polarized fluorescence intensities were collected at a rate of 40 ms per set for 10 s (see Methods).

The time courses of a typical set of the eight raw polarized intensities measured from an individual ATR-labeled actin monomer within a filament are shown in Fig. 3. Except for the noise, which is typical on this recording, all eight fluorescence intensity traces are essentially flat until they simultaneously bleach to the background level in one step. This behavior indicates that the detected photons in excess of the background came from one fluorophore. A linear combination of the eight intensities that is roughly independent of fluorophore orientation is shown as the black trace in the fifth panel down (I_Tot). As described in Methods, for each data point, the eight intensities were fitted to the equations in Supplementary Material Appendix A to determine the 3D orientation in the microscope coordinate frame, amplitude of slow-wobble mobility of the fluorophore, and intensity factor I_Fit (blue trace in Fig. 3, panel 5). The fitted intensity factor is in good agreement with I_Tot minus background. θ and φ are the axial and azimuthal angles of the fluorophore's absorption/emission dipole moment relative to the optical axis of the microscope (Fig. 2 a and Fig. 3, panel 6). Because of the symmetries of the polarizations used, θ and φ were determined to within a fourfold degeneracy. Although the measured values are presented with θ and φ each between 0° and 90°, the degeneracy indicates that the actual value of φ may be equal to φ, 180° − φ, 180° + φ, or 360° − φ. This degeneracy, combined with the mirror symmetry of the fluorophore's dipole moment, implies θ could also be equal to 180° − θ. β and α are the axial and azimuthal angles relative to the actin axis (Fig. 2 b and Fig. 3, panel 7). These values are also reported with each between 0° and 90°. The degeneracy here indicates α may be α, 180° − α, 180° + α, or 360° − α, and β may be β or 180° − β. As expected, when the polarized intensities are relatively constant, the orientation is unchanged. δ is the half-angle of the cone describing restricted diffusion of the fluorophore on the time scale 4 ns ≪ τ ≪ 10 ms (slow wobble; Fig. 2 and Fig. 3, panel 8), likely representing the amplitude of μs mobility of the protein domain to which the fluorophore is attached. the half-angle of the cone representing restricted diffusion of the fluorophore on the time scale τ ≪ 4 ns, was fixed at 25° for this analysis.

FIGURE 3.

Single molecule data. Typical data trace from a single rhodamine molecule attached to a sparsely labeled actin filament. Raw polarized fluorescence intensities have units of photocounts per 10 ms gate; total intensities have units of photocounts per 40 ms cycle. Polarized intensity subscripts indicate excitation/detection polarizations as defined in Methods. I_Tot is a weighted sum of the fluorescence intensities according to the expression given in Methods. I_Fit is the corresponding intensity less background determined from the fit to the data (proportional to K—see Methods). The single discrete decrease of all intensities to background levels at ∼6 s is due to photobleaching of the fluorophore. Angles are defined as in Fig.2.

The angles θ, φ, and δ were also determined for the data with the fast motion parameter, 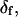allowed to vary. determined this way was 29° ± 11°. Values obtained for the other adjustable parameters (θ, φ, and δ) were nearly the same whether 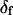was adjustable or not. However, because uncertainties on the fitted values of θ, φ, and δ were higher when 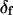was allowed to vary, and because the fitted value of 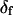reasonably matched the value determined for densely labeled actin filaments (see below), the main data analysis fixed 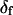at 25°.

For each molecule, average values 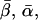and 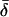were calculated from the temporal traces. The distributions of 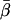- and -values (Fig. 4) show that the 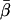-values were more closely grouped than the 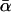-values, as expected for a population of fluorophores uniformly distributed around the actin axis. The mean values of 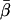and 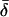for 148 individual ATR-labeled actin monomers were 49.6° ± 0.8° and 37° ± 1°, respectively (mean ± SE).

FIGURE 4.

Distribution and standard deviations of single molecule measurements. Histograms show the distributions of average angle measurements from 148 individual molecules. The associated standard deviations calculated for each molecule are plotted versus each angle.

The precision of the angles measured with 40 ms time resolution was determined by calculating the mean values and standard deviations from the time-resolved measurements for each individual molecule, as shown in Fig. 4. There was no apparent correlation between average angle values and the corresponding standard deviations. For α, β, θ, φ, and δ measurements, the average standard deviations were 16°, 9°, 10°, 14°, and 17°, respectively.

To examine the source of noise in the temporal traces of probe angles, simulated polarized intensities were also calculated using Eqs. A.3 (Supplementary Material, Appendix A), assuming Poissonian distributed photon shot noise (39). These simulated intensities were determined for a fixed value of δ (30°) and a range of α, β, θ, and φ. The root mean-squared deviations between fits to these simulated intensities and the corresponding angles were 13°, 7°, 6°, 10°, and 11° for α, β, θ, φ, and δ, respectively, close to the standard deviations calculated from the measured single molecule data. This result indicates that the major source of noise on the single molecule data was photon shot noise.

Order parameters 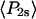and 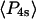for the static 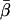distribution (see Methods) were 0.14 ± 0.02 and −0.33 ± 0.01, respectively. The order parameters 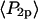and 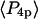describing the slow-wobble cone were 0.67 ± 0.02, and 0.29 ± 0.03, respectively. These values and their products are plotted (see Fig. 6, black symbols) and are compared below with order parameters measured on densely labeled F-actin filaments to estimate accuracy of the measured single molecule angles.

FIGURE 6.

Comparison of ensemble and single molecule order parameter measurements. The solid triangle and square show 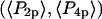and respectively, determined according to Eqs. 2 and 3 from the distribution of 148 single molecule measurements of β shown in Fig. 4. The product of these values (see Eq. 4) is shown as the solid circle. The open circle indicates the order parameters determined by summing all of the single molecule intensities and then analyzing these sums as though they were from a densely labeled filament. Dark and shaded diamonds indicate the order parameters determined for densely labeled horizontally aligned (along the x axis) and vertically aligned (along the y axis) filaments, respectively. All physical angular distributions fall within the area bounded by the solid lines.

Measurement of densely labeled F-actin

Densely labeled F-actin filaments, containing 10% ATR-labeled and 10% AEDANS-labeled actin monomers, were bound to a myosin-coated fused silica slide and preferentially aligned with the flow direction along either the x axis or y axis of the microscope coordinate frame as described in Methods. Images of the AEDANS or ATR fluorescence were used to locate individual filaments on the surface. At this density, the fluorescence intensity appeared uniform along the filaments.

Polarization ratios, as defined in Methods, were calculated for each spot, and combined into distributions (Fig. 5). Filaments included in the analysis were oriented within 10° of the x or y microscope axis, indicated by “H” or “V” superscripts, respectively.

FIGURE 5.

Polarization ratios for densely labeled F-actin. Each blue box plot shows the distribution of polarized intensity ratio measurements (as defined in Methods) from 76 horizontally oriented (parallel to the x axis) densely labeled actin filaments. Each green box plot shows the distribution from 45 vertically oriented (parallel to the y axis) filaments. Large red dots show the polarized intensity ratios calculated from the sum of polarized intensities measured from 160 individual molecules on sparsely labeled actin filaments. For each box plot, black dots correspond to the 5–95% range of the distribution; horizontal lines correspond to the 10–90% range; top and bottom of the colored box correspond to the 25–75% range; and the line inside of the colored box corresponds to the median (50% distribution point). The “H” and “V” superscripts correspond to polarization ratios measured on horizontal (vertical) actin filaments.

If the calibration factors X₁, X₂, X₁₂, and C_d (Supplementary Material) are correct, then consideration of the symmetries between the different excitation polarizations and different filament orientations results in the following expected equalities:

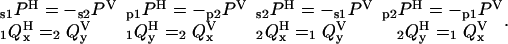Agreement between these equations and the measured polarization ratios for the densely labeled filaments (Fig. 5) indicates that the calibration factors have been determined accurately.

A simple check of the fidelity of the single molecule intensity measurements is to sum the polarized intensities from all 160 individual molecules interrogated in the sparsely labeled filament experiments as if they were in one “H”-oriented filament. Ratios of these totals are shown as red dots in Fig. 5 and agree well with the polarization ratios measured from actual densely labeled filaments.

The orientation distribution of the rhodamine probes on the densely labeled filaments was described in the form of and order parameters following the procedure described in Methods and in Dale et al. (16). As expected, there was no significant difference between the order parameter values determined for “horizontally” and “vertically” oriented filaments.

The measured value of (second rank order parameter describing subnanosecond wobble) was 0.866 ± 0.004 (mean ± SE; n = 121 filaments). This value corresponds to rhodamine probe motion, on a timescale much faster than its 4 ns fluorescence lifetime, within a hard-edged wobble cone with half-angle of 25° (16,40). This agrees reasonably well with the value of 29° ± 11° (corresponding 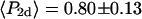) obtained for 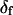in the single molecule experiments above. The values of 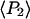and determined from all densely labeled actin data were 0.147 ± 0.003 and −0.136 ± 0.003, respectively. These order parameters represent the combined static and slow wobble (on the timescale 4 ns ≪ t ≪ 10 ms) distributions and are plotted in Fig. 6. The description in Methods (Eq. 4) and Bell et al. (38) indicates that the products of the order parameters determined from the single molecule measurements for the different timescales (i.e., 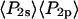) should be equal to the order parameters determined from the densely labeled filaments (i.e., 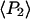). As shown in Fig. 6, the products of the single molecule order parameters (solid circle) are very close to those measured with the densely labeled filaments (diamonds).

DISCUSSION

Single molecule fluorescence polarization (SMFP) was used to measure the orientation of individual rhodamine probes labeling Cys³⁷⁴ of actin monomers copolymerized into filaments with unlabeled actin. The 3D orientation was measured and reported relative to the microscope laboratory coordinate frame (θ and φ), and with respect to the axis of the actin filaments (β and α). The distributions of these angles (Fig. 4) for individual molecules spread uniformly around the actin axis as expected. θ should take on values greater than or equal to β, the axial angle of the probe relative to the actin. Indeed, here the distribution of θ extends from nearly 90° to a fairly sharp cutoff near the mean measured value for β (). φ should exhibit values less than or equal to β, and the measured distribution of φ does extend from very low angles up to a cutoff near 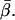In the actin frame, the azimuthal angle, α, is distributed fairly uniformly over its range of possible angles (0–90°), whereas β occupies a single narrow peak close to 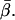All of these distributions are as expected for the axially symmetric sparsely labeled F-actin. In addition, the value of 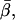49.6° ± 0.8°, is close to the value, 45°, that is obtained for the axial angle of the rhodamine chromophore when the crystal structure of rhodamine-labeled actin (Protein Data Bank reference 1J6Z (41)) is aligned with monomers in a model of the actin filament (42), and the rhodamine dipole moment is assumed to lie between the carbons bearing its two dimethyl amino groups.

Accuracy and precision of measurements

The standard deviation of the measurements taken every 40 ms for a given molecule is an indication of the precision of the individual measurements. Here the measurements have an average standard deviation of 10° for θ and 14° for φ. These levels of statistical uncertainty are low enough to make this SMFP technique useful for detecting and quantifying motions within many protein systems. For example, the technique was used to detect structural changes in myosin V during processive motility, where calmodulin light chains tilted by ∼45° (or, likely, 75°, taking symmetries into account) each time the molecule stepped along actin (22). X-ray crystallography studies have implied similar or larger domain rotations in many other systems including DNA polymerase (43), F₁-ATPase (3,6), the potassium ion channel (10,11,14), and translation elongation factors (44).

The standard deviations on the measured angles were close to those predicted by a computer simulation that assumed statistical uncertainties under similar recording conditions were dominated by photon shot noise in the signal and background intensities. This implies that similar precision could be achieved on shorter timescales, provided that comparable counts per measurement interval were maintained by increasing the excitation laser power. Maintenance of the angular precision by increasing laser intensity proportional to the measurement frequency should hold until the intensity becomes large enough to saturate the fluorophore, (e.g., the time between excitations is comparable to the fluorescence lifetime). Saturation would occur with rhodamine at an excitation intensity ∼100-fold higher than that used here. Thus, submillisecond time resolution should be achievable, although with a corresponding reduction of the observation time (∼5 s in the present experiments) due to photobleaching.

To test the accuracy of the SMFP measurements and to determine whether any major artifacts caused systematic angular deviations, the angles and mobilities measured on a series of single molecules were compared to ensemble measurements on heavily labeled, similarly aligned actin filaments. Also, in the absence of systematic errors in the single molecule technique, ratios of summed single molecule intensities should be equivalent to ratios of multi-molecule intensities, as was found (Fig. 5).

The ensemble experiments cannot be used to measure the detailed distribution of molecular β-angles, but they produce two order parameters of that distribution, 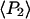and 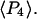The orientation distribution described by 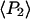and 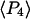encompasses the static distribution of β as well as broadening of the orientation distribution generated by wobbling motions slower than the fluorescence lifetime (4 ns). SMFP measurements, on the other hand, determine both of these β-distributions, so these order parameters can be calculated directly.

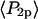As described in Methods and in Bell et al. (38), the aggregate order parameters equivalent to and measured by the ensemble experiment can be calculated by multiplying the order parameters ( and 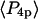) derived from the extent of microsecond motions (δ) in the SMFP experiment by those describing the static distribution ( 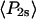and 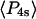). As seen in Fig. 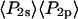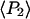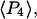6, the products of the order parameters ( and ) measured with SMFP are indeed close to and respectively, determined from the ensemble measurements. The slight differences between the SMFP products and the ensemble order parameters are difficult to interpret directly in terms of angle differences since the ensemble measurements do not directly report individual angles or their distributions. However, if the distributions of β are modeled as either single Gaussian profiles or maximum entropy distributions (45) for both the sparsely and densely labeled filaments, the difference between and from the ensemble measurements and and 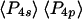from SMFP, corresponds to a difference in the peak angles of the Gaussians or maximum entropy distributions of ∼2°. This comparison indicates that systematic errors in the single molecule measurements compared to the ensemble measurements are very low.

Comparison with other single molecule techniques

Single molecule methods, particularly mechanical measurements using optical traps and single molecule fluorescence imaging techniques, have opened a new and powerful avenue for investigations of biophysical systems. These techniques reveal details of the functionally relevant mechanisms by directly measuring the trajectory of reactions and by avoiding averaging of populations that inevitably obscures some information (see Introduction, and Forkey et al. (23) and references therein). Orientations of single fluorophores have been measured by a number of novel polarization-sensitive microscopies. Several groups have reported the use of polarizations in the plane of the microscope slide (i.e., in the x-y plane) to measure the orientation, φ, of the projection of a single fluorophore's dipole onto the x-y plane (20,21,46–53). To determine the axial angle, θ, as well, Bopp et al. (19,54) and Empedocles et al. (55) used unique fluorophores with cylindrically symmetric degenerate dipole moments. Dickson et al. (56) and Bartko et al. (57,58) used the effect of spherical aberration on the shape of a single fluorophore's point spread function to estimate both θ and φ. Although these approaches have yielded a wealth of new information about the motions of individual macromolecules, none is ideally suited to measuring the 3D orientation with millisecond time resolution of an individual conventional fluorophore having a nondegenerate dipole moment.

The present technique utilizes an evanescent wave generated by totally internally reflected excitation beams with temporally modulated polarization. The p-polarization (electric field parallel to the scattering plane) generates an electric field with a strong polarization component along the z axis. Such polarization is not available with excitation light propagated along the microscope optical axis. Comparison of the fluorescence between intervals of excitation with this z polarized evanescent wave versus that with x- and y-polarization provides robust discrimination between probe absorption dipoles aligned near the optical axis from those nearer the x-y plane. The z-polarized evanescent wave has a small (∼5%) component along the x axis as well (for path 1 excitation; see Fig. 1), but this effect is easily accounted for in the analysis (Methods and Supplementary Material, Appendix A). The s-polarized excitation beam produces a purely y-polarized evanescent wave (for path 1). SMFP is only sensitive to the angle of the detected single fluorophore and is relatively insensitive to lateral motions, laser intensity variations, and mechanical vibrations. As implemented here, the detected angles are ambiguous with respect to reflection across the x-y, x-z, and y-z planes. Some of these symmetries could be removed, however, by directing or polarizing the illumination along intermediate axes (59,60). The ability of this new technique to measure both the axial and azimuthal angles on a millisecond timescale, or better, makes it a powerful tool for real-time investigations of biological structural dynamics.

In addition to reporting the 3D orientation averaged over the measurement time, this SMFP technique also enables determination of the extent of motion (δ) on the timescale shorter than the measurement time (10 ms here), but longer than the fluorescent lifetime (4 ns for rhodamine). Presumably, rotational motions on this microsecond timescale are due to thermal motions of the protein subunits. A conventional fluorescence polarization measurement made on an ensemble of molecules is not capable of separating the effect of motion on this timescale from that of a broad static orientation distribution. Thermal motions on this timescale have been implicated in a number of important biological processes, including the movement of molecular motors such as myosin and kinesin (61–63) and the movement of a cellular leading edge by actin polymerization (64). Although more complex pulse-probe techniques (38,65) do make rotational motions on the microsecond timescale accessible in bulk samples, interpretation of these measurements is complicated by the presence of the ensemble. Such complications are not present in the single molecule experiments reported here.

Motions of actin monomers in a filament

Previous measurements (reviewed in Egelman (24)) of actin motions on the microsecond timescale were obtained with ensemble measurements using electron paramagnetic resonance, saturation transfer electron paramagnetic resonance (66–68), transient absorption anisotropy, and transient phosphorescence anisotropy (69,70). These measurements indicate substantial intrafilament torsional motion on the 100 μs timescale, and imply a filament torsional rigidity of roughly 2 × 10⁻²⁷ Nm². Static electron micrographs show a large component of rotation between successive monomers in filaments (on the order of 5–6°) beyond that associated with the average twist of the filament helix, implying similar values for torsional rigidity (71,72). In contrast, single molecule in vitro measurements, relying on imaging of rotations of beads attached to individual actin filaments (73,74), suggest that the torsional rigidity is more than an order of magnitude larger, roughly 5 × 10⁻²⁶ Nm². This result would imply much smaller relative rotational motions between adjacent actin monomers in the filament. Although it is possible that labeling of Cys³⁷⁴ or incorporation of phalloidin may modify the torsional rigidity of F-actin, there is no correlation between these variables and the different torsional rigidities reported in the references cited above. In fact, Yoshimura et al. (69) found no difference in measured torsional rigidity between filaments that were phalloidin stabilized, and those that were not.

An accurate measurement of the torsional rigidity and the associated thermal motions of individual actin filaments is important for understanding the contribution of such motions to the interaction of F-actin with other proteins. For instance, it has been shown that under some conditions in an in vitro motility assay, myosin applies a rotational torque to actin filaments (60,75), and that binding of cofilin/ADF to actin filaments changes the helical periodicity (76). If thermal motions in the isolated filament easily access torsional angles similar to those promoted by actin-binding proteins, then accessory proteins, or even a motor, may stabilize an otherwise transient structure of the filament. However, if the isolated filament is stiffer, then the binding proteins must actively generate a torque.

The average half-width of wobbling rotational motions of the rhodamine fluorophore on the microsecond timescale (δ, formally 4 ns ≪ t ≪ 10 ms) measured here was 37°. The torsional rigidity implied by this extent of wobble depends on the separation between attachment points of the actin to the slide surface, through individual myosin molecules. If the torsional rigidity were 5 × 10⁻²⁶ Nm², a rotational motion of amplitude ∼40° would occur if the attachment points were ∼34 μm apart (74). This distance is much longer than the typical filament used and would lead to large lateral motions of the filaments (77), which were not observed at the myosin densities used to secure the filaments to the surface. By contrast, a lower torsional rigidity, i.e., 2 × 10⁻²⁷ Nm², as deduced from the ensemble probe and electron microscopy studies, would imply a separation of ∼1.4 μm between attachments. This separation is consistent with the firm association of the filaments with the surface and lack of lateral motions observed with our standard method of attachment. The measurements reported here, therefore, support the lower of the two previously published values for torsional rigidity: ∼10⁻²⁷ Nm².

A factor that might cause error in the measurements reported here is that the labeled actin monomers were assumed to undergo centrosymmetric wobbling motion about an average orientation. There is some evidence that the dynamic motions within actin are anisotropic (74). Other potential artifacts of ensemble experiments using extrinsic probes, however, such as inhomogeneous length distribution in the sample or azimuthal rotations of the whole filament, do not apply to the measurements reported here on individual actin filaments attached to the surface. Concerns regarding sample preparation for electron microscopy are also not relevant to the current measurements. In the works cited above that found much higher tortional rigidity, the small beads used to report the rotational mobility of actin filaments were either close to a surface (74) or trapped in an optical tweezer (73). Either of these geometries may have restricted the motions of the beads, although both groups considered this possibility and controlled for it. Therefore the reason for their outlying value for torsional stiffness is not known.

The current measurements, then, in addition to validating the new SMFP technique, provide strong support for the low actin filament torsional rigidity values obtained from many previous studies, while avoiding potential concerns about ensemble averaging and sample preparation.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.