Enzyme Activity and Flexibility at Very Low Hydration

Abstract

Recent measurements have demonstrated enzyme activity at hydrations as low as 3%. This raises the question of whether hydration-induced enzyme flexibility is important for activity. Here, to address this, picosecond dynamic neutron scattering experiments are performed on pig liver esterase powders at 0%, 3%, 12%, and 50% hydration by weight and at temperatures ranging from 120 to 300 K. At all temperatures and hydrations, significant quasielastic scattering intensity is found in the protein, indicating the presence of anharmonic, diffusive motion. As the hydration increases, a temperature-dependent dynamical transition appears and strengthens involving additional diffusive motion. The implication of these results is that, although the additional hydration-induced diffusive motion in the protein detected here may be related to increased activity, it is not required for the enzyme to function.

INTRODUCTION

There have been numerous experimental and theoretical studies of protein hydration water and its effects on protein dynamics and function (1–11). Two classes of hydration water may be defined. The first consists of individual, internal water molecules that may be reactants in a catalyzed reaction and/or may be integral parts of a protein structure, providing stereospecific interactions (12–15). The second class is the ubiquitous surface hydration shell. It is the influence of this second class on protein dynamics and function which is the subject of this work.

It is widely believed that hydration is necessary for enzyme catalytic function, that dry enzymes are nonfunctional (16,17), and that, below a threshold hydration level, enzymes are inactive. Hydration may be necessary for catalytic function and/or for the diffusion of substrate and product. However, estimates of the degree of hydration required for enzyme activity vary (14,18–21). A commonly discussed threshold is 0.2 g of water/g of protein (14,18–21). The apparent hydration threshold for activity in some enzymes has led to suggestions that this is the critical hydration level at which enzyme dynamics qualitatively change, ‘loosening up’ the enzyme to permit catalysis (22). However, much of the data on which this threshold concept is based arise from experiments where activity is measured in dry enzymes using solid substrates so that the threshold may arise from a diffusional limitation on substrate and/or product rather than from any requirement for surface hydration (23,24).

There have been reports of enzyme activity in organic solvents at very low (<2%) hydrations (22). One reason for this activity might be that some of the organic solvent replaces molecular functions of water at the protein surface. An alternative is that the organic solvent may simply provide a medium for the diffusion of substrate and product. Similar results have been found in applications-directed studies of enzymes at low hydrations where both substrate and product are gaseous (25,26). Powdered esterases hydrated to <4% by weight and exposed to ethyl butyrate vapor exhibit activity, i.e., the production of ethanol (23). There is, in these cases, no evidence found for a threshold, and activity is possible at very low hydration levels.

If enzyme activity can occur at very low hydration levels, and if at these levels protein flexibility is reduced, then our view of the dynamic requirement for enzyme activity and stability may be profoundly affected. Exploring the variation of the dynamics of enzymes with hydration and comparing this with nondiffusion-limited activity should assist in resolving these questions.

Incoherent neutron scattering (INS) is a particularly useful tool for determining the hydration-dependent dynamics of proteins. INS probes motions on length scales of the order of Å and timescales ranging from femtoseconds to nanoseconds (27). In this work, INS experiments were performed on powders of the enzyme pig liver esterase at hydration levels of 0%, 3%, 12%, and 50% so as to determine the influence of the hydration level on the dynamics of enzyme. Since the incoherent scattering cross section of the hydrogen atom is an order of magnitude larger than that of the other atoms present in the system, the measured spectrum is dominated by the incoherent single-particle hydrogen scattering. We probe here the hydration dependence of the so-called dynamical or “glass” transition in temperature-dependent protein dynamics (28). This transition, at which anharmonic motions become more apparent, is a sensitive measure of change in flexibility (29). Also examined is the hydration dependence of the quasielastic scattering intensity, which provides information on the presence of diffusive motions in the sample. The results indicate that increasing the hydration level of the enzyme powder increases the activity and that this is accompanied by a strengthened dynamical transition. However, diffusive motion is present at all hydrations and temperatures studied, and the hydration-induced anharmonic motions are not required for activity.

METHODS

Activity measurements

Details of this experiment are published elsewhere (23). A brief description is given here. The vapor phase activity measurements were conducted at room temperature (298 K). Control experiments included “no-enzyme” and autoclaved enzyme labels, hydrated at the same relative humidity, running in parallel with each experiment. In both cases, the rates of ester hydrolysis were found to be zero. Hydration of the heat denatured enzyme label was found to be the same as for the active enzyme label. The enzyme hydrated to >0.6 h was regarded as the 100% control value, as at this point it has been found that enzymes display dilute solution thermodynamics and the mobility of the bound hydration layer is close to that of the bulk solvent. Quantification of ester hydrolysis was based on measuring ethanol production. A minimum of three replicates were run at each hydration. Enzyme activity was defined as nanomoles of ethanol produced per minute per milligram of enzyme powder used in the label.

Sample preparation and equilibration

Pig liver esterase (150 units/mg, EC 3.1.1.1) was obtained from Sigma (St. Louis, MO) and further partially purified using Fast Flow Q Sepharose. The enzyme was hydrogen/deuterium exchanged by twice dissolving the protein in 99.9% D₂O at 10 mg/ml, for 20 h at 4°C, and then lyophilized.

A completely anhydrous enzyme powder was prepared by extensive drying in the aluminium sample holder. The lyophilized powder was initially packed into the sample holder at 4°C to prevent back exchange. The sample was then placed in a dessicator under vacuum, over phosphorus pentoxide, for 1 week at room temperature. From previous gravimetric studies it was found that the resulting hydration after such treatment was <1% (w/w). The sample was finally rapidly (<60 s) sealed in a low humidity environment of ∼13% relative humidity to reduce any adsorption of water. After 60 s exposure at this humidity, the hydration increased by <0.2%. To prepare protein powders at higher hydrations, the original enzyme powder was hydrated to successively higher hydrations by equilibration with the appropriate saturated salt solution. The salts used to prepare the saturated solutions were dissolved in D₂O several times and rotary evaporated to near dryness, so as to exchange as much of the water of crystallization as possible.

Neutron scattering

The dynamic neutron scattering experiments were performed on the IN5 time-of-flight spectrometer at the Institut Laue-Langevin, Grenoble. The incident neutron wavelength was 5.1 Å. All data were collected with the sample holder oriented at 135° relative to the incident beam. The samples were contained in aluminium flat-plate cells, of 0.3 mm thickness. Spectra were measured at 295 K and, in an additional set of experiments, with a temperature ramp starting at 120 K and increasing to 290 K in steps of 10 K every half an hour. The measured transmission for all the samples was 0.96, indicating that multiple scattering was negligible. The elastic intensity was determined by integrating detector counts over the energy range of the instrumental resolution (≈100 μeV). The detectors were calibrated by normalizing with respect to a standard vanadium sample. The cell scattering was subtracted, taking into account attenuation of the singly scattered beam. Finally, the scattering was normalized with respect to the scattering at the lowest measured temperature, and the lowest measured scattering vector, q.

The elastic incoherent scattering intensity S_inc(q, E = 0), where E is the energy transfer and q is the scattering wave vector, was used to obtain the mean-square displacement, 〈u²〉, by using the relationship (30)

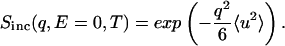(1)

A plot of lnS_inc(q, E = 0, T) vs q² was fitted to a straight line in the linear regime of q (0.8 < q < 1.4 Å⁻¹). The slope yields 〈u²〉. As the scattering was normalized with respect to the 120 K intensities, the 〈u²〉 determined is equal to (〈u²〉_T − 〈u²〉₁₂₀), where 〈u²〉_T is the absolute mean-square displacement at temperature T.

An alternative approach also used for obtaining 〈u²〉 is directly from the elastic peak by summing S_inc(q, E = 0, T) over a range of small q values so as to obtain the integrated elastic intensity S_INT(T) (31). Assuming that q is small enough over the integration range used that Eq. 1 still holds, then S_INT ∝ − 〈u²〉. This method has the advantage that it does not rely on fitting the low q region of the scattering data, this being often a difficult task owing to noise in the data. Again, the scattering intensities were normalized to those at 120 K.

Determination of the quasielastic scattering intensity as a function of temperature was performed by integrating the difference between the spectrum of the sample (normalized to the elastic intensity) and the normalized vanadium spectrum, i.e.,

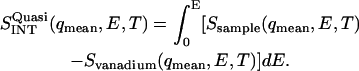(2)

Since vanadium is a pure elastic scatterer, 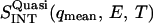is the quasielastic scattering of the sample. The quantity 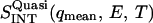was calculated by summing the differences between the intensities of the sample and vanadium in the energy range 0 < E < 0.5 meV and normalized to those at 120 K.

RESULTS

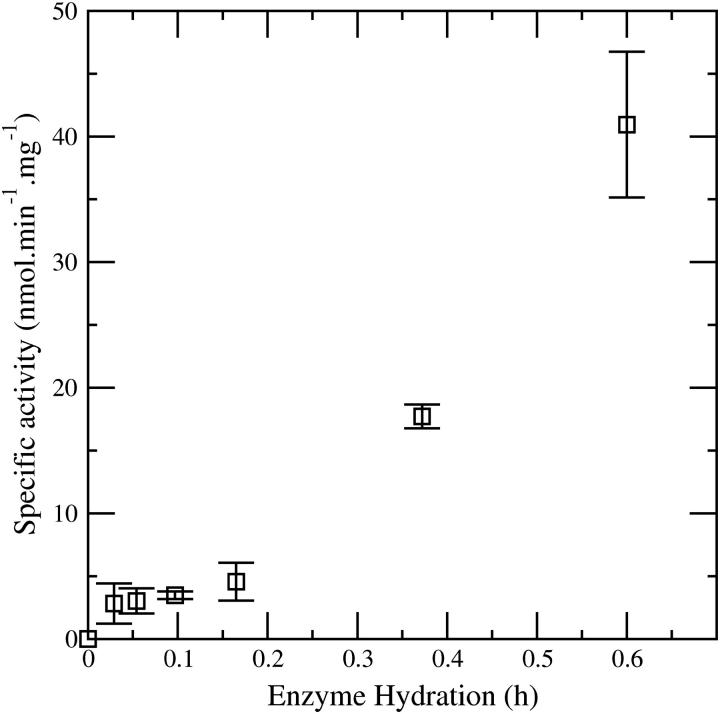
The effect of enzyme water content on the vapor phase activity of the pig liver esterase enzyme is shown in Fig. 1. The enzyme reaction, which involves exposing the powdered esterase to ethyl butyrate vapor so as to form ethanol, is hydrolytic and hence activity in the complete absence of water is precluded. However the figure clearly demonstrates significant enzyme activity at hydrations as low as 3%.

FIGURE 1.

Effect of enzyme water content on the vapor phase activity of pig liver esterase. Data taken from Lind et al. (23).

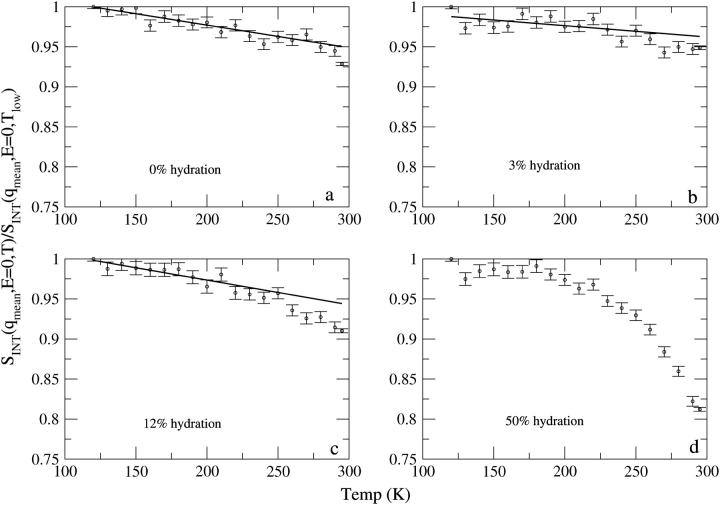
The integrated elastic neutron scattering intensity, S_INT, is shown as a function of temperature for the four esterase samples in Fig. 2. For the 50% hydration sample, there is a clear change in slope of temperature dependence of the elastic intensity at T ≈ 200–230 K, which becomes steeper at higher temperatures. This change is observed over the temperature range at which the dynamical transition has been previously identified in various proteins with neutron scattering instruments of similar energy resolutions (32). For the 12% hydration sample, there is also a change in the slope of the elastic intensity, although less marked. For the 3% sample, there is also a small, but statistically significant, change in slope. In contrast, for the 0% sample, the plot remains linear over 120–280 K. However, the point at 295 K does drop below the straight-line extrapolation. The possible significance of this is further investigated below.

FIGURE 2.

Normalized integrated elastic intensities as a function of temperature. Due to the lack of clarity in linear behavior of the data as a function of temperature, integrated elastic intensities as a function of temperature for 50% hydration sample have not been fitted to a straight line.

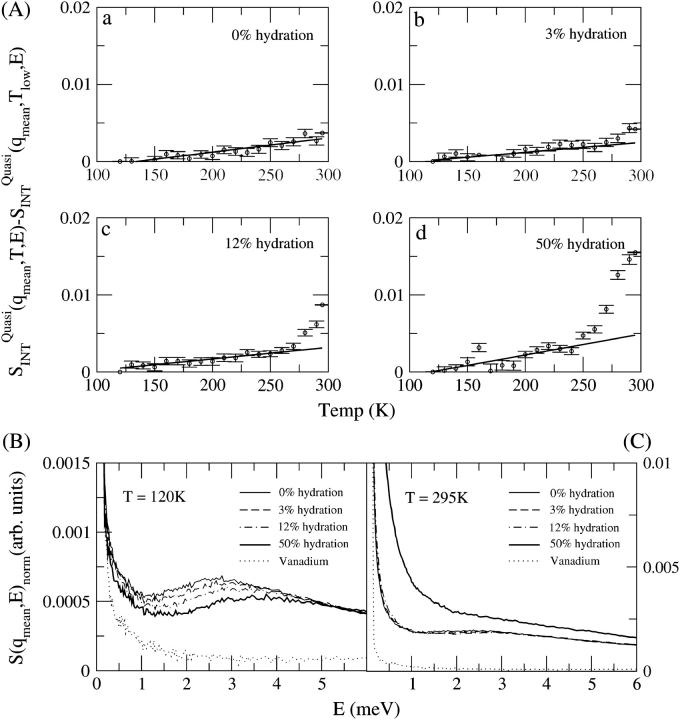
Nonvibrational motions, such as jump or continuous diffusion, lead to quasielastic broadening under the elastic peak (33). In Fig. 3 A is shown the variation of the integrated quasielastic intensity with temperature. This quantity is complementary to the elastic intensity, i.e., a change in the gradient of the elastic scattering should be accompanied by an increase in the quasielastic scattering, indicating increased diffusive motion in the system. The term “diffusive” here indicates stochastic motion that encompasses various types of relaxation processes involving restricted diffusion, such as rotational jumps between defined sites or diffusion in a confined volume. Fig. 3 A shows that the quasielastic scattering intensity is nonzero for all temperatures studied. The presence of nonzero quasielastic scattering at 120 K and 295 K is clear in Fig. 3, B and C, by comparison of the sample scattering with the vanadium control which defines the elastic peak shape. This indicates that there is significant nonvibrational (diffusive) motion in the samples, even at temperatures below those at which the integrated elastic intensity changes are seen in Fig. 2. However, at the temperatures where changes are seen in the integrated elastic intensity, there are also transitions in the quasielastic scattering. Again, the 3% sample shows a significant increase in quasielastic intensity for T = 270–295 K. In contrast, for the 0% sample the 295 K sample shows no significant deviation from linear behavior with T. Broadening under the elastic peak, i.e., the presence of quasielastic intensity, is observed at all hydration levels as shown in Fig. 3, B and C, including the 0% hydration system, confirming the presence of diffusive motion in all samples at 120 K and 295 K. The shape of the quasielastic scattering at 295 K does not differ significantly between the 0%, 3%, and 12% hydration samples. However, a significant increase in quasielastic intensity is observed when the hydration is increased to 50%.

FIGURE 3.

(A) 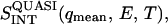a measure of quasielastic scattering as functions of temperature and hydration for (a) 0%, (b) 3%, (c) 12%, and (d) 50% hydration. (B) The dynamic structure factor S(q, E) at different levels of hydration at 120 K. (C) The dynamic structure factor S(q, E) at different levels of hydration at 295 K. Height of the spectra in B and C were normalized to 1 for zero energy transfer to visualize the variation in shape of the quasielastic intensity.

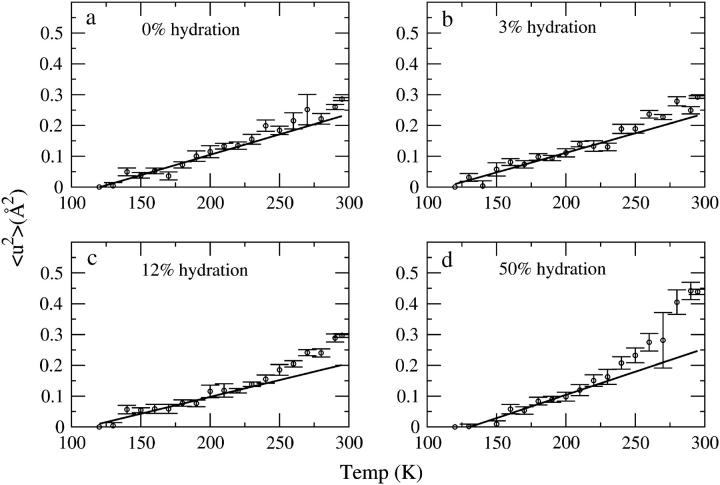
The mean-square displacement, 〈u²〉, as a function of temperature calculated using Eq. 1 is shown in Fig. 4. In the 0% and 3% hydration systems, there is a small but statistically significant deviation from linearity of 〈u²〉 for T > 250 K in the 3% sample and T > 280 K at 0%. This deviation becomes stronger in the systems hydrated to 12% and 50%. In the 50% sample, again the temperature at which the deviation becomes significant is reduced to 240 K.

FIGURE 4.

〈u²〉 as a function of temperature for (a) 0%, (b) 3%, (c) 12%, and (d) 50% hydration. The 〈u²〉 values are normalized to the lowest temperature (120 K) at which measurements were made. The 〈u²〉 obtained by integrating the elastic intensity exhibited closely similar behavior as a function of temperature and hence is not shown here.

DISCUSSIONS AND CONCLUSIONS

Many experiments and computer simulations have provided evidence for a hydration dependence of both protein dynamics and function (8,9,34–37). Here we have probed the relationship between dynamics, hydration, and function for an enzyme at very low hydrations.

One, possibly simplistic, view of the relationship between protein dynamics and activity is that a harmonic vibrating protein, trapped in a single potential energy well, is nonfunctional and that diffusive, anharmonic motions are required for activity. Vibrational dynamics leads to inelastic neutron scattering (peaks at nonzero energy transfer), whereas diffusive dynamics leads to quasielastic scattering. Therefore, activity would require the presence of quasielastic scattering intensity.

These results indicate that at all temperatures and hydrations at which activity has been detected and, indeed, even at 0% hydration, there is diffusive dynamics in the protein, as evidenced by nonzero quasielastic intensity. Therefore a requirement of the presence of quasielastic intensity (diffusive motion) for enzyme activity is not ruled out by this work. The results indicate that at low temperatures, even below the dynamical transition anharmonic, diffusive, nonvibrational motion occurs on the picosecond timescale. Although apparent linear behavior of the mean-square displacement, as seen in the samples below the transition, is consistent with harmonic motion, linearity does not exclude a quasielastic origin per se. Furthermore, there is also evidence from previous experiments that quasielastic scattering exists at temperatures below dynamical transition temperatures (7,9,11). This observation is also in accord with recent molecular dynamics simulation results, which indicate that deviation from harmonic dynamics in a small protein in vacuo is apparent at temperatures as low as 120 K (38,39) and also with experimental results demonstrating the appearance of a transition at similarly low temperatures in a membrane protein (37). In experiments on hydrated powders or enzyme solutions, the change in slope at 200–250 K was found to be dependent on the energy resolution (32,40), indicating that the apparent position of the dynamical transition depends on the timescale explored (41,42) consistent with molecular dynamics simulations that indicate that the transition does not involve an abrupt change from harmonic to anharmonic dynamics (43). At a low enough temperature, the quasielastic scattering should no longer be visible, as the associated relaxation time will have moved to slower timescales than can be detected on the instrument.

Previous picosecond neutron scattering studies concluded that the protein dynamical transition, as manifested by an increase in the gradient of the temperature dependence in proteins, is observed only above certain hydration levels (36,8). In this work, we also observe a clear hydration dependence of the change in dynamical behavior with temperature. This dependence concerns both the temperature at which the deviation from linear behavior occurs and the magnitude of the change above that temperature. Whereas at 50% hydration the change becomes apparent in the 200–230 K range and leads to 〈u²〉 of 0.45 Ų at 295 K, at 3% hydration and 12% hydration the temperature at which the dynamical change occurs is increased to 250–270 K and the amplitude at 295 K reduced to 0.3 Ų (Fig. 4). The 0% hydration sample shows a small but statistically significant deviation at T > 280 K.

The surface coverage associated with any given level of hydration by weight depends on the size of the enzyme. For the esterase examined here the approximate surface coverages are 10%, 40%, and 170% for the 3%, 12%, and 50% hydration samples, respectively. The change in dynamical behavior in the 3%, 12%, and 50% hydration samples may be due to the surface solvent molecules present on the surface of the protein facilitating an increase in the amplitude of anharmonic motions by lowering energy barriers for jumping between minima (5,6,43), again in accord with findings from molecular dynamics simulations (44,45). This would also explain why the temperature at which the dynamical behavior begins to change decreases with increasing hydration. The correlation between hydration and increased activity in Fig. 1 means that it is likely that the hydration-induced dynamical changes observed here may facilitate activity. However, the presence of activity in the absence of these extra motions indicates that they are not an absolute requirement.