Molecular Dynamics of a Protein Surface: Ion-Residues Interactions

Abstract

Time-resolved measurements indicated that protons could propagate on the surface of a protein or a membrane by a special mechanism that enhanced the shuttle of the proton toward a specific site. It was proposed that a suitable location of residues on the surface contributes to the proton shuttling function. In this study, this notion was further investigated by the use of molecular dynamics simulations, where Na⁺ and Cl⁻ are the ions under study, thus avoiding the necessity for quantum mechanical calculations. Molecular dynamics simulations were carried out using as a model a few Na⁺ and Cl⁻ ions enclosed in a fully hydrated simulation box with a small globular protein (the S6 of the bacterial ribosome). Three independent 10-ns-long simulations indicated that the ions and the protein's surface were in equilibrium, with rapid passage of the ions between the protein's surface and the bulk. However, it was noted that close to some domains the ions extended their duration near the surface, thus suggesting that the local electrostatic potential hindered their diffusion to the bulk. During the time frame in which the ions were detained next to the surface, they could rapidly shuttle between various attractor sites located under the electrostatic umbrella. Statistical analysis of the molecular dynamics and electrostatic potential/entropy consideration indicated that the detainment state is an energetic compromise between attractive forces and entropy of dilution. The similarity between the motion of free ions next to a protein and the proton transfer on the protein's surface are discussed.

INTRODUCTION

Biological reactions, such as binding of a ligand to its receptor, insertion of an ion into an ion channel, and protein folding, occur at the interface between a protein and its surrounding solvent. Accordingly, before such a reaction takes place, the surfaces of the reactants should lose some of their solvation shell. What is more, the interactions between the protein and the innermost water molecules will modulate the physical-chemical properties of the first solvation shell of the macromolecule. For these reasons, the protein-solvent interface has been excessively studied by the use of various experimental and theoretical methods (1–26); for recent reviews, see references 27–29. These studies focused on the hydration pattern of the proteins. However, a complete description of the protein-solvent interface cannot be accomplished without a consideration of the surface residues and the salt ions, which are an integral part of all physiological systems.

Protein-salt interactions have been studied both experimentally and theoretically. The effects of salt on the stability and solubility of protein (i.e., salting-in and salting-out) have been known for a long time. Furthermore, salt ions were experimentally found to be bound to the surface of the protein lysozyme (30). Yet, owing to the experimental difficulties in studying the dynamics of ions on protein surfaces on the molecular scale, ligand exchange reactions that involve small ions on the protein surface can only be studied using computer simulations. For this reason, we carried out molecular dynamics (MD) simulations of a model protein, in a study of the various aspects of ion propagation near the surface of the protein. The S6 protein, selected for this study, is a part of the bacterial 30S ribosome central domain (31) and has no physiological function associated with ion transport on its surface. The S6 is a globular protein of 101 amino acids, 32 of which are charged at a physiological pH. Moreover, all its amino acids are at least partially exposed to the bulk and no residue is totally buried in the protein matrix. To be consistent with the chemical experiments that have been carried out in our lab with the S6 Q16H/S17C double mutant, we have performed our simulations using the same mutant protein.

To this end, most studies of ion propagation around macromolecules investigated the dynamics of ions near membranes (32–35). The phospholipid membrane forms an almost homogeneous structure; hence, once a sufficient number of ions was added, the results could be analyzed using statistical measures such as the distribution of the ions relative to the membrane normal.

Soluble proteins, unlike membranes, do not have a defined geometrical form, and the ions are not distributed homogeneously around them. Therefore, statistical analysis of ion distributions around the surface of such proteins would be meaningless. However, when only a small number of ions is present in the solution, their dynamics can be studied directly by monitoring the distance between each ion and the protein, or certain moieties on its surface, as reported by Pettit and co-workers (36–39).

Our interest in the protein-water interface stemmed from the kinetic measurements of proton transfer at the surface of proteins (40–48). Reactions of a free proton with the protein surface were studied directly by use of the laser-induced proton pulse technique (49–52). In these studies, proteins were dissolved or suspended in a solution containing photoacid. Photoacids are molecules whose pK_as are dramatically reduced when excited to their first electronic singlet state (53–56). The excitation of the photoacid molecules led to a rapid proton release into the solution. After the momentary acidification of the solution, surface groups such as histidine, aspartate, and glutamate became transiently protonated. Using probe molecules attached to the protein, the kinetics of the proton transfer reactions on the protein surface could be analyzed. It was noted in these studies that residues which according to the crystal structure of the protein are up to 10–15 Å apart, could form proton-attractive domains and share the proton among them at a very fast rate, exceeding the upper limit of diffusion-controlled reactions as characterized by the Debye-Smoluchowski equation (52,57,58). To account for the fast rate, it was suggested that the dynamics of the protein generate transient situations, in which the residues get sufficiently close to allow a proton transfer over a short distance. What is more, the passage of the proton is accelerated by the electrostatic potentials that bias the diffusion of the proton between the donor-acceptor sites. It was also reasoned that, if such a mechanism is operative, it should be a general feature of the protein surfaces and not limited to a specific protein or to the nature of the charged particle.

In this study, we wish to demonstrate that the protein surface has the ability to attract small charged molecules, to hold them near the protein surface for relatively long durations and to shuttle them between its surface residues. For this reason, we wished to study events that involved a low concentration of ions, so that most of the ion attractor sites (i.e., oppositely charged amino acids) would be vacant, and the transfer of ions from site to site could be observed and analyzed. Accordingly, we have conducted our simulations of a protein in a fully hydrated system, in the presence of a small number of salt ions (between 4 and 16 ion pairs). Three simulations were performed under different conditions, as summarized in Table 1.

TABLE 1.

Summary of the MD runs

Name	Duration	Protonation states	No. of Cl− ions	No. of Na+ ions	Formal salt concentration
MD_N	10 ns	Normal*	4	4	33 mM
MD_S	10 ns	Normal*	16	16	133 mM
MD_E22p	10 ns	Glu-22 protonated	5	4	33 mM

^*N-terminus, lysine, and arginine residues are protonated; C-terminus, aspartate, and glutamate are unprotonated.

The simulations revealed that certain domains on the protein surface could detain an ion in their immediate vicinity. The detained ions did not lose their freedom of motion. Rather, they were confined to the vicinity of the ion attractors for a long duration (up to several hundreds of picoseconds), indicating that the local electrostatic field strongly biased their Brownian motions.

METHODS

Molecular dynamics simulations

Three different molecular dynamics simulations (see Table 1) were performed using the GROMACS 3.1.4 package of programs (59,60), with the GROMACS force field, which is a modified version of the GROMOS87 force field (61–65). The calculations were carried out using the structure of the S6 ribosomal protein (Protein Data Bank code 1RIS) determined by Lindahl and co-workers (66) that was downloaded from the Protein Data Bank (67). The starting structure was prepared by replacing the side chains of residues Glu-16 and Ser-17 with histidine and cysteine, respectively. The protein was embedded into a box containing SPC model water (68) that extended to at least 8 Å between the protein and the edge of the box. Although more complex water models are nowadays frequently used in the simulation of proteins, we chose to use the SPC, as it was found to give superior results for simulations of solutes in water when compared to more sophisticated water models (69), especially at interfaces (70). The total number of water molecules was 6677. Four Na⁺ and four Cl⁻ ions, corresponding to a salt concentration of ∼30 mM, were added to the system by replacing the water molecules in random positions.

Before the dynamics simulation, internal constraints were relaxed by energy minimization. After the minimization, an MD equilibration run was performed under position restraints for 20 ps. A 10-ns-long production MD run was performed after the equilibration. During the MD run, the LINCS algorithm (71) was used to constrain the lengths of hydrogen-containing bonds; the waters were restrained using the SETTLE algorithm (72). The time step for the simulation was 2 fs. The simulations were run under NPT conditions, using Berendsen's coupling algorithm (73) to keep the temperature and the pressure constant (P = 1 bar, τ_P = 0.5 ps; T = 300° K; τ_T = 0.1 ps). Van der Waals forces were treated using a cutoff of 12 Å. Long-range electrostatic forces were treated using the particle mesh Ewald method (74). The coordinates were saved every 0.5 ps.

The procedure described above was repeated twice, to create two simulations of 10 ns each, under slightly different initial conditions. In one simulation, Glu-22 was protonated before the solvation, and five Cl⁻ ions were used instead of four to cancel the total charge of the protein. In the other simulation, 16 Na⁺ ions and 16 Cl⁻ ions were used, resulting in a total salt concentration of 120 mM.

The different simulation terms are summarized in Table 1.

Estimation of the electrostatic contribution to the ion binding energy

The free-energy change involved in the binding of ions to the protein surface can be calculated directly from the MD simulations. However, due to the rapid movement of the ions, it is difficult to quantitate the favorable electrostatic term involved with the ion binding. For this reason, the electrostatic contribution to the binding energies was calculated based on selected conformations, using the continuum electrostatic approach and distant-dependent screening factors. These calculations are intended for a rough estimation of the electrostatic contributions to the binding energy. It should be mentioned that a more accurate treatment can be performed using advanced methods, such as semimicroscopic protein dipoles Langevin dipoles (PDLD/S) (75–79) or linear interaction energy (LIE) (80–84). However, such calculations are not within the scope of this article.

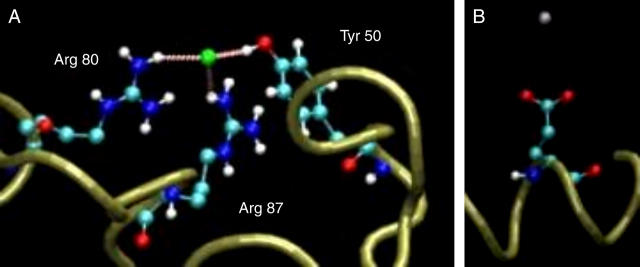
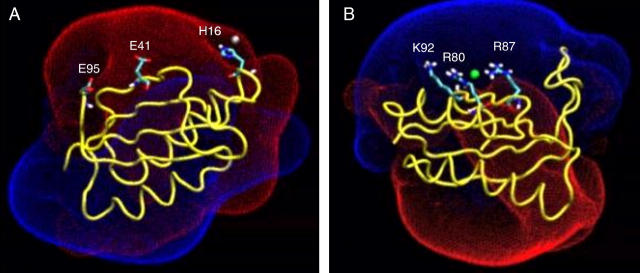
The calculations were performed using two configurations: one in which the protein binds a chloride ion to its most attractive site (see Fig. 5 A) and the other in which a Na⁺ ion is located in the vicinity of the carboxylate of Glu-31 (see Fig. 5 B).

FIGURE 5.

The bound ions and their immediate vicinity. (A) A chloride ion bound to residues Arg-80, Arg-87, and Tyr-50. The minimal distances between the ion and the residues were 2.24, 2.86, and 2.02 Å for Arg-80, Arg-87, and Tyr-50, respectively. (B) A sodium ion bound to Glu-31. The minimal distance between the ion and the protein is 4.34 Å.

The calculations of the electrostatic contribution to the binding energies were calculated by Eq. 1:

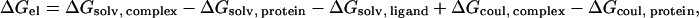(1)

where ΔG_solv and ΔG_coul refer to the Poisson-Boltzmann (PB) and pairwise Coulombic energy terms associated with the transfer of the solute from a continuum medium with a low dielectric constant (ɛ = 4, 10, 20, or 40) to a continuous medium with the dielectric constant of water (ɛ = 78.4).

The calculations were carried out as follows. First, the structure of the protein, ions and solvent was extracted from the MD simulation. To make sure that the structure did not contain any unfavorable interactions between the atoms, the system was energy minimized using the GROMACS program (59,60). After the minimization, the coordinates of the protein and the ion were used for the calculation of ΔG_el. The solvation energies were calculated using APBS (85), with a grid spacing of 0.33 Å. To make sure that the calculations were independent of the grid size, they were repeated using a grid spacing of 0.4 Å, which had a marginal effect on calculated ΔG_el (the largest difference was 0.10 kcal mol⁻¹). All calculations were carried out by solving the nonlinear Poisson-Boltzmann equation for the protein in a solution of 50 mM NaCl.

Following Johnson and Parson (86), the electrostatic contributions to the binding energies were also calculated based on distant-dependent screening factors (DDSF). This allows the usage of a simpler form of ΔG_el:

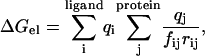(2)

q_i are the ligand atomic charges, q_j are the protein atomic charges, r_ij is the distance between atom i of the ligand and atom j of the protein, and f_ij is a function that scales the interaction between atoms i and j based on r_ij; f_ij was given by (87):

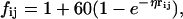(3)

where η is an empirical factor that can vary between 0.1 and 0.18. In these calculations, we used η = 0.14.

Other calculations and visual presentation

The electrostatic potential around the protein was calculated using the program APBS (85), with a solute dielectric value ɛ = 2, solvent dielectric value ɛ = 78.4, and a grid spacing of 0.4 Å.

All protein figures were created using the VMD computer program (88).

The volumes of the protein and its surroundings were calculated using the computer program VOLBL (89).

The analysis of the secondary structure elements of the protein was performed using the program “do_dssp”, which utilizes the DSSP program (90).

RESULTS

The overall dynamics of the protein, solvent, and ions

The stability of the protein during the simulation was evaluated by the root mean square deviation (RMSD) of the protein backbone, and by monitoring its secondary structure elements during the simulations. As documented in Table 2, the backbone RMSD was steady over time, exhibiting fluctuations that reached maximal values of 2.7–2.8 Å in the different simulations. This consistency indicates that the protein was stable under the simulation conditions. Furthermore, the protein retained its secondary structure elements as the simulations proceeded, as indicated by the number of amino acids that retained their secondary structure elements (helices, sheets, turns, etc.) during the simulation (see Table 2). The variations in the number of structured residues reflect temporal disordering on the residues adjacent to the random coil domains of the protein.

TABLE 2.

Different dynamical properties of the simulated molecules

Run	Protein backbone RMSD	Water diffusion coefficient*	Cl− diffusion coefficient*	Na+ diffusion coefficient*	The number of amino acids in secondary structural elements†
MD_N	2.8 Å	4.021 ± 0.089	2.06 ± 0.48	1.79 ± 0.35	75 ± 5
MD_S	2.8 Å	3.956 ± 0.025	2.10 ± 0.33	1.54 ± 0.27	72 ± 4
MD_E22p	2.7 Å	4.124 ± 0.023	2.03 ± 0.25	1.23 ± 0.51	72 ± 5

^*10⁻⁵ cm² s⁻¹.

^†Calculated by do_dssp; see the Methods section.

To characterize the overall dynamics of the solvent, the values of the diffusion coefficient of the water were calculated from their mean square displacement. The calculated values (3.956–4.124 10⁻⁵ cm² s⁻¹; Table 2) are larger than the experimental diffusion coefficient of water (2.4 × 10⁻⁵ cm² s⁻¹ in room temperature). This deviation is attributed to the SPC model (91) for water molecules used in the simulations. Other simulations of SPC type water (92) have yielded values (4.1–4.3 10⁻⁵ cm² s⁻¹) that are comparable with ours, indicating that the higher diffusion coefficient is a feature of the model and not a flaw of the simulation.

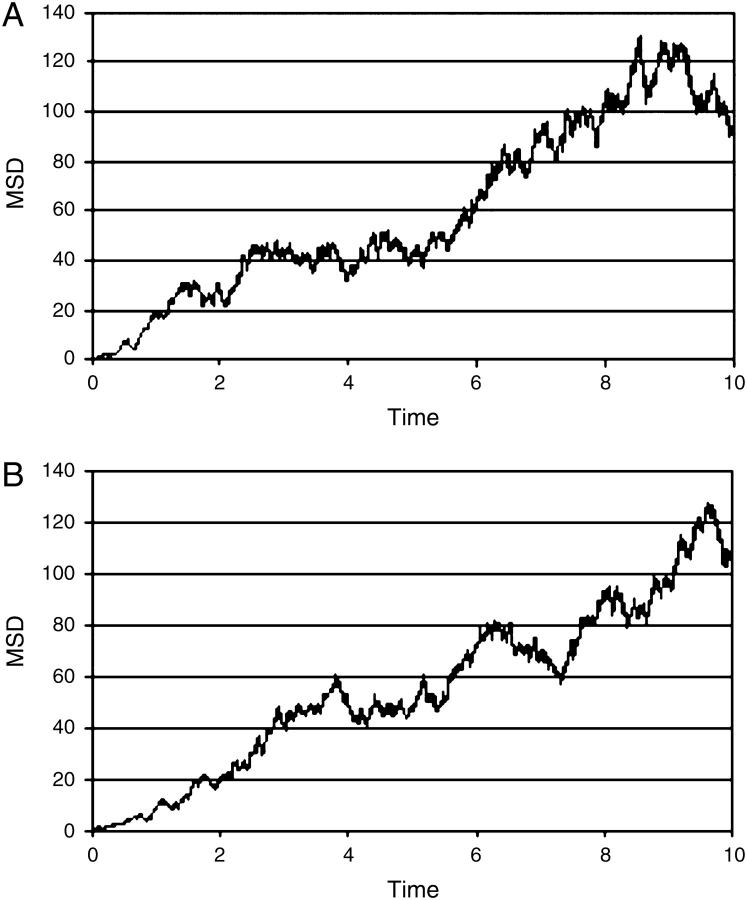
The mean square deviation (MSD) of the ions was calculated with respect to their initial (random) placement. The variation of the MSD as a function of simulation time for the simulation MD_N is presented in Fig. 1. The calculated diffusion coefficients of the ions were 2.06 ± 0.48 10⁻⁵ cm² s⁻¹ and 1.79 ± 0.35 10⁻⁵ cm² s⁻¹ for the Cl⁻ and Na⁺ ions, respectively (see Table 2). These values are comparable with the experimental results (2.03 10⁻⁵ and 1.33 10⁻⁵ cm² s⁻¹ for the Cl⁻ and Na⁺ ions (93,94). This is an indication that, despite the simplicity of the water model and the small number of ions, the simulation of the Brownian motion of the ions is realistic. The diffusion coefficients calculated using a larger number of ions (16 pairs of ions, simulation MD_S; see Table 2) yielded essentially the same results. Finally, we wish to indicate that our results are compatible with the results reported by Pfeiffer and co-workers (2.03 ± 0.25 10⁻⁵ cm² s⁻¹ and 1.23 ± 0.51 10⁻⁵ cm² s⁻¹ for the Cl⁻ and Na⁺ ions, respectively), who conducted an MD simulation of the betaARK1 PH domain in the presence of 30 mM salt (95).

FIGURE 1.

The mean square deviations (MSD) of the Cl⁻ (A) and Na⁺ (B) ions as a function of simulation time, calculated over the simulation MD_N. The MSDs are given in nanometers squared and the time is given in nanoseconds.

Contacts between the ions and the protein

Quantitation of the interactions between the ions and the protein necessitates the usage of parameters that can describe the location of the ions relative to the protein surface. In MD simulations of ions near membrane surfaces, as performed by Mukhopadhyay et al. and by Pandit et al. the authors relied on atomic densities and radial distribution functions (33,35). However these indices cannot be applied in this case for two reasons. The irregularity of the protein surface renders the radial distribution functions inadequate. Moreover, the small number of ions results in large fluctuations of the calculated densities. To avoid these difficulties, we adopted the ion-protein distance as a parameter for the quantitation of the ions' locations. A similar parameter was used for the studies of ion distributions in the vicinity of peptides (36–39).

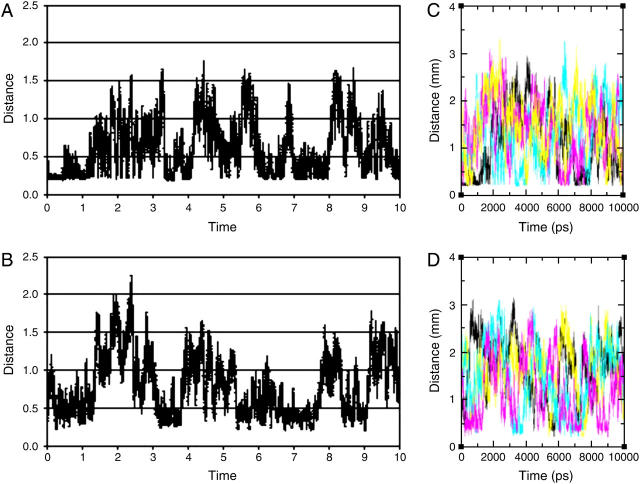
The variations with time of the minimal distance between the protein and any of the ions, during the simulation MD_N, are presented in Fig. 2. The distance varies from a contact distance of ∼2 Å up to ∼22 Å. Yet, the distribution of the minimal distances versus time is not random; there are distinct time frames where at least a single ion is located close to the protein for hundreds of picoseconds. In principle, such states can result either from a certain ion being attracted to the protein surface for a long time, or from rapid exchange of ions between the bulk and attractive sites on the protein. To discriminate between the two cases, we took advantage of the small number of ions, which allowed the individual monitoring of each ion.

FIGURE 2.

The minimal distance, in nanometers, between any of the Cl⁻ (A); any of the Na⁺ ions (B); individual Cl⁻ ions (C; each of the four ions is colored differently) or individual Na⁺ ions, and the protein as a function of simulation time, calculated over the simulation MD_N. The distances in nanometers and the time is given in nanoseconds. The absolute minimal distance (∼0.2 nm) is dictated by the steric interferences between the van der Waals radii of the ions.

The minimal distance between each ion and the protein is shown in Fig. 2, frames C and D. A close inspection of the ions' motion reveals that each ion, when coming close to the protein, tends to remain there. Thus, the relatively long time stretch, when an ion appears to be next to the protein, reflects a true detainment of an ion near the protein surface, rather than a rapid turnover of several ions.

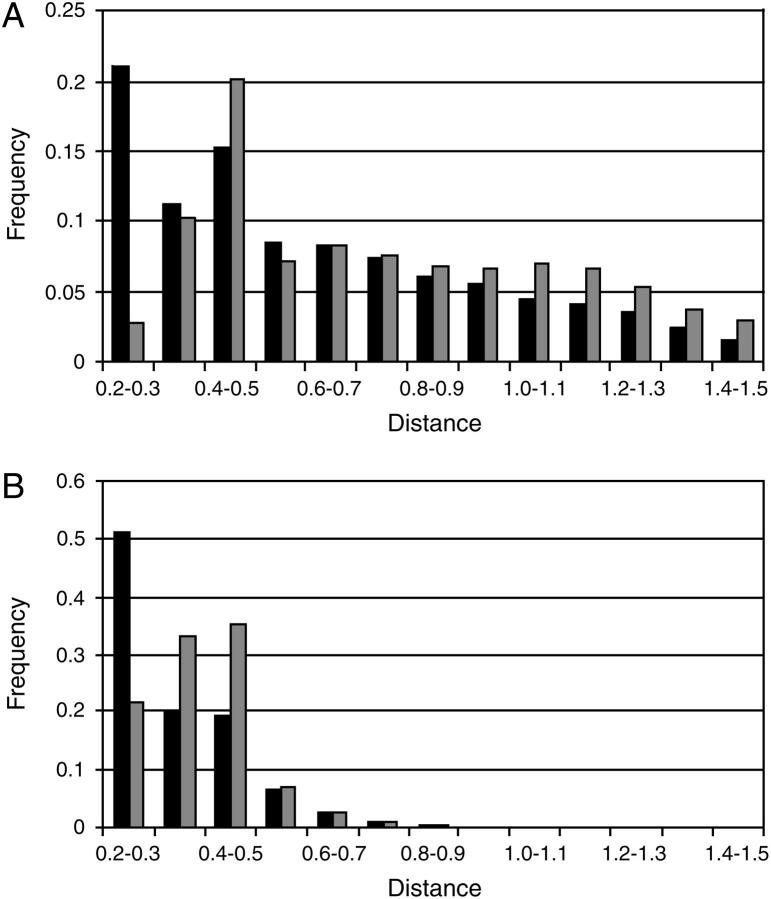
The results presented in Fig. 2 were further analyzed by study of the distribution of the minimal distances between the ions and the protein. Fig. 3 A presents the distribution function of the minimal distances between the ions and the protein as a histogram. It can be seen that, for the Cl⁻ ions (panel A), the functions have two maxima (at d = 0.2–0.3 nm and at d = 0.4–0.5 nm), whereas for the Na⁺ ions (panel B), there is only one maximum (at d = 0.4–0.5 nm). These observations are in agreement with the radial distribution functions of the salt ions, relative to the C-terminus and N-terminus of the penicillamine enkephalin peptide, as calculated in Marlow and Pettitt (38). In their simulations, the radial ion distributions had maxima at 0.27 and 0.47 nm (Na⁺), and at 0.23 and 0.49 nm (Cl⁻). These values are consistent with the tendency of the ions to be retained near the protein, either at a van der Waals contact distance or separated by a single solvation layer.

FIGURE 3.

The distribution functions for the minimal distances between the Cl⁻ ions (black) or Na⁺ ions (gray) and the protein, in the simulations MD_N (A) and MD_S (B). The distances are given in nanometers. Only the main part of the distribution is shown.

The minimal distance distribution functions were also calculated for the simulations MD_S and MD_E22p. In the case of the simulation E22p, the distribution was essentially the same as in Fig. 3 A (data not shown). In the simulation MD_S, in which the salt concentration was 120 mM, the minimal distances between the ions and the proteins are smaller (Fig. 3 B), in accordance with the higher concentration of ions in the solution.

The apparent delay of the ions near the protein can be quantitatively evaluated by an estimation of the time needed for the ion to diffuse out of a space element of comparable size. As a test case, let us consider an ion located at a contact distance (2 Å) from an atom on the protein. Unless there is a force that limits its freedom of motion, the ion will diffuse toward the bulk. Using Einstein's expression 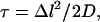we can estimate that the ion will propagate to 6 Å, normal to the protein's surface, within ∼40 ps. As seen in Fig. 2, there are time frames, extending up to a few hundreds of picoseconds, in which the ions appear to remain <6 Å from the protein. When an ion is delayed near the protein for such a long time period, its motion must be biased by the presence of the protein.

Quantitation of the ions' interaction with the protein's surface

The tendency of the ions to be detained near the protein surface is not evenly distributed over the protein's surface, and some residues are more attractive than the others. This feature can be precisely quantitated by means of the probability of finding an ion at a cutoff distance from the attractive domain of each amino acid. The cutoff distance used to define the detained state was based on the minimal distance distributions presented in Fig. 3. For simulations MD_N and MD_E22p, the cutoff distance was defined as 6 Å, based on the characteristic minimal distance between the ions and the protein (4–5 Å; Fig. 3 A). As the ion affinity does not vanish instantaneously, the cutoff distance was set to 6 Å. For the simulation at the higher ionic strength (MD_S), the cutoff distance was reduced to 5 Å; see Fig. 3 B. Ions that are located next to the protein surface, within the cutoff distance, are defined as detained. This term signifies their ability to execute a random walk but under restrictions that retain them near the surface, longer than expected for an unbiased free diffusing particle.

The attractiveness of each residue was calculated by the probability of finding an ion within the cutoff distance from the atoms of the attractor domain of the residues, namely: the OE oxygen atoms in aspartate, OD oxygen atoms in glutamate, HE or HH hydrogen atoms in arginine, HZ hydrogen atoms in lysine, the C-terminal oxygens, and the hydrogen atoms of the N-terminal amine. The results of these calculations are presented in Tables 3–8 (see also the Supplementary Material).

TABLE 3.

The probability of finding the Cl⁻ ions in a detained state, in which an ion is located within 6 Å of the terminal group hydrogens of the N-terminus, arginine, or lysine, or the hydrogen from the OH group of Tyr-50, calculated over the simulation MD_N

Residue	Probability	Detainment energy (kcal/mol)
Tyr-50	0.11	−0.84
Arg-80	0.28	−1.53
Arg-87	0.24	−1.41

Only residues associated with the protein during >5% of the simulation time, or discussed in the text, are included in the table. A table that details the interactions with all residues is given in the Supplementary Material.

TABLE 4.

The probability of finding the Na⁺ ions in a detained state, in which an ion is within 6 Å of the carboxylate oxygens of the C-terminus, aspartate, or glutamate and the unprotonated imidazole nitrogen of His-16, calculated over the simulation MD_N

Residue	Probability	Detainment energy (kcal/mol)
Asp-15	0.06	−0.45
His-16	0.03	−0.02
Glu-31	0.07	−0.55
Glu-41	0.08	−0.64
Glu-42	0.005	1.07
Glu-95	0.12	−0.90
Phe-97 (C-terminus)	0.08	−0.64

Only residues associated with the protein during >10% of the simulation time, or discussed in the text, are included in the table. A table that details the interactions with all residues is given in the Supplementary Material.

TABLE 5.

The probability of finding the Cl⁻ ions in a detained state, in which an ion is within 6 Å of the terminal group hydrogens of the N-terminus, arginine, or lysine, or the hydrogen from the OH group of Tyr-50, calculated over the simulation MD_E22p

Residue	Probability	Detainment energy (kcal/mol)
Arg-2	0.09	−0.54
Tyr-50	0.06	−0.28
Lys-54	0.08	−0.46
Arg-80	0.23	−1.20
Arg-87	0.11	−0.67

Only residues associated with the protein during >5% of the simulation time, or discussed in the text, are included in the table. A table that details the interactions with all residues is given in the Supplementary Material.

TABLE 6.

The probability of finding the Na⁺ ions in a detained state, in which an ion is located within 6 Å of the carboxylate oxygens of the C-terminus or aspartate, is calculated over the simulation MD_E22p

Residue	Probability	Detainment energy (kcal/mol)
Glu-41	0.11	−0.85
Glu-42	0.02	0.23
Glu-95	0.02	0.23
Phe-97 (C-terminus)	0.11	−0.85

Only residues associated with the protein during >5% of the simulation time, or discussed in the text, are included in the table. A table that details the interactions with all residues is given in the Supplementary Material.

TABLE 7.

The probability of finding the Cl⁻ ions in a detained state, in which an ion is located within 5 Å of the terminal group hydrogens of the N-terminus, arginine, or lysine, calculated over the simulation MD_S

Residue	Probability	Binding energy (kcal/mol)
Arg-80	0.12	−0.08
Arg-87	0.14	−0.18
Lys-92	0.01	1.48

Only residues associated with the protein during >5% of the simulation time, or discussed in the text, are included in the table. A table that details the interactions with all residues is given in the Supplementary Material.

TABLE 8.

The probability of finding the Na⁺ ions in a detained state, in which an ion is located within 5 Å of the carboxylate oxygens of the C-terminus, aspartate, or glutamate and the unprotonated imidazole nitrogen of His-16, calculated over the simulation MD_S

Residue	Probability	Detainment energy (kcal/mol)
Glu-24	0.06	0.38
Glu-41	0.10	0.05
Glu-95	0.08	0.19
Phe-97 (C-terminus)	0.02	1.06

Only residues that are associated with the protein during >5% of the simulation time, or that are discussed in the text, are included in the table. A table that details the interactions with all residues is given in the Supplementary Material.

Before an examination of the results presented in Tables 3–8 takes place, let us calculate the basal probability of finding an ion within the 6-Å layer surrounding the protein. This can be done by relating the volume of the layer (39.18 nm³) to the total volume of the aqueous phase in the simulation box (217.7 nm³). Assuming that the protein is totally inert with respect to the ions' distribution, each of the ions present in the solution is expected to be within the 6-Å layer 22% of the time.

To estimate for how much of the total simulation time an ion will be located near a certain residue, let us consider the most solvent-exposed amino acid, Phe-97 at the C-terminus. The volume available at the 6-Å layer surrounding Phe-97 is 1.04 nm³, which is 0.5% of the volume of the aqueous phase in the simulation box. Consequently, for an inert protein and four Na⁺ or Cl⁻ ion pairs, we should expect to find either a sodium or a chloride ion in the detained state for ∼2% of the simulation time. Any deviation of the observed probability of detainment from 2% is a quantitation of the attractiveness or repulsiveness of the residue. Examination of the results, given in Tables 4 and 6, indicates that this residue detains sodium ions in its vicinity, above the level of homogenous ion distribution.

Further inspection of the results indicates that not all charged residues have the same ability to attract ions. Few residues were able to attract an ion in their vicinity for up to 20–30% of the simulation time, whereas others hardly affected the ion's spatial mobility. When simulation MD_N is compared with the simulation MD_E22p, similar features are observed. Considering the chloride ions, the same pair of residues forms the strongest ion attractor site (Arg-80 and Arg-87; see Tables 4 and 6). Similarly, the strongest sodium attractors in the simulation MD_N were Glu-41, Glu-95, and the C-terminus, whereas in the simulation MD_E22p the strongest attractors were Glu-41 and the C-terminus (Tables 3 and 5).

In the presence of higher ionic strength, 120 mM, the capacity of the protein to detain ions in its vicinity is practically lost. At this salt concentration, the intensive ionic screening (κ⁻¹ ∼ 10 Å) practically smoothes the variation of the electrostatic potential, and the frequency of the ion's presence near the various charged residues is more homogeneous, as expected from a system where the number of ions exceeds the number of attractive sites.

In summary, we can assign ion attractor sites, which differ in their intensity, to the protein's surface. The effect is sensitive to ionic screening and weakens due to saturation of the surface by ions. Despite the difference between the simulations, the same residues emerged as strong ion attractors, leading to the conclusion that the strong ion attractor sites are a feature of the protein structure and not of the simulation setup.

The detainment energy

To quantitate the affinity of the attractor sites for the ions, we employed a two-state model as an operational definition for the ion affinity. In the two-state model, the ion is defined as detained if it is located less than a cutoff distance from the protein. Otherwise, it is considered free.

According to this definition, the equilibrium constant for detainment (K_det) is calculated as (33,96):

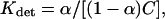(4)

where C is the concentration of the ions and α is the time fraction that the site is associated with an ion as given in Tables 3–8 (second column). Accordingly, the energy associated with the detainment is calculated by the expression

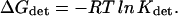(5)

The energies, which were calculated for the different residues that detain the ions, are given in the third column of Tables 3–8.

The energy associated with the detained state is relatively small, in the order of ΔG_det ≈ −k_BT or less. This value implies that the detainment events are consequences of a rather weak force. Yet, the strong attractor sites are well distinguished, having detainment energies of ΔG_det ≈ −k_BT or less, whereas the weaker attractor sites have ΔG_det > 0.

In the case of the sodium ions, all the attractor sites are of the same chemical nature; however, there are marked differences between the detainment energies associated with the sites. Thus, the capacity of a site to detain an ion is not attributed only to the residue itself. Rather, it is a reflection of multiple interactions of many moieties on the protein's surface. For example, such interactions account for the difference between the ion-attracting ability of the neighboring residues Glu-41 and Glu-42 (see Tables 4 and 6).

Although some differences between the stronger and weaker ion attractors were still observed in the simulation with 120 mM salt, when accounting for the higher salt concentration, the detainment energies are much smaller and even the strongest sites have ΔG_det ∼ 0 or higher. Thus, we can clearly state that the detainment energy is sensitive to ionic screening and is mostly contributed by the local electrostatic potential.

The electrostatic potential around the protein

The electrostatic potential surrounding the protein (at I = 50 mM) is displayed in Fig. 4. The potential field consists of two main lobes, one positive and the other negative; the ions are attracted to the oppositely charged lobes, and interact with the residues enclosed within this space.

FIGURE 4.

The electrostatic potential surface around the protein. (A) Residue His-16 (which is transiently located in the vicinity of the ion) and the two attractor sites Glu-41 and Glu-95 are presented under the positive Coloumb cage umbrella. (B) Residues Arg-80 and Arg-87, which are the strongest ion attractors, and Lys-92, which is located in their vicinity and forms a weak ion attractor, are presented as the ion is detained by Arg-80 and Arg-87. The Coulomb cages for the positive (blue) and negative (red) domains are drawn at the distance where the electrostatic potential equals 1 k_BT/e.

The negative Coulomb cage is characterized by a linear array of attractors. During the molecular dynamics, the Na⁺ ion can be observed to shuttle along the attractors. Such bind-and-release events are demonstrated in the animation, which is provided in the supporting information. At the first frame of the movie, the ion is associated with Glu-95 (simulation MD_N, t = 700). It then escapes from the vicinity of Glu-95 and diffuses into the bulk. During its diffusion, it is reattracted to the protein and becomes detained by Glu-41 (t = 890). The ion's encounter with Glu-41 is brief. After ∼20 ps, it diffuses away from Glu-41 and, within a few tens of picoseconds, associates with His-16. Histidine residues are not usually ion attractors. However, His-16 is located under the negative Coloumb cage umbrella (see Fig. 4 A) and briefly detains the sodium ion (see Tables 4 and 6) for almost 100 ps, before shifting to Glu-41. Finally, the ion is driven into the bulk solvent, where it freely diffuses away from the protein surface.

The positive Coulomb cage (Fig. 4 B) has one central attractor area made of two arginines (Arg-80 and Arg-87). Residue Lys-92 is located in the vicinity of the Arg-80/Arg-87 pair, but is a much weaker attractor (see Table 2), indicating that the local environment near a certain residue is a crucial factor in determination of its ability to detain oppositely charged ions. It is of interest to note that, in the presence of the two arginine residues, the OH moiety of Tyr-50 also becomes an ion attractor.

The thermodynamic constituents of the binding energy

The energies associated with the detainment of the ions were based on the analysis of the MD simulation. It would be of interest to test whether similar binding energies could also be obtained through structural thermodynamic formalism, where the individual contributions of the electrostatic and entropic terms could be accounted for. There are several formalisms for the decomposition of protein-ligand binding energies, including the PDLD/S method under the linear response approximation treatment (97–99), LIE (80–84), and continuum electrostatic-based free-energy calculations (100). In the section below, we limit ourselves to the latter formalism, which is conceptually simple and easy to follow in the case of the detainment of a small ion by a protein.

Following Froloff et al. (100), the binding free energy can be estimated in the form:

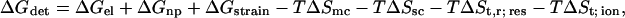(6)

where ΔG_el is the electrostatic contribution to the detainment energy, ΔG_np is the nonpolar contribution due to a change in the exposed surface area, ΔG_strain is the change in free energy due to local distortions in the structures of the protein and the ligand after ligand binding, TΔS_mc accounts for the loss of backbone torsional freedom, TΔS_sc accounts for the loss of side-chain torsional freedom, and TΔS_{t,r; res} and TΔS_{t; ion} account for the loss of translational and rotational freedom of the binding residues and for the loss of the translational freedom of the ion upon its detainment. When calculating the binding of a small ion to a protein, ΔG_strain can be neglected. ΔG_np and TΔS_sc are also negligible because the binding of a small ion hardly modulates the exposure of the binding residues to the solvent interface (for elaboration of these terms, see Froloff et al. (100)). The loss of backbone torsional freedom of the residues after the binding of the ions is also expected to be negligible, i.e., TΔS_sc ∼ 0.

The value of ΔS_{t,r; res} depends on the thermal motion of the atoms, which is proportional to their root mean square fluctuations (RMSF). Comparison of the RMSF of the residues of the Cl⁻-detaining site during the time of detainment, versus the RMSF of the same residues when the site is free, revealed no significant difference. We therefore assume that the binding of the ion hardly influences the rotational and translational freedom of the binding residues, i.e., ΔS_{t,r; res} ∼ 0.

Accordingly, we can simplify Eq. 6 in the case of the binding of an ion to the protein surface, as:

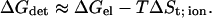(7)

The electrostatic contribution to the detainment energy was calculated for two conformations of the protein when the ion was detained, taken from the simulation MD_N. These conformations are shown in Fig. 5. The calculations are performed by solution of the Poisson-Boltzmann equation, where the solutes are treated in atomic detail, whereas the solvent is represented by a continuum. For these calculations, the dielectric constants of the solutes (protein and bound ions) and the solvent must be given as input. Although the choice of a dielectric constant for the solvent is straightforward (ɛ = 78.4), the dielectric constant assigned to the solvated protein may assume different values, depending on the system under study.

It should be mentioned that the assignment of a uniform dielectric constant for a protein is physically meaningless; the hydrophobic inner core, solvent-exposed surface, and residues that border water-bound cavities should be described by different dielectric coefficients (101–107). When a certain dielectric constant is applied to the solute in the calculation of ΔG_el, it should be treated as a parameter that depends on the model used (78). For example, Miyashita and co-workers have calculated the binding energies for protein-protein association, using different values of the solutes' dielectric, between ɛ = 2 and ɛ = 20 (108). Miyashita and co-workers have found reasonable agreement with the experiment when the dielectric constants of the proteins were ɛ = 10–20. On the other hand, Muegge and co-workers stated that when charged groups are considered, the protein dielectric constant should be as high as ɛ = 40 or even higher (98). Following these workers we calculated the value of ΔG_el where the dielectric constant assigned for the solutes was set as 4, 10, 20, and 40. The corresponding values of ΔG_el are given in Table 9.

TABLE 9.

The contributions for the free energies of detainment (see Eq. 5)

	PB calculation*
	ɛ = 4	ɛ = 10	ɛ = 20	ɛ = 40	DDSF†	TΔSt, ion	ΔGb‡
Na+	−10.0	−3.6	−1.7	−1.1	−7.2	2.5	−0.55
Cl−	−18.9	−7.2	−3.5	−2.2	−8.3	2.1	−1.26

^*Calculated by Eq. 1.

^†Calculated by Eq. 2.

^‡Reference energy, calculated throughout the 10-ns simulation using Eq. 5.

The energies are presented in kcal mol⁻¹; ɛ is the dielectric constant as used for the calculation of ΔG_el (see Methods).

It should be stated that the macroscopic treatment offered by solving the PB equation for the calculation of ΔG_el is not accurate enough, because the protein inner dipoles are not considered (78). An alternative approach is to calculate ΔG_el by an application of distant-dependent screening factors to the Coulomb equation (Eq. 2; see Methods). This simple treatment gave satisfactory results when used for the calculation of the electrostatic interactions in the photosynthetic reaction center (86). Therefore, the calculations of ΔG_el were repeated using Eq. 2, and the corresponding values of ΔG_el are given in Table 9.

Although the electrostatic energy favors the detained state, the entropy term given in Eq. 5 favors the free state of the ion. By treating the ions in the bulk as ideal, noninteracting particles, the change of entropy upon the detainment of the ion can be estimated by:

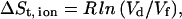(8)

where V_d is the volume element available for the detained ion and V_f the volume available for the free ion. Following the operational definition of the detained state, the ion can be located within a range of 6 Å away from the nearest protein atom. Accordingly, we can estimate the free space sampled by that of the detained ion as the volume of a spheric shell with an outer radius of 0.6 nm and an inner radius that is determined by the Van der Waals exclusion distance around the ion (∼0.2 nm), i.e., V_d = 0.87 nm³. When the ion is diluted in the bulk, the average volume that it occupies is a function of its concentration in the solution. For a solution of 0.03 M, V_f = 55.37 nm³.

The entropic loss upon detainment of the free Na⁺ ion (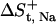) is calculated to be −8.25 cal mol⁻¹ K⁻¹. The calculation of 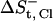is more complex, as the ion interacts with two bulky positive residues (Arg-80 and Arg-87) and, to a lesser extent, with the O-H dipole of Tyr-50 in the best attractor site. Thus, the space it can sample while remaining within 6 Å of the nearest attractor atom is larger than that attributed to the sodium ion, and is estimated as 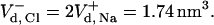The special geometry of the Cl⁻ attractor domain thus allows it to retain a higher freedom of motion. In parallel, the electrostatic attraction operating on the Cl⁻ is stronger than that affecting the Na⁺ (Table 9). The combination of the two factors leads to a higher detainment energy of the Cl⁻ with respect to the Na⁺.

The energy associated with the detainment of the ions throughout the MD simulation (as calculated by Eq. 5) is displayed in Table 9. As apparent from this table, when TΔS is considered and a dielectric value of 10 < ɛ ≤ 20 is assigned for the solvated protein, the calculated detainment energy covers the range of its actual detainment energy. This range of dielectric constants is in accordance with the calculations of Miyashita and co-workers (108). The DDSF calculation led to slightly too-favorable detainment energies compared to the molecular dynamics simulations, presumably because these functions were designed to treat electrostatic calculations inside proteins rather than on the protein surface. When the calculation is based solely on ΔG_el, a dielectric value of ɛ = 40 should be assigned to the protein, in agreement with Muegge et al. (98). This representation compensated for the energy needed for the structural reorganization of the protein (see also Warshel and Russell and others (109,110)).

The effect of water polarizability on the potential energy function

It remains to be ascertained that our conclusions, which are based on a force-field potential energy model, are valid despite the lack of explicit treatment for the electronic polarizability of the solutes and the water. The usage of potential energy models that can take the electronic polarizability into account is clearly desired in MD simulations, especially when interfaces that include ionic solutions are involved. However, although polarizable force fields are developed for protein simulations (111,112) such calculations cannot be applied for simulations of even moderately sized proteins such as the S6. On the other hand, neglect of the polarization can influence the results of simulations that involve the interface of an ionic solution in several ways, as discussed below.

It had been widely believed that when considering ionic solutions near air or hydrophobic interfaces, the ions are more likely to be found in the bulk of the liquid rather than near the air-water interface. This notion was rejected based on both experimental results (113) and MD simulations (114,115). Using an MD simulation with a polarizable force-field function, Jungwirth and Tobias have shown that, when simulating concentrated (1.2 M) solutions of NaCl in water, the Cl⁻ ions are in fact more likely to be located close to the water-air interface (114). This phenomenon could not be reproduced using the methods described in the current manuscript (see Supplementary Material). In contrast, the methods that we employed qualitatively reproduce the increase of surface tension in a solution of 1.2 M NaCl relative to pure water (see Supplementary Material).

Owing to the lower salt concentration in the simulations reported above (0.03–0.12 M), and due to the fact that the ions are detained by charged residues (rather than a hydrophobic surface), the failure to reproduce the results obtained by Jungwirth and Tobias is not expected to affect the behavior of the ions at the protein-water interface.

The realistic description of ion solvation in polarizable versus conventional force fields was previously tested by Grossfield and co-workers (48). There were no significant differences between the conventional force fields and the polarizable one in a variety of calculations, including the equilibrium ion-water distances and interaction energies in ion-water dimers, and the location of the solvation shells. On the other hand, differences of up to 10% have been found in the free energies of solvation of both individual ions and whole salts. Although the energies calculated by the polarizable force field were closer to the experimental values in the case of the free energy of solvation obtained for salt solutions, a difference of 10% is not expected to affect the general picture of ion detainment by the protein surface, as larger difference in the detainment energies are found between the simulations MD_N and MD_E22p. It should also be noted that the solvent electronic polarization had only little effect in simulations of monovalent ions in solution (116). However, when one deals with protein interiors the effect of using polarizable force fields can be significant (79).

DISCUSSION

In this study, we have reported three 10-ns-long MD simulations of the S6 ribosomal protein surrounded by a few ions. The dynamics of the ions were analyzed by considering individual ion bind and release events. The biological function of the S6 ribosomal protein is not associated with ion binding, but we could identify residues that function as local ion attractor sites. This demonstrates that the observed features are general and not specific to a certain biological function. The simulations indicated that the protein was able to detain ions to its immediate vicinity, 6 Å or less from its surface, for time frames as long as hundreds of picoseconds. In the detained state, the ions did not lose their freedom of motion: they were able to shuttle between nearby attractor sites, with a restriction that lowered their probability of moving far from the protein. This restriction is attributed to the electrostatic potential. As the ion could hop near and between attractor sites in the detained state, even residues that are not expected to function as ion attractors (such as His-16 and Tyr-50) can temporarily function as efficient ion attractors.

The simulations revealed fast exchange of the ions between the protein's surface and the bulk, thus reflecting competition between two forces: the electrostatic attraction that favors the detainment and the entropic drive that prefers the free state of the ion. Throughout most of the simulation time, the ion diffuses in a Brownian motion in the bulk, but once an ion is trapped by the protein's Coulomb cage, it is drawn to the nearest attractor site. Sooner or later, depending on the strength of the attractor site, the ion will escape its detainment and will either diffuse within the Coulomb cage to another attractor or diffuse out of it. When ions are scarce in the solution, a detained ion has a higher probability of encounter with the nearby attractor sites, compared to ions present in the bulk solvent, as the detained ion is already located on the other site's vicinity and is under the Coloumbic umbrella. There is a strong resemblance between the mechanism of ion motion next to the protein and the proton-collecting antenna reported for bacteriorhodopsin (117) or cytochrome c oxidase (118,119). These domains consist of clusters of carboxylate moieties that function as proton binding sites. The protonation on any carboxylate of the cluster leads to rapid proton exchange reactions that finally deliver the proton to the immediate vicinity of the proton-conducting channel of the protein. In this study, we generalized the system by substituting the proton, with its special chemistry, by more inert ions: Na⁺ and Cl⁻. Both bear a single charge, yet they do not form a covalent bond with the protein, and their diffusion mechanism is a simple self-diffusion rather than the Grotthuss mechanism of the proton (120). With these ions, we could follow the propagation along the surface of the protein without the complications emerging from the breaking of covalent bonds or the special diffusion pattern of the proton.

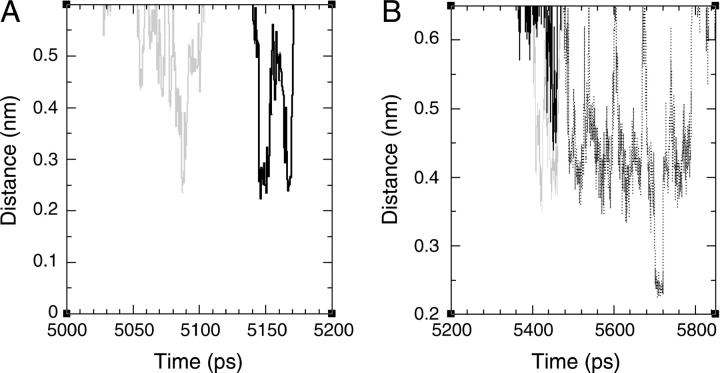
Two examples of rapid movements of ions from residue to residue are given in Fig. 6. The figure depicts the minimal distance between a single ion and two attractor sites, as it varies with time. Panel A depicts the dynamics of a Cl⁻ ion over ∼200 ps. During this time frame, the ion spent ∼50 ps near residue Arg-47. Then, for ∼50ps, it diffused out of the detainment layer to be rearrested in the vicinity of Lys-54. Panel B represents the same scenario for a Na⁺ ion. In this case, the ion rapidly shifts between three residues and the overall period, where the three attractors detain the ion, extends to ∼0.5 ns. Such events are seen throughout all simulations (two examples from the simulations MD_E22p and MD_S are given in the Supplementary Material). When the salt concentration is low, these events can be interpreted as a demonstration of the antenna effect: an ion is first attracted to a single site and then transferred to another. Thus, this study demonstrates that the antenna effect is a common feature of the protein surface, and is not limited only to proton-transferring proteins.

FIGURE 6.

(A) The distance between one of the chloride ions and the hydrogen atoms attached to the guanido group of Arg-47 (gray) or to the amino group of Lys-54 (black), as a function of simulation time, during the simulation MD_N. The ion rapidly moves from the vicinity of Arg-47 to the vicinity of Lys-54. (B) The distance between one of the sodium ions and the carboxylate oxygens of Glu-31 (points), Glu-38 (solid line), and Glu-66 (gray) as a function of simulation time, during the simulation MD_N. The ion is first associated with Glu-38 and Glu-66 and then with Glu-31.

Interestingly, there is also resemblance between the mechanism of ion motion next to the protein and proton transport near phospholipid membranes, as studied by molecular dynamics simulations (121). In their study, Smondyrev and Voth have found that proton diffusion was delayed as it penetrated into the polar regions of the lipid membranes due to two factors. First, it moved into confined regions bordered by the lipids. This is similar to the detainment of the Cl⁻ ions in the confined region formed by Arg-80 and Arg-87 (Fig. 5 A). Second, hydronium ions were found to form bridges between adjacent lipid molecules in the simulation reported by Smondyrev and Voth. This is similar to the binding of the ions by several residues (for example, see Fig. 6 B).

In summary, we conclude that the interaction between the protein surface and salt ions in dilute salt solution should be studied currently by conventional MD simulations, as used here. Experimental methods such as HSQC NMR, isothermal titration calorimetry, and differential scanning calorimetry can be used for the study of ion binding at binding sites (122), but their ability to detect ion binding at the protein surface is questionable; whereas more advanced simulation methods are too computationally expensive to be used. As discussed above, the usage of polarizable force-field energy functions is not expected to change our description of the ion dynamics at the protein salt interface.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.