Abstract
A large amount of data and observations on inositol 1,4,5-trisphosphate (IP3) binding to the IP3 receptor/Ca2+ channel, the steady-state activity of the channel, and its inactivation by IP3 can be explained by assuming one activation and one inhibition module, both allosterically operated by Ca2+, IP3, and ATP, and one adaptation element, driven by IP3, Ca2+, and the interconversion between two possible conformations of the receptor. The adaptation module becomes completely insensitive to a second IP3 pulse within 80 s. Observed kinetic responses are well reproduced if, in addition, two module open states are rendered inactive by the current charge carrier Mn2+. The inactivation time constants are 59 s in the activation, and 0.75 s in the adaptation module. The in vivo open probability of the channel is predicted to be almost in coincidence with the behavior in lipid bilayers for IP3 levels of 0.2 and 2 μM and one-order-higher at 0.02 μM IP3, whereas at 180 μM IP3 the maximal in vivo activity may be 2.5-orders higher than in bilayers and restricted to a narrower Ca2+ domain (∼10 μM-wide versus ∼100 μM-wide). IP3 is likely to inhibit channel activity at ≤120 nM Ca2+ in vivo.
INTRODUCTION
Release of Ca2+ ions from the endoplasmic reticulum (ER) is essential to many cellular processes (1,2). Calcium is released via the opening of its ER channel, the inositol 1,4,5-trisphosphate receptor (IP3R), whose complex behavior undergoes marked changes as the receptor is either incorporated into planar lipid bilayers or preserved in its native membrane environment (3–13). The reasons for the extreme variation (reaching as high as ≃20-fold) found in its peak open-probability are not clear. It is well established, however, that the IP3R activity is tightly regulated by cytosolic factors such as Ca2+, IP3, and free ATP, but the underlying mechanisms have remained poorly defined and are often confusing. It is not surprising, then, that there is no general consensus among existent models of the IP3 receptor (4,9,10,14–19), and that even though models (see Refs. 20 and 21 for review) have evolved in explaining increasing amounts of data, the current understanding of the calcium release regulation is still far from complete.
The ER Ca2+ channel is recognized as a tetrameric complex that binds IP3 and Ca2+ and is able to promote release of calcium ions into the cytosol. Three IP3 receptor isoforms are expressed in mammalian cells: IP3R type-1 (IP3R1), IP3R type-2 (IP3R2), and IP3R type-3 (IP3R3). The IP3R1 sequence contains 2749 amino acids and determines three structurally different parts: a large N-terminal cytoplasmic arm (∼65–80% of full length), a putative six-membrane-spanning domain near the C-terminus, which contributes to the pore structure; and a short C-terminal cytoplasmic tail (22,23).
IP3 has been found to bind to the 226–578 residue domain, which is near the NH2-terminus of each monomer (23,24). Mutational analysis revealed that the IP3 binding domain contains four segments (indexed here as DS1–4) covering the regions 241–249, 265–269, 504–508, and 568–569, respectively, which are determinant for ligand binding (24). In most biochemical studies IP3 bound to the receptor with Kd ∼50 nM and Hill coefficient ≃1 (4,10,24–29). It has been estimated that in the purified receptor each subunit binds one IP3 molecule to a single medium affinity site (30), but several recent findings in microsomes, with higher concentrations used of the radioactive ligand, cannot be explained unless a second IP3 binding site, of low affinity (Kd ∼10 μM, nH ≃ 1), is present on the IP3R1 (4) with equal abundance as the 50 nM site (4,10). Meanwhile, a third site with high affinity (Kd ≃ 1 nM) appears with extremely low frequency (<1%) in microsomal preparations (4,10), which brings into question its belonging to the IP3R1 (see below).
Ca2+ binds to seven sites residing on the cytoplasmic region of the receptor monomer and to one luminal site (23,31,32). The affinity of the luminal site and that of one cytoplasmic site have been determined (31,32), Kd = 0.3 μM (h = 1) and Kd = 0.8 μM (h = 1), respectively. With constant levels of IP3, the open probability of the channel depends on cytosolic Ca2+ in a bell-shaped manner, which is currently attributed to regulation by two distinct classes of activating and inhibitory Ca2+ sites, although some models can reproduce it with the aid of a single Ca2+ regulatory site (10). The IP3R1 sensitivity to activation and inhibition by Ca2+ most likely results from the calcium binding sensor (1932–2270 residues in IP3R1), which may include several Ca2+ binding sites (12).
It has been shown that another regulating factor, ATP, affects the activity of the channel (7,8). ATP binds to two-to-three putative sites situated on the regulatory cytoplasmic domain of the IP3R1 (23,33–36). Initially it has been estimated that in the purified receptor ATP binds to a single high affinity (Kd = 17 μM) site on the monomer (30). Recent studies have proved that the regions 1773–1780 and 2015–2021 of the purified IP3R1 bind ATP with high (Kd = 1.6 μM) and low affinity, respectively (35,36). The lower affinity site is conserved between IP3R isoforms. For the type-3 receptor the Kd is 177 μM (35). Binding of ATP can both stimulate and inhibit the receptor, depending on the Ca2+ concentration; however, the mechanisms are not clear. A simple, Hill-modified, ATP-dependence of the Ca2+ dissociation constant in the activation region (where Po increases with Ca2+, here for Ca2+ levels <60 μM) suggests that ATP has a functional Kd of 270 μM and h = 1 (7), whereas in the inhibition region ([Ca2+] > 60 μM) an ATP increase from 0 to 500 μM leads to a decrease of the Ca2+ dissociation constant from ∼100 to ∼50 μM (8). It appears thus that ATP enhances both activation and inhibition of the channel by Ca2+.
Regulation of IP3R1 activity by IP3 and Ca2+ has been approached with models of increasing complexity. Even though early models (14,37) succeeded in reproducing the biphasic dependence of Po on Ca2+ on the basis of three regulatory sites (one IP3-, one activating Ca2+-, and one inhibitory Ca2+ site), the right dependence of Po on both Ca2+ and IP3 was achieved later, by including a low affinity IP3 site (4). However, better fit to Po and open dwell-time data was obtained with a more complex, 125-state model (10), which assumed a single Ca2+ regulatory site and two IP3 sites (of medium and low affinity) in each monomer. The Po dependence on Ca2+ at 2 μM IP3 can be reproduced as well with different combinations of regulatory sites, as, for example, in the model of Swillens et al. (15,16)—where the assumed regulatory sites are the medium-affinity IP3, two Ca2+ activating sites, and two Ca2+ desensitizing sites.
In this article we analyze different sets of published data on IP3R binding and single channel activity, and show that the stationary activity of the IP3R type-1 (IP3R1) in both native and artificial membranes as well as various puzzling properties of the IP3 binding to the ER membrane can be consistently explained by a unique gating mechanism involving triple allosteric interactions between Ca2+, IP3, and free ATP binding to the channel molecule, but with different receptor sensitivity to particular ligands under different experimental conditions. Nevertheless, since to this end we use exclusively equilibrium data, the IP3R gating model is then adapted to reproduce channel inactivation in the sustained presence of IP3. Time trends of channel's open probability after two-pulse IP3 stimulation can be found closely similar to the experimental ones.
The model assumes that the activity of the Ca2+ channel is determined by the opening of three independent gates, each belonging to a certain region of the receptor, termed a module. One module is activated whereas another is inhibited by Ca2+. They are therefore called the activation module (AMo) and the inhibition module (IMo), respectively, whereas the remaining module, termed the adaptation module (AdMo), is considered to contribute to channel inactivation. The whole model is constructed on the basis of considering the tetramer receptor as a complex unit, so it describes how IP3 binds globally to each module, not to the corresponding portion of each monomer within a certain module. That allows us to assume that each module provides a single equivalent IP3 binding site. Then the Hill coefficient that defines IP3 binding to such a site gives the mean number of IP3 molecules that at an instant bind all four monomers at the locus of IP3 binding in the corresponding module.
Some of the model outputs pertain to the following:
The prediction of four IP3 binding sites on each receptor subunit, presumably located on the DS1–4 segments; three of these sites are implicated in channel gating.
The modulation by ATP of (IP3-dependent) channel activation and inhibition by Ca2+, effected by ATP binding at two sites on the receptor and allosteric regulation of Ca2+ and IP3 binding.
The description of Ca2+ inhibitory effects on IP3 binding, comprising alternative effects on affinity or the number of available binding sites.
The involvement in channel gating of a spontaneous or ligand-induced interconversion between two receptor conformations.
The description of channel inactivation by IP3 observed in two-pulse experiments, involving the transient kinetic response to successive IP3 additions; the rates of spontaneous conformation interchanges are determinant for the timescale of inactivation.
The prediction of the in vivo steady-state activity of the channel, which shares both similarities and differences with the behavior observed in bilayer experiments.
METHODS
Analysis of steady-state channel activity
Calculation of channel open probability and open/close dwell-times is done according to a previously published method (18), considering 0.2-ms temporal resolution of single channel recordings (8) in Xenopus oocytes and the IP3R1 reactions assumed in the present model. In the analysis of data obtained with the channel in lipid bilayers we have not corrected for missed events; however, the resolution therein is better (40 μs; see Ref. 10), and errors should be very small, at least for the open probability (18).
At equilibrium
 |
(1) |
where Pad denotes the probability that the AdMo gate is open, and is assumed to be constant. Here and throughout the article, h denotes Hill coefficient, k is the rate constant, K is the dissociation constant, Po is the open probability of the channel, Pm is the open gate probability of the m-type module, and [X] is the concentration of the X species. A site's occupancy is valued 1 (or 0) if the ligand is (or is not) bound to that site.
Where not specified, h = 1 for all ATP binding reactions. The rate of IP3 dissociation is 5 s−1 (15) unless otherwise stated, whereas the ATP dissociation rate constant is set to 0.05 s−1 for all ATP sites in the activation module (see Channel Inactivation).
To obtain the equilibrium open gate probability of every module we consider first-order kinetics for all state transitions, using mass balance equations to describe the time variation in state fractions, and the thermodynamical constraints, as
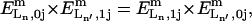 |
(2) |
where  is the equilibrium constant of the binding reaction of the n-type ligand Ln (n = 1, 2, or 3, corresponding to Ln ≡ IP3, Ca2+ and ATP, respectively) in the m-type module when the occupancies of the other two ligand sites are i and j, respectively, written in the order IP3, Ca2+, and ATP. The on-rates are of the form
is the equilibrium constant of the binding reaction of the n-type ligand Ln (n = 1, 2, or 3, corresponding to Ln ≡ IP3, Ca2+ and ATP, respectively) in the m-type module when the occupancies of the other two ligand sites are i and j, respectively, written in the order IP3, Ca2+, and ATP. The on-rates are of the form 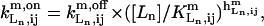 where
where 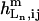 is the Hill coefficient of Ln binding to its site in the m-type module, with the other two ligand sites having occupancies i and j, respectively.
is the Hill coefficient of Ln binding to its site in the m-type module, with the other two ligand sites having occupancies i and j, respectively. 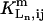 is the dissociation constant of Ln under the same conditions.
is the dissociation constant of Ln under the same conditions.
Equilibrium state probabilities are calculated numerically by solving the ordinary differential equations (ODEs) describing kinetics of each state fraction and extracting the solution values in steady state. Within analyses of channel activity at steady state, inactivation is not considered (see Channel Inactivation), so transitions to inactive states in Figs. 1 and 2 are not included in the equations.
FIGURE 1.
States and transitions within activation and inhibition modules of the IP3R1. Open and shaded circles represent states with open and closed gates, respectively. Ligands bound to the module are marked by symbols inside the circles. Detailed state transitions have common forms in both modules (m ≡ act or m ≡ inh in the activation and inhibition modules, respectively) and are represented without reference to the gate configuration (open/closed). The state denoted AI in the activation module can enter an inactive form (solid circle) when the charge carrier Mn2+ binds to a inner site of the channel.
FIGURE 2.
The adaptation module of the IP3R1 is operated by IP3, Ca2+ and the interconversion between two possible conformations, C1 and C2, with open and, respectively, closed gates. The state AdI is rendered inactive (solid circle) when Mn2+ (or K+) binds to an inner site of the channel.
It is assumed that both IP3 and Ca2+ bind with h = 1 to their sites in the adaptation module. According to the reactions, both IP3 and Ca2+ can bind to their respective sites with two different affinities, depending on the module state. The respective dissociation constants are denoted  (i, j = 1 or 2) when the ligand L binds to its site with the module being in conformation Ci and then changing conformation to Cj. The apparent affinity of each ligand for its site is determined by the module state distribution and the two distinct dissociation constants characteristic to the ligand. The apparent Kd values derive from fbound = [L]free/([L]free + Kd), where L is the ligand (IP3 or Ca2+) and fbound is the fraction of L-bound states in steady state, calculated according to the respective reaction scheme. The peculiar structure of the adaptation module state diagram determines a constant value for the total fraction of states in one of the two possible conformations, as well as for the apparent Kd of both ligands. These properties were numerically tested over large ranges of IP3 and Ca2+ concentrations. The rate constant k21 corresponding to the spontaneous change from conformation C2 to C1 is calculated from equating the open gate probability of the adaptation module to Pad = k21/(k12 + k21), where k12 is the rate of spontaneous conversion from C1 to C2.
(i, j = 1 or 2) when the ligand L binds to its site with the module being in conformation Ci and then changing conformation to Cj. The apparent affinity of each ligand for its site is determined by the module state distribution and the two distinct dissociation constants characteristic to the ligand. The apparent Kd values derive from fbound = [L]free/([L]free + Kd), where L is the ligand (IP3 or Ca2+) and fbound is the fraction of L-bound states in steady state, calculated according to the respective reaction scheme. The peculiar structure of the adaptation module state diagram determines a constant value for the total fraction of states in one of the two possible conformations, as well as for the apparent Kd of both ligands. These properties were numerically tested over large ranges of IP3 and Ca2+ concentrations. The rate constant k21 corresponding to the spontaneous change from conformation C2 to C1 is calculated from equating the open gate probability of the adaptation module to Pad = k21/(k12 + k21), where k12 is the rate of spontaneous conversion from C1 to C2.
When analyzing the single channel data of Mak et al. (6–9), two distinct values are obtained for each measured quantity, τo, namely, Po (mean open time), and τc (mean close time). The actual value corresponds to the real value, which would be obtained if all the events were recorded (i.e., time resolution τd = 0), whereas the apparent value corresponds to the measured value, obtained with τd = 0.2 ms. The difference between the two values reflects errors in discriminating open from closed channel events, which determine part of the events to be missed during recordings. The kinetic parameters derived from fit to these data (presented in Table 1, column CA-nm) are the only rate constants appearing in the calculation of τo and τc at steady state (see Appendix 2 in Ref. 18).
TABLE 1.
Parameter values derived from model fit to different data of channel activity, IP3 binding to cerebellar membranes, and channel inactivation
| Value
|
||||||
|---|---|---|---|---|---|---|
| Parameter | CA-lb | CA-nm | B-I | B-II | B-III | In |
| Activation module | ||||||
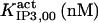 |
210 ± 10 (220)* | 220 | 130* | 220 | 8* | 220 |
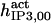 |
1.75 ± 0.25 (2)* | 1 | 1 | 1 | 1 | 1 |
 |
50* | 220–300* | 260* | 2500* | n.d. | 2500* |
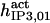 |
1.75 ± 0.25 (2) | 1 | 1 | 1 | n.d. | 1 |
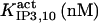 |
210 ± 10 (220) | 220 | 130 | 220 | 12† | 220 |
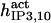 |
1.75 ± 0.25 (2) | 1 | 1 | 1 | 1 | 1 |
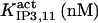 |
50 | 220–300 | 260 | 2500 | n.d. | 2500 |
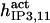 |
1.75 ± 0.25 (2) | 1 | 1 | 1 | n.d. | 1 |
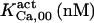 |
585 ± 15 (580)* | 550 ± 50 (520)*‡§ | 550 | 550 | 450* | 600* |
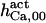 |
1.55 ± 0.15(1.8)* | 1.65 ± 0.15 (1.8)*‡§ | 2* | 2 | 2 | 1.5* |
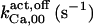 |
103.3¶ | 175± 25 (180)*‖§ | n.d. | n.d. | n.d. | 180 |
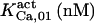 |
8 | 10 ± 2 (8)*‖ | 8 | 8 | n.d. | 8 |
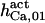 |
2.2 | 2.25 ± 0.25 (2.2)*‖ | 2.2 | 2.2 | n.d. | 2.2 |
 |
103.3¶ | 375 ± 75 (400)*‖ | n.d. | n.d. | n.d. | 400 |
 |
585 ± 15 (580) | 550 ± 50 (520) | 550 | 550 | 550 | 600 |
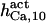 |
1.55 ± 0.15 (1.8) | 1.65 ± 0.15 (1.8) | 2 | 2 | 2 | 1.5 |
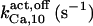 |
103.3¶ | 175 ± 25 (180) | n.d. | n.d. | n.d. | 180 |
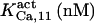 |
8 | 10 ± 2 (8) | 8 | 8 | n.d. | 8 |
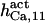 |
2.2 | 2.25 ± 0.25 (2.2) | 2.2 | 2.2 | n.d. | 2.2 |
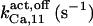 |
103.3¶ | 375 ± 75 (400) | n.d. | n.d. | n.d. | 400 |
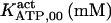 |
750 ± 250† | 390 ± 210† | 310† | 109† | n.d. | 2500† |
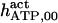 |
1 | 1.3 ± 0.1 (1.2) | 1 | 1 | n.d. | 1 |
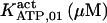 |
685 ± 285† | 175 ± 15 (169)† | 25† | 8.8† | n.d. | 132† |
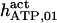 |
1 | 1.3 ± 0.1 (1.2) | 1 | 1 | n.d. | 1 |
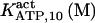 |
0.04† | 0.39 ± 0.21† | 0.62† | 1.2† | n.d. | 29† |
 |
1 | 1.3 ± 0.1 (1.2) | 1 | 1 | n.d. | 1 |
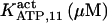 |
50 (20)* | 175 ± 15 (169)‡ | 50 | 100* | n.d. | 1500* |
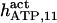 |
1 | 1.3 ± 0.1 (1.2)‡ | 1 | 1 | n.d. | 1 |
| Inhibition module | ||||||
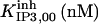 |
52.5 | 8.45*** | 28* | 300* | 13* | 300* |
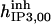 |
1.5 | 6 | 1.185* | 1.185 | 1.2* | 1 |
 |
52.5 ± 2.5 (55)* | 11.5 ± 0.5 (12)*†† | 28 | 300 | n.d. | 300 |
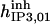 |
1.5 ± 0.3 (1.3)* | 6 ± 0.25 (6)*†† | 1.185 | 1.185 | n.d. | 1 |
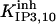 |
190 ± 136 μM† | 213 ± 33 nM† | 610 μM† | 37 mM† | 31 mM† | 34 M† |
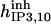 |
1.5 | 6 | 1.185 | 1.185 | 1.2 | 1 |
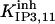 |
121.5 ± 70 μM† | 165 ± 11 nM† | 464 ± 85 nM† | 11.5 mM† | n.d. | 4.2 M† |
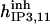 |
1.5 ± 0.3 (1.3) | 6 ± 0.25 (6) | 1.185 | 1.185 | n.d. | 1 |
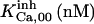 |
90 | 90 | 120* | 100* | 90 | 100* |
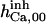 |
2.5 | 2.75 ± 0.25 (3)*** | 1.75* | 2* | 2.5 | 3* |
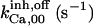 |
81¶ | 20*‖‖ | n.d. | n.d. | n.d. | 20 |
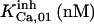 |
85 ± 5 (50)* | 90 | 120 | 100 | n.d. | 100 |
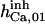 |
2.55 ± 0.05 (2.7)* | 1.35 ± 0.05 (1.3)*†† | 1.75 | 2 | n.d. | 3 |
 |
81¶ | 5 ± 4.9 (2)*‖ | n.d. | n.d. | n.d. | 2 |
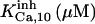 |
104 | 104‡‡ | 104 | 104 | 104 | 104 |
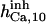 |
1.5 | 4‡‡ | 1.75 | 2 | 2.5 | 3 |
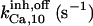 |
81¶ | 180*§ | n.d. | n.d. | n.d. | 180 |
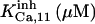 |
52 | 52‡‡ | 0.8 ± 0.1 (0.9)* | 52 | n.d. | 52 |
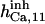 |
1.35 ± 0.15 (1.2)* | 4‡‡ | 1.75 | 2 | n.d. | 3 |
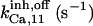 |
81¶ | 50*‖ | n.d. | n.d. | n.d. | 50 |
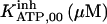 |
17 ± 7.5† | 0.75 ± 0.41† | 17† | 17† | n.d. | 17† |
 |
12.9 ± 7.1† | 9 ± 4.9† | 17† | 17† | n.d. | 17† |
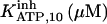 |
17 | 17§§ | 17 | 17 | n.d. | 17 |
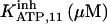 |
9.8 ± 1† | 1.56† | 0.005† | 6.25† | n.d. | 6.25† |
| Adaptation module | ||||||
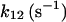 |
0.065¶ | 185 ± 35 (170)*‖§ | n.d. | n.d. | n.d. | 0.065* |
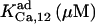 |
0.072¶ | 25¶ | 0.072 | 2.5 | 0.072 | 2.5* |
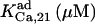 |
58† | 1.4 ± 0.6† | 58† | 80.3† | 58† | 80.3† |
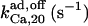 |
800¶ | 2¶ | n.d. | n.d. | n.d. | 500* |
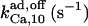 |
1.3¶ | 2¶ | n.d. | n.d. | n.d. | 50* |
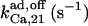 |
4.8¶ | 2¶ | n.d. | n.d. | n.d. | 50* |
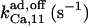 |
1.6¶ | 2¶ | n.d. | n.d. | n.d. | 50* |
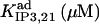 |
15¶ | 0.2¶ | 6.5 ± 1.5 (5) | 5 | 0.22 | 1.1 ± 1 (0.6)* |
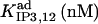 |
18† | 3600 ± 2800† | 10† | 156† | 0.3† | 34 ± 31 (19)† |
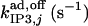 ¶¶ ¶¶
|
3¶ | 5‖‖ | n.d. | n.d. | n.d. | 5‖‖ |
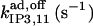 |
0.025¶ | 5‖‖ | n.d. | n.d. | n.d. | 5‖‖ |
| Pad | 0.034* | 0.81 ± 0.04 (0.07)*‖ | 0.034 | 0.15 | 0.034 | 0.15* |
| Apparent | ||||||
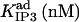 |
528*** | 853 ± 280 (670) *** | 230 ± 53 (177)* | 882* | 7.8* | 194 ± 177 (106)*** |
| Apparent | ||||||
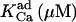 |
2.05*** | 5.86 ± 1.45*** | 2.05 | 14.2 | 2.05 | 14.2*** |
| IP3 site abundancies | ||||||
| nA:nI:nAd:nhi | 1:1:1:(n.d.) | 1:1:1:(n.d.) | 1:1:1:(0.0125*) | 1:1:1:0.0125 | 1:1:1:(0.02*) | 1:1:1:(n.d.) |
CA-lb and CA-nm stand, respectively, for channel activity in lipid bilayers (data from Ref. 4) and in nuclear membranes (data from Refs. 6–8). The values in parentheses of column CA-lb are obtained with data of Moraru et al. (10) and are used in the graph of Fig. 8. The values in parentheses of column CA-nm are common to all graphs in Figs. 3–6. B-I and B-II correspond to binding data of Moraru et al. (10), obtained with 0.5 mM ATP at 0° and 22°C, respectively, and B-III to data of Cardy et al. (29), obtained with 0 ATP at 2°C. The parameter values collected in column In are obtained from fit to the data of Hajnoczky and Thomas (18), shown in Figs. 11 and 12. The data have been obtained at 35°C, in the presence of 2 mM ATP. The values in parentheses of column In are used in simulations in Figs. 11–13.
Variable parameters.
Derived according to the thermodynamical equilibrium constraint; values are representative for 1 μM Ca2+.
Estimated from fit to data on modulation by IP3 of Po's Ca2+-dependence at 0 mM ATP (Ref. 8; and see this article, Fig. 3, lower panel) and dwell-time data with 33 nM IP3 and 0 mM ATP (8) (not shown).
Estimated from fit to data on modulation by IP3 of Po's Ca2+-dependence at 0.5 mM ATP (Refs. 6,8,9; and see this article, Fig. 3, upper panel).
Taken from the literature (30).
j = {10}, {20}, or {21}.
Taken from the literature (15).
Calculated from equilibrium values of total binding to the adaptation module.
All the data analyzed in the article are estimated from published articles. Whenever possible, effort has been made to have model parameter values as close as possible among data sets. The criterion has been used all over the fit procedure in analyses of channel activity, IP3 binding, and channel inactivation, and the values selected in Table 1 are obtained on this basis. Particular attention has been given to the confrontation between model parameters fit to the data obtained with IP3 binding to cerebellar microsomes (10) and those obtained, respectively, with studies on membrane permeability of intracellular Ca2+ stores in permeabilized hepatocytes (38), because the cellular conditions defined with the two experimental procedures involve the highest degree of similarity among all the data analyzed in this article, and are closest to the in vivo conditions.
The highest number of data was provided by experiments performed with Xenopus oocytes. The informative data on the dependence of IP3R1 inhibition on ATP are quite few; however, we estimated that the inhibition module is saturated by ATP at 0.5 mM. In particular, from our findings, ATP binding to the activation module results to have low affinity. Therefore the nominal InMo-dissociation constant KATP, 10 is fixed at the 17 μM value of the high affinity site (30). We first fit the model to the data obtained at 10 μM IP3, including Po, open-, and close-dwell-times (6,8). At this level, inhibition is maximal (6,9), meaning that the inhibition module is saturated with IP3. We obtain the parameters indexed with superscripts (‖) in the column CA-nm of Table 1. For the ATP dependence of receptor activation, Po is approximated to Pact × Pad since the inhibition module has, effectively, no Ca2+ bound. Then the rest of the parameters defining binding of ATP to the activation module (labeled with (‡) in Table 1) are estimated from fit to other data (7). The three remaining parameter values (indexed with (††) in Table 1) are extracted from fit of IP3 and Ca2+ dependencies of the Po (6,8,9). Parameters labeled with (¶) in the adaptation module are estimated exclusively from dwell-time information. The procedure is repeated for 0 ATP-data.
Because of the lack of sufficient data, some of the parameter values are shared among other sets, especially 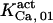 and
and 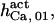 or
or 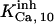 and
and 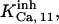 which are taken from the Xenopus set, whereas
which are taken from the Xenopus set, whereas 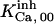 is dissipated from the CA-lb set. The consistency of the results validates this option. In analyses of IP3 binding, Pad and
is dissipated from the CA-lb set. The consistency of the results validates this option. In analyses of IP3 binding, Pad and 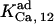 are each tested on two values, obtained with the sets CA-lb or In, and the best fit is kept. Where not specified, certain values of Table 1 copy the most reliable value among columns. If such a value does not provide reasonable fit, it is treated as a variable. The same principle applies also for various K- and h-parameters characterizing a certain ligand in AMo and IMo, within every single column of the table. All these simplify the fitting to a reasonable number of parameters. For example, with the fit in Figs. 4 and 5, eight and five parameters are estimated, respectively; in this particular case, the fitting is performed in two stages. First, the best fit is obtained separately for each set of data. Then, the common parameters are varied in a common range covering the values already obtained, and the best parallel fit is selected. With these values, the fitting moves forward to the data on the modulation by IP3 of the Po values Ca2+ dependencies at 0 or 0.5 mM ATP. From the fit shown in Fig. 3 (upper panel), three parameter values are determined. The fit of the data in Fig. 3 (lower panel) and related dwell-time data at 33 nM IP3 (8) (not shown) provides two other parameter values. For other data presented in Figs. 7 and 10, twelve and, respectively, six variable parameters are required. Fig. 9 (upper and lower panels) is obtained with 10- and six-parameter fits, respectively.
are each tested on two values, obtained with the sets CA-lb or In, and the best fit is kept. Where not specified, certain values of Table 1 copy the most reliable value among columns. If such a value does not provide reasonable fit, it is treated as a variable. The same principle applies also for various K- and h-parameters characterizing a certain ligand in AMo and IMo, within every single column of the table. All these simplify the fitting to a reasonable number of parameters. For example, with the fit in Figs. 4 and 5, eight and five parameters are estimated, respectively; in this particular case, the fitting is performed in two stages. First, the best fit is obtained separately for each set of data. Then, the common parameters are varied in a common range covering the values already obtained, and the best parallel fit is selected. With these values, the fitting moves forward to the data on the modulation by IP3 of the Po values Ca2+ dependencies at 0 or 0.5 mM ATP. From the fit shown in Fig. 3 (upper panel), three parameter values are determined. The fit of the data in Fig. 3 (lower panel) and related dwell-time data at 33 nM IP3 (8) (not shown) provides two other parameter values. For other data presented in Figs. 7 and 10, twelve and, respectively, six variable parameters are required. Fig. 9 (upper and lower panels) is obtained with 10- and six-parameter fits, respectively.
FIGURE 4.
Model fit to data of Mak et al. (6,8) obtained with the channel in the nuclear membrane, and 10 μM IP3 and 500 μM ATP on the cytosolic side. Dashed and solid lines characterize actual and apparent values, respectively, of the quantity represented in each graph.
FIGURE 5.

Model fit to data of Mak et al. (8) obtained with 10 μM IP3 and 0 ATP on the cytosolic side. Other details as in Fig. 4.
FIGURE 3.
The [Ca2+]cyt dependence of the IP3R1 open probability in the presence of 500 μM or 0 ATP, exhibited by channels within nuclear membranes of Xenopus oocytes. Curves are theoretical fits to the data and predictions for IP3 concentrations other than those used in experiments. Values next to curves represent IP3 concentrations in nM, unless otherwise specified. In the upper panel, data from Ref. 6 are represented as solid triangles, solid squares, open circles, solid circles, and open triangles, corresponding to 10 nM, 20 ± 3 nM, 33 ± 6 nM, 100 nM, and 10 μM IP3, respectively. The second and third datasets are to be confronted with the two regions delimited by dashed lines (squares to the 17–23 region, open circles to the 27–39 domain), to correct for variations in the IP3 level. In the lower panel, open and solid circles represent data of Mak et al. (8), obtained with 0 ATP, and 33 nM or 10 μM IP3, respectively.
FIGURE 7.
The [Ca2+]cyt dependence of the IP3R1 open probability at 500 μM ATP, exhibited by channels incorporated in lipid bilayers. Data, taken from Kaftan et al. (4) and Moraru et al. (10), and shown as solid and open circles, squares, and triangles, are obtained with 10, 20, 200 nM, and 180 μM IP3, respectively. Theoretical curves are obtained with the present model.
FIGURE 10.
The IP3 binding to cerebellum membranes at different [Ca2+]cyt. Data (from Ref. 29) correspond to 2 nM (open circles) and 1.1 μM (solid circles) Ca2+, respectively.
FIGURE 9.
The IP3 binding to cerebellum membranes at different [Ca2+]cyt and two different temperatures. Data are from Moraru et al. (10) and correspond, in the upper panel, to 0 (solid circles), 0.1 μM (open circles), 0.5 μM (triangles), and 10 μM (squares) Ca2+, respectively. In the lower panel, open and solid circles are data obtained with 0 and 10 μM Ca2+, respectively.
Analysis of IP3 binding
In the IP3 binding analyses we assume that the receptor has an IP3 regulatory site with apparent Kd = 10 μM (h = 1), and that an additional, high affinity site is present in microsome preparations, with 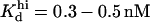 (h = 1) as we obtained from fit to the data. The high affinity IP3 site is assumed to bind IP3 through a simple one-step reaction and results to be located on IP3Rs other than the IP3R type-1 (see the last row in Table 1 and explanations in the text). In addition to these two classes of IP3 sites, three other classes of sites, each one belonging to a receptor module, contribute to the total quantity of bound IP3.
(h = 1) as we obtained from fit to the data. The high affinity IP3 site is assumed to bind IP3 through a simple one-step reaction and results to be located on IP3Rs other than the IP3R type-1 (see the last row in Table 1 and explanations in the text). In addition to these two classes of IP3 sites, three other classes of sites, each one belonging to a receptor module, contribute to the total quantity of bound IP3.
IP3 bound to the receptor is calculated by summing the products of the following terms, each one corresponding to a certain class of IP3 binding sites: site abundance, apparent number of IP3 molecules bound to the IP3 sites of the respective site class, and receptor concentration. The apparent number of IP3 molecules bound to a certain module is determined by summing the fraction of each IP3 bound-state within that module, times the Hill coefficient of IP3 binding to the respective state. Site abundances are denoted nA, nI, nAd, and nhi in the lowest row of Table 1 and correspond to the IP3 sites located on the activation, inhibition, and adaptation modules, and, respectively, to the high-affinity IP3 site existent in the respective microsome preparation. For each of the activation, inhibition, and adaptation modules the fraction of states with bound IP3 equals the sum of the steady-state probabilities corresponding to the module being in one of the four possible states with the IP3 site occupied. The IP3-bound state fraction of the high-affinity site is computed as 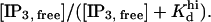 The receptor concentration is calculated such that the same apparent Kd values are obtained as derived from the original Scatchard plots (10,29).
The receptor concentration is calculated such that the same apparent Kd values are obtained as derived from the original Scatchard plots (10,29).
Simulation of channel inactivation
The time variation of Po after IP3 stimulation is calculated numerically by solving the kinetic equations (ODEs) corresponding to the reactions in each module, followed by multiplication of all three open gate probabilities at every instant. Inactivation of a certain state is equated by subtracting from the ODE right-hand side a term of the form fst/τst, where fst is the instantaneous fraction of that state and τst its inactivation time constant.
The cytosolic conditions are fixed by levels of 2 mM ATP and 300 nM Ca2+, and the time constant for IP3 degradation is τIP3 = 12 min (calculated from data in Ref. 38). Addition of 7.5 μM IP3 takes place firstly at t1 = 0 and then at a specified moment after the first pulse. The IP3 concentration varies according to the equation
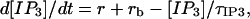 |
(3) |
where the rate of IP3 addition is r = 7.5 μM/Δt in the time interval (ta,ta + Δt) starting with the moment ta of IP3 addition, and r = 0 otherwise. The time of IP3 addition is Δt = 1 s; however values Δt <1 s lead to similar results. The basal IP3 production rate rb = [IP3]b/τIP3 with the basal level of IP3 set to [IP3]b = 1 nM.
The variation in the Mn2+ content inside the stores is obtained by considering the same constant value of the single channel current for all the IP3Rs. The rate of Mn2+ increase is given by the Mn2+ current through the membrane, which is proportional to the open probability of the IP3Rs. Each Mn2+ profile is then obtained, in arbitrary units, by integrating Po over time after the moment of Mn2+ addition, which is specified for each trace. It is assumed that quenching of fura-2 fluorescence by Mn2+ (obtained experimentally) is proportional to the Mn2+ content (calculated by model simulation), so both traces should have identical time courses. On some simulated traces a Gaussian noise is superimposed with standard deviation chosen so as to yield a noise magnitude similar to that observed experimentally in the fluorescence signal (38).
RESULTS
Model construction
We proposed previously (18) a model, and we have found it was the minimal one, to describe Po, τo, and τc dependence on Ca2+ at saturating levels of IP3 (10 μM), as well as both ATP- and Ca2+-dependence of Po in the activation region. The model was defined with three 4-state modules that drive independent gates responsible for activation/inhibition/inactivation of the channel. Here we improve that model to describe more data and reproduce the Po, τo, and τc dependence on Ca2+, IP3, and ATP, as well as the IP3 binding characteristics and the inactivation of the channel.
It is important to stress the major idea of the modeling procedure. Such an empirical formulation of the Po dependence with Ca2+ and IP3 as found to describe the data in Xenopus oocytes (6,7) can be explained by at least three independent gates, of which two depend, at steady state, on Ca2+ and IP3 concentrations whereas the others do not. To simplify the model, we consider only three such gates that act independently, leading to channel activity only when all of them are simultaneously open. For each gate-associated module now we introduce molecular mechanisms able to explain various experimental observations. The state-transition diagram of each module is constructed as the simplest state-configuration that agrees with all of the findings taken into account.
The activation module of the IP3 receptor is responsible for the stimulation of channel in the low-domain of cytosolic calcium concentrations, where the inhibitory effect of Ca2+ is absent. The module is operated by Ca2+ and ATP (18) as one can readily deduce from direct observation of the Po, τo, and τc data obtained with the channel in the outer nuclear membrane of Xenopus oocytes (6,7). The dwell-time data in conjunction with the Po-data can only be explained by allosteric regulation of the activation module by Ca2+ and ATP (18), which requires at least four states of the module. Interestingly, with the receptor reconstituted into lipid bilayers (4,10) the activation module appears also to be IP3-regulated since with 20 nM IP3 the IP3R1 activity in the activation region is 10-fold reduced as with 200 nM or higher IP3 concentrations. Although the data in the former set is not sufficient to evidence that feature (as seen in Fig. 3 here, it is not clear from the data whether AMo is sensitive to variations in IP3 in the Xenopus nuclear membrane), we collect both observations and draw the conclusion that gating in the activation module is allosterically controlled by IP3, Ca2+, and ATP.
To make this statement one has to assume that the gating mechanisms are the same in both membrane systems and the resulting differences in channel behavior are purely quantitative. In fact this is exactly the basic rationale of the article, for we intended to see whether the variability observed in different data can be explained by considering the same molecular processes and, if so, to find the quantitative differences in ligand affinities and Hill coefficients associated to each data set obtained under different experimental conditions. One major observed discrepancy, which is discussed in this section, comes from the observation that under closely similar conditions on the cytosolic side of the receptor the maximal activity of the channel appears to vary ∼20-fold in the two different membrane systems mentioned before. Other sources of variability will be addressed in the next sections.
So, the state-structure of the activation module is defined with allosteric regulation by IP3, Ca2+, and ATP, and the corresponding state-transition diagram is shown in Fig. 1.
Upon further raising cytosolic [Ca2+], the channel becomes increasingly inhibited. In this region, the behavior is dominated by the inhibition module, which is less active, whereas the activation gate may remain continuously open. As the data indicate (4,5–8,10), IP3 is an important modulator of the calcium inhibitory effect (18). The inhibition module can therefore exist in one of at least four states. We characterize this module better than in our previous work (18), with more recent results on IP3R1 regulation by ATP (8) included in the present analysis. These data require ATP to modulate channel inhibition by Ca2+. Taken together, all the data mentioned above point to the existence of three regulatory sites within IMo, namely one ATP, one IP3, and one Ca2+ binding site, and a similar state distribution within AMo and IMo (see Fig. 1) derives naturally after a summary inspection of the Po data. The difference is that Ca2+ binding in the AMo opens the AMo gate; Ca2+ binding in the IMo closes the IMo gate; ATP binding in the AMo stimulates opening of the AMo gate by Ca2+; and ATP binding in the IMo reduces opening of the IMo gate by Ca2+.
The two modules are not sufficient to reproduce the observed behavior of the channel, since with appropriate Ca2+ levels both gates virtually remain continuously open (the open gate probability in both modules is ≃1). Therefore, to obtain agreement with experimental data in both cases (native and artificial membranes), including Po, τo, and τc data, the model is constrained to include one other regulatory module, the adaptation module, characterized by constant (i.e., Ca2+, IP3, and ATP-independent) and subunitary steady-state probability of the open gate, Pad. It follows then that Pad represents the maximal open probability of the channel reached at steady state.
The model predicts that the Ca2+, IP3 and ATP dependence of channel's activity at equilibrium is determined by the AMo and IMo modules only. However, we found that the model established in the simplest possible form (see below) is not able to simulate several observed features related to the inactivation of the channel by Ca2+ and IP3. In vivo kinetic studies on Ca2+ release indicate that after double IP3 pulse delivery to Xenopus oocytes, the second release event gets weaker if the interval between pulses is successively increased up to 30 s, and the process occurs with a half-time of ∼10 s. For a 30-s interval, the inhibition of the release is ∼80% relative to the case of simultaneous IP3 delivery. Metabolism of IP3 is slow both in Xenopus oocytes (half-life 60 s, see Ref. 39) and in permeabilized hepatocytes (half-life 12 min., calculated from the data of Ref. 38), so it is more likely that the observed release inhibition is due to a ligand-induced inactivation of the IP3R1 rather than IP3 degradation, as suggested by Callamaras and Parker (39). In favor of this, other measurements (5) of the IP3R1 activity in the nuclear membrane of the oocyte evidenced an inactivation process at the receptor level, with a time constant of 30 s (discussed later, in Channel Inactivation). Calcium release events after IP3 photolysis in Xenopus oocytes (40) show IP3-dependent time courses that are similar (17) to those obtained from superfusion of 45Ca-loaded hepatic microsomes (41). In these and other similar (42) cases the release is fast, at variance with the slow channel inactivation detected in hepatocytes, where the unwanted effects of the cytosolic and luminal Ca2+ dynamics on the ion permeation properties were avoided by eliminating the Ca2+ fluxes (38). The type-2 IP3 receptor (IP3R2) is the major expressed subtype in hepatocytes, with ∼80% abundance (43). In this cell type the Ca2+ channel is subjected to an IP3- and Ca2+-dependent slow inactivation (38), and channel inhibition reaches ∼70% after preincubation with 7.5 μM IP3 for 30 s.
Given these and other similarities (e.g., the dual effect of cytosolic calcium on the open probability) between type-1 and type-2 receptors, we assume that the ligand-dependence of channel inactivation is common to both forms. To strengthen this choice, we observe that:
Both IP3R1 and IP3R2 exhibit intrinsic inactivation.
The fraction of IP3R2 in hepatocytes is 0.8 of total IP3Rs.
In hepatocytes the intrinsic IP3Rs inactivation displays, depending on the preincubation time, one or two exponential components of equal weights.
If inactivation were different between IP3R subtypes, at least one more exponential component would be detected, of smaller pool size. So, we will consider that inactivation follows the same time course in IP3R1 and IP3R2 and use identical inactivation parameter values for both receptor types. As we will discuss in a subsequent section, the differences between IP3R1 and IP3R2 with regard to the calcium effect on the receptor affinity toward IP3 are explained here by regulation due to AMo and IMo only, since, according to our model, channel inactivation does not affect that (see the next sections). Moreover, we have found that most of the observed differences between IP3R subtypes can be understood as consequences of variations in parameter values (not shown). The same treatment applies also for the differences in the Ca2+ and IP3 ranges of action on a channel's Po (8,11,12,44).
We were not able to fully explain inactivation assuming that gating dynamics of the adaptation module are independent of Ca2+ and IP3 (not shown). We have reasoned then that the adaptation element has to contribute as well to channel inactivation, and is therefore considered to be driven by Ca2+ and IP3 binding reactions, yet yielding in steady state a constant (i.e., not dependent on Ca2+, IP3, and ATP concentrations) open probability of the adaptation gate.
We consider that the adaptation module has a two-ligand (namely Ca2+ and IP3) pattern, constrained by two experimental observations:
The channel recovers from inactivation after IP3 removal or Ca2+ buffering (38).
In lipid bilayers the two components of the open dwell-time distribution appear to vary with the Ca2+ concentration (10).
The latter observation is not consistent with the IP3R1 model above unless the adaptation module has at least one open state whereby the gate is closed by Ca2+ binding. In addition, to reproduce channel inactivation we add allosteric reactions in completion of the kinetic diagram, similarly to the one-ligand case (45), where, to obtain constant open gate probability, the exact adaptation condition must apply (45). That such a strong and inflexible constraint can apply to ligand binding reactions is hardly conceivable; instead, the exact adaptation requirement can be more readily met by transitions reflecting conversions between different conformations of the module.
Based on these observations, we obtain the transition- and state-configuration in the two-ligand (IP3 and Ca2+) AdMo module as presented in Fig. 2. It is assumed that every time IP3 or Ca2+ bind to, or dissociate from their AdMo sites, the module changes conformation, and, in addition, there is an auto-switch mode determined by spontaneous conversion between two possible conformations (C1 and C2) of the receptor. This particular combination between an autonomous change mode and the existence of only two possible conformations ensures that the exact adaptation requirement is always met, with no need to unnaturally force the respective transition rates. With the present module structure we obtain (not shown) that indeed the equilibrium open gate probability does not depend on IP3 and Ca2+ concentrations, and neither does the apparent affinity of either ligand.
It will be certainly difficult to test such a molecular description of the adaptation module. However, the fact that it can reproduce IP3R inactivation, whose mechanisms are unknown at present, makes it a good starting point and, corroborated by several other observations discussed below, lends support for other experiments designed to clarify the nature of inactivation. Recent findings on the three-dimensional structure of the IP3R1 indicate (23,46) that the receptor presents two different conformations, which viewed from the top have either a square- or a windmill-like appearance (S- and W-conformations). The second conformation is favored at high Ca2+ concentration. However, it is not induced exclusively by Ca2+ binding to the receptor, since even in the absence of Ca2+ (and IP3, too) the ratio of states W/S is ∼0.5 (this supports our hypothesis on the spontaneous conversion mode). There are two possible reasons for this behavior. One is that Ca2+ is an allosteric factor that is affecting the rate of the IP3R structural changes. The other one is that the same state conversion, S-to-W, can be performed in two different ways: induced by Ca2+ binding or through a Ca2+-independent step. The first scenario applied to the adaptation module involves that the equilibrium open gate probability depends on Ca2+ concentration. Therefore, our model agrees with the second possibility. The Ca2+-independent step is considered as a spontaneous state conversion, which can take place even in the absence of the ligands. The main assumption here is that Ca2+, by binding to the adaptation module in either S/W conformation, acts as a molecular switch and triggers irreversibly a mechanism that destabilizes the respective conformation, which then changes rapidly. In this two-step process (Ca2+ binding-conformation change) Ca2+ binding is the rate limiting step, so the reaction scheme in Fig. 2 can apply. Conversely, Ca2+ dissociation from the adaptation module switches off the activated mechanism and the receptor resumes its initial configuration. The same mechanism is introduced for IP3, too, and is incorporated into the same module, because the roles of IP3 and Ca2+ in IP3R inactivation are interdependent (38).
There are two other possible limitations of the adaptation modeling approach. The first is that the effect of 1 or 10 μM IP3 on the receptor conformation was undetectable (23). However, the possibility that IP3 binding to the adaptation module or the IP3 effect itself on the receptor conformation could be affected during the respective experimental maneuvers cannot be neglected, and that would explain why such an effect was not observed. A second apparent discrepancy between our model and the data is the observed increase, up to approximately six, of the windmill/square-state ratio in the presence of calcium (23), whereas, according to our model, this ratio should remain constant at equilibrium. A plausible explanation would be that equilibrium was not yet reached at the moment of image recording, and the W/S ratio increase was observed during the transitory regime in the activation module, which develops after calcium application. Existent evidence supporting this idea is the fact that the rapidness of the practical procedures, from receptor purification to application onto the carbon grids for electron microscopy, is critical for the detection of the Ca2+-dependent structural changes (23). This means that images recorded after a sufficiently long time indicate that the W/S ratio is unchanged whether calcium (or IP3) is present or not, and that would be an important confirmation of the model prediction. This point is also strengthened by the finding of one other group (47), which established in the absence of calcium a pinwheel-like structure of the IP3R, which is more similar (23) to the windmill-like aspect of the receptor top-view, found to predominate when calcium is present. It has been suggested (23) that in the respective study the receptor has been locked in that state during purification, freezing, and thawing. Nevertheless, it seems highly improbable that all of the IP3Rs in the sample preparation be locked in the same open state at an early stage of the experiment. Alternatively, the differences between various experimental strategies used in these experiments (e.g., different purification methods, different detergents, or different pH) can determine apparent discrepancies between results, and this issue has been discussed (47). It is therefore possible that the equilibrium W/S ratio, which, according to our model, should be the same in either the absence or the presence of calcium, depends with high sensitivity on the actual experimental conditions. Further diversity is evident at higher pH (8.3), where the IP3R1 appears with a flowerlike structure (22) in the absence of calcium. This is consistent with the square-shaped reconstituted image obtained by Hamada and collaborators (23), but the structural details in the side view of the three-dimensional map are different (23).
Channel activity at steady state
The high dimension of the present IP3R1 model system (83 total states, with 43 open states) can be easily reconciled with the small number, namely 2, of distinct open time components detected experimentally (5,8,10). Using rate constant values given in Table 1, column CA-nm, for the transitions within the AMo and IMo, one obtains a two-component open-time histogram with 0.5 mM ATP if IP3 and Ca2+ binding/dissociation are much slower than the rates of spontaneous conformation change, which are high in this case. As one can see later on, with one other data set (see Channel Inactivation) the conformational modifications appear to be very slow. However, the transition rates may be modified during reconstitution (45) or may vary from one system to another (17), so we obtain two distinguishable open time constants similar to those reported in each case (5,8,10), with appropriate kinetic parameters given in Table 1.
In this way, with the three-module (3M-) IP3R1 model the dependence of the channel open probability and dwell-times on all three cytosolic factors, IP3, Ca2+, and ATP, can be accurately reproduced with parameter values given in Table 1. Fit of the model to the various data on steady-state channel activity is presented in Figs. 3–8.
FIGURE 6.
Number of events during 1000 single-channel recordings. Point values and error bars are calculated with the use of open and close time data of Mak et al. (6,8) obtained with the channel in the nuclear membrane, 10 μM IP3, and 0 or 0.5 mM ATP on the cytosolic side of the channel. Dashed and solid lines represent actual and apparent numbers of events, respectively.
FIGURE 8.
The IP3 dependence of the IP3R1 open probability exhibited by channels incorporated in lipid bilayers, with 0.16 μM Ca2+ and 500 μM ATP on the cytosolic side. Data shown as open and solid circles are from two different experiments performed under the same conditions; see Refs. 4 and 10, respectively.
Moreover, the ATP stimulation of Po in the activation domain is obtained (not shown) closely similar to the fit in Fig. 5 of our previous article (18), where data from Xenopus oocytes were used (8). The dominant ATP binding reaction leading to this effect is effected within the AMo with an estimated affinity (given by Kd = 160–190 μM, h = 1.2–1.4) similar to the one (Kd = 270 μM, h = 1) reported before (7) in Xenopus, whereas in bilayers the affinity for ATP of cerebellar IP3R1 (10) appears 2.5 times higher (Kd = 50 μM, h = 1) than obtained from functional characterization of the rat IP3R1 expressed in Sf9 cells and reconstituted into planar lipid bilayers (Kd = 130 μM, h = 1) (11,12). In the activation module we obtain that ATP increases the Ca2+ affinity: from Kd = 0.55 μM at 0 ATP one goes to Kd = 10 nM at saturating ATP in both types of membranes. Given the lack of data, the AMo sensitivity to IP3 in oocyte membranes is not well defined (it is not clear whether IP3-Kd is constant or is increased by ATP), but the data obtained with bilayers indicate that ATP increases IP3 affinity from Kd = 210 nM at 0 ATP to Kd = 50 nM at saturating ATP.
Within the inhibition module, surprisingly, the 3M-model predicts a very high cooperativity (h = 6, higher than h = 4 ± 0.5 obtained by Mak et al., see Ref. 6, with a biphasic Hill equation) of IP3 in binding its IMo site in oocyte nuclear membranes, as compared to the low value (h = 1.5 ± 0.3) obtained with the receptor reconstituted into bilayers. Similarly, in the same native environment, Ca2+ shows high cooperativity (h = 4, as obtained by Mak et al., see Refs. 7 and 8) in binding to its IMo site at saturating IP3 levels, but exhibits reduced cooperativity (h = 1.35 ± 0.15) in bilayers, though its affinity is the same. Interestingly, at saturating levels of ATP, Ca2+ inhibits IP3 binding, leading, in bilayers, to a variation from Kd = 52.5 nM in the absence of calcium, to Kd = 121 μM at high levels of calcium, whereas the corresponding variation in nuclear membranes is from Kd = 17 nM to Kd = 165 nM. Reciprocally, Ca2+ binding is strongly affected by IP3, and its Kd at saturating ATP varies from 0.09 μM in the absence of IP3 to 52 μM at high IP3 in both membranes, but the Hill coefficient changes in different ways. Finally, the effects of ATP are less dramatic on both IP3 and Ca2+ within the inhibition module.
Since the cytosolic conditions are closely similar in those studies, the differences obtained in the receptor sensitivity to each ligand might be induced by a luminal factor, loss of an accessory protein and/or by alteration of the protein-protein/protein-lipid interactions associated to the membrane.
At the end of this section, it should be mentioned that the model fits into the Po, τo, and τc data if there are only one AMo and one IMo per channel molecule, whereas on the regulation of the adaptation module the equilibrium data analyzed so far do not impose any restriction except that, at steady state, the open gate probability is constant.
IP3 binding to the ER membrane
Calcium has been reported to induce almost complete reduction of IP3 binding to cerebellum membranes at pH 8.3 (29,48), to cause partial—up to ≃70% at pH 7.35 (10), and up to ≃50% at pH 7.0 (29)—inhibition under more physiological conditions, or to have no effect on IP3 binding to the purified receptor (25). The inhibition was initially found to be apparent only, and was associated to the activation of an endogenous phospholipase C that produces competitive IP3 (49) but this scenario was contradicted by subsequent determinations under different conditions (10). In some studies an effective inhibition resulted exclusively from a Ca2+-mediated decrease of the apparent affinity of the receptor for IP3 (10,26,50), whereas Cardy et al. (29) found the mechanism to be a reduction in the maximal number of IP3 binding sites with no change in the affinity for IP3 or the Hill coefficient.
For comparison, in hepatocytes, cytosolic Ca2+ increases the affinity of the receptors (mostly IP3R2) for IP3 (51), whereas in RINm5F cells, which express predominantly the type-3 IP3R (42), there is no effect at 0.1 mM (42) or 1 mM (29) Ca2+. However, there is a maximum increase of 100% in IP3 binding at 500 nM Ca2+ (29) and a complex regulation by calcium of the number of exposed IP3 binding sites and the affinity for IP3.
We found that our gating model is able to integrate even such contradictory data of IP3 binding. Here we discuss only IP3 binding properties of the type-1 IP3R. Best model fit to the data are shown in Figs. 9 and 10. To obtain consistency with the results of Kaftan et al. (4) and Moraru et al. (10), the high (Kd ∼1 nM) and low (Kd ∼10 μM) affinity IP3 sites (4) are included in determinations related to their data. However, since the type-1 is the most frequent (95–99%) isoform of cerebellar IP3Rs (52), it is likely that the 1 nM affinity site actually belongs to the other isoforms of the receptor, so that its low (∼1%) abundance (see Refs. 4 and 10; see also this article, Table 1, here) might simply reflect their low expression level found in microsome preparations. Nevertheless, the consistent contribution of the low affinity site in microsomes (4) indicates clearly that the 10 μM site is located on the IP3R1, and we will include it in proportion 1:1:1:1 with respect to the three regulatory IP3 sites of the model. Its affinity does not vary with temperature (4), so the corresponding Kd is set to 10 μM in both calculations based on the two sets of data obtained at 0°C and 22°C, respectively.
Interestingly, the IP3 affinity for the its IMo-site in lipid bilayers at 22°C appears close to that detected in microsomes at 0°C, not 22°C as expected, suggesting an increased molecular rigidity of the receptor in planar bilayers, or the interaction between the channel and an accessory protein in fractionated membranes, interaction that might become effective at higher temperatures. We also notice that the channel with IP3 and ATP bound to their sites in the inhibition module has an extremely low affinity (52 μM) of the inhibitory Ca2+ site in all preparations at 22°C, as compared to the medium affinity (0.8 ± 0.1 μM) found at 0°C.
At saturating levels of ATP the activation module appears desensitized to IP3 in cerebellum microsomes at room temperature, with a ∼50-fold lower affinity for IP3 than in bilayers. The most dramatic effect of increasing the temperature in microsomes is the 10-fold decrease in IP3 affinity for its AdMo site with ATP bound to the module, as well as for its IMo site in the absence of Ca2+; at saturating levels of Ca2+ and ATP the IMo IP3 site is largely desensitized at 22°C (Kd = 11 mM), as also happens with the receptor in bilayers.
Cardy et al. (29) found that Ca2+ regulates, presumably through the intermediate of an accessory protein, the interconversion between two conformations of the receptor, one with high affinity for IP3 (Kd ∼10 nM) and the other one having the IP3 site either occluded or of extremely low affinity. Consistent with this mechanism, our fit to the data (shown in Fig. 10) results in a virtually inaccessible IP3 site (Kd = 31 mM) within the inhibition module when the Ca2+ site is occupied. For comparison, at saturating [Ca2+], IP3 binds with medium affinity to the channel molecule in Xenopus nuclear membranes, whereas the IP3 affinity in the absence of calcium is similar to that obtained from channel recordings in Xenopus nuclei, but with Hill coefficient consistently different (1 as compared to 6). However, Ca2+ affinity for the IMo site appears to be identical in both experiments. As for the activation module, IP3 appears to increase channel's affinity for Ca2+, which is of the same order as obtained with the other data sets, and reciprocally, Ca2+ increases the affinity for IP3, which however appears one-order-higher than in the other experiments, possibly reflecting the effect of the high pH.
At high ATP and in the absence of calcium, IP3 binds with similar affinity to AMo and IMo; it appears then that IP3 binds to a unique class of sites. At increasing [Ca2+], however, the dominant feature is determined by Ca2+ depressing IP3 binding to its IMo site, whereas the AMo IP3 site contributes with an increase in the apparent affinity for IP3 of the channel molecule. For instance, at 22°C in the presence of ATP (see Table 1, column B-II) there is no IP3 bound in the inactivation module faced to saturating calcium, but the receptor appears to bind IP3 with low affinity (Kd = 2 μM in the activation module). Extrapolation of the curves in the lower panel of Fig. 9 evidences the corresponding reduction in the maximal binding sites (not shown) which is similar to the phenomenon reported under different conditions (2°C in absence of ATP). In fact, this situation is evident also under reconstitution of the receptor in lipid bilayers (see Table 1, column CA-lb), where, at high levels of Ca2+ and ATP, the inhibition module has an extremely low affinity for IP3. These results provide indirect evidence that the mechanism proposed by Cardy et al. (29) can manifest even with different microsomal preparations, and show that when one single parameter (temperature; see Table 1, columns B-II and B-III) is modified between experiments otherwise similar, the resulting variations in ligand binding may lead to the interpretation with apparently different mechanisms.
In all of the cases discussed in this section, the summated contribution of the three IP3 binding sites predicted by the model to belong each to a single gating module looks similar to the contribution of an apparently unique class of sites. As seen also from the values determined by model fit, all the three sites are of similar, i.e., medium (∼100 nM) apparent affinities. We propose that each IP3R1 monomer has four IP3 binding sites (one of low affinity, three of medium affinity), presumably located in the four determinant segments of the IP3 binding domain, which are known to contain conserved basic residues that interact with the phosphate groups of IP3 (24). Except the case of the Xenopus IP3 receptor, the obtained nH  1 for all the three modules indicate that binding of one molecule of IP3 to a certain site on a monomer prevents binding to a related site on any other subunit. In Xenopus, nH = 6 indicates that six molecules bind cooperatively to the inhibition module of the receptor. Presumably, two IP3 molecules bind three of the four monomers at the IMo site location each, and binding is highly cooperative. The prediction can be tested by binding assessment on Xenopus nuclear membranes.
1 for all the three modules indicate that binding of one molecule of IP3 to a certain site on a monomer prevents binding to a related site on any other subunit. In Xenopus, nH = 6 indicates that six molecules bind cooperatively to the inhibition module of the receptor. Presumably, two IP3 molecules bind three of the four monomers at the IMo site location each, and binding is highly cooperative. The prediction can be tested by binding assessment on Xenopus nuclear membranes.
It is likely that the low affinity (Kd = 10 μM) site resides on one of the two IP3 binding determinant segments of the IP3R1 which are closer to the C-terminal (DS3, DS4), since the GST protein fused to the 341–604 fragment of the receptor obtained from cerebellar microsomes binds IP3 with similar affinity (Kd = 4.7 μM) (27). Additionally, breakup of the IP3 binding core into two fragments (F1, 226–317 and F2, 346–604) by mild trypsin digestion does not alter the capacity for IP3, the specificity or affinity of the receptor evaluated for the medium-affinity binding component (27). This, from the perspective of our model, indicates that the two fragments (F1, F2) bind IP3 independently. Moreover, in mixtures of GN and GC constructs (GST proteins fused to the 1–343 and, respectively, the 341–604 fragment), beside the low-affinity binding contribution, one other component, of medium-affinity, is evident in the Scatchard plots (27). We interpret these findings by the existence of a medium-affinity IP3 site on each of the segments DS1 and DS2, whereas the domain 341–576 may contain a low- as well as a medium-affinity site. Our model differs from that of Yoshikawa et al. (27), who proposed that F2 binds IP3 with low affinity whereas F1 cannot bind IP3 but potentiates binding affinity. Their conclusion is based on the assumption that a monomer has a single IP3 site. Ours relies on the assumption that the GN construct is incapable of binding IP3 by itself but is able to bind IP3 in a GC-GN fused conformation resembling that in the actual spatial configuration of the receptor, as suggested by the Kd value's similarity (11 nM of GC-GN versus 19 nM of the native receptor; see Ref. 27). In favor of a four-site model, in the experiments by Moraru et al. (10) most preparations have a maximal binding capacity of ≃154 pmol/mg of protein. In some cases, however, a fourfold reduction in the number of available sites is observed (Bmax ≃ 40 pmol/mg) without change in affinity (10), suggesting alteration of IP3 binding ability in three of four IP3 sites of similar affinities, rather than prevention of IP3 binding to three of four monomers within all the receptors in the preparation. The results of Cardy et al., too, indicate (at high Ca2+ levels) a reduction with either 35% or 50% of the maximal observed number of available sites (29), explicable by Ca2+-induced suppression of IP3 binding to one of three or two of four sites. More suggestive evidence for the existence of four sites comes from data on IP3R3 which, depending on the level of Ca2+, may present discrete values of Bmax, in proportion extremely close to 1:2:4 (inset of Fig. 5 and Table 1 of Ref. 29). Furthermore, the fact that Ca2+ both stimulates and inhibits IP3 binding to type-3 receptors (29) indicates by itself the existence of two different IP3 sites of medium affinity (Kd ≃ 2 and 14 nM, respectively; see Ref. 29), regulated by Ca2+ in different ways. In our model these are represented by the AMo- and IMo-IP3 sites. It is also unlikely that an accessory protein (29) can decrease the number of exposed IP3 sites in various preparations in a precise, quantal manner. Rather, our model predicts that IP3R has four sites for IP3 in each monomer, and that IP3 can bind only one medium-affinity site in the purified receptor (30), but can bind all four sites in vivo.
With regard to ATP, it has been found to inhibit cold IP3 binding to the rat cerebellar membrane with IC50 = 0.5 mM and to the purified receptor protein with IC50 = 2 mM (30). Our model predicts that such an inhibition derives from the modulation of the adaptation module state by ATP. In the presence of Ca2+, complete (30) inhibition by ATP of IP3 binding is obtained for two data sets (columns B-II and In in Table 1, with an inhibition ATP constant (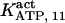 ) of 0.1 and 1.5 mM, respectively (not shown). This is in agreement with the data. Stimulation of channel activity of the purified receptor is most effective at 0.6 mM ATP (30), is twofold-valued in the IP3R from aortic sarcoplasmic reticulum at 0.1 mM (53), or has an IC50 = 0.04 mM ATP (54). This also agrees with our results that ATP binding to the activation module site increases Ca2+ binding affinity to its activating site (ATP modulatory Kd is obtained in the range 0.02–1.5 mM, Table 1). The high affinity for ATP of its site in the inhibition module (Kd = 17 μM) has been previously determined (30), and is intermediate between the values of Kd = 1.6 and possibly 177 μM of the two ATP sites determined by another group (36) but is quite distant to the observation that 45Ca release from lipid vesicles is inhibited between 0.1 and 1 mM ATP (55). Nevertheless, the kinetic parameters of the inhibition module would be better estimated if more data were available on inhibition of channel activity by Ca2+ and ATP.
) of 0.1 and 1.5 mM, respectively (not shown). This is in agreement with the data. Stimulation of channel activity of the purified receptor is most effective at 0.6 mM ATP (30), is twofold-valued in the IP3R from aortic sarcoplasmic reticulum at 0.1 mM (53), or has an IC50 = 0.04 mM ATP (54). This also agrees with our results that ATP binding to the activation module site increases Ca2+ binding affinity to its activating site (ATP modulatory Kd is obtained in the range 0.02–1.5 mM, Table 1). The high affinity for ATP of its site in the inhibition module (Kd = 17 μM) has been previously determined (30), and is intermediate between the values of Kd = 1.6 and possibly 177 μM of the two ATP sites determined by another group (36) but is quite distant to the observation that 45Ca release from lipid vesicles is inhibited between 0.1 and 1 mM ATP (55). Nevertheless, the kinetic parameters of the inhibition module would be better estimated if more data were available on inhibition of channel activity by Ca2+ and ATP.
Channel inactivation
Stationary Po data such as those analyzed in the first section are obtained from current recordings with channels that remain active sufficiently long. For this reason, these steady state data do not include the slow inactivation component of channel activity. However, one detailed analysis of single channel recordings with sufficient number of events has revealed that IP3R1 inactivates with a time constant of ≃30 s in the presence of 10 μM IP3 (5), whereas kinetic studies on ER membrane permeability in hepatocytes with two-IP3-pulse protocol (38) have shown two components with rate constants and weights that depend on the time of IP3 preincubation. This translates into the contribution of three actual kinetic components as follows: with no preincubation, two exponential components are evident—of which one is fast (time constant ≃1.8 s) and one is slow (time constant ≃17 s). With 180-s preincubation, the fast component is lacking, whereas there is a slow component, however, of different (lower) rate (time constant ≃50 s) as compared to that obtained in the first case (38).
From our numerical investigations we concluded that agreement of the 3M-model with the data could not be obtained, unless:
The channel inactivates upon conducting the ionic current.
There are two modules, namely the activation and the adaptation modules, that each generate an inactivated state.
The first restriction is imposed by the equilibration of the fluorescence quenching by Mn2+ entry through the IP3-dependent permeation pathway. In the opposite case, if there were no inactivation, the Mn2+ content in the stores would increase continuously—Po is not zero at the IP3 and Ca2+ levels used in that study—which is not the case (see Fig.1 c, trace 1, in Ref. 38). Moreover, inactivation manifests in the conduction period only, since fluorescence quenching remains at high levels even after IP3 preincubation periods as long as 180 s. This implies the existence of inner sites acting as triggers for inactivation, when the charge carrier (either K+ as in Ref. 5, or Mn2+ as in Ref. 38) binds them.
The second restriction is related to the three observed inactivation components, of weights that vary with the preincubation time. As shown in Fig. 11, inactivation kinetics can be explained on the right timescale and with correct time course with multiplication of the three independent module components. The 3M-model was fit to the data presented in Fig. 1 of Hajnoczky and Thomas (38). The best-fit parameter values (given in the last column of Table 1) were used to create the simulations in Fig. 11, which are quite close to the experimental traces, seen in Fig. 1 in Hajnoczky and Thomas (38). The adaptation component leads to the dominant fast-release with no-IP3 preincubation period, followed by a gradual decrease of its contribution as the preincubation is prolonged. After ∼50-s preincubation, application of the second IP3 pulse produces no further response transposed onto the AdMo open gate probability trace, and this determines the almost complete disappearance of that component from the fluorescence signal. Since this component is associated with the fast-inactivation rate, one AdMo open state with IP3- and Ca2+-bound (called AdI state in Fig. 2) is assumed to inactivate at high rate (with a time constant of 0.75 s, as we obtained). The choice of the state undergoing inactivation as an IP3- and Ca2+-bound state is imposed by the first experimental observation mentioned in the second paragraph. However, there are two IP3- and Ca2+-bound open states in the adaptation module, but the correct response was obtained with inactivation originating from the C2-conformation state. As seen in Fig. 11, with no preincubation, there is a rapid (in <0.5 s) increase in the open probability of the adaptation gate, determined by accumulation in the AdI state, followed by fast inactivation of that state. The fraction of remaining open states is low and decreases gradually as the AdMos of numerous channels cycle between states and continue to inactivate when reaching the AdI-state. During this period the decline of the channel Po is dominated by the slower kinetics of the AMo gate, which shows two distinct components. The medium component (time constant 20 s) is given by rearrangement of AMo states after IP3 stimulation and its timescale depends on the rate of ATP binding to AMo, which is slow (rate constant 0.05 s−1). The slow component is determined by inactivation at low-rate (time constant = 59 s, double the ≃30 s-value reported in Xenopus oocytes with K+ as a current carrier; see Ref. 5) of the IP3-, Ca2+-, and ATP-bound open state of the activation module (denoted AI in Fig. 1).
FIGURE 11.
Simulated inactivation of the IP3R1 in the continuous presence of IP3R. The Mn2+ content in the stores, expressed in arbitrary units in the upper panel, corresponds, from the lower to the upper trace, to preincubation with IP3 for 0, 20, and 180 s, respectively. Here t = 0 is the moment of Mn2+ addition, coincident with application of the second IP3 pulse. Lower panels depict kinetics of open gate probability in each IP3R1 module before and after addition of IP3. The first IP3 pulse initiates at t = 0. The second IP3 pulse is applied at t = 20 and 180 s, respectively.
When the channel is faced to IP3 for 15 s, the available AI- and AdI-state fractions are consistently reduced at the time of Mn2+ addition. In this case both the fast- and the medium-release components appear with diminished weight. However, the final Mn2+ content in the stores almost reaches the same value as before, because the contribution of the inhibition module to the overall membrane permeability is increased, as shown in Fig. 11. The slow release after preincubation with IP3 for 180 s is determined by inactivation at low-rate (time constant = 59 s) of the AI state in the activation module, and the lack of the faster release components is partially compensated by activation of more open states in the inhibition module by the second pulse of IP3.
Since the fast inactivation component has not been detected with single channel recordings where the current carrier is either Ca2+ (3), K+ (5,6), or Ba2+ (4,10), it is presumably induced solely by Mn2+ binding to an inner site, whereas the slow inactivation may be triggered by Mn2+ as well as by K+.
We have to distinguish between two modes of receptor inactivation: intrinsic inactivation by IP3 and Ca2+, and inactivation by the current charge carrier Mn2+ or K+. Intrinsic inactivation by IP3 and Ca2+ derives from state dynamics of the adaptation module, which responds gradually weaker to the second IP3 pulse (Fig. 11). Complete loss of IP3R1 receptivity to IP3 is observed at interpulse times ≥80 s. The timescale of the process is dictated by the rates of the spontaneous conformation interchanges. The calculated half-time dependence on the time of preincubation with IP3 comes out to be in good agreement with the experimental one (Fig. 12). Inactivation by cytosolic Ca2+ (38) is explained in the same manner, but the discussion is not enlarged here. Intrinsic inactivation is modulated by inactivation due to specific cations (Mn2+, K+ but probably not Ca2+ or Ba2+). K+ is an important modulator of Ca2+ release (18,56). We suggest also that IP3R1 inactivation by K+ may contribute to termination of Ca2+ release in vivo and could be the cause for the damping of local Ca2+ oscillations in permeabilized cells within 15–20 s (56).
FIGURE 12.
Kinetics of channel inactivation depends on the time of preincubation with IP3. On the ordinate it is represented the time to half-maximum of the Mn2+ content trace obtained after preincubation with IP3 for the duration represented on the abscissa. The data are from Hajnoczky and Thomas (38); solid line is obtained by model calculation.
We have noticed that the sensitivity of the inhibition module in bilayers at 22°C is similar to that in fractionated membranes at 0°C, not 22°C. Added to this, the similarity of ligand affinities obtained with the inactivation data set (obtained in permeabilized hepatocytes at 35°C) and those obtained with data on cerebellar microsomes at 0°C suggests that this degree of sensitivity to IP3 and Ca2+ is a fundamental characteristic of IP3 receptors of the endoplasmic reticulum in mammalian cells under physiological conditions. Rather than the effect of a protein associated to the ER membrane (suggested above), it is more likely that the intact membrane is a more rigid medium embedding the receptor, since receptor behavior in intact membranes is more closely related to that in fractionated membranes at 0°C, not 22°C.
Consistent differences are obtained with the Xenopus IP3R1, particularly related to the high cooperativity in IP3 and Ca2+ binding to the inhibition module, and to the high open gate probability of the adaptation module. Fig. 13 shows the predicted in vivo open probability of the channel in dependence on IP3 and Ca2+. Channel activity remains low (Po ≤ 1.7%) and confined to a narrow range of cytosolic Ca2+ (<3 μM) even at 2 μM IP3, with the peak reached at 0.25 μM Ca2+, in coincidence with results obtained in bilayers (3,4,10). At increasing IP3, the activity augments and the Ca2+ domain is enlarged, with rightward-shifting of both the maximum Po and the half-maximum inhibition Ca2+, as seen also in bilayers. However, the channel closes at ≥10 μM Ca2+ even at IP3 levels as high as 180 μM IP3, in contrast with the predictions in bilayers or Xenopus nuclear membranes. It is expected then that the channel readily closes when high Ca2+ gradients develop at the mouth of the open channel, since in the presence of cytosolic Ca2+ buffering and diffusion the local Ca2+ becomes already ≥ 10 μM when the current ≥10 fA. For instance, with 30 μM Ca2+ inside the store and the channel conducting a current of 8 fA, the Ca2+ concentration averaged over a distance of 40 nm from the channel mouth reaches 9 μM, whereas with 80 fA conducted, the channel is faced to ≥50 μM Ca2+ (18). In the case of clustered receptors, the concentration at the channel/cytosol interface reaches 170 μM for a release current of 0.8 pA (57). Calcium release is produced intermittently, during open-channel periods which alternate with closed-channel intervals. With intermediate currents of 0.1 pA established upon opening of the channel, the concentration rises within 1–2 μs at >50 μM in the vicinity of the channel (15,18,57). According to our findings, at this calcium level the channel should then instantly close due to saturation in the inhibition module. The calcium profile at the channel mouth drops below the [Ca2+] threshold for complete inhibition (e.g., 2 μM for 10 μM IP3, Fig. 13) in <1 ms (15,18,57) and the channel can reopen. The IP3R activity during release depends critically on cytosolic and luminal diffusion and buffering, as well as on the upper threshold of cytosolic [Ca2+] that permits the receptor to activate. The threshold value depends on the IP3 level (Fig. 13).
FIGURE 13.
Predicted in vivo channel open probability at 500 μM ATP. Calculation is done according to the 3M-model, using parameter values defined in Table 1, last column. Numbers next to each curve represent IP3 concentration, in μM.
Knowledge of how the ER calcium channel functions in vivo is essential for an accurate description of various calcium-dependent processes. At the moment the Po of IP3R1 in vivo is not known (12). However, all Ca2+ flux measurements performed with permeabilized cells (58), isolated brain microsomes (59), and Xenopus oocytes (60,61) have shown that IP3-induced calcium release is completely blocked by concentrations of Ca2+ in the 5–10 μM range, which is in good agreement with the present predictions. From our estimations, it appears that at resting cytosolic Ca2+ levels of ≤120 nM, IP3 inhibits channel opening by Ca2+ (Fig. 13). This should protect cells from sustained Ca2+ release in rapid processes in which cytosolic Ca2+ transients remain local. In contrast, elevation of global calcium at concentrations higher than 120 nM would allow rapid activation of channels everywhere in the cell.
DISCUSSION
In numerous experiments, high variability has been found in IP3 binding to the IP3R1 receptor, with apparent Kd ranging from ≃8 nM (29) to 20 nM (27), 100 nM (25,26), or even 300 nM (10), as well as in the activity of the IP3R1/Ca2+ channel, with peak open probability ranging from ∼0.04 (4,10) to 0.2 (12), ∼0.3 (13), or even ∼0.8 (6,8). Because Ca2+ is one of the key regulator factors of the IP3 receptor, concentrated effort has been oriented toward the understanding of its action mechanisms. Although Ca2+ activating and inhibitory effects on channel gating have been systematically found in various determinations of channel activity, contradictory scenarios emerged from IP3 binding experiments, where the data seem to support the existence of different Ca2+ effects on IP3 binding in different microsome preparations.
The present study emerged from the observation that the IP3R behavior does not change qualitatively under different experimental conditions. It is then assumed that a unique gating mechanism characterizes this behavior. This particular assumption provides a huge advantage because it allows us to use information from a large number of data and observations and construct the model by recreating the picture of IP3R regulation from disparate pieces. The model structure is quite different from that of other theoretical models of the receptor in that it uses an autonomous module decomposition able to explain the activation, inhibition, and inactivation of the channel. Although various reduced forms of the model can explain separate findings, they are not in agreement with some other data. All of the mechanisms assumed by the model are selected to explain disparate observations and then combined so that the complete model becomes able to reproduce the entire amount of observations discussed here. These are focalized on three main points:
The regulation of the steady-state channel activity by Ca2+, IP3, and ATP. The data we use have been obtained with the channel either incorporated in lipid bilayers or studied in its native membrane environment. Both bell- and square-shaped Ca2+-dependencies of Po are reproduced; Ca2+-dependencies of Po and dwell-times at various IP3 and ATP levels are well fitted.
The puzzling properties of IP3 binding to the receptor, associated with the inhibitory effect of Ca2+ on IP3 binding, which is mediated either by decrease in IP3 affinity or by reduction of the maximal number of binding sites. Inhibition of IP3 binding by ATP is also supported by the model.
The inactivation of the receptor by IP3. Kinetic responses of the receptor assessed by two-pulse IP3 application are accurately reproduced. Time-dependent reduction in the receptor response to the second stimulation pulse is explained. Two inactivation modes are evidenced: intrinsic receptor inactivation by Ca2+ and IP3, and inactivation due to conduction of a specific cation (Mn2+ or K+ but, most likely, not Ca2+ or Ba2+). The timescale for intrinsic receptor inactivation is dictated by the rates of spontaneous conformation changes of the receptor.
The Ca2+ inhibitory effect on IP3 binding to the receptor has been reported to be effected either through variation of the receptor affinity for IP3 or through decrease of the maximal number of IP3 binding sites, and thought to be either direct or indirect. Findings that suggest the role of a calcium-binding membrane protein that associates with the receptor to regulate its sensitivity to IP3 come from confrontations between experiments of IP3 binding to crude membranes and, respectively, to the purified receptor (25). Although with the receptor embedded in the membrane IP3 binding is effectively regulated by Ca2+, the Ca2+ effect vanishes completely in the purified receptor. Our model converges to this picture if calcium escapes from the allosteric effect of IP3 and ATP in both the activation and the inhibition modules of the purified receptor (i.e., Ca2+ Kd values are constant within both modules), suggesting that the membrane-associated protein induces a conformation that permits IP3 and ATP to regulate Ca2+ binding in both modules. In addition, this mechanism would also explain the actual insensitivity to Ca2+ found by one group (49) in bovine cerebellum membranes, where the involved protein might be lacking. We did not, however, obtain the Ca2+ decoupling from the allosteric trios when we used activity data of the channel expressed in lipid bilayers. This suggests that the triple allosteric regulation is in fact intrinsic to the IP3 receptor but may be not a robust mechanism and thus may be easily altered by various experimental maneuvers. Additionally, receptor protein folding may depend on the structure of the lipid environment and assembly of the receptor as a tetramer may be required for various binding and gating events (28). Nevertheless, we obtained a good convergence of the model parameters with two data sets expressing conditions closer to the in vivo environment, but the convergence is specifically related to the mammalian-cell type.
The 3M-model of the IP3 receptor predicts that four IP3 sites lie on each monomer. The hypothesis is confronted with various experimental observations. We find no contradiction between the model and the known properties of the receptor. Two medium affinity sites may reside on the sequence domain 226–317 of the IP3R1, whereas the region 341–576 might have one medium- and one low-affinity IP3 binding site. Some discrepant findings could be reconciled by the existence of multiple sites in each subunit. For example, electron microscopy reveals that gold-albumin attached to heparin (a competitive antagonist of IP3) binds to a single site on each monomer and the distance between sites is ≥10 nm (28), in agreement with the large size of the IP3R structure (12–25 nm) (22,23,28,30), whereas by using IP3 dimers linked by molecules of varying length the estimated distance between sites would be ≃1.5 nm (28). This spacing has been associated with the separation between sites on different monomers within the receptor and it has been therefore concluded that the four IP3 sites of the receptor are placed centrally, close to the channel pore. A larger distance (≃8 nm), found for increased IP3 binding, has been attributed to interreceptor interactions of long IP3 dimers (28). We propose that, since the albumin and gold are themselves large (>5 nm) (28), heparin cannot bind but a single site of a monomer (located toward the periphery of the IP3R; see Ref. 46), which would explain why no more than four heparin-gold molecules are detected to bind the receptor. The presumptive multiple sites on a monomer would be separated by ≤2 nm, whereas IP3 sites on different subunits would be separated by ≥8–10 nm.
The present model of IP3R1 can be used in the same form for the type-2 and -3 IP3 receptors. From numerical studies other than those shown here, data obtained with these receptors (8,11,12,29,41,42,44) can be well fitted by the model. This would be useful to the study of the functional importance of any differences in rate constants between receptor subtypes (17). Besides the Ca2+ and IP3 effects on channel activity or ligand binding, various kinetic responses of the receptor to IP3 or Ca2+ application can also be explained by the model (not shown). Based on measurements of 45Ca release in permeabilized cells, it has been proposed that in the absence of IP3 Ca2+ rapidly inhibits IP3R2, as well as IP3R3, whereas binding of IP3 protects IP3R2 from inhibition by calcium, but fails to do that in IP3R3 (42). It has been suggested that in both receptors IP3 binding causes exposure of an activating Ca2+ binding site. The molecular interpretation disagrees (42) with other findings from single channel recordings of the type-3 receptor (8). Theoretical considerations (17) on the IP3R2 kinetics also caution that the time course of release after addition of large amounts of Ca2+ may be not sufficient to determine whether binding of IP3 shields the Ca2+ inhibitory site, since the response can be simulated with a model that excludes this possibility. Although we have found that our model, too, can generate IP3R2 and IP3R3 receptor kinetics similar to those observed for release kinetics (41,42), the influence of luminal and cytosolic calcium dynamics around the channel should be thoroughly investigated by numeric simulations incorporating calcium fluxes, ion diffusion, and buffering (16,18,57). When assessed in this way (56), the correct meaning of the data obtained from superfusion experiments reflects a biexponential decay of the release, originating from the Ca2+ concentration dynamics rather than channel state dynamics. To analyze inactivation of the receptor, we use findings from experiments where the measurement of ionic permeability is decoupled from the effect of Ca2+ dynamics. For this reason, the respective data represent faithful determinations of the Ca2+ channel function in response to Ca2+ and IP3. In fact, all the data used in this article specifically refer to intrinsic properties of the IP3 receptor, determined in the absence of Ca2+ fluxes.
In conclusion, our results support the idea that essentially the same gating mechanisms are in the core of the IP3R1 events observed in various studies in the absence of calcium fluxes, but, as the variations in the parameter values related to different data (see Table 1) reflect it, the receptor expresses different sensitivity under different experimental conditions. However, it appears that although the modules remain functional after reconstitution of the channel into planar bilayers, the receptor sensitivity to IP3 is particularly increased within the ATP bound-activation module, where the IP3 Kd decreases four times, as well as in the inhibition module with no Ca2+ bound, where the IP3 Kd decreases six times. Likewise, the sensitivity of the activation module to ATP is one-order-higher in bilayers than in permeabilized cells, but remains unchanged in microsomes. ATP decreases IP3 binding to the activation module up to 10-fold, with the exception of cerebellar IP3R1 incorporated in bilayers.
We have previously analyzed the possibility that the IP3R1 channel closes upon Ca2+ binding to a luminal site and found it able to explain a series of experimental findings (18). We could explain channel inactivation by 0.6–1 mM luminal Ca2+ in absence of ATP (62); apparent invariability of Po at low luminal calcium levels (6,37); decreased open channel duration observed in the presence of calcium in the trans chamber (37); decrease of channel Po at high levels of luminal Ca2+ (37); or the shallow decrease of the largest component of the open dwell-time histogram with increasing luminal [Ca2+] (62). We found that high concentrations of luminal calcium reduce the maximal Po (Fig. 5 in Ref. 18; and also results not shown, in agreement with the data in Ref. 37). The mechanism can be incorporated into the present model by adding a regulatory luminal site and its associated gate, which would act independently of the cytosolic conditions. The enlarged model would then approach the IP3R1 regulation by cytosolic Ca2+, IP3, ATP, and luminal Ca2+, supplementing all its present features with modulation by luminal Ca2+.
Our present model differs from the more recent model by Fraiman and Dawson (19), who consider a regulatory luminal Ca2+ site to explain the differences in the shape and magnitude of the Po([Ca2+]cyt) dependence observed in bilayer experiments (3) and in patch recordings on nuclei of Xenopus oocytes (6). They assume that IP3R1 behavior depends on the cation used as a charge carrier in single channel recordings and the observed differences derive from using either monovalent or divalent cations for current recordings. Our model does not include this possibility, but finds a different possible cause, originating from 1), different affinity and Hill coefficient of IP3 binding to the inhibition module; and 2), change in the equilibrium IP3R1 preferential conformation mode.
These and many other differences between experiments may originate, as discussed in this article, from different lipid environments, detergents, preparation, purification methods, pH, or other related conditions. Furthermore, as previously observed (12), earlier nuclear patch-clamp experiments (13) performed with a monovalent cation (140 mM K+) as a current carrier yielded a narrow bell-shaped dependence and a relatively low Po, similar to those obtained in bilayers with fluxes carried by Ca2+ (3) or Ba2+ (4,11,12), not to the square Ca2+ dependence and high Po found in nuclear patches with an identical 140 mM K+ current source (6). Additionally, both studies (6,13) were performed on nuclei from Xenopus oocytes, thus eliminating variations due to cell-specificity of the receptor structure. All this lends further support for our model.
References
- 1.Berridge, M. J. 1993. Inositol trisphosphate and calcium signaling. Nature. 361:315–325. [DOI] [PubMed] [Google Scholar]
- 2.Clapham, D. E. 1995. Calcium signaling. Cell. 80:259–268. [DOI] [PubMed] [Google Scholar]
- 3.Bezprozvanny, I., J. Watras, and B. E. Erlich. 1991. Bell-shaped calcium response curves of Ins(1,4,5)P3- and calcium-gated channels from endoplasmic reticulum of cerebellum. Nature. 351:751–754. [DOI] [PubMed] [Google Scholar]
- 4.Kaftan, E. J., B. E. Ehrlich, and J. Watras. 1997. Inositol 1,4,5-trisphosphate and calcium interact to increase the dynamic range of InsP3 receptor-dependent calcium signaling. J. Gen. Physiol. 110:529–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mak, D.-O. D., and J. K. Foskett. 1997. Single-channel kinetics, inactivation, and spatial distribution of inositol (1,4,5) trisphosphate (IP3) receptor in Xenopus oocyte nucleus. J. Gen. Physiol. 109:571–587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mak, D.-O. D., S. McBride, and J. K. Foskett. 1998. Inositol 1,4,5-tris-phosphate activation of inositol 1,4,5-trisphosphate receptor Ca2+ channel by ligand tuning of Ca2+ inhibition. Proc. Natl. Acad. Sci. USA. 95:15821–15825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mak, D.-O. D., S. McBride, and J. K. Foskett. 1999. ATP regulation of type 1 inositol 1,4,5-trisphosphate receptor channel gating by allosteric tuning of Ca2+ activation. J. Biol. Chem. 274:22231–22237. [DOI] [PubMed] [Google Scholar]
- 8.Mak, D.-O. D., S. McBride, and J. K. Foskett. 2001. ATP-dependent adenophostin activation of inositol 1,4,5-trisphosphate receptor channel gating: kinetic implications for the durations of calcium puffs in cells. J. Gen. Physiol. 117:299–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mak, D.-O. D., S. McBride, and J. K. Foskett. 2003. Spontaneous channel activity of the inositol 1,4,5-trisphosphate (InsP3) receptor (InsP3R). Application of allosteric modeling to calcium and InsP3 regulation of InsP3R single-channel gating. J. Gen. Physiol. 122:583–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Moraru, I. I., E. J. Kaftan, B. E. Ehrlich, and J. Watras. 1999. Regulation of type 1 inositol 1,4,5-trisphosphate-gated calcium channels by InsP3 and calcium. J. Gen. Physiol. 113:837–849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tu, H., Z. Wang, E. Nosyreva, H. De Smedt, and I. Bezprozvanny. 2005. Functional characterization of mammalian inositol 1,4,5-trisphosphate receptor isoforms. Biophys. J. 88:1046–1055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tu, H., Z. Wang, and I. Bezprozvanny. 2005. Modulation of mammalian inositol 1,4,5-trisphosphate receptor isoforms by calcium: a role of calcium sensor region. Biophys. J. 88:1056–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Stehno-Bittel, L., A. Luckhoff, and D. E. Clapham. 1995. Calcium release from the nucleus by InsP3 receptor channels. Neuron. 14:163–167. [DOI] [PubMed] [Google Scholar]
- 14.De Young, G. W., and J. Keizer. 1992. A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc. Natl. Acad. Sci. USA. 89:9895–9899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Swillens, S., P. Champeil, L. Combettes, and G. Dupont. 1998. Stochastic simulation of a single inositol 1,4,5-trisphosphate-sensitive Ca2+ channel reveals repetitive openings during “blip-like” Ca2+ transients. Cell Calcium. 23:291–302. [DOI] [PubMed] [Google Scholar]
- 16.Swillens, S., G. Dupont, L. Combettes, and P. Champeil. 1999. From calcium blips to calcium puffs: theoretical analysis of the requirements for interchannel communication. Proc. Natl. Acad. Sci. USA. 96:13750–13755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sneyd, J., and J.-F. Dufour. 2002. A dynamic model of the type-2 inositol trisphosphate receptor. Proc. Natl. Acad. Sci. USA. 99:2398–2403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Baran, I. 2003. Integrated luminal and cytosolic aspects of the calcium release control. Biophys. J. 84:1470–1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fraiman, D., and S. P. Dawson. 2004. A model of IP3 receptor with a luminal calcium binding site: stochastic simulations and analysis. Cell Calcium. 35:403–413. [DOI] [PubMed] [Google Scholar]
- 20.Dupont, G. 1999. Spatio-temporal organization of cytosolic Ca2+ signals: from experimental to theoretical aspects. Comm. Theor. Biol. 5:305–340. [Google Scholar]
- 21.Falcke, M. 2004. Reading the patterns in living cells—the physics of Ca2+ signaling. Adv. Phys. 53:255–440. [Google Scholar]
- 22.da Fonseca, P. C. A., S. A. Morris, E. P. Nerou, C. W. Taylor, and E. P. Morris. 2003. Domain organization of the type 1 inositol 1,4,5-trisphosphate receptor as revealed by single-particle analysis. Proc. Natl. Acad. Sci. USA. 100:3936–3941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hamada, K., A. Terauchi, and K. Mikoshiba. 2003. Three-dimensional rearrangements within inositol 1,4,5-trisphosphate receptor by calcium. J. Biol. Chem. 278:52881–52889. [DOI] [PubMed] [Google Scholar]
- 24.Yoshikawa, F., M. Morita, T. Monkawa, T. Michikawa, T. Furuichi, and K. Mikoshiba. 1996. Mutational analysis of the ligand binding site of the inositol 1,4,5-trisphosphate receptor. J. Biol. Chem. 271:18277–18284. [DOI] [PubMed] [Google Scholar]
- 25.Supattapone, S., P. F. Worley, J. M. Baraban, and S. H. Snyder. 1988. Solubilization, purification, and characterization of an inositol trisphosphate receptor. J. Biol. Chem. 263:1530–1534. [PubMed] [Google Scholar]
- 26.Yoneshima, H., A. Miyawaki, T. Michikawa, T. Furuichi, and K. Mikoshiba. 1997. Ca2+ differentially regulates the ligand-affinity states of type 1 and type 3 inositol 1,4,5-trisphosphate receptors. Biochem. J. 322:591–596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yoshikawa, F., H. Iwasaki, T. Michikawa, T. Furuichi, and K. Mikoshiba. 1999. Cooperative formation of the ligand-binding site of the inositol 1,4,5-trisphosphate receptor by two separable domains. J. Biol. Chem. 274:328–334. [DOI] [PubMed] [Google Scholar]
- 28.Riley, A. M., S. A. Morris, E. P. Nerou, V. Correa, B. V. L. Potter, and C. W. Taylor. 2002. Interactions of 1,4,5-trisphosphate (IP3) receptors with synthetic poly(ethylene glycol)-linked dimers of IP3 suggest close spacing of the IP3-binding sites. J. Biol. Chem. 277:40290–40295. [DOI] [PubMed] [Google Scholar]
- 29.Cardy, T. J. A., D. Traynor, and C. W. Taylor. 1997. Differential regulation of types-1 and -3 inositol trisphosphate receptors by cytosolic Ca2+. Biochem. J. 328:785–793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Maeda, N., T. Kawasaki, S. Nakade, N. Yokota, T. Taguchi, M. Kasai, and K. Mikoshiba. 1991. Structural and functional characterization of inositol 1,4,5-trisphosphate receptor channel from mouse cerebellum. J. Biol. Chem. 266:1109–1116. [PubMed] [Google Scholar]
- 31.Sienaert, I., H. De Smedt, J. B. Parys, L. Missiaen, S. Vanlingen, H. Sipma, and R. Casteels. 1996. Characterization of a cytosolic and a luminal Ca2+ binding site in the type I inositol 1,4,5-trisphosphate receptor. J. Biol. Chem. 271:27005–27012. [DOI] [PubMed] [Google Scholar]
- 32.Sienaert, I., L. Missiaen, H. De Smedt, J. B. Parys, H. Sipma, and R. Casteels. 1997. Molecular and functional evidence for multiple Ca2+-binding domains in the type 1 inositol 1,4,5-trisphosphate receptor. J. Biol. Chem. 272:25899–25906. [DOI] [PubMed] [Google Scholar]
- 33.Marshall, I. C. B., and C. W. Taylor. 1993. Regulation of inositol 1,4,5-trisphosphate receptors. J. Exp. Biol. 184:161–182. [DOI] [PubMed] [Google Scholar]
- 34.Taylor, C. W., and D. Traynor. 1995. Calcium and inositol trisphosphate receptors. J. Membr. Biol. 145:109–118. [DOI] [PubMed] [Google Scholar]
- 35.Maes, K., L. Missiaen, P. De Smet, S. Vanlingen, G. Callewaert, J. B. Parys, and H. De Smedt. 2000. Differential modulation of inositol 1,4,5-trisphosphate receptor type 1 and type 3 by ATP. Cell Calcium. 27:257–267. [DOI] [PubMed] [Google Scholar]
- 36.Maes, K., L. Missiaen, J. B. Parys, P. De Smet, I. Sienaert, E. Waelkens, G. Callewaert, and H. De Smedt. 2001. Mapping of the ATP-binding sites on inositol 1,4,5-trisphosphate receptor type 1 and type 3 homotetramers by controlled proteolysis and photoaffinity labeling. J. Biol. Chem. 276:3492–3497. [DOI] [PubMed] [Google Scholar]
- 37.Bezprozvanny, I., and B. E. Erlich. 1994. Inositol (1,4,5)-trisphosphate (InsP3)-gated Ca channels from cerebellum: conduction properties for divalent cations and regulation by intraluminal calcium. J. Gen. Physiol. 104:821–856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hajnoczky, G., and A. P. Thomas. 1994. The inositol trisphosphate calcium channel is inactivated by inositol trisphosphate. Nature. 370:474–477. [DOI] [PubMed] [Google Scholar]
- 39.Callamaras, N., and I. Parker. 2000. Phasic characteristic of elementary Ca2+ release sites underlies quantal responses to IP3. EMBO J. 19:3608–3617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Parker, I., Y. Yao, and V. Ilyin. 1996. Fast kinetics of calcium liberation induced in Xenopus oocytes by photoreleased inositol trisphosphate. Biophys. J. 70:222–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dufour, J.-F., I. M. Arias, and T. J. Turner. 1997. Inositol 1,4,5-trisphosphate and calcium regulate the calcium channel function of the hepatic inositol 1,4,5-trisphosphate receptor. J. Biol. Chem. 272:2675–2681. [DOI] [PubMed] [Google Scholar]
- 42.Swatton, J. E., and C. W. Taylor. 2002. Fast biphasic regulation of type 3 inositol trisphosphate receptors by cytosolic calcium. J. Biol. Chem. 277:17571–17579. [DOI] [PubMed] [Google Scholar]
- 43.De Smedt, H., L. Missiaen, J. B. Parys, M. D. Bootman, L. Mertens, L. Van den Bosch, and R. Casteels. 1994. Determination of relative amounts of inositol trisphosphate receptor mRNA isoforms by ratio polymerase chain reaction. J. Biol. Chem. 269:21691–21698. [PubMed] [Google Scholar]
- 44.Ramos-Franco, J., D. Bare, S. Caenepeel, A. Nani, M. Fill, and G. Mignery. 2000. Single-channel function of recombinant type 2 inositol 1,4,5-trisphosphate receptor. Biophys. J. 79:1388–1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sachs, F., F. Qin, and P. Palade. 1995. Models of Ca2+ release channel adaptation. Science. 267:2010–2011. [DOI] [PubMed] [Google Scholar]
- 46.Hamada, K., T. Miyata, K. Mayanagi, J. Hirota, and K. Mikoshiba. 2002. Two-state conformational changes in inositol 1,4,5-trisphosphate receptor regulated by calcium. J. Biol. Chem. 277:21115–21118. [DOI] [PubMed] [Google Scholar]
- 47.Serysheva, I. I., D. J. Bare, S. J. Ludtke, C. S. Kettlun, W. Chiu, and G. A. Mignery. 2003. Structure of the type 1 inositol 1,4,5-trisphosphate receptor revealed by electron cryomicroscopy. J. Biol. Chem. 278:21319–21322. [DOI] [PubMed] [Google Scholar]
- 48.Worley, P. F., J. M. Baraban, S. Supattapone, V. S. Wilson, and S. H. Snyder. 1987. Characterization of inositol trisphosphate receptor binding in brain. Regulation by pH and calcium. J. Biol. Chem. 262:12132–12136. [PubMed] [Google Scholar]
- 49.Mignery, G. A., P. A. Johnston, and T. C. Südof. 1992. Mechanism of Ca2+ inhibition of inositol 1,4,5-trisphosphate (InsP3) binding to the cerebellar InsP33 receptor. J. Biol. Chem. 267:7450–7455. [PubMed] [Google Scholar]
- 50.Hannaert-Merah, Z., J.-F. Coquil, L. Combettes, M. Claret, J.-P. Mauger, and P. Champeil. 1994. Rapid kinetics of myo-inositol trisphosphate binding and dissociation in cerebellar microsomes. J. Biol. Chem. 269:29642–29649. [PubMed] [Google Scholar]
- 51.Pietri, F., M. Hilly, and J.-P. Mauger. 1990. Calcium mediates the interconversion between two states of the liver inositol 1,4,5-trisphosphate receptor. J. Biol. Chem. 265:17478–17485. [PubMed] [Google Scholar]
- 52.Wojcikiewicz, R. J. H. 1995. Type I, II, and III are unequally susceptible to down-regulation and are expressed in markedly different proportions in different cell types. J. Biol. Chem. 270:11678–11683. [DOI] [PubMed] [Google Scholar]
- 53.Ehrlich, B. E., and J. Watras. 1988. Inositol 1,4,5-trisphosphate activates a channel from smooth muscle sarcoplasmic reticulum. Nature. 336:583–586. [DOI] [PubMed] [Google Scholar]
- 54.Bezprozvanny and Erlich. 1993. ATP modulates the function of inositol 1,4,5-trisphosphate-gated channels at two sites. Neuron. 10:1175–1184. [DOI] [PubMed] [Google Scholar]
- 55.Ferris, C. D., R. L. Huganir, and S. H. Snyder. 1990. Calcium flux mediated by purified inositol 1,4,5-trisphosphate receptor in reconstituted lipid vesicles is allosterically regulated by adenine nucleotides. Proc. Natl. Acad. Sci. USA. 87:2147–2151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Nguyen, T., W. C. Chin, and P. Verdugo. 1998. Role of Ca2+/K+ ion exchange in intracellular storage and release of Ca2+. Nature. 395:908–912. [DOI] [PubMed] [Google Scholar]
- 57.Thul, R., and M. Falcke. 2004. Release currents of IP3 receptor channel clusters and concentration profiles. Biophys. J. 86:2660–2673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Iino, M. 1990. Biphasic Ca2+ dependence of inositol 1,4,5-trisphosphate-induced Ca2+ release in smooth muscle cells of the guinea-pig taenia caeci. J. Gen. Physiol. 95:1103–1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Finch, E. A., T. J. Turner, and S. M. Goldin. 1991. Calcium as a co-agonist of inositol 1,4,5-trisphosphate induced calcium release. Science. 252:443–446. [DOI] [PubMed] [Google Scholar]
- 60.Parker, I., and I. Ivorra. 1990. Inhibition by Ca2+ of inositol trisphosphate-mediated Ca2+ liberation: a possible mechanism for oscillatory release of Ca2+. Proc. Natl. Acad. Sci. USA. 87:260–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Yao, Y., and I. Parker. 1992. Potentiation of inositol trisphosphate-induced Ca2+ mobilization in Xenopus oocytes by cytosolic Ca2+. J. Physiol. 458:319–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Thrower, E. C., H. Mobasheri, S. Dargan, P. Marius, E. J. A. Lea, and A. P. Dawson. 2000. Interaction of luminal calcium and cytosolic ATP in the control of type 1 inositol (1,4,5) trisphosphate receptor channels. J. Biol. Chem. 275:36049–36055. [DOI] [PubMed] [Google Scholar]














