Effects of Organelle Shape on Fluorescence Recovery after Photobleaching

Abstract

The determination of diffusion coefficients from fluorescence recovery data is often complicated by geometric constraints imposed by the complex shapes of intracellular compartments. To address this issue, diffusion of proteins in the lumen of the endoplasmic reticulum (ER) is studied using cell biological and computational methods. Fluorescence recovery after photobleaching (FRAP) experiments are performed in tissue culture cells expressing GFP–KDEL, a soluble, fluorescent protein, in the ER lumen. The three-dimensional (3D) shape of the ER is determined by confocal microscopy and computationally reconstructed. Within these ER geometries diffusion of solutes is simulated using the method of particle strength exchange. The simulations are compared to experimental FRAP curves of GFP–KDEL in the same ER region. Comparisons of simulations in the 3D ER shapes to simulations in open 3D space show that the constraints imposed by the spatial confinement result in two- to fourfold underestimation of the molecular diffusion constant in the ER if the geometry is not taken into account. Using the same molecular diffusion constant in different simulations, the observed speed of fluorescence recovery varies by a factor of 2.5, depending on the particular ER geometry and the location of the bleached area. Organelle shape considerably influences diffusive transport and must be taken into account when relating experimental photobleaching data to molecular diffusion coefficients. This novel methodology combines experimental FRAP curves with high accuracy computer simulations of diffusion in the same ER geometry to determine the molecular diffusion constant of the solute in the particular ER lumen.

INTRODUCTION

Most cellular processes depend on the diffusion of macromolecules and substances of small molecular weight, such as metabolites and ions. The presence of internal membranes restricts diffusion in general to specific organelles and compartments. The technique of fluorescence recovery after photobleaching (FRAP) is often used to determine how substances move within confined geometries, or within cellular membranes. In FRAP, an area of a live cell that contains the fluorescently tagged molecules of interest is bleached using strong light from a laser, and the movement of nonbleached molecules from the adjacent areas into the bleached area is recorded and analyzed over time. When applied quantitatively, this technique allows the determination of molecular diffusion coefficients for fluorescent molecules including soluble and membrane-bound proteins (1).

The use of FRAP is rapidly increasing with the availability of methods to tag intracellular proteins with green fluorescent protein (GFP) and its derivatives. This method allows visualization of the protein and enables measurements of its dynamics in living cells. Diffusion constants (D) of GFP and GFP-tagged proteins have been reported for the cytosol (2), nucleus (3), endoplasmic reticulum (ER) (4,5), mitochondria (6), Golgi complex (7,8), and for different membranes of the cell (9–11). Although theoretical descriptions of particle diffusion in two-dimensional (2D) membranes have been derived for a variety of situations including nonplanar membranes (12), binding, particle crowding (13), and mobile as well as immobile obstacles (14,15), no such theory exists for the three-dimensional (3D) lumen of compartments.

To obtain molecular diffusion constants from fluorescence recovery curves, the dependence of the curve's shape on the molecular D needs to be modeled. Fitting such a model to an experimentally determined recovery curve yields the measured D. Current modeling techniques do not take fully into account that the organelles in which the fluorescent molecules are confined often have a complex three-dimensional shape, and that they may only occupy a fraction of the bleached and nonbleached volumes. Moreover, diffusion is either calculated as motion in a plane rather than in three dimensions (4), or by using a semiempirical model based on time-dependent (anomalous) diffusion in two dimensions (16).

The importance of accounting for the specific geometry of the organelle increases with increasing complexity of the organelle's shape and with decreasing volume fraction in the bleached and nonbleached volumes. This issue has been frequently discussed in the literature (4,17), but no procedure exists to estimate the magnitude of the uncertainty introduced, let alone to calculate more accurate molecular diffusion coefficients from FRAP curves.

Theoretical considerations by Sciaky et al. (8) came to the conclusion that the effectively observed diffusion constant in a homogeneous isotropic collection of tilted tubes in three dimensions is three times lower than the molecular diffusion constant along each tube. The assumptions made about the tube geometry and the distribution of tilting angles are not connected to a specific organelle geometry and the connectivity between the tubes was neglected.

The question of connectivity was addressed by Ölveczky and Verkman (18). Using the classical method of random walk (19) they performed computer simulations to calculate solute diffusion in an orthogonal meshwork of interconnected cylinders. Random walk is an intuitive method for simulating diffusion and is suitable for handling complex geometries. Its slow convergence rate, however, hampers the accuracy of the results. Ölveczky and Verkman found that the apparent diffusive transport in the cylinder meshwork is about half as fast as in free space. Moreover, they found the diffusion to effectively appear anomalous even if the molecular diffusion is normal. This showed that geometry does have a significant impact on apparent diffusion, and that diffusion constants will be underestimated by models neglecting the confinement. The shape of real organelles may, however, not be accurately mimicked by random artificial cylinder meshes.

Siggia et al. (20) used finite differences (21) to computationally solve the diffusion equation in the imaging plane of the observation microscope. The geometry was treated by taking a smoothed postbleach fluorescence intensity micrograph as initial value. In the course of the simulation, the geometry was, however, no longer explicitly taken into account, mainly due to numerical limitations of the employed finite difference method. A statistically averaged model for confined diffusion was introduced in an attempt to compensate for this. Depending on the particular geometry model, variations in the apparent diffusion constant of up to a factor of three were observed (20). The model relies on the basic assumption that the local density of fluorescence equally represents the density of connections in a reticular network. As already stated in the original publication (20), the validity of the model is questionable when 3D effects become important, or when image regions of saturated pixel intensities exist. The former situation will, for example, occur when two compartments that overlap in the projection are in fact disconnected in 3D.

A more recent approach by Braga et al. (22) made use of finite difference simulations to derive a FRAP model in the nucleoplasm. Their model thoroughly considers the initial condition of the recovery dynamics by taking into account the 3D intensity distribution of the bleaching laser beam as well as premature recovery during bleaching. They report a molecular diffusion constant of 33.3 ± 3.6 μm²/s for GFP in the nucleoplasm of HeLa cells. This work as well did not account for the geometric shape of the compartment under consideration. The model as well as the simulations were done in 3D free space. For short times this certainly is a valid assumption for the nucleoplasm. Compartments of more complex shape, such as, e.g., the ER or mitochondria, cannot be expected to be treated accurately with this scheme.

Finite differences are based on numerical approximations of the derivatives of the governing equations. These approximations result in reformulating the governing partial differential equations as sets of linear systems of equations that can be solved computationally. For simple geometries, the resulting algebraic systems can be structured (e.g., in tridiagonal matrices), so that efficient numerical solvers can be applied, resulting in computations that scale linearly with the number of the discretization points. However, the efficiency of grid-based methods is drastically reduced when discretizing complex geometries. The resulting discretized equations fail to have the “nice” structure associated with simpler geometries, resulting in fuller systems whose solution often scales with the square or even the cube of the computational elements. Moreover, the generation of the grid in complex geometries is not a trivial task, although several methods are available to render such procedures automatic. In addition, the order of the accuracy of the numerical approximation of the governing equations is reduced near complex boundaries.

A more accurate three-dimensional analysis of diffusion in complex-shaped organelles is needed to overcome the limitations of present methods to measure molecular diffusion constants from FRAP data, and to provide much-needed validation of the various models and methods currently in use.

In this article, we describe simulations using the method of particle strength exchange (PSE) ((23); cf. Supplementary Material) to estimate the influence of organelle shape on FRAP of a lumenal solute. The same simulations also lead to a novel method enabling more accurate measurements of molecular diffusion constants in vivo. The PSE is a deterministic particle method to simulate diffusion (24). The method is based on replacing the Laplace operator with an integral operator that is subsequently discretized using particle locations as quadrature points. This deterministic method is orders of magnitude more accurate than random walk for the same number of particles. The grid-free character of PSE avoids the geometric limitations of finite differences, thus allowing fully resolved 3D simulations in realistic whole-organelle geometries using ∼10⁶ particles. Resolving a full ER using random walk would require some 10¹⁰ particles (cf. Supplementary Material), which is infeasible on present-day workstation computers. Fully resolved simulations eliminate the need for modeling either the geometry or the process of confined diffusion, and effectively allow assessment and refinement of existing FRAP models.

As an application we consider FRAP experiments in the ER, a characteristic example of a complex-shaped organelle. The ER is generally described as a highly convoluted, interconnected, closed network of tubular and lamellar structures in three dimensions (25). To obtain realistic geometries of the ER, live tissue culture cells expressing a soluble, resident, recombinant protein (ssGFP–KDEL; (26)) are imaged. Using this marker and a stack of serial confocal sections, we can experimentally define and computationally reconstruct the 3D shape of the ER. These shapes are then used to simulate diffusion within them, and to compute the corrected molecular diffusion constant in the vicinity of the bleached portion of the ER lumen.

In this article, we distinguish between “molecular diffusion coefficients” and “apparent diffusion coefficients”. The former ones are those that are determined by single-molecule techniques such as single-molecule tracking (27,28) or fluorescence correlation spectroscopy (29), and whose values have to be used in the diffusion equation to computationally model the process. The latter ones are those coefficients determined by coarse-grained methods such as FRAP, averaging over a certain observation volume. These values depend on the geometry of the observation volume. Deriving molecular diffusion coefficients from apparent ones is important for comparisons of experiments made in different organelles or cells as well as for mathematical modeling and computational simulations.

MATERIALS AND METHODS

Cells and DNA construct

VERO cells were grown on coverslips at 37°C in Dulbecco's minimal essential medium supplemented with 10% fetal calf serum, 2 mM glutamine, 100 g/ml penicillin, 100 units/ml streptomycin (GibcoBRL; Life Technologies, Eggstein, Germany) at 37°C in a 5% CO₂ incubator and were used in all experiments. Cells were transiently transfected with a reporter gene containing the ER targeting signal sequence fused to GFP and the ER retention sequence (ssGFP–KDEL; derived from pCMV/myc/ER/GFP, Invitrogen, Carlsbad, CA) using Superfect (Sigma, St. Louis, MO). Alternatively, cells were transfected using Nucleofactor by amaxa (Köln, Germany) according to the protocol for COS-7 cells (Kit V, program A24). Briefly, 1×106 VERO cells were pelleted and resuspended in 100 μl of solution V, and electroporated with 1–2.5 μg of DNA. The electroporated cells were resuspended in 350 μl MEM. Of this solution, 100 μl were seeded on one 18-mm coverslip and incubated over night (15 h) at 37°C and 5% CO₂; 12–16 h posttransfection cells were imaged live on a temperature-controlled stage at 37°C.

Photobleach experiments

FRAP experiments were performed on an inverted Zeiss LSM510 confocal microscope, using the 488-nm line of a 30 mW Argon/2 laser with a 100×, 1.4 N.A. objective. A defined region of interest (ROI; 4 × 4 μm) was photobleached at full laser power (100% power, 100% transmission, 20 iterations); recovery of fluorescence was monitored by scanning the ROI at low laser power (50% power, 3% transmission). The scanning laser intensity did not significantly photobleach the specimen over the time course of the experiment. Images were acquired as 8-bit TIFF files (512 × 512 pixel frame) and processed using NIH Image 1.62. The average fluorescence in the ROI and the average background were determined from the images. After subtracting the background, the fluorescence values were normalized according to Phair and Misteli (3) to correct for the loss in fluorescence caused by imaging. To be able to compare FRAP curves from different cells, these values F(t) were further normalized by their respective asymptotic value F(t → ∞), determined as outlined in the Supplementary Material. FRAP(t) = F(t)/F(t → ∞) is shown in all the figures.

Z-sectioning and reconstruction of ER geometries

Before FRAP analysis, 50 0.1 μm optical z-sections of the cell to be bleached were collected with a lateral resolution of 0.18 μm/pixel. The image file series were reconstructed as a 3D gray level iso-surface in space using Imaris 3 (BitPlane, Zurich, Switzerland), and the same number of voxels as the section images had pixels. Detached parts of the surface were removed and only the largest contiguous shape was kept. Its surface was discretized in Imaris and stored as a triangulation using planar triangles. The intensity threshold used for the iso-surface was set as high as possible to still yield a connected domain. Error analysis of the 3D reconstructions using artificial ER-like geometries has shown this threshold to be optimal (see Supplementary Material). After reconstruction, the triangulation was checked for consistency. It was required to enclose a connected space and to not contain any surface intersections or holes in the surface.

Measurement of the fractal dimension

Among the numerous definitions of fractal dimensions (see, e.g., Table 1 in Cross (30)), we use the generalized Renyi dimensions (31)

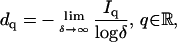(1)

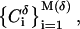which are based on the Renyi entropies I_q, defined as follows: assume a disjoint partitioning of the embedding Euclidean space Eⁿ, n = 2, 3, into Cartesian cells each of volume δ. Let p_i be the probability for the geometry under consideration to fill cell C_i. The Renyi entropies are then given by

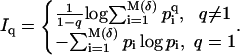(2)

The Renyi dimensions d_q are always positive and their values decrease with increasing q, converging to a limit d_∞. For q = 0, the dimension d₀ is identical to the capacity (box counting) dimension. We considered the Renyi dimensions q = −1, 0, 1, 2 to verify the fractal scaling behavior; i.e., check that d₋₁ > d₀ > d₁ > d₂ holds over a sufficiently large range of length scales. To estimate the Renyi dimensions, the probabilities p_i need to be approximated. This was done by uniformly scattering 500 random points per triangle of the reconstructed triangulated surface of the ER (∼300 million points in total) and then counting the number of such points falling into every Cartesian cell C_i. Dividing this count by the total number of scattered points approximates p_i for the cells. The grid defining the cells C_i was then coarsened and the whole procedure repeated until the number of cells in any direction fell below two. To minimize spurious effects from the random number generator or aliasing effects due to grid sampling, the whole algorithm was repeated with five different random seeds and six different, slightly shifted, bounding boxes for the cell mesh. The measured entropies were averaged from all 30 repetitions. The Renyi dimensions were determined as least squares regressions of the corresponding entropies versus the logarithm of the box sizes at each reduction step.

Governing equation for diffusion

Isotropic diffusion of a scalar quantity in the three-dimensional space of the ER lumen is described by the spatiotemporal evolution of the local concentration 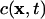for a time interval 0 < t ≤ T. The governing partial differential equation for a constant molecular diffusion coefficient D is given by:

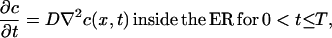(3)

where ∇² is the Laplace operator. The initial concentration field in the ER is specified by 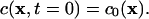As soluble proteins do not spontaneously cross the ER membrane the assumed boundary condition for diffusion of soluble proteins in the ER lumen is the zero-flux Neumann condition

where n is the outer unit normal on the ER membrane and ∇_xc is the gradient of the concentration field c with respect to the location 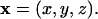Bold symbols denote vector quantities.

Diffusion simulation using random walk

The random walk method (19) in m dimensions (m = 1, 2, 3) starts by either uniformly or randomly placing N particles p at initial locations 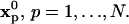Each particle is assigned a strength of 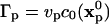where v_p is the particle's volume. The particles then undergo an m-dimensional random walk by changing their positions at each positive integer time step n according to:

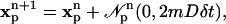(4)

where 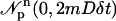is a vector of independent, identically distributed Gaussian random numbers with each element having mean zero and variance 2mDδt; D is the molecular diffusion constant and δt is the simulation time step. The boundary condition was treated by reflecting particles at the boundary.

Diffusion simulation using particle strength exchange

The PSE method as introduced by Degond and Mas-Gallic (23) approximates the Laplace operator by an integral operator that allows consistent evaluation on the particle locations. This integral operator is found to be:

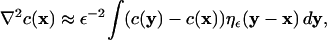(5)

where 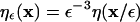is a kernel function in 3D that has to fulfill the moment conditions stated in references (23,24). The approximation error of the operator is O(ε^r) with r being the order of the method and ε the core size of the particles. Using the rectangular quadrature rule with the locations 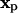of the N particles as quadrature points and dropping the error term leads to the discrete version of the approximated operator:

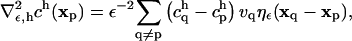(6)

where v_q is the volume of particle q such that 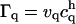is the rectangular rule quadrature approximation for the strength 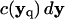(mass in the context of diffusion). The quadrature error is O(h/ε)^s where s is the number of continuous derivatives of the kernel function 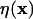and h is the interparticle spacing. The approximation c^h to the continuous concentration c at any location and time can be reconstructed from the values 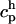at particle locations using

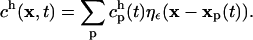(7)

The final PSE scheme reads:

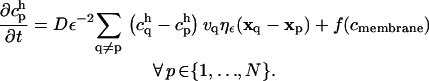(8)

The function f(c) is used to account for the boundary condition at the ER membrane. The homogeneous boundary conditions are treated using the method of images (cf. Supplementary Material). Because the kernel η_ε is chosen to be local, only the nearest neighbors of each particle significantly contribute to its sum. Hence, the computational cost of the method scales linearly with the number of particles. Details about the PSE methods are contained in the Supplementary Material.

RESULTS

The influence of dimensionality

We report first 2D and then 3D simulations to study the influence of dimensionality in the absence of complex shapes.

We compare simulation results from a 2D plane and a 3D box. Diffusion is simulated using the method of random walk as described in Materials and Methods. Both 2D simulations in the plane [0, L] × [0, L], and 3D simulations in the box [0, L] × [0, L] × [0, L] are conducted with the same molecular diffusion constant D = 1.56 × 10⁻⁴ L²/δt (scaled with the domain length L and the simulation time step δt). Zero-flux boundary conditions are imposed, which means that no mass is allowed to leave the domain. The bleached areas for the two cases are [0.5L, 0.75L] × [0.5L, 0.75L] and [0.5L, 0.75L] × [0.5L, 0.75L] × [0, L], respectively. All simulations use 10⁵ particles and are repeated five times to obtain ensemble averaged results.

The results show that the fluorescence recovery curves on the 2D square plane and the 3D cubic box do not significantly differ (Fig. 1 a in Supplementary Material). This implies that dimensionality does not have a detectable influence on the simulated FRAP curves under zero-flux boundary conditions, if the initial condition is independent of the third direction, and when the intersection planes between the bleached area and the organelle lumen form an axes-parallel rectangle or box. This is a more restrictive requirement for dimensionality invariance than the one stated by Siggia et al. (20). As soon as confinement or the three-dimensional structure of the organelle start to be important, i.e., if the intersection surface is not a simple box, dimensionality cannot be neglected any more, as we will show next.

The influence of confinement in complex shapes

To study the effects of organelle geometry, we make the transition from the 3D box to “real” ER geometries. We express a well-characterized, fluorescent, recombinant protein (ssGFP–KDEL; Terasaki et al. (26)) in the ER of VERO cells. The protein is synthesized with a cleavable signal sequence sufficient for ER-lumenal targeting. At the C-terminus, it has a KDEL sequence that serves as an ER localization sequence and prevents secretion (32). The molecular diffusion of the closely related ssYFP–KDEL has been shown to be nonanomalous, i.e., it does not exhibit subdiffusive properties on molecular length and timescales (M. Weiss, personal communication, 2002). The proposed simulation method, thus, solves the normal diffusion equation as stated in the Materials and Methods section. Using confocal fluorescence microscopy and a set of serial confocal sections (z-stacks), the 3D shape of the ER filled with the fluorescent protein is defined in 19 different cells (Fig. 1 a). The stacks are used to computationally reconstruct the 3D shape of the ER (Fig. 1 b), and the ER surface is represented by a connected, closed mesh of triangles (Fig. 1 c) as outlined in the Materials and Methods section.

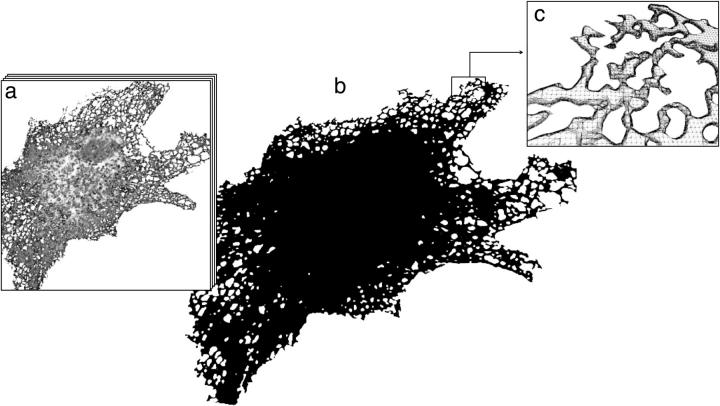
FIGURE 1.

Three-dimensional reconstruction of an ER sample from a VERO cell. (a) The reconstruction is done starting from a stack of 50 serial sections with Δz = 0.1 μm from confocal microscopy of a VERO cell expressing ssGFP–KDEL. (b) Computer visualization of the triangulated 3D reconstruction consisting of 739,956 triangles. (c) Detail view of the top right section of the reconstruction with individual triangles shown. Hidden lines are removed for better clarity. Note that due to microscope resolution limitations, only the peripheral areas are trustworthy. FRAP simulations are thus only made close to the cell periphery.

The ER reconstructions are used as computational domains for the PSE simulations of diffusion of lumenal solutes (cf. Supplementary Material). The speed of diffusive recovery is determined by the geometry of the organelle near the bleached region. The specific shape of the organelle far from the region of interest is insignificant. Still our simulations include the entire ssGFP–KDEL-labeled ER of each cell because it is not clear what boundary conditions would have to be imposed around an isolated ER subregion.

Using PSE, diffusion of a solute such as ssGFP–KDEL in the lumen of all reconstructed ER samples is simulated with an assumed zero-flux boundary condition implying that the protein cannot cross the membrane. The numerical (root mean square) error is as low as 6 × 10⁻³ in all simulations.

Details of the method, its assessment, and a validation case can be found in the Supplementary Material. Computer-generated images of ER samples at different stages of simulated recovery are shown in Fig. 2, a–d. The local concentration of unbleached solute is shown as a density cloud inside the reconstructed ER structure. The bleached volume is depicted by its outline. The solute can be seen to diffuse into the bleached region from the edges, and the rate by which each element in the bleached region recovers depends on the distance from the edge and on the local geometry.

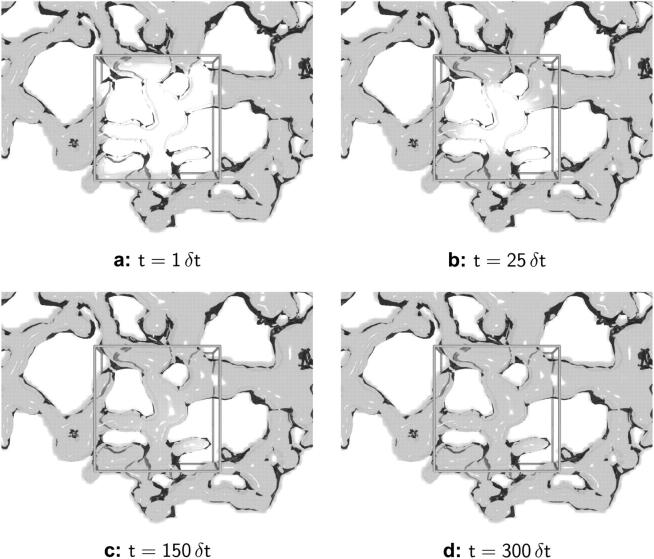
FIGURE 2.

Snapshots of concentration distribution from a sample PSE simulation in a reconstructed ER geometry. The results at times t = 1 δt (a), t = 25 δt (b), t = 150 δt (c), and t = 300 δt (d) are shown for a molecular diffusion constant of D = 3 × 10⁻⁵ b²/δt. All units are scaled with the simulation time step δt and the lateral edge length b of the bleached region. The ER membrane is visualized as a transparent surface and the concentration of green fluorescent protein as a volume density cloud inside it. The bleached region is represented by the outline of a cube. Only the part of the ER around the bleached region is shown.

To study the effects of confinement in the ER lumen, we compare the PSE simulations of diffusion in the ER samples to the aforementioned simulations in the cubic 3D box. Only bleached regions in the cell periphery are considered because the geometry of the dense perinuclear ER is not well resolved (cf. Fig. 1 b).

When the same molecular diffusion constant is used in both simulations, much faster recovery is observed in the box (cf. Fig. 1 b in Supplementary Material). Depending on the actual ER geometry, the apparent diffusion constant observed in the ER is 1.8–4.2 times lower than the one observed in the box. Ignoring the effect of 3D confinement in complex geometries, thus, leads to significant underestimation of molecular diffusion constants.

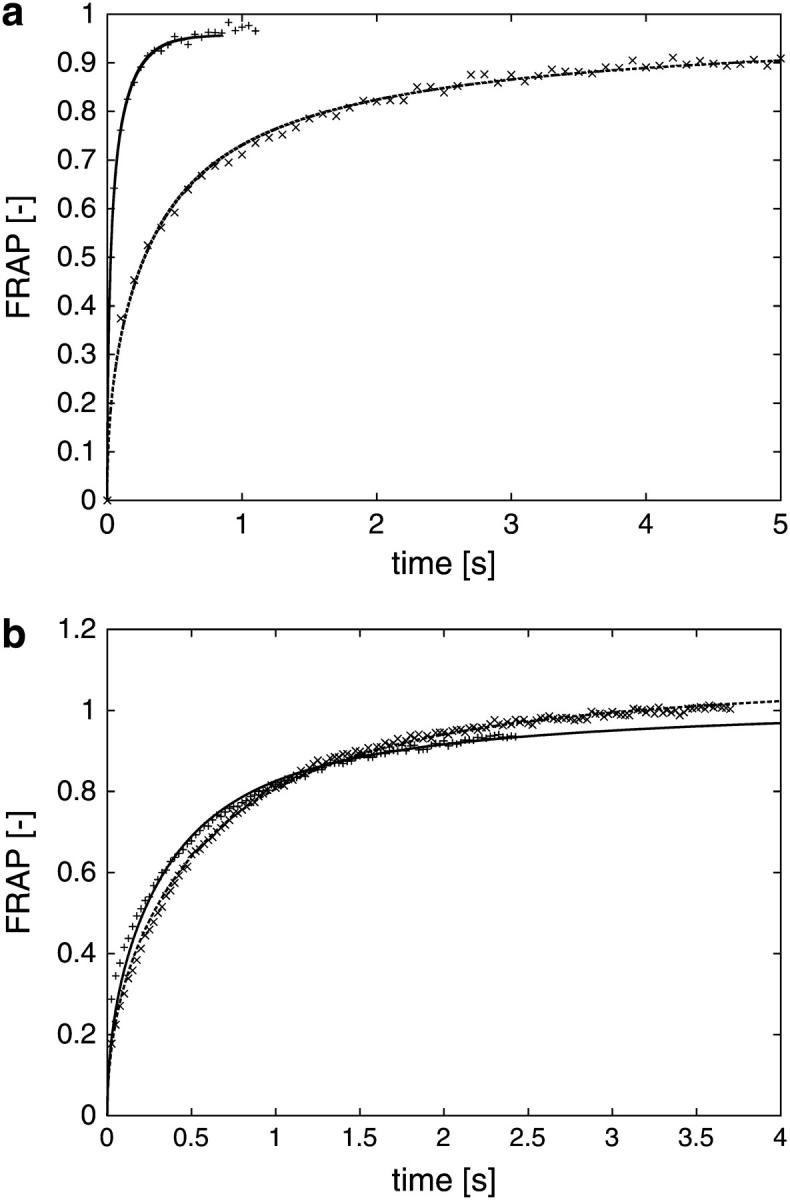
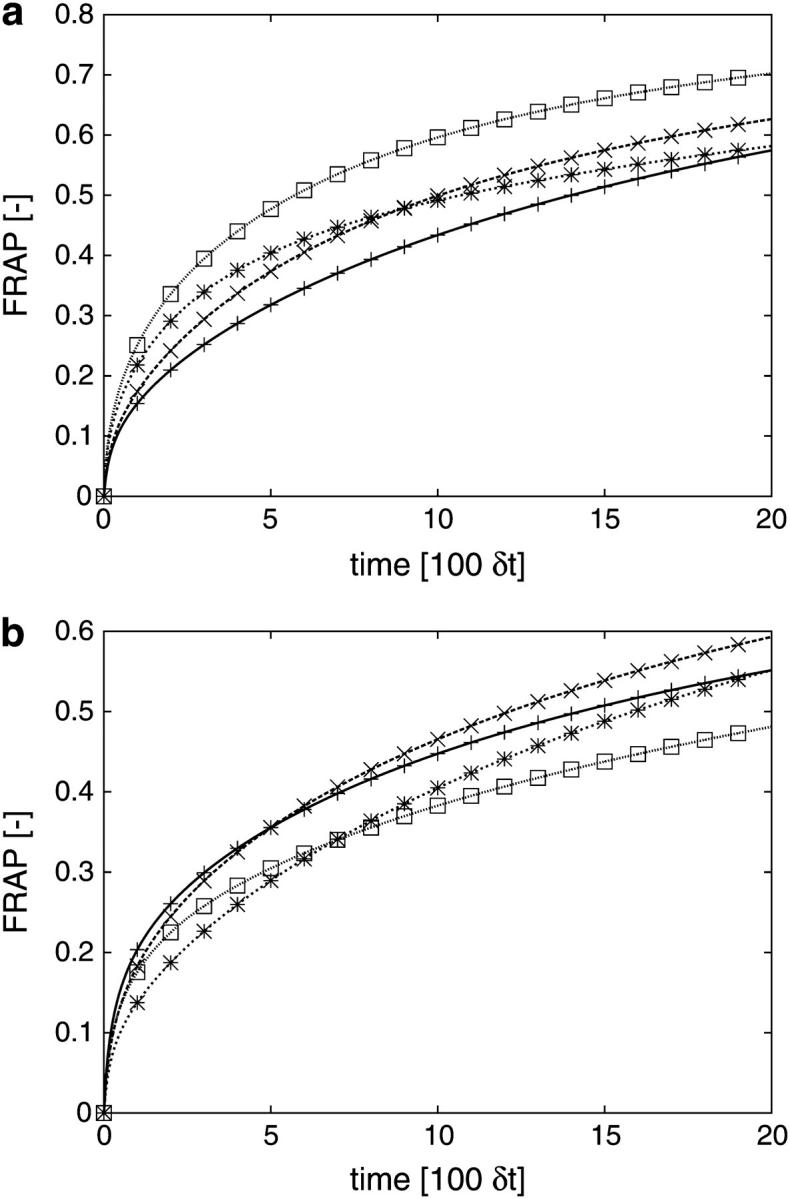
The complexity of the ER geometry is quantified using the notion of fractal dimensions (33). To test whether the ER membrane can be viewed as a continuous fractal surface in 3D space, the reconstructed ER from nine cells are analyzed in the computer as outlined in the Materials and Methods section. For the ER shapes the capacity dimension d₀ is 2.4 ± 0.1. The fractal scaling persists over 1.7 orders of magnitude in length scales ranging from 0.01 cell diameters to 0.5 cell diameters. The fractal scaling is confirmed by the correct ordering of the Renyi dimensions (cf. Materials and Methods). The bleached region in a standard FRAP experiment usually has a diameter or edge length of ∼0.1 cell diameters. This means that at length scales relevant to FRAP, the ER surface is complex enough to exhibit fractal characteristics. The laws of lateral diffusion in the membrane as well as of diffusion inside the lumenal space change when considering a fractal domain (34–36). In particular, the expected mean square displacement of a normally diffusing particle during the time period δt is not given by 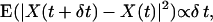but by Barlow and Perkins (34)

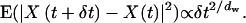(9)

X(t) denotes the position of the particle at time t and d_w is called the “dimension of the walk”. Confined diffusion in the ER is thus expected to appear anomalous (37) at length scales comparable to the size of the bleached region, even if the underlying molecular diffusion is normal (18,38,39). This is a direct effect of the complexity of the ER geometry, and the experimental results reported by Weiss et al. (29) give evidence that the observed anomaly is purely caused by the geometry of the organelle and is independent of molecular structure and events.

Comparison to experimental data

To compare the results obtained from the computations with experimental data, FRAP experiments are conducted in ssGFP–KDEL expressing cells for which the ER shape is first established from a 3D confocal reconstruction as described above. In the bleached regions, the ER occupies on the average one-third of the total volume. Using the PSE method, simulated FRAP curves are computed in the same geometries as those used in the actual experiment. This is done for 12 different FRAP experiments in eight different cells. The simulated curves are then fitted to the experimentally measured FRAP curves using time stretching only (cf. also Siggia et al. (20)). Stretching time by a factor of f and at the same time multiplying D by 1/f leaves the solution unchanged, as the diffusion constant can be incorporated into the governing equation as a scaling in time (cf. Materials and Methods).

As shown in Fig. 3 a for two of the cases, the simulated and experimentally determined FRAP curves are virtually indistinguishable after fitting. Similar overlap is observed in all instances. We conclude that the simulations are consistent and accurate enough to capture geometric effects, and can be used to predict effects of organelle geometries on FRAP as well as to derive geometry-corrected molecular diffusion constants from FRAP data.

FIGURE 3.

(a) Simulated FRAP curves compared to experimental measurement data for different ER. The computer simulations are done using the method of particle strength exchange as outlined in the Materials and Methods section. The experiment is a standard FRAP experiment, preceded by the recording of a stack of serial sections used for the reconstruction of the geometry. The simulated FRAP curves (lines) are stretched in time to fit the experimental data (symbols). As time and diffusion constant are inversely proportional, this allows us to estimate the molecular diffusion constant while fully taking the specific geometry into account (cf. main text). For the two examples shown, the molecular diffusion constants are determined to be 34.4 μm²/s (faster curve, +), and 34.2 μm²/s (slower curve, ×), respectively. All curves are normalized by their asymptotic value to allow comparison. (b) Simulated FRAP curves compared to experimental measurement data for different locations of the bleached region. Two FRAP experiments, followed by corresponding PSE simulations, performed for two different, but overlapping, bleached regions in the same ER. The result after fitting the simulation results (lines) to the measurement (symbols) is shown. The two bleached regions are given in microscope coordinates as: × (191,190)–(229,228) and + (218,196)–(256,234), corresponding to 4 × 4 μm, and the molecular diffusion constants are 1.8 μm²/s (×) and 1.6 μm²/s (+), respectively. All curves are normalized by their asymptotic value to allow comparison.

Fig. 3 b shows a similar comparison between simulated and experimentally measured FRAP curves for two different bleached regions in the same ER. The two bleached regions are overlapping; the recovery curves thus expected to be similar.

Fig. 4 visually compares the fluorescence recovery dynamics from an experiment and the corresponding simulation. Note that the experimental images show confocal sections whereas the simulation visualization shows the top view onto the closed three-dimensional object. The recovery percentages of simulation and experiment match within ±1%.

FIGURE 4.

Visual comparison between FRAP experiment and computer simulation. Micrographs from a standard FRAP experiment (cf. Materials and Methods) are compared to visualizations from the corresponding computer simulation. The case corresponds to the slower curve in Fig. 3 a and the reconstructed geometry shown in Fig. 1. Experimental images were acquired every 100 ms with a spatial resolution of 0.18 μm/pixel. The simulation entailed 6.8 million particles and comprised the whole ER (cf. Materials and Methods). The figure only depicts the portion of the ER in the vicinity of the region of interest. The molecular diffusion coefficient is determined from the fit shown in Fig. 3 a to be 34.2 μm²/s. The bleached region is indicated by its outline. No experimental image was acquired during bleaching. Note that the experimental images show a confocal section through the middle of the cell, whereas the visualizations from the simulation show the top view onto a closed three-dimensional geometry. The recovery percentages of the simulation match those of the experiment to within ±1%.

The influence of the particular geometry

The observed variation in the factor of underestimation is due to the different shapes of the individual ER samples. This is illustrated in Fig. 5 a where simulated recovery curves for different ER geometries are compared. All simulations are done using the same value for the molecular diffusion constant. Still, the recovery curves and recovery half-times scatter over a wide range. Not surprisingly, changes in the size or the position of the bleached area in the same ER lead to similar variations (Fig. 5 b). The specific local geometry of the organelle around the bleached area is thus responsible for variations of about a factor of 2.5 in the observed diffusion constant. Methods trying to deduce molecular D values using an approximate model geometry or statistically averaged shape models are unable to account for this situation.

FIGURE 5.

(a) Comparison of simulated FRAP curves for four different ER samples. All simulations are done using the same computational diffusion constant and the same simulation parameter settings (see Supplementary Material for details). All curves are normalized by their asymptotic value to allow comparison (cf. Supplementary Material). The variation observed in the FRAP curves is therefore only caused by the different geometries of the ER samples. The recovery half-times vary within the interval [5.7…14.2] × 100δt. (b) Comparison of simulated FRAP curves for different bleached areas in the same ER sample. The bleached regions are given by the microscope coordinates of their bottom left and top right corners as follows: □ (225,125)–(300,200); * (350,200)–(400,250); + (250,125)–(300,175); × (80,300)–(130,350). Simulation parameters and computational D are kept constant (cf. Supplementary Material). All curves are normalized by their asymptotic value to allow comparison.

A proposed method for determining molecular diffusion constants from FRAP data in the lumen of complex-shaped organelles

Putting the pieces together, our simulations and experiments lead to a novel method of determining molecular diffusion constants from FRAP data. The procedure is as follows:

1. After transfection and incubation, the organelle of interest is imaged as a z-stack of serial confocal sections. After this recording of the geometry, the actual FRAP experiment is performed. It is important that the organelle under consideration does not significantly move or deform during this step.

2. The z-stack of images is used to determine the reconstructed surface of the organelle as an iso-surface of pixel intensity. Various commercial and free software packages are available to do this. The iso-value is chosen such that the topological features of the organelle are conserved (e.g., the ER should be connected).

3. The reconstructed volume is used as the computational domain for PSE simulations of diffusion using scaled units of time and an arbitrary, scaled, computational diffusion coefficient. The initial condition is given by the FRAP setup.

4. The computed fluorescence recovery curve is fitted to the measured data points using a linear least squares fit in time.

5. The molecular diffusion constant in the experiment is calculated from the computational diffusion constant, the timescale factor (from the fit) and the length scale factor (from microscope/camera resolution).

In one of our examples, the simulation uses a computational D of 75 (in scaled simulation units). To convert from scaled simulation units to physical units, the time- and lengthscales need to be determined. The lengthscale is known from the pixel resolution of the z-stack images and the voxel size used in 3D reconstruction. In our example, images are acquired with 0.18 μm/pixel (cf. Materials and Methods). In 3D reconstruction the same number of lateral voxels is used as the z-stack images have pixels. The size of an individual voxel is set to 66.7 (arbitrary units). One simulation length unit thus corresponds to 2.7 nm in physical units.

The timescale factor is determined by fitting (in time) the simulated recovery curve to the experimental one. In our example, we find that (time unit) = 1.6 × 10⁻⁵ s. The molecular diffusion constant in the experiment thus is (unit length)²/(unit time) times the computational one, yielding about D = 34.2 μm²/s for this example.

Together with geometry-resolving simulations, this scaling of units allows us to determine geometry-corrected diffusion constants of fluorescently labeled proteins in the organelle lumen. We determine the molecular diffusion constant of ssGFP–KDEL in the ER lumen of VERO cells to be 34 ± 0.95 μm²/s, averaged from eight computer-evaluated FRAP experiments. Depending on the particular ER geometry, the molecular diffusion constant obtained without correcting for organelle shape is 1.8–4.2 times lower. Ignoring the effect of shape thus leads to underestimation of molecular diffusion constants.

The reported diffusion constant of pure GFP in water at room temperature is 87 μm²/s (4). This indicates that the material filling the ER lumen is of >2.5-fold higher viscosity than water.

Assessment of the method

The diffusion constants of GFP in the ER lumen are reported in the literature as ∼10 μm²/s (4). Our value being ∼3.5 times larger is consistent with our previous result that neglecting the geometry will lead to underestimation of the molecular diffusion constant by a factor of 1.8–4.2. This is further supported by work of Weiss and colleagues, where fluorescence correlation spectroscopy (a molecular-level method that directly determines molecular diffusion constants) was used to measure the molecular D of the closely related ssYFP–KDEL in the ER lumen of HeLa cells. The value obtained by Weiss and colleagues is 30 μm²/s (M. Weiss, personal communication, 2002), which is in nice agreement with our results, given that two different cell types are considered.

A thorough comparison with the method of Siggia (20) was conducted on FRAP experiments of ssGFP–KDEL in the ER lumen of VERO cells. Great care was taken to record nonsaturated images and meet all requirements of both methods. Comparing two different bleached regions from the same ER we observe that the molecular diffusion constants determined by the method presented in this article are much less scattered than the ones obtained using Siggia's program. Even though we have no reason to expect the molecular D to be constant throughout the entire ER, variations of a factor of three, as predicted by Siggia's method, seem unlikely.

The sensitivity of our method is assessed using an alternative transfection method (cf. Materials and Methods). Again, two different spots of the same ER are bleached and analyzed. Evaluating the corresponding FRAP experiments of ssGFP–KDEL in the ER lumen using the method set out in this article, molecular diffusion constants of 1.13 μm²/s and 1.63 μm²/s are determined for the two areas.

CONCLUSIONS AND DISCUSSION

The combined use of single-cell FRAP experiments, 3D reconstruction techniques, and high accuracy computer simulations allows us to estimate the magnitude of the influences of dimensionality, confinement, and specific organelle geometry on the apparent diffusion of solutes observed by FRAP.

The results demonstrate that for complex-shaped organelles neither the confinement caused by the 3D shape of the organelle, nor the specific geometry of the sample can be neglected when experimental fluorescence recovery data are used to derive molecular diffusion constants. Models used to calculate diffusion in the ER or any other intracellular organelle have to take these influences into account if they should be free of systematic errors. Unless corrected, molecular diffusion constants are underestimated. In the case of the ER, the correction factors are in the two- to fourfold range. The actual magnitude depends on the complexity of the particular 3D shape as well as the local density of small-scale structures. If one is interested in determining molecular weights based on measured molecular diffusion constants, this corresponds to an 8- to 64-fold error in weight because the diffusion cross-section area of the molecule depends quadratically on the molecular diffusion constant. For membrane-bound proteins the situation is even worse as their radius depends exponentially on the diffusion constant (40).

The results in this article indicate that it is possible to perform accurate and fully resolved computer simulations in experimentally recorded whole-organelle shapes from serial confocal sections. This enables the estimation of the geometry-induced uncertainties in the calculation of molecular diffusion constants obtained by FRAP. The employed numerical method of PSE (23) is crucial in doing so, because it avoids many of the problems that grid-based methods have in complex geometries, and its convergence is fast enough to limit the number of particles needed for a simulation to feasible ranges. The computational cost of the PSE algorithm is low enough for it to be used in quantitative analysis of FRAP experiments. The simulation of a full ER sample with ∼5 × 10⁵ particles takes roughly 20 min on a 3-GHz Intel Pentium IV computer. Because the simulation algorithm is easily parallelized, this time can be proportionally reduced by using a cluster of computers or several workstations connected by a network. The computer time for 3D reconstruction and initialization of the simulation algorithm is ∼2–5 min.

We have also shown that the ER is a fractal shape at length scales important to FRAP. Diffusion is thus expected to appear anomalous at these length scales, even if the underlying molecular diffusion is normal. This is in agreement with the simulations described by Ölveczky and Verkman (18) and the experimental results reported by Weiss et al. (29,39). The observed anomaly is a direct effect of the complexity of the ER geometry and needs not be connected to any molecular events.

What do our findings mean in practical terms? When monitoring diffusion of solutes in cellular organelles with defined boundaries and a complex shape, FRAP analysis is likely to give underestimated diffusion constants unless properly corrected. To perform the correction one needs information about the shape of the organelle inside and outside the bleached volume. This information must be digital, and is most easily obtained by 3D confocal microscopy. Using the simulation algorithm described together with the 3D geometry of the organelle, one can determine a corrected value of the molecular diffusion constants derived from FRAP experiments in the same, defined geometry. Our data suggest that the corrected values for the ER in the peripheral cytoplasm will be two to four times larger than the uncorrected ones. The apparent diffusion constants determined in different ER samples are found to vary with a factor of 2.5 for the same molecular D. For analysis of many biological processes this difference will be of considerable significance. Because the computational cost and applicability of the simulation algorithm do not depend on the complexity of the shape, it is also well suited for treating organelles or intracellular structures other than the ER.

The limitations of our approach involve the resolution of light microscopy. We find that a sufficiently detailed geometry of the ER can only be obtained in peripheral regions of the cytoplasm where the cell is thin and the ER relatively coarse. It is important that the bleached region of any FRAP experiment to be evaluated with this method is located in well-resolved areas of the organelle. The speed of diffusive recovery is determined by the intersection areas between the bleached volume and the organelle lumen. The specific shape of the organelle far away from the region of interest is of no importance. Still the whole organelle is considered in our simulations to have an estimate of the total fluorescence reservoir and to avoid postulating hypothetical boundary conditions. Another limitation of the method is that it cannot be applied to organelles that change their shape during a FRAP experiment or in the time between recording the geometry and performing the FRAP measurement. The ER is, however, quite a stationary organelle as judged from our experiments. Its shape remains largely unchanged during the few seconds of geometry recording and FRAP. A limitation of our simulation technique is that it cannot be applied to membrane components and their lateral diffusion. The reason is that restricted diffusion on membranes is governed by a different equation than diffusion in the enclosed space. Ongoing work is concerned with extending the PSE technique to this problem.

The main advantage of our approach is that it does not need a model geometry or a statistical model. This minimizes the number of assumptions and ad hoc simplifications needed and effectively relaxes some of the constraints and prerequisites current methods impose on the experimental data. The particular comparison to the method of Siggia (20) shows that our method is well capable of handling saturated images, as they are only used for the geometry reconstruction and no density information is extracted from them. As a side effect this allows much better signal/noise ratios to be achieved during the microscopic video recording and helps reducing errors and uncertainties in the geometry. By construction, our method is not hampered by 3D effects and no assumption about the connection density of the ER is made.

From the point of view of geometry, current methods of determining diffusion constants are valid when applied to relatively flat surfaces and completely volume-filling compartments. However, for intracellular organelles uncorrected diffusion constants must be interpreted with caution. The method set out in this article can be used to assess and validate current models and methods of FRAP analysis, or to directly obtain corrected molecular diffusion constants in the specific organelle geometry at hand.

Combining the presented organelle geometry treatment with realistic FRAP initial conditions (22,41) enables more accurate fluorescence recovery analysis. This will be even more important as better microscopy techniques become available to resolve the 3D shape and structure of intracellular compartments and organelles.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.