Abstract
We describe a model of the mechanical properties of the cell plasma membrane using a finite-temperature particle-dynamics simulation of the whole cell, in which a two-dimensional network of virtual particles embedded in a three-dimensional closed surface represents the membrane. The particles interact via harmonic potential and dihedral angle potential and are subject to a constant area constraint. The evolution of the positions of the particles yields the equilibrium state of the membrane and allows determination of the membrane thermal fluctuations and the elastic moduli. We show that time-averaging of the cell-model configurations allows quantitative comparison with experimental data on membrane fluctuations and elastic moduli of the red blood cell.
INTRODUCTION
The mechanical properties of plasma membranes have been shown in recent years to play an important part in physiology and cell biology. An archetypal system for study is the red blood cell (RBC) membrane, the elastic character of which determines many of the flow properties of blood and enables the red blood cells to transverse the capillaries. The RBC membrane consists of a mixed lipid-protein bilayer, an attached intracellular network called the membrane cytoskeleton, and an extracellular glycocalyx (a layer of glycoproteins covering the outer surface of the cell), thought to have little or no affect on the mechanical properties. The main component of the cytoskeletal network is the protein spectrin. Spectrin cross-links with very short actin filaments, resulting in junctional nodes that are approximately five- or sixfold coordinated in spectrin. Although the red cell is unique, in that it contains no cytoplasmic cytoskeleton or organelles, the complexes of the proteins that make up its associated membrane skeletal network and give it its elastic properties also occur in the plasma membranes of other cell types.
The RBC at rest assumes a biconcave discoid shape with a diameter of ∼8 μm and it is capable of passing through capillaries with less than half the diameter. To allow the RBC to deform inside a capillary, the resistance to deformation of the RBC membrane must not be too large. The resistance, on the other hand, must not be too small, otherwise the cell's integrity would not be preserved during normal flow in the circulatory system. Bending deformability of the RBC membrane is also shown by its mechanical out-of-plane and in-plane fluctuations with amplitudes in the range of 10–400 nm (1–3).
A long-standing problem in the study of RBC structure is that the observation of thermal fluctuations of nanometer-size seems to be consistent only with a vanishingly small shear modulus (2), whereas static deformation experiments such as micropipette aspiration (4) report a large shear modulus. Strey et al. (2) studied the flickering of RBC to derive the mean-square amplitudes of the first three azimuthal eigenmodes and they obtained a shear modulus, μ, 100-times smaller than the static value measured by micropipette aspiration, μ = 6 × 10−6 N/m (4), with a fluorescent multiparticle tracking system μ = 1–10 × 10−6 N/m (3) or by optical tweezers, μ = 2.5 × 10−6 N/m (5) and μ = 11.1–17.7 × 10−6 N/m (6). They concluded that the shear resistance for small deformations vanishes and therefore it does not contribute to thermal shape fluctuations.
We have chosen to analyze the problem considering both shear and bending moduli in the attempt to reconcile a finite value of the shear modulus with the presence of the nanometer-scale fluctuations observed experimentally. The essential assumptions of the model are that the membrane preserves a constant global area under thermal fluctuations and its mechanical behavior can be described by two material parameters, an out-of-plane bending modulus, B, which describes the resistance to bending, and an in-plane shear modulus, μ, which describes the resistance to shape changes of the membrane surface. It is usually assumed that the bending modulus, B, is dominated by the microscopic properties of the lipid bilayer. Equivalently the shear modulus, μ, is thought to be dominated by the microscopic properties of the cytoskeleton, although protein-protein interactions or domains of lipids in solid-state form can also contribute. Throughout the article, we shall use “membrane” to refer to the composite structure formed by the lipid bilayer, its integral proteins, and associated membrane skeleton.
MODEL DETAILS
Our model envisages the RBC membrane as a two-dimensional network consisting of N particles arranged in a regular triangulation. We emphasize that these are virtual particles that represent discrete areas of the membrane. For small deformation, a two-dimensional network with sixfold symmetry can be described by two elastic moduli—the area compression modulus KA and the shear modulus, μ (7). In our model we keep the global surface area constant, so we can assume that KA ∼ ∞. The two-dimensional network is embedded in a three-dimensional closed surface where it is allowed to fluctuate in all directions (see Fig. 1 a). Equations of motion of the virtual particles are solved in a molecular-dynamics fashion (8,9) to derive the time-evolution of the system and calculate the time-dependent properties.
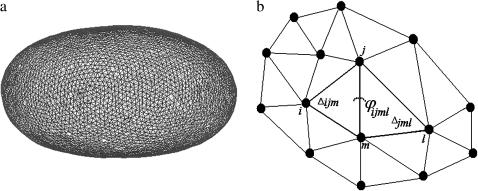
FIGURE 1.
Particle-network representing the whole-cell model is reported in a. In b we illustrated a portion of the network and the dihedral angle φijml between the adjacent triangles Δijm and Δjml.
Each particle is tethered to its six nearest-neighbors (see Fig. 1 b) by linear springs, giving a potential energy of
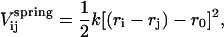 |
(1) |
where k is the spring constant, which is the same for all the particles, ri is the position of particle i, and r0 is the equilibrium distance between particles. The value of r0 fixes the minimum wavelength of the membrane fluctuations. We chose r0 to be close to the average length of the spectrin filaments (∼100 nm). This is the minimum length for which it is reasonable to expect the particles to be homogeneous. If a smaller length-scale is chosen (for example, that of membrane thickness) it would be necessary to consider heterogeneous particles to account for inhomogeneity at the molecular scale.
A dihedral angle potential is applied between adjacent triangles. This potential is used in molecular dynamics simulations to describe interactions arising from torsional forces in molecules (8,9). The expression of the dihedral angle potential we used is (10)
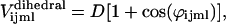 |
(2) |
where φijml is the dihedral angle between the triangles Δijm and Δjml (see Fig. 1 b). This potential has a minimum when two adjacent triangles are co-planar. Intuitively it can be seen as a mechanism for the particles to resist out-of-plane bending. The dihedral angle potential is commonly used as a procedure for curvature discretization in a triangulation (11) and it can be shown that the continuum limit of Eq. 2 is the Kantor and Nelson's bending energy for solid membranes (12). Aronovitz and Lubensky (13) stressed that this bending energy is in general different from the bending energy which Helfrich used to describe a fluid membrane (14). However, for the small displacements that occur in our system, the bending energies for solid and fluid membranes are identical. Furthermore, Gompper and Kroll (15) reported a more general expression for the bending energy that includes the effect of changes in area of triangular elements. They showed that when equilateral triangles are used, the area dependency cancels out. Since we use equilateral triangles as the equilibrium configuration, the effect of dynamic area changes will be negligible on average because of our constant area constraint.
We stress here that the bending and shear moduli are not independent (16), so in general it is not possible to change k (or D) and independently change the value of μ (or B). Details are given below about the derivation of μ and B that we adopted in our work.
In general the free energy of a system is given by two contributions, F = E–TS. In the case of a spring-network, for example, the energetic contribution E is given by the sum of 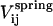 over all the particles. The entropic contribution TS depends in general on the number of configurations available to the system at a particular state. Both contributions influence the system elasticity. A clear sign that the elasticity is entropy-dominated is that the shear modulus increases when the temperature increases. It is not clear yet which of the two contributions is the dominant one in determining the RBC membrane elasticity (7). In the present model the elasticity of the system is dominated by the energetic contribution. This should not restrict our analysis since we study membrane fluctuations at a given temperature and with a given shear modulus. Furthermore, the constraint is readily overcome since removing bonds between neighboring particles within our model allows simulation of a system where the entropy can be the dominant contribution to the elasticity (17).
over all the particles. The entropic contribution TS depends in general on the number of configurations available to the system at a particular state. Both contributions influence the system elasticity. A clear sign that the elasticity is entropy-dominated is that the shear modulus increases when the temperature increases. It is not clear yet which of the two contributions is the dominant one in determining the RBC membrane elasticity (7). In the present model the elasticity of the system is dominated by the energetic contribution. This should not restrict our analysis since we study membrane fluctuations at a given temperature and with a given shear modulus. Furthermore, the constraint is readily overcome since removing bonds between neighboring particles within our model allows simulation of a system where the entropy can be the dominant contribution to the elasticity (17).
As in any standard molecular dynamics simulation, we define the temperature, T, of the system as
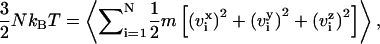 |
(3) |
where N is the number of the particles; kB is the Boltzmann constant (1.3805 × 10−23 J/K); 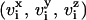 are the velocity components of particle i; m is the mass of the particle; and 〈…〉 represents the time-average. The temperature is kept constant to the desired value using a Nosé-Hoover thermostat (8,9). The value used for the temperature is T = 309 K (∼37 C).
are the velocity components of particle i; m is the mass of the particle; and 〈…〉 represents the time-average. The temperature is kept constant to the desired value using a Nosé-Hoover thermostat (8,9). The value used for the temperature is T = 309 K (∼37 C).
Since the lipid bilayer is relatively incompressible, we require that the global surface area of the membrane, defined as the sum of the areas of all triangles by which the surface is tessellated, remains constant. To do this we apply Lagrange's method of undetermined multipliers. We chose the global area, Atot, to be the value given by triangles whose sides are all equal to the equilibrium length, r0:
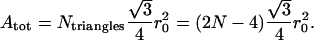 |
(4) |
In Eq. 4 we used the relationship Ntriangles = 2N − 4, which is generally true for a triangulation of the surface of simply connected bodies. In this work we are interested in calculating the amplitude of the fluctuations to derive bulk membrane properties like the shear and bending moduli. A full description of the dynamics of the red blood cell fluctuations should include the induced flow inside and outside the cell, so it should take into account the viscoelastic properties of the membrane and the equations governing the flow of the cytoplasm and the cell environment. Brochard and Lennon (18) pointed out that the induced flow of the cytoplasm is the most significant among these contributions. Tuvia et al. (19) studied the influence of extracellular fluid macroviscosity (EFM) on RBC membrane fluctuations. They stressed that thermally driven membrane fluctuations cannot be damped by an increase of EFM. They stated that the partial attenuation of the fluctuations they observed with elevation of EFM can be associated with metabolic forces, which are, to some extent, responsible for the fluctuations; however, they did not specify the nature of the metabolic forces.
The system used in the simulations consists of N particles (vertices) embedded in a closed surface. For the initial particle-configuration we followed Discher et al. (20), who used two parallel sheets in the form of a hexagon. Each particle on the perimeter of one sheet is connected to two particles on the perimeter of the other sheet. There are six “corners” on each hexagonal sheet, each of which has only fivefold coordination. The minimum number of fivefold defects required by topology for the triangulation of a spherical surface is 12 and so this configuration represents one possible triangulation of a spherical surface. All particles move in space but the connectivity is fixed, in that each particle has a fixed set of neighbors: 12 particles have five neighbors and all the others have six neighbors.
The molecular dynamics simulations were performed using the DL_POLY simulation package version 2.12 developed in Daresbury Laboratory, Cheshire, UK (10). The equations of motion of the particles were integrated using a Verlet leapfrog integration algorithm in conjunction with a Nosé-Hoover thermostat. We developed a subroutine that applies Lagrange's method of undetermined multipliers to keep the total surface area constant.
Because of computational time-demand considerations we used N = 5582 for number of particles. In most simulations we used an equilibrium length r0 = 100 nm. The area per particle, Aparticle, is given by
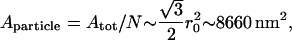 |
(5) |
where the total area is Atot ∼5 × 107 nm2. This value is approximately half the surface area of a real red blood cell (∼108 nm2).
We used two values of the spring constant, k1 = 5 × 10−6 N/m and k2 = 25 × 10−6 N/m, and two values of the dihedral-angle potential constant, D1 = 6 × 10−20 J and D2 = 60 × 10−20 J. We chose these values because the derived shear and bending moduli are in the range of the experimental measurements. We observed that using higher values of the k and D gives an increasingly rigid behavior of the model-network. On the other hand, lower values of k and D generate crumpled configurations, which were not worth studying with the present model that lacks a repulsive interaction between particles and a constraint on the cell volume. Therefore, we performed four main simulations combining the two chosen values of k and D. As we report in the following section, during the simulations we were able to keep track of the thermal fluctuations and to estimate the shear and bending moduli of the membrane.
DEVELOPMENT OF THE MODEL
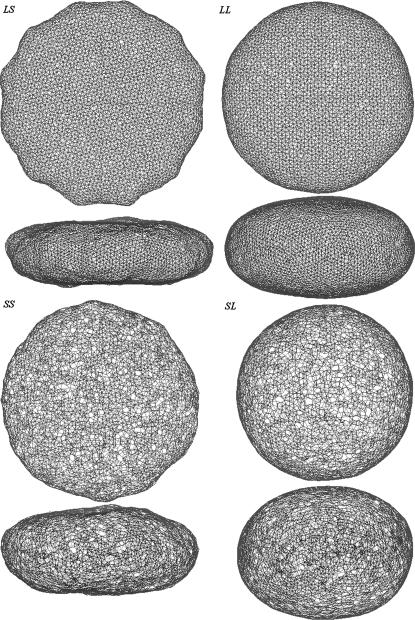
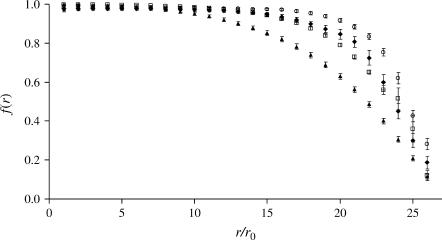
We observed a common feature of the evolution of the shape of the cell models. After an equilibration phase (∼107 time steps), the cell model attains an oblate shape for any of the values of k and D used (see Fig. 2). The oblate shape persists up to the maximum simulation time we reached (4 × 107 time steps). This is also evident in the behavior of the correlation function (reported in Fig. 3). The correlation function is defined as 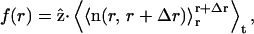 where
where 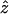 is the z-coordinate unit vector, 〈…〉t is the time-average, and
is the z-coordinate unit vector, 〈…〉t is the time-average, and 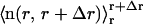 is the instantaneous average of the unit vectors perpendicular to the triangles that fall within r and r+Δr from the cap-center. In any flat region of the membrane, f(r) has a value close to unity.
is the instantaneous average of the unit vectors perpendicular to the triangles that fall within r and r+Δr from the cap-center. In any flat region of the membrane, f(r) has a value close to unity.
FIGURE 2.
Overall shape of the cell: top and side views for four different cases. Case LS, k = 25 × 10−6 N/m, B = 6 × 10−20 J. Case LL, k = 25 × 10−6 N/m, B = 60 × 10−20 J. Case SS, k = 5 × 10−6 N/m, B = 6 × 10−20 J. Case SL, k = 5 × 10−6 N/m, B = 60 × 10−20 J.
FIGURE 3.
Correlation function, 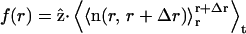 versus r/r0. Case LS (○), k = 25 × 10−6 N/m, B = 6 × 10−20 J; Case LL (□), k = 25 × 10−6 N/m, B = 60 × 10−20 J; Case SS (♦), k = 5 × 10−6 N/m, B = 6 × 10−20 J; and Case SL (▴), k = 5 × 10−6 N/m, B = 60 × 10−20 J.
versus r/r0. Case LS (○), k = 25 × 10−6 N/m, B = 6 × 10−20 J; Case LL (□), k = 25 × 10−6 N/m, B = 60 × 10−20 J; Case SS (♦), k = 5 × 10−6 N/m, B = 6 × 10−20 J; and Case SL (▴), k = 5 × 10−6 N/m, B = 60 × 10−20 J.
It is not the purpose of our current work to investigate the overall shape of the red blood cell. Further work is needed to assess how the shape is affected by the presence of the 12 defects at the rim of the cell. Moreover a mechanism to keep the total volume constant needs to be introduced in the model to study the overall shape of the cell. However, we observed that once the system has reached equilibrium, the volume fluctuations account for <1% of the total volume. This feature corresponds well to the cell behavior observed in the experiments, where the volume remains essentially constant. This allows us to infer that our findings are not significantly affected by volume fluctuations.
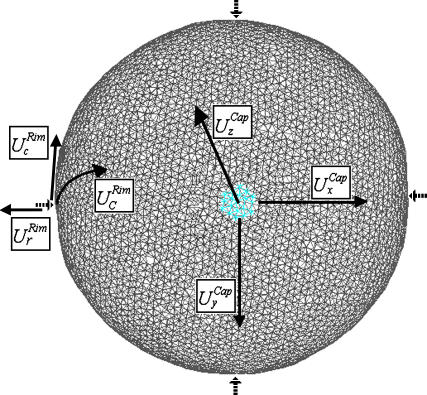
The center of the cell cap is almost flat and parallel to the x-y plane. We exploited this feature and decided to monitor a small portion of the membrane in this region to study the thermal fluctuations. We consider 19 particles located at the center of the cell cap (the lighter patch in Fig. 4), which correspond to an area of ∼1.6 × 105 nm2. We define the average of the z-displacement of the 19 particles as the out-of-plane instantaneous fluctuations of the patch. We also keep track of the positions of single particles, which correspond to fluctuations of the smallest area accessible to our model (∼9740 nm2). More specifically, we monitor the particle at the center of the cap and four other particles at orthogonal positions around the cell (see dashed arrows in Fig. 4) and monitor the displacements of the particles in the membrane plane (in-plane fluctuations). Our resolution is comparable with the resolution used in flicker measurements. Tuvia et al. (19), for example, measured membrane fluctuations over a cell patch with an area of 2.5 × 105 nm2 using point-dark-field microscopy.
FIGURE 4.
View of the cell from the top. The lighter spot represents the 19-particle patch. The four dashed-arrows indicate the positions where the rim fluctuations are taken. The solid arrows indicate the directions along which the amplitudes, U, are taken.
To derive an estimate of the shear modulus we consider the 19-particle patch and we use the average of the x- and y-displacements of the 19 particles as the in-plane fluctuations of the patch. The estimate of the shear modulus is obtained using the expression reported by Lee and Disher (3),
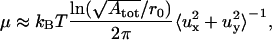 |
(7) |
where ux and uy are the in-plane fluctuations of the patch in the x- and y-directions, respectively. In Eq. 7,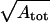 represents the maximum wavelength of the fluctuations, and r0 represents the minimum wavelength. To test the validity of Eq. 7 we performed preliminary simulations of a triangular network in two-dimensional space with periodic boundary conditions. We used Eq. 7 to calculate the shear modulus and compared the results with an analytical expression reported by Discher et al. (21) for the shear modulus of a two-dimensional regular triangulation at zero temperature,
represents the maximum wavelength of the fluctuations, and r0 represents the minimum wavelength. To test the validity of Eq. 7 we performed preliminary simulations of a triangular network in two-dimensional space with periodic boundary conditions. We used Eq. 7 to calculate the shear modulus and compared the results with an analytical expression reported by Discher et al. (21) for the shear modulus of a two-dimensional regular triangulation at zero temperature,
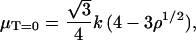 |
(8) |
where ρ is the density of the patch relative to the stress-free state. We performed the two-dimensional simulations at two different temperatures, T = 309 K (reduced temperature, 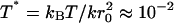 ), and T = 10 K (T* ≈ 5 × 10−4), respectively. In both cases Eq. 7 agrees within the variance with the analytical values predicted by Eq. 8. This also suggests that the temperature does not significantly affect the shear modulus for the range of temperatures we used.
), and T = 10 K (T* ≈ 5 × 10−4), respectively. In both cases Eq. 7 agrees within the variance with the analytical values predicted by Eq. 8. This also suggests that the temperature does not significantly affect the shear modulus for the range of temperatures we used.
To derive the bending modulus we used the formulae reported by Helfrich and Servuss (14),
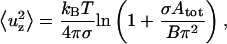 |
(9) |
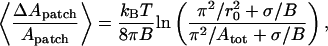 |
(10) |
which are derived in the harmonic approximation and under the condition of small fluctuations, which is satisfied when tan ϑ ≪ 1, where ϑ is the tilt angle of the membrane with respect to the x-y plane. In particular Eq. 9 is valid for 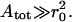 In Eqs. 9 and 10, σ is the lateral tension,
In Eqs. 9 and 10, σ is the lateral tension, 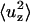 is the out-of-plane mean-squared displacement of the membrane cap, and ΔApatch is the difference between the true area of the 19-particle patch and the projected area of the patch on the x-y plane.
is the out-of-plane mean-squared displacement of the membrane cap, and ΔApatch is the difference between the true area of the 19-particle patch and the projected area of the patch on the x-y plane.
From each simulation we can easily calculate 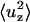 and 〈ΔApatch/Apatch〉, so we can derive the relative values of B and σ using Eqs. 9 and 10. In the case in which the lateral tension is zero, Eqs. 9 and 10 simplify to
and 〈ΔApatch/Apatch〉, so we can derive the relative values of B and σ using Eqs. 9 and 10. In the case in which the lateral tension is zero, Eqs. 9 and 10 simplify to
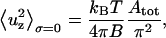 |
(11) |
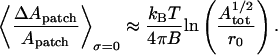 |
(12) |
However, we found that these equations gave different and inconsistent values of B in our models and so we used Eqs. 9 and 10 and allowed the existence of lateral tension in all further analyses. This gave a much smaller value of B. It is noteworthy that Strey et al. (2) reported that the lateral tension had no influence on their RBC membrane fluctuation measurements and used Eq. 11 to derive the bending modulus from their measurements obtaining a bending modulus B = 20–70 × 10−20 J. However, this value is larger than most of those reported by other authors: B = 21 × 10−20 J (22); B = 18 × 10−20 J (23); B = 1.3–3.0 × 10−20 J (18); and B = 2.3 × 10−20 J (24).
RESULTS AND DISCUSSION
In Table 1 we report the main results of our simulations. The first two rows show the values of k and D we used as inputs in four different simulations, the results of which are displayed in the columns LS, LL, SS, and SL. The following six rows report the root-mean-squared (RMS) amplitude, U, of the fluctuations:
Cap out-of-plane fluctuations,
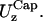
Cap in-plane fluctuations,
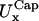 and
and 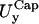 in the x- and y-directions, respectively.
in the x- and y-directions, respectively.Rim out-of-plane fluctuations,
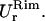
Rim in-plane fluctuations,
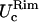 and
and 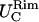 along the smaller and bigger curvatures, respectively.
along the smaller and bigger curvatures, respectively.
The results for the shear modulus obtained using Eq. 7, and for the bending modulus and lateral tension obtained using Eqs. 9 and 10 are also reported in the table. We observe that the RMS amplitudes of the fluctuations for one-particle case and for the 19-particle patch case are very similar. This means that the particles in the patch are all moving together. Both the 19-particle patch and one-particle RMS amplitudes are within the variance of the results reported in Table 1.
TABLE 1.
Main results from four simulations
| LS | LL | SS | SL | |
|---|---|---|---|---|
| k (10−6 N/m) | 25 | 25 | 5 | 5 |
| D (10−20 J) | 6 | 60 | 6 | 60 |
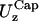 (nm) (nm) |
55 (9) | 22 (6) | 55 (8) | 35 (6) |
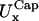 (nm) (nm) |
14 (2) | 12 (2) | 28 (4) | 23 (3) |
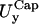 (nm) (nm) |
15 (2) | 14 (2) | 30 (3) | 29 (5) |
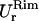 (nm) (nm) |
23 (1) | 16 (2) | 42 (7) | 25 (7) |
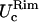 (nm) (nm) |
16 (1) | 16 (1) | 30 (2) | 28 (3) |
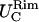 (nm) (nm) |
24 (3) | 16 (2) | 36 (5) | 28 (3) |
| μ (10−6 N/m) | 6.7 (0.7) | 11 (1) | 1.5 (0.1) | 2.1 (0.3) |
| B (10−20 J) | 3.7 (0.5) | 31 (2) | 3.1 (0.3) | 23 (3) |
| σ (10−6 N/m) | 0.5 (0.2) | 2.6 (1) | 0.5 (0.1) | 0.8 (0.2) |
First two rows: values of k and D used. Third row: out-of-plane RMS fluctuations of the cap. Fourth and fifth rows: cap in-plane RMS fluctuations (x- and y-directions, respectively). Sixth row: rim out-of-plane RMS fluctuations. Seventh and eighth rows: rim in-plane RMS fluctuations (along smaller and bigger curvatures, respectively). Ninth row: shear modulus obtained using Eq. 7. Tenth and eleventh rows: bending modulus and lateral tension obtained using Eqs. 9 and 10. The variance is reported in parentheses.
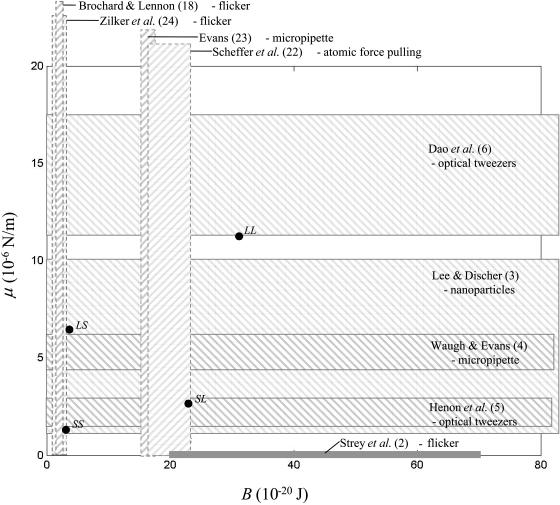
The first notable result in Table 1 is that the fluctuations, in particular the out-of-plane fluctuations, are in the nanometer scale (∼20–60 nm) as observed in experimental measurements (1,2). This is significant because these fluctuations are observed in conjunction with values of the shear and bending moduli that are of the same order of magnitude of those measured experimentally. Case LS in Table 1 is particularly interesting: 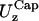 is 55 nm; the calculated bending modulus, B = 3.7 × 10−20 J, agrees well with experimental measurements, 1.3–3 × 10−20 J (18), and 2.3 × 10−20 J (24), as does the calculated shear modulus, μ = 6.7 × 10−6 N/m, with the relative experimental values, 6 × 10−6 N/m (4), 1–10 × 10−6 N/m (3), and 2.5 × 10−6 N/m (5). Moreover,
is 55 nm; the calculated bending modulus, B = 3.7 × 10−20 J, agrees well with experimental measurements, 1.3–3 × 10−20 J (18), and 2.3 × 10−20 J (24), as does the calculated shear modulus, μ = 6.7 × 10−6 N/m, with the relative experimental values, 6 × 10−6 N/m (4), 1–10 × 10−6 N/m (3), and 2.5 × 10−6 N/m (5). Moreover, 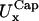 and
and 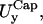 calculated with our simulation (14 and 15 nm), are quite close to the experimental values, 17–19 nm (3). Fig. 5 shows our results for μ and B together with an indication of the experimental measurements obtained with different techniques.
calculated with our simulation (14 and 15 nm), are quite close to the experimental values, 17–19 nm (3). Fig. 5 shows our results for μ and B together with an indication of the experimental measurements obtained with different techniques.
FIGURE 5.
Values of the shear modulus μ and bending modulus B calculated as described in the text compared with experimental values measured by different methods as reported in the literature. The calculated values, LS, SS, LL, and SL (·), refer to the combinations of k and D used in the calculations (see caption of Fig. 2). The shaded horizontal boxes enclosed by solid lines represent the range of experimental values reported by different authors (mean ± SD or range of values) for the shear modulus μ (10−6 N/m), whereas the vertical boxes enclosed by dotted lines represent the range of values reported for the bending modulus B (10−20 J). The method of measurement is also indicated. Strey et al. (2) report a value for both μ and B estimated by flicker measurements; the value of B is indicated by the width of the box, but their value of μ was <0.16 (10−6 N/m), and therefore the height of the box is not a true indication of their reported modulus.
For each of the four cases, 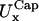 and
and 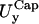 coincide within the variance. This means that the flat portion of the membranes behaves like an isotropic two-dimensional network. Furthermore, in cases LL, SS, and SL,
coincide within the variance. This means that the flat portion of the membranes behaves like an isotropic two-dimensional network. Furthermore, in cases LL, SS, and SL, 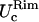 and
and 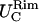 coincide within the variance, showing an isotropic behavior. In case LS, on the other hand, where the differences between the two principal curvatures are more pronounced (see Fig. 2),
coincide within the variance, showing an isotropic behavior. In case LS, on the other hand, where the differences between the two principal curvatures are more pronounced (see Fig. 2), 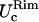 and
and 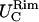 do not coincide. The fluctuations in that region are not isotropic. Lee and Discher (3) studied the thermal fluctuation of the red blood cell by measuring the displacement of a fluorescent nanoparticle attached to the membrane. They found isotropic fluctuations when the particle was centrally attached in a spherical contour of the cell, but anisotropic fluctuations when the particle was located in a highly strained region where the principal curvatures were different. We observed the same phenomenon with the out-of-plane fluctuations. The different values of
do not coincide. The fluctuations in that region are not isotropic. Lee and Discher (3) studied the thermal fluctuation of the red blood cell by measuring the displacement of a fluorescent nanoparticle attached to the membrane. They found isotropic fluctuations when the particle was centrally attached in a spherical contour of the cell, but anisotropic fluctuations when the particle was located in a highly strained region where the principal curvatures were different. We observed the same phenomenon with the out-of-plane fluctuations. The different values of 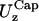 and
and 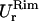 reported in Table 1 are also due to the different curvature in the two regions.
reported in Table 1 are also due to the different curvature in the two regions.
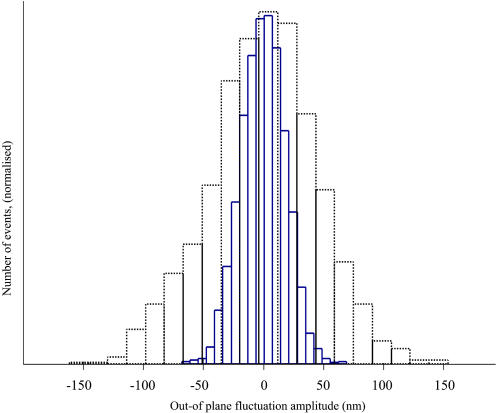
In Fig. 6 we show the histogram of the out-of-plane fluctuation amplitude for the case LS (k = 25 × 10−6 N/m, D = 6 × 10−20 J) and for the case LL (k = 25 × 10−6 N/m, D = 6 × 10−19 J). Thermal fluctuations follow a Gaussian distribution. We observe in both cases shown in Fig. 6 that the amplitude can be approximated by a Gaussian distribution and the amplitude for the case LL is narrower due to the higher value of the dihedral constant D. This is expected since a higher value of D gives a higher value of the bending modulus, which induces a lower RMS amplitude in the out-of-plane fluctuations. Equivalently, the RMS amplitude of the in-plane fluctuations is lowered by higher values of the shear modulus, which are obtained using a higher value of the spring constant k.
FIGURE 6.
Histogram of the out-plane fluctuation amplitude. (Dotted line) Case LS (k = 25 × 10−6 N/m, D = 6 × 10−20 J). (Solid line) Case LL (k = 25 × 10−6 N/m, D = 6 × 10−19 J).
In Table 1, simulations using the same dihedral constant give similar bending moduli, suggesting that the bending resistance is not affected significantly by the value of the spring constant k for the range of values we used. The results for the shear modulus show a more interesting behavior. The shear modulus for cases LL and SL obtained with Eq. 7 agrees well with the prediction of Eq. 8. The shear moduli obtained with Eq. 7 for cases LS and SS, instead, are 40% and 30% lower than the prediction of Eq. 8. We believe that this deserves more detailed analysis, which we report in the Appendix.
The lateral tension reported in Table 1 ranges between 0.5 and 2.6 × 10−6 N/m. These values are three or four orders-of-magnitude smaller than the isotropic lysis tension, 3–12 × 10−3 N/m (25). We stress that the lateral tension proscribes the use of Eqs. 11 and 12, which are valid only for vanishingly small values of the lateral tension.
CONCLUSIONS
The model we implemented showed itself able to describe the elastic properties of the red blood cell membrane related to thermal fluctuations. We demonstrated that it is possible to observe nanometer-scale fluctuations in conjunction with values of the shear and bending moduli similar to those obtained experimentally. In particular, given the microscopic parameters k and D and the assumption of constant area, the model reproduces the experimental values of the fluctuation amplitudes, the shear and bending moduli. We must emphasize that the constraint of constant area is an important feature of the model, since without it the model would show, in general, different dynamics. Moreover, it is essential to use Eqs. 9 and Eq. 10 properly. We found that the approximate expressions in Eqs. 11 and 12 give incorrect and inconsistent values of the bending modulus, due to the presence of a non-vanishingly small lateral tension. This highlights the importance of measuring 〈ΔApatch/Apatch〉 (or related quantities) when studying membrane fluctuations experimentally and of properly choosing the minimum wavelength appearing in Eqs. 9 and 10.
APPENDIX
In this section we analyze the behavior of the shear modulus reported in Table 1. The shear modulus for cases LL and SL agrees well with the prediction of Eq. 8, which is valid for T = 0 K. This suggests that the shear modulus is not affected by the temperature or by the out-of-plane fluctuations of the system. In cases LS and SS, instead, the shear modulus obtained with Eq. 7 is 40%, and 30%, respectively, lower than the prediction of Eq. 8. We believe that this softening of the shear modulus can be explained using rescaling arguments reported by Aronovitz and Lubensky (13,26). These authors used renormalization group techniques to study the crumpling transition and the fluctuations around a flat phase of flexible D-dimensional crystalline membranes embedded in d-dimensional space. They reported that for fluctuations of wavelength, λ, greater than the nonlinear length, ξnl, the shear modulus is renormalized and behaves as μ(λ) = (1/λ)η, the nonlinear length being defined as 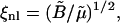 for D = 2, where
for D = 2, where 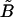 and
and 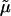 are the bare elastic moduli divided by the temperature. Using T = 309 K and the values of D and μT=0 (Eq. 8) to derive ξnl, the following values are obtained:
are the bare elastic moduli divided by the temperature. Using T = 309 K and the values of D and μT=0 (Eq. 8) to derive ξnl, the following values are obtained: 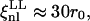
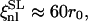
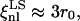 and
and 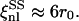 For the shear modulus to be renormalized and then to undergo softening, the critical exponent η must be positive and the fluctuation wavelengths of the system must be larger than ξnl. In cases LL and SL the nonlinear length is comparable with the size of the system, and for this reason the renormalization of the shear modulus is less significant. In cases LS and SS, instead, ξnl is much smaller than the size of the system and the conditions for the softening of the shear modulus are met.
For the shear modulus to be renormalized and then to undergo softening, the critical exponent η must be positive and the fluctuation wavelengths of the system must be larger than ξnl. In cases LL and SL the nonlinear length is comparable with the size of the system, and for this reason the renormalization of the shear modulus is less significant. In cases LS and SS, instead, ξnl is much smaller than the size of the system and the conditions for the softening of the shear modulus are met.
To corroborate further the conclusion that the softening of the shear modulus can be ascribed to renormalization, we performed simulations on a hexagonal sheet (open surface) with the same characteristics as the LS case. We used hexagonal sheets with three different diameters, namely, 40r0, 60r0, and 100r0. We obtained the following values for the shear modulus: μ(40r0) = 9.9(0.1), μ(60r0) = 9.0(0.3), and μ(100r0) = 8.2(0.3) 10−6 N/m, which show that the shear modulus diminishes as the size of the system increases. These are preliminary results and more systematic work should be done, but they seem to show an interesting behavior. Considering that our system is realistic in terms of size and range of elastic moduli, we can infer that the renormalization group may play an important role in the understanding of red-blood cell mechanical properties.
References
- 1.Krol, A. Y., M. G. Grinfeldt, S. V. Levin, and A. D. Smilgavichus. 1990. Local mechanical oscillations of the cell surface within the range 0.2–30 Hz. Eur. Biophys. J. 19:93–99. [DOI] [PubMed] [Google Scholar]
- 2.Strey, H., M. Peterson, and E. Sackmann. 1995. Measurement of erythrocyte membrane elasticity by flicker eigenmode decomposition. Biophys. J. 69:478–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lee, J. C. M., and D. E. Discher. 2001. Deformation-enhanced fluctuations in the red cell skeleton with theoretical relations to elasticity, connectivity, and spectrin unfolding. Biophys. J. 81:3178–3192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Waugh, R., and E. A. Evans. 1979. Thermoelectricity of red blood cell membrane. Biophys. J. 26:115–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hénon, S., G. Lenormand, A. Richert, and F. Gallet. 1999. A new determination of the shear modulus of the human erythrocyte membrane using optical tweezers. Biophys. J. 76:1145–1151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dao, M., C. T. Lim, and S. Suresh. 2003. Mechanics of the human red blood cell deformed by optical tweezers. J. Mech. Phys. Solut. 51:2259–2280. [Google Scholar]
- 7.Boal, D. 2002. Mechanics of the Cell. Cambridge University Press, Cambridge, UK.
- 8.Allen, M. P., and D. J. Tildesley. 1987. Computer Simulation of Liquids. Clarendon Press, Oxford, UK.
- 9.Sadus, R. J. 1999. Molecular Simulation of Fluids: Theory, Algorithms and Object-Orientation. Elsevier Press, Amsterdam, The Netherlands.
- 10.Smith, W., and T. R. Forester. 1999. The DL_POLY_2 Molecular Simulation Package. http://www.cse.clrc.ac.uk/msi/software/DL_POLY. [DOI] [PubMed]
- 11.Seung, H. S., and D. R. Nelson. 1988. Defects in flexible membranes with crystalline order. Phys. Rev. A. 38:1005–1018. [DOI] [PubMed] [Google Scholar]
- 12.Kantor, Y., and D. R. Nelson. 1987. Crumpling transition in polymerized membranes. Phys. Rev. Lett. 58:2774–2777. [DOI] [PubMed] [Google Scholar]
- 13.Aronovitz, J. A., and T. C. Lubensky. 1988. Fluctuations of solid membranes. Phys. Rev. Lett. 60:2634–2637. [DOI] [PubMed] [Google Scholar]
- 14.Helfrich, W., and R. M. Servuss. 1984. Undulations, steric interaction and cohesion of fluid membranes. Nuovo Cimento. 3D:137–151. [Google Scholar]
- 15.Gompper, G., and D. M. Kroll. 1996. Random surface discretizations and the renormalization of the bending rigidity. J. Phys. (France). 6:1305–1320. [Google Scholar]
- 16.Nelson, D. R., and L. Peliti. 1987. Fluctuations in membranes with crystalline and hexatic order. J. Phys. E. 48:1085–1092. [Google Scholar]
- 17.Plischke, M., D. C. Vernon, B. Joós, and Z. Zhou. 1999. Entropic rigidity of randomly diluted two- and three-dimensional networks. Phys. Rev. E. 60:3129–3135. [DOI] [PubMed] [Google Scholar]
- 18.Brochard, F., and J. F. Lennon. 1975. Frequency spectrum of the flicker phenomenon in erythrocytes. J. Phys. E. 36:1035–1047. [Google Scholar]
- 19.Tuvia, S., A. Almagor, A. Bitler, S. Levin, R. Korenstein, and S. Yedgar. 1997. Cell membrane fluctuations are regulated by medium macroviscosity: evidence for a metabolic driving force. Proc. Natl. Acad. Sci. USA. 94:5045–5049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Discher, D. E., D. H. Boal, and S. K. Boey. 1998. Simulations of the erythrocyte cytoskeleton at large deformation. II. Micropipette aspiration. Biophys. J. 75:1584–1597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Discher, D. E., D. H. Boal, and S. K. Boey. 1997. Phase transitions and anisotropic responses of planar triangular nets under large deformation. Phys. Rev. E. 55:4762–4772. [Google Scholar]
- 22.Scheffer, L., A. Bitler, E. Ben-Jacob, and R. Korenstein. 2001. Atomic force pulling: probing the local elasticity of the cell membrane. Eur. Biophys. J. 30:83–90. [DOI] [PubMed] [Google Scholar]
- 23.Evans, E. A. 1983. Bending elastic modulus of red blood cell membrane derived from buckling instability in micropipette aspiration tests. Biophys. J. 43:27–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zilker, A., M. Ziegler, and E. Sackmann. 1992. Spectral analysis of erythrocyte flickering in the 0.3–4-μm−1 regime by microinterferometry combined with fast image processing. Phys. Rev. A. 46:7998–8001. [DOI] [PubMed] [Google Scholar]
- 25.Evans, E. A., R. Waugh, and L. Melnik. 1976. Elastic area compressibility modulus of red cell membrane. Biophys. J. 16:585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Aronovits, J., L. Golubovic, and T. C. Lubensky. 1989. Fluctuations and lower critical dimensions of crystalline membranes. J. Phys. [E]. 50:609–631. [Google Scholar]