Abstract
The magnetic field dependence of the proton-spin-lattice relaxation rate in rotationally immobilized proteins shows that the one-dimensional character of the protein primary structure causes a dramatic increase in the population of low-frequency motions from 10 kHz to 20 MHz. As a consequence, the probability and rate at which functionally critical conformational states are thermally sampled in a protein are dramatically increased as well, when compared with a three-dimensional lattice structure. Studies of protein dynamics often focus on time periods far shorter than those associated with catalytic function, but we show here that the magnetic field dependence of the proton nuclear spin-lattice relaxation rate in rotationally immobilized proteins reports unambiguously the structural fluctuations in the frequency range from 10 kHz to 20 MHz. This relaxation rate decreases with increasing Larmor frequency according to a power law that derives from the distribution of dynamical states, the localization of the structural disturbances, and the spatial distribution of hydrogen atoms in the structure. The robust theoretical foundation for the spin-relaxation process, loosely characterized as a direct spin-phonon coupling, shows that the disturbances propagate in a space of reduced dimensionality, essentially along the stiff connections of the polypeptide chain. The reduced dimensionality traps the disturbance and changes the efficiency for energy redistribution in the protein and the processes that drive nuclear spin relaxation. We also show that the Larmor frequency dependence of the protein-proton-spin-lattice relaxation rate constant is related to the frequency dependence of force constants and mean-square displacement commonly observed or calculated for proteins. We believe that these approaches give additional physical insight into the character of the extremely low-frequency protein dynamics.
INTRODUCTION
Structural fluctuations in proteins and other macromolecules provide access to functional conformations that result in concerted and critical changes directly coupled to chemical reactivity, transport, or functional control (1–5). The complex dynamical spectrum of a folded polymeric structure may span many decades in frequency or time (6,7), although most recent discussions of protein dynamics focus on timescales of nanoseconds and shorter. However, these time periods are far shorter than those associated with biological functions. Other experiments and theories are thus necessary to report on protein dynamics on a much longer timescale. Here, we report on the protein dynamics in the frequency range from 10 kHz to 20 MHz or the time range from tens of microseconds to 10 nanoseconds, by using the proton magnetic relaxation dispersion (MRD), i.e., the magnetic field dependence of the spin-lattice relaxation rate constant, 1/T1. The frequency range explored is well below the one usually addressed by high-resolution NMR methods (5) and complementary to, but more extensive than, transverse relaxation dispersion measurements (8). MRD reports on protein dynamics over a range from fast and localized motions to slow and delocalized collective motions which may involve the whole protein.
To probe the intramolecular protein dynamics, we focus on MRD measurements of rotationally immobilized proteins. These systems are excellent models for the spin relaxation in whole tissues, and the theoretical description we have developed accounts well for the magnetic field dependence of spin-lattice relaxation time constants in tissues. In addition to the practical implications of this quantitative theory for clinical medicine, the experiment and the theory provide important insights for intramolecular protein dynamics that impact molecular function and its mechanism.
The rotational immobilization eliminates the high-resolution spectra usually associated with proton NMR spectroscopy in liquids. However, the strong dipolar couplings magnetically connect all the protons to provide a broad homogeneous NMR spectrum consisting of one line ∼25 kHz wide. The spin-spin communication within the immobilized protein-proton spin system is rapid. Dynamics that relax one portion of the protein-proton population then affect the total proton population so that the dynamical report provided by the protons collectively includes all motions that modulate proton-proton couplings; i.e., the observable proton spin relaxation provides a global report of protein dynamics.
Nuclear spin relaxation is stimulated by the spin coupling to the magnetic noise at the resonance frequency that derives from the relative motions of the spin-bearing components. The MRD provides a direct characterization of these noisemaking motions from milliseconds to picoseconds by changing the observation window, which is linear in the magnetic field strength (9–12). Here we probe the low-frequency domain where rapid internal motions such as methyl group rotation are not competitive relaxation pathways (13). Because there is no rapid rotational averaging, the usual approaches to spin relaxation using common spectral density models are inappropriate. The successful quantum theoretical description of these experiments, which we have developed, is based on simple assumptions that we summarize here and are supported in detail by experiment. A crucial component of this description rests on the fact that the stiff connections in the protein structure are along the polypeptide chain, which makes the system approximately one-dimensional in some respects, not three-dimensional. The key point that follows from the dimensionality reduction is that the structural fluctuations in the protein are far more prevalent in the frequency range usually associated with protein function than expected based on three-dimensional models which are our common experience. Last, we show that non-affine relations exist between the proton-spin-lattice relaxation rate and commonly encountered frequency dependences of force constants and mean-square displacements. Though MRD measurements explore a much lower frequency range than most other techniques, these relations give additional physical insight to low-frequency protein dynamics.
METHOD AND RESULTS
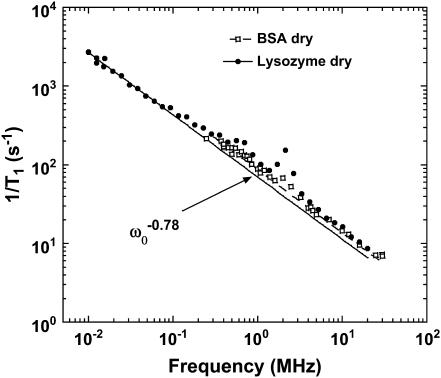
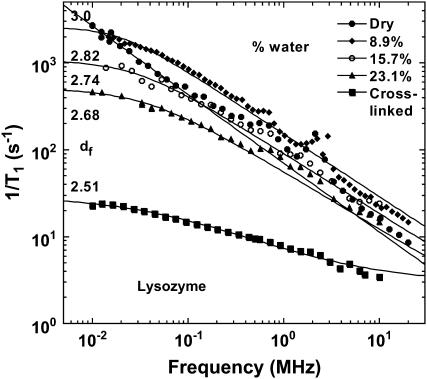
Fig. 1 shows typical proton MRD profiles for lyophilized bovine serum albumin (14) and lysozyme obtained at room temperature using a fast-field-cycling spectrometer from Stelar Instruments (Mede, Italy). The lyophilization procedure is described in Lester and Bryant (14). For both systems, the protein-proton-spin-lattice relaxation rate is described by a power law in the Larmor frequency, 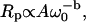 with A as a constant and b = 0.78. Fig. 2 shows MRD profiles for various hydrations of lysozyme. Here the measured 1/T1 differs from Rp because of cross-relaxation between water and protein protons (14–16). As a consequence, the relaxation rates in the low field plateau region decrease with increasing hydration. Fig. 2 also shows measurements on lysozyme gels where the molecular rotation has been inhibited by glutaraldehyde cross-linking. Results for cross-linked serum albumin are similar; thus, the essential features do not depend on water content or the protein identity.
with A as a constant and b = 0.78. Fig. 2 shows MRD profiles for various hydrations of lysozyme. Here the measured 1/T1 differs from Rp because of cross-relaxation between water and protein protons (14–16). As a consequence, the relaxation rates in the low field plateau region decrease with increasing hydration. Fig. 2 also shows measurements on lysozyme gels where the molecular rotation has been inhibited by glutaraldehyde cross-linking. Results for cross-linked serum albumin are similar; thus, the essential features do not depend on water content or the protein identity.
FIGURE 1.
The proton spin-lattice relaxation rate recorded as a function of the magnetic field strength plotted as the proton Larmor frequency for samples of dry lysozyme and BSA at room temperature. The solid line presents the best fit of the data with Eqs. 3a and 3b and b = 0.78. This value of b leads to a value df = 3 from Eq. 3b, which indicates a uniform distribution of protons. The peaks at 2.8, 2.4, and 0.8 MHz in the relaxation rate profile are caused by proton relaxation coupling to the amide nitrogen when the 14N energies match the proton Zeeman levels.
FIGURE 2.
The proton spin-lattice relaxation rate recorded as a function of the magnetic field-strength plotted as the proton Larmor frequency for lysozyme samples hydrated to various degrees (weight %) at room temperature. The solid lines are the best fits to the data using Eqs. 3a and 3b. The two parameters adjusted are b and the exchange rate constant between the protein protons and the water proton populations. The value df is obtained from b according to Eq. 3b.
THEORY
The interpretation of these measurements is built on a quantum theory of the nuclear spin relaxation induced by time fluctuations of the proton dipole-dipole interaction, Hdip(t), between spins in a disordered or non-crystalline solid (17–21). This interaction is expanded as a superposition of pairwise contributions 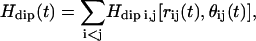 which depends mainly on the interspin distance rij(t) and the angle θij(t) between rij and the constant magnetic field B0. Motions that change the remaining azimuthal angle φij do not change the dipolar coupling between two protons at magnetic fields significantly above the local dipolar field strength. This description closely follows the basic features of the mathematical model presented by Abragam (22), except that even in a protein crystal, the local structure, as sensed by the proton-proton dipolar connectivity, is disordered—i.e., the protons do not form a uniform three-dimensional array. However, the proton dipolar interactions are still modulated by fluctuations of the interspin vectors, rij, in the approximation of small displacements, uij, compared to equilibrium distances, Rij (e.g., rij(t) = Rij + uij(t)) (18). This approximation is justified for proteins by the general preservation of modest Debye-Waller factors deduced from x-ray scattering determinations of protein structure in the crystal. We have extended the model for relaxation caused by a direct spin-phonon process (18). The strong magnetic field dependence and linear temperature-dependence of the spin-lattice relaxation rate support this model and eliminate the Raman process in the temperature range above 270 K (22). Only the phonons in the neighborhood of the Larmor frequency contribute to nuclear spin relaxation. In the following, we outline the three contributions responsible for the magnetic field dependence of protein-proton-spin-lattice relaxation rate Rp that yield a quantitative expression for the frequency dependence of Rp, and that allow us to probe the internal protein dynamics from the data displayed in Figs. 1 and 2.
which depends mainly on the interspin distance rij(t) and the angle θij(t) between rij and the constant magnetic field B0. Motions that change the remaining azimuthal angle φij do not change the dipolar coupling between two protons at magnetic fields significantly above the local dipolar field strength. This description closely follows the basic features of the mathematical model presented by Abragam (22), except that even in a protein crystal, the local structure, as sensed by the proton-proton dipolar connectivity, is disordered—i.e., the protons do not form a uniform three-dimensional array. However, the proton dipolar interactions are still modulated by fluctuations of the interspin vectors, rij, in the approximation of small displacements, uij, compared to equilibrium distances, Rij (e.g., rij(t) = Rij + uij(t)) (18). This approximation is justified for proteins by the general preservation of modest Debye-Waller factors deduced from x-ray scattering determinations of protein structure in the crystal. We have extended the model for relaxation caused by a direct spin-phonon process (18). The strong magnetic field dependence and linear temperature-dependence of the spin-lattice relaxation rate support this model and eliminate the Raman process in the temperature range above 270 K (22). Only the phonons in the neighborhood of the Larmor frequency contribute to nuclear spin relaxation. In the following, we outline the three contributions responsible for the magnetic field dependence of protein-proton-spin-lattice relaxation rate Rp that yield a quantitative expression for the frequency dependence of Rp, and that allow us to probe the internal protein dynamics from the data displayed in Figs. 1 and 2.
Normal mode expansion
In the approximation of small displacements uij compared to equilibrium distances Rij, one can expand the time-dependent spatial parts of the proton dipole-dipole interaction up to their first-order contributions: 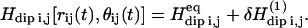 We show in Korb and Bryant (18) how this expansion can be put in a form appropriate for calculations by writing the displacement vector uij(t) in a normal coordinate expansion, where the longitudinal displacements (u‖) modify only the interspin distance rij, and the displacements (u⊥) perpendicular to the interspin distance modify only the angle θij. Calculations show that
We show in Korb and Bryant (18) how this expansion can be put in a form appropriate for calculations by writing the displacement vector uij(t) in a normal coordinate expansion, where the longitudinal displacements (u‖) modify only the interspin distance rij, and the displacements (u⊥) perpendicular to the interspin distance modify only the angle θij. Calculations show that 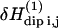 may be written as a linear combination of the gradients of u expressed in this normal coordinate system (‖, ⊥). The transition rate per unit of volume induced by the time-dependent perturbation
may be written as a linear combination of the gradients of u expressed in this normal coordinate system (‖, ⊥). The transition rate per unit of volume induced by the time-dependent perturbation 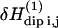 is calculated with the Golden rule for time perturbation theory of harmonic oscillators. This contribution enters as the square of the dipole-dipole perturbation
is calculated with the Golden rule for time perturbation theory of harmonic oscillators. This contribution enters as the square of the dipole-dipole perturbation 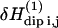 averaged over the Zeeman and lattice Boson states, which, at high temperature, finally gives
averaged over the Zeeman and lattice Boson states, which, at high temperature, finally gives 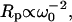 where ω0 is the proton Larmor frequency.
where ω0 is the proton Larmor frequency.
Density of vibrational states
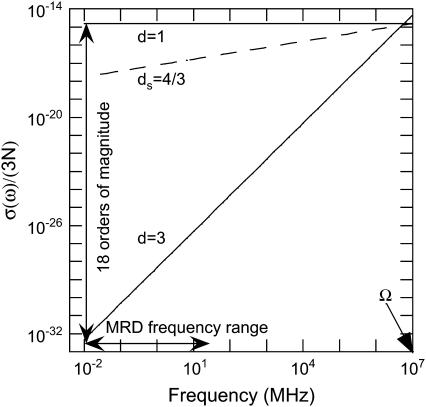
The summation of the transition rate over the lattice Boson states is replaced by an integration over the density of vibrational states σ(ω), and Rp thus becomes proportional to σ(ω). The question now is what expression of density of vibrational states should be used for a disordered system like a protein. The usual Debye description for the vibrational distribution of states, σ(ω) ∝ ωd−1 for a d-dimensional system of N atoms, is drastically dependent of the dimensionality (see Fig. 3). One notes a dramatic increase (18 orders of magnitude) of σ(ω) at low-frequency range probed in a MRD experiment when reducing the dimensionality from d = 3 to d = 1. The importance of the dimensionality is implied by previous work of Kimmich, who found the same power-law exponents (b = 0.8) for the proton MRD of polypeptide chains (polyglycine) that present no side chains and proteins, which do have side chains (23,24). From the first principles of proton NMR relaxometry, this result unambiguously demonstrates that the dynamics probed in these MRD experiments reflect those of the protein backbone. The motions that dominate the shape of the magnetic field dependence of the proton-spin relaxation at room temperature in the very low-frequency range are thus associated with the backbone of the polypeptide chain and not with the side chains. We note a critical point here. The structural fluctuation itself is not one-dimensional; atoms move in three dimensions and involve backbone as well as side chains of the protein. However, the propagation of the structural disturbance is of reduced dimensionality; i.e., the propagation of the structural disturbance is not in three dimensions, but largely restricted to one, which is along the chain. This is the reason that two parameters enter the theory, one characterizing the distribution of protons in space, and one for the effective dimensionality of the propagation. Therefore, vibrational density of states and consequently Rp is dramatically enhanced in the low-frequency range compared with the three-dimensional case (see Fig. 3). To take into account such an anisotropic propagation of disturbance, the usual Debye description for the vibrational distribution of states, σ(ω) ∝ ωd−1 for a d-dimensional system of N atoms, is then modified (25) to
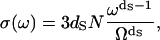 |
(1) |
with Ω the maximal frequency in the problem and with the normalization requirement of 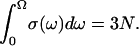 Here ds, called a spectral dimension, is <2 for systems that are not three-dimensional crystals. The value ds is related to the propagation of the structural disturbance or the number of sites sampled by a random exploration of the space characterized by a fractal distribution of mass of dimension df. Both experiment and simulation suggest that ds is 4/3 for percolation systems (25,26). According to Alexander and Orbach, ds depends both on the internal geometry of the fractal and the way it is internally connected (25). They note also that, concerning the vibrational problem, ds depends also on the way the fractal is embedded in the external space and on the nature of the terms in the harmonic expansion that determine its rigidity. This is precisely why it is called spectral dimension. In summary, the 1H relaxation rate, Rp, is proportional to
Here ds, called a spectral dimension, is <2 for systems that are not three-dimensional crystals. The value ds is related to the propagation of the structural disturbance or the number of sites sampled by a random exploration of the space characterized by a fractal distribution of mass of dimension df. Both experiment and simulation suggest that ds is 4/3 for percolation systems (25,26). According to Alexander and Orbach, ds depends both on the internal geometry of the fractal and the way it is internally connected (25). They note also that, concerning the vibrational problem, ds depends also on the way the fractal is embedded in the external space and on the nature of the terms in the harmonic expansion that determine its rigidity. This is precisely why it is called spectral dimension. In summary, the 1H relaxation rate, Rp, is proportional to 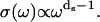
FIGURE 3.
Frequency dependence in MHz of the normalized density of vibrational distribution of states σ(ω)/3N calculated from Eq. 1 for different dimensionalities d (3, dS = 4/3 and 1). The range of frequency (104 − 2 × 107 Hz) probed by magnetic relaxation dispersion is indicated by an arrow. The frequency, Ω ≈ 1013 Hz, corresponds to the highest vibrational mode. One notes a dramatic increase (18 orders of magnitude) of the density of vibrational states at low-frequency when reducing the dimensionality from d = 3 to d = 1.
Localization and scaling in proteins
The structural disturbance in the dry and disordered protein is confined or spatially limited; its extent, 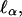 ranges from a minimal size, a that may be less than the size of the monomer unit, up to the size of the protein, and is related to the frequency of the fluctuation ωα ∈ {ωmin, Ω}. This model considers a process of overdamping of vibrational modes of frequency ω > ωα on a region of size
ranges from a minimal size, a that may be less than the size of the monomer unit, up to the size of the protein, and is related to the frequency of the fluctuation ωα ∈ {ωmin, Ω}. This model considers a process of overdamping of vibrational modes of frequency ω > ωα on a region of size 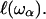 On random strongly disordered fractals, this corresponds to the strong localization model where
On random strongly disordered fractals, this corresponds to the strong localization model where 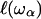 is defined as the localization length. From a mathematical point of view, such a localization is expressed through an exponential spatial decay of the displacement vector through a normalized wave function
is defined as the localization length. From a mathematical point of view, such a localization is expressed through an exponential spatial decay of the displacement vector through a normalized wave function 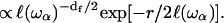 The localization greatly affects the values of the gradient of spin displacements ∇u and thus Rp. Scaling arguments show that the product of the volume of localization,
The localization greatly affects the values of the gradient of spin displacements ∇u and thus Rp. Scaling arguments show that the product of the volume of localization, 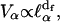 for a given frequency ωα and the number of modes,
for a given frequency ωα and the number of modes, 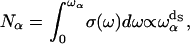 outside this volume Vα, is a constant (see (25)),
outside this volume Vα, is a constant (see (25)),
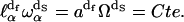 |
(2) |
This relation leads to an anomalous dispersion relation 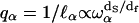 between q space and frequency. The quantity df is the fractal dimensionality associated with the distribution of protons in the protein structure. We have computed fractal dimensions df for the spatial distribution of protons based on the crystal structure of lysozyme and other globular proteins and find that they agree with the values derived from treating df as an adjustable parameter in fitting the proton MRD data (18). The values of df are those expected for systems that form percolation networks. For the α-carbons, this is dominated by the connectivity of the polypeptide chain (27,28). Thus, the primary motion is along the stiff connections of the polypeptide chain. Calculations show that the proton relaxation rate Rp is proportional to the square of the gradient of the displacement vector as
between q space and frequency. The quantity df is the fractal dimensionality associated with the distribution of protons in the protein structure. We have computed fractal dimensions df for the spatial distribution of protons based on the crystal structure of lysozyme and other globular proteins and find that they agree with the values derived from treating df as an adjustable parameter in fitting the proton MRD data (18). The values of df are those expected for systems that form percolation networks. For the α-carbons, this is dominated by the connectivity of the polypeptide chain (27,28). Thus, the primary motion is along the stiff connections of the polypeptide chain. Calculations show that the proton relaxation rate Rp is proportional to the square of the gradient of the displacement vector as 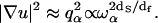 By comparison, in a Euclidean space of dimension d where ds = df = d, one has a normal dispersion behavior without any damping qα ∝ ωα (existence of phonons) and
By comparison, in a Euclidean space of dimension d where ds = df = d, one has a normal dispersion behavior without any damping qα ∝ ωα (existence of phonons) and 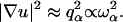 A consequence of such anomalous dispersion is that the radii of localization at the two extremes of our frequency range,
A consequence of such anomalous dispersion is that the radii of localization at the two extremes of our frequency range, 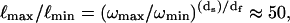 changes from essentially the limit of the bond lengths to the approximate size of the protein molecule. Thus, Rp is proportional to
changes from essentially the limit of the bond lengths to the approximate size of the protein molecule. Thus, Rp is proportional to 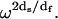 We note that the term localization is used to distinguish the spatial extent of the structural disturbance from very short wavelength modes that may be appropriate to hard three-dimensional crystals. We emphasize that at the low-frequency limit of the MRD, the length scale of the fluctuation is approximately the diameter of the protein.
We note that the term localization is used to distinguish the spatial extent of the structural disturbance from very short wavelength modes that may be appropriate to hard three-dimensional crystals. We emphasize that at the low-frequency limit of the MRD, the length scale of the fluctuation is approximately the diameter of the protein.
Frequency dependence of proton-spin-lattice relaxation rate in dry proteins
The three contributions described above coming from normal modes, density of vibrational states, and localization combine to yield 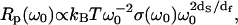 where T is the temperature. By comparison, in a Euclidean space of dimension d, this relation becomes
where T is the temperature. By comparison, in a Euclidean space of dimension d, this relation becomes 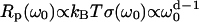 (22). Considering both longitudinal (‖) and transverse (⊥) motions associated to the normal modes u‖ and u⊥ and characterized by their density of vibrational states given by Eq. 1 with maximal frequencies Ω‖ and Ω⊥ yields the quantitative expression (18,20) of
(22). Considering both longitudinal (‖) and transverse (⊥) motions associated to the normal modes u‖ and u⊥ and characterized by their density of vibrational states given by Eq. 1 with maximal frequencies Ω‖ and Ω⊥ yields the quantitative expression (18,20) of
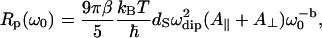 |
(3a) |
where
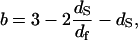 |
(3b) |
and 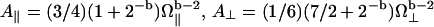 ; β is a numerical factor (β ≈ 3) associated with the effective size of the proton dipolar coupling, ωdip/2π = 11.3 kHz; and Ω‖ and Ω⊥ correspond to the frequencies of the highest vibrational modes parallel and perpendicular with the polypeptide chain, taken as the amide (I) and (II) modes at 1560 cm−1 and 200 cm−1, respectively (29). The frequency dependence of Rp (Eq. 3) and the anomalous dispersion (Eq. 2) thus allow us to probe the internal protein dynamics from the fast localized motions to the slow cooperative delocalized motions.
; β is a numerical factor (β ≈ 3) associated with the effective size of the proton dipolar coupling, ωdip/2π = 11.3 kHz; and Ω‖ and Ω⊥ correspond to the frequencies of the highest vibrational modes parallel and perpendicular with the polypeptide chain, taken as the amide (I) and (II) modes at 1560 cm−1 and 200 cm−1, respectively (29). The frequency dependence of Rp (Eq. 3) and the anomalous dispersion (Eq. 2) thus allow us to probe the internal protein dynamics from the fast localized motions to the slow cooperative delocalized motions.
DISCUSSION
MRD protein data
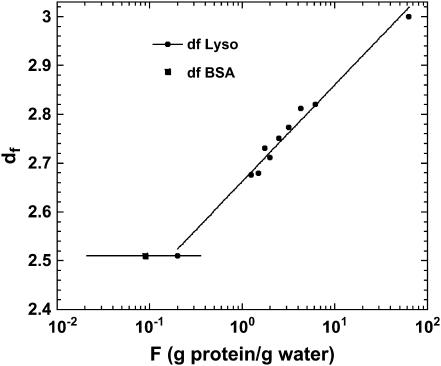
For the dry proteins shown in Fig. 1, only the longitudinal motions (‖) are needed due to highly steric constraints. Equation 3a fits the data well with b = 0.78, which corresponds to df = 3 according to Eq. 3b, i.e., the same as the Euclidean dimension. This result is a limiting value that implies that the distribution of protons in space is essentially uniform and that the protein structure in the lyophilized solid is more uniform than in the hydrated crystal, for which we deduce a value of df = 2.5 from the hydrogen atom positions implied by the x-ray structure. Similar b values have been found for polypeptides and other proteins (23,24), which demonstrates that the dynamics probed in the MRD experiments reflect propagation along the protein backbone. In the presence of water, only the lower frequency transverse term A⊥ is required and dominates because Ω⊥/Ω‖ ≈ 1/8. The solid lines through the hydrated protein data of Fig. 2 are obtained using the expressions in Eq. 3 in combination with the solution to the problem of magnetic coupling between the mobile water protons and the protein protons (19). Only two parameters were adjusted: the values of df and of the exchange rate constant between the two spin populations. The value of df changes essentially logarithmically as a function of the ratio of the number of protein protons to the number of water protons from 3 for the dry protein to 2.5 for a fully hydrated protein (Fig. 4). Such a weak variation of the fractal dimension, which represents a single parameter characterization of the three-dimensional distribution of protons in space, implies that the protein structure changes in small local incremental steps rather than by large scale or global cooperative transitions as the protein adjusts to increasing water content from the lyophilized state. Further, the decrease in the fractal dimension, df, implies that the proton distribution changes from essentially uniform in the lyophilized protein to significantly non-uniform in the fully hydrated state. This change almost certainly involves an increase in free volume in the native structure that may be occupied by water in the cases where the volume increments are sufficiently large. A consequence of an increase in free volume is increased local motion, which is reflected in the fact that the perpendicular components of Eq. 3 dominate the hydrated cases.
FIGURE 4.
The fractal dimension df of the proton distribution obtained from Fig. 2 with use of Eqs. 3a and 3b and plotted against the ratio F between the protein-protons and the water-protons at equilibrium. The continuous line is a logarithmic fit to the data.
The relaxation dispersion profiles in both Figs. 1 and 2 are monotonically decreasing functions of increasing frequency. A consequence of this observation is that the data do not support a model of any periodic motions of the protein structure. That is, if putative low-frequency breathing motions were periodic, there would be a peak in the relaxation dispersion profile. None is observed; therefore, all motions detected by the MRD experiment are stochastic.
The successful description of these data rests on the fundamental theoretical assumptions about the effective dimensionality of the system and the consequences for the vibrational distribution of states. The term vibrational is used for convenience; the MRD experiments show clearly that all dynamics sampled are stochastic. The assumption that σ(ω) is described by Eq. 1 with ds of 4/3 is strongly supported by these MRD data. The generality of this value for linear disordered systems has been discussed by Orbach and co-workers (30,31). If this description was wrong, Eqs. 3a and 3b would fail to describe the measurements by many orders-of-magnitude (22). Thus, the effective dimensionality that describes the critical dynamics of the protein as sensed by the proton spins throughout the molecule is far closer to 1 than 3 in the frequency range studied.
Fig. 3 shows that the one-dimensional character of the polypeptide chain in the folded protein increases the low-frequency mode density in the protein by ∼18 orders of magnitude compared with the uniform three-dimensional crystal lattice, which is not a fruitful model for the protein in the frequency range studied here. We note that as the frequency increases toward Ω, the effects of dimensionality are eliminated and at the highest frequencies and shortest distances, the system will appear three-dimensional. Indeed, simulations of high-frequency dynamics in proteins suggest that the three-dimensional approaches are appropriate (32–34). This dramatic increase has important consequences for the magnetic field dependence of image contrast in MRI experiments (19), but the biophysical implications are general. Although the protein clearly has a three-dimensional structure, the strong connectivity is that of a polypeptide chain. The interactions that lead to the higher order structures or the folded structure of the protein are very weak compared with the covalent connectivity of the primary chain. The propagation of the structural disturbance is then primarily along the covalent connections, which are more than an order-of-magnitude stronger than the interactions between side chains or even hydrogen-bond connections between different portions of the chain. The character of the model is not that we ignore the motions that appear in the side chains. Indeed, most of the protons that we detect in the experiment are located on side-chain carbon atoms. Rather, the essence of the model is that the side-chain motions follow the structural disturbances propagating along the main chain in these low-frequency regimes. That is, the propagation is approximately one-dimensional, not the resulting motions of the protons detected. We also note the significant distinction between the total cohesive energy of the folded protein that depends strongly on the integrated contribution of the relatively weak interactions involving side chains and how a structural disturbance propagates through the structure, which is primarily along the stiff connections. As pointed out by Orbach, in a different context (31), the one-dimensional character of the stiff connections in chain molecules effectively confines structural fluctuations and modifies energy flow in the system that affects such fundamental characterizations as the heat capacity. Finally, these experiments show that the power spectrum for the protein noise is not characterized as “white” or by an exponentially decaying time-correlation function common to the case of aqueous solutions, but rather by the power law of Eq. 3. In consequence, fluctuations are much more prevalent in the frequency range associated uniquely with protein function, as shown unambiguously by the data in Figs. 1 and 2.
Frequency dependences of force constants and mean-square displacements in coarse-grained fractal proteins
Equation 2 reveals an important argument of our theoretical model that considers a process of overdamping of vibrational modes of frequency ω on a region of size 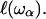 On random strongly disordered fractals, this corresponds to the strong localization model where
On random strongly disordered fractals, this corresponds to the strong localization model where 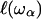 is defined as the localization length. As the fractal is denser at the small length scales, it is plausible that its elastic constants
is defined as the localization length. As the fractal is denser at the small length scales, it is plausible that its elastic constants 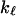 will also become scale-dependent. In consequence, it will deform in a non-affine way under external stresses. If we coarse-grain the fractal protein by collapsing all portions of size
will also become scale-dependent. In consequence, it will deform in a non-affine way under external stresses. If we coarse-grain the fractal protein by collapsing all portions of size 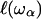 to points and construct a new network on this scale, this will eliminate all modes with frequency ω > ωα and one can ascribe a mass
to points and construct a new network on this scale, this will eliminate all modes with frequency ω > ωα and one can ascribe a mass 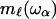 to this point and express the frequency dependence of the elastic constant
to this point and express the frequency dependence of the elastic constant 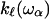 relevant at this length scale as
relevant at this length scale as
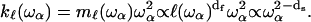 |
(4) |
To estimate the strain, we can estimate the frequency dependence of the mean-square displacement 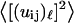 due to the “vibrations” on the size
due to the “vibrations” on the size 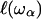 as
as
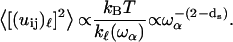 |
(5) |
The frequency dependence of such mean-square displacement is thus a power law that becomes 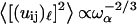 when substituting ds = 4/3 into Eq. 5. This dependence is very close to the one calculated by Doruker and co-workers for a coarse-grained anisotropic network model (35). In other words, this power law proves the reality of the density of vibrational states given in Eq. 1.
when substituting ds = 4/3 into Eq. 5. This dependence is very close to the one calculated by Doruker and co-workers for a coarse-grained anisotropic network model (35). In other words, this power law proves the reality of the density of vibrational states given in Eq. 1.
Connections between MRD relaxation and force constants or mean-square displacement data
To relate the MRD data to more conventional data concerned with dynamics of proteins, it is tempting to connect the frequency dependence of Rp(ω0) given in Eq. 3 with the frequency dependence of the force constants 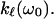 A direct comparison of the power laws given in Eqs. 3a and 4 thus leads to
A direct comparison of the power laws given in Eqs. 3a and 4 thus leads to
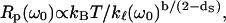 |
(6) |
where b is given into Eq. 3b. Finally, substituting Eq. 5 into Eq. 6 permits comparison of the frequency dependence of Rp(ω0), which we measured with the frequency dependence of the mean-square displacement that is calculated or measured by other techniques:
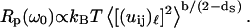 |
(7) |
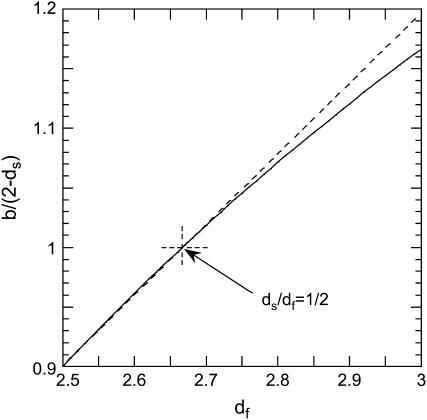
This relation shows that the frequency-dependence Rp(ω0), which we probe with MRD, may be related to that for the mean-square displacements. We show, in Fig. 5, that the relation between these two components is non-affine where the exponent b/(2 − ds) varies between 0.9 and 1.2 in the range of 2.5 ≤ df ≤ 3. In the case of a fully hydrated protein for which one has 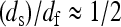 and b ≈ 2 − ds, Eq. 7 simplifies
and b ≈ 2 − ds, Eq. 7 simplifies 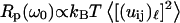 and Rp(ω0) becomes proportional (and not equal) to the frequency dependence of the mean-square displacements. The only difference is that we probe, with the MRD measurements, very much lower frequencies than those sampled by most other spectroscopic techniques. Although the present theory does not yield a precise value for the mean-square displacement, we believe that this comparison is important and gives more physical insight into the real dynamics probed by the MRD experiments.
and Rp(ω0) becomes proportional (and not equal) to the frequency dependence of the mean-square displacements. The only difference is that we probe, with the MRD measurements, very much lower frequencies than those sampled by most other spectroscopic techniques. Although the present theory does not yield a precise value for the mean-square displacement, we believe that this comparison is important and gives more physical insight into the real dynamics probed by the MRD experiments.
FIGURE 5.
The computed variation of the exponent of the mean-square displacement of Eq. 7 versus the fractal dimension, df, is shown as a solid line. The exponent is 1 for dS/df = 1/2. The dashed line is a guide for the eye and indicates a linear dependence.
CONCLUSION
We have presented proton MRD experiments from 10 kHz to 20 MHz of more or less hydrated proteins and proteins confined in gel by cross-linking. These MRD experiments sense the very-low-frequency stochastic motions of the protein that modulate the proton-proton dipolar couplings in the structure.
The interpretation of the data has been made through an extension to disordered protein systems of the well-known quantum description of a direct spin-lattice relaxation process coming from acoustical lattice vibrations (phonons) in crystals. For a direct spin-lattice relaxation process only a first-order expansion of the time-dependent spatial part of the proton dipole-dipole interaction between spins is needed. This supposes that the spin displacement vectors, expressed in a normal mode coordinate system, always stay an order-of-magnitude smaller than the equilibrium interspin vectors. Such a direct spin-phonon process in a disordered solid accounts quantitatively for experiments and depends on the dynamical distribution of vibrational states, the localization of the disturbances along and transverse to the peptide chains, and the spatial distribution of protons in the protein structure. In the very-low-frequency range explored, the localization of the disturbance can extend over the whole protein.
We have shown through scaling relations that calculated MRD frequency behavior of dry and hydrated protein is related to the frequency behavior of force constants and mean-square displacements of the detected protons and is similar in character to characterizations of protein dynamics at much higher frequency ranges. We have also shown that the fractal dimensionality of the proton distribution in space, which is a very crude characterization of the protein structure, changes continuously with hydration from the dry to fully hydrated state.
Last, it is shown that the dimensionality of the disturbance propagation is reduced from 3 to nearly 1, and the strong connectivity along the polypeptide chain dramatically increases the density of stochastic motions in the low-frequency regime, from 10 kHz to 20 MHz. A consequence of the reduction of the effective dimensionality for the disturbance propagation in the low-frequency region sampled by the present experiments is a large increase in the density of low-frequency modes. This permits the protein to sample functionally critical conformations in the frequency range that is most relevant for enzymatically critical fluctuations, much more often than would be the case for a uniformly connected three-dimensional solid.
Acknowledgments
This work was supported by the National Institutes of Health, The University of Virginia, and the Centre National de la Recherche Scientifique, France.
References
- 1.Daniel, R. M., R. V. Dunn, J. L. Finney, and J. C. Smith. 2003. The role of dynamics in enzyme activity. Annu. Rev. Biophys. Biomol. Struct. 32:69–92. [DOI] [PubMed] [Google Scholar]
- 2.Frauenfelder, H., and B. McMahon. 1998. Dynamics and function of proteins: the search for general concepts. Proc. Natl. Acad. Sci. USA. 95:4795–4797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Frauenfelder, H., B. H. McMahon, R. H. Austin, K. Chu, and J. T. Groves. 2001. The role of structure, energy landscape, dynamics, and allostery in the enzymatic function of myoglobin. Proc. Natl. Acad. Sci. USA. 98:2370–2374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Reat, V., H. Patzelt, M. Ferrand, C. Pfister, D. Oesterhelt, and G. Zaccai. 1998. Dynamics of different functional parts of bacteriorhodopsin H-2H labeling and neutron scattering. Proc. Natl. Acad. Sci. USA. 95:4970–4975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wand, A. J. 2001. Dynamic activation of protein function: a view emerging from NMR spectroscopy. Nat. Struct. Biol. 8:926–931. [DOI] [PubMed] [Google Scholar]
- 6.Brooks, B., and M. Karplus. 1983. Harmonic dynamics of proteins: normal modes and fluctuations in bovine pancreatic trypsin inhibitor. Proc. Natl. Acad. Sci. USA. 80:6571–6575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Go, N., T. Noguti, and T. Nishikawa. 1983. Dynamics of small globular protein in terms of low-frequency vibrational modes. Proc. Natl. Acad. Sci. USA. 80:3696–3700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Korzhnev, D. M., X. Salvatella, M. Vendruscolo, A. A. Di Nardo, A. R. Davidson, C. M. Dobson, and L. E. Kay. 2004. Low-populated folding intermediates of Fyn SH3 characterized by relaxation dispersion NMR. Nature. 430:586–590. [DOI] [PubMed] [Google Scholar]
- 9.Halle, B., V. P. Denisov, and K. Venu. 1999. Multinuclear relaxation dispersion studies of protein hydration. In Biological Magnetic Resonance. N.R. Krishna and L.J. Berliner, editors. Kluwer Academic/Plenum, New York. 419–484.
- 10.Kimmich, R., and E. Anoardo. 2004. Field-cycling NMR relaxometry. Prog. Nucl. Magn. Reson. Spectrosc. 44:257–320. [DOI] [PubMed] [Google Scholar]
- 11.Noack, F. 1986. NMR field-cycling spectroscopy: principles and applications. Prog. Nucl. Magn. Reson. Spectrosc. 18:171–276. [Google Scholar]
- 12.Victor, K., A. Van-Quynh, and R. G. Bryant. 2005. High frequency dynamics in hemoglobin measured by magnetic relaxation dispersion. Biophys. J. 88:443–454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shirley, W. M., and R. G. Bryant. 1982. Proton-nuclear spin relaxation and molecular dynamics in the lysozyme-water system. J. Am. Chem. Soc. 104:2910–2918. [Google Scholar]
- 14.Lester, C. C., and R. G. Bryant. 1991. Water-proton nuclear magnetic relaxation in heterogeneous systems: hydrated lysozyme results. Magn. Reson. Med. 22:143–153. [DOI] [PubMed] [Google Scholar]
- 15.Henkelman, R. M., X. Huang, Q. S. Xiang, G. J. Stanisz, S. D. Swanson, and M. J. Bronskill. 1993. Quantitative interpretation of magnetization transfer. Magn. Reson. Med. 29:759–766. [DOI] [PubMed] [Google Scholar]
- 16.Bryant, R. G., D. Mendelson, and C. C. Lester. 1991. The magnetic field dependence of protein-protein spin relaxation in tissues. Magn. Reson. Med. 21:117–126. [DOI] [PubMed] [Google Scholar]
- 17.Korb, J. P., A. Van-Quynh, and R. G. Bryant. 2001. Proton spin relaxation induced by localized spin-dynamical coupling in proteins. Chem. Phys. Lett. 339:77–82. [Google Scholar]
- 18.Korb, J. P., and R. G. Bryant. 2001. The physical basis for the magnetic field dependence of proton spin-lattice relaxation rates in proteins. J. Chem. Phys. 115:10964–10974. [Google Scholar]
- 19.Korb, J. P., and R. G. Bryant. 2002. Magnetic field dependence of proton spin-lattice relaxation times. Magn. Reson. Med. 48:21–26. [DOI] [PubMed] [Google Scholar]
- 20.Korb, J. P., and R. G. Bryant. 2004. Magnetic field dependence of proton spin-lattice relaxation of confined proteins. C. R. Phys. 5:349–357. [Google Scholar]
- 21.Korb, J. P., A. Van-Quynh, and R. G. Bryant. 2001. Low-frequency localized spin-dynamical coupling in proteins. C. R. Acad. Sci. IIC. 4:833–837. [Google Scholar]
- 22.Abragam, A. 1961. The Principles of Nuclear Magnetism, Chapt. IX, Sect. 4c. Oxford University Press, Oxford, UK.
- 23.Winter, F., and R. Kimmich. 1985. 14N-1H and 2H-1H cross-relaxation in hydrated proteins. Biophys. J. 48:331–335. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
24.Kimmich, R., and F. Winter. 1985. Double-diffusive fluctuations and the
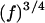 law of proton spin-lattice relaxation in biopolymers. Prog. Colloid Polym. Sci. 71:66–70. [Google Scholar]
law of proton spin-lattice relaxation in biopolymers. Prog. Colloid Polym. Sci. 71:66–70. [Google Scholar] - 25.Alexander, S., and R. Orbach. 1982. Density of states on fractals: fractons. J. Physique Lett. 43:L625–L631. [Google Scholar]
- 26.Courtens, E., R. Vacher, J. Pelous, and T. Woigner. 1988. Observations of fractons in silica aerogels. Europhys. Lett. 6:245. [Google Scholar]
- 27.Stapleton, H. J., J. P. Allen, C. P. Flynn, D. G. Stinson, and S. R. Kurtz. 1980. Fractal form of proteins. Phys. Rev. Lett. 45:1456–1459. [Google Scholar]
- 28.Allen, J. P., J. T. Colvin, D. G. Stinson, C. P. Flynn, and H. J. Stapleton. 1982. Protein conformation from electron spin relaxation data. Biophys. J. 38:299–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Miyazawa, T., T. Shimanouchi, and S. Mizushima. 1958. Normal vibrations of N-methyl acetamide. J. Chem. Phys. 29:611–616. [Google Scholar]
- 30.Aharony, A., S. Alexander, O. Entin-Wohlman, and R. Orbach. 1987. Scattering of fractons, the Ioffe-Regel criterion, and the 4/3 conjecture. Phys. Rev. Lett. 58:132–135. [DOI] [PubMed] [Google Scholar]
- 31.Orbach, R. 1986. Dynamics of fractal networks. Science. 231:814–819. [DOI] [PubMed] [Google Scholar]
- 32.Bahar, I., B. Erman, R. L. Jernigan, A. R. Atilgan, and D. G. Covell. 1999. Collective motions in HIV-1 reverse transcriptase: examination of flexibility and enzyme function. J. Mol. Biol. 285:1023–1037. [DOI] [PubMed] [Google Scholar]
- 33.Haliloglu, T., I. Bahar, and B. Erman. 1997. Gaussian dynamics of folded proteins. Phys. Rev. Lett. 79:3090–3093. [Google Scholar]
- 34.Bahar, I., A. R. Atilgan, and B. Erman. 1997. Direct evaluation of thermal fluctuations in proteins using a single parameter harmonic potential. Fold. Des. 2:173–181. [DOI] [PubMed] [Google Scholar]
- 35.Doruker, P., R. L. Jernigan, and I. Bahar. 2002. Dynamics of large proteins through hierarchical levels of coarse-grained structures. J. Comput. Chem. 23:119–127. [DOI] [PubMed] [Google Scholar]