Abstract
The opening of basepairs plays a key role in DNA replication and transcription, and in the action of DNA repair and modification enzymes. In this article, we have used proton exchange to define the energetics of the pathways for basepair opening in two DNA 17-mer duplexes. The rates of exchange of imino protons with solvent protons were measured by NMR spectroscopy for each DNA duplex, as a function of the concentration of exchange catalyst and of temperature. The measurements provided the rates and the equilibrium constants of the opening reactions for individual basepairs at different temperatures. These temperature dependences were used to calculate the enthalpies and the free energies of the barrier to opening and of the open state for each basepair. The results reveal the existence of three distinct patterns of enthalpy changes in the opening reactions. The patterns differ from each other in the location of the kinetic opening barrier relative to the open state. Neighboring bases, which are one or more positions removed from the opening basepair, influence the enthalpic pattern of the opening pathway. The free energies of the opening barriers are found to be linearly related to the free energies of the open state. This correlation is analyzed in terms of rate-equilibrium free energy relationships previously observed in other systems, and suggests that the transition state in the opening reaction is closer to the native closed state of the basepair than to its open state.
INTRODUCTION
Opening of basepairs in DNA is a structural fluctuation necessary for the biological functioning of the molecule. The double helix must open and unwind in DNA replication and transcription, such that the sequence of bases can be copied into a new DNA molecule or into mRNA. The opening (or flipping) of basepairs is also necessary for the chemical modification of DNA bases and for the repair of damaged ones (1). For example, DNA methylation by methyltransferases requires that the target base be flipped out of the double helix (1). Similarly, repair of base lesions by DNA glycosylases requires extrusion of the damaged base from the helical stack and its move into the active site of the enzyme (2). Recently, it has been proposed that basepair opening processes could provide a mechanism for recognition of specific base sequences by DNA modification and repair enzymes (1,3,4). In these proposals, the sequence-specific recognition is thought to be coupled to the mechanism for flipping out the base. The target base is selected as having an energetic propensity to open, or to be opened by the enzyme, which is higher than that of other bases. In view of these proposals and of widely spread roles of basepair opening reactions in the biological function of DNA, the molecular and energetic mechanisms by which DNA basepairs open have been the objects of sustained interest.
The current understanding of the molecular pathways for basepair opening in DNA and their energetics is based on molecular dynamics simulations. These studies have revealed the detailed conformational changes of the basepair and its neighbors during opening (5–7), the existence of an energetic coupling between DNA bending and basepair opening (8,9), energetic preferences for opening into the major or the minor groove (10,11), and the influence of enzymes upon the basepair opening propensities (4,12). However, experimental evidence on the nature and the energetics of the opening pathways is scarce. This article attempts to fill this gap by an experimental investigation using NMR spectroscopy and imino proton exchange. NMR measurements of imino proton exchange have been previously used to obtain the rates of opening of basepairs in a variety of DNA duplexes (13,14). The results have demonstrated that the opening rates are strongly dependent on the DNA conformation, e.g., B- versus Z-form (15), and base sequence (16–20). The enthalpy changes in basepair opening have been reported for several DNA dodecamers by this laboratory (17,18,21). This work extends these previous investigations by a study of the two DNA molecules shown in Fig. 1. Each DNA contains 17 basepairs. The sequences of the central 13 bases are the same as those in two sites from the origin of replication of bacterial chromosomes (22). The sites are generally abbreviated according to their location on the chromosome as L (left) and M (middle). The same abbreviation is being used henceforth for the two DNA duplexes investigated. This study provides a complete characterization of the enthalpy and free energy changes that are associated with the activation barriers and the equilibria in opening of selected basepairs in these two DNA 17-mers. The results, together with those previously reported for DNA dodecamers, provide new insights into the nature of the basepair opening pathways and their energetics.
FIGURE 1.
The base sequences of the two DNA duplexes investigated. The opening reactions of the basepairs shown in boldface have been characterized in this article.
MATERIALS AND METHODS
DNA samples
Each strand of the DNA molecules of interest was synthesized on a DNA synthesizer (Applied Biosystems, Foster City, CA) using solid-support phosphoramidite chemistry. The DNA was purified by reverse-phase HPLC on a PRP-1 column (Hamilton, Reno, NV) as described (23). The counterions were replaced with Na+ ions by repeated centrifugation through Centricon YM-3 tubes (Amicon, Bedford, MA) using 0.5 M NaCl. The DNA was desalted by repeated centrifugation against water. Each DNA duplex was annealed by equilibrating the corresponding two oligonucleotides in a water bath at 80°C for 30 min, followed by slow cooling down. The DNA concentrations were determined using extinction coefficients calculated as described by Cantor and co-workers (24): 336 OD units/μmole for duplex L and 329 OD units/μmole for duplex M. Accordingly, the DNA concentrations in the samples used for NMR were 1.7 mM for duplex L and 2.0 mM for duplex M, in 0.1 M NaCl with 1 mM EDTA at pH between 8 and 9. The samples also contained 1 mM triethanolamine, which was used to determine the pH of the sample directly inside the NMR tube, at each temperature of interest, as we have described (20). For proton exchange measurements, increasing concentrations of ammonia were obtained by adding to the DNA sample small aliquots of stock ammonia solutions (0.5–5 M) in 0.1 M NaCl with 1 mM EDTA at pH 8.5. The final concentration of ammonia in the sample was measured by 14N NMR using a Varian VXR-400 NMR spectrometer operating at 9.4 T, as we have described (20). The concentration of ammonia base at each temperature was calculated from the total ammonia concentration (C0) and the pH as
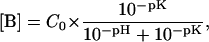 |
(1) |
where the pK value of ammonia at each temperature was used (25).
NMR experiments
The NMR experiments were performed on a Varian INOVA 500 spectrometer operating at 11.75 T. One-dimensional NMR spectra were obtained using the Jump-and-Return pulse sequence (26). The proton exchange rates were measured by transfer of magnetization from water, as described previously (14,27). Twenty-five values of the exchange delay in the range from 2 to 600 ms were used in each experiment, and the observation was with the Jump-and-Return pulse sequence.
Imino proton exchange in DNA
Characterization of basepair opening processes in DNA relies upon the exchange properties of imino protons, i.e., N1H in guanines and N3H in thymines. The current model for exchange of these protons is a two-state model in which the base (or the basepair) undergoes a local conformational change from a closed to an open state. The exchange occurs from the open state. This state is exchange competent because the imino proton is accessible to proton acceptors present in solution, and its hydrogen bond is transiently broken (28,29). The exchange rate observed experimentally depends upon the concentration of proton acceptor B as (28)
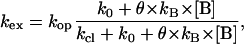 |
(2) |
where kop and kcl are the rates of opening and closing of the corresponding basepair; k0 is the rate of exchange of the imino proton from the open state of the basepair in the absence of the proton acceptor; kB is the rate constant for transfer of the proton to the acceptor in isolated nucleotides; and θ is a factor that accounts for differences in the rate of proton transfer between isolated nucleotides and open DNA basepairs, e.g., restricted accessibility of the acceptor to the imino proton in the open base. As Eq. 2 shows, the limiting value of the exchange rate at high concentrations of proton acceptor (i.e., k0 + θ × kB × [B] ≫ kcl or EX1 regime of exchange) is the rate of opening of the corresponding basepair.
In this work, we have used ammonia base as the proton acceptor in imino proton exchange. Previous studies have shown that, due to its small size and lack of charge, ammonia is the proton acceptor of choice for investigation of basepair opening in DNA (13,29). The rates of opening and closing of each basepair were obtained by fitting the experimentally measured exchange rate as a function of the concentration of ammonia base to Eq. 2. The rate constants kB for transfer of the imino proton from thymine or guanine to ammonia base have been calculated previously as a function of temperature (17). The results have shown that the rate constants are nearly temperature-independent, in agreement with experiments on isolated mononucleotides (30). For example, for the temperature range used in this work (namely, 10–35°C), they range from 4.0 × 108 to 4.3 × 108 M−1 s−1 for thymine, and from 8.8 × 108 to 1.2 × 109 M−1 s−1 for guanine (17). The factor θ was assumed to have a value of 1 and to be independent of temperature (29). The equilibrium constant for the opening reaction was calculated from the opening and closing rates as
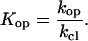 |
(3) |
RESULTS
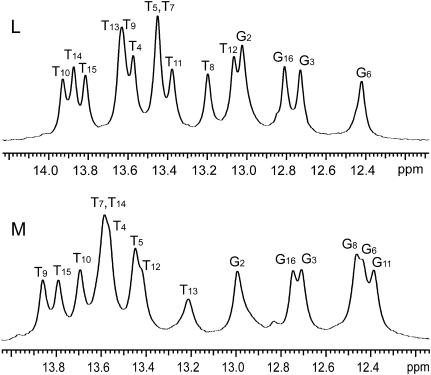
The NMR resonances of imino protons (i.e., N1H in guanines and N3H in thymines) in the two DNA 17-mer investigated are shown in Fig. 2. Their assignments to individual protons were obtained previously by our laboratory using 1H-1H NOESY experiments. These NOESY experiments have also indicated that the conformation of the two DNA duplexes is in the B-form family (31).
FIGURE 2.
NMR resonances of imino protons of the two DNA duplexes investigated in 0.01 M phosphate buffer containing 0.1 M NaCl, and 1 mM EDTA, in 90%H2O/10%D2O at pH 7.5 and at 20°C.
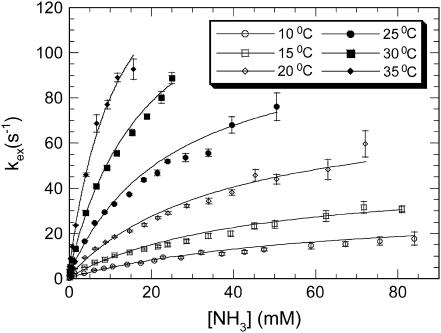
The rates of exchange of imino protons with solvent protons were measured as a function of the concentration of ammonia base at six temperatures in the range from 10 to 35°C. The dependence of the exchange rates on ammonia-base concentration is illustrated in Fig. 3 for the imino proton of AT8 basepair in duplex L. The figure also shows the fits of the exchange rate as function of ammonia base concentration to Eq. 2. These fits were used to obtain the opening rate kop and the opening equilibrium constant Kop for individual basepairs (Materials and Methods). The values of kop and Kop in the two DNA duplexes are given in Tables S1–S4 in Supplementary Material. The values at 20°C have also been reported in a recent publication from our laboratory (32). For GC/CG basepairs at 20°C, most opening rates are ∼20 s−1, whereas the opening equilibrium constants are ∼(1–2) × 10−7. For AT/TA basepairs, the opening rates range from 16 to 240 s−1, and the equilibrium constants range from 28 × 10−7 to 340 × 10−7. These ranges are typical for the opening rates and equilibrium constants previously observed in DNA duplexes of various base sequences (13,18,20,29,33).
FIGURE 3.
Dependence of the exchange rate of T8 imino proton in duplex L on ammonia-base concentration at the temperatures investigated. The curves represent nonlinear least-squares fits to Eq. 2.
Characterization of the pathways for basepair opening and their energetics requires determination of both the rates and the equilibrium constants of the opening reactions as a function of temperature. In turn, this requires the full definition of the dependence of the exchange rates on ammonia concentration (Eq. 2) at each temperature. We were able to obtain the complete dependence of the exchange rates on ammonia concentration for 14 basepairs of the two duplexes for at least four temperatures (Tables S1–S4 in Supplementary Material). These basepairs are indicated in boldface in Fig. 1. For the other basepairs, the full dependence of the exchange rates on ammonia concentration could not be defined, for two reasons. First, at some temperatures and/or ammonia base concentrations, the imino proton resonances of the corresponding basepairs are not resolved in the NMR spectra (for example, resonances from T9 and T13, and resonances from T5 and T7 in duplex L; Fig. 2). Second, for some imino protons, the exchange rates increase rapidly upon raising the temperature and/or the ammonia concentration (for example, T13 in duplex M and the guanine imino protons from the two terminal GC/CG basepairs in both duplexes; data not shown). At the highest temperatures and ammonia concentrations of interest, the exchange rates become too fast to be measured accurately in experiments of transfer of magnetization from water (kex > ∼100 s−1; for example, T8 imino proton in duplex L at 35°C; Fig. 3). Thus, the opening rates for these basepairs could not be measured.
The energetic parameters of the opening reactions for the basepairs shown in boldface in Fig. 1 were obtained from the temperature dependence of the opening rates and equilibrium constants, kop and Kop, respectively. The temperature dependence of the opening rates was analyzed on the basis of the transition-state theory using the equation (34)
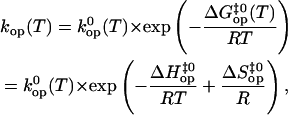 |
(4) |
where 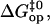
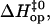 and
and 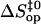 are the free energy, enthalpy, and entropy changes in the activation process; T is the absolute temperature; R is the universal gas constant; and
are the free energy, enthalpy, and entropy changes in the activation process; T is the absolute temperature; R is the universal gas constant; and 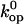 is the pre-exponential factor defining the maximum rate of the reaction in the absence of an activation barrier. The pre-exponential factor was assumed to be that of Eyring's theory (34),
is the pre-exponential factor defining the maximum rate of the reaction in the absence of an activation barrier. The pre-exponential factor was assumed to be that of Eyring's theory (34),
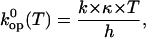 |
(5) |
where k is Boltzmann's constant, h is Planck's constant, and κ is the transmission coefficient (assumed to be 1). To insure that the values of the energetic parameters are free of statistical compensation effects, we have used the M-linear regression algorithm introduced by Krug and co-workers (35). In this algorithm, Eq. 4 is modified as
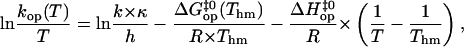 |
(6) |
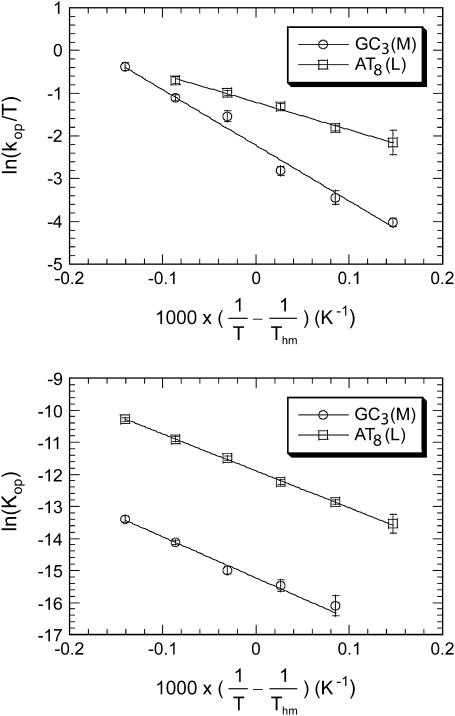
where Thm is the harmonic mean of the experimental temperatures Ti (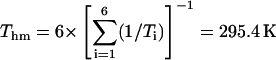 ). The opening rates kop were fitted as a function of
). The opening rates kop were fitted as a function of 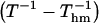 to Eq. 6. Representative examples of these fits are shown in Fig. 4, and all the fits are reported in Figs. S1 and S2 in Supplementary Material. The values of the activation parameters
to Eq. 6. Representative examples of these fits are shown in Fig. 4, and all the fits are reported in Figs. S1 and S2 in Supplementary Material. The values of the activation parameters 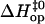 and
and 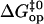 obtained from these fits are summarized in Tables 1 and 2, respectively.
obtained from these fits are summarized in Tables 1 and 2, respectively.
FIGURE 4.
Illustration of the dependence of the opening rates (upper panel) and equilibrium constants for opening (lower panel) on temperature. Circles represent results for GC3 in the M duplex, and squares represent results for AT8 in the L duplex. The lines are linear fits to Eq. 6 (upper panel) and Eq. 8 (lower panel).
TABLE 1.
Enthalpy changes (kcal/mol) in basepair opening reactions in the two DNA duplexes investigated
| L Duplex
|
M Duplex
|
|||||
|---|---|---|---|---|---|---|
| Position | Basepair | 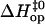 |
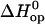 |
Basepair | 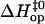 |
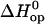 |
| 3 | GC | 25 ± 2 | 25 ± 2 | GC | 26.1 ± 0.8 | 26 ± 2 |
| 4 | AT | 13 ± 3 | 19.3 ± 0.3 | |||
| 5 | ||||||
| 6 | CG | 21 ± 1 | 12 ± 1 | |||
| 7 | ||||||
| 8 | AT | 13 ± 1 | 22.9 ± 0.7 | |||
| 9 | TA | 17 ± 1 | 16.7 ± 0.4 | |||
| 10 | TA | 29.1 ± 0.6 | 24.2 ± 0.9 | TA | 8 ± 1 | 14.0 ± 0.8 |
| 11 | TA | 24 ± 1 | 19.2 ± 0.2 | CG | 22 ± 2 | 10 ± 2 |
| 12 | AT | 21.6 ± 0.6 | 22.9 ± 0.8 | |||
| 13 | ||||||
| 14 | TA | 28.4 ± 0.8 | 24 ± 1 | |||
| 15 | TA | 29 ± 1 | 24.0 ± 0.1 | TA | 18 ± 3 | 18 ± 4 |
TABLE 2.
Free energy changes (kcal/mol) in basepair opening reactions in the two DNA duplexes investigated at Thm = 295.4 K
| L Duplex
|
M Duplex
|
|||||
|---|---|---|---|---|---|---|
| Position | Basepair | 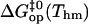 |
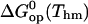 |
Basepair | 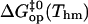 |
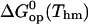 |
| 3 | GC | 15.15 ± 0.04 | 8.81 ± 0.05 | GC | 15.24 ± 0.02 | 8.94 ± 0.05 |
| 4 | AT | 14.69 ± 0.04 | 7.08 ± 0.01 | |||
| 5 | ||||||
| 6 | CG | 15.28 ± 0.03 | 9.12 ± 0.04 | |||
| 7 | ||||||
| 8 | AT | 14.65 ± 0.02 | 6.98 ± 0.02 | |||
| 9 | TA | 14.27 ± 0.03 | 6.64 ± 0.01 | |||
| 10 | TA | 15.40 ± 0.01 | 7.31 ± 0.01 | TA | 14.13 ± 0.05 | 6.49 ± 0.03 |
| 11 | TA | 14.84 ± 0.02 | 6.58 ± 0.01 | CG | 15.33 ± 0.06 | 8.94 ± 0.06 |
| 12 | AT | 15.02 ± 0.01 | 7.13 ± 0.01 | |||
| 13 | ||||||
| 14 | TA | 15.08 ± 0.02 | 7.05 ± 0.02 | |||
| 15 | TA | 14.18 ± 0.03 | 6.24 ± 0.01 | TA | 13.97 ± 0.06 | 5.86 ± 0.09 |
The temperature dependence of the opening equilibrium constants Kop was analyzed on the basis of van't Hoff's equation,
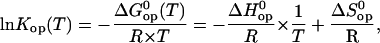 |
(7) |
where 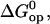
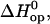 and
and 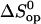 are the standard free energy, enthalpy, and entropy changes for the opening equilibria. The experimental Kop values were fitted to the following modified van't Hoff equation, according to the M-linear regression algorithm (35):
are the standard free energy, enthalpy, and entropy changes for the opening equilibria. The experimental Kop values were fitted to the following modified van't Hoff equation, according to the M-linear regression algorithm (35):
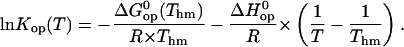 |
(8) |
Representative examples for these fits are shown in Fig. 4, and all the fits are reported in Figs. S3 and S4 in Supplementary Material. The values of 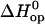 and
and 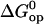 obtained from these fits are summarized in Tables 1 and 2.
obtained from these fits are summarized in Tables 1 and 2.
DISCUSSION
The results presented in Table 1 show that the enthalpy changes in basepair opening span large ranges of values. For the activation enthalpies the range is ∼20 kcal/mol, from 8 to 29 kcal/mol. Similarly, the enthalpy changes for the opening equilibria span ∼16 kcal/mol, from 10 to 26 kcal/mol. The values are not directly correlated with the nature of the basepair. For example, for GC/CG basepairs, the enthalpy changes in opening equilibria are ∼25 kcal/mol for GC3 in the two duplexes, and ∼12 kcal/mol for CG6 in duplex L and CG11 in duplex M. This finding suggests that the enthalpy changes are strongly influenced by the surrounding base sequence.
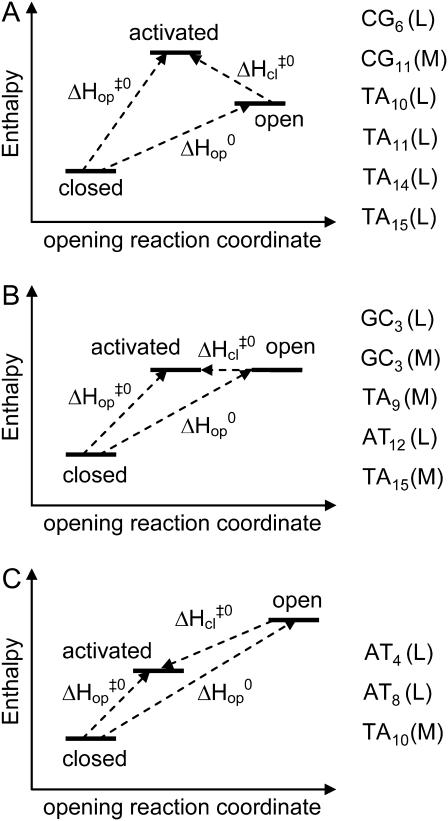
Closer analysis of the results presented in Table 1 reveals that the patterns of enthalpy changes along the opening pathways differ between various basepairs. For some basepairs, such as CG6, TA10, TA11, TA14, and TA15 in duplex L, and CG11 in duplex M, the enthalpy of the activated state is higher than that of the open state (Fig. 5 A). In contrast, for other basepairs, namely, AT4 and AT8 in duplex L and TA10 in duplex M, the enthalpy of the activated state is less than that of the open state (Fig. 5 C). Furthermore, for several basepairs, such as GC3 and AT12 in duplex L, and GC3, TA9, and TA15 in duplex M, the enthalpy of the open state does not differ significantly from that of the activated state (Fig. 5 B). These results clearly demonstrate that the pathways for basepair opening in DNA are not unique. They differ from each other in the relative magnitude of the activation and equilibrium enthalpy changes. These differences affect how the enthalpy of the open state compares with the enthalpy of the barrier to opening.
FIGURE 5.
Schematic representation of the patterns of enthalpy changes observed in this article.
The existence of different opening pathways has been previously inferred from molecular dynamics simulations of opening processes. Most studies to-date have calculated the free energy changes in the system as the base breaks away from its paired state and becomes accessible to solvent (4,6,7,11). The base sequences investigated consist of repeating dinucleotide motifs, which often are recognition sites for DNA C5-methyltransferases, e.g., d(GCGC) (4,6,7), or purine tracts, e.g., (dA)n or d(GA)n (10,11). Different free energy profiles were obtained for AT and GC basepairs in various surrounding sequences. These results support our finding that different pathways for basepair opening are accessible in DNA. A recent theoretical study has used transition-path sampling to describe the kinetic pathway for flipping of the terminal cytosine in the short DNA duplex d(CGC)/d(GCG) (36). The results identify the transition state as the state in which the Watson-Crick hydrogen bonds are broken and the stacking energies are comparable to the thermal energy. No changes in the interaction energies were observed in going from the transition to the fully open state. This behavior parallels the enthalpy changes that we observed for GC3 and AT12 in duplex L, and GC3, TA9, and TA15 in duplex M (Fig. 5 B).
Our present investigation does not allow us to describe the molecular mechanisms responsible for the different pathways of opening that we observed. Nevertheless, based on the molecular dynamics results discussed above, we may expect the opening pathway of a given basepair to be influenced by the nature and orientation of its nearest neighbors. This expectation is supported by our results for several basepairs. For example, the pathway for opening CG6 in duplex L is similar to that for opening CG11 in duplex M (i.e., 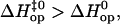 Fig. 5 and Table 1). These two basepairs have the same nearest-neighbor base context, i.e., 5′-AGA-3′/5′-TCT-3′. Similarly, TA10 and TA14 in duplex L are located in the sequence context 5′-TTT-3′/5′-AAA-3′, and for both,
Fig. 5 and Table 1). These two basepairs have the same nearest-neighbor base context, i.e., 5′-AGA-3′/5′-TCT-3′. Similarly, TA10 and TA14 in duplex L are located in the sequence context 5′-TTT-3′/5′-AAA-3′, and for both, 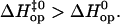 For other basepairs, however, the two nearest neighbors do not fully determine the pattern of enthalpy changes during opening. For example, AT8 and AT12 in duplex L are both located in the 5′-ATA-3′/5′-TAT-3′ context. Yet,
For other basepairs, however, the two nearest neighbors do not fully determine the pattern of enthalpy changes during opening. For example, AT8 and AT12 in duplex L are both located in the 5′-ATA-3′/5′-TAT-3′ context. Yet, 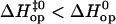 for AT8, and
for AT8, and 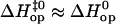 for AT12. Different pathways for opening are also observed for the TA basepairs in the 15th positions of the two duplexes, despite the fact that both basepairs are located in the context 5′-TTG-3′/5′-CAA-3′ (Fig. 5). These findings suggest that bases beyond the nearest neighbors can also influence the pattern of enthalpy changes during opening of a given basepair. A mechanism by which this could happen is revealed by results of computational studies (6,7). The results show that, after escaping from their paired states, the bases do not move away from the helix, on a pathway perpendicular to the helix axis. Instead, they turn out-of-plane and follow the directions of the grooves where they contact sites on the DNA, which are up to three positions removed from the open basepair. These contacts are close enough that hydrogen bonds, direct or water-mediated, can form between the open base and neighboring basepairs. Although short-lived, such contacts profoundly affect the energetic pattern of the opening pathway (6,7), as observed in this article.
for AT12. Different pathways for opening are also observed for the TA basepairs in the 15th positions of the two duplexes, despite the fact that both basepairs are located in the context 5′-TTG-3′/5′-CAA-3′ (Fig. 5). These findings suggest that bases beyond the nearest neighbors can also influence the pattern of enthalpy changes during opening of a given basepair. A mechanism by which this could happen is revealed by results of computational studies (6,7). The results show that, after escaping from their paired states, the bases do not move away from the helix, on a pathway perpendicular to the helix axis. Instead, they turn out-of-plane and follow the directions of the grooves where they contact sites on the DNA, which are up to three positions removed from the open basepair. These contacts are close enough that hydrogen bonds, direct or water-mediated, can form between the open base and neighboring basepairs. Although short-lived, such contacts profoundly affect the energetic pattern of the opening pathway (6,7), as observed in this article.
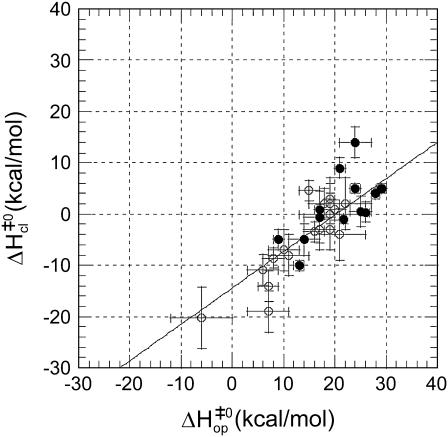
An alternative way to look at the different patterns of enthalpy changes observed in this work is to express the differences between the enthalpies of the opening barrier and those of the open state as activation enthalpies during the closing step:
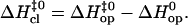 |
(9) |
In these terms, the three patterns of enthalpic changes shown in Fig. 5 correspond to 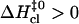 (Fig. 5 A),
(Fig. 5 A), 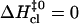 (Fig. 5 B), and
(Fig. 5 B), and 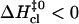 (Fig. 5 C). The closing activation enthalpies
(Fig. 5 C). The closing activation enthalpies 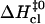 calculated based on Eq. 9 are plotted versus opening activation enthalpies
calculated based on Eq. 9 are plotted versus opening activation enthalpies 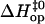 in Fig. 6. The figure also includes results previously obtained by our laboratory for the central six basepairs in the following DNA dodecamers: [5′-d(CGCAAATTTGCG)-3′]2 (21), [5′-d(CGCACATGTGCG)-3′]2 (18), [5′-d(CGCAGATCTGCG)-3′]2 (18), [5′-d(CGCGAATTCGCG)-3′]2 (17), and [5′-d(CGCGAATTTGCG)-3′]2 (17). The plot indicates the existence of a linear correlation between
in Fig. 6. The figure also includes results previously obtained by our laboratory for the central six basepairs in the following DNA dodecamers: [5′-d(CGCAAATTTGCG)-3′]2 (21), [5′-d(CGCACATGTGCG)-3′]2 (18), [5′-d(CGCAGATCTGCG)-3′]2 (18), [5′-d(CGCGAATTCGCG)-3′]2 (17), and [5′-d(CGCGAATTTGCG)-3′]2 (17). The plot indicates the existence of a linear correlation between 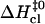 and
and 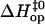 values. The correlation is such that, when the activation enthalpy for the opening step is ∼20 kcal/mol,
values. The correlation is such that, when the activation enthalpy for the opening step is ∼20 kcal/mol, 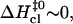 and no further enthalpy change occurs upon going from the activated to the open state (Fig. 5 B). When the opening activation enthalpy exceeds 20 kcal/mol, then
and no further enthalpy change occurs upon going from the activated to the open state (Fig. 5 B). When the opening activation enthalpy exceeds 20 kcal/mol, then 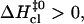 and the enthalpy of the open state of the basepair is less than that of the activated state (Fig. 5 A). In contrast, when the opening activation enthalpy is <20 kcal/mol, then
and the enthalpy of the open state of the basepair is less than that of the activated state (Fig. 5 A). In contrast, when the opening activation enthalpy is <20 kcal/mol, then 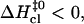 and a further increase in enthalpy occurs in going from the activated to the open state (Fig. 5 C). These observations suggest that the patterns of enthalpy changes observed experimentally are determined by the height of the enthalpy barrier to opening. As discussed above, the height of the barrier is, in turn, influenced by the neighboring bases, one or more positions away from the opening basepair.
and a further increase in enthalpy occurs in going from the activated to the open state (Fig. 5 C). These observations suggest that the patterns of enthalpy changes observed experimentally are determined by the height of the enthalpy barrier to opening. As discussed above, the height of the barrier is, in turn, influenced by the neighboring bases, one or more positions away from the opening basepair.
FIGURE 6.
Correlation between activation enthalpy changes in basepair opening (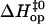 ) and in basepair closing (
) and in basepair closing (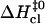 ). The results obtained in this work are shown with solid symbols. Previous results from our laboratory on several DNA dodecamers described in the text are shown with open symbols. The line represents a linear fit with the equation
). The results obtained in this work are shown with solid symbols. Previous results from our laboratory on several DNA dodecamers described in the text are shown with open symbols. The line represents a linear fit with the equation 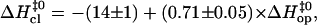 and a correlation coefficient of 0.84.
and a correlation coefficient of 0.84.
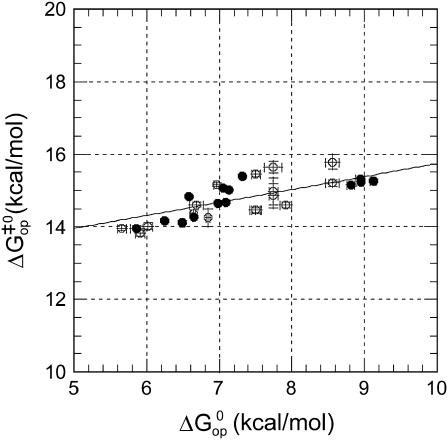
Further insight into the energetics of the pathways for basepair opening is provided by the free energy changes in the activation steps and in the opening equilibria, which are shown in Table 2. One notes that the ranges of values for these opening free energies are narrower than those for opening enthalpies, namely, ∼1.5 kcal/mol for 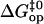 and ∼3.5 kcal/mol for
and ∼3.5 kcal/mol for 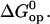 This is due to the presence of enthalpy-entropy compensation in the opening processes, as previously shown by our laboratory (18,20,21). The activation free energy changes
This is due to the presence of enthalpy-entropy compensation in the opening processes, as previously shown by our laboratory (18,20,21). The activation free energy changes  are plotted versus the equilibrium free energy changes
are plotted versus the equilibrium free energy changes 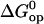 in Fig. 7. In addition to the DNA 17-mers investigated in this work, the figure also includes the corresponding free energy changes for several DNA dodecamers previously studied by our laboratory, namely, [5′-d(CGCAAATTTGCG)-3′]2 (21), [5′-d(CGCACATGTGCG)-3′]2 (18), [5′-d(CGCAGATCTGCG)-3′]2 (18), and [5′-d(CGCGAATTCGCG)-3′]2 (17). For these dodecamers, the free energy changes were calculated with Eqs. 4 and 7, using the reported kop and Kop values at 25°C. The plot reveals that the activation free energies
in Fig. 7. In addition to the DNA 17-mers investigated in this work, the figure also includes the corresponding free energy changes for several DNA dodecamers previously studied by our laboratory, namely, [5′-d(CGCAAATTTGCG)-3′]2 (21), [5′-d(CGCACATGTGCG)-3′]2 (18), [5′-d(CGCAGATCTGCG)-3′]2 (18), and [5′-d(CGCGAATTCGCG)-3′]2 (17). For these dodecamers, the free energy changes were calculated with Eqs. 4 and 7, using the reported kop and Kop values at 25°C. The plot reveals that the activation free energies  are linearly related to the equilibrium free energy changes
are linearly related to the equilibrium free energy changes 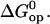 In considering this correlation, it should be noted that the
In considering this correlation, it should be noted that the 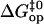 values calculated based on Eq. 6 are affected by uncertainties in the value(s) of the pre-exponential factor
values calculated based on Eq. 6 are affected by uncertainties in the value(s) of the pre-exponential factor 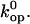 The pre-exponential factor used in our analysis (Eq. 5) is that of the original transition-state theory, and corresponds to the frequency of vibration of a single covalent bond (34). The opening of basepairs in DNA is certainly a more complex process, involving breakage of hydrogen bonds, perturbations of stacking interactions and of hydration, etc. Hence, one expects the pre-exponential factor for the opening reaction to be lower than the
The pre-exponential factor used in our analysis (Eq. 5) is that of the original transition-state theory, and corresponds to the frequency of vibration of a single covalent bond (34). The opening of basepairs in DNA is certainly a more complex process, involving breakage of hydrogen bonds, perturbations of stacking interactions and of hydration, etc. Hence, one expects the pre-exponential factor for the opening reaction to be lower than the 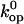 value that we assumed, and this would affect the calculated values of
value that we assumed, and this would affect the calculated values of 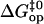 (Eq. 6). For example, a 10-fold decrease in
(Eq. 6). For example, a 10-fold decrease in 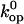 would lower the activation barrier
would lower the activation barrier 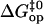 by 1.4 kcal/mol. Nevertheless, in the first approximation, we could assume that the deviations of pre-exponential factors for the basepairs investigated from the assumed value (Eq. 5) are comparable. In this case, the
by 1.4 kcal/mol. Nevertheless, in the first approximation, we could assume that the deviations of pre-exponential factors for the basepairs investigated from the assumed value (Eq. 5) are comparable. In this case, the 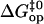 values would be affected at similar extents, and the ordinate intercept of the fitted line in Fig. 7 would be lower, but its slope would remain the same.
values would be affected at similar extents, and the ordinate intercept of the fitted line in Fig. 7 would be lower, but its slope would remain the same.
FIGURE 7.
Correlation between activation and equilibrium free-energy changes in basepair opening in the DNA duplexes investigated at 22°C (shown with solid symbols). The line represents a linear fit to the equation 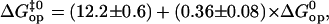 and a correlation coefficient of 0.8. Previous results from our laboratory on several DNA dodecamers described in the text shown with open symbols.
and a correlation coefficient of 0.8. Previous results from our laboratory on several DNA dodecamers described in the text shown with open symbols.
Linear correlations between activation and equilibrium free energies have been previously observed in a large variety of chemical and biochemical reactions (37,38). Leffler (39) first noted these linear correlations for changes in a chemical reaction induced by variations in structure (e.g., new substituents) or in the solvent. The changes in the activation free energy of the reaction are linearly related to the changes in the free energy difference between reactants and products. The slope α provides a description of the transition state: when α is close to 1, the transition state resembles the product, and when α is close to 0, the transition state resembles the reactant. These rate-equilibrium free energy relationships have been widely used to characterize transition states in biochemical reactions, including protein folding (38,40,41). By the same approach, we could use the results shown in Fig. 7 to infer about the transition state in basepair opening in DNA. The slope of 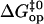 versus
versus 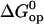 is α = 0.36 ± 0.08. This suggests that the properties of the transition state are intermediate between the properties of the closed state and those of the open state, and are likely to be closer to those of the native closed state.
is α = 0.36 ± 0.08. This suggests that the properties of the transition state are intermediate between the properties of the closed state and those of the open state, and are likely to be closer to those of the native closed state.
In summary, in this article we have shown that different pathways of basepair opening exist in DNA. The pathways differ from each other in how the enthalpies of the transition state compare with the enthalpies of the open state. This energetic variability is determined by the base sequence context of the opening basepair. Characterization of the conformational changes that occur in each pathway awaits future molecular dynamics studies of basepair opening processes in DNA of various sequences.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
Acknowledgments
This work was supported by a grant from the National Institutes of Health (No. GM65159).
References
- 1.Roberts, R. J., and X. Cheng. 1998. Base flipping. Annu. Rev. Biochem. 67:181–198. [DOI] [PubMed] [Google Scholar]
- 2.Fromme, J. C., A. Banerjee, and G. L. Verdine. 2004. DNA glycosylase recognition and catalysis. Curr. Opin. Struct. Biol. 14:43–49. [DOI] [PubMed] [Google Scholar]
- 3.Krosky, D. J., F. P. Schwarz, and J. T. Stivers. 2004. Linear free energy correlations for enzymatic base flipping: how do damaged basepairs facilitate specific recognition? Biochemistry. 43:4188–4195. [DOI] [PubMed] [Google Scholar]
- 4.Huang, N., and A. D. MacKerell, Jr. 2005. Specificity in protein-DNA interactions: energetic recognition by the (cytosine-5-)-methyltransferase from HhaI. J. Mol. Biol. 345:265–274. [DOI] [PubMed] [Google Scholar]
- 5.Giudice, E., P. Varnai, and R. Lavery. 2001. Energetic and conformational aspects of A:T basepair opening within the DNA double helix. Chem. Phys. Chem. 2:673–677. [DOI] [PubMed] [Google Scholar]
- 6.Banavali, N. K., and A. D. MacKerell, Jr. 2002. Free energy and structural pathways of base flipping in a DNA GCGC containing sequence. J. Mol. Biol. 319:141–160. [DOI] [PubMed] [Google Scholar]
- 7.Varnai, P., and R. Lavery. 2002. Base flipping in DNA: pathways and energetics studied with molecular dynamics simulations. J. Am. Chem. Soc. 124:7272–7273. [DOI] [PubMed] [Google Scholar]
- 8.Ramstein, J., and R. Lavery. 1988. Energetic coupling between DNA bending and basepair opening. Proc. Natl. Acad. Sci. USA. 85:7231–7235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fuxreiter, M., N. Luo, P. Jedlovszky, I. Simon, and R. Osman. 2002. Role of base flipping in specific recognition of damaged DNA by repair enzymes. J. Mol. Biol. 323:823–834. [DOI] [PubMed] [Google Scholar]
- 10.Giudice, E., and R. Lavery. 2003. Nucleic acid basepair dynamics: the impact of sequence and structure using free-energy calculations. J. Am. Chem. Soc. 125:4998–4999. [DOI] [PubMed] [Google Scholar]
- 11.Giudice, E., P. Varnai, and R. Lavery. 2003. Basepair opening within B-DNA: free energy pathways for GC and AT basepairs from umbrella sampling simulations. Nucleic Acids Res. 31:1434–1443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Huang, N., N. K. Banavali, and A. D. MacKerell, Jr. 2003. Protein-facilitated base flipping in DNA by cytosine-5-methyltransferase. Proc. Natl. Acad. Sci. USA. 100:68–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gueron, M., and J. L. Leroy. 1995. Studies of basepair kinetics by NMR measurement of proton exchange. Methods Enzymol. 261:383–413. [DOI] [PubMed] [Google Scholar]
- 14.Russu, I. M. 2004. Probing site-specific energetics in proteins and nucleic acids by hydrogen exchange and NMR spectroscopy. Methods Enzymol. 379:152–175. [DOI] [PubMed] [Google Scholar]
- 15.Kochoyan, M., J. L. Leroy, and M. Gueron. 1990. Processes of basepair opening and proton exchange in Z-DNA. Biochemistry. 29:4799–4805. [DOI] [PubMed] [Google Scholar]
- 16.Leroy, J. L., E. Charretier, M. Kochoyan, and M. Gueron. 1988. Evidence from basepair kinetics for two types of adenine tract structures in solution: their relation to DNA curvature. Biochemistry. 27:8894–8898. [DOI] [PubMed] [Google Scholar]
- 17.Moe, J. G., and I. M. Russu. 1992. Kinetics and energetics of basepair opening in 5′- d(CGCGAATTCGCG)-3′ and a substituted dodecamer containing G·T mismatches. Biochemistry. 31:8421–8428. [DOI] [PubMed] [Google Scholar]
- 18.Folta-Stogniew, E. J., and I. M. Russu. 1994. Sequence-dependence of basepair opening in a DNA dodecamer containing the CACA/GTGT sequence motif. Biochemistry. 33:11016–11024. [DOI] [PubMed] [Google Scholar]
- 19.Dornberger, U., M. Leijon, and H. Fritzsche. 1999. High basepair opening rates in tracts of GC basepairs. J. Biol. Chem. 274:6957–6962. [DOI] [PubMed] [Google Scholar]
- 20.Chen, C., and I. M. Russu. 2004. Sequence-dependence of the energetics of opening of AT basepairs in DNA. Biophys. J. 87:1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Moe, J. G., E. Folta-Stogniew, and I. M. Russu. 1995. Energetics of basepair opening in a DNA dodecamer containing an A3T3 tract. Nucleic Acids Res. 23:1984–1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kornberg, A., and T. A. Baker. 1992. DNA Replication. W.H. Freeman, New York.
- 23.Coman, D., and I. M. Russu. 2002. Site-resolved energetics in DNA triple helices containing G·TA and T·CG triads. Biochemistry. 41:4407–4414. [DOI] [PubMed] [Google Scholar]
- 24.Cantor, C. R., M. M. Warshaw, and H. Shapiro. 1970. Oligonucleotide interactions. III. Circular dichroism studies of the conformation of deoxyoligonucleotides. Biopolymers. 9:1059–1077. [DOI] [PubMed] [Google Scholar]
- 25.Weast, R. C. 1987. CRC Handbook of Chemistry and Physics, 67th Ed. CRC Press, Boca Raton, FL.
- 26.Plateau, P., and M. Gueron. 1982. Exchangeable proton NMR without base-line distortion, using new strong-pulse sequences. J. Am. Chem. Soc. 104:7310–7311. [Google Scholar]
- 27.Mihailescu, M. R., and I. M. Russu. 2001. A signature of the T→R transition in human hemoglobin. Proc. Natl. Acad. Sci. USA. 98:3773–3777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Englander, S. W., and N. R. Kallenbach. 1984. Hydrogen exchange and structural dynamics of proteins and nucleic acids. Q. Rev. Biophys. 16:521–655. [DOI] [PubMed] [Google Scholar]
- 29.Gueron, M., E. Charretier, J. Hagerhorst, M. Kochoyan, J. L. Leroy, and A. Moraillon. 1990. Structure and Methods. R.H. Sarma, and M. H. Sarma, editors. Adenine Press, Schenectady, NY. 113–137.
- 30.Leroy, J. L., X. Gao, M. Gueron, and D. J. Patel. 1991. Proton exchange and internal motions in two chromomycin dimer-DNA oligomer complexes. Biochemistry. 30:5653–5661. [DOI] [PubMed] [Google Scholar]
- 31.Coman, D. 2004. Structural energies of DNA double and triple helices and their interactions with metal ions by NMR spectroscopy. PhD thesis. Wesleyan University, Middletown, CT.
- 32.Coman, D., and I. M. Russu. 2005. Basepair opening in three DNA unwinding elements. J. Biol. Chem. 280:20216–20221. [DOI] [PubMed] [Google Scholar]
- 33.Moe, J. G., and I. M. Russu. 1990. Proton exchange and basepair opening kinetics in 5′-d(CGCGAATTCGCG)-3′ and related dodecamers. Nucleic Acids Res. 18:821–827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Glasstone, S., K. J. Laidler, and H. Eyring. 1941. The theory of rate processes. In The Kinetics of Chemical Reactions, Viscosity, Diffusion, and Electrochemical Phenomena. McGraw-Hill, New York and London.
- 35.Krug, R. R., W. G. Hunter, and R. A. Grieger. 1976. Enthalpy-entropy compensation. II. Separation of the chemical from the statistical effect. J. Phys. Chem. 80:2341–2351. [Google Scholar]
- 36.Hagan, M. F., A. R. Dinner, D. Chandler, and A. K. Chakraborty. 2003. Atomistic understanding of kinetic pathways for single basepair binding and unbinding in DNA. Proc. Natl. Acad. Sci. USA. 100:13922–13927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Leffler, J. E., and E. Grunwald. 1963. Rates and Equilibria of Organic Reactions. Dover, New York.
- 38.Jencks, W. P. 1969. Catalysis in Chemistry and Enzymology. McGraw-Hill, New York.
- 39.Leffler, J. E. 1953. Parameters for the description of transition states. Science. 117:340–341. [DOI] [PubMed] [Google Scholar]
- 40.Matouschek, A., and A. R. Fersht. 1993. Application of physical organic chemistry to engineered mutants of proteins: Hammond postulate behavior in the transition state of protein folding. Proc. Natl. Acad. Sci. USA. 90:7814–7818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sanchez, I. E., and T. Kiefhaber. 2003. Hammond behavior versus ground state effects in protein folding: evidence for narrow free energy barriers and residual structure in the unfolded state. J. Mol. Biol. 327:867–884. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.