Probing Vesicle Dynamics in Single Hippocampal Synapses

Abstract

We use fluorescence correlation spectroscopy and fluorescence recovery after photobleaching to study vesicle dynamics inside the synapses of cultured hippocampal neurons labeled with the fluorescent vesicle marker FM 1–43. These studies show that when the cell is electrically at rest, only a small population of vesicles is mobile, taking seconds to traverse the synapse. Applying the phosphatase inhibitor okadaic acid causes vesicles to diffuse freely, moving 30 times faster than vesicles in control synapses. These results suggest that vesicles move sluggishly due to binding to elements of the synaptic cytomatrix and that this binding is altered by phosphorylation. Motivated by these results, a model is constructed consisting of diffusing vesicles that bind reversibly to the cytomatrix. This stick-and-diffuse model accounts for the fluorescence correlation spectroscopy and fluorescence recovery after photobleaching data, and also predicts the well-known exponential refilling of the readily releasable pool. Our measurements suggest that the movement of vesicles to the active zone is the rate-limiting step in this process.

INTRODUCTION

Most neurons communicate via chemical synapses. In this process, vesicles in the axon termini (boutons) of the presynaptic cell dock at the active zone and undergo exocytosis in response to action potential triggered Ca²⁺ influx, emptying neurotransmitter into the synaptic cleft. The bouton replenishes lost vesicles by recycling portions of the plasma membrane to create new vesicles via endocytosis. In the 1990s, Betz and colleagues (1) developed the fluorescent marker FM 1–43 that labels recycling vesicles. By imaging dye accumulation or depletion at the synapse, one can study vesicle recycling and exocytosis in a variety of preparations including central synapses (2–4). Together with electrophysiological studies, these experiments provide strong evidence that synaptic vesicles are divided into distinct functional pools. These include a readily releasable pool (RRP) that stains with FM 1–43 and is likely docked and a reserve pool (RP) that is also labeled but is twice as large (4) and is remote from the active zone (5–7). Interestingly, the majority of vesicles in these synapses do not become labeled at saturating levels of fluorescent staining, and thus do not participate in recycling; these vesicles comprise the resting pool. Electrophysiological studies show that stimulation at even moderate frequencies (10 Hz) (8) depletes the RRP faster than the RP can replenish it (9–11). Thus, the dynamics of RP vesicles influence the efficacy of synaptic transmission.

Several studies suggest that vesicles are associated with a variety of structural proteins (cytomatrix) within the synapse and with motor proteins (12–17). Much of this work has focused on the synapsin family of phosphoproteins, which tethers vesicles to actin filaments (18–20). In response to Ca²⁺ entry, these proteins become phosphorylated and release vesicles (21,22), making these vesicles available to join the RRP.

Despite these observations, a physical picture of how RP vesicles move to the active zone is still lacking, particularly in central synapses. For example, recovery of the RRP, known as “refilling”, is also observed in the absence of Ca²⁺ influx (23) when vesicle fusion is stimulated with the application of hypertonic sucrose solution (8,9,12,24–26). This Ca²⁺-independent refilling displays a similar exponential recovery to that observed in response to membrane depolarization (8,9,27). Traditionally, this empirical observation is thought to reflect the mobilization of RP vesicles to the active zone (23). However, previous studies in these and other synapses containing synapsin find no measurable vesicle motion in either resting or electrically stimulated synapses (28,29). Moreover, Pyle and co-workers provide evidence that refilling is due to the rapid endocytosis of docked vesicles commonly known as “kiss and run” (24), rather than vesicle movement. Also, recent measurements by Deak et al. (30) demonstrate that synaptobrevin-2 is critical for rapid endocytosis and that removing this protein slows refilling by a factor of three. Together, these findings cast doubt on the role of vesicle movement in refilling. In addition, the RRP recovers even more slowly after sustained exocytosis compared to the faster refilling described above (10,31). The mechanism for this form of synaptic depression is unknown, although vesicle motion has been implicated (24). Lastly, the role of actin in vesicle mobility in these synapses has recently come into question (32). Thus, it remains unclear how RP vesicles move to the active zone and how this process is regulated.

Studying vesicle dynamics in most central synapses is challenging primarily due to bouton size. These small (∼0.1 μm³) boutons are packed with hundreds of synaptic vesicles that are ∼40 nm in diameter, which is well below the diffraction limit of visible light. Therefore, imaging synaptic vesicles directly using light microscopy (33) is problematic. Here we report the use of fluorescence correlation spectroscopy (FCS) (34) to study vesicle dynamics in small central synapses for the first time by recording the fluorescence intensity fluctuations of FM 1–43 labeled synaptic vesicles in cultured hippocampal neurons. These fluctuations reflect the movement of vesicles in and out of a diffraction-limited laser spot (Gaussian radius w = 0.11 μm). Together with fluorescence recovery after photobleaching (FRAP) (35), our results indicate that there exists a small fraction (∼27%) of mobile vesicles that exhibit slow restricted motion within an immobile vesicle cluster. This motion is sped up ∼30-fold after applying the phosphatase inhibitor okadaic acid (OA), suggesting that the vesicles' sluggish dynamics are due to phosphorylation-regulated binding within the bouton. To explain these data, a model consisting of a pool of diffusing vesicles that reversibly stick to and release from the cytomatrix is constructed. This simple model agrees well with both the FCS and FRAP data, and it also reproduces the previously observed exponential refilling of the RRP.

MATERIALS AND METHODS

Primary cell culture

Cultures of dissociated embryonic rat hippocampal neurons were prepared as described previously (36). Cells were used for experiments after 12–18 days in culture.

Fluorescence labeling

The culture was constantly perfused with room (∼23°C) or low (14–16°C) temperature HEPES-buffered saline (HBS) solution containing the following (in mM): NaCl 150, KCl 3, CaCl₂ 3, MgCl₂ 2, HEPES 10, glucose 5, and pH 7.3 for all experiments unless stated otherwise. Synapses were loaded with dye by perfusing cells with HBS containing 10–15 μM FM 1–43 (Synaptogreen, Biotium, Hayward, CA) and 50–90 mM KCl for 60 s, followed by perfusion with HBS containing only dye for 30 s. This was followed by a fast perfusion of dye-free (typically Ca²⁺-free) HBS for 10 min at a rate >2 ml/min. In some experiments, 300 μM ADVASEP-7 (Biotium) was added for 1 min to the dye-free HBS, beginning 1 min after the initiation of the fast perfusion (37). The majority of images of FM 1–43 puncta were taken with a charge-coupled device (CCD) camera (Hamamatsu C9100-12, Hamamatsu City, Japan), using the same microscope and fluorescent filters as described for FCS below.

Fixation

Synapses used in experiments with fixed cells were loaded with AM 1–43 (Biotium) using a similar protocol to the one described above. Cells were then placed in 4% paraformaldehyde for 30 min, followed by rinsing several times in phosphate-buffered saline (PBS). Cells were stored in PBS up to the time of the experiment.

FCS measurements

Fluorescence correlation spectroscopy (FCS) was used to investigate the vesicle dynamics of the recycling pool. The experiments were carried out on an inverted microscope (Nikon TE300, Melville, NY), using a 100× 1.3 numerical aperture oil immersion lens. Light from a Xenon arc lamp was projected into the back port through a Nikon fluorescence attachment (Nikon TE-FM), an excitation filter (Chroma D470/40, Rockingham, VT), a converging lens (f = 30 cm), and a 50/50 beam splitter. The other input to the beam splitter consisted of two aligned parallel laser beams. An argon laser beam (λ = 488 nm) was used as the excitation beam and was focused by the microscope objective to a diffraction-limited spot. A HeNe (λ = 632 nm) laser beam was used to mark the position of the excitation spot, which does not exit the filter cube (Chroma HQ510LP, Q497LP). The FM 1–43 labeled puncta were visualized under epifluorescence and positioned onto the HeNe spot by a manual or a motorized microscope stage (SD Instruments, Grants Pass, OR). Measurements were performed with all light sources blocked except for the excitation laser (∼0.5 μW). A confocal geometry was used in which the fluorescence intensity I(t) from the synapse was imaged onto a 50 μm pinhole placed in the side port and was measured using an avalanche photodiode (APD) (EG & G SPCM-100, Wellesley, MA) and an autocorrelator (ALV-5000, Langen, Germany). The pinhole, the collection optics, and the excitation spot define the Gaussian detection volume or the “light box” () with a radius w = 0.11 μm, calibrated by performing FCS on dyes with a known diffusion coefficient. This radius is consistent with the size of the confocal detection volume measured by scanning subresolution (40 nm) fluorescent beads (Fig. 1) and represents the distance that a freely diffusing object must traverse for the correlation function to decrease by 50% (38). The raw fluorescence intensity I(t) was typically binned to 10 ms and then fit to an exponential curve I_B(t) = I₀exp(−t/t_B), which accounts for the photobleaching (typically t_B > 200 s). The fluorescence intensity-intensity autocorrelation function G(τ) = 〈δI(t)δI(t + τ)〉/〈I(t)〉² was calculated, where δI(t) = I(t) − I_B(t) and 〈…〉 represents a time average.

FIGURE 1.

FCS measures vesicle dynamics in single synapses. (A) A schematic of the FCS detection volume (light box) is shown overlying a typical large synapse labeled with FM 1–43 (scale bar 0.5 μm). (B) A plot of the normalized intensity measured by scanning the detection volume along the long (▵) and the short (▪) axes of this synapse as well as along a 40 nm fluorescent bead (○). A plot of the Gaussian light box I = I₀exp(−r²/2w²) (solid line), where w = 0.11 μm, is also shown. (C) The intensity trace measured from a single synapse is fit to an exponential function (shaded trace) and is used to calculate the autocorrelation function G(τ) shown in (D) (see Materials and Methods).

FRAP measurements

FRAP measurements were made using the same experimental setup as described above for FCS with slight modification. The intensity of the excitation beam was increased to ∼100 μW for ∼0.5 s to bleach the synapse by moving a neutral density filter out of the light path using a solenoid actuator. This bleaching was moderate, reducing the intensity in the light box to 35.40% ± 0.05% of its original value. Camera images of bleached synapses showed a decrease in the total synaptic fluorescence of 13% ± 2%. The estimated size of the mobile pool was adjusted to reflect this loss. During the bleaching the APD was blocked to avoid saturation and damage. The APD was unblocked within ∼100 ms of the completion of the bleaching. The autocorrelator recorded the intensity throughout the experiment. The intensity before bleaching I_pre was average for 5 s. At t = 0 the bleaching was completed, the APD was unblocked, and the fluorescence intensity I(t) was recorded. The fraction of fluorescence recovery was calculated as R(t) = [I(t) − I(0)]/[I_pre − I(0)].

For the fluctuation analysis of the FRAP experiments, the fluorescence intensity after bleaching I(t) was fit to an exponential recovery I_R(t) = I₁ − I₀exp(−t/t_R). Similar to FCS experiments, the fluorescence intensity-intensity autocorrelation function G(τ) = 〈δI(t)δI(t + τ)〉/〈I(t)〉² was calculated, where δI(t) = I(t) − I_R(t).

Application of OA

A total of 2 μM OA (LC Laboratories, Woburn, MA), diluted from frozen stock solutions aliquoted in dimethylsulfoxide (DMSO), was added after dye loading such that the final concentration of dimethylsulfoxide did not exceed 0.1%. For experiments using OA, regions of interest (ROIs) were drawn around synapses that appear as fluorescent puncta, as well as neuronal processes labeled nonspecifically. Normally, nonspecific labeling is estimated by measuring the fluorescence remaining in puncta after exhaustive exocytosis. Since electrically stimulated exocytosis may be altered by OA, nonspecific labeling in regions of neuronal processes devoid of puncta was used to estimate the nonvesicular contribution to the synapses' fluorescence before and after adding OA. A decrease in background fluorescence was observed upon adding OA. This secondary effect is small but cannot be explained entirely by photobleaching. If one assumes that the decrease in background intensity is uniform, then the fraction of dye lost to this secondary effect is <10% of the puncta's initial fluorescence. The fading in puncta greatly exceeded this change in background and is not due to exocytosis (39) (Appendix A). The difference between fading in the synapses and fading in the background was attributed to the dispersion of vesicles.

Synapse size

We measured synapse size by scanning individual puncta via scanning stage confocal microscopy as shown in Fig. 1 B. However, this process is rather slow. To gather sufficient statistics, the synapse area was measured by plotting the intensity along the long and short axes of camera images of fluorescent puncta. The baseline intensity was subtracted from each intensity profile and the full width half maximum (FWHM) was calculated. The intensity profile was approximated as a Gaussian function, allowing the FWHM to be converted to a Gaussian radius, w_I. This image intensity profile represents the actual synapse shape profile convolved by the point spread function (PSF) of the microscope (see Appendix B, Fig. 9 B). If all three profiles are assumed to be Gaussian, than the radius w_s along a given axis s of the synapse can be estimated as 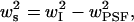where 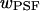is the Gaussian radius of the PSF. The synapse and light box area were calculated by approximating the synapse as an ellipse of area 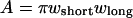and the light box as a circle of area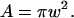

Synaptic motion

Synaptic boutons are dynamic structures whose shape and size evolve with time (40). Such synaptic motion could contribute to the measurement of fluorescence intensity fluctuations and fluorescence recovery if the fluorescent synapse moves relative to the fixed laser beam. To determine the contribution of this motion, we used video fluorescence microscopy to record the center of mass position of individual synapses labeled with FM 1–43 (see Fig. 3 A). The video rate was three frames per second. This measurement was compared to the intrinsic drift of the experimental setup by recording the position as a function of time of 0.42 μm diameter fluorescein isothiocyanate-labeled beads adsorbed onto a glass coverslip. Puncta and beads were identified manually, and the center of mass position 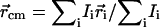for each 1 × 1 μm² ROI containing a punctum was calculated for each frame, where I_i and 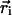are the fluorescence intensity and position, respectively, of the ith pixel in the ROI. The average 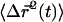was calculated for 30 synapses and is plotted versus t (see Fig. 3 B). The slope of this line is equal to 4D_CM, where the effective diffusion coefficient of the center of mass is D_CM = 5.4 × 10⁻¹⁵ cm²/s. As will be shown below, this diffusion coefficient is about three orders of magnitude smaller than the vesicle dynamics measured by FCS or FRAP.

FIGURE 3.

Synapse center of mass motion does not contribute to the FCS measurement. (A) The inset displays the trajectory of the center of mass of a typical synapse (0.3 s/step, totaling T = 90 s, scale 5 nm). The mean squared displacement calculated from this synapse's trajectory is plotted below the inset. (B) The average 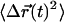was calculated for 30 synapses and is displayed (top line with error bars) along with a linear fit (shaded line) of slope 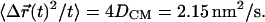The average mean-square displacement 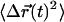for 0.42 μm fluorescent beads (bottom solid line, with the thickness exceeding the error, n = 75) adsorbed to a glass coverslip is displayed along with a linear fit (shaded line) of slope 4D_CM = 0.22 nm²/s.

All errors and error bars represent the mean ± SE, unless stated otherwise.

RESULTS

FCS measures sluggish vesicle dynamics

A typical synaptic vesicle FCS measurement is depicted in Fig. 1. Here the laser spot and detection volume (light box) is positioned onto a synaptic bouton labeled with FM 1–43 (Fig. 1 A). It is important that vesicles can leave the light box for fluorescence intensity fluctuations to be observed. The lateral dimensions of this typical large synaptic bouton are measured by scanning the detection volume across the synapse, which are displayed in Fig. 1 B. The narrow lateral dimension of the bouton is less than twice the width of the light box. In addition, the height of the synapse is comparable to the narrow lateral dimension, whereas the height of the light box is 3–5 times larger than its width (41). Thus, motion perpendicular to the coverslip is not detected (42). This natural confinement can be taken into account, and the vesicles can be treated as if they are moving in a constrained two dimensional system (42). The area of an ensemble of labeled synapses was measured from camera images resulting in an average area of 0.34 ± 0.02 μm² (n = 33). This area is 9 ± 2 times larger than the area of the light box (0.038 ± 0.009 μm²) and is consistent with the average cross sectional area of ∼0.3 μm² measured from electron micrographs of cultured hippocampal synaptic boutons (5). The ratio of synapse to light box size is also consistent with photometric measurements that show that the total amount of fluorescence emanating from these synapses is an order of magnitude larger than the fluorescence measured in a typical FCS measurement (Appendix B). In the FCS measurements, we also took advantage of the great heterogeneity in bouton sizes (43) by selecting large boutons such as the one shown in Fig. 1. These boutons are similar in size to those displayed as examples of normal architecture in several electron microscopy studies (5,7,44). Hence, the light box is small enough that vesicles can exit this volume, which is required for observing fluorescence fluctuations.

Fig. 1 C displays the fluorescence intensity from a single synapse as a function of time. Here the number of photons measured during each time bin decays at a modest rate due to photobleaching and can be corrected after fitting to an exponential function (see Materials and Methods). In addition to the overall decay of the time trace, one observes intensity fluctuations resulting from putative vesicle motion. The fluorescence intensity autocorrelation function G(τ) calculated from this time trace is shown in Fig. 1 D. Here, G(τ) quantifies the correlation between pairs of fluorescence intensity fluctuations observed a time τ apart. As vesicles redistribute, these correlations decay, providing information about the underlying dynamics.

These measurements were repeated for an ensemble of labeled synapses (n = 39), each with an integration time of T = 200 s. As shown in Fig. 2 A, there is a great deal of heterogeneity within the ensemble, particularly in the amplitude of the correlation function G(0) (coefficient of variation c_G(0) = 0.92). This large variation is not surprising and has been observed in several other measurements in these synapses, such as synapse size and release probability (8,43,45). These factors along with the variation in the arrangement and the number of vesicle clusters may contribute to the heterogeneity in the observed dynamics. For a subset of these synapses (n = 23), the FCS measurement was repeated at a different location (at least one light box diameter away) within the same synapse. We find that the variation in G(0) within the synapse is ∼½ of that between synapses, indicating that about one-half of the heterogeneity is intrinsic to the population of synapses. The correlation between measurements within the same synapse is demonstrated in Fig. 2 C. To examine the average behavior of vesicles in these synapses, the autocorrelation functions from individual boutons were averaged (Fig. 2 B). The amplitudes of these fluctuations are orders of magnitude greater than those measured in the synapses of fixed cells, demonstrating that the fluctuations are inherent to the living synapses.

FIGURE 2.

Synapses are heterogeneous. (A) Ensemble of G(τ)'s measured from 39 different synapses. (B) The average of the correlation functions in A is plotted (•) with the amplitude G(0) = 0.016 ± 0.002 and the correlation time τ_½ = 2.82 ± 0.4 s marked. The green line represents the fit to the stick-and-diffuse model (τ_B = 4.5 ± 1.1 s, τ_U = 2.1 ± 1.5 s, τ_D = 0.19 ± 0.17 s). The blue line with error bars represents the average correlation function for low temperature (14–16°C) exposed synapses (τ_½ = 10.5 ± 0.3 s, n = 16). The solid squares represent the average correlation function for synapses labeled with dye and fixed with paraformaldehyde (n = 41). For both the control and the fixed synapses, the error bars (mean ± SE) are the same size or smaller than the points. (C) The spatial heterogeneity was measured by making two FCS measurements spaced at least one light box diameter away within the same synapse (n = 23). The G(0) of the first measurement is plotted against G(0) of the second measurement and scatter about the line of slope one. The intrasynaptic heterogeneity is 58% of the intersynaptic heterogeneity

The correlation time is one important parameter that can be extracted from the autocorrelation function. Our experiment yields a correlation time of τ_½ = 2.8 ± 0.4 s, where G(τ_½) = ½G(0). We can gain physical intuition about this number by relating it to a diffusion coefficient and an effective viscosity of the vesicles' surroundings. If we assume that τ_½ corresponds to a diffusion time τ_½ = w²/D, then we find an effective diffusion coefficient of D = 4.3 ± 0.7 × 10⁻¹¹ cm²/s. This diffusion constant is ∼8000 times larger than that measured for synaptic motion using video fluorescence microscopy (Fig. 3 and Materials and Methods). Thus, the observed FCS fluctuations cannot be attributed to any relative motion between the synapse and the laser spot. Assuming that the vesicles diffuse in a medium characterized by a single viscosity coefficient, the Stokes-Einstein relation (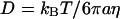) yields an effective viscosity η = 25 poises for T = 293 K for the vesicle radius a = 20 nm. This viscosity is 2,500 times larger than water and ∼100 times larger than expected for inert particles of this size diffusing in the cell (46). Accordingly, one of the goals of this work is to understand the source of this large correlation time and to develop a model of the vesicle motion that will help us understand the observed dynamics.

To further probe vesicle dynamics we also examined the temperature dependence of vesicle motion (47). Increasing the temperature to near physiological temperatures increases the rate of spontaneous exocytosis and thus the depletion of FM 1–43 from the puncta. This severely restricts the time available for performing time averaging techniques such as FCS, particularly when an ensemble of synapses is required to collect statistics. Instead, we examined the effect of lowering the temperature (14–16°C) on vesicle dynamics. Not only was the fluorescence in these lower temperature puncta more stable, but the vesicle dynamics measured in these synapses were significantly slower (τ_½ = 10.5 ± 0.3 s) than those in control synapses measured at room temperature (τ_½ = 2.82 ± 0.4 s) (Fig. 2 B). This temperature dependence offers further confirmation that we are observing physiological vesicle motion.

Recycling vesicles consist of a mobile and an immobile pool

FRAP measures the mobility of fluorescent objects by monitoring the fluorescence intensity as it recovers within an area previously bleached by an intense laser beam (35). Compared to FCS, it is more suited for measuring slow dynamics and can provide complementary information about mobility and the fraction of mobile particles. The same FCS experimental setup as described above was used to measure FRAP of FM 1–43 labeled vesicles within the synapse. Fig. 4 A shows a labeled synapse before and ∼1 min after a portion of the synapse has been bleached. In addition, the same synapse is displayed after application of high K⁺ bath solution. The diminished fluorescence throughout the bouton, including the bleached region, indicates that vesicles within the synapse are still able to undergo exocytosis and that the synapse is still viable after photobleaching. In addition to the traditional analysis of FRAP data described below, we also calculated G(τ) for the FRAP signal and compared it to G(τ) measured during FCS experiments where no photobleaching had occurred. The inset to Fig. 4 B shows that the average correlation function measured after photobleaching closely resembles the average correlation function for control synapses. Hence, vesicle dynamics are not significantly altered by photobleaching.

FIGURE 4.

FRAP resembles refilling of RRP. (A) A synapse labeled with FM 1–43 is shown before and ∼1 min after an area is photobleached with a laser. The same synapse is also shown after high K+ bath is applied. The images are displayed twice, emphasizing the high (H) and low (L) end of the gray scale (scale bar 0.5 μm). (B) A sampling of FRAP curves (n = 12) randomly chosen from the full ensemble (n = 47). The normalized, ensemble-averaged correlation function calculated from the fluctuations in the FRAP measurements (green trace) is plotted along with the corresponding correlation function from FCS measurements (black trace) in the inset. (C) The average FRAP response of the entire ensemble is plotted with error bars (standard deviation) and is fit to a double exponential (dotted line) A(f(1 − exp(−t/τ_F)) + (1 − f(1 − exp(−t/τ_S))) with τ_S = 4 s, τ_F = 40 s, A = 0.15, and f = 0.58. Rescaled refilling data (see Discussion) of the RRP measured by Morales et al. (12) (▪, scaling factor 0.10) and Stevens and Wesseling (31) (▵, scaling factor 0.16) reveal short and long time refilling, respectively. The solid red line is the fit of the simplified stick-and-diffuse model to the fast refilling experiments with fitting parameters τ_B = 4.32 s and τ_U = 0.59 s. The inset shows the same data on a semilog scale to emphasize early times.

The recovery from an ensemble of synapses and the average recovery are displayed in Fig. 4, B and C, respectively. Similar to the measurements of G(0), there is significant heterogeneity in the asymptotic level of fluorescence recovery (coefficient of variation c_R = 0.35). The average recovery is ∼15%, indicating that a vast majority of labeled vesicles are not mobile and explaining why the bleached area in Fig. 4 A remains dark (29). The fluorescence recovery has two identifiable timescales. The fast timescale τ_F ≈ 4 s agrees well with the correlation time τ_½ = 2.8 ± 0.4 s measured by FCS. The slow timescale τ_S ≈ 40 s, which is comparable to the total FCS integration time T, is not accessible in those measurements.

The amplitude of the correlation function G(0) measured by FCS is the variance of the number of labeled vesicles in the light box. For the average correlation function displayed in Fig. 2 B, G(0) = 0.016 ± 0.002. For freely diffusing particles, the fluctuations of the number of particles in the light box obey Poisson statistics with the result G(0) = 1/〈N〉, where 〈N〉 is the average number of fluorescently labeled particles in the light box. However, for a system containing an immobile population, G(0) = 〈N_M〉/〈N〉² (48), where 〈N〉 = 〈N_M〉 + 〈N_I〉 + 〈N_B〉 and 〈N_M〉 and 〈N_I〉 are the average number of mobile and immobile vesicles, respectively, in the light box. 〈N_B〉 is the amount of background fluorescence in units of vesicles. Measuring the fluorescence remaining in puncta after sustained exocytosis gives 〈N_B〉/〈N〉 = 0.39 ± 0.01 (Appendix B). Also, FRAP measurements performed on unloaded puncta show no measurable fluorescence recovery, indicating that the background fluorescence fraction (〈N_B〉) does not contribute to the measured vesicle dynamics. We can estimate the average number of vesicles in our light box (〈N_I〉 + 〈N_M〉 = 0.61〈N〉) by solving the above expression for 〈N〉 = (〈N_M〉/〈N〉)/G(0), where 〈N_M〉/〈N〉 can be measured by the asymptotic level of the FRAP curve in Fig. 4 C. This level must be adjusted for the total synaptic fluorescence remaining after bleaching, which is 87% ± 2%. The remaining fluorescence recovers to 16.2% ± 0.9% on the timescale of the FRAP experiment (∼70 s), which is comparable to the FCS integration time. Hence, G(0) reflects only a fraction of this recovery, and the above 〈N_M〉/〈N〉 is an upper bound. (The FRAP signal recovers to ∼10% in 10τ_½ (∼30s), which perhaps is a more appropriate value to compare with G(0) but is not rigorous. This value is consistent with the scaling factor for fast refilling considered in the Discussion.) This yields 〈N_I〉 + 〈N_M〉 < 6.0 ± 0.4 labeled vesicles in the light box and < 54 ± 15 total labeled vesicles in a typical synapse. This is consistent with the majority of studies involving quantal dye uptake (4,6) and counting of labeled vesicles with electron microscopy via photoconversion (7), which show that the total number of labeled vesicles in the average synapse is 25–30, with one study measuring as many as 120 (49). This result confirms that our earlier estimate of the ratio of the synapse to light box area is reasonable. More importantly, it demonstrates that both G(0) and the asymptotic level of FRAP are small because there exists a large population of immobile recycling vesicles, with 〈N_I〉/(〈N_I〉 + 〈N_M〉) = 73% ± 2% on the timescale of minutes.

Phosphorylation frees vesicles

The phosphatase inhibitor OA has been shown to increase the mobility of synaptic vesicles at the neuromuscular junction (28,50), although this phenomenon may not be universal among different synapse types (39). It is thought that this occurs primarily by shifting the population of synapsin proteins to the phosphorylated state, which releases vesicles from the synaptic cytoskeleton (18,20,51). Other studies such as those by Sankaranarayanan et al. (32) suggest that vesicles in hippocampal synapses bind to other structural proteins rather than actin. Therefore, the stickiness of the synaptic cytoskeleton or other structural proteins may explain the observed slow dynamics of these vesicles.

To explore this idea, we examined the effect of OA on hippocampal synapses labeled with FM 1–43. Images show that OA tends to fade and smear the majority (∼90%) of puncta, with the average punctum losing >70% of its vesicles (Fig. 5 A). This large value indicates that the application of OA frees vesicles that were previously immobile. We also used FCS to measure the effect of OA on the dynamics of these vesicles. The measurements show that these puncta can be divided into two distinct groups, sensitive and resistant, based on their correlation time (Fig. 5 B). Resistant puncta are 50% brighter and exhibit dynamics whose decay time is too long for the average correlation function to converge. Similar effects of OA treatment were observed by Betz et al. (50) in the neuromuscular junction. In contrast, sensitive puncta are dimmer and exhibit dynamics whose average decay time is τ_½ = 0.10 ± 0.04 s, which is ∼30 times faster than the control synapses. The average correlation function changes its form significantly and can be described well by free diffusion in a confined geometry (Fig. 5 B). These dynamics agree reasonably well with the diffusion time measured for inert particles of this size in cells (46) as well as synaptic vesicles in ribbon type synapses that lack synapsin (52,53). Thus, eliminating the phophorylation-dependent binding of RP vesicles to the cytomatrix allows them to diffuse freely.

FIGURE 5.

OA frees vesicles. (A) Fluorescence image of FM 1–43 labeled synapses before and 15 min after continuous application of 2 μM OA (scale bar 5 μm). By measuring the labeling of neuronal processes, one can estimate the nonspecific contribution to the puncta's fluorescence (see Materials and Methods). The remaining intensity is due to vesicles (∼80%); >70% of this vesicular fluorescence is lost to diffusion after 15 min in OA. (B) The average autocorrelation function from OA-sensitive synapses (n = 7) is plotted (solid line) along with a fit (shaded line) to two-dimensional (2D) free diffusion with one dimension confined to twice the light box size (42). The cumulative histogram displayed in the inset shows that synapses can be divided into two groups, sensitive (▪) and resistant (○), based on their correlation times. Note that a log scale is used to display the widely separated correlation times.

DISCUSSION

Our experiments suggest that the motion of synaptic vesicles can be measured with FRAP and FCS in cultured hippocampal neurons at the level of single synaptic boutons despite their small size. The small G(0) measured by FCS and the slight asymptotic recovery measured independently by FRAP are both consistent with the picture that a large fraction of recycling vesicles are immobile. Together these quantitative measurements provide an estimate for the number of labeled vesicles in the light box and the synapse, which agrees with previous measurements using fluorescent and electron microscopy in these synapses (4,6,7,49). Also, results from both techniques indicate that mobile vesicles take on the order of seconds or longer to move across the bouton. Control FCS experiments performed on labeled vesicles in synapses of fixed cells indicate that this motion is intrinsic to living synapses and that the FCS signal in live synapses is not due to fluctuations in laser intensity or other instrument noise. Further, vesicle dynamics in synapses is about three orders of magnitude faster than synaptic motion and mechanical drift measured by video fluorescence microscopy. Finally, the timescale of vesicle dynamics and its temperature dependence agrees with the time required to refill the RRP, which we discuss in detail below. These facts strongly imply that we are indeed measuring the dynamics of synaptic vesicles.

Vesicles exhibit stick-and-diffuse dynamics

Several results lead us to believe that the observed slow vesicle motion is not free diffusion. First, the effective diffusion coefficient for vesicle motion is ∼100 times smaller than that measured for inert particles of the same size diffusing in cells (46). Next, we observe that the effective diffusion constant changes by a factor of ∼4 when the temperature is lowered by ∼8°C. In contrast, the Stokes-Einstein relationship for ideal diffusion predicts only a 3% change for the same decrease in temperature. Also, the motion of synaptic vesicles is altered significantly by the application of the phosphatase inhibitor OA, which results in vesicles diffusing freely with an apparent diffusion coefficient that is 30 times larger than control synapses. Lastly, we compared the experimental correlation function to the correlation function predicted for one and two dimensional diffusion, as well as for free diffusion in confined geometries (42). In all cases the fits were marginal (see Appendix C, Fig. 11). Hence, phosphorylation-dependent vesicle binding to the synaptic cytomatrix is likely the source of the sluggish dynamics, and normal vesicle motion is not simply free diffusion.

Motivated by our experimental results and the of body of work on synapsin (18–20), we constructed a model of diffusing vesicles that stochastically bind to and release from the synaptic cytomatrix via a Poisson process (Fig. 6). When the vesicles are unbound, they are free to diffuse with a diffusion constant, D, so that the characteristic diffusion time over the light box is τ_D = w²/D. In the free state, vesicles become bound at a rate 1/τ_U. Once bound, the vesicles become free again with an unbinding rate 1/τ_B. Therefore, the unbound and bound states last for average times τ_U and τ_B, respectively. The correlation function for this model can be expressed in terms of an infinite sum, allowing G(τ) to be calculated numerically (Appendix C). Fig. 2 B shows that the fit of the stick-and-diffuse model to the FCS data is quite good, with the fitting parameters τ_B = 4.5 ± 1.1 s, τ_U = 2.1 ± 1.5 s, and τ_D = 0.19 ± 0.17 s.

FIGURE 6.

Refilling of the RRP is modeled by stick-and-diffuse dynamics. A schematic of the stick-and-diffuse model depicts mobile vesicles stochastically alternating between a bound and a free state. Bound vesicles become free at a rate the inverse of the average time they remain stuck. Free vesicles diffuse with a diffusion coefficient D and become stuck at a rate In addition to mobile vesicles that undergo stick-and-diffuse dynamics, there exists an immobile pool of vesicles, which remains bound on timescales much longer than the transient binding times of the mobile pool. Refilling of the RRP can be modeled by including docking sites that act as perfect sinks.

Therefore, our picture of vesicle dynamics is as follows. The majority of recycling vesicles are immobile, and even mobile vesicles spend ∼70% (τ_B/(τ_U + τ_B)) of their time bound. When bound, these vesicles remain stuck for an average time of ∼5 s. Once unbound, the vesicles are free to move about the bouton, becoming bound again after an average time of ∼2 s. Since τ_U/τ_D ≈ 10, the vesicles can visit an area much larger than the light box while free. Note that the fit of the model to the experimental autocorrelation function is sensitive to τ_U and τ_B but insensitive to τ_D as long as τ_D ≪ τ_U. Despite the large uncertainty in τ_D, the free diffusion time obtained in our fits is consistent with the diffusion time measured in the presence of OA (τ_½ = 0.10 ± 0.04 s).

Although mobile vesicles spend a majority of their time bound, it is important to make a distinction between mobile vesicles that bind transiently and vesicles that reside in the immobile pool. Since the sticking time τ_B is much smaller than the integration time, these mobile vesicles contribute to both G(0) and to the amount of fluorescent recovery after photobleaching. In contrast, the immobile pool vesicles remain bound on timescales on the order of, or larger than, the duration of the FCS and FRAP experiments. Thus, the immobile pool is a long-lived state compared to the transient binding of the mobile vesicles, and the small G(0) and incomplete fluorescence recovery can only be explained by the existence of two distinct vesicle populations. A population of immobile vesicles has been observed in these (29) and in other synapses (28,54) and may be characteristic of many synapses.

Mobilization of vesicles is the rate-limiting step for refilling the RRP

Refilling experiments monitor the recovery of exocytosis after the entire RRP of vesicles has fused. Although other mechanisms have been proposed (24), this phenomenological observation is thought to reflect the mobilization of RP vesicles to the active zone (23). However, this had not previously been addressed by direct measurements of vesicle mobility. The majority of studies show that the refilling process can be fit by a single exponential with a relaxation time of 3–10 s. This agrees with the typical correlation time τ_½ = 2.8 s and the fast fluorescence recovery time τ_F ≈ 4 s measured in our experiments. This agreement suggests that vesicle movement to the active zone might be the rate-limiting step in refilling. If this is true, then this movement alone should be able to explain the exponential recovery. Fig. 4 C shows refilling data measured by Morales et al. (2000) that has been rescaled to overlie the averaged data from the FRAP experiments. We see that the refilling of the RRP follows an identical time course as the fast (τ_F) recovery of fluorescent vesicles into the light box. Next we asked if the fast FRAP and refilling data could be explained by the stick-and-diffuse dynamics used to model the FCS experiments. To simplify the analysis we set τ_D = 0, since the diffusion time is an order of magnitude faster than the other timescales. At t = 0, a fraction F = τ_U/(τ_U + τ_B) of mobile vesicles are free. Additional vesicles continue to unbind in an average time τ_B. Once free the vesicles diffuse and, because τ_D = 0, distribute instantaneously with uniform probability throughout the synapse. Hence the time for refilling the light box or the active zone, approximated as a perfect sink (4), is determined solely by τ_B and has the form (1 − F × exp(−t/τ_B)). The fit of the simplified stick-and-diffuse model to the refilling data is shown in Fig. 4 C. A separate fit for the FRAP experiment was not done since the refilling and FRAP data coincide. Despite the simplicity of the model, the parameters optimized to fit the refilling and FRAP experiments (τ_B = 4.32 s, τ_U = 0.59 s) agree reasonably well with those optimized independently to fit the FCS measurements (τ_B = 4.5 ± 1.1 s, τ_U = 2.1 ± 1.5 s). The stick-and-diffuse model of synaptic vesicle dynamics is consistent with both FCS and FRAP results, as well as the previously observed refilling of the RRP. These results, however, do not rule out other mechanisms of refilling such as rapid endocytosis (24).

In contrast to the fast refilling described above, the RRP recovers more slowly after extensive exocytosis (10,11,31). The mechanism of this form of synaptic depression is unknown although several mechanisms, including vesicle mobilization, have been suggested (24). In addition to fast refilling, Fig. 4 C also shows rescaled data measured by Stevens and Wesseling (31) for the refilling of the RRP after depression was induced with 150 action potentials at 9 Hz. The slow component (τ_S) of the FRAP signal matches the slow recovery of the RRP after the sustained activity. (Experiments that measure both the fast and slow component of refilling simultaneously (31) also fit the average FRAP data well (data not shown).) Therefore, the slow recovery of the RRP is consistent with the mobilization of vesicles. One possible mechanism for the slow synaptic depression is that after extensive exocytosis the rate of refilling of the RRP is limited by the rate at which immobile vesicles join the mobile pool. The slow refilling is not seen in the traditional refilling experiments because the brief application of hypertonic solution only depletes the RRP. In contrast, sustained electrical activity depletes both the RRP and the mobile pool faster than they can be replenished by the immobile pool, resulting in depletion, but with slower recovery. Hence, the slow timescale for refilling appears only after both the docked and the mobile pools undergo exocytosis. In contrast, our experiments do not rely on exocytosis, allowing us to observe vesicle mobilization more directly. We conjecture that immobile vesicles become free at minimal levels in resting synapses and that this process manifests as the slow (τ_S) fluorescence recovery measured in our experiments. If the limited availability of immobile vesicles is truly responsible for the slow recovery of the RRP, then this process is likely to be a key regulatory point in the vesicle cycle (54). This idea is consistent with experiments that show that OA frees immobile vesicles, suggesting that the size of the immobile pool is regulated by phosphorylation. Additional experiments should address these issues.

APPENDIX A: APPLICATION OF OA DOES NOT INCREASE EXOCYTOSIS

Previous work in other preparations has shown that application of OA disrupts the synaptic vesicle cluster, with no evidence of increased exocytosis reported (39,50). To confirm that OA does not result in the release of dye via exocytosis, we monitored postsynaptic currents in our culture preparation in the presence of OA. Fig. 7 shows current traces recorded under voltage clamp from a single cell within a densely connected network. Under normal conditions (Fig. 7 A), postsynaptic currents are infrequent. No discernable change is observed when 2 μM or greater OA is added to the extracellular bath (Fig. 7 B). In contrast, perfusing the culture in high K⁺ solution results in numerous postsynaptic responses (Fig. 7 C). Identical behavior was observed in all experiments (n = 3). Thus, the loss of fluorescence in FM 1–43 labeled puncta upon addition of OA is not due to exocytosis.

FIGURE 7.

Application of OA does not increase exocytosis. Twenty current traces recorded every 10 s from a single cell under voltage clamp in the presence of (A) normal bath solution and (B) normal bath solution with 4 μM OA added. (C) High K⁺ bath solution. Note the different scale, demonstrating that synapses in the network are release competent given the proper stimulus. Each experimental condition was presented sequentially from A to C. Within each condition, blue traces were recorded earlier, red traces later. The top graph in each panel displays the traces superimposed on a 2D plot, whereas the bottom graph shows each trace separated along the y axis.

APPENDIX B: FCS DETECTION VOLUME IS A SMALL PORTION OF THE SYNAPSE

The area of the light box is ∼10 times smaller than that of the synapse, suggesting that the FCS measurement observes a small fraction of the total labeled vesicles in the synapse. To confirm this, we calibrated the mean intensity measured by the avalanche photodiode (APD) during the FCS experiment against the total fluorescence of FM 1–43 labeled puncta. This time-averaged intensity measured by the APD should represent a small fraction of the total fluorescence emanating from the labeled synapse. To measure the total fluorescence intensity, synapses were loaded with FM 1–43 using the same protocol as used in the FCS experiments. The FM 1–43 loaded synapses were illuminated with a Xenon arc lamp, and an image (Fig. 8 A) was taken with a camera using a specified gain and exposure time. The synapses were unloaded by perfusing the coverslip three times with high K+ solution without dye, and a second image (Fig. 8 B) was taken using the same settings. The two images were aligned, and a 1.0 μm circular ROI was drawn around each punctum. The total intensity and the difference intensity for each ROI was calculated (n = 82 puncta). The histograms for both the starting and difference (unloaded) intensities are displayed in Fig. 8, D and E, respectively. The mean starting and difference intensities are 2.8 and 1.9 million counts per second, respectively. These values indicate that ∼30% of the puncta's fluorescence is not released upon stimulation. A synapse-by-synapse analysis shows that 39% ± 1% of the puncta's fluorescence remains, and this value is used to estimate the nonspecific background labeling.

FIGURE 8.

The total fluorescence of FM 1–43 labeled synapses. Image of a field of FM 1–43 labeled puncta before (A) and after (B) unloading with three rounds of high K+ bath solution. (C) The difference image of B subtracted from A. Identical ROIs were drawn around puncta in A and B, and the total intensity was calculated for each ROI. (D) A histogram of the starting intensities for three experiments is displayed in counts on the CCD camera per second. (E) A histogram of the difference intensities for the same experiments.

The intensities of these puncta measured by the camera in the front port could then be calibrated against FCS intensities measured by the APD in the side port of the microscope. This calibration actually involves calibrating two sets of instruments: the APD and the laser used in the FCS experiment against the lamp and the camera used in the above unloading experiment. We describe these calibrations below.

First, we calibrated the 16-bit scale of the camera against the photons counted by the APD. Since intensity is the number of photons per area per second, we must find the area over which the APD together with the pinhole integrate the incoming photons under wide field illumination. Formally, the pinhole in front of the APD convolves the image that the APD detects. Similarly, we convolved the image that the camera detects with a window function, W, to properly calibrate the intensities. To measure this window function, we imaged subresolution 40 nm fluorescent beads illuminated with the arc lamp. This image of subresolution beads reveals the PSF of the optical system. The image of individual beads were projected into the side port and scanned across the pinhole and APD at a known velocity (0.313 μm/s). Several of these line scans (Fig. 9 A) were averaged to give I_APD (Fig. 9 C). Likewise, images of the beads from the same coverslip and with the same illumination were imaged by the camera mounted in the front port. Line scans along a single row of pixels though the middle of the beads (Fig. 9 B) were averaged to give the PSF displayed in Fig. 9 C. Notice that in Fig. 9 C the camera's line scan along a row of pixels (PSF) is narrower than the line scan measured by the APD. This is due to the fact that the camera is measuring the PSF of the microscope, whereas the APD is measuring the PSF convolved by some window function. To mimic the effect of the pinhole, we convolve the line scan measured by the camera (PSF) with a square window function W of various sizes d until it matches the line scan measured by the APD (Fig. 9 C).

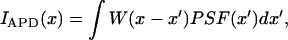where 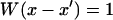for and 0 otherwise. As the window size increases, the convolved PSF spreads out and approaches the line scan measured by the APD, with the best match being a window ∼5.5 pixels or 440 nm measured in the object plane. When one applies the magnification of the side port of 80×, one finds a window of 35 μm. This agrees well with physical size of the pinhole, which is 50 μm.

FIGURE 9.

Calculating the window function. A total of 40 nm fluorescein isothiocyanate-labeled beads were sparsely adsorbed onto a glass coverslip that was mounted onto a motorized stage and were illuminated with an arc lamp. (A) The intensity of individual beads recorded by the APD as their image is scanned across the pinhole. (B) The intensity of individual beads from the same sample plotted along a row of pixels in the CCD image. (C) The average intensity profile measured by the APD in A (▪) and by the camera in B (•) is plotted along with the average camera profile convolved by a square window function of size 3 × 3 (▵), 5.5 × 5.5 (□), and 7 × 7 (⋄) pixels.

To calibrate the counts measured by the camera into photons measured by the APD, we labeled a dendrite with FM 1–43 and illuminated it with the same arc lamp as above. The dendrite's image was both captured by the camera (Fig. 10 A) in the front port and scanned across the pinhole and APD in the side port (open squares Fig. 10 C). The position of the pinhole in reference to the camera image is measured by illuminating the sample with the laser spot, to which the pinhole has been aligned, and taking an image with the camera (Fig. 10 B). A line scan in the x direction along the pixels of the camera image was then convolved by a two dimensional 5.5 × 5.5 pixel square window. This convolution integrates the intensity in the square window as it moves along the image and is meant to mimic the pinhole being scanned across the dendrite. The convolved line scan along the camera image (solid squares) as well as the scan across the APD and pinhole (open squares) are displayed in Fig. 10 C. After rescaling, the two curves collapse onto each other, reaffirming the correct choice of the window function used in the convolution. The result of the rescaling is that one photon measured by the APD in the side port is equivalent to 39 counts measured by the camera in the front port (on a 16-bit scale at the given camera settings). With additional calculations, we find that our calibration agrees within a factor of ∼2 of the manufacturer's specifications.

FIGURE 10.

Counts on the CCD camera calibrated in terms of counts on the APD. (A) A schematic of a square window function being scanned across an image of a dendrite labeled with FM 1–43 and illuminated with an arc lamp. The y coordinate for the window function is given by the position of the laser spot shown in B. (C) This convolved intensity profile (▪) is scaled to the intensity profile measured by the APD as the dendrite's image is physically scanned across the pinhole (□). This scaling factor calibrates the counts on the 16-bit scale of the camera into photon counts measured by the APD. Notice that the two curves collapse onto each other, indicating that the window function used in the convolution is accurate. The same dendrite is then illuminated with the laser spot, and the image is scanned across the same pinhole and APD as above (○). This is scaled to best match the scan using the APD and arc lamp. This scaling factor provides the calibration of the lamp intensity in terms of the laser intensity.

FIGURE 11.

Fit of FCS data to free diffusion is marginal. The average correlation function shown in Fig. 2 B is replotted (black line) along with fits to free diffusion models in one (green line) and two (blue line) dimensions, with diffusion times of τ_D = 1.1 and τ_D = 2.7, respectively. The fit to 2D free diffusion with 1D confined to twice the light box size (42) is also shown (red line) and overlies the 1D fit. However, for confined diffusion τ_D = 2.0, which is slightly closer to the 2D diffusion constant. All fits were corrected for finite integration time (Appendix D).

Now we can express the total counts in the labeling experiment shown in Fig. 8 in terms of photons collected by the APD per unit time. If we multiply 1/39 photons per count by the average total fluorescence emanating from the synapse during 1 s, we can get the number of photons per second that the APD would measure with the same illumination. For the fully labeled synapse this would be 72.2 × 10³ photons/s.

The last step is to calibrate the different excitation sources, laser and xenon arc lamps, used in the two experiments. To do this we scan the same dendrite in the same location as above with a laser intensity typically used in the FCS measurements (∼0.005 μW) and measure the fluorescence intensity. This can be directly compared to the analogous scan of the dendrite illuminated by the arc lamp described above. Both are scanned in the same manner and measured with the same APD and pinhole. The scan of the dendrite with the laser is plotted (open circles) in Fig. 10 C. Notice that the profile of the dendrite is narrower when excited with the laser than with the lamp. This improved resolution is a well-known effect in laser confocal microscopy. The fluorescence emitted (as detected by the pinhole and APD) via laser excitation is ∼4.5 times greater than that of the lamp. Therefore, a fully labeled synapse excited entirely by the laser would yield ∼320 kHz measured by the APD.

Finally, we can compare the DC intensity in our FCS experiment with the total fluorescence emanating from the synapse. We use laser intensities from ∼0.0025 μW to ∼0.01 μW. Therefore, if the entire synapse was contained within the light box of the FCS experiment, the DC intensity would lie between 160 kHz and 640 kHz. Counting rates in our measurement are 5–70 KHz. This is about an order of magnitude smaller than the synapse's total fluorescence and agrees with the ratio of the light box to the synapse size.

APPENDIX C: STICK-AND-DIFFUSE MODEL

In this appendix, we derive the ensemble average subtracted correlation function for the stick-and-release model. The time average subtracted correlation function can then be obtained using the results of Appendix D.

In the stick-and-release model, the mobile vesicles are assumed to alternate between a state in which they are bound to the cytomatrix (stuck) and a second state in which they are free to diffuse with a diffusion time τ_D = w²/D, where w is the width of the laser beam and D is the diffusion constant. They release with a rate 1/τ_B when bound and bind with a rate 1/τ_U when free. Therefore the vesicles, on average, will be bound for a time τ_B before freeing and be free for a time τ_U before binding. In steady state, the probability that a vesicle is bound is τ_B /(τ_B + τ_U) and free is τ_U /(τ_B + τ_U).

The ensemble average subtracted intensity autocorrelation function is

where d is the dimension and P(u,t) is the probability density that the vesicle is free for a total time u out of a time interval t ≥ u. The probability density P(u,t) can be obtained by summing over the probabilities of having the total free time u in total time t occurring in n different intervals. This gives

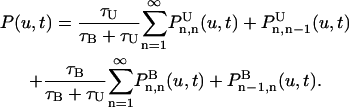Here is the probability that a vesicle is initially free has total free time u during the interval t in n free intervals and m bound intervals. is the same except the vesicle is initially bound.

Therefore the correlation function G_o(t) can be written as an infinite sum. This sum must be evaluated numerically and can be fairly complicated. However two limits are readily stated. If the diffusion time τ_D is long compared to the free time and sticking time, then the dynamics are essentially the same as a random walk with a longer time between steps. Therefore the correlation function will be the same as diffusion with a longer effective diffusion time:

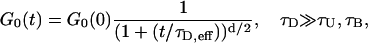where the effective diffusion time is

In contrast, if the diffusion time is small compared to the other two timescales, the sum in P(u,t) is dominated by the P₁₀ and P₀₁ terms. The correlation function is just the sum of an exponential and diffusion correlation functions

This is the limit that we observe in our experiments. Note that in this limit, the correlation function for times t ≫ τ_D is independent of the short time dynamics and is therefore independent of the dimension d.

APPENDIX D: FCS DATA CORRECTED FOR FINITE INTEGRATION TIME

The intensity variations measured in most FCS experiments is the correlation of the deviation of the intensity from the time average intensity. In contrast, most theoretical analysis concerns the deviation of the intensity from its ensemble average value. The time average and the ensemble average intensities are the same if the integration time is much larger than the longest correlation time in the system. However, this is not the case in our experiment.

In this appendix, we derive the relation between the ensemble average subtracted autocorrelation function and the time average subtracted autocorrelation function. We introduce the notation 〈x〉 and 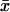to indicate the ensemble average and time average, respectively. The ensemble average subtracted correlation function is then

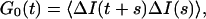where ΔI(t) = I(t) − 〈I〉. We assume a steady-state process so that G₀(t) is independent of s. Assuming a total integration time of T, the time average intensity is

The deviation of the intensity from the time average intensity is

where 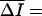Ī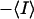 is the difference between the ensemble average and time average intensity. Therefore the time average subtracted correlation function G_T(t) can be written in terms of the ensemble average subtracted correlation function as

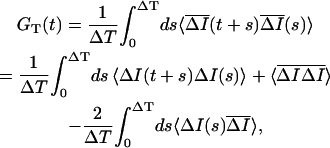where ΔT = T − t. The last two terms can be written in terms of the ensemble subtracted correlation function:

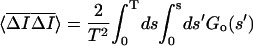and

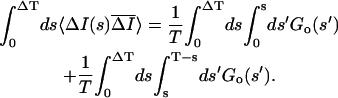Combining the terms gives the time average subtracted correlation function in terms of ensemble subtracted correlation function

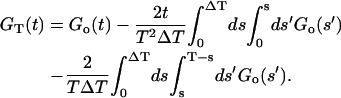Notice that the time average subtracted correlation function is always smaller than the ensemble average value. If the integration time is much larger than the correlation time, the two correction terms are negligible and G_T(t) ≈ G_o(t). On the other hand, if the correlation time is not much smaller than the integration time, the correction terms become important and the time average subtracted correlation function can even become negative. As shown in Fig. 2 B, the correction is important in our experiments even though the correlation time is <1/70th of the integration time.