Liquid-Like Water Confined in Stacks of Biological Membranes at 200 K and Its Relation to Protein Dynamics

Abstract

Confined water is of considerable current interest owing to its biophysical importance and relevance to cryopreservation. It can be studied in its amorphous or supercooled state in the “no-man's land”, i.e., in the temperature range between 150 and 235 K, in which bulk water is always crystalline. Amorphous deuterium oxide (D₂O) was obtained in the intermembrane spaces of a stack of purple membranes from Halobacterium salinarum by flash cooling to 77 K. Neutron diffraction showed that upon heating to 200 K the intermembrane water space decreased sharply with an associated strengthening of ice diffraction, indicating that water beyond the first membrane hydration layer flowed out of the intermembrane space to form crystalline ice. It was concluded that the confined water undergoes a glass transition at or below 200 K to adopt an ultraviscous liquid state from which it crystallizes to form ice as soon as it finds itself in an unconfined, bulk-water environment. Our results provide model-free evidence for translational diffusion of confined water in the no-man's land. Potential effects of the confined-water glass transition on nanosecond membrane dynamics were investigated by incoherent elastic neutron scattering experiments. These revealed no differences between flash-cooled and slow-cooled samples (in the latter, the intermembrane space at temperatures <250 K is occupied only by the first membrane hydration layers), with dynamical transitions at 150 and 260 K, but not at 200 K, suggesting that nanosecond membrane dynamics are not sensitive to the state of the water beyond the first hydration shell at cryotemperatures.

INTRODUCTION

Confined water is an essential component of biological systems, in which it plays various vital roles, including contributions to the organization of macromolecular structure and participation in enzyme catalysis (1). Studies of confined water in nonbiological models have been largely motivated by their potential relevance to biological systems such as the interior of cells or macromolecular and membrane surfaces (2), which are significantly more difficult to study because of their complexity. Understanding the properties of confined water over a wide temperature range is important for applications such as cryopreservation in medicine and food science. Insight into confined water properties should also yield valuable information on a controversial and lively debated issue: the behavior of bulk water at cryotemperatures (3–6).

Bulk water can be in a supercooled, liquid state below 273 K (0°C) if crystallization is prevented, but it necessarily crystallizes into ordinary hexagonal ice as the temperature approaches 235 K, the point of homogeneous nucleation at atmospheric pressure (7). Crystallization can be bypassed, however, by flash cooling from the liquid phase to form hyperquenched glassy water (HQGW), or by low-pressure vapor deposition on a cold plate to form amorphous solid water (ASW) (for reviews, see works by Mishima and Stanley (3), Angell (8), Debenedetti and Stillinger (9), and Mayer (10)). High-density amorphous ice can be obtained if hexagonal ice is subjected to high pressure (10 kbar) at 77 K (11). High-density amorphous ice (density of 1.17 g/cm³ at zero pressure) transforms into low-density amorphous ice (LDA, 0.94 g/cm³) at zero pressure and 117 K (12). LDA, ASW, and HQGW are of similar structure and density and are generally acknowledged to undergo a glass transition, at which the water molecules gain rotational mobility (13) upon warming (at 136 K for ASW and HQGW and at 129 K for LDA (10,14,15). Further warming to 150 K leads to formation of crystalline cubic ice (10). Evidence has been presented that translational diffusion occurs concomitantly with crystallization (16) and, consequently, water in the temperature window between the glass transition and crystallization has been termed “ultraviscous” (3). The existence of ultraviscous water, however, remains controversial (4–6) and it has been proposed that glassy water directly transforms into the crystalline state at 150–160 K (17). In either case, the liquid (or glassy) state of bulk water cannot be studied between 150 and 235 K because of crystallization. Consequently, this temperature range has been called a “no-man's land” (3).

The study of confined water (18–22) allows one to enter the no-man's land experimentally (23). Water molecules in direct contact with the confining medium—interfacial water—have a similar room temperature (293 K) structure as supercooled bulk water 30 K below room temperature (263 K) (24). Interfacial water is more H-bonded than bulk water at the same temperature (25) and does not form crystalline ice even at 77 K (24). Confined water beyond the interfacial region has been reported to crystallize into a distorted form of cubic ice, in contrast to bulk water, which crystallizes into ordinary hexagonal ice (26). Water confined by hydrophilic surfaces exhibits a molecular layering with a mean periodicity of 2.5 Å (27–28). Computer simulations of 2D confined interfacial water in hydrophilic nanopores suggested the formation of two well-defined layers that are already in a glassy state at ambient temperature, displaying very low mobility with respect to bulk water (19). Beyond these two layers, water shows bulk-like character. The effect of confinement has been reported to decrease with decreasing dimensionality of confinement (20); water confined in one dimension between parallel sheets of mica has been shown to have a mobility at room temperature very close to that of bulk water down to at least the first hydration layer (18).

Coupling between macromolecular dynamics and the surrounding water, which would greatly benefit from a better understanding of confined water behavior, remains an important issue for study (29–33). It is widely acknowledged that intramolecular motions, associated with transitions between substates in the conformational energy landscape of proteins, are essential for biological function and activity (34,35). The energy landscape is organized in tiers, each characterized by the height of the energy barriers separating different substates. On the top level, transitions between a small number of substates separated by relatively high energy barriers (31), result in slower conformational changes on the microsecond to millisecond timescale involved in enzyme catalysis (36,37), for example. In the bottom tiers, faster thermal motions on the atomic level, occurring on a timescale between 10⁻⁷ and 10⁻¹² s, correspond to local fluctuations with small barriers and are believed to act as a lubricant for the slower conformational changes (38).

Thermal motions exhibit a so-called dynamical transition, as shown by Mössbauer e.g., (39) and neutron spectroscopy studies (40,41; for a review, see Gabel et al. (42)). The dynamical transition, occurring at 150–250 K in proteins and biological membranes (40,41,43–46), marks the onset of nonharmonic motions and has been shown to be crucial for certain proteins to function optimally (47,48). There are enzymes, however, that are able to perform part of their catalytic function well below the dynamical transition (49) or to turn over at a rate expected from normal Arrhenius behavior (50,51).

Solvent fluctuations and viscosity have been shown to influence protein dynamics (48,52,53), and protein motions have been termed “solvent-slaved” (54) if their temperature dependence follows that of dielectric solvent fluctuations, “hydration-shell-coupled” if they follow those in the hydration shell (32), and “nonslaved” if they exhibit an intrinsic, solvent-independent temperature dependence (31). It has been shown by Mössbauer spectroscopy that fluctuations in the heme-iron of myoglobin, for example, exhibit a temperature dependence similar to the mobility of hydration water (55). Computer simulations have suggested that solvent fluctuations determine protein motions above the dynamical transition, whereas intrinsic protein motions dominate below the transition (30). Picosecond fluctuations of xylanase in various cryosolvents of different glass-transition temperatures have been monitored by incoherent elastic neutron scattering experiments (29). These studies suggested that the dynamical transition of a protein takes place at a temperature determined by either the protein or the solvent, depending on which component has the higher transition temperature. Even though protein motions are generally accepted to be influenced by solvent motions, the question as to whether or not a solvent glass transition directly triggers a protein dynamical transition remains a delicate issue that needs further investigation. In the work presented here, purple membranes, containing 75% (w/w) protein and 25% lipid, were used to study the cryotemperature behavior of water confined in the membrane stack and its effects on protein dynamics.

The purple membrane (PM) from halophilic Archaea (56) is constituted of only one type of protein, the light-driven proton pump bacteriorhodopsin (57), and a set of defined lipids. Native PM is organized in a 2D crystalline lattice. The lattice is maintained upon isolation and confers rigidity to the ∼0.5-μm-diameter planar patches of proteolipid complex (58). Drying a suspension of PM fragments produces regular stacks, with a lamellar spacing that can be varied from 49 Å (the thickness of the vacuum-dried membrane) to 109 Å (viz. 60 Å of water between adjacent membrane fragments) by equilibration under different ambient relative humidities (59–65). Slowly cooling a hydrated stack of PM to below 273 K has been shown to result in supercooling of the confined water. A sharp decrease in lamellar spacing between 270 and 243 K, depending on the initial degree of hydration at room temperature, has been attributed to the flow of water out of the intermembrane space, where confinement hampers crystallization, toward less confined regions outside stacks, where it can crystallize (64). Dehydration upon slow cooling also has been observed with stacks of planar lipid membranes (66).

In this study, flash cooling was employed to trap water confined in stacks of purple membranes in an amorphous state. Upon subsequent warming, the lamellar spacing of the stack decreased abruptly at 200 K, as monitored by neutron diffraction, and ice diffraction appeared, indicating that water flowed out of the intermembrane space to crystallize outside the stack. Only the first hydration layer remained associated with the membrane surface, and the experiment establishes that water beyond that shell can exhibit long-range translational diffusion at such low temperatures. The observation provided circumstantial evidence for the existence of a glass transition at or below 200 K in confined water, from an amorphous to an ultraviscous liquid-like state (3). Incoherent elastic neutron scattering to study nanosecond dynamics, carried out on the same sample, revealed identical behavior in both flash- and slow-cooled samples, with dynamical transitions at 150 and 260 K and no indication of a transition at 200 K, suggesting that nanosecond protein motions are independent of the state of intermembrane water beyond the first hydration layer at temperatures <260 K.

MATERIALS AND METHODS

Sample preparation and characterization

PM were isolated from Halobacterium salinarum strain S9 as described previously (56). H₂O was exchanged against D₂O by three successive centrifugation steps (100,000 × g, 10°C, 60 min). The pellet, containing ∼200 mg PM, was spread out in a flat rectangular aluminum container (surface area 4 × 3 cm², neutron path length 0.5 mm) and partially dried over silica gel to ∼0.3 g D₂O/g PM as determined by weighing. The sample was subsequently equilibrated for several days in a relative humidity atmosphere of 100% D₂O. Sample water was exchanged with D₂O for reasons related to the neutron scattering experiments (see below), but the behavior of H₂O is not expected to differ substantially, since the isotope effect in bulk water has been reported to shift characteristic transition temperatures by ≤6 K (67). The container was closed with an aluminum cover with an airtight indium seal. The procedure led to an orientation of the membrane fragments parallel to the container surface with a mosaicity of ∼25 ° as measured by neutron diffraction. The same sample was employed for both the neutron diffraction and neutron scattering experiments. Flash cooling was achieved by plunging the container into liquid nitrogen. The sample was rapidly transferred into an “orange” cryostat (Institut Laue-Langevin (ILL), Grenoble, France) and precooled to 100 K (for the diffraction experiments) or 50 K (for the scattering experiments). A higher cooling rate of flash cooling, by immersing the sample container into a vacuum-prepared mixture of solid and liquid nitrogen (a nitrogen slush), gave essentially the same results.

Neutron diffraction experiments

Neutron diffraction experiments were carried out on the D16 diffractometer at the ILL with a wavelength of 4.53 Å. In a first experiment on the flash-cooled sample, the temperature was raised from 100 to ∼300 K and then slow-cooled back to 120 K. During both heating and slow cooling, the temperature was changed in 5-K steps and was kept constant for 28 min after each step. In a second experiment, the temperature was changed after flash cooling from 100 to ∼300 K with a plateau of several hours at 170, 210, 230, 250, 260, 270, 280, and 300 K during which data were acquired at 29-min intervals. Lamellar spacing, d, was determined by monitoring the first-order Bragg peak of the membrane stack, and the unit-cell parameter, a, of the 2D lattice was determined from the in-plane reflections of the trigonal PM lattice. Ice formation was monitored by integrating the intensities of part of the most prominent powder ring, which correspond to spacings of 3.67 Å (Q = 1.71 Å⁻¹; originating either from amorphous ice, the (1 1 1) reflection of cubic ice, or the (0 0 2) reflection of hexagonal ice) and 3.91 Å (Q = 1.61 Å⁻¹; (1 0 0) reflection of hexagonal ice).

Incoherent elastic neutron scattering experiments

Neutron scattering experiments are perfectly suited to measure protein dynamics on an atomic level. This is because the wavelength (a few Å) and energy (a few meV) of cold and thermal neutrons match interatomic distances and energies of macromolecular thermal motions (corresponding to the picosecond–nanosecond timescale). Neutrons are scattered by atomic nuclei and are sensitive to isotope effects. The incoherent-scattering signal of hydrogen atoms is almost two orders of magnitude larger than those of other atoms present in biological samples and of deuterium. As a consequence, and since hydrogen atoms are uniformly distributed throughout a biological macromolecule, incoherent neutron scattering experiments probe dynamics averaged over the entire biological sample (“global” dynamics). On the picosecond–nanosecond timescale, the motions of H-atoms reflect the dynamics of the larger chemical groups, such as the amino acid side chains to which they are bound. In D₂O-hydrated PM samples, the contribution of the hydration water to the incoherent scattering signal is negligible and experiments probe essentially the global membrane dynamics (the BR and lipid components).

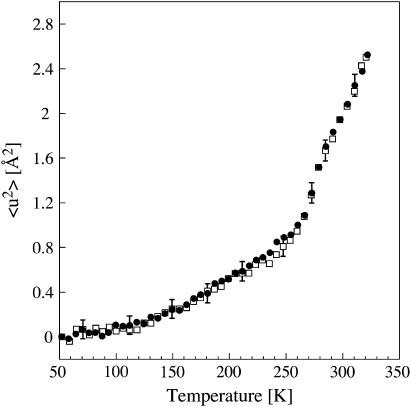
Incoherent elastic neutron scattering experiments probe motions in a time and space window determined by the energy resolution (ΔE) and accessible scattering-vector, Q, range (Q = 4πsinθ/λ, where 2θ is the scattering angle and λ is the neutron wavelength) of the neutron spectrometer. Experiments were performed on the IN16 spectrometer at the ILL, in elastic mode, with a wavelength of 6.275 Å and an energy resolution of 1 μeV (68), corresponding to a length-time window of a few Ångstroms in 1 ns. The elastic scattered intensity was analyzed according to a Gaussian approximation that is valid for Q² 〈 u² 〉 ≤ 2 (69): S_T(Q, 0 ± ΔE) = const. exp(−1/6Q²〈u²〉). 〈u²〉 is the mean-square displacement at a given temperature T, corresponding to the full extension of the movement. The mean-square displacement plotted in Fig. 5 represents the global, averaged, dynamics of atoms in the sample (excluding hydration D₂O, which contributes only weakly to the scattering) for motions occurring in 1 ns or shorter times, localized in a length window of a few Ångstroms.

FIGURE 5.

Mean-square displacements (〈u²〉) of motions faster than 1 nanosecond in flash-cooled (• and slow-cooled (□) PM as a function of temperature as measured on IN16. Every data point corresponds to 26 min of acquisition, during which the temperature increased by 6 K. Errors are shown for selected data points.

After flash cooling, the sample temperature was changed linearly as a function of time from 50 to ∼320 K (at 0.23 K/min). Data were collected in time intervals of 26 min, during which the temperature increased by 6 K. When 320 K was reached, the sample was slowly cooled back to 50 K in 2.5 h. Data were then collected again during heating to 320 K, at the same rate as described above. Sample container and absorption-corrected intensities were normalized by the value corresponding to the lowest temperature (T₀ = 50 K). Error calculations assumed Poisson statistics for the measured intensities (I) and variance (I) = I. The mean-square displacement 〈u²〉 was obtained from linear fits of ln[(S_T(Q, 0 ± ΔE)/S_50K(Q, 0 ± ΔE)] versus Q². Data were analyzed in the Q-range from 0.4 to 1.24 Å⁻¹. The errors associated with the linear fit (and therefore on 〈u²〉) were calculated using Igor Pro, Version 4.3, WaveMetrics, by weighting each intensity data point according to its statistical error. The 〈u²〉 values were plotted as a function of sample temperature T. IN16 has a unique provision, which permits the measurement of diffraction and inelastic scattering simultaneously up to a Q value of 2 Å⁻¹ (70), and it was used to monitor ice diffraction peaks.

RESULTS AND DISCUSSION

Liquid-like water flows out from between purple membranes at 200 K

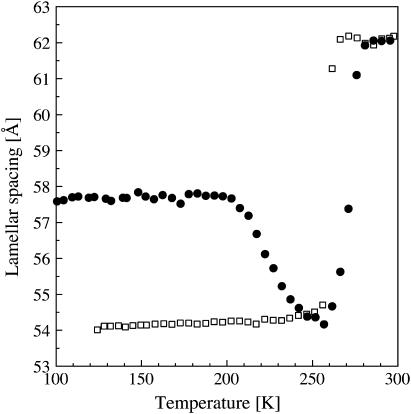
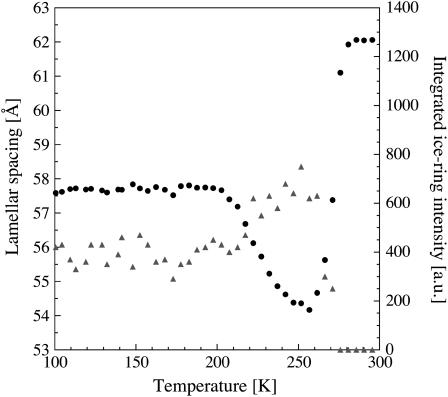
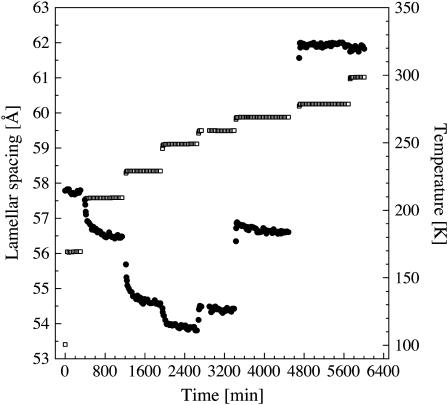
Flash-cooling PM stacks led to a decrease in lamellar spacing from 62 Å at room temperature to 58 Å at 100 K, i.e., to a reduced intermembrane space of ∼9 Å (Fig. 1). Given the mean periodicity of 2.5 Å of water layers confined by hydrophilic surfaces (27,28), this value corresponds to three to four layers of water between adjacent membranes. The lamellar spacing after flash cooling (58 Å) did not depend on the initial room temperature value, which ranged between 59 and 69 Å for different samples examined. The lamellar spacing after flash cooling was equally insensitive to increased flash-cooling rates when the sample holder was immersed in nitrogen slush rather than in liquid nitrogen (see Materials and Methods). Only 3–4 water layers (viz. the two “first hydration layers”, each in direct contact with a membrane surface, and one to two “second hydration layers”) can be vitrified at the cooling rates employed in our experiments. Water beyond the second hydration layers drains from the intermembrane space during flash cooling, indicating that it is characterized by a considerably higher mobility, in line with observations on globular proteins (71). Flash cooling led to the concomitant appearance of a sharp diffraction peak at Q = 1.71 Å⁻¹ (corresponding to a d-spacing of 3.67 Å). A diffraction peak at Q = 1.61 Å⁻¹ (corresponding to a d-spacing of 3.91 Å) was not detected. Upon slow-heating, the lamellar spacing remained constant up to 200 K. It decreased abruptly upon further heating to reach a minimum value of 54 Å at 260 K (Fig. 1), with a concomitant monotonic increase in intensity of the diffraction peak at Q = 1.71 Å⁻¹ (Fig. 2). Above 260 K, the lamellar spacing increased again and, at 280 K, reached the initial value of 62 Å, determined at room temperature before flash cooling (Fig. 1). A diffraction peak at Q = 1.61 Å⁻¹ appeared at 260 K, continued to grow, and disappeared again upon further heating to ∼273 K (not shown). Upon slow cooling from 300 K, the lamellar spacing started to decrease at 260 K to reach a minimum value of ∼54 Å at 240 K (Fig. 1), with a concomitant appearance of diffraction peaks at Q = 1.61 and 1.71 Å⁻¹ (not shown). No abrupt change in lamellar spacing at 200 K was seen during slow cooling.

FIGURE 1.

Lamellar spacings of stacks of purple membranes as a function of temperature as determined by neutron diffraction on D16. (•) Lamellar spacing after flash cooling upon heating from 100 to 300 K; (□) lamellar spacings during subsequent slow cooling from 300 to 120 K. Errors in lamellar spacings were estimated to be ∼0.2 Å. The time interval between successive data points was 28 min.

FIGURE 2.

Integrated intensity of the diffraction peak at Q = 1.71 Å⁻¹ (▴) and lamellar spacings (•) of flash-cooled stacks of purple membranes as a function of temperature upon heating from 100 to 300 K.

The abrupt decrease in the lamellar spacing of PM stacks after flash cooling and slow heating to 200 K, with concomitant strengthening of the ice diffraction, indicated that water beyond the first hydration layer displayed liquid-like behavior at that temperature and drained out to crystallize outside the intermembrane spaces in which ice formation is prevented by the 1D confinement. The observation offers proof for a glass transition in the confined water beyond the first membrane hydration layer, from an immobile amorphous state below 200 K to a mobile state, at or below 200 K, viz. of long-range translational diffusion of ultraviscous water in the no-man's land of Mishima and Stanley (3). The decrease by 4 Å in lamellar spacing between 200 and 260 K corresponds to ∼1–2 water layers leaving the membrane stacks. Two layers of water (corresponding to 5 Å = 54 – 49 Å, with 49 Å being the thickness of the dry membrane) remain in the intermembrane space, each in direct contact with a membrane surface. Above 260 K, water from melting ice returned to the intermembrane space and the lamellar spacing increased again to its initial room temperature value. Upon subsequent slow cooling, the membrane stacks dehydrated down to a lamellar spacing of 54 Å at 120 K, corresponding to two first-hydration layers, as previously reported (64).

Based solely on the observation of a diffraction peak at Q = 1.71 Å⁻¹, it is not possible to distinguish between cubic and amorphous ice (24). However, this peak appears concomitantly with the decrease in lamellar spacing, both upon flash cooling and upon subsequently raising the temperature from 200 to 260 K; it must, therefore, originate from water that flowed out of the intermembrane spaces. It is highly unlikely that amorphous intermembrane water turns liquid at 200 K, leaves the intermembrane space, and is deposited as amorphous ice outside the membrane stacks, since there would be no gain in free energy. We concluded, therefore, that cubic ice forms when flash-cooled amorphous water returns to equilibrium by crystallizing outside the membrane stacks. Cubic ice recrystallizes into hexagonal ice at 260 K as seen by the decrease in intensity of the peak at Q = 1.71 Å⁻¹ and the appearance of a peak at Q = 1.61 Å⁻¹. Hexagonal ice is formed during slow cooling at 260 K. A similar observation of liquid-like solvent being transported at ∼200 K out of a confined space has been made with flash-cooled 3D protein crystals (72). In this case also, the transported solvent formed crystalline ice at the borders of the confined space (i.e., at the protein crystal surface).

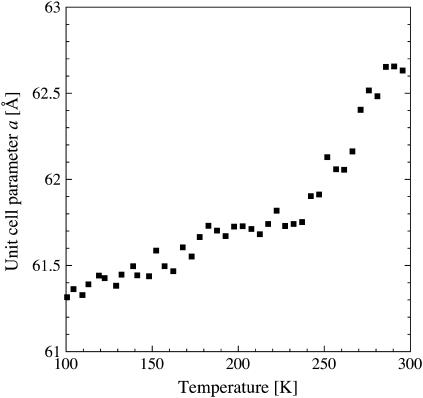
It might be argued that the sudden decrease in lamellar spacing at 200 K is the consequence of a structural change within the membrane plane. This is ruled out, however, by the temperature dependence of the unit-cell dimension a of the 2D PM lattice (Fig. 3). After flash cooling, the unit-cell parameter a showed a biphasic linear behavior upon heating from 100 to 300 K with a change in slope at 250 K, yet not at 200 K. The behavior of a as a function of temperature is strikingly reminiscent of the dynamical transition in the mean-square displacement characterizing PM thermal motions, measured by incoherent elastic neutron scattering (see below).

FIGURE 3.

Unit cell parameter a of the two-dimensional PM lattice as a function of temperature. (▪) a after flash cooling upon heating from 100 to 300 K. The error in a was estimated to correspond to ∼0.1 Å. The time interval between successive data points was 28 min.

To gain insight into the characteristic times of lamellar spacing changes after flash cooling, the temperature was increased stepwise with sufficiently long time intervals at constant temperature to allow the lamellar spacing to equilibrate (Fig. 4). Dehydration of the flash-cooled membrane stacks above 200 K, and rehydration above 260 K, appeared to proceed in steps, involving the same intermediate spacings, viz. 54.5 (corresponding to ∼2 water layers) and 56.5–57 Å (corresponding to ∼3 water layers), which is in line with the reported layering effect of confined water (27,28). Rehydration above 260 K was immediate on the timescale of our experiments (∼30 min per data point in Figs. 1–4), whereas dehydration appeared to be a slow process with relaxation times between 105 min (at 210 K) and 67 min (at 230 K). Most probably, this timescale reflects the macroscopic relaxation time for rearrangement of the membrane fragments and not the molecular diffusion of water molecules. Information about the molecular relaxation time of intermembrane water in flash-cooled stacks of purple membranes has been obtained from dielectric loss spectroscopy (73). At 200 K, a characteristic time in the order of microseconds has been found. Dielectric spectroscopy probes movements of individual dipole moments, however, so that the diffusion coefficient of ultraviscous intermembrane water at 200 K, a collective-transport measure, remains to be determined.

FIGURE 4.

Lamellar spacings (•) of flash-cooled stacks of purple membranes as a function of experimental time. The temperature (□) was increased stepwise from 100 to 300 K after flash cooling. Errors in lamellar spacings were estimated to be ∼0.2 Å. The time interval between successive data points was 29 min.

Glass transition of intermembrane water beyond the first hydration layer does not trigger a dynamical transition of nanosecond motions in purple membranes

Does the glass transition in the second hydration layer water directly trigger a dynamical transition in the membrane itself? To address this issue, we determined the mean-square displacements of flash- and slow-cooled PM as a function of temperature by incoherent elastic neutron scattering. Upon heating the flash-cooled sample, Bragg peaks at Q = 1.71 Å⁻¹ and at Q = 1.61 Å⁻¹ appeared at 200 K and at 260 K, respectively. After subsequent slow cooling, both peaks were present during heating between 50 and 273 K (not shown). This confirmed that the state of the flash-cooled sample was the same for the IN16 and D16 experiments. The IN16 spectrometer measures movements occurring in times <∼1 ns. Only the membrane dynamics were analyzed, since the contribution of D₂O to the incoherent scattering signal is negligible (see Materials and Methods). The mean-square displacements in flash- and slow-cooled stacks of purple membranes were found to be essentially identical (Fig. 5), with two dynamical transitions, at 150 and 260 K, and no transition observed at 200 K. We conclude that the glass transition of intermembrane water beyond the first-hydration layer does not trigger a dynamical transition of motions in PM occurring in up to a nanosecond. In other words, slow water motions (the molecular relaxation time at the glass transition is typically in the order of 100 s (8)) do not influence fast (nanosecond) membrane dynamics. Our results do not exclude, however, that the water glass transition influences slower membrane motions and/or that water motions couple to nanosecond membrane motions at a temperature at which their relaxation time is in the order of nanoseconds.

Our results show that translational diffusion of water molecules in the flash-cooled PM stacks between 200 and 260 K does not affect membrane dynamics on the nanosecond timescale. At first glance, this seems contradictory to molecular dynamics simulations of globular proteins, which suggest that the onset of solvent translational mobility drives the protein dynamical transition (74,75). However, the contradiction is only apparent because these and other simulations (see, e.g., Vitkup et al. (30)) included only one hydration layer. Our results establish, therefore, that the importance of translational diffusion for the protein dynamical transition is limited to the first hydration layer. In the terminology of Frauenfelder (32), our results suggest that nanosecond motions in PM at temperatures below 260 K are hydration-shell-coupled motions that do not follow the temperature dependence of bulk-solvent fluctuations.

SUMMARY

We have employed neutron diffraction and incoherent scattering to address the behavior of amorphous water confined in thin films by native biological membranes and its relation to protein dynamics. The second hydration layers show long-range translational diffusion upon heating at 200 K, as revealed by a decrease in lamellar spacing, which is ascribed to draining of water molecules from the intermembrane space. This shows that amorphous water confined in one dimension by biological membranes transforms into an ultraviscous liquid above its glass transition before crystallization. Water beyond the second hydration layers cannot be vitrified with the cooling rates employed in our study and is, therefore, substantially more mobile. The first hydration layers remain in contact with the membrane surface throughout the entire temperature range studied. Incoherent neutron scattering shows that water confined in native biological membranes starts to display liquid-like behavior at least 60 K below the dynamical transition temperature of nanosecond protein motions in the membrane. Consequently, the solvent glass transition does not trigger a protein dynamical transition of nanosecond motions.