Molecular Dynamics Simulations of the 136 Unique Tetranucleotide Sequences of DNA Oligonucleotides. II: Sequence Context Effects on the Dynamical Structures of the 10 Unique Dinucleotide Steps

Abstract

Molecular dynamics (MD) simulations including water and counterions on B-DNA oligomers containing all 136 unique tetranucleotide basepair steps are reported. The objective is to obtain the calculated dynamical structure for at least two copies of each case, use the results to examine issues with regard to convergence and dynamical stability of MD on DNA, and determine the significance of sequence context effects on all unique dinucleotide steps. This information is essential to understand sequence effects on DNA structure and has implications on diverse problems in the structural biology of DNA. Calculations were carried out on the 136 cases embedded in 39 DNA oligomers with repeating tetranucleotide sequences, capped on both ends by GC pairs and each having a total length of 15 nucleotide pairs. All simulations were carried out using a well-defined state-of-the-art MD protocol, the AMBER suite of programs, and the parm94 force field. In a previous article (Beveridge et al. 2004. Biophysical Journal. 87:3799–3813), the research design, details of the simulation protocol, and informatics issues were described. Preliminary results from 15 ns MD trajectories were presented for the d(CpG) step in all 10 unique sequence contexts. The results indicated the sequence context effects to be small for this step, but revealed that MD on DNA at this length of trajectory is subject to surprisingly persistent cooperative transitions of the sugar-phosphate backbone torsion angles α and γ. In this article, we report detailed analysis of the entire trajectory database and occurrence of various conformational substates and its impact on studies of context effects. The analysis reveals a possible direct correspondence between the sequence-dependent dynamical tendencies of DNA structure and the tendency to undergo transitions that “trap” them in nonstandard conformational substates. The difference in mean of the observed basepair step helicoidal parameter distribution with different flanking sequence sometimes differs by as much as one standard deviation, indicating that the extent of sequence effects could be significant. The observations reveal that the impact of a flexible dinucleotide such as CpG could extend beyond the immediate basepair neighbors. The results in general provide new insight into MD on DNA and the sequence-dependent dynamical structural characteristics of DNA.

INTRODUCTION

Basepair sequence effects on structure and dynamics are a key issue in understanding the biochemistry and biology of DNA at the molecular level. Most information on sequence effects to date has been limited to the 10 unique dinucleotide steps. However, recent, more extensive considerations of the problem indicate that dinucleotide steps are sensitive to at least nearest neighbor sequence context. The minimum structural unit which reveals nearest neighbor sequence context effects is the tetranucleotide step, of which there are 136 unique sequence permutations. At present, the experimental structural database of DNA tetranucleotide steps at atomic resolution, derived primarily from x-ray crystallography and emerging results from NMR spectroscopy, is quite sparse. However, the ability to model DNA structure in solution using all-atom molecular dynamics (MD) simulations has improved significantly in recent years (1–6), and the study of sequence and sequence context effects has now become accessible to simulations carried out on high performance computers.

This series of articles describes a project aimed at obtaining MD trajectories including water and counterions for all unique tetranucleotide base sequences. This project involves the participation of nine independent research laboratories that initiated this project at a Workshop in Ascona, Switzerland, in June of 2002, referred to as the “Ascona B-DNA Consortium” (ABC). Overall, we seek to obtain MD trajectories for the 136 unique DNA tetranucleotides embedded in 39 DNA oligomers having repeating sequences. The oligomers are each 15 nucleotide pairs in length and are capped on both ends by GC pairs. All MD simulations were performed with a consensus protocol using the AMBER suite of programs (7) and the parm94 force field of Cornell et al. (8). This force field, although not the only option, has been verified in test cases to produce good overall agreement between calculated and observed DNA structures in crystals and in solution (9,10). MD trajectories of 15 nanoseconds (ns) have been obtained for each of the 39 oligomers. In Work I of this series (11), we presented the research design, MD protocol, convergence and stability, and informatics considerations, and reported results on sequence context effects in d(CpG) steps. In this work, we provide results from the structural analysis of all the 136 unique tetranucleotides.

Background

The general background necessary to this research was presented in some detail in Work I. We present here only a concise summary of salient information together with references to published work in the field of MD on DNA that has appeared in the interim. The initial motivation for this study was the investigation of first neighbor context effects on the structures of DNA dinucleotide steps, which requires knowledge of the structures of all 136 unique tetranucleotides. Experimental oligonucleotide structures from crystallography or NMR spectroscopy at the tetranucleotide step level are available for only a limited number of specific cases. Even so, surveys of these structures have raised the possibility of significant sequence effects (12–14). An extensive theoretical consideration of the problem to date is due to Packer et al. (15,16), who presented detailed considerations based on the minimization of stacking energies for tetranucleotide steps as described by empirical energy functions.

New NMR experiments based on residual dipolar coupling (RDC) offer the possibility of obtaining higher resolution structures of oligonucleotides in solution (17) and may have sufficiently high resolution to accurately resolve DNA fine structure. Presently, NMR/RDC structures of DNA oligonucleotides are just beginning to appear in the literature (18–20). MD simulations on each of these sequences have been carried out and are found to be generally in close accord with NMR-derived solution structures (9,21). In the case of dodecamers containing the dA6 motif, independent MD in solution were carried out starting from the x-ray crystal structure and the NMR solution structure and canonical B-form DNA (21). The results converged rapidly to a structure in close proximity to the observed NMR solution structure. The current ideas on sequence-dependent bending and curvature of B-DNA have been recently reviewed by Beveridge et al. (22) and Zhurkin et al. (23).

Recent surveys of the field of MD on DNA are available from several sources (2–6,24). The AMBER parm94 (8) is a “second generation” parameterization of the nucleic acids force field for MD using explicit solvent models for proper treatment of electrostatics. MD using AMBER and parm94 provided the first well-behaved MD trajectories of the DNA double helix (6,25–28). Known shortcomings in parm94 still include a sensitive problem in the coupling of base-sugar torsions and a systematic tendency toward somewhat underwound structures. A modification known as parm99 has recently been proposed (29) which improves twist but appears less sensitive to changes in the environment (high salt, ethanol), leading the ABC group to use the parm94 force field, well characterized with respect to experimental data on prototype cases (9,30). Leading references to force field alternatives are provided in Work I. A new version on nucleic acids force field for GROMOS (31) as well as CHARMM (32) has recently appeared, but extensive force field comparisons are beyond the scope of this study.

Updating the literature on studies of sequence effects on DNA deformability since Work I of this series, Matsumoto and Olson (33) reported normal mode analysis of oligonucleotide DNA using knowledge-based potentials obtained from high-resolution crystal structures. The results successfully accounted for the bending persistence length and stretching modulus of DNA and indicated a sensitivity of twisting force constants to the basepair sequence. An MD study of two 18-basepair DNA oligomers was recently reported by Lankas et al. (34). In these two sequences, all 10 unique dinucleotide basepair steps are represented, which provides a point of comparison with some of the results of this study. A marked trend in relative flexibility in roll, pyrimidine(Y)-Purine(R) > purine-purine > purine-pyrimidine was noted in the study, and the YpR steps were also found to be the most flexible in tilt and partially in twist, supporting previous results (35). Slide-rise, twist-roll, and twist-slide elastic couplings of various degrees were observed. A possible correlation of motions on a length scale of 2–3 basepairs was noted, which falls in the neighborhood of first neighbor context effects. A set of basepair step sequence-dependent bending force constants was recently obtained from electron paramagnetic resonance studies by Okonogi et al. (36). Ho and co-workers (37) are assembling a crystallographic data set of DNA structures involving all permutations of the inverted repeat sequence d(CCnnnN₆N₇N₈GG) where N₆, N₇, and N₈ are any of the four naturally occurring nucleotides and the ns are the corresponding bases to maintain self-complementarity. The presented data based on 29 of the possible 64 permutations of the trinucleotides correlate sequence and environment with the B, A, and Holliday junction-like structural classes and their variability.

An issue of particular interest in MD on DNA is the motion of mobile counterions, which may also contribute interesting sequence effects (38–40) and have been noted from previous studies to be slow to converge (30). Varnai and Zakrzewska (41) performed MD simulations on d(CCCATGCGCTGAC) and studied the behavior of mobile counterions Na⁺ and K⁺. The ions, as expected, preferentially sampled electronegative sites around the DNA, but direct ion association with nucleotide bases occurred in <13% of the trajectory. Interesting ion- and sequence-specific effects were observed in which preferential direct binding of Na⁺ ions occurred at a minor groove site, whereas the larger K⁺ ions favored a site in the major grove. This introduces a degree of complexity not apparent from just examining the electrostatic potential of DNA (42). Little evidence of minor groove narrowing correlated with ion binding was observed, a topic around which there has been a diversity of opinion (38–40).

Extended studies on the d(CGCGAATTCGCG) sequence (43) indicate that DNA conformational and helicoidal parameters including groove widths have relaxation times of ∼500 ps or less. The rule of thumb is to sample 10 times the relaxation time of all the indices of interest for a particular application (44). This indicates that 5 ns trajectories should be sufficient in the absence of substate problems (see below), and we are well in excess of that in the 15 ns trajectories carried out in phase I of this project. Observed diffusion constants indicate that motions of mobile counterions in the environment of DNA will be relatively slow to converge. Ponomarev et al. (43) reported a benchmark indicating that ion occupancies can take up to 100 ns to stabilize. However, in the same calculation, the DNA parameters were found to be well stabilized at 5 ns and not sensitive to the fine details of ion convergence. The calculated DNA counterion radial distribution functions were found to be essentially unchanged after 3–5 ns, indicating that mean field effects of ions are dominant in DNA structure and that the excess sampling to get ion occupancies converged is a matter of granularity of the ion distributions.

DNA has the potential for contributions from manifold thermally accessible substates (45,46). Known examples of this are the B_I-B_II transitions (47), α/γ crankshaft motions (48), and YpR hinge motions (49). The last have been noted to play an important role in structures of protein-bound DNA (13) as well as DNA curvature (22). Rich and co-workers (50) have observed a correlated α/γ transition in A-form DNA from the preferred g−/g+ state, which they called A_I, to a less common and less constricted t/t state they labeled A_II. Sundaralingam and co-workers (51) have noted that distortions in the α/γ on the 5′-side of the sugar are more common in A-DNA, whereas conformational changes in the ɛ/δ on the 3′-side are more common in the B-form DNA. Indications from the crystallographic database and MD are that certain basepair steps show high flexibility, whereas those involved in A-tracts are relatively rigid (35,52–54). This raises the question of which are more susceptible to sequence context effects, rigid or flexible steps. One could argue either way since more rigid steps could either resist deformation or respond as a unit whereas flexible steps are more malleable but could absorb perturbations more easily. The problem this poses to a simulation arises from the need to sample all thermally accessible substates adequately to obtain an ensemble of snapshots which properly represent the dynamical structure of the DNA.

The d(CpG) step in all its possible neighboring sequence contexts was chosen for preliminary analysis as described in Work I, since x-ray structures indicate that this and possibly other YpR steps have a potential for context-dependent substates (49,52). The results were surprising in several respects. First, although many structural and dynamic features of the oligomers studied have converged to stable values, the results indicate that slow backbone transitions prevent a complete sampling of the conformation space of B-DNA in the MD on CpG steps. For the same reason it is not yet possible to characterize all the consequences of such backbone transitions, which can occur independently or be coupled together, and which can influence the structural and dynamic behavior beyond the junction where the transition occurs. If we filter out such effects, the remaining conformational sampling appears to be reasonably balanced but also suggests that the surrounding sequence has a very small effect on the properties of the CpG step. This indicates that any difference in the underlying potential as a consequence of the surrounding sequence is probably only a fraction of a kcal/mol.

The preliminary analysis obtained in Work I for the dCpG step anticipates at least some of the problems involved and issues to be considered. However, before drawing any general conclusions, it is clearly necessary to complete the analysis of all 136 unique tetranucleotides. At this point all simulations from the initial phase of ABC are completed and analyzed. The data obtained will hopefully allow us to obtain an increasingly clear view of sequence context effects, to better understand the importance of such phenomena as conformational substates, and also to define how end effects and length effects can influence the behavior of DNA fragments.

METHODOLOGY

All simulations have been carried out using the AMBER 6 or AMBER 7 suite of programs (7) and the parm94 force field (8). The simulations cover 39 double-stranded DNA oligomers, each being 15 basepairs in length. The sequences of these oligomers are discussed below. A consensus protocol was adopted for simulation in which the solute molecule is a 15 basepair oligonucleotide with 28 potassium ions added to achieve system electroneutrality. The DNA with its counterions was simulated in a truncated octahedral box having a face-to-face dimension of ∼70 Å, which allows for a solvent shell extending for at least 10 Å around the DNA. The starting configuration has the oligomer in a canonical B-form. The ions are randomly placed around the oligomer and located at least 5 Å from any atom of the solute and at least 3.5 Å from one another in the initial structure. Ion interactions with other atoms are based on the potentials developed by Aqvist (55). The neutral ion-oligomer complex was solvated with TIP3P water molecules (56). Simulations are performed with periodic boundary conditions in which the central cell contains ∼8000 water molecules. Considering the DNA, counterions, and solvent water, the total system consists of ∼24,000 atoms.

The preparations for MD simulations consist of an initial minimization followed by slow heating to 300 K at constant volume over a period of 100 ps using harmonic restraints of 25 kcal mol⁻¹ Å⁻² on the solute atoms. These restraints are slowly relaxed from 5 to 1 kcal mol⁻¹ Å⁻² during a series of five segments of 1000 steps of energy minimization and 50 ps equilibration using constant temperature (300 K) and pressure (1 bar) conditions via the Berendsen algorithm (57) with a coupling constant of 0.2 ps for both parameters. The final segment consists of 50 ps equilibration with a restraint of 0.5 kcal mol⁻¹ Å⁻² and 50 ps unrestrained equilibration. The simulations were then continued for a total of 15 ns at constant temperature and pressure conditions, using the Berendsen algorithm (57) with a coupling constant of 5 ps for both parameters. Electrostatic interactions were treated using the Particle Mesh Ewald (PME) algorithm (58) with a real space cutoff of 9 Å, cubic B-spline interpolation onto the charge grid with a spacing of ∼1 Å. SHAKE constraints (59) were applied to all bonds involving hydrogen atoms. The integration time step was 2 fs. Center of mass translational motion was removed every 5000 MD steps to avoid the methodological problems described by Harvey et al. (60). The trajectories were extended, as noted above, to 15 ns for each oligomer, and conformations of the system were saved every 1 ps for further analysis.

Rather than performing separate calculations on all 136 tetranucleotides using 136 different oligomers (for example, placing each tetranucleotide within a longer duplex surrounded with some standard sequence), we carried out the calculations on oligomers with repeating tetranucleotide sequences (ABCDABCDABCD…). Moving a 4-base “reading frame” along the oligomer, we locate successively ABCD, BCDA, CDAB, and DABC tetranucleotides. The length of the oligomers was chosen to be 15 basepairs, a compromise between the necessity to avoid end effects and the computational expense of the simulations. This strategy enables all 136 tetranucleotides to be studied using only 39 oligomers. We cap the ends of each oligomer with a single GC pair to avoid fraying. This implies that a given 15 basepair oligomer contains 3¼ tetranucleotide repeats 5′-G-D-ABCD-ABCD-ABCD-G-3′, where A,B,C,D are any deoxyribonucleotide. This choice means that if we decide to ignore two basepairs at either end of the oligomer, to avoid potential artifacts from end effects, there will still be two distinct copies of each unique tetranucleotide (ABCD, BCDA, CDAB, DABC) within the remaining 11 basepair fragment. MD trajectories for these 39 oligonucleotides provide a basis for comparing the properties of two copies of each tetranucleotide. Note this is valuable for the study of convergence as well as sequence context effects. The backbone conformational angles and helicoidal parameters of the DNA structure in the MD trajectory were calculated using the program Curves 5.3 (61) and stored in our relational database management system to facilitate mining of this voluminous dataset.

Many questions, including those of interest to this project, involve comparing the results of two chosen MD simulations, or, one chosen simulation with all the others. In the relatively brief history of MD on DNA, the primary tool for this task has been the root mean-square difference (RMSD) between structures or between derived parameters from structures following optimal alignment. In MD simulation, one obtains, in any given trajectory, an ensemble of structural “snapshots”, i.e., the dynamical structure. Previous studies have computed the average structure from this ensemble, calculated after placing a representative number of snapshots in optimal alignment followed by a few cycles of post facto energy minimization which ensures that the average structure assumes a physically reasonable form. Typically the time evolution of RMSD is obtained by calculating the RMSD between each of the MD snapshots and the computed average structure. However, an MD average structure can be misleading when the dynamical structure from MD involves substates. Furthermore, the snapshots which comprise the dynamical ensemble of the DNA from MD are typically 1–2 Å RMSD from the average structure. However, none of the snapshots actually match average structure. This naturally raises a question about the suitability of average structures at all in MD analysis.

In response, a method for comparing MD results has been applied which avoids the use of MD average structures and makes comparisons only on the basis of actual snapshots included in the MD ensemble (S. B. Dixit, S. Ponomarev, K. M. Thayer, and D. L. Beveridge, unpublished). Comparing the results of the dynamical structure from any two MD simulations, the first step is to generate the matrix of RMSD differences for all n structures, where n is the number of MD snapshots considered. In previous works this has been referred to as a two-dimensional (2D) RMSD plot (46). The characteristics of a 2D RMSD plot are interesting per se in the identification of substates (46,62). However, our primary use of this information in this project comes in the generation of a plot of the probability of observing a given RMSD between all snapshots in both simulations, the RMSD probability denoted as P(rmsd). It is of interest to distinguish two cases at this point: a), the P_intra (rmsd) in which the RMSD of all structures with all other structures in a given trajectory are displayed to ascertain the extent of thermal motions, and b), the P_inter (rmsd) in which the structures from one distribution are compared with those of another. The question of whether the results of the two MD simulations are similar or not in RMSD probability analysis reduces to comparing the P_intra (rmsd) and P_inter (rmsd) distributions. For two simulations in which the P(rmsd) results are identical, these should be the same.

In this study we compare the probability distributions of angular RMS deviations calculated for the backbone dihedral angles (α, β, γ, ɛ, ζ) involved in connecting consecutive nucleotides, the phase and amplitude of the sugar pucker, and the torsional angle χ connecting the sugar and the base in the tetranucleotide, with reference to every other conformation adopted by that tetranucleotide in the trajectory and also the conformations adopted by the second occurrence of the same tetranucleotide sequence in the database. The use of angular (internal) coordinates for the RMSD calculation instead of the usual Cartesian coordinates results in the use of a smaller number of variables to define the structure of a section of the DNA and also avoids the problem associated with fitting of structures to a reference frame before an RMSD calculation is performed in Cartesian space. The results in this article employ the backbone conformational and basepair helicoidal parameters of DNA as defined by Dickerson et al. (63,64) and implemented in the Curves program (65). For a recent article dealing with the derivation of DNA structural parameters, see Lu and Olson (66).

When two P(rmsd) results differ, one may compare the two distributions using statistical tests to determine the confidence level with which one may infer the two sets of structures to have been drawn from the same general population. The standard statistical test for the similarity in such situations is the χ² test for independence (67), which can be readily applied. An alternative, more rigorous information theoretic approach applicable in the case of complex distributions is to calculate the “Kullback-Leibler (KL) Distance”, D_KL, which is a measure of the divergence between a “true” probability distribution, p, and a “target” probability distribution, q (68). For discrete probability distributions, p = {p₁, …, p_n} and q = {q₁, …, q_n}, D_KL is defined as

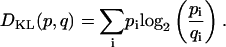For continuous probability densities, the sum is replaced by an integral. The value D_KL is always positive and equal to zero only if p_i = q_i. D_KL is not, in general, symmetric and hence we employ the mean of D_KL(p,q) and D_KL(q,p). This equation based on expected log likelihood ratio between the two distributions is a metric of the relative entropies and can be viewed as the bits of information required to convert one distribution to another. Such an approach to compare the RMSD probability distribution provides a single index for examining the difference between two MD results in a way that avoids the necessity of working with possibly problematic average structures.

RESULTS

The completed data set in this project contains the results of 39 independent 15 ns MD trajectories on DNA 15-mers of various sequence composition, with each of the 136 unique tetranucleotide steps represented at least twice. The complete 15 ns of the postequilibrated trajectory are included in the analysis presented here. The data set contains almost 600,000 coordinate sets. All the trajectories are globally very stable over the complete simulation length and the mass-weighted all-atom RMSD with reference to the simulation average is in the range of 2–4 Å. The A-rich sequences favor a more B-like form in solution, whereas the G-rich sequences present a tendency toward (but not identical to) canonical A-like structure. The average mass-weighted all-atom RMSD of the 39 DNA trajectories with respect to the canonical B-form is ∼4.8 Å and ∼4.9 Å with respect to the canonical A-form DNA. The poly(A) sequence at an RMSD of 3.7 Å with respect to the canonical B-form structure is the most B-like, whereas poly(G) is the farthest from the canonical B-form structure with an RMSD of 6.2 Å and ∼4.6 Å from the A-from structure. Note that the RMSD between the canonical A and B forms of DNA for a 15-mer DNA sequence is itself ∼7 Å. The differences in the A- and B-“like” structures in the MD model are largely observed as a combination of basepair inclination, x-displacement, roll, and helical twist. There are no clear cut transitions to the C3′-endo (north) conformation of the sugar pucker which would be affirmative of transitions between the B and A forms. The solution state structures are not exactly the same as the canonical models of DNA because the atomistic models provide greater fine structural details of the system. The occurrence of such sequence-dependent intermediate structures outside the regime of canonical A or B form has also been reported in crystallography (69).

In Work I, we presented preliminary results on the dCpG dinucleotide step in all sequence contexts. Our analysis revealed that in certain cases, conformational transitions to nonstandard B-form conformational states occurred. Two types of these conformational transitions were prominent: a), B_I/B_II transitions (47), which are reversible within the nanosecond timescale, resulting from coupled changes in the ɛ and ζ values, and b), α/γ flips (48), in which the nonstandard form persisted to an extent that raised a concern about whether or not a sufficient sampling of the conformational space of B-DNA was being achieved. Thus, in the analysis of the complete database, we must address first and foremost the extent to which such long-lived nonstandard substates cause a sampling problem.

Conformational substates of DNA backbone

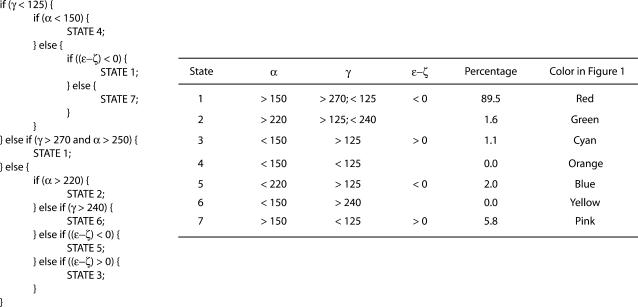
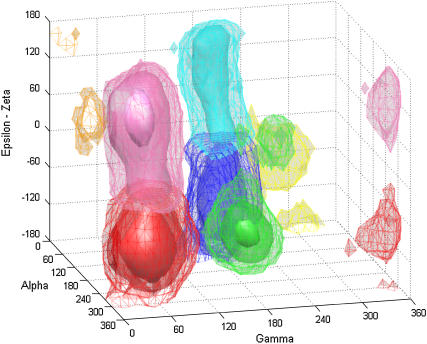
In the canonical B-form DNA obtained from fiber diffraction, the α/γ angles are ∼314°/36° (i.e., g−/g+), whereas during MD, noncanonical substates with α/γ values around g+/t are observed. Transitions between the B_I and B_II states are observed when the value of ɛ/ζ changes from t/g− with (ɛ–ζ) value around −90° to g−/t with (ɛ–ζ) value around +90°. On the basis of distinct combinations of α, γ, and (ɛ−ζ) values adopted, in accordance with the simple classification presented in Table 1, we were able to organize all the DNA backbone conformations in our database into seven putative substates. (For brevity, we refer to these “backbone conformational substates” as just “substates” in the rest of the article.) Similar classes of backbone angles were observed in the work of Varnai et al. (48) in which they explored the free energy surface of the central GpC dinucleotide step in the d(GTCAGCGCATGG) sequence. Fig. 1 shows the probability distribution as a function of α/γ/(ɛ–ζ) values for all the backbone positions in the complete database. This plot is based on a total of 11,700,000 data points, corresponding to the product of 39 DNA trajectory × 10 nucleotide positions (chosen to avoid end effects) × 2 strands × 15,000 snapshots (i.e., sampling structures every picosecond). Note that although the dihedral angles have usually been classified in terms of their values being close to g+/g−/t etc. in the past, we have simply classified the data in terms of the clusters observed in the 3D plot in Fig. 1. States such as 3 and 5 present a range of values that spans across both the g+ and t in case of α, whereas the value of γ is essentially near t. A 2D plot presenting the classification in terms of just the α and γ angles is available in the supplementary material (Supplement 1). General approaches to a consistent identification of the number of sub- or metastable states present in a given time series are discussed in I. Horenko, E. Dittmer, F. Lankas, J. Maddox, P. Metzner, and C. Schuette (unpublished), including the example of an analysis of a 100 ns trajectory of one of the ABC oligomers described here.

TABLE 1.

Algorithm used to classify the DNA backbone conformations into substates 1 to 7 and the resultant classification

FIGURE 1.

3D plot of DNA backbone conformations in the complete database as a function of α, γ, and (ɛ−ζ) values, showing the presence of distinct substates. The color code is as follows: red, state 1; green, state 2; cyan, state 3; orange, state 4; blue, state 5; yellow, state 6; and pink, state 7. Three levels of isosurface are shown: mesh, transparent, and solid coressponding to population densities of 1, 10, and 10,000, respectively.

As seen from Fig. 1, the most densely populated state 1 corresponds to the B_I form, the standard conformation in B-form DNA. Next in importance is state 7, which corresponds to the B_II form of DNA. The angles α and γ are present at their canonical values in both these states with the distinction being in the value of the difference (ɛ − ζ) (both these states are shown in red and pink in Fig. 1). States 5 and 3 (in blue and cyan in Fig. 1) correspond to the noncanonical states due to the α/γ transition, with the subclassification due to the concerted presence of B_I and B_II, respectively. State 2 (in green in Fig. 1) appears when the dihedral γ makes the transition to t, whereas α continues to exist in the standard g-state. States 4 and 6 (shown in orange and yellow in Fig. 1) are scantily populated but distinct, occurring near α and γ values of g+/g+ and g+/g−, respectively. Overall ∼90% of the backbone conformations exist in the regular B_I form (state 1) and another ∼6% in the B_II form (state 7). Thus ∼96% of the backbone conformations exist in the normal α/γ state, whereas the other ∼4% occupies the nonstandard α/γ conformational values.

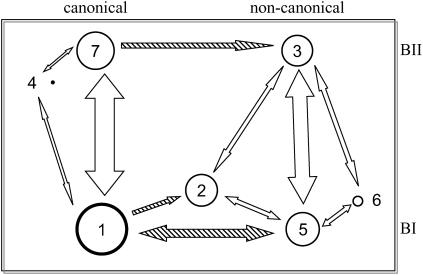
Analysis of the transitions occurring between the seven states indicates that some pathways are preferred over others, and the transitions occurring along these pathways are not necessarily reversible in all the cases (Table 2). The most frequent reversible transitions occur between B_I and B_II states of ɛ and ζ torsions, from state 1 to 7 and from state 5 to 3. These results are summarized in Fig. 2. Transitions involving α/γ torsions are far less frequent and often irreversible. Transitions from state 1 to 5 (both in B_I) and those from state 7 to 3 (both in B_II) clearly prevail over the reverse transitions. There are no direct transitions observed from state 1 to 3, although there are indirect pathways involving transitions through state 5 or state 2. Once a backbone makes a transition from state 1 to 2, the only way out appears to involve a move into either state 3 or 5 since no reverse transition from state 2 back to 1 was seen. Note the transient population of states 4 and 6, which thus appear only marginally stable in MD simulations. State 4 flips back to the canonical α/γ state (off-pathway intermediate) and state 6 transits to states 3 or 5 within <0.1 ns. In agreement with these data, states 4 and 6 along with α/γ in t/t were observed as metastable, whereas state 2 was an intermediate on the pathway to state 3 in earlier free energy studies of a GpC step (48). In all, of the 21 possible paths between the 7 states reported here, only 11 are traversed of which 9 were reversible and 2 were unidirectional.

TABLE 2.

Observed frequency of transitions between various DNA phosphodiester backbone states in the database and their time features in nanoseconds

Transition*	Frequency	Average time	Std. dev. time	Maximum time
“1–7”	7205	1.0	1.7	14.8
“7–1”	7209	<0.1	0.2	2.6
…
…
“5–3”	748	0.2	0.6	11.4
“3–5”	747	0.1	0.4	3.1
“1–5”	44	2.5	1.9	7.5
“6–5”	30	<0.1	<0.1	0.1
“5–6”	27	0.2	0.3	1.3
“5–2”	24	0.2	0.5	2.1
“1–2”	16	2.1	1.8	6.0
“2–5”	14	1.8	2.5	7.5
“3–2”	14	0.4	0.7	2.9
“2–3”	11	0.2	0.3	1.0
“7–3”	11	0.3	0.4	1.3
“5–1”	9	1.1	1.6	5.0
“1–4”	8	3.5	4.2	12.5
“4–7”	8	<0.1	<0.1	<0.1
“3–6”	6	0.9	1.5	4.2
“4–1”	6	<0.1	<0.1	0.2
“6–3”	6	<0.1	0	<0.1
“7–4”	6	0.1	<0.1	0.2

^*Data may be read as follows: There were 7205 cases in the database where a backbone conformation makes a transition from state 1 to state 7 (“1–7”). Before each of these transitions, the backbone was in state 1 for an average time of ∼1 ns, the standard deviation among these lifetimes was 1.7 ns, and the longest among these was ∼14.8 ns. Note that in the absence of well-sampled data with regard to transitions other than 1–7 and 7–1, the reported average times and standard deviations are only of rough qualitative value.

FIGURE 2.

Schematic of the various conformational states observed in the DNA backbone and the observed transitions between them. The size of the circles is approximately proportional to the population of the various conformational substates, and the thickness of the lines is roughly proportional to the number of transitions observed. The shaded arrows are highly unbalanced in directionality.

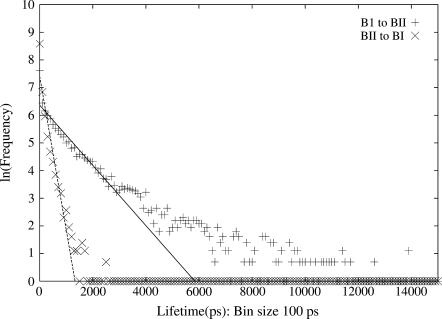
The B_I-B_II transitions observed in the MD are reversible and occur as short blips in all the trajectories at most of the positions, with a few exceptions. The mean lifetime in the B_I and B_II states can be calculated from the inverse of the slope in the ln(frequency) versus lifetime plot, which is shown in Fig. 3, based on a histogram of lifetimes of the B_I and B_II states. Considering the linear section of the B_I to B_II transition curve between 0–3000 ps, a mean lifetime of 918 ps for the B_I state is obtained. Similarly, from the linear section of the B_II to B_I transition curve between 0–1000 ps, the calculated mean lifetime of the B_II state is ∼180 ps. In the absence of sufficient data, it is not possible to obtain an accurate estimate of the mean lifetimes in the other states, although the average time observed in the available data as reported in Table 2 might provide some insight into their nature.

FIGURE 3.

The ln(frequency) of lifetimes in states B_I and B_II shown with “plus” sign and BII to BI shown with the “cross” sign as a function of the lifetime (in 100 ps) in the starting state. The slope of the line gives the mean lifetime in states B_I and B_II, respectively.

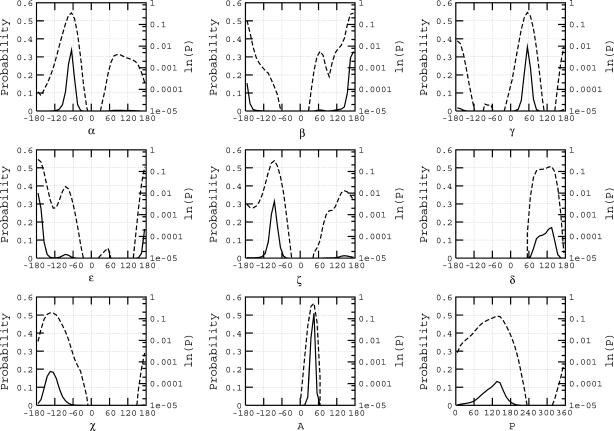
The graph in Fig. 4 shows the probability distributions of the backbone dihedral angles, the sugar pucker and amplitude, and the value of the glycosydic χ-angle in the complete database. Most of these parameters predominantly take on values close to that in the canonical B-form structure. A small population adopts nonstandard values as in the case of ɛ and ζ, which present two small secondary peaks around g− and t, respectively. The log plot of the probability distribution is included in these graphs to highlight the presence of nonstandard populations in the curves for α and γ. As noted earlier, >96% of the properties exist near the canonical B-form values. With regard to the sugar pucker, the pyrimidines in MD tend to exhibit a skewed distribution of sugar phase with higher population about ∼125° in contrast to the purines, which have a more balanced distribution centered about ∼140° (Supplement 2). Experimentally, the sugar pucker distribution is expected to rapidly interconvert between the C2′-endo (south) and C3′-endo (north) with pyrimidines presenting a higher tendency for C3′-endo sugar pucker population than purines, but it is technically challenging to track these conformation switches. The average MD data are in accord with the average values from NMR homo- and heteronuclear dipolar coupling data (71) based on a two-state model, although the MD does not present an explicit two-state distribution of the phase angle. On the other hand, the MD data present a noticeable O4′-endo (east) population especially in the case of pyrimidines, which contribute to lowering the population mean of the sugar pucker. The existence of east population has been recognized in earlier literature, but this is largely in the case of unusual nucleotides which are chemically modified (72).

FIGURE 4.

Probability distribution of the DNA conformational angles α, β, γ, ɛ, ζ, δ, and χ, and the amplitude (A) and phase (P) of the sugar. The solid line presents the normalized probability distribution plotted with reference to the primary y axis, and the dotted line presents the same data on the log scale shown in the secondary y axis.

Effect of substates on helicoidal parameters

The change in backbone torsion angles between the various substates has the strongest impact on the properties of the adjacent 5′ dinucleotide basepair step. The impact of backbone conformational change is strongest when transitions have occurred simultaneously on both the strands of the basepair step. Table 3 presents the data on the observed frequency of the simultaneous occurrence of any two combinations of backbone conformational substates on the two opposite strands at every basepair position in the complete database. The lack of symmetry in the frequency of substates in the two strands, especially for states 3 and 5, may originate from a sequence composition preference for the transition, since the occurrence of the 16 dinucleotide steps in the two strands is not symmetric in the DNA sequences analyzed. The other possible origin of this lack of symmetry is that the database may not yet be completely converged with regard to the presence of such substates.

TABLE 3.

Observed percentage frequency of concurrent occurrence of the indicated backbone conformational states at the 3′ side to a given basepair step in the two complementary strands

	Strand 2
	State	1	2	3	4	5	6	7	Total
Strand 1	1	82.824	1.096	0.677	0.002	2.525	0.009	2.838	89.972
	2	0.755	0.146	0.112	0.0002	0.001	0.0002	0.537	1.552
	3	0.526	0.140	0.071	0.000	0.001	0.002	0.5087	1.249
	4	0.001	0.0002	0.0002	0.000	0.000	0.000	0.001	0.002
	5	1.412	0.010	0.002	0.000	0.000	0.000	0.055	1.479
	6	0.007	0.0002	0.000	0.000	0.000	0.000	0.001	0.008
	7	4.117	0.173	0.160	0.000	0.135	0.000	1.153	5.738
	Total	89.643	1.565	1.022	0.002	2.662	0.011	5.095	100.000

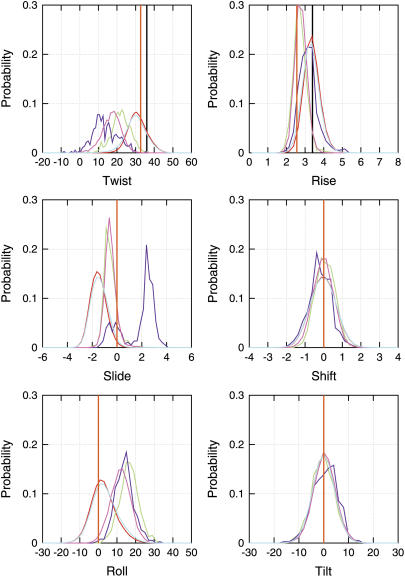
Fig. 5 presents the probability distribution of interbasepair step properties in the complete database and a classification such that the backbone conformation on the adjacent 3′ end of both the DNA strands is in states 1, 2, 3, or 7. We do not find basepair steps with the backbone conformation on the adjacent 3′ end of both the strands in states 4, 5, and 6 simultaneously, although there are cases of different combinations of these states. Although the population of basepair steps with the two strands in states 2, 3, or 7 is small (see Table 3), we see a significant difference in distribution pattern of their corresponding basepair step helical parameters, highlighting the correlation between the backbone and base geometries. Basepair steps with a combination of backbone conformational states in the opposite strands present intermediate geometries in comparison to the extreme values observed when the two complementary strands are in the same state. In Fig. 5, the most prominent effect is seen in the case of twist, slide, roll, and rise. The maximum in the helical twist distribution in the case of state 1 is ∼30° ± 6°, considerably lower than the value of 36° ± 19° observed in a survey of 88 B-form DNA structures in the Nucleic Acid Database (NDB) (73) and the 36° in fiber B-DNA (74). The helical twist in the MD structures is actually closer to the mean helical twist of 33° ± 5° in a survey of 68 A-form DNA in the NDB. The data based on 29 crystal structures reported by Hays et al. (37) present a much sharper distinction between the B and A forms, with the average helical twist being reported at 35.6 and 30.4 degrees, respectively. The mean helical twist in state 3 of the MD, i.e., α/γ in g+/t and ɛ/ζ in B_II form is ∼10°, significantly lower than in the other states. This observation suggests that the occurrence of such substates contributes to the known undertwisting in the parm94 force field (30). Another structural parameter which shows strong differences between the various substates and the canonical B-form value is the slide, which on average has a value below −1 Å, closer to the mean value of −1.5 Å observed in A-form DNA structures in the NDB, whereas the B-form structures in the NDB show a mean around −0.1 Å, the canonical B-form value being 0.0 Å. Interestingly, slide for state 3 takes on a characteristically different positive value. Finally, alternative backbone substates also exhibit large positive roll values ∼15°. Analysis of the intrabasepair parameters such as the shear, stretch, stagger, buckle, propeller twist, and opening indicates very little impact of these noncanonical substates.

FIGURE 5.

Normalized probability distribution of the six interbasepair step parameters, classified on the basis of the conformational state of the neighboring 3′ side backbone angles of the two DNA strands. Cases where the backbone conformation of both the strands in state 1 is shown in red, state 2 in green, state 3 in blue, and state 7 in pink. The distribution in the complete database is shown in cyan. Note that since the normalized probability distributions for each of the state distributions are plotted, the heights of the curves appear the same but the fraction of population in each of the states is not the same.

Sequence dependence of conformational substates

Fig. 6, A and B, presents the various substates occurring at all the nucleotide backbone positions as a function of time for DNA sequences with the repeating tetranucleotides AAGC and AATC. These sequences are examples of two of the most extreme cases among the 39 simulations, with regard to the number of substate transitions observed in a given trajectory. In the AATC sequence, 4 out of the central 10 basepair backbone positions show these unusual transitions, whereas the AAGC sequence shows no such transitions. The corresponding graphs for the other 37 trajectories in the database is available in the supplementary material (Supplement 3). Only 8 out of the 39 trajectories show no transitions except those between B_I and B_II. The rest exhibit a transition in at least one of the 10 central steps in the DNA sequence. In all, there are 68 cases of α/γ flips in the complete database, and these have been observed at all the positions along the DNA sequence. There is no clear correlation between transitions in consecutive positions or on complementary strands of the DNA at the same positions, and both cases have been observed. Unlike the transitions between the B_I and B_II states which occur reversibly, in most of the transitions involving the dihedrals α and γ (with the exception of 5 out of the 68 cases), once a transition to a nonstandard α/γ state occurs, the particular backbone position remains in the same state until the end of the trajectory as seen in the case of AATC in Fig. 6, B. An extreme example is provided by the backbone dihedral at position 7 in the GGCT sequence, which transits to the nonstandard α/γ substate at almost the very beginning of the trajectory and remains in this state for the rest of the 15 ns trajectory. The almost “irreversible” nature of these transitions suggests that the sampling of the energy surface may be incomplete or an imbalance in the potential energy surface of the backbone dihedral angles might be present.

FIGURE 6.

Plot depicting the occurrence of the seven backbone conformational substates at all the backbone positions in the DNA sequence over the complete 15 ns trajectory. The status of the backbone conformations in two strands at each position is shown in the two lines, the lower one for the first strand and the higher line for the second strand. The data for two trajectories based on the (A) AAGC and (B) AATC sequences are shown. The color code is as follows: black, state 1; red, state 2; green, state 3; blue, state 4; yellow, state 5; brown, state 6; and gray, state 7.

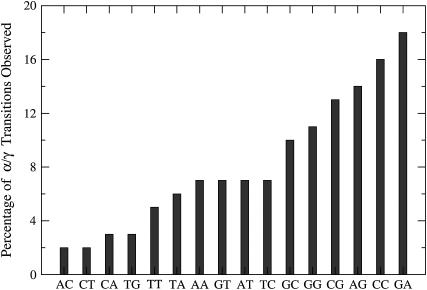
A sequence preference for the bases flanking the backbone phosphodiester position making the conformational transition to states with the unusual α/γ values is observed. Fig. 7 plots the frequency of occurrence of these backbone conformational transitions for each of the unique dinucleotide steps in the single-stranded DNA as a percentage fraction of the total number of the dinucleotide steps in the database. Considering both DNA strands, there are ∼40–60 copies of each of the dinucleotide steps in the database. Some of the dinucleotide steps exhibit an order of magnitude higher probability to transit to noncanonical α/γ states in comparison to others, suggesting a sequence preference. A more detailed analysis of the preferences as a function of the nucleotides on the 5′ and 3′ end is available in the supplementary material (Supplement 4). It appears to be possible that the nucleotides on the 5′ and 3′ end might also play a role in determining these sequence preferences. As an interesting case, we observe that the AGT sequence (i.e., GT dinucleotide with A on the 5′ end) is noteworthy because all sequences in the database with this combination (there are eight cases) have been involved in α/γ transitions. However, given the rarity of these transitions, longer simulations may be required to confirm the statistical significance of these results. It is nevertheless encouraging to note that the GA step shows the highest probability for the unusual transitions in our calculations and is also found to be the predominant step showing the g+/t conformational state of the α/γ pair in the protein-bound DNA structures solved by x-ray crystallography (75).

FIGURE 7.

Percentage of the phosphodiester backbone positions that transition to a nonstandard conformational state for all the dinucleotide steps in the simulated database.

Convergence of tetranucleotide structures

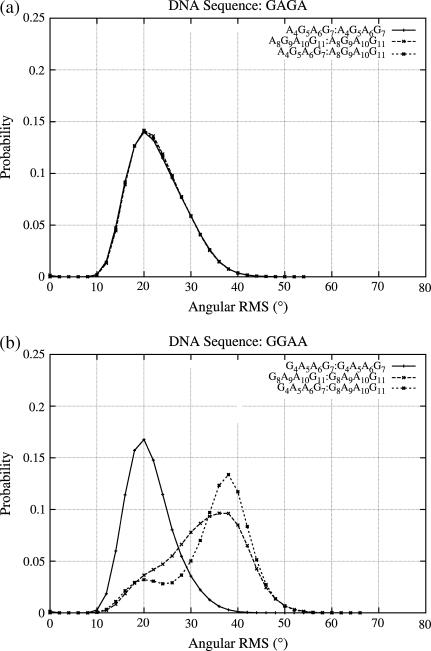
We next address the issue of MD structural convergence at the level of tetranucleotide structures. Since the sequences were designed so that there are at least two copies of each of the 136 unique tetranucleotides in the database, one measure of convergence would be to study the similarity of these multiple copies. The probability distribution of the angular 2D RMS data, discussed in the methods section, is employed to carry out this comparison. Fig. 8, a and b, shows two example cases, the first corresponding to the tetranucleotide A₄G₅A₆G₇ and A₈G₉A₁₀G₁₁, the subscript denoting the position of the nucleotide, in the DNA sequence GAGA. The two copies of this tetranucleotide show exactly the same structural behavior at both positions in the DNA sequence. The second graph (Fig. 8 b) presents the data for G₄A₅A₆G₇ and G₈A₉A₁₀G₁₁ in the DNA sequence GGAA, which shows the largest difference in the distribution of angular RMS values between the two tetranucleotide copies. The corresponding data for all the other tetranucleotide sequence positions in the simulated trajectories (39×4) is available in the supplementary material (Supplement 5). Analyzing the individual components contributing to the major difference in the RMS distribution of the two tetranucleotide structures reveals that α, γ, and β, that is, those torsions directly involved in backbone transitions, are the primary contributors. This observation is supported by an analysis of the tetranucleotides which undergo no transitions other than B_I-B_II (such as AAGC) and show little difference between the RMS plots of equivalent tetranucleotide copies. Hence, large structural differences between tetranucleotide copies are mainly the result of substate transitions.

FIGURE 8.

Normalized probability distribution of the angular RMS differences between copies of the tetranucleotides at a particular position and comparison with the structures of the same tetranucleotide at different positions along the DNA sequence. Top image compares A₄G₅A₆G₇ and A₈G₉A₁₀G₁₁ tetranucleotides in the DNA sequence GAGA, and bottom image compares the G₄A₅A₆G₇ and G₈A₉A₁₀G₁₁ tetranucleotides in the DNA sequence GGAA.

This result is encouraging since it implies that the position of a tetranucleotide within a given DNA oligomer has little impact on its dynamical properties and we do not have to worry about possible “positional effects”. However, it also implies that any fine analysis of DNA sequence effects based on parm94 requires filtering the simulation data to remove tetranucleotide conformations in which noncanonical α/γ transitions have occurred. But alarmingly, after filtering all the cases involved in α/γ transitions, data are presently available for only 95 of the 136 unique tetranucleotides.

Effect of sequence context on dinucleotides

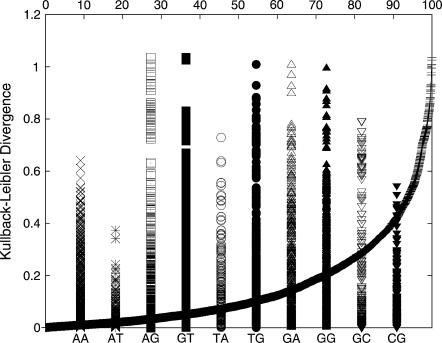
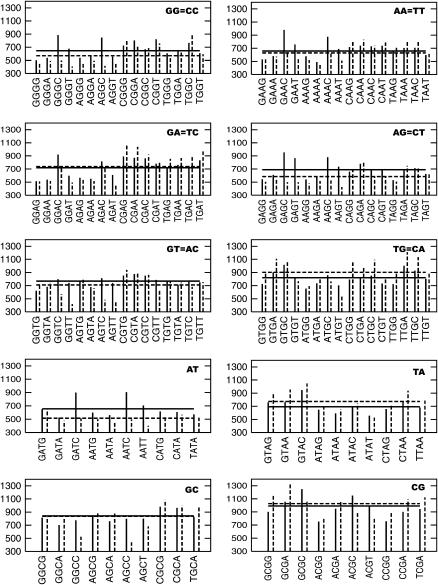
To study the effect of the flanking basepairs on the structure of a dinucleotide, the angular RMS probability distributions similar to Fig. 8, but based on the backbone and sugar parameters for the section connecting the two basepairs in the dinucleotide, were obtained for each of the available cases. The probability distribution of each dinucleotide angular RMS data is compared with the distribution of every other dinucleotide of the same kind, and the differences can be attributed to the impact of the flanking basepairs on the central dinucleotide. The KL divergence value between all pairs of dinucleotide steps is shown in Fig. 9. D_KL values close to zero represent similar distributions, whereas significantly different distributions show larger differences in the RMS data. The smooth curve presents the cumulative percentage of the dinucleotide pairs presenting a particular KL value. Although some pairs of dinucleotides in the database exhibit close to zero KL divergence, the largest divergence is ∼1.1. Of the dinucleotide pairs, ∼90% exhibit a KL distance <0.4. The KL distance in the angular RMS distribution of B_I/B_II states for a given nucleotide step are in the range of 0.1–0.2. The individual bars present the distribution of KL values within the set of each dinucleotide step data. In the case of symmetry-related copies of the dinucleotides which do not present any of the unusual transitions, the KL distance is <0.2. The AT and CG dinucleotides show the least divergence in the KL values, leading to the conclusion that these dinucleotides are least affected by the flanking sequences. In contrast, the GG, GA, and AG present some of the largest effects of the flanking sequences. Interestingly, the remaining purine-purine step, AA, is comparatively less affected. Among the pyrimidine-purine steps, the effect of flanking sequence on the TG step is large compared to those of TA and CG.

FIGURE 9.

D_KL between the RMS probability plots for the various dinucleotide steps in states 1 and 7. The smooth curve plotted with reference to the secondary x axis shows the cumulative percentage of all the dinucleotide pairs with a D_KL less than any particular value.

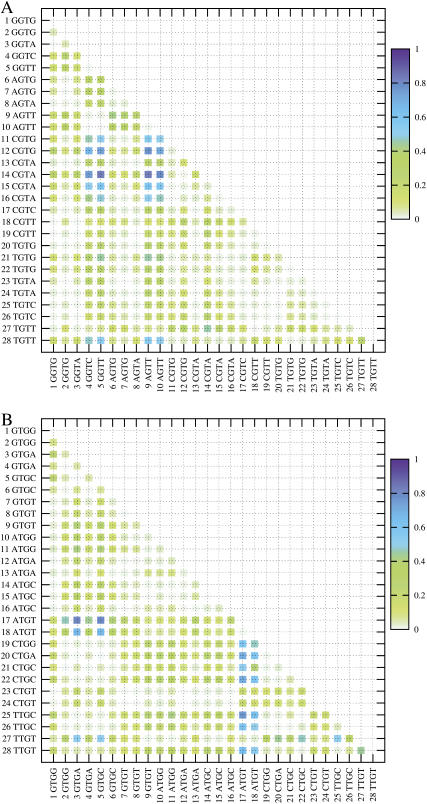
A more detailed 2D plot highlighting the differences in the KL value within a set of dinucleotides with different flanking sequences is shown in Fig. 10 for the cases of GT and TG dinucleotides. The data for the other dinucleotides can be found in the supplementary material (Supplement 6). One can immediately recognize patterns and blocks of data that distinguish the structure of the GT dinucleotide depending on the basepair flanking the dinucleotide step. The most significant differences are observed between the CGTR and the RGTY sequences, but interestingly the differences between TGTR and RGTY are not as distinct (where R and Y refer to purines and pyrimidines, respectively). The KL distance between the RGTR steps, such as the block of GGTG and AGTG, is fairly small. Although the GGTG block is distinct from the RGTY block, the difference between the GGTG and YGTR block is small. For the TG step in Fig. 10, B, one can immediately notice that 5′-flanking A and 3′-flanking T have distinct effects on the TG step in comparison to the other flanking sequences.

FIGURE 10.

2D matrix plot showing D_KL between all pairs of the dinucleotides with different flanking sequences. (A) The central dinucleotide is GT. (B) The central dinucleotide is TG. The light green shades indicate low D_KL and hence similar structures, and the shades of blue indicate differences in structure. Data from only states 1 and 7 were used in this plot.

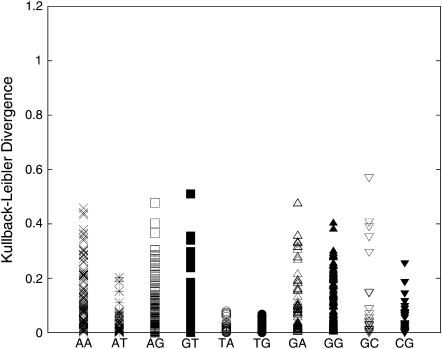
Fig. 11 shows a plot similar to Fig. 9 but only for dinucleotides not involved in α/γ transitions over the complete 15 ns of trajectory. Although the volume of data is now significantly reduced, the data here indicate that close to 99% of the dinucleotide pairs have a KL distance <0.4, compared to only 90% in Fig. 9. Although dinucleotides such as TA and TG showed large KL differences before such filtering (Fig. 9), the differences reduce to <0.2 in this analysis, signifying only minor structural effects due to different flanking sequences. This large difference in the data shown in Fig. 9, where only those sections of the data are removed which are in the nonstandard α/γ state, and Fig. 11, where the complete dinucleotide data which get involved in the α/γ transition are neglected, suggests that the steps which undergo transitions to nonstandard substates are more prone to exhibit greater fluctuations and structural differences even before the α/γ transitions occur. A last point which can be made from this graph is the spread in values for YR steps (notably, TA, TG, and CG). Although TA and TG steps are usually considered flexible, they show the least impact of flanking sequences, judged from their KL values in this figure. This suggests that the intrinsic flexibility of YR attenuates the impact of the flanking sequence. On the other hand, more rigid RR/YY steps might be expected to be more affected by their sequence context as observed in the larger KL distance for the RR/YY and RY steps. The detailed 2D plot comparing the KL distances of the RMS differences between each pair of the dinucleotide steps is available in the supplementary material (Supplement 7).

FIGURE 11.

D_KL between the RMS probability plots for the various dinucleotide steps in the database after neglecting all cases which were involved in α/γ transitions.

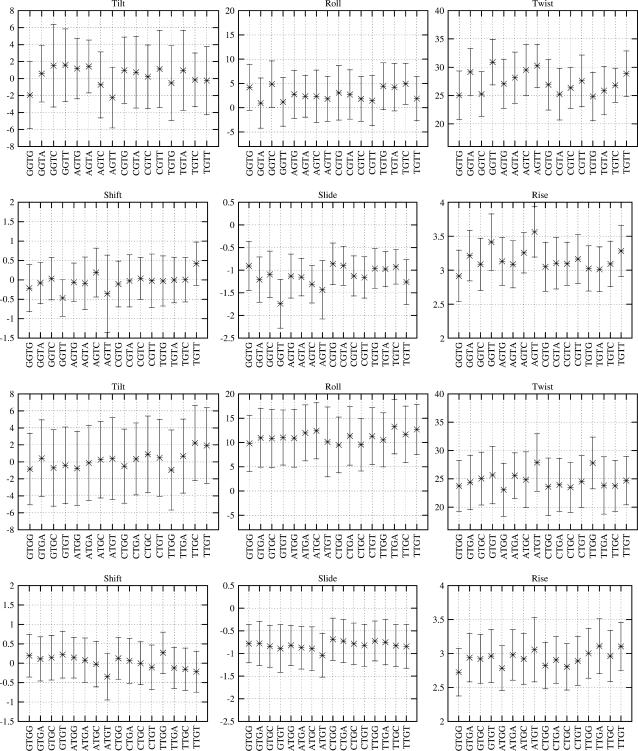
Although the subtle effects of flanking sequences on the dinucleotide structure are already apparent on the basis of the KL divergence values, we can better understand these effects by comparing the basepair step helicoidal parameters for each of the dinucleotide. Fig. 12 presents the six basepair step parameters for the dinucleotide steps GT and TG with all the possible flanking sequences. The corresponding plots for the rest of the dinucleotide steps are available in the supplementary material (Supplement 8). There are clear differences in general across the various groups of dinucleotide steps similar to those seen in the KL distance value plot for the TG and GT steps (Fig. 10). Although the average roll for the GT steps is small, in the range of 0–5°, the corresponding range for the TG steps is much higher. Similar differences in the general tendency of the dinucleotide properties are observed in the case of twist, rise, slide, and tilt, although the nature of some of these parameters limits the range of observed values. Comparing the effect of the flanking sequence on a particular dinucleotide step, the results become much more complex to analyze. In many cases, the average values differ by as much as one standard deviation, suggesting that they could be significant.

FIGURE 12.

Comparison of the six interbasepair step properties of the dinucleotide steps TpG and GpT with all the possible unique flanking sequences. The data presented here are the mean and one standard deviation of the respective parameters, considering only the snapshots with the α/γ backbone conformation close to the canonical state, i.e., g−/g+.

The average of the mean square fluctuations in the backbone conformational angles for the different tetranucleotides and dinucleotides is a unique measure of the flexibility observed in these steps. This is shown in Fig. 13 and can be used to study the effects of flanking sequence on the flexibility of a dinucleotide step. At the dinucleotide level, as seen from Fig. 13, the average flexibility of the YpY/RpR steps is much smaller than that of the YpR steps. Among the RpY steps, the flexibility of the ApT step is comparable to that of the most rigid RpR steps, whereas the GpT/ApC and GpC steps have intermediate flexibility between those of the RpR and YpR. Thus, the difference in the flexibility of GpG, ApA, and ApT steps on the rigid end of the scale and CpG on the more flexible extreme is quite clear. While comparing the average flexibility of the tetranucleotides, the distinctions become much less. Comparing the average flexibility of the tetranucleotides and the corresponding central dinucleotides, we observe that there is a strong effect of the flanking sequence on the flexibility of the GpG, ApG, and ApT steps whereas it is very small in the case of ApA, GpA, and CpG. Proceeding from the dinucleotide to the tetranucleotide level (observed by following the horizontal lines in Fig. 13 for the dinucleotide and tetranucleotide data), the flexibility of sequences with central GG, AA, AG, GT, and AT sequences increases, i.e., the flanking sequences make a larger contribution to the flexibility of these tetranucleotides. On the other hand, in the case of the YpR steps, the flexibility shows no change or a small decrease on including the flanking sequences. Thus we can conclude that at the tetranucleotide level, the flexible step flanking a particular central dinucleotide tends to affect the resultant character of the structural unit to a greater extent, i.e., rigid RpR/YpY steps when present in isolation are more prone to experience the effect of the neighboring steps when viewed at the tetranucleotide level. On the other hand, RpR/YpY steps flanked on both the sides with other purines, i.e., the polypurine sequences tend to be among the most rigid tetranucleotides, indicating the cooperative nature of these structural effects. In addition, we observe significant difference in the behavior of the ATAT and GCGC sequences. Although CGCG or GCGC is one of the most flexible tetranucleotides, interestingly TATA or ATAT is among the most rigid.

FIGURE 13.

Mean-square fluctuations in the backbone conformational angles of each of the 10 unique dinucleotide steps and all their corresponding tetranucleotides. The solid vertical lines present the average mean square fluctuations from the P_inter and P_intra RMSD for each tetranucleotide step, and the corresponding dinucleotide data are shown as a dotted line. The solid and dotted horizontal lines are the average of all the tetranucleotide and dinucleotide data in the graph, respectively.

The effect of the highly flexible CpG and CpA on the structure of positions farther than the immediate neighbor is consistently large, indicating that the tetranucleotide by itself does not capture the complete structural effect of such steps. For example, most of the dinucleotides in the presence of G on the 5′ end and C on the 3′ end, such as the GGGC or GAAC sequence, show very large flexibility. The origin of this large flexibility has to be the CpG that would be present outside the tetranucleotide (the DNA sequences which were simulated have the repeating tetranucleotides, i.e., the GGGC is present in the sequence ···GGGCGGGC···) since the GpG and GpC dinucleotides which constitute this tetranucleotide unit are known to be comparatively rigid by themselves. The dinucleotides GT and GC present exceptions to this behavior understandably due to the cooperative effects discussed above in polypurine and polypyrimidine sequences. This indicates that analysis of context effects at the hexanucleotide level might be necessary in the case of some sequences.

DISCUSSION

The current generation of molecular simulation force fields and the methodology employed give stable MD trajectories which encourage us to inquire about the sequence-directed structural properties of DNA and their origin in greater detail. Analysis of the trajectories in the database developed here reveals that substates involving transitions to noncanonical values for backbone conformational angles α and γ is only a small percentage of the total (<5%), but they are present at some time or the other in most of the trajectories, and the associated conformational changes have a significant impact on the DNA structure. The natural presence of such noncanonical conformational substates in DNA structure when complexed with proteins is confirmed in the recent analysis of high-resolution x-ray crystal structures conducted by Hartmann and co-workers (48,75), and hence the observation of such transitions in the MD are interesting. However the paucity of experimental information regarding these substates leaves a lot of questions unanswered. For instance, the available crystal structure data indicate that in the unbound B-form DNA, ∼79% of the population exists in the B_I state whereas ∼18% exists as B_II. Our simulation presents a ratio of 92%/7% for the B_I and B_II forms, respectively. In their selected survey of 60 free and 64 protein-bound DNA structures (75), they observe mainly the canonical α/γ angles in the uncomplexed form of B-DNA but find ∼2% of DNA structures in the noncanonical g+/g− state of α/γ, associated with particular regions making crystal contacts in the system. In the protein-bound structures of DNA, they also observe the g+/t and t/t conformational states although the crystal structures appear to exhibit a somewhat greater preference for the g+/g− as the noncanonical α/γ substate. In the MD simulations of unbound DNA studied here, g+/t conformation predominates, whereas the t/t occurs as an extremum of the former distribution, and g+/g− is comparatively rare.

In the absence of time-resolved experimental data on the lifetimes of the noncanonical α/γ and other substates of the backbone, it is difficult to judge the accuracy of the observed long-lived substates in simulations. Such substates do, however, raise concerns over the quality of sampling during 15 ns simulations. Notably, α/γ transitions may constitute significant “traps” in the potential energy surface, pseudo/nonergodic situations, which cannot be well characterized in such simulation times. This simulation database, albeit theoretical, has provided us with useful insight into the mean lifetimes of the B_I and B_II substates. It would be interesting to experimentally verify the B_I/B_II lifetimes estimated from simulations in this study. Further characterization of the other substates of free DNA and their protein-bound forms clearly needs to be pursued in simulations both from the perspective of trying to understand the fine structure of DNA and refining the force field used in the simulation. The fact that the crystal structures selectively exhibit noncanonical values of the backbone torsion angles at a few positions suggests that these substates are natural and long lived, with lifetimes possibly much longer than what can presently be simulated by the protocol employed in this study. NMR studies involving T₁ρ measurements (76) have revealed that conformational exchange of dinucleotide steps such as TpA occur in the submillisecond timescale, well beyond the realm of current MD simulation. This issue raises a very useful role for simulations based on the implicit solvent models such as the generalized Born method (77) or the Poisson-Boltzmann method (78), which are computationally much less demanding and hence can simulate longer timescales to address this problem. However, the dynamics in a continuum solvent are of questionable accuracy and still require a considerable amount of characterization and verification studies (79).

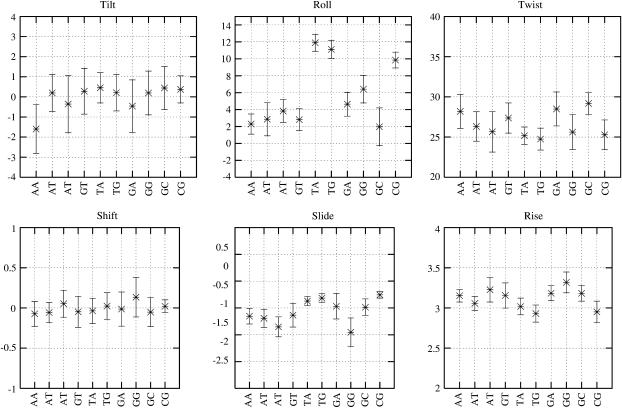
In terms of the basepair step helicoidal parameters, the dinucleotide steps present clear differences which can be classified in terms of the general preferences of the YpR, RpY, and RpR/YpY steps (35). The corresponding MD values are shown in Fig. 14. Among the angular parameters, the difference in mean between the lowest and highest values are ∼5° in twist, 10° in roll, and 2° in tilt whereas the standard deviations in each distribution are usually <2°. Hence, although it would be difficult to distinguish basepair steps on the basis of tilt, differences in twist and roll values should be recognizable. The basepair step roll clearly follows the Calladine's steric clash model (80) wherein the YpR and GpG steps present large roll into the major groove. Interestingly, although the Calladine rule suggests that RpY and ApA steps roll into the minor groove, the MD structures present these dinucleotides with small but positive average roll, i.e., small roll into the major groove. The average twist for the YpR steps are in general lower than the RpR and RpY steps, and the difference becomes even more prominent in terms of the roll values wherein the YpR steps present a predominantly large and positive roll value. In very good agreement with the crystal structure analysis of Dickerson and co-workers (12), the GpC and GpA steps which were noted to exhibit a high twist profile (HTP) indeed exhibit the highest average twist in our MD simulations and the CpG, GpG, and ApG present a low twist profile (LTP) (Fig. 14). The difference in average twist of the dinucleotides in the HTP and LTP groups is ∼5° in the MD model. Among the translational parameters rise, slide, and shift, the difference would be much less predictable since the range of observed values are fairly narrow, 0.4 Å for the rise, 0.7 Å in slide, and 0.2 Å in shift whereas the corresponding standard deviations are in the range of 0.1–0.2 Å. Yet, the average values in the database indicate anticorrelated changes in rise and slide values with the following trend: rise (YpR) < rise (RpY) < rise (RpR) and slide (RpR) < slide (RpY) < slide (YpR).

FIGURE 14.

Average basepair step values observed in the MD simulation database for all the unique dinucleotide steps and the standard deviation in the data as a result of different flanking steps. Data from only states 1 and 7 were used in this plot.

It has been suggested that the stacking interactions in a dinucleotide which are directly related to the basepair step helicoidal properties is the primary determinant of DNA structure and the backbone only adopts conformations accordingly (35). Previous theoretical analysis of tetranucleotide properties by Hunter, Packer, and co-workers (16,81) was based on the assumption that twist was the only basepair step parameter dependent on the backbone conformation. The MD results, on the other hand, indicate that change in the basepair step twist, slide, roll, and rise follow the changes in the backbone conformation.

The MD analysis of DNA structure presented here has provided significant new insight which is corroborated by the available structural data derived experimentally. At the same time it has also highlighted issues about the behavior of DNA structure in MD methods at a new level of sensitivity, which requires a reexamination of the accuracy of nucleic acid force fields. Most of the force fields including AMBER (8) and CHARMM (82) to an extent, have been developed with a “build up” approach wherein the guiding criteria are to use a minimum number of parameters and accurately reproduce the conformation and energy profile for a selected set of constituent small molecules in high level quantum mechanical study. The parameters are then assumed to be transferable to the larger macromolecule. The parm94 force field has significantly achieved this goal while adopting the minimalist approach to the force field development but understandably such an approach has limitations in being able to capture all the complex sequence-directed structural properties of DNA which would show up only in longer sequences of the molecule. The alternate “top down” approach adopted by Langley in the development of the Bristol-Myers Squibb (BMS) force field (83) for nucleic acid involves iteratively refining the torsion terms to reproduce the structural data determined from the available high-resolution structures. Such a “knowledge-based” approach wherein the macromolecular properties are considered target data for parameter optimization is fraught with our inability to clearly discriminate between sequence-directed versus crystal-packing effects in the x-ray crystallographic structures of DNA.

With regard to the parm94 force field, the correlation between the backbone conformational angles and the twist in the adjacent basepair step suggests that sorting out the recognized issue of undertwisting (30) in this force field could pave the way for a better understanding of the behavior of the backbone conformations and vice versa. Note that the parm99 version (29) of the AMBER force field, which improves the simulated average sugar pucker, χ-angles and the helical twist also exhibits the long-lived substates of the α/γ torsion angles as observed in the work of Varnai and co-workers (48). Further, the changes in the force field in going from parm94 to parm99 also introduced an inability to stabilize the A-form DNA structure in ethanol or with hexa-amine cobalt (III) ions. Extensive calibration studies of the intrinsic torsion angle energetics in the parm94 and parm99 version of AMBER and CHARMM 22 and 27 nucleic acids force fields using model compounds reported by Bosch et al. (84) provides further insight on this issue. Comparisons to ab initio calculations has revealed that although the recent versions of the force fields are fairly well balanced, the location and height of the energy barriers separating different conformers are not quantitatively reproduced, leaving room for improvement.

Issues with nucleic acid force fields are not limited to the force field applied here. Simulations with the CHARMM 27 force field (32,85) show rapid basepair opening, little minor groove narrowing in A-tract regions, the BMS force field appearing to overstabilize DNA into a crystal-like geometry (83), and the new GROMOS 45A4 parameter set (31) appearing to overstabilize canonical A-form geometries. The detailed analysis provided here, with consideration of limitations seen with this force field and others, provides insight on the directions in which the force field description may be refined. This is a subtle and complex issue to fine tune, given the highly coupled nature of these structural parameters and the potential long timescale conformational changes among these structural substates. Despite these caveats related to the applied force fields, we have witnessed considerable success in simulation of nucleic acid structure throughout the community in problems ranging from DNA bending and flexibility, RNA structure motifs, drug-DNA interaction, to probing unusual nucleic acid structure.

SUMMARY AND CONCLUSIONS

Based on 39 different MD simulations of DNA oligomers containing all the 136 unique tetranucleotides, we have been able to decipher in detail many of the fine structural properties of DNA not yet available from crystallography or NMR. We have been able to observe a range of structural substates distinct from the canonical B-form, largely controlled by preferences for backbone conformational angles. We see strong correlations between the backbone conformational angles and the helicoidal properties of DNA such as twist, rise, and slide, which together define the fine structure. The detailed simulations provide us with insight into the lifetimes of some of these substates which needs to be confirmed experimentally. The mean lifetimes of the B_I and B_II forms of the DNA are estimated to be ∼918 ps and 180 ps, respectively, in these simulations. With regard to the transitions in the backbone dihedrals α and γ, we observe persistent noncanonical substates which either indicate insufficient sampling during the 15 ns of simulation undertaken here or an ergodic problem in the potential energy surface described by the force field, causing the structure to be “trapped” in these long-lived conformational substates. The detailed simulations and analysis pursued here have pushed the MD study of DNA to the limit in terms of both the number of trajectories available and their length to provide new insight on the directions in which the force field description may be refined. We have been able to compile a complete database of the geometrical parameters for all the dinucleotide steps and address the effect of all possible flanking basepair combinations on the central dinucleotide structure. Among the more striking results obtained from analyzing the tetranucleotide steps, one can note that although YpR steps are intrinsically flexible they also appear to be least affected by the neighboring basepairs. Conversely, these steps have a significant structural impact when adjacent to a RpR or RpY step, which are intrinsically rather rigid.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org and the author's website at http://sdixit.web.wesleyan.edu/ABCII.