Interfacial Tryptophan Residues: A Role for the Cation-π Effect?

Abstract

Integral membrane proteins are characterized by having a preference for aromatic residues, e.g., tryptophan (W), at the interface between the lipid bilayer core and the aqueous phase. The reason for this is not clear, but it seems that the preference is related to a complex interplay between steric and electrostatic forces. The flat rigid paddle-like structure of tryptophan, associated with a quadrupolar moment (aromaticity) arising from the π-electron cloud of the indole, interacts primarily with moieties in the lipid headgroup region hardly penetrating into the bilayer core. We have studied the interaction between the nitrogen moiety of lipid molecule headgroups and the π-electron distribution of gramicidin (gA) tryptophan residues (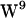, , , 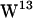and 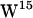) using molecular dynamics (MD) simulations of gA embedded in two hydrated lipid bilayers composed of 1-palmitoyl-2-oleoylphosphatidylethanolamine (POPE) and 1-palmitoyl-2-oleoylphosphatidyl-choline (POPC), respectively. We use a force field model for tryptophan in which polarizability is only implicit, but we believe that classical molecular dynamics force fields are sufficient to capture the most prominent features of the cation-π interaction. Our criteria for cation-π interactions are based on distance and angular requirements, and the results from our model suggest that cation-π interactions are relevant for 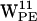, , 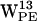, 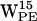and, to some extent, 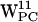and 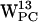. In our model, does not seem to engage in cation-π interactions with lipids, neither in POPE nor POPC. The criteria for the cation-π effect are satisfied more often in POPE than in POPC, whereas the H-bonding ability between the indole donor and the carbonyl acceptor is similar in POPE and POPC. This suggests an increased affinity for lipids with ethanolamine headgroups to transmembrane proteins enriched in interfacial tryptophans.

INTRODUCTION

A ubiquitous feature of membrane–spanning proteins seems to be a preference of tryptophan (W) and tyrosine (Y) residues at the interfacial lipid headgroup region (1). Statistical analysis of membrane protein sequences indicates that this preference is a general feature (2,3). The preference has been discussed in terms of so-called anchoring by flanking residues in the sense that the aromatic or charged residues serve as to symmetrically anchor membrane-spanning proteins at the interfacial regions in the membrane (1,4–6). Studies with small membrane adsorbed model peptides and model transmembrane helical proteins suggest that the preference for aromatic residues at the interface is related to distinct interfacial interactions (7–14).

Yau et al. (14) studied the interaction between tryptophan analogs with different hydrogen bonding and electric dipole interaction abilities and phosphatidylcholine membranes. They found that the analogs reside in the vicinity of the glycerol moiety where they all caused modest changes in acyl chain organization and that penetration of the analogs into the bilayer core was not increased by reduction of hydrogen bonding or electric dipole interaction ability, which rules out simple amphiphatic or dipolar interactions as the dominant modes of tryptophan-lipid interaction (14). Rather these results suggest that the interfacial preference is related to its flat rigid paddle-like structure of tryptophan associated with the quadrupolar moment (aromaticity) arising form the indole π-electron cloud (see also Gaede et al. (15)). Our aim is to establish to what extent cation-π interactions play a role for the interaction between tryptophans and the lipid headgroup region and thus lipid-protein interactions in general.

Cation-π interactions in biological systems are considered one of the driving forces in molecular recognition (16–19). The dominating component in cation-π interactions is the electrostatic attraction of the positive cationic charge toward the quadrupole created by the π-electron distribution of the aromatic ring (16). The role of cation-π interactions in protein and peptide conformational states has been studied by means of interactions between positively charged lysine and arginine residues (the ammonium NH₃⁺ and guadinium C(NH₂)₃⁺ groups, respectively) and the aromatic six-membered ring centers of phenylalanine, tyrosine, and tryptophan (17,20).

The polarizability of the out-of-plane charge distributions associated with the aromatic ring (21) combined with the polarized nature of the positively charged ion preclude an adequate description of cation-π interactions in terms of additive potentials (17). However, when exploring complex biological phenomena in large systems such as the interactions between tryptophans in membrane-spanning proteins with hydrated lipid bilayers, additive potentials currently constitute the best approximation for addressing the biological importance of this interaction.

Molecular dynamics (MD) simulations have become an established tool to study structure and dynamics of complex biomolecules (22–24), and increased computer power and improved algorithms have enabled studies of larger systems on a nanosecond timescale. Lately there has been a rapid development of simulations of lipid bilayers with interfacially associated peptides (8,20,25) as well as embedded membrane-spanning proteins (26–31 and references therein).

In current MD force fields, electronic polarizability is not treated explicitly (32); rather polarizability is included implicitly in the form of partial atomic (electrostatic) charges that typically overestimate molecular dipoles (32,33). Although the polarizability of the π-electron distribution is not accounted for explicitly, current pairwise additive electrostatic (Coulomb) forces capture the basic physics of the cation-π interaction (17,34). We use the CHARMM27 parameter set (35) and employ geometric selection criteria to identify lipid nitrogen cation candidates for cation-π interactions with tryptophan in a model membrane protein. Specifically we have investigated the interaction between the cations of lipid molecules (NH₃⁺ in 1-palmitoyl-2-oleoyl-sn-glycerophosphatidylethanolamine (POPE) and N(CH₃)₃⁺ in 1-palmitoyl-2-oleoyl-sn-glycerophosphatidylcholine (POPC)) and the π-electron distribution of gramicidin (gA) tryptophan residues.

With four tryptophans (, , 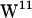, 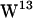and 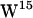) positioned at different depths in each interface, a gA dimer can be seen as a model for a transmembrane-spanning protein enriched in interfacial tryptophans (for reviews on gA, see Anderson and Koeppe (36), Roux (37), and Koeppe and Anderson (38)), and gA has been the model protein in several MD studies of lipid-protein interactions (29,31,39–41).

Although 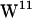, , 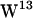and all have unique regions of side-chain (χ₁,χ₂) torsion angles, two 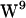rotamers are present in gA dimer NMR structures known as the 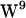/ 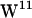sandwich and the / 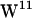stacked conformation (PDB:1JNO and PDB:1MAG, respectively). We have analyzed tryptophan-lipid headgroup interaction using the gA structure 1MAG in which the tryptophans assume the / stacked conformation. The reason for our choice is 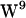in 1MAG is closer to the bilayer center than 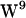in 1JNO (cf. Allen et al. (40)). Thus the range of positions for the eight tryptophans in 1MAG spans a larger region in the interfacial region during our simulation than would the tryptophans in 1JNO.

POPE and POPC can be seen as models of lipid bilayers with different propensity to form nonbilayer structures (42–44), which is known to affect gA conduction (45,46).

We have addressed five questions that arise when considering the anchoring effect of interfacially located tryptophans. i), What configurations do the four tryptophan residues in each gA monomer adopt in the POPC and POPE bilayers? ii), Which of the tryptophans are favorably positioned to meet chosen distance and angular requirements for cation-π interactions? iii), What is the relative importance of the quadrupolar moment arising from the centroid of the six-membered ring versus the quadrupolar moment arising from the centroid of the five-membered ring? iv), How does the lipid cation type (NH₃⁺ versus N(CH₃)₃⁺ ) influence the cation-π interaction? v), And to what extent is anchoring due to cation-π interactions and to hydrogen bonding of the NH-indole group to the lipid molecules, respectively?

To address the first question, we analyze motional flexibility in terms of order parameters for tryptophan in the two different lipid environments. To answer the second, third, and fourth questions, we study i), distributions of distance vectors (see Materials and Methods) between either the five- or six-membered geometric centroid or the tryptophan (indole) geometrical center and the closest lipid nitrogen atom, and ii), angles between these distance vectors and vectors normal to the indole plane. To answer the final question, we monitor hydrogen bonds between the tryptophan indole NH and the lipid carbonyls.

MATERIALS AND METHODS

Molecular dynamics simulations

Fully hydrated POPE and POPC lipid bilayers were simulated as follows. First a randomized POPE bilayer consisting of 204 lipids was generated. Then the gA dimer (Protein Data Bank (PDB) coordinate file 1MAG) was inserted (for PDB, see Berman et al. (47)). The entire system was arranged in a periodic rectangular box with dimensions of 122.0 × 112.7 × 77.0 ų, and the bilayer was hydrated with 16,227 water molecules using Solvate (48) ensuring a hydration of 33 water molecules per POPE molecule. In simulations of the gA/POPC system, the amine hydrogen atoms in the ethanolamine lipid headgroups of the POPE bilayer were replaced by methyl groups preserving box and hydration parameters. The two systems included a total of 47.409 atoms (gA/POPE) and 49.239 atoms (gA/POPC). The seemingly large system size that was chosen as the (radial) persistence length of protein-lipid mismatch is known to be about the magnitude of the mismatch itself, i.e., 10–15 Å for gA in POPE and POPC (26,49). A snapshot of the gA/POPE simulation is shown in Fig. 1.

FIGURE 1.

Simulation system. (a) Snapshot showing the final configuration of gA in a hydrated POPC bilayer after 10 ns of simulation. (b) Same for the gA/POPE system. Lipids and tryptophan side chains are displayed without their hydrogen atoms. For clarity, some lipid molecules in front of gA are not shown. Water molecules occupying the channel are displayed as van der Waals spheres. Each gA dimer channel (PDB:1MAG) shown in ribbons representation is made from two monomers, one from each monolayer leaflet. The four tryptophans in each monomer are indicated by colors as follows: (orange), 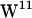(dark cyan), 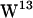(light cyan), and 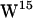(blue). (c) A snapshot of lipid-tryptophan interactions (depicted as dotted lines). Left, a hydrogen bond between the NH moiety of a tryptophan and a lipid carbonyl group. Right, a cation-π interaction between a tryptophan and a lipid cationic nitrogen.

The MD simulations were performed with NAMD (50) using the CHARMM27 parameter set (51) on 16, 32, 64, or 128 Pentium 4 processors (52). One nanosecond simulation time took on average 1.9 days. Standard parameters for lipid molecules and TIP3P water were used. The protein/lipid/water systems were initially minimized and equilibrated in the NPT ensemble, i.e., at constant temperature (T = 310 K) and pressure (P = 1 atm) for 250 ps with the protein fixed. The protein was subsequently released, and the full systems were energy minimized. NPT simulations were then conducted for 10 ns with T and P specified as above. Full periodic boundary conditions were imposed in all simulations, and the particle mesh Ewald method (53) was used for computation of electrostatic forces. A time step of 1 fs was employed, and coordinates were written at 0.5 ps intervals. Equilibration was reached after 4 ns judged by the emergence of a steady-state value of the root mean square deviation of the system atom coordinates between two consecutive writings. All results presented are based on the last 6 ns of simulation.

Analysis

The resulting trajectories were analyzed and displayed using visual molecular dynamics (VMD) (54) and OriginPro 7.5 (OriginLab, Northampton, MA). Throughout the text, specific tryptophans are denoted W and indexed with superscript for residue number (9, 11, 13, or 15) followed by a letter denoting monomer location (U for upper and L for lower, or U,L when referring to both) and a subscript denoting the type of lipid bilayer (PE or PC). Orientation of the tryptophan residues was characterized by two order parameters S_N and S_L (see Fig. 2 a) (8,20,55). S_N = (3cos²θ − 1)/2 where θ is the angle between the protein longitudinal axis d_protein and n_indole the normal vector for the plane of the indole. S_N has two extreme values: −0.5 means that n_indole ⊥ d_protein and S_N = 1 means that n_indole ∥ d_protein. S_L = (3cos²β − 1)/2 where β is the angle between d_protein and a vector d_indole from the C_β to C_γ of the tryptophan residue. If S_L = 1, d_indole ∥ d_protein. If S_L = −0.5, d_indole ⊥ d_protein. The distance between a point in space, i.e., a cation candidate for a cation-π interaction and the indole (see below), is defined relative to the indole plane as a projection of the distance vector d onto the indole plane, yielding the projected distance r and the height h, the latter being normal to the indole plane (see Fig. 2 b).

FIGURE 2.

(a) Tryptophan nomenclature and order parameter defining vectors. (b) The distance vector d_{6 − π} from any nitrogen (blue sphere) to the indole geometric centroid and its projection r onto the indole plane and its projection h along the indole plane normal. Each projection is characterized by the coordinate s0 nset (r,h), where r = |r| and h = |h|.

For cation-π interactions, three distance vectors d_C6-π, d_C5-π, and d_C56-π between the tryptophan and the geometric center of the closest ammonium group were evaluated at each time step. d_C6-π was computed as the distance vector from the geometric centroid of the six-membered ring of the indole to the cation. d_C5-π was computed as the distance vector from the geometric centroid of the five-membered ring of the indole to the cation. d_C56-π was computed as the distance vector from the geometric center between the ɛ² and δ² carbons defining the border between the five- and six-membered ring to the cation. Based on the analysis of Chipot et al. (56), we impose two geometric constraints onto the distance vectors: i), a length cutoff of 7 Å, and ii), a 120° selection cone ensured by an angular constraint depicting only distance vectors forming angles <60° with the indole plane normal (see Fig. 3). These constraints serve to define subsets of candidates for cation-π interactions.

FIGURE 3.

Lipid nitrogen indole cation-π interactions and indole NH-lipid carbonyl hydrogen bonding interactions. For cation-π interactions, the dotted lines depict the cutoff for the distance vector d_C6-π (d_C5-π, and d_C65-π are treated in the same way) from the indole geometric centroid to the cationic lipid nitrogen (dark blue) (see also text). For a 120° cone selection, interaction candidates are limited to the nitrogen atoms for which the angle χ = ∠ d,n_indole is <60°. Indole NH-lipid carbonyl hydrogen bonding interaction are defined by r_(N-)H…_{O = C,} the vector (with a maximal cutoff length of 3.5 Å) from the indole NH-group to lipid carbonyls (red). θ = ∠ r_N-H,r_(N-)H…_{O = C} is the angle between the director for the indole NH group r_N-H and the vector r_(N-)H…_{O = C} from the hydrogen to the carbonyl oxygen atom.

For hydrogen bonding, donor candidates were selected as the closest oxygen atom in a lipid carbonyl group within a maximal cutoff distance of 3.5 Å from the indole group NH electron acceptor. The donor-H-acceptor angle θ = ∠ r_N-H,r_(N-)H…_{O = C} is defined as the angle between the director for the indole NH group r_(N-)H and the vector r_(N-)H…_{O = C} from the hydrogen to the carbonyl oxygen atom (see Fig. 3), and in our analysis we apply a donor-H-acceptor angle cutoff of θ = ∠ r_N-H,r_(N-)H…_{O = C} = 60°.

RESULTS

For both POPC and POPE, the average position and orientation of the tryptophans (S_L and S_N ) are essentially the same relative to the bilayer plane throughout the simulation (S_L(POPC) = 0.27 ± 0.07, S_L(POPE) = 0.19 ± 0.06, S_N(POPC) = −0.43 ± 0.03, S_N(POPE) = −0.44 ± 0.03; values given as mean ± SD for all tryptophans). The only exception is 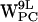, which undergoes a transition between two energy minima (cf. Allen et al. (40)).

To study if cation-π interaction could constitute (part of) the mechanism behind tryptophan interfacial preference, we analyzed whether our distance and angular requirements were satisfied. The indole group is a large asymmetric planar structure and it is not obvious whether the cation-π effect arises predominately from the centroid of the six-membered ring or the centroid of the five-membered ring or is due to the electron distribution of the entire indole group. We therefore investigated the three different cases, and this is shown in Fig. 4. The minimum distance between the indole and the lipid nitrogen is shown as (r,h) plots (as defined in Fig. 2 b) for d_C6-π, d_C5-π, and d_C65-π for . Apart from a few outliers in Fig. 4, a, c, and e, there is little difference with or without the cone selection shown in Fig. 3. Most distances between the cations and the centroids are <4 Å and within the 120° cone, indicating that they are likely candidates for cation-π interactions.

FIGURE 4.

Scatter plot of the (r,h) projection as defined in Fig. 2 c obtained during 500 ps of d_C6-π d_C5-π, or d_C65-π with and without a 120° cone selection (χ ≤ 60°, cf. Fig. 3) for 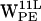. The horizontal line indicates the indole plane. (a) (r,h) plot for d_C6-π vectors with cone selection. (b) (r,h) plot for d_C6-π vectors without cone selection. (c–d) (r,h) plot for d_C5-π vectors analyzed as in a and b. (e and f) (r,h) plot for d_C65-π vectors analyzed as in a and b.

For the d_C5-π distance vector selection, a subset of the vectors scatter in the (r,h) area around (−12Å, −10Å) (see Fig. 4 c). These sets represent nitrogens picked up on the far side of the gA molecule, when only the distance selection criterion is applied. When the 120° cone restriction is added, these spurious candidates disappear and a uniform scatter pattern emerges, essentially independent on the exact position of the centroid (Fig. 4, b, d, and f).

In the following analysis presented in Figs. 5–8, we will therefore use the criterion based on the d_C6-π vectors only, a 7 Å distance limit, and a 120° selection cone. First we consider the dynamics of the minimal distance distribution for all the tryptophans in the upper and lower monomers. Fig. 5 shows the temporal development in the (r,h) coordinates for d_C6-π in POPE. For all tryptophans, d_C6-π generally explores extended regions of the (r,h) plane, reflecting the highly dynamic nature of the interfacial region. The differences in scatter areas for the four tryptophans reflect the differences in location of the gA dimer and thus of the tryptophan C_α atoms in the lipid bilayer. Neithe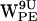r nor (the tryptophans with C_α closest to the bilayer midplane) d_C6-π vectors satisfies the requirements for a cation-π interaction with the lipid nitrogen (see Fig. 5, a and e) as defined in Fig. 3. For both 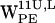(Fig. 5, b and f) a subset of d_C6-π vectors are within the cone and range criteria for a cation-π interaction. For 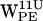(Fig. 5 b) the d_C6-π vectors initially lie outside the selection cone, whereas after ∼1.5 ns the interaction is favored for ∼2.5 ns before the d_C6-π vectors again fall outside the selection cone. A somewhat similar pattern is seen 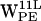for . For the d_C6-π vectors also locate in part in the selection cone. For (Fig. 5 c), the d_C6-π vectors initially exceed our cutoff, but with time they concentrate in a region closer to the centroid with a significant subset of the d_C6-π vectors within the selection cone. The pattern for is more complicated (Fig. 5 g). The d_C6-π vectors now spend a substantial amount of time in the region h < 0. Although the cone selection criterion is satisfied in both the h < 0 and h > 0 cone for some d_C6-π vectors, all vectors are longer than 7 Å, and most of the d_C6-π vectors are centered around (r,h) = (9 Å, 2 Å) and thus outside the selection cones. Of the eight gA tryptophans, the two C_α atoms of are closest to the aqueous phase. For 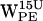some d_C6-π projections are within the selection cone (Fig. 5 d), however, with few distances <7 Å. For , a substantial subset of d_C6-π is well within the h > 0 cone and have distances below 7 Å (Fig. 5 h).

FIGURE 5.

Time-resolved (r,h) scatter plot of projected d_C6-π vectors for gA/POPE. (0,0) represents the six-membered ring centroid. Open and black-filled circles on the line intersecting h = 0 indicate equidistance to any C-atom of the six-membered ring and the distance to the most distant C-atom of the five-membered ring, respectively. The dashed line delineates the cone selection for h > 0. Colors indicate (r,h) sets as a function of time indicated in picoseconds (see inset for spectral timescale). 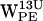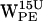(a–d) , , , and (r,h) projections. (e–h) , , , 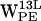and 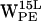(r,h) projections.

FIGURE 6.

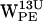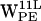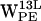Density plots of (r,h) for d_C6π for gA/POPE. (a–d) Density plots of (r,h) for d_C6-π projections for , , , and . (e–h) Density plots of (r,h) for d_C6-π projections for , , , and .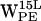

FIGURE 7.

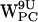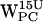(a–h) Time-resolved (r,h) scatter plots of d_C6-π projections for gA/POPC. Colors indicate (r,h) sets as a function of time indicated in ps. (a–d) , , , and (r,h) d_C6-π projections. (e–h) , , 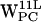, 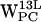and 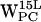(r,h) d_C6-π projections. Legend as in Fig. 5.

FIGURE 8.

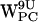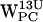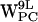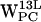Density plots of (r,h) for d_{C6 − π} for gA/POPC. (a–d) Density plots of (r,h) for d_C6-π projections for , , , and . (e–h) Density plots of (r,h) for d_C6-π projections for , , , and .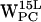

Fig. 5 provides information about distances and angles, but information about the number of possible interactions at a given (r,h) position is not accessible. Therefore we plotted the (r,h) projections of the d_C6-π vectors in a density plot, shown in Fig. 6.

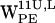For , the density analysis confirms and extends the information obtained in Fig. 5, a and e. The d_C6-π vectors projections scatter mainly in a single region close to the plane of the indole beyond 10 Å from the centroid. For , the (r,h) cloud is centered approximately at (r,h) = (12 Å, 4 Å), and for , the cloud is centered around (r,h) = (11 Å, 1 Å) (see Fig. 6, a and e). For both and , the density scatter plots have several regions of high density (Fig. 6, b, c, f, and g). 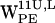For both and 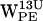, some high density regions are within the cone selection and distances <7 Å, thus fulfilling our criteria for cation-π interaction. and 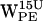both have high density regions beyond the selection criteria for cation-π interaction (see Fig. 6, d and g). 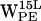has a moderately dense region for h > 0 within the selection cone, but a dense region h < 0 falls outside (see Fig. 6 h).

We now turn to gA/POPC where Figs. 7 and 8 are analog to Figs. 5 and 6 for gA/POPE.

When comparing the time-resolved scatter plots for d_C6-π (r,h) projections for POPE (Fig. 5) with the similar plots for POPC (Fig. 7), some features are common. For both systems, 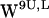(Figs. 5, a and e, and 7, a and e) d_C6-π vector projections scatter well beyond the selection criteria for cation-π interactions; the projections (Fig. 7, a and e) scatter points are centered around (14 Å, 3 Å) a bit farther away from the centroid compared with the projections (Fig. 5, a and e) that center around (12 Å, 3 Å). For 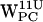(Fig. 7 b) very few (r,h) sets fall within the selection criteria, and for (Fig. 7 f), they all fail to meet the selection criteria. This is in contrast to the corresponding results for 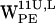(Fig. 5, b and f), where both residues find candidates for cation-π interactions. 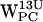(Fig. 7 c) has a subset of (r,h) sets around (3 Å, 4 Å), well within the selection criteria at the end of the simulation (Fig. 7 c), whereas for (Fig. 7 c), the subset that fulfills the selection criteria is farther away, centered around (7 Å, 8 Å). 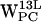(Fig. 7 g) and 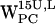(Fig. 7, d and h) do not have any (r,h) sets that meet the selection criteria. When comparing 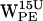(Fig. 5 d) with 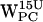(Fig. 7 d), the scatter regions overlap significantly. For 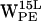(Fig. 5 h) and 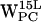(Fig. 7 h), both (r,h) sets scatter in a crescent-like pattern centered around (12 Å, 4 Å) in POPC and (7 Å, 2 Å) in POPE, respectively.

The density plot for POPC d_C6-π (r,h) projections is shown in Fig. 8. For (Fig. 8, a and e) no density regions are within the selection criteria, consistent with the results in Fig. 7, a and e) For 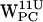(Fig. 8 b) a low density region is visible around (6 Å, 3 Å), but the highest density is seen in the indole plane some 8 Å away from the centroid, failing to meet our selection criteria. The density plot for the 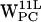projections (Fig. 8 f) shows no regions within our selection criteria. For 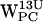(Fig. 8 c) a low-density region is seen around (4 Å, 4 Å), whereas a somewhat denser region is seen for 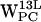, centered at (5 Å, 6 Å), thus more far away from the centroid (Fig. 8 g). For 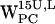, no favorable conditions for cation-π interactions were detected.

The results presented so far indicate that conditions for cation-π interactions are less favorable in POPC than in POPE. This could be compensated for by an increase in hydrogen-bonding ability to the carbonyl group in POPC compared to POPE. We therefore analyzed the hydrogen-bonding ability in POPE and POPC for all tryptophans using a 3.5 Å cutoff distance and a donor-H-acceptor angle cutoff of θ = ∠ r_N-H,r_(N-)H…_{O = C} = 60° and compared hydrogen bonding lifetimes with cation-π interaction lifetimes. The lifetimes of hydrogen bonds and cation-π in upper and lower tryptophans show no significant differences between the upper and lower tryptophans, although the number of interactions varies due to gA center-of-mass displacements relative to the bilayer midplane during the simulations and an associated long autocorrelation time (results not shown). We have therefore performed lumped statistics on the upper and lower tryptophans, and this is shown in Fig. 9.

FIGURE 9.

(a) Distribution of individual lifetimes for hydrogen bonds between the lipid carbonyls and the NH group of the indole for gA/POPE (light shaded) and gA/POPC (dark shaded). Measurements were made every 0.5 ps during 6 ns. (b) Distribution of individual lifetimes for cation-π interactions for gA/POPE (light shaded) and gA/POPC (dark shaded); sampling as in a. (c) Normalized survivor plots for hydrogen bonds and cation-π interactions in gA/POPE and gA/POPC. In this analysis, the 6 ns period was divided into 50 ps segments, and for each segment, the interactions were followed until each interaction ceased (sampled every 0.5 ps). Finally, counts for the 120 segments were summed and normalized. The distributions were fitted with biexponential functions (dashed curves) and the fitting parameters are listed in Table 1.

Fig. 9 a shows the number of hydrogen bonds as a function of their lifetimes in POPE and POPC. The distributions are exponential with most lifetimes <2 ps, and the bin-count ratios of the lifetimes in POPE/POPC are close to 1 except for the first bin ratio where it is 0.75, reflecting the somewhat larger number of short-lived hydrogen bonds in POPE compared to POPC. In comparison, the same type of analysis for the cation interaction (shown in Fig. 9 b) reveals that the number of cation-π interactions is at least threefold higher in POPE than in POPC.

To relate interaction lifetimes to the energetics, we analyzed the length of each interaction within 50 ps time segments, revealing the stability of the individual interactions. This is shown in Fig. 9 c. Each of the four interactions analyzed reveal a biexponential distribution of lifetimes, and the fitting parameters are listed in Table 1.

TABLE 1.

Fitting parameters for the distributions in Fig. 9 c

	τs/ps	τl/ps	Ps	Pl = 1 − Ps
H-bond POPC	1.19	41.19	0.47	0.53
H-bond POPE	1.43	28.02	0.42	0.58
Cat-π POPC	0.72	8.80	0.45	0.55
Cat-π POPE	0.25	8.60	0.28	0.72

Each distribution is fitted to the equation 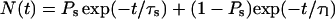, with r² > 0.97.

likely reflects vibrational dynamics of the interaction, whereas 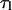probably is related to lipid translation and rotational movements.

From the τ values in Table 1, we can estimate the relative strength of the cation-π interaction over hydrogen bonding in POPE and POPC. τ is related to the dissociation constant k for the transition state as

(1)

where x denotes the short (s) or long (l) time constant. Assuming that A is invariant with respect to interaction and bilayer type, we can write the total energy ratio between cation-π and hydrogen bond interactions as

(2)

For POPE 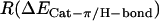= 0.63 and for POPC 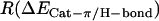= 0.41, thus in POPE 1.5 times more of the interaction energy is present in the form of cation-π interactions compared to hydrogen bonds than is the case for POPC.

DISCUSSION

MD simulations constitute an effective tool for exploring lipid-protein interactions in atomic detail. The vast amount of experimental data on gA channel structure and function in a lipid environment (cf. Koeppe et al. (38)) allows for a critical examination of the computed trajectories (31,37,39,57,58). Using gA as a model for a tryptophan “anchored” membrane-spanning protein, we show that tryptophan lipid-headgroup interactions are complex, involving both hydrogen bonding and cation-π interactions, and that the interaction with the lipid headgroup depends on tryptophan orientation and localization as well as on the chemical nature of the headgroup.

Tryptophan orientation

Our tryptophan order parameters results are consistent with torsion angle values reported from other MD simulations (39). Except for 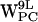, no major changes in torsion angle values occur in our simulations, consistent with fluorescence spectroscopy studies suggesting that the tryptophans are conformationally restricted by their lipid environment (59). A recent NMR study of the orientation of “free” tryptophans in phospholipids bilayers supports the notion of motion restriction dictated by a multitude of interactions, including cation-π interactions with the lipids (15).

Tryptophan orientation in gA has been studied experimentally (59–62) and theoretically (39,40,63). For 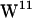, , and 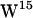unique regions of side-chain (c₁,c₂) torsion angles have been proposed (62,64–66), whereas two rotamers for 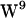have been proposed in dimyristoylphosphatidylcholine (DMPC): one resulting in aligning approximately parallel to 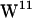(sandwich configuration PDB:1JNO) (64–66), and one resulting in 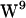aligning approximately parallel to (stacked conformation PDB:1MAG) (62,67).

The 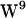/ sandwich configuration, observed in sodium dodecyl sulfate micelles (65,66), DMPC (68,69), consistent with experimental average ring orientations (60), and supported by MD simulations (40), is likely to be the dominating conformer. However, (40) note that the two rotamers (1JNO and 1MAG) are within 1 kcal/mol of each other, in apparent contrast to the suggestion that the 1MAG structure has a large repulsive stacking interaction between 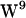and 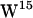. Thus we do not see that the tryptophan stabilization observed with the 1MAG structure in our simulations stems from a particularly unfavorable conformation.

Cation-π interactions

We have investigated the role of cation-π interactions in the tryptophan motion restriction observed theoretically (40) and experimentally (15,59). In neither POPE nor POPC is 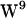participating in cation-π interactions with lipids according to our analysis, although the result could be model dependent. 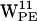, , 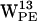and 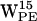all seem good candidates for participating in cation-π interactions, whereas only 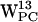shows a tendency to cation-π interact. One reason for a more pronounced cation-π effect in POPE compared to POPC could be steric hindrance caused by the more bulky N(CH₃)₃⁺ group in POPC relative to the NH₃⁺ group in POPE. Indeed, the density plots (Fig. 8) for POPC do show scatter densities farther away from the centroid than what is found for POPE (Fig. 6). This could suggest that the cation-π effect is more important for protein-PE interaction than for protein-PC interaction. If the lack of cation-π stabilization in PC is not compensated for in other ways, for example by an increased number of hydrogen bonds between the PC lipid and the protein (see below), then the cation-π effect could contribute to an enrichment of PE lipids around membrane-spanning proteins with aromatic interfacial residues.

In our study we have characterized cation-π interactions based on geometrical selection criteria using an existing force field. However, polarizability is only present in our simulation implicitly in the form of partial atomic charges that typically overestimate molecular dipoles (32,33). In particular, this implies that the cation-π effects are underestimated at large angles. Future attempts to refine cation-π interactions in greater detail will therefore depend on the development of force fields based on improved tryptophan parameters (60) as well as potentials for induced polarizability (31,70,71).

Hydrogen bonding

In addition to indole cation-π interactions, the NH-group of the indole can act as electron acceptor hydrogen for the carbonyl oxygen atom donor. This was observed both in POPE and POPC (Fig. 9). MD simulations of a gA heterodimer constructed as one 1MAG monomer and one 1JNO monomer embedded in a DMPC bilayer revealed that hydrogen bonding for the 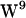/ 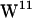sandwich configuration (1JNO) was much more pronounced than for the 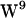/ stacked configuration (1MAG) without any major difference in the magnitude of conformational fluctuations (39). The absence of large-scale W movements is consistent with our observations based on the 1MAG structure, and neither in POPE nor POPC is 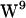engaged in hydrogen bonding to the lipid carbonyl. This does not rule out, however, that tryptophans hydrogen bond to water, which seems to be the dominant type of tryptophan hydrogen bonding (with exceptions) (39), noting that 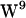faces the hydrophobic core, where only a few potential hydrogen bonding waters will be available. For 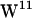and 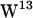, strong hydrogen bonding to the lipid carbonyl is present in both POPE and POPC, whereas 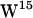is generally too far away for carbonyl hydrogen bonding in either bilayer but closer to the aqueous phase than the other tryptophans, providing good opportunities for hydrogen bonding to water. In general, our simulations suggest that the major lipid hydrogen bonding tryptophans are and 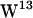with no major difference between POPE and POPC, consistent with the observation that tryptophan motions seem equally restricted in POPC and POPE. The fast component of the hydrogen bond lifetimes (see Fig. 9 c) is similar to the 0.9 ps mean lifetime of indole hydrogen bonds with water previously reported (72), and the slow component is consistent with these authors' observations of lipid-indole hydrogen bonds lasting >25 ps.

The fact that hydrogen bonding does not seem to compensate for the lower number of possible cation-π interactions in PC together with the observation that in POPE more of the interaction energy is due to cation-π interactions than to hydrogen bonds compared to the case in POPC (see Table 1 and Eq. 2) indicate that cation-π interactions play a stronger role for anchoring of aromatic residues to PE headgroups than to PC headgroups in the annulus of lipids surrounding membrane-spanning proteins.

Possible effects of ionic strength

The simulations were done in the absence of any ions in the aqueous phase, which potentially might influence cation effects and hydrogen bonding in the interfacial region, but we note that the interaction between monovalent ions (e.g., Na⁺, Cl⁻) and lipids are generally assumed to be weak with dissociation constants in the physiological range of 100–500 mM (73). However, MD simulations of POPC have revealed significant effects on the lateral lipid self-diffusion (74). For dipalmitoylphosphatidylcholine (DPPC) bilayers, MD simulations suggest that on average each Na⁺ is coordinated with carbonyls and phosphates of two lipid headgroups, whereas Cl⁻ seems more loosely adsorbed (75). The presence of Na⁺ close to the indole ring could enable a favorable interaction with the π-electron cloud, thus competing with the ammonium or guadinium moiety of the lipid headgroup for a cation-π interaction with the indole. The ammonium moiety is larger than the guadinium moiety, which could imply that Na⁺ would have better access in the latter case, but it would then also feel a stronger repulsion from the headgroup positive charge. Thus these effects may cancel out in the sense that Na⁺ would affect POPC and POPE to the same extent, although we admit this is still an open issue as we are not aware of any detailed (MD) analyses of Na⁺ interaction with PE bilayers. Finally we note that the hydration of the lipid headgroup remains relatively stable upon simulated Na⁺ addition (75), suggesting that no major water molecule rearrangements take place in that region. In conclusion, we acknowledge that ion adsorption may change the electrostatic properties in the headgroup region, but there are no strong reasons to believe that the effects will affect our overall conclusions.

Implications for lipid-protein interactions

How can our observation that PE headgroups seem to interact more favorably with interfacial tryptophans than PC headgroups be reconciled with metastable nonspecific mechanisms for modulation of protein function by the host bilayer, e.g., via bilayer elasticity (49,76)? POPE has a more negative monolayer equilibrium curvature compared to POPC (77). Thus POPE bilayers will be in a state of curvature frustration, and the stored frustration energy can modulate protein function (78). The monolayer equilibrium curvature is reflecting the effective shape of the lipid molecules where the effective headgroup size is determined by a combination of steric and electrostatic forces as well as polarization of interfacial water in the headgroup region. In this view, the effects of curvature frustration on the protein are dependent on the nature of the flanking or anchoring residues. Further, the exact position of these residues modulate the effective hydrophobic length of transmembrane proteins (79,80). The cation-π interactions between lipids and proteins can thus be regarded as i), realizations of the effect of monolayer equilibrium curvature on transmembrane proteins, and ii), codeterminants of the transmembrane proteins effective hydrophobic length. Taken together this provides a mechanism for indirect regulation of protein function (and localization) based on the hydrophobic matching ability of the lipid membrane.

CONCLUSION

Using an existing force field we have studied cation-π interactions in the interaction between interfacial anchoring residues of transmembrane proteins and the surrounding lipid bilayer. Our results show that cation-π interactions for interfacial tryptophan residues depend on both the tryptophan position relative to the bilayer-water interface and on the chemical nature of the lipid headgroup. Ethanolamine headgroups are favored over choline headgroups, whereas the hydrogen-bonding ability between tryptophan and lipid carbonyls is largely independent of the chemical nature of the headgroup. The cation-π interaction translates into two effects: one anchoring the protein to the bilayer, and one indirectly affecting membrane lateral stress on the protein as well as the effective hydrophobic length of membrane-spanning segments of integral membrane proteins.