Extending a Spectrin Repeat Unit. II: Rupture Behavior

Abstract

A spectrin repeat unit was subject to extension using cyclic expansion nonequilibrium molecular dynamics. Periodic boundary conditions were used to examine the effects of the contiguous α-helical linker on the force response. The measured force-extension curve shows a linear increase in the force response when the spectrin repeat unit is extended by ∼0.4 nm. After that point, the force response peaks and subsequently declines. The peak in the force response marks the point where the spectrin repeat unit undergoes a change in its material properties from a strongly elastic material to a mostly viscous one, on the timescales of the simulations. The force peak is also correlated with rupture of the α-helical linker, and is likely the event responsible for the peaks in the sawtooth-pattern force-extension curves measured by atomic force microscopy experiments. Rupture of the linker involves simultaneously breaking approximately four hydrogen bonds that maintain the α-helical linker. After this initial rupture, the linker undergoes simple helix-to-coil transitions as the spectrin repeat unit continues to be extended. The implications of linker rupture in the interpretation of unfolding and atomic force microscopy experiments are also discussed.

INTRODUCTION

Spectrin is a filamentous protein that is primarily responsible for the elasticity of the red blood cell, or erythrocyte. The ∼200-nm-long spectrin tetramer is formed by the head-to-head association of two heterodimers. The primary structure of the spectrin monomers exhibits a repeating sequence consisting of 106 amino acids (1). NMR and x-ray crystallography have shown that a particular selection of the 106-amino-acid repeating sequence (2) folds into three antiparallel α-helices (where the helices are labeled A, B, and C, and the B-helix is aligned antiparallel to the A- and C-helices; see (3,4)). This triple-helix structure is commonly referred to as the spectrin repeat unit. Many experimental studies, such as x-ray crystallography (5–7), temperature- and urea-induced unfolding (8,9), and atomic force microscopy (AFM) (10,11), as well as homology modeling (1) and atomistic simulations (12–14), have been performed to understand the relationship between the molecular structure of the repeat units and the function, or material properties, of larger-scale spectrin assemblies. In particular, the secondary structure of the polypeptide chain linking repeat units, or just the linker, has often played a key role in explaining the elasticity (1,5–7,9,15) and forced unfolding behavior (10,11,14) of multiple-repeat spectrins. In contrast to earlier assumptions about the secondary structure of the linker (1,15), recent crystal structures of multiple-repeat spectrins (3,5–7,16,17) have indicated that the linker forms a contiguous α-helix. This article presents novel simulations of a spectrin repeat unit, which were constructed to examine how a contiguous α-helical linker affects the properties of a multiple-repeat spectrin. The companion article (part I) (18) explored how the linker affects the elastic properties, or its near-equilibrium response. This work focuses more on understanding how the structure of spectrin, and in particular the linker, changes when it is subject to extensions large enough to unfold the individual repeat units, such as those imposed using AFM.

Spectrin was first studied using AFM by Rief et al. (19) The force-extension curves of native α-spectrin, a recombinant construct of six spectrin repeats, and α-actinin (which belongs to the spectrin superfamily and is composed of spectrin repeat units) all gave a sawtooth-pattern with force peaks of 25–35 pN (at pulling speeds of 0.08–0.8 nm/ms) and peak-to-peak spacings of ∼31.7 nm. The peaks were attributed to the force required to rupture one spectrin repeat unit. The peak-to-peak spacing was close to that expected for completely unfolding a 106-amino-acid spectrin domain. This led the authors to conclude that the repeat units unfold in an all-or-none fashion, similar to previous AFM results on immunoglobulin and fibronectin type III domains (20–22). Furthermore, Rief et al. (19) proposed that the mechanism for the rupture event responsible for the AFM force peaks involves breaking the core hydrophobic interactions maintaining the triple-helix bundle.

More recent AFM studies (10,11,13,23), which analyzed hundreds to thousands of force-extension curves, have revealed more complex behavior. Lenne et al. (23) studied an engineered spectrin consisting of four identical repeat units. The distribution of peak-to-peak lengths was found to be bimodal with short elongation events centered at 15.5 nm and long elongation events centered at 31 nm. The short elongation events were attributed to the existence of at least one stable intermediate between the folded state and the completely unfolded state. Subsequent simulation and mutation studies suggested that the stable intermediate involves kinking of helix B near a proline residue (13).

AFM studies of two-, three-, and four-repeat spectrins also gave bimodal as well as some very broad peak-to-peak distributions (10,11), depending on the number of repeat units in the molecule. But in contrast to Lenne et al. (23), the bimodal distributions peaked at 22 nm and 42 nm, and the authors assigned the long elongation events to tandem unfolding, where two adjacent repeat units unfold at the same time, although the precise mechanism by which tandem unfolding would occur is still not clear. Originally, it was thought that when one repeat unit unfolded (presumably by the mechanism suggested by Rief et al. (19)), disruption of hydrogen bonds in the linker would propagate into the adjacent unit and destabilize the hydrophobic core, thereby causing the adjacent repeat unit to unfold (10). However, later experiments that examined the relationship between tandem unfolding and the α-helical content seemed to suggest that the loss of α-helical structure in the linker actually decreased the tendency for tandem unfolding (11). In other words, the presence of an α-helical linker would seem to propagate unfolding to adjacent repeat units. Of course, the molecular mechanism by which spectrin unfolds under an applied force has not previously been determined, making any discussion of the mechanism of tandem unfolding unclear.

Molecular dynamics (MD) simulations have played a key role in elucidating the relationship between molecular structures and forced unfolding experiments. This is especially true in the case of titin, where steered molecular dynamics (SMD) (24–26) simulations showed that the force peaks observed in AFM experiments correspond to the force required to rupture several β-sheet hydrogen bonds in parallel (26–29). But in contrast to simulations of the titin domains, SMD simulations of single- and double-repeat spectrin units (12–14) have not previously shown a distinctive force-peak that could be related to specific changes in the molecular structure. Instead, more gradual unfolding was observed, where the terminal helices (the ones that were being pulled on) elongated, which disrupted the hydrophobic core and allowed the repeat unit to unfold.

When using either AFM or MD simulation to study the forced-unfolding behavior of repeating structures such as spectrin, it is often convenient to reduce the system size to only a small number of repeat units. In doing so, it is assumed that there is little coupling between repeat units and that understanding how a single- or double-repeat spectrin unfolds will provide considerable insight into the properties of the full spectrin filament. However, when using a small section of spectrin to understand the larger structure, the boundary conditions imposed on the system must be carefully considered. This is especially true in the case of spectrin, where the linker region that connects adjacent repeat units has a specific secondary structure, that of a contiguous α-helix. Any subdivision of the full spectrin filament into a smaller number of repeat units will obviously disrupt the native structure of the linkers, and any artifacts introduced due to this subdivision must be addressed. As mentioned above, SMD has previously been employed to study the forced-unfolding behavior of spectrin (12–14). However, the particular choice of boundary conditions used (i.e., the way in which the SMD biasing force was applied) for these systems may exhibit properties that are not commensurate with either those of the full spectrin filament or those of the several-repeat spectrins studied by AFM. The primary difficulty is that SMD was imposed on the two terminal atoms which, in a larger filament, would have belonged to a contiguous α-helix and any force on the end of the filament would have been distributed throughout the α-helix. In an AFM experiment, the AFM tip has a radius of curvature of approximately the size of four spectrin repeat units (10) and thus the force on the spectrin molecule is distributed over a much larger surface and not localized on the two terminal atoms (the spectrin AFM experiments have used adsorptive rather than covalent interactions to attach the molecules to surface and tip). These issues were perhaps less critical in the SMD simulation of titin unfolding (26–29), where the linkers did not have a well-defined secondary structure, and thus the force on a single titin domain could be considered to originate from specific atoms.

The approach used in this work is designed to alleviate some of the issues discussed above and involves making use of periodic boundary conditions to attach a spectrin repeat unit to its own periodic image, thereby incorporating an intact and contiguous α-helical linker without introducing any free noncontiguous helical ends. This situation can be thought of as a simulation of an interior spectrin repeat unit (i.e., surrounded by other repeat units). The relationship between the force-extension response and the molecular structure was probed using a method called cyclic expansion nonequilibrium molecular dynamics (NEMD), which imposes a uniform strain field on the system. In the companion article (18), this method was used to demonstrate that a contiguous α-helical linker can significantly increase the elasticity of a spectrin repeat unit. In this article, it will be shown that the linker also plays an important role in the unfolding behavior. Specifically, the simulations suggest that the force peaks observed in AFM experiments can be attributed to rupture of the α-helical linker.

METHODS

The simulation conditions and methods are described in detail in the companion article (18), but will be briefly summarized here. The initial coordinates for all simulations were based on the solution NMR structure of the 16th repeat unit of chicken-brain α-spectrin (4) (Protein Data Bank ID 1AJ3). The residues that were not resolved in the NMR structure were manually added to adopt an α-helical conformation using the Swiss-PDBViewer (30). The C-terminus of the spectrin repeat unit was covalently bound, via a peptide bond, through the periodic boundary conditions to the N-terminus to form a contiguous α-helix, as observed in crystal structures of multiple-repeat spectrins (3,5,6,16,17). Explicit water was used to solvate the system, which was then equilibrated for 10 ns under a constant NPT ensemble. Starting conditions for the nonequilibrium simulations were obtained from configuration snapshots of this equilibration trajectory.

The force-extension response of the spectrin repeat unit was calculated using cyclic expansion NEMD (31–36). In short, cyclic expansion NEMD subjects the system to an oscillating strain rate given by

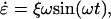(1)

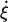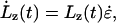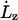where is the strain rate, ξ is the amplitude of oscillation, and ω is the frequency (and λ = 2π/ω is the period). This strain rate is only applied along the z direction of the simulation cell, such that the length of the spectrin repeat unit is governed by where is the extension rate, or pulling speed. The strain rate given by Eq. 1 is imposed on the system through the equations of motion. The equations of motion (see the companion article (18)) are similar to the usual Nosé-Hoover NPT equations of motion (37), except that the strain rate in the z direction is predetermined by Eq. 1. The strain rate in the x and y directions is such that it maintains, on average, zero stress in these directions.

As discussed in the companion article (18), the instantaneous force acting on the system is F_ω = 〈P_zzV〉/L_z (where P_zz is the instantaneous value of the pressure tensor (38) in the z direction and V is the volume of the simulation cell). This relationship, which is easy to measure using MD, is a consequence of the employed periodic boundary conditions and the equations of motion. The equilibrium force response is obtained in the limit of ω→0. In practice, this value is obtained by averaging P_zzV/L over all trajectories performed at a particular ω and extrapolating the averages to ω = 0. But since NEMD can only sample a finite range of frequencies, the true ω→0 limit is not always obtained by extrapolation. Evidence that the extrapolation is not equal to the ω→0 limit is often observed in the form of a strong frequency or extension-rate dependence, as discussed in Results. In this case, the extrapolated force response gives an upper limit to the equilibrium force response and indicates that, on timescales of the NEMD simulation, a large amount of irreversible work must be done on the system to impose the applied extension.

NEMD simulations of water under conditions very similar to those in the spectrin simulations were used as a control. As shown in the companion article (18), the force response from bulk water is negligible at the pulling speeds used in the spectrin NEMD simulations. Therefore, any force response measured can be directly attributed to the presence of spectrin, and not the bulk water.

The companion article (18) was primarily concerned with examining the force response of a spectrin repeat unit under small extensions in the linear region of the force-extension curve. This article expands on the earlier work by probing a larger range of extensions using two different sampling methods. The first method, which is referred to as the NEMD window sampling method, involved chaining together several cyclic expansion NEMD simulations. This was accomplished by first taking the maximum amplitude configurations from the slowest frequency cyclic expansion NEMD trajectories reported in part I, and equilibrating them under constant length for 500 ps. These new equilibrated structures were then subject to cyclic expansion NEMD to obtain the force response for that region of the force-extension curve. The maximum amplitude structures from these NEMD simulations were again equilibrated at constant length for 500 ps and the process was repeated to cover four NEMD windows, or ranges of length. All windows were subject to the same NEMD amplitude ξ = 0.02 and NEMD periods, ranging from λ = 500 to 4000 ps. For every period in each window, 4–7 trajectories starting from different initial configurations were calculated.

The second method involved performing cyclic expansion NEMD on equilibrated systems sampled from the original constant NPT equilibration trajectory, but with varying amplitudes ranging from ξ = 0.01 to 0.09 and periods from λ = 200 to 2000 ps (giving rise to pulling speeds ranging from 0.2–12 nm/ns). This method is referred to as the amplitude-scan method. For these simulations, both the extension (t = 0 to λ/2) and contraction (t = λ/2 to λ) trajectories are reported (i.e., both halves of the NEMD cycle). For every period at each amplitude, 10 trajectories starting from different configurations were calculated.

A quantitative measurement of the structural changes of spectrin was obtained by measuring the number of linker hydrogen bonds as a function of extension in the amplitude scan trajectories. For the purposes of this article, the linker was defined as including residues 100–110 and 1–16. A hydrogen bond was counted only if the distance between backbone nitrogen and oxygen atoms was <3.5 Å and the hydrogen-nitrogen-oxygen angle was <35°. The molecular visualization program VMD (39) was used for this analysis.

RESULTS

NEMD windows

In any MD simulation that involves measuring a force-extension response, care must be taken to distinguish between contributions that arise from the underlying conservative forces and those that arise from nonconservative forces. Cyclic expansion NEMD is ideally suited for these purposes. By measuring the phase relationship between the imposed extension or extension rate and the force response, one can determine whether the system behaves primarily as an elastic material (involving conservative forces) or if it responds with strong viscous (i.e., nonconservative) forces. An elastic material gives a force response that is in phase with the extension, whereas a viscous material gives a force response that is in phase with the extension rate. In the companion article (18) it was shown that for small extensions of ∼3 Å, spectrin behaves primarily as an elastic material. Therefore, to determine how the material properties change as a function of length, the spectrin repeat unit studied here was subject to cyclic expansion NEMD over four ranges, or windows, of extension.

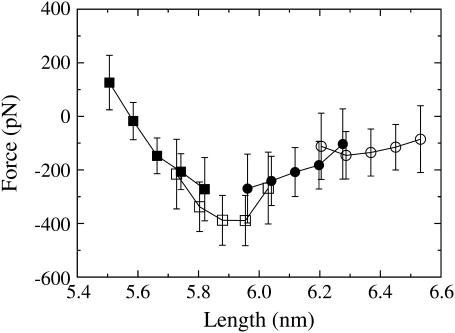
Fig. 1 shows the extrapolated force-extension curve for each of the NEMD windows. The sampling windows overlap because the starting configurations for window 1 were all sampled from an equilibrium trajectory integrated under a constant NPT ensemble. This ensemble gives a distribution of initial lengths, which carries over to subsequent windows. Window 1 sampled the force response over lengths of ∼5.50–5.80 nm, window 2 sampled 5.70–6.05 nm, window 3 sampled 5.95–6.30 nm, and window 4 sampled 6.20–6.55 nm.

FIGURE 1.

The extrapolated force-extension curve using NEMD window sampling. Each point type corresponds to a different window: window 1 is shown as solid squares, window 2 as open squares, window 3 as solid circles, and window 4 as open circles.

As discussed in detail in the companion article (18), the force response in window 1 was found to be mostly linear with little frequency dependence, and could be accurately described by a linear elastic constitutive equation. Fig. 1 shows that this linear force-extension response breaks down in window 2, where the magnitude of the force peaks at 400 ± 100 pN at ∼5.9 nm. As will be shown in a later section, this force peak corresponds to the force required to rupture the α-helical linker. The peak is followed by a quick decline in the magnitude of the force through window 3 and then levels off to an almost constant force of ∼100 pN in window 4.

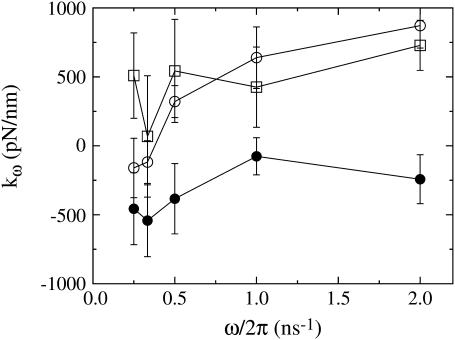
One of the ways in which the material properties of the spectrin repeat unit were measured was by calculating an effective spring constant for each window as a function of the NEMD frequency ω (Fig. 2 shows results for windows 2–4; see Fig. 3 of part I for window 1). In windows 1–3, the measured spring constant was relatively insensitive over the range of imposed frequencies, although it did significantly decrease as the repeat unit was extended. In contrast, window 4 gives a strong positive spring constant (meaning that the force-extension curve is downward-sloping) of 870 ± 160 pN/nm at high frequencies and a weak negative (upward-sloping), essentially zero, spring constant of −160 ± 215 pN/nm at low frequencies. This trend is indicative of a viscous effect and suggests that there are some slow relaxation processes that occur after the linker has ruptured. Indeed, the trajectories that were subject to slow frequencies in window 4 give a force response that is largely in phase with the extension rate and out of phase with the extension (data not shown), again indicating the presence of viscous forces. These results show, on these timescales, that as the spectrin repeat unit is extended, it undergoes a transition from a strong elastic material to a mostly viscous one. As will be shown later, the peak in the force-extension curve and the changes in material properties are due to rupture of the α-helical linker connecting repeat units.

FIGURE 2.

Spring constants measured as a function of frequency for each NEMD window (window 1 is shown in the first article). Each point type corresponds to a different window: window 2 is shown as open squares, window 3 as solid circles, and window 4 as open circles. In window 4, spectrin responds with a strong elastic component only at higher frequencies.

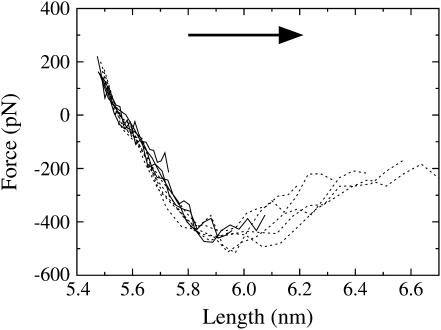
FIGURE 3.

The extrapolated force-extension curve upon extension for several NEMD amplitudes (ξ = 0.010–0.040 shown as solid lines, ξ = 0.050–0.090 shown as dashed lines). The arrow indicates the direction of pulling (extension). Error bars have been omitted for clarity, but are similar in magnitude to Fig. 1 (i.e., ±100 pN).

Amplitude scan

The rupture process observed in the force-extension curve described above was examined in more detail by performing cyclic expansion NEMD over a set of NEMD amplitudes. The amplitudes used here (ξ = 0.010–0.090) covered a similar range of lengths (5.50–6.70 nm) as spanned in the NEMD window trajectories. But in this case, both the extension and contraction halves of the NEMD cycle were calculated. By monitoring the hysteresis in the force response, information about the reversibility of the rupture process was obtained.

Results from the extension trajectories are shown in Fig. 3. Each line in this figure is the extrapolated force response of the spectrin repeat unit at a particular NEMD amplitude. In the linear region of the force-extension curve, ∼5.5–5.8 nm, the force response for all amplitudes is the same to within the error of ±100 pN. In this region, both the amplitude scan and NEMD window sampling are in agreement. However, after ∼5.9–6.0 nm, the force responses for each amplitude diverge. The reason for this divergence is that, although all amplitudes sampled the same extension rate frequencies ω, the larger amplitude trajectories were subject to larger extension rates (Eq. 1). This indicates that after the peak in the force-extension curve, the system is far enough away from equilibrium that a linear extrapolation of the forces with respect to these frequencies is not equivalent to the ω→0 limit. In other words, after rupture, the spectrin repeat unit responds with strong frequency-dependent forces (i.e., viscous forces that relax on a longer timescale than these simulations). These viscous forces were also observed in this region of the force-extension curve in the NEMD window sampling trajectories described above.

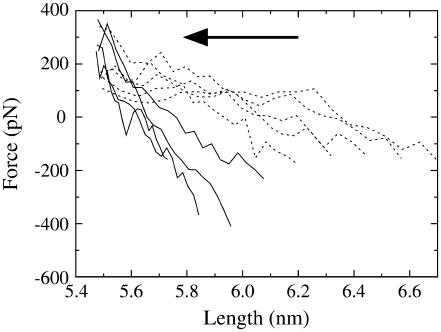
The extrapolated force response for each amplitude on contraction is given in Fig. 4. This figure shows that before the rupture point is reached, the extension and contraction force-extension curves are nearly identical. However, once the spectrin repeat unit is extended beyond 5.9–6.0 nm, a large hysteresis develops. The force that the spectrin repeat unit experiences is thus critically dependent on whether it has been extended beyond the rupture point. Up to this point, the force response is essentially linear, and the zero of the force-extension curve is close to the equilibrium length. Once the repeat unit has ruptured, the zero of the force response shifts out to larger lengths and the effective spring constant decreases.

FIGURE 4.

The extrapolated force-extension curve upon contraction for several NEMD amplitudes (ξ = 0.010–0.040 shown as solid lines, ξ = 0.050–0.090 shown as dashed lines). The arrow indicates the direction of pulling (contraction). Error bars have been omitted for clarity, but are ∼±100 pN.

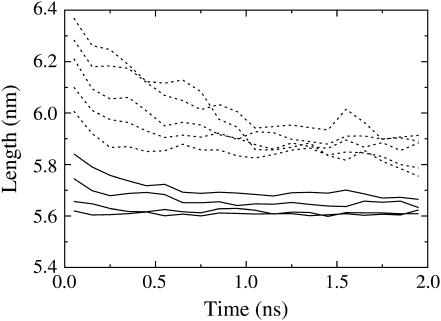
To determine how accurately Fig. 4 represents the actual dynamics of the spectrin repeat unit, a set of simulations were performed, which were not subject to the length constraints imposed by cyclic expansion NEMD. In these simulations, the final configurations of the slowest (period λ = 2000 ps) extension amplitude scan trajectories were allowed to evolve under a normal constant NPT ensemble for 2 ns. The average position (over 10 initial configurations) as a function of time is plotting for each NEMD amplitude in Fig. 5. This figure is in good agreement with the conclusions drawn from Fig. 4. For example, Fig. 4 shows that when the spectrin repeat unit is extended to 6.2 nm, the zero in the force response on contraction occurs at ∼6.0 nm. Of course, the force response beyond the rupture point is largely dependent on the pulling speed and the zeros of the force-extension curve would also be expected to differ, depending on how fast the system is pulled. Beyond the rupture point, the zero of the force response occurs approximately half-way along the force-extension curve (Fig. 4). This means that for the slowest (λ = 2000 ps) contraction trajectories performed, the system was forced to the zero point in ∼500 ps. Fig. 5 shows that after 500 ps, a system that started with a length of 6.2 nm relaxed to a length of 6.0 nm. Therefore, the contraction force-extension curves of Fig. 4 appear to govern the actual motion of the system, at least over the timescales on which it was calculated.

FIGURE 5.

Average length as a function of time for several different starting lengths when the system was allowed to evolve under a constant NPT ensemble. Trajectories that started from the maximum extension of amplitudes ξ = 0.010–0.040 are shown as solid lines, whereas those from ξ = 0.050–0.090 are shown as dashed lines.

As more time is allowed, the system continues to relax to smaller lengths than those suggested by Fig. 4. But it is clear from Fig. 5 that the spectrin repeat unit does not easily return to its equilibrium length once it has been extended past the rupture point. Instead, this figure shows that even after 2 ns, the system relaxes to two different lengths, depending on whether it was extended beyond ∼6.0 nm.

STRUCTURAL ANALYSIS

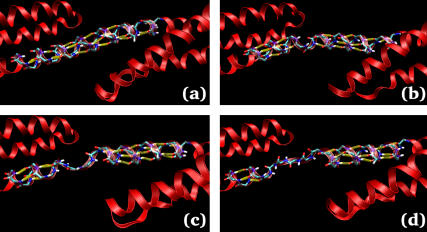
Visual inspection of the trajectories reveals that the structure of the linker region can be used to explain features of the force-extension curves described above. Fig. 6 shows several snapshots of the linker at different lengths, where the hydrogen bonds have been highlighted with yellow bars (see Methods for the criteria used to assign a hydrogen bond). In the linear region of the force-extension curve, the backbone hydrogen bonds maintaining the α-helix in the linker are all well formed (Fig. 6 a). Shortly after the force peak, four linker hydrogen bonds break, which is equivalent to approximately one turn of the α-helix (Fig. 6 b). Therefore, the linear region of the force-extension curve likely corresponds to stretching the linker hydrogen bonds, while the force peak can be attributed to the force required to break these hydrogen bonds. The initial rupture of one turn of the α-helix behaves like a nucleation event, as subsequent extension of the spectrin repeat unit results in rupture of adjacent hydrogen bonds as seen in Fig. 6, c and d. Furthermore, this behavior can help to explain the origin of the irreversibility of the rupture process observed in Figs. 4 and 5. When the system is allowed to relax (or forced back to its equilibrium length using cyclic expansion NEMD), reformation of the α-helical linker would require that several hydrogen bonds all come into alignment at the same time. This would be an extremely rare event and is not observed on the timescales of the simulation.

FIGURE 6.

Configuration snapshots showing the hydrogen-bond rupture and subsequent unzipping of the linker α-helix. Hydrogen bonds are indicated by the yellow bars. The snapshots were taken at extensions of (a) 5.62 nm, (b) 6.07 nm, (c) 6.19 nm, and (d) 6.54 nm. This figure was made with the help of VMD (39).

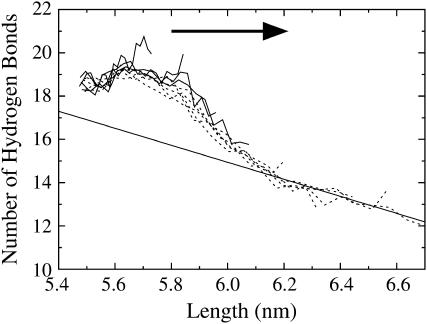
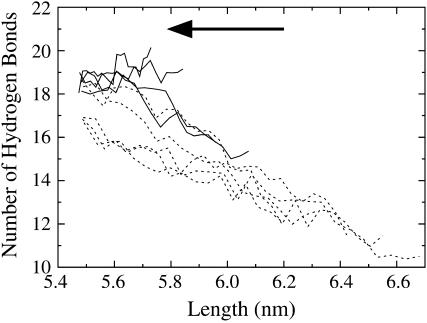
A more exact description of the structural changes can be obtained by counting the number of hydrogen bonds in the linker region as the system is extended. Fig. 7 shows the average number of linker hydrogen bonds as a function of length for the extension amplitude scan trajectories. In the linear region of the force-extension curve, 5.5–5.8 nm, the number of linker hydrogen bonds is almost constant. One exception to this trend involves the slow, low amplitude trajectories (λ = 2000 ps, ξ = 0.010), where the average number of hydrogen bonds actually increase by approximately two bonds when spectrin is extended from 5.5 to 5.7 nm. This effect is due the fact that, at equilibrium, the boundary conditions forced the linker to bend slightly to attach to its periodic image. This bend reduces the average number of linker hydrogen bonds. When the system is slowly extended, the bent linker is allowed to straighten and consequently allows for the formation of more hydrogen bonds. For the larger amplitude trajectories (ξ > 0.010), the faster extension rates do not give the linker enough time to straighten as much and thus do not reform hydrogen bonds as readily (although a slight, ∼0.5 hydrogen-bond, increase can still be observed between lengths of 5.5–5.7 nm for all amplitudes).

FIGURE 7.

Linker hydrogen bonds as a function of spectrin length for the extension-half of the NEMD cycle (slow trajectories, λ = 2000 ps; ξ = 0.010–0.040 shown as solid lines, ξ = 0.050–0.090 shown as dashed lines). The arrow indicates the direction of pulling (extension). Error bars have been omitted for clarity, but are ∼±1 hydrogen bond. The line drawn is a linear fit to the data beyond 6.1-nm extension and corresponds to a helix-to-coil transition extension of 0.254 ± 0.026 nm, close to the expected value of 0.23 nm.

When the spectrin repeat unit is extended beyond the linear region of the force-extension curve, the number of linker hydrogen bonds sharply drops by approximately four bonds between lengths of 5.8 and 6.1 nm. As indicated by Fig. 6 b, this four-hydrogen-bond drop corresponds to the rupture of one turn of the linker α-helix. Beyond the rupture point, the number of linker hydrogen bonds decreases more slowly. A linear fit to the data shown in Fig. 7 beyond 6.1 nm revealed that for every hydrogen bond that breaks, the length of the spectrin repeat unit increased by 0.25 ± 0.03 nm. The end-to-end length of a single amino acid is ∼0.38 nm and the length of one turn of an α-helix is 0.54 nm (40). Since there are 3.6 amino acids per turn of the α-helix, when a residue converts from being in an α-helical conformation to that of an extended random coil, the end-to-end length of the polypeptide is expected to increase by 0.23 nm. The agreement between this estimate and the measured decrease suggests that after one turn of the α-helix has ruptured (i.e., beyond 6.1 nm), the linker unfolds via a simple helix-to-coil transition.

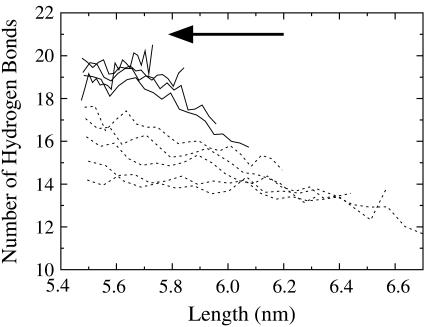
The number of linker hydrogen bonds measured in the contraction trajectories also offers some insight into the rupture process. As shown in Fig. 8, the broken linker hydrogen bonds reform if the spectrin repeat unit has not been extended beyond ∼6.1 nm. Beyond this length (i.e., after one turn of the α-helical linker has ruptured), the hydrogen bonds do not completely reform. Fig. 8 shows the results from trajectories subject to NEMD periods of λ = 2000 ps. However, when the system is subject to much faster cyclic expansion NEMD (λ = 200 ps; Fig. 9), the linker hydrogen bonds actually reform more readily. This is a consequence of the fact that at the fast pulling speeds, the ruptured sections of the α-helix have not had enough time to fully randomize and still contain some α-helical structure, even though the hydrogen bonds have ruptured. When the system is forced back, the hydrogen bonds are aligned enough to reform. When the pulling speed is decreased, the ruptured sections are given enough time to become random coil elements where exceedingly slow speeds would be required for the hydrogen bonds to align and reform.

FIGURE 8.

Linker hydrogen bonds as a function of spectrin length for the contraction-half of the NEMD cycle (slow trajectories, λ = 2000 ps; ξ = 0.010–0.040 shown as solid lines, ξ = 0.050–0.090 shown as dashed lines). The arrow indicates the direction of pulling (contraction). Error bars have been omitted for clarity, but are ∼±1 hydrogen bond.

FIGURE 9.

Linker hydrogen bonds as a function of spectrin length for the contraction-half of the NEMD cycle (fast trajectories, λ = 200 ps; ξ = 0.010–0.040 shown as solid lines, ξ = 0.050–0.090 shown as dashed lines). The arrow indicates the direction of pulling (contraction). Error bars have been omitted for clarity, but are ∼±1 hydrogen bond.

DISCUSSION

The results presented above provide a general picture for the initial stages of spectrin unfolding under an imposed extension. For small displacements, the spectrin repeat unit gives a linear force response that arises primarily from stretching the α-helical hydrogen bonds in the linker. Eventually, this stretching reaches a threshold, the force peaks, a full turn of the α-helix quickly ruptures, and the force drops. This is followed with one-by-one breaking of adjacent hydrogen bonds, or what can be thought of as unzipping of the α-helical linker.

Previous forced unfolding MD simulations of both single- (12,13) and double-repeat (14) spectrins failed to observe any specific molecular-level rupture events that could be responsible for the AFM force peaks. Although linker rupture was observed in some of the recent double-repeat simulations of Ortiz et al. (14), the large noise in the measured force-extension curve makes any definitive conclusions (about, for example, force barriers) problematic. The critical difference between the previous simulations and those reported here is our use of periodic boundary conditions to allow for a contiguous α-helical linker. In a contiguous α-helix, the backbone of each residue forms two hydrogen bonds with nearby residues. On the other hand, in an isolated single- or double-repeat spectrin, the terminal α-helices are not contiguous, so the four residues near the termini can only form one hydrogen bond each. The situation is similar to starting with adjacent linkers that have already ruptured. Indeed, after rupture of the linker α-helix, the NEMD simulations reported here are qualitatively and quantitatively similar to the pulling simulations of a single isolated repeat unit reported by Paci and Karplus (12) and Altmann et al. (13). Although Paci and Karplus (12) and Altmann et al. (13) probed extensions large enough to completely unravel the entire repeat unit, the peak average forces (∼200 pN) were all significantly lower than those observed in this study (∼400 pN). Furthermore, these 200-pN peak forces were observed in regions that were shown here, using cyclic expansion NEMD, to involve strong viscous forces that would likely be diminished on experimental timescales. The NEMD simulations reported here, in conjunction with these previous SMD simulations, thus demonstrate that once the two adjacent linkers surrounding a repeat unit have ruptured, no significant force barriers need to be overcome for the repeat unit to continue unfolding (at least, none larger than those required to rupture the linkers in the first place). Rupture of the linker is thus an initial, or nucleating, unfolding event; following which, the structure readily unfolds.

The above considerations strongly suggest that the force peaks observed in AFM experiments are the result of rupture of the α-helical linker region connecting repeat units. The mechanism of the rupture event (i.e., the initial stages of unfolding) involves breaking approximately four parallel hydrogen bonds followed by sequential unzipping of the nearby hydrogen bonds. This mechanism is in sharp contrast to the one originally suggested by Rief et al. (19), where the rupture event was proposed to involve unbundling of the three helices. Despite any evidence supporting such a mechanism, it is possible that these long timescale tertiary structure rearrangements could occur and are just not being sampled over the timescales examined in these NEMD simulations. Nevertheless, in real systems such as the AFM experiments or the cellular-level spectrin network, the observed force response can be thought of as a superposition of multiple frequency-dependent responses spanning the entire frequency spectrum (as required by equipartition of energy). That is, the observed unfolding mechanism could be a composite effect resulting from multiple unfolding mechanisms, occurring over different frequency domains. The NEMD simulations reported here indicate the presence, and describe the details, of a high-frequency rupture mechanism that could exist in conjunction with other very different low-frequency responses. Despite these considerations, the NEMD simulations suggest a plausible mechanism for the rupture events observed in AFM experiments.

A similar mechanism has been observed in the immunoglobulin (26–28) and fibronectin type III (29) domains of the muscle elasticity protein titin. Spectrin and titin both play a similar physiological role by providing cellular elasticity and are both arranged into a sequence of repeating domains. Titin has also been the subject of AFM experiments (20,21,41–43) and gives a sawtooth-pattern force-extension curve similar to spectrin, although the peaks are significantly larger. However, the structure of the repeating domains of spectrin and titin are vastly different. The spectrin repeat unit is constructed of three α-helices, and the repeating domains of titin are composed of several β-sheets. Despite these large structural differences, spectrin and titin both share a similar unfolding mechanism. SMD simulations of the titin domains were able to show that the force peaks observed by AFM are due to the force required to rupture several parallel hydrogen bonds, which compose a β-sheet (26–29). After this initial rupture, the structure of the protein is such that the remaining β-sheets were able to be unzipped, where the hydrogen bonds ruptured sequentially rather than in parallel. The rupture event for both the spectrin and titin repeating domains appear to involve disruption of secondary structure elements and not the tertiary structure proposed in the original AFM experiments (19,20). It is intriguing that Nature would choose a structure composed of repeating domains for two different elasticity proteins, and perhaps even more interesting that rupture of these domains would follow a similar mechanism involving hydrogen-bond rupture, even though the structure of the domains are completely different. However, it is still not clear what, if any, role these rupture processes play under physiological conditions.

An important difference between the rupture mechanisms of spectrin and titin is the location of the rupture. Although the rupture event in titin occurs between β-sheets of the folded domain, spectrin ruptures at the linker connecting repeat units. Of course, the whole idea of what constitutes the spectrin repeat unit and what constitutes the linker is somewhat arbitrary. Spectrin was originally identified as being composed of repeating units when an examination of the primary structure of spectrin revealed a ∼106-amino-acid repeating sequence (1,44). Winograd et al. (2) were able to show that a particular selection, or phasing, of the repeating sequence resulted in a stable, folded single-repeat structure. This sequence was later shown to fold into a triple-helix structure (3,4), which is now referred to as the spectrin-repeat unit. Using this definition of a repeat unit, experimental unfolding results suggest that the repeat units do not unfold independently. Instead, temperature- and urea-induced unfolding experiments indicate that in a double-repeat spectrin, both repeat units unfold in concert (8). Furthermore, Kusunoki et al. (7) were able to show that, while both single- and double-repeat spectrins undergo a single unfolding transition, triple-repeat spectrins undergo two transitions. This would again indicate some cooperativity in the unfolding of repeat units. Excluding the single-repeat case, these experiments indicate an interesting trend, where for N repeat units, N−1 unfolding transitions are observed. Although forced-unfolding and temperature- or urea-induced unfolding of proteins do not necessarily follow the same unfolding pathways, this trend could be a consequence of linker rupture being the initial unfolding barrier to both types of unfolding. In a multiple-repeat structure with N repeat units, there are N−1 linkers, which would each give rise to a separate unfolding event. From a functional standpoint (i.e., when considering unfolding), it might be more useful to consider a “shifted” repeat unit, where the center of the repeat unit is the linker region instead of the triple-helix. With this definition of a shifted repeat unit, the temperature-induced unfolding experiments (7,8) would suggest that the shifted repeat units do, in fact, unfold independently, where each of the N−1 shifted repeat units undergo an unfolding event. Single-repeat structures thus correspond to a special case, which fold into significantly less stable structures than multiple-repeat spectrins (8).

One important issue concerning unfolding is the mechanism by which the unzipping of the linker stops. These simulations suggest that it is relatively easy to break α-helical hydrogen bonds once the initial rupture event takes place. If this trend continued, then the entire structure of a multiple-repeat spectrin would easily unfold after just one linker ruptured. Obviously, this is not supported by the experimental evidence. Instead, there must be some structural feature of spectrin that prevents the entire structure from being unzipped after one linker has ruptured. One hypothesis to explain this behavior begins by considering an unfolding experiment of a triple-repeat spectrin molecule, where the helices are labeled A_i, B_i, and C_i, and where i is the position of the repeat unit. Now suppose that the C₁A₂ linker (i.e., the linker connecting repeat units 1 and 2) ruptured upon forced extension. As the system is elongated, the hydrogen bonds in the C₁A₂ linker region will continue to rupture until the entire C₁A₂ helix has unzipped. At this point, the force would no longer be applied in the same direction on the B₁ and B₂ helices, since the B-helices are all aligned antiparallel to the A- and C-helices. Stabilizing interactions between the B₁ and A₁ helices and the B₂ and C₂ helices could plausibly be enough to prevent further unzipping. However, once an adjacent linker unfolds, such as linker C₂A₃, the B₂ helix would be isolated and no longer stabilized enough to resist unfolding. Consequently, this whole process would give rise to multiple different peak-to-peak extension lengths in the AFM force-extension curve, depending on whether adjacent linkers have ruptured. Bimodal and very broad AFM peak-to-peak distributions have been observed, but have been attributed to either a stable intermediate (23) or to tandem unfolding (10,11). These bimodal or broad distributions may at least partially be a consequence of linker rupture and the mechanism by which helix unzipping stops. Of course, the scenario described above is only one hypothesis; there could be different mechanisms to halt unzipping of the whole structure. These issues cannot be directly addressed with the present boundary conditions, because there is only one repeat unit and one linker, and must be examined with large-extension simulations of multiple-repeat spectrin structures.

Although these simulations offer some insight into the structural changes that occur when spectrin is subject to pulling by AFM, a direct quantitative comparison of the rupture forces between the NEMD simulations and the AFM experiments is not appropriate for several reasons. First of all, as discussed in the companion article (18), the boundary conditions prohibit interrepeat bending. The periodically replicated system corresponds to a perfectly linear hyperstretched multiple-repeat spectrin molecule. This means that the force response obtained using NEMD arises solely from stretching the repeat unit and thus provides information about the linear force required to rupture an individual domain. On the other hand, AFM experiments measure how much force is required on the end of the molecule to rupture a domain. Part of the force response would be due to the force required to straighten some of the bending between repeat units as it is extended. As discussed above, bending of the linker can affect the hydrogen-bond network. In fact, bending of the linker region as spectrin is straightened out in an AFM experiment may facilitate unfolding by destabilizing the linker hydrogen bonds.

Another reason why a quantitative comparison between simulations and AFM experiments is not appropriate is the fact that the NEMD simulations are restricted to pulling speeds approximately six orders-of-magnitude faster than experiment. Rupture forces are known to be dependent on pulling speed (19,20,24,45,46); but due to large irreversible contributions to the force, simple extrapolation of the rupture force to experimental timescales is not generally valid (25). In the case of spectrin unfolding, this inability to extrapolate rupture forces to experimental timescales is clearly exhibited by the divergence of the extrapolated force responses at different NEMD amplitudes after rupture (Fig. 3).

But perhaps the most significant difference between these simulations and experiment is that in an experiment, the length of the repeats units can fluctuate (46,47). Instantaneous fluctuations of the force on, or the length of, a repeat unit can rupture a domain, without that force ever propagating to the AFM tip. With cyclic expansion NEMD, the force is measured with respect to a predetermined length that is not allowed to fluctuate. The importance of this distinction can be illustrated by imagining an idealized AFM experiment of a perfectly straight spectrin molecule containing several repeat units. In this idealized AFM experiment, let the equilibrium length of a repeat unit be l₀. When the AFM cantilever moves away from the surface, the average length of each repeat unit increases by some amount, 〈l〉 = l₀ + Δ_AFMl, where Δ_AFMl is the average displacement per repeat unit imposed by the AFM. The average displacement of each repeat unit from equilibrium gives rise to a force on the cantilever. Although the average end-to-end length of spectrin is well controlled in an AFM experiment, the lengths of the individual repeat units are still subject to thermal fluctuations; so at any given time, the length of a repeat unit may not be equal to the average length imposed by the AFM. Suppose that a small thermal fluctuation increases the length of one repeat unit. If the fluctuation was small enough that rupture has not occurred, then the large linear restoring force that arises due to the increase in length will drive the repeat unit back toward the average length 〈l〉. On timescales six orders-of-magnitude larger than those in the NEMD simulations, a fluctuation large enough to bring a repeat unit over the force barrier can become probable. If a large fluctuation results in rupture, then on atomistic timescales, as shown in Figs. 4 and 5, the ruptured repeat unit will relax to a length larger than the equilibrium length l₀. Since the ruptured repeat unit can have a larger length for a given force, the other repeat units in the chain will be able to relax toward their equilibrium length. The average length of the remaining folded repeat units thus becomes 〈l〉 < l₀ + Δ _AFMl, and results in a drop in the measured force. The ruptured repeat unit is easily extensible, so the force will only slowly rise as the cantilever is moved until it becomes large enough for a fluctuation to again rupture another repeat.

Experimentally, it has been shown that once a repeat unit has been completely unfolded via AFM, it takes on the order of seconds to refold (19,23). But even when the repeat unit has only been partially unfolded (i.e., after rupture of just few turns of the linker α-helix), it is not likely that it would be able to refold, even on experimental timescales. Refolding during the course of an AFM experiment would require a decrease in the length of the ruptured repeat unit and a corresponding increase in the length of adjacent repeat units. So in order to refold, the ruptured repeat unit would not only have to overcome its own intrinsic folding barrier, but would also have to overcome the additional barrier imposed by extending the adjacent repeat units.

As a final note, the rupture process observed in these simulations has an interesting interpretation in terms of a simple protein folding model. Protein folding can be described as diffusion in a multidimensional configuration space (48). The folded state corresponds to a small region of this configuration space that has a lower potential energy. Protein folding thus involves a search in configurational space for the folded state. This type of a model captures the fact that folding involves a decrease in both the energy and entropy of the system. The decrease in entropy is due to the fact that the folded state has access to fewer configurations than the unfolded state. In terms of this model, the linear region of the force-extension curve corresponds to small perturbations of the folded state. When the spectrin repeat unit is extended beyond the point where the linker hydrogen bonds break, it is forced to leave the folded region and has access to a much larger configuration space. This larger configuration space comes in the form of the linker being able to access a greater number of φ- and ψ-backbone angles. When the hydrogen bonds are broken, the system will diffuse in the expanded configuration space and can get so far away from a folded-like structure that it essentially gets lost in configuration space, where random sampling of a folded structure is highly unlikely. This inhibits refolding on MD timescales even when the length of spectrin is brought back to its folded length. Refolding will only occur if the system is allowed enough time to search though the available space for the folded state. This model also suggests that if the system is not allowed to diffuse in the unfolded space for very long, it may not get lost, and can return to the folded state when the length is decreased. These features of this simple model were observed in these simulations, where more linker hydrogen bonds were able to reform on contraction when the imposed NEMD frequency was high (e.g., Fig. 9).

CONCLUSIONS

These are the first simulations that directly attribute a specific molecular-level rupture event to the peaks in the AFM force-extension curve of spectrin. These NEMD simulations were able to show that rupture of the linker region connecting spectrin repeat units seems to be the most likely event responsible for the AFM force peaks. A precise account of the initial rupture process was also presented, which involves simultaneously breaking approximately four parallel hydrogen bonds that maintain the α-helix. After rupture, the adjacent hydrogen bonds break one-by-one and unzip the helix.

If linker rupture is the primary unfolding event, many experimental results may need to be reinterpreted. First of all, rupture of the linker suggests that defining a shifted repeat unit would aid in the interpretation of urea- and temperature-induced unfolding experiments. Using this definition basically transforms complicated cooperative unfolding transitions of the standard repeat unit into independent unfolding of shifted repeat units. Furthermore, the bimodal and very broad distribution of unfolding lengths measured using AFM, which have been attributed to the existence of a stable intermediate of a single repeat unit or complete tandem unfolding of repeat units, may instead be at least partially a consequence of whether adjacent repeat units have already unfolded.

Finally, it should be emphasized that many of these results were obtained only through careful consideration of the boundary conditions used to simulate a spectrin repeat unit. Specifically, the periodic boundary conditions employed allowed simulation of a spectrin repeat unit without any noncontiguous α-helical linkers. However, it may be necessary in the future to run simulations of multiple-repeat spectrin structures where periodic boundary conditions could become problematic, and in which case any artifacts that might arise due to noncontiguous linkers must be addressed. One solution might be to cap the terminal helices by introducing artificial bonds to prohibit unfolding of the end linkers, thereby only allowing interior linkers the ability to unfold.