Mechanics of Enveloped Virus Entry into Host Cells

Abstract

Enveloped viruses such as HIV-1 enter their hosts by first establishing a contact region at the cell surface, which is stabilized by the formation of receptor-ligand complexes. We show that the favorable contact energy stemming from the formation of the receptor complexes in the interaction zone is sufficient to drive the engulfment of the virus by the cell. Using a continuum model, we show that the equilibrium engulfment depth and the force driving the engulfment are functions of the virus size and the complex formation energy. Resistance to engulfment is dominated by the elastic deformation of the cytoskeleton.

Enveloped viruses interact with their host cell through specific binding interactions between glycoproteins on their envelope and receptors on the cell surface. In particular, human immunodeficiency virus type 1 (HIV-1) infects T lymphocytes and macrophages by initiating binding interactions between the surface subunit of the HIV-1 envelope glycoprotein, gp120, and the primary host-cell receptor CD4 (Fig. 1). CD4 binding promotes a conformational change in gp120, which mediates gp120 binding to the coreceptor CCR5 for HIV-1 R5-tropic viruses (1). Binding of gp120 to CCR5 triggers further conformational changes in gp120, which exposes a fusion peptide that inserts into the cell membrane, mediating fusion between viral and cell membranes (2). Structure-based models of binding interactions of viruses such as HIV-1 with their receptors are emerging (1,2). However, the biophysical factors (e.g., virus size and cell stiffness) that may control the overall energetics of virus-cell attachments in general, and HIV-1-cell interactions in particular, are not well understood. Moreover, whether a virus is coated partially or completely by the plasma membrane before infection is unknown and the role of the cytoskeleton in viral entry is unclear.

FIGURE 1.

Virus-cell interaction zone. For HIV-1, gp120/CCR5 binding complexes mediate the formation of the contact zone. To maximize the contact energy, the cell deforms to accommodate the virus. The energies of the engulfment process as a function of the engulfment depth, h, can be estimated.

By considering the elastic deformations of the cell membrane and cytoskeleton, and the interaction between the virus and the host cell, we show that the binding energy of the receptor-ligand complex can drive the engulfment of the viral particle. Depending on the density of the complexes in the interaction zone, it may be energetically favorable for the viral particle to be completely coated by the cell membrane. Fig. 1 shows the geometry of the virus-cell interaction zone. The depth of the virus engulfment is labeled as h. Although most of our numerical estimates describe the interaction between HIV-1 and a cell, our model can explain the interaction of any spherical enveloped virus with its host cell mediated by receptor-ligand binding. Three energies determine the final engulfment depth: 1), 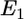: the favorable energy of gp120-receptor complex formation, which is proportional to the number of receptor complexes in the interaction zone. 2), 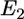: the unfavorable distortion energy of the plasma membrane. 3), : the unfavorable energy due to the deformation of the virus and cell body. The equilibrium engulfment depth, 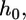is obtained by minimizing the total energy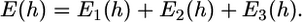

HIV-1 is a relatively small particle (∼50 nm in radius) encased in a glycoprotein coated membrane. In this article, we do not fix the virus radius because different viruses, as well as different strains of the same virus, can vary in size. The Young's modulus of the virus is expected to be much larger than the cell because of the capsid underneath the viral-lipid membrane. In contrast, the cell is tens of microns in size, enclosed by a soft and flexible plasma membrane. Thus, when the virus and cell interact, most of the deformations occur in the cell. The relative deformation is given by the ratio of the Young's moduli. Given this configuration, all the relevant energies can be estimated analytically. The favorable contact energy between the virus and the cell, 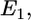is proportional to their contact area, A. Thus, 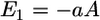and 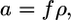where f is the free energy gained per gp120-receptor complex and ρ is the complex density in the contact zone. The complex formation kinetics has been measured (3), thus 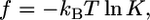where K is the equilibrium constant of receptor formation upon glycoprotein binding. 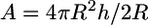is the area of contact between the cell and virus. There are 219 gp120 proteins on the surface of HIV. Thus, the receptor-ligand complex density is ∼ Each complex gains 10–20 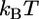of free energy upon formation, giving

The mechanics of the elastic cell membrane is well described by the Canham-Helfrich theory. When the engulfment occurs, the cell membrane bends and stretches. Thus, the energy of the membrane after engulfment is

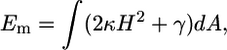where H is the mean-curvature of the membrane, κ and γ are the bending modulus and surface tension of the membrane, respectively. For typical cells, (4), and 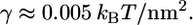The Gaussian curvature does not contribute to the elastic energy since the topological class of the cell remains unchanged. For the configuration in this study, the mean curvature is H=1/2R. The change in the membrane energy is the difference in the membrane energy before and after the engulfment. We obtain

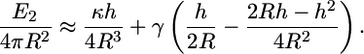The final contribution to the energy of engulfment is the elastic energy of the cytoskeleton. The cell can be modeled as an elastic solid whose Young's modulus is on the order of 10 kPa or less (5); the Poisson ratio of the cell is taken to be 1/2. From the classic theory of elasticity, it can be shown that the contact region between two uniform and isotropic elastic solids is bounded by a circle (6). The deformation of the virus and the cell is described by a sphere. The corresponding deformation energy can be solved exactly (6). In the limit where the cell is much larger than the virus, the energy is

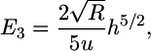where

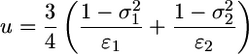and 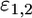are the Young's moduli of the cell and the virus, and 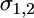are their respective Poisson ratios. We note that the purely elastic energy presented here does not account for the viscoelasticity of the cytoskeleton and the heterogeneity of the cell (7).

Combining all the energies, we obtain

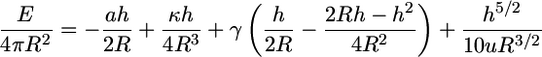for which the equilibrium engulfment depth, 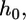is the root of the equation 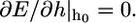Fig. 2 shows our central result. We find that 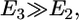indicating that cytoskeleton deformation is the dominant effect that determines the engulfment depth. The force driving the engulfment, 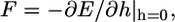varies between 20 pN and 50 pN depending on a (Fig. 2, inset). An estimate of the cytoskeleton deformation timescale is 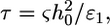where 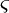is the drag coefficient of cytoskeleton fibers in fluid. For typical cells, 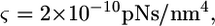and τ is 50 μs if However, the kinetics of gp120-receptor formation is considerably slower (3). Therefore, the engulfment time is likely to be controlled by the slow formation of the complexes.

FIGURE 2.

(A) Total energy, E, of the cell-virus interaction as a function of the virus engulfment depth. The equilibrium depth is given by the minimum of the curves where receptor formation energy, a, is a parameter. The inset shows the equilibrium engulfment depth, 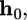as a function of a. The virus is completely engulfed if 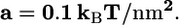(B) Contours of the equilibrium virus engulfment depth, 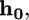as a function of the virus radius, R, and the receptor energy, a. (Inset) The engulfment force for 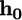; R, 50 nm.

The estimates in this article represent an equilibrium analysis of virus-cell interaction. We have assumed that the cell is static, i.e., no cytoskeletal growth occurs. The cell is, however, dynamic. It is likely that the initial contact between the virus and cell can trigger cytoskeleton rearrangement. Moreover, inhibition of actin cytoskeleton regulators limits infection (8). The timescale of this rearrangement is on the order of minutes. Nevertheless, our analysis unambiguously shows that the driving force toward engulfment is already present in the receptor formation alone, indicating that the remaining processes of membrane fusion and virus entry are much easier if the viral particle is already largely engulfed. The timescale of engulfment and the actual forces during the process deserve careful experimental scrutiny. The extension of recent single molecule micromanipulation experiments (3) may reveal the energetics, engulfment forces, and dynamics of virus entry.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.