Theoretical Evaluation of Voltage Inducement on Internal Membranes of Biological Cells Exposed to Electric Fields

Abstract

Several reports have recently been published on effects of very short and intense electric pulses on cellular organelles; in a number of cases, the cell plasma membrane appeared to be affected less than certain organelle membranes, whereas with longer and less intense pulses the opposite is the case. The effects are the consequence of the voltages induced on the membranes, and in this article we investigate the conditions under which the induced voltage on an organelle membrane could exceed its counterpart on the cell membrane. This would provide a possible explanation of the observed effects of very short pulses. Frequency-domain analysis yields an insight into the dependence of the voltage inducement on the electric and geometric parameters characterizing the cell and its vicinity. We show that at sufficiently high field frequencies, for a range of parameter values the voltage induced on the organelle membrane can indeed exceed the voltage induced on the cell membrane. Particularly, this can occur if the organelle interior is electrically more conductive than the cytosol, or if the organelle membrane has a lower dielectric permittivity than the cell membrane, and we discuss the plausibility of these conditions. Time-domain analysis is then used to determine the courses of the voltage induced on the membranes by pulses with risetimes and durations in the nanosecond range. The particularly high resting voltage in mitochondria, to which the induced voltage superimposes, could contribute to the explanation why these organelles are the primary target of many observed effects.

INTRODUCTION

Exposure of a biological cell to electric field can lead to a variety of biochemical and physiological responses. If the field is sufficiently strong, the exposure can cause a significant increase in the electric conductivity and permeability of the cell plasma membrane (1). Provided that the exposure is neither too strong nor too long, this phenomenon (referred to as electroporation or electropermeabilization) is reversible. Using electroporation, many molecules to which the cell plasma membrane is otherwise impermeable can be introduced into the cells or inserted into their plasma membrane. Due to its efficiency, this method is rapidly becoming an established approach for treatment of solid cutaneous and subcutaneous tumors (2,3), and it also holds great promise for gene therapy (4).

As a cell is exposed to an external field, this leads to an inducement of a voltage on the cell plasma membrane. This voltage is proportional to the field strength and superimposes onto the resting voltage present on the membrane under physiological conditions, typically ∼−70 mV (5). According to the theory of electroporation, a voltage on the membrane reduces the energy necessary for rearrangements of the membrane lipids that result in formation of aqueous passages (hydrophilic pores) and consequently in increased conductivity and permeability of the membrane. Consequently, as the voltage increases, so does the probability of formation of such passages. The resting voltages that are normally present on the cell membrane and on the organelle membranes—the largest is in mitochondria, ∼−140 mV (6)—are clearly insufficient for this, as electroporation is not observed under physiological conditions. With exposures to electric fields leading to total voltages of several hundreds of millivolts, however, electroporation of the cell membrane becomes readily achievable and observed in experiments. Both the theory of electroporation (7,8) and recent computational studies based on molecular dynamics (9–11) corroborate that as the membrane voltage increases, so does the rate of formation of metastable aqueous passages in the membrane.

The fields used for electroporation are most often delivered in the form of unipolar rectangular pulses, with typical amplitudes of several hundred volts per centimeter, durations ranging from tens of microseconds up to milliseconds, and risetimes in microseconds. In the first few microseconds after the onset of the pulse, these exposures induce a voltage in the range of several hundred millivolts on the cell membrane, and this voltage persists until the end of the pulse. Also within microseconds, this leads to the onset of electroporation, detected as a steep increase in electrical conductivity and permeability of the membrane (12,13). Although they are used less commonly, bipolar rectangular pulses (14–16) and sinusoidal or sine-modulated rectangular pulses (17,18) are also efficient in achieving electroporation.

The exposure of a cell to an electric field also induces voltages on the organelle membranes in the cell interior, but these voltages are several orders of magnitude smaller than the voltage induced on the cell membrane. As such they are far too low for electroporation, and although the cell membrane is rendered permeable, the organelle membranes are left unaffected.

However, in a number of recent articles it has been reported that with much stronger (typically tens or hundreds of thousands of volts per centimeter) but much shorter (typically tens or hundreds of nanoseconds) pulses, the situation seems to be reversed, with the cell membrane affected less than some internal cell structures (19–24). In many cases, a mitochondria-dependent apoptosis was observed, which could be due to electroporation of these organelles (25–27). For brevity, the high-intensity, nanosecond-duration pulsed electric fields used in these experiments are often referred to by the acronym nsPEF, and we will also adopt this practice in this article.

In this article we explore one possible theoretical explanation of the observed effects of nsPEF on intracellular membranes. Namely, as discussed above, the steady-state value of the voltage induced on the cell membrane is always much larger than its counterpart on an organelle membrane. But as the duration of an electric pulse is decreased into the submicrosecond range, this becomes less and less relevant, because such an exposure is too short for the two voltages to come close to their steady-state values, and the time courses of their inducement become important. These time courses depend on a number of geometric and electric parameters, and the aim of this article is to investigate whether there is a range of plausible values of these parameters for which the voltage on the organelle membrane can temporarily exceed the voltage on the cell membrane. This explanation has been proposed before based on considerations of a more qualitative nature (19) and later on numerical studies performed on a finite-elements model with a spherical mesh geometry (28). In this article, we derive the analytical expressions for the induced voltages, which allows for a theoretical analysis of the role of each model parameter. In “Derivation of the induced voltages” we derive the expressions for the induced voltages for the case where each region is characterized by an electric conductivity and a dielectric permittivity, whereas in “Results and Discussion” we analyze the dependence of the induced voltages on each of the parameters and discuss the results.

DERIVATION OF THE INDUCED VOLTAGES

The model of a cell with an organelle

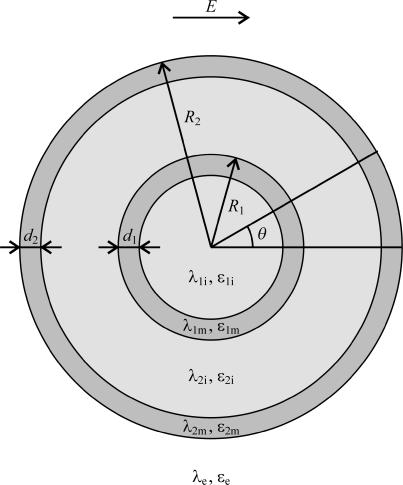
For a valid treatment of the membrane voltage induced by alternating fields with frequencies in the megahertz and gigahertz range, or by pulsed fields with risetimes in the submicrosecond range, electric conductivities as well as dielectric permittivities of the membranes and the surrounding aqueous media have to be taken into account. An analytical treatment of such a system is possible only if the cell is the only object distorting the otherwise uniform electric field, and moreover only in geometries where the cell and its membrane can be expressed as coordinate surfaces. Throughout this article, the treatment will therefore be restricted to a single cell with a spherical geometry, for which these requirements are met. The simplest case is that of a spherical cell with a uniform interior (i.e., containing no organelles), which is widely used in theoretical studies of cells exposed to electric fields, e.g., in derivation of the Schwan equation (29,30) and its extensions (31–34). The simplest model of a cell with an organelle is then obtained by incorporating into the cell another spherical body surrounded by a concentric shell (Fig. 1). Although incorporation of a single organelle is clearly an oversimplification in modeling the interior of a realistic biological cell, such a model is still suitable for analyzing the voltages induced on the cell membrane and on organelle membranes (35,28). Namely, concerning exposures to external fields, the crucial aspect here is a topological one: an organelle membrane is completely surrounded by the cell membrane and thereby—to an extent—electrically shielded by it. The extent of shielding in an alternating field depends on its frequency, and in a pulsed field on the risetime and duration of the pulses. These dependences will be the main subject of the study presented in this article.

FIGURE 1.

The model of a spherical cell with a concentric spherical organelle. The model consists of five regions, each characterized by an electric conductivity (σ, in S/m) and a dielectric permittivity (ɛ, in As/Vm). From the center outwards, the regions are the organelle interior (subscript index “1i”), the organelle membrane (“1m”), the cytosol (“2i”), the cell plasma membrane (“2m”), and the cell exterior (“e”). The organelle radius and the cell radius are denoted by R₁ and R₂, respectively, and their membrane thicknesses by d₁ and d₂, respectively.

With an exposure of the cell shown in Fig. 1 to a uniform electric field, the spatial distribution of the electric potential is obtained by solving the Laplace equation in spherical coordinates (36). In each of the five regions of the model, it has the general form

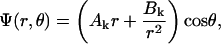(1)

with r the radius measured from the center, θ the angle with respect to the direction of the field, and with constants A_k and B_k specific for each region. Finiteness of the electric potential at r = 0 implies B_i1 = 0, and from uniformity of the field at r → ∞ it follows that A_e = −E. The remaining eight constants (A_1i, A_1m, B_1m, A_2i, B_2i, A_2m, B_2m, and B_e) are determined by the conditions of continuity of the electric potential, Ψ, and the normal component of the electric current density, 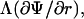at each of the four boundaries between the regions. In frequency-domain (FD) analysis, Λ is the complex conductivity (admittivity) of a region, σ + jωɛ, where ω is the angular frequency of the field, and in time-domain (TD) analysis, it is the admittivity operator, 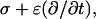where 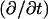is the differential operator transforming a function into its time derivative. Thus, the pair of continuity requirements pertaining to the boundary between the organelle membrane and the cytosol can be written as

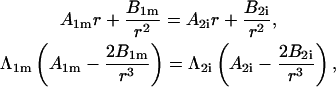(2)

where in the and in the 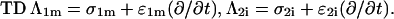Analogous pairs of conditions characterize the other three boundaries. The direct dealing with differential operators in the TD can be avoided by transferring the treatment into the complex-frequency space, as described in more detail in “Analysis in the time domain”.

The solutions for the eight constants are relatively lengthy expressions, because in general each of them incorporates the geometric and electric parameters of all five regions of the model, but algebraically their exact determination is elementary, because they form a well-defined system of eight equations with eight unknowns. The solutions for the somewhat simpler system of three regions, i.e., for a spherical cell devoid of an organelle, are given in Kotnik et al. (32). For the spherical cell with an organelle, the derivation of all the constants is available as Supplementary Material to this article found at the home page of the journal, but for brevity it will be omitted here.

Once all the constants are determined, the voltage induced on a membrane is determined as the difference between the potentials Ψ(r, θ) at the inner and outer surface of this membrane. This yields Eq. 3 for the voltage induced on the cell plasma membrane, and Eq. 4 for the voltage induced on the organelle membrane where M is in both cases given by Eq. 5.

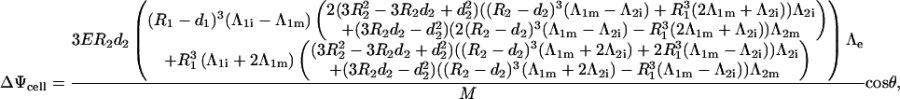(3)

and for the voltage induced on the organelle membrane (Eq. 4).

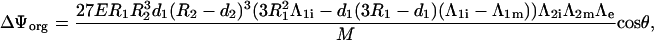(4)

where M is given by (Eq. 5).

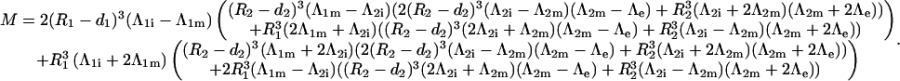(5)

The substitution Λ = σ + jωɛ for each of the five regions provides the starting point for analysis of ΔΨ_cell and ΔΨ_org in the FD, and the substitution 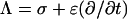does the same for the TD.

Analysis in the frequency domain

The frequency domain is the natural setting for an exposure of a cell to sinusoidal electric fields. Fixing the geometric and electric parameters of the model, inserting for E the amplitude of the field, and writing explicitly Λ = σ + jωɛ, the induced voltages ΔΨ_cell and ΔΨ_org become functions of a single variable, namely ω, the angular frequency of the field. For a fixed ω, the values of ΔΨ_cell and ΔΨ_org are complex numbers, with |ΔΨ_cell|, |ΔΨ_org| corresponding to the amplitudes of the induced voltages, and arg(ΔΨ_cell), arg(ΔΨ_org) to their phase shifts with respect to the external field. It should be emphasized that these values characterize the sinusoidal steady states that are established after the transients occurring at the onset of the field are over.

By considering ΔΨ_cell and ΔΨ_org as functions of ω, it is then determined very straightforwardly whether there is a range of parameter values and field frequencies where ΔΨ_org can—at least temporarily—exceed ΔΨ_cell. The results of such analysis are presented in “Voltages induced by a sinusoidal field”.

The approach described above can be extended to other periodic time courses of the field representable as uniformly convergent Fourier series. The induced voltages are then given by the series of voltage components induced by individual field components in the Fourier series.

Analysis in the time domain

The time domain is the natural setting for exposures of a cell to aperiodic fields, as well as to periodic fields for which the Fourier series is nonuniformly convergent. This class clearly contains a rectangular and a trapezoidal (i.e., having nonzero risetime and falltime) pulse, but it also contains periodic trains of such pulses, as the uniform convergence requirement fails at the pulse edges, which is usually referred to as the Gibbs phenomenon (37). As mentioned in “The model of a cell with an organelle”, the most convenient approach here is an interim transfer of the treatment to the complex-frequency space. Denoting the complex frequency by s, the differentiation with respect to time is thereby transformed into multiplication by s, and time courses are replaced by their Laplace transforms. Fixing again the geometric and electric parameters of the model, inserting for E the Laplace transform of the time course of the electric field, L[E(t)] = E(s), and writing explicitly Λ = σ + ɛs, the expressions for ΔΨ_cell and ΔΨ_org become functions of s. The time courses of the induced voltages are then obtained as inverse Laplace transforms, ΔΨ_cell(t) = L⁻¹[ΔΨ_cell(s)] and ΔΨ_org(t) = L⁻¹[ΔΨ_org(s)]. This yields the complete time courses, including the transients.

Provided that E(s) is a polynomial in s, ΔΨ_cell and ΔΨ_org are rational functions (i.e., fractions of polynomials) of s, and the inverse Laplace transforms are obtained easily. The method is also applicable to all other cases for which the Laplace transform of E(t) and the inverse Laplace transforms of ΔΨ_cell and ΔΨ_org can be obtained explicitly. For many of the conceivable time courses of the electric field, the transforms can be found in standard tables (38), whereas for other sufficiently regular functions they can be derived by means of the Laplace transform integral (39) and the Bromwich integral (39), respectively. For more intricate cases, discretization of time and application of the unilateral Z-transform instead of the Laplace transform would still allow one to obtain approximate solutions.

Limitations of the described approaches

In this article, the cell is modeled as a shelled sphere containing another shelled sphere—a single organelle. This allows for analytical derivation but is generally an evident oversimplification, both in assuming spherical shapes and in reducing the actual multitude of organelles to a single one (to an extent, the analytical approach can also be extended to spheroidal and ellipsoidal cell shapes (44,45)). However, as already mentioned in “The model of a cell with an organelle”, these assumptions are acceptable for the purpose of studying the membrane shielding due to its primarily topological nature. As a consequence, the qualitative conclusions obtained with this geometry are also valid more generally, but the precise quantitative picture for a particular cell and organelle geometry would have to be determined (in general numerically) in that geometry.

In “Analysis in the frequency domain” and “Analysis in the time domain” we have implicitly assumed that the conductivities and the permittivities featuring in Λ are constants. Strictly speaking, this is only accurate if the variation of the field is slow enough for negligible effects of dielectric relaxation. For exposures to sinusoidal fields, this is the case up to tens or hundreds of megahertz for lipids (40), and up to tens of gigahertz for aqueous solutions (41). Above these frequencies, the conductivities and the permittivities become functions of the field frequency (42), and for precise results this has to be accounted for. In Kotnik and Miklavčič (34), this approach is pursued in the FD using a simple Debye relaxation model for a cell without an organelle, which could be applied in the same way to the case with an organelle. However, in this article a clear picture of the role of each parameter is more important than a high precision of the results, and to avoid obscuring this picture, we choose not to introduce dielectric relaxation into the model.

The FD and the TD approach presented in “Analysis in the frequency domain” and “Analysis in the time domain” are both based on the Laplace equation, which does not account for the fact that the electric field propagates in waves and with finite velocity. On timescales where this becomes important, a correct treatment would have to proceed from the more general Helmholtz equation (43). However, the frequencies for which the field wavelength becomes comparable to the size of a cell are in the range of terahertz, which is far above the frequencies of the sinusoidal fields we will investigate here. Similarly, the time required for the electric field to traverse the cell is in the range of femtoseconds, which is far below the risetimes, durations, and falltimes of the pulsed fields (nsPEF) that will be considered here.

Finally, in the treatment presented in this article it is assumed that unless they exceed the threshold value sufficient for electroporation, the induced voltages do not affect the electric properties of the membranes. Some membrane components, most notably the voltage-gated channels, can respond actively to induced voltages considerably lower than the electroporation threshold, thereby altering the electric properties of the membrane. The open channels could result in increased membrane conductivity, hindering further increase of membrane voltage and possibly preventing electroporation. This clearly cannot be the case with the cell plasma membrane, as its electroporation is readily achievable with a wide range of pulse parameters. The possible role of voltage-sensitive constituents of the organelle membranes in the observed effects is discussed briefly in “Curvature of organelle membranes”.

RESULTS AND DISCUSSION

The aim of this article is to evaluate the voltages induced by nsPEF, which will be approximated as having a trapezoidal shape. As described in the preceding sections, the natural setting for this is the TD, in which this aim will be pursued in “Voltages induced by a trapezoidal pulse”. However, there are four geometric and 10 electric parameters that have to be investigated with respect to their influence on ΔΨ_cell and ΔΨ_org, and a trapezoidal pulse is characterized by a risetime, an amplitude, a duration pertaining to this amplitude, and a falltime. For a first insight into the role of the parameters, and for a selection of those to be investigated further, a clearer picture is provided by treating an exposure of a cell to a sinusoidal field, which is characterized only by its amplitude and frequency. Along these lines, “Voltages induced by a sinusoidal field” investigates the influence of each of the parameters in the FD, and a much smaller subset of parameters chosen on the basis of this investigation is then used in “Voltages induced by a trapezoidal pulse” in the TD with trapezoidal pulses.

Voltages induced by a sinusoidal field

The purpose of this section is to determine whether in an exposure of a cell to a sinusoidal field, there is a range of parameter values for which |ΔΨ_org| can exceed |ΔΨ_cell|, or equivalently, for which the ratio |ΔΨ_org| / |ΔΨ_cell| can exceed the value of 1. The expressions for ΔΨ_cell and ΔΨ_org in “The model of a cell with an organelle” show that this ratio depends on practically all the geometric and electric parameters of the model. The only exceptions are σ_e and ɛ_e, because the numerators of ΔΨ_cell and ΔΨ_org are proportional to Λ_e = σ_e + jωɛ_e, whereas their denominators are identical, so that in the ratio |ΔΨ_org| / |ΔΨ_cell| all occurrences of Λ_e cancel out. The simplest method for investigation of the role of the remaining 12 parameters is by means of parametric studies, in which one parameter is varied through a given range while the others are kept at their default values. Restriction to one variable at a time does not completely elucidate the behavior of a function of 12 variables, but the results of such parametric studies are easy to interpret, and will also suffice for the aims of this article.

Table 1 gives the default values and variation ranges of the parameters. The choice of default values is based on the typical data found in the literature, and the limits of the variation ranges were chosen in an attempt to confine each parameter to physically realistic, or at least plausible values. For the reasons discussed in the above paragraph, σ_e and ɛ_e do not enter the parametric studies, and thus the table gives only their default values, which are needed when the two voltages themselves are of interest, and not only their ratio.

TABLE 1.

Default values and variation ranges for parametric studies

Parameter	Default value	Variation range
σ1i [S/m]	0.3*	0.1–1.0
ɛ1i [As/Vm]	6.4 × 10−10†	(3.5–7.0) × 10−10
σ1m [S/m]	3 × 10−7‡	10−8–10−5
ɛ1m [As/Vm]	4.4 × 10−11§	(1.8–8.8) × 10−11
σ2i [S/m]	0.3¶	0.1–1.0
ɛ2i [As/Vm]	6.4 × 10−10†	(3.5–7.0) × 10−10
σ2m [S/m]	3 × 10−7‖**	10−8–10−6
ɛ2m [As/Vm]	4.4 × 10−11**	(1.8–8.8) × 10−11
σe [S/m]	1.2††	–
ɛe [As/Vm]	6.4 × 10−10†	–
R1 [μm]	3	1–8
d1 [nm]	5	3–15
R2 [μm]	10	5–100
d2 [nm]	5‡‡	3–7

^*Set equal to σ_2i.

^†Physiological saline at 35°C (46,41).

^‡Set equal to σ_2m.

^§Set equal to ɛ_2m.

^¶(47,48).

^‖From Hu et al. (49), using the conversion given in Arnold et al. (50).

^**(51).

^††Blood serum at 35°C (52).

^‡‡(6).

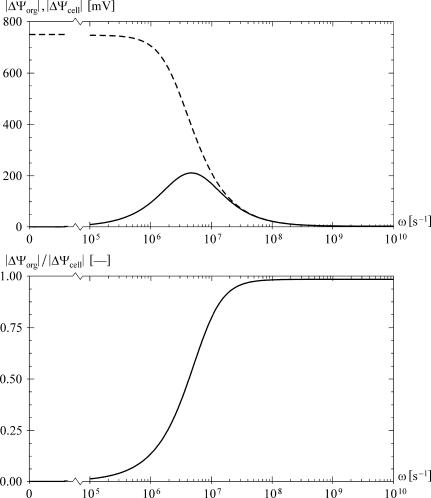
Each of the parametric studies was performed for ω spanning the range from 10⁵ to 10¹⁰ s⁻¹, yielding a set of data that can be visualized clearly in a contour plot of the ratio |ΔΨ_org| / |ΔΨ_cell| as a function of frequency and the studied parameter. As shown in Fig. 2, with the default values assigned to all parameters, this ratio does not exceed the value of 1 for any frequency. A similar result is obtained if the two membranes are assigned realistic dielectric permittivities but zero electric conductivities (35).

FIGURE 2.

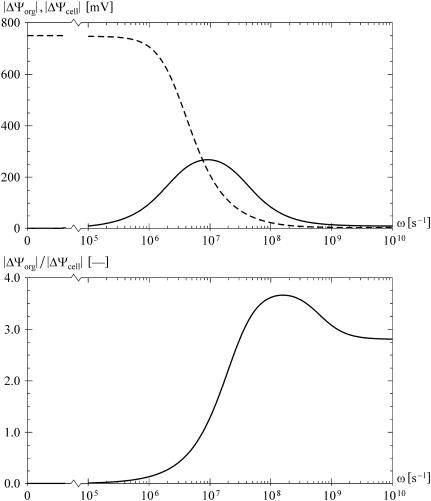
The frequency dependence of the voltages induced in an alternating field (ω = 2πν, where ν is the frequency in Hz), with default values used for all the parameters. The top plot shows the amplitudes of the voltages, |ΔΨ_org| (solid) and |ΔΨ_cell| (dashed), for E = 5 × 10⁴ V/m and θ = 0, and the bottom plot gives the ratio |ΔΨ_org| / |ΔΨ_cell|. As the frequency increases, |ΔΨ_cell| strictly decreases, whereas |ΔΨ_org| has a peak, but never exceeds |ΔΨ_cell|.

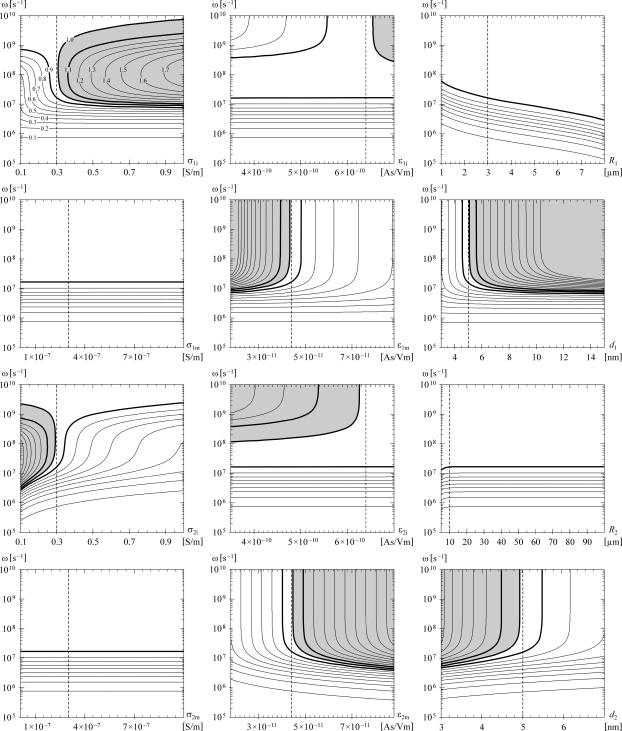
However, in eight of the 12 parametric studies, for sufficiently high frequencies the ratio |ΔΨ_org| / |ΔΨ_cell| does exceed 1 in a certain range of parameter values. The contour plots showing the results of the parametric studies are given in Fig. 3, from which two clear properties emerge. First, in the higher megahertz range, either a small increase of σ_1i above its default value, or a small decrease of σ_2i below its default value suffices for |ΔΨ_org| to exceed |ΔΨ_cell|. And second, in the higher megahertz range and in the gigahertz range the same is the case for a decrease of ɛ_1m and for an increase of ɛ_2m. A more general formulation is that the ratio |ΔΨ_org| / |ΔΨ_cell| can exceed the value of 1 if the organelle interior has a higher electric conductivity than the cytosol, or if the organelle membrane has a lower dielectric permittivity than the cell membrane. The effect of σ_1i > σ_2i is due to the fact that with the increase of field frequency, the shielding of the cell interior by the plasma membrane weakens, and the electric current flowing through the cell becomes concentrated in the organelle interior. The effect of ɛ_1m < ɛ_2m is also easily explained, as the voltage inducement is faster on the membrane with the lower dielectric permittivity.

FIGURE 3.

The ratio |ΔΨ_org| / |ΔΨ_cell| as a function of one of the model parameters and the angular frequency of the field. As shown explicitly in the top left panel, the contours mark the multiples of 0.1, and the region where this ratio exceeds the value of 1 is shaded gray. The thicker contours correspond to the ratio values of 0.9 (white on both sides of the contour), 1.0 (white on one side, gray on the other), and 1.1 (gray on both sides). In each plot, the dashed vertical corresponds to the default value of the studied parameter, so that the values along this vertical are as in Fig. 2 b.

For the condition σ_1i > σ_2i, the organelle interior would have to contain either a higher total concentration of ions with respect to the cytosol, or a larger fraction of ions with higher mobility (e.g., more potassium and less sodium). In a recent computational analysis, the concentration of potassium ions in the intermembrane space of the mitochondria was estimated at between 175 and 207 mM (53), which is indeed significantly higher than in the cytosol, where it is typically ∼140 mM (5). Among the membranes, the ones with the lowest dielectric permittivity are pure lipid bilayers, and hence for the condition ɛ_1m < ɛ_2m, the membrane of the organelle under consideration would generally have to contain a smaller fraction of proteins than the cell plasma membrane. This is, however, markedly not the case for the inner mitochondrial membrane, where proteins represent ∼76% of the mass, which is a higher fraction than in any other membrane (5).

The parametric studies also show that |ΔΨ_org| / |ΔΨ_cell| can exceed 1 if d₁ is significantly larger than its default value of 5 nm. More generally, a sufficient condition is that the organelle membrane should be thicker than the cell membrane, d₁ > d₂. This is realistic for some organelles, such as the nucleus and the mitochondria, as they have a double membrane, and in mitochondria the two membranes are moreover separated by several nanometers of intermembrane space (6). Still, with a thicker membrane, a proportionally larger voltage is required for the same electric field within the membrane. As a consequence, if the electric field in the membrane is the decisive factor in electroporation, with d₁ > d₂ the condition |ΔΨ_org| / |ΔΨ_cell| > 1 is not sufficient for the organelle membrane to be electroporated, but instead roughly |ΔΨ_org| / |ΔΨ_cell| > d₁ / d₂ would be required.

Finally, a region with |ΔΨ_org| > |ΔΨ_cell| is also reached in the parametric studies of ɛ_1i and ɛ_2i. More generally, this is the case for sufficiently high frequencies provided that ɛ_1i > ɛ_2i. However, as the organelle interior and the cytosol are both aqueous solutions, it is reasonable to assume that ɛ_1i and ɛ_2i are very similar. The choice of variation ranges for these two parameters primarily reflects the dependence of dielectric permittivities on the temperature, but because the cell is too small to contain significant temperature differences, change of the temperature by cooling or heating the cell suspension or a tissue will have nearly the same effect on the two permittivities.

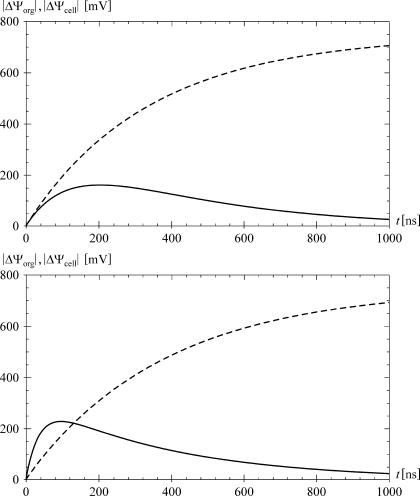
Further analysis reveals that if the cell and organelle membranes are identical in their electric properties and their thickness, and if the cytosol is electrically identical to the organelle interior, then |ΔΨ_org| < |ΔΨ_cell| at any field frequency. It should perhaps be stressed here that for such parameter values, the faster charging of the organelle membrane cannot cause ΔΨ_org to exceed ΔΨ_cell, even if the shielding of the organelle by the cell membrane is disregarded. Namely, without shielding, the rate of voltage inducement on a spherical object is inversely proportional to its radius, but the voltage plateau is directly proportional to the radius, so that on a larger object the induced voltage is necessarily larger at all times. This is clear from the fact that 1 − exp(−t/τ) < K(1 − exp(−t/(Kτ))) for K > 1 and t > 0; the two functions are equal at t = 0, and for their respective derivatives at t > 0 we have exp(−t/τ)/τ < exp(−t/(Kτ))/τ. As a consequence, the voltage induced on the cell membrane is always larger than its counterpart on the organelle membrane. At low field frequencies the shielding intensifies this effect, as the voltage on the organelle membrane starts decreasing even during the exposure (Fig. 5 illustrates this for an exposure to a direct field).

FIGURE 5.

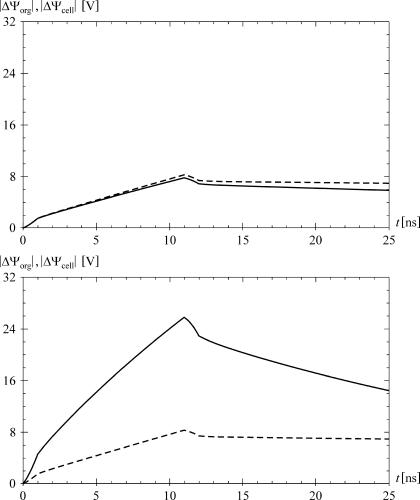
The time courses of ΔΨ_org (solid) and ΔΨ_cell (dashed) induced by an onset of a direct field with an amplitude of 5 × 10⁴ V/m and a risetime of 1 ns. The top panel shows the case for the default parameter values, and the bottom panel for σ_1i = 0.5 S/m, ɛ_1m = 3.0 × 10⁻¹¹ As/Vm, d₁ = 10 nm, and default values for the other parameters. The time course of ΔΨ_org reaches a peak after 203 ns in the top plot, and after 86 ns in the bottom plot. In the top plot ΔΨ_org never exceeds ΔΨ_cell, whereas in the bottom plot it does for the first 117 ns.

However, as Fig. 3 shows, if some parameters are shifted from their default values, the outcome can change significantly. As an illustration, in Fig. 4 we assume that σ_1i = 0.5 S/m, ɛ_1m = 3.0 × 10⁻¹¹ As/Vm, and d₁ = 10 nm, while keeping the other nine parameters at their default values. This study shows that on a cell characterized by the chosen parameter values, with an exposure to an alternating field with a frequency in the range of tens and hundreds of megahertz, the induced voltage on the organelle could exceed its counterpart on the cell membrane by a factor of >3. Obviously, this is only relevant provided that σ_1i can actually differ that much with respect to σ_2i, and similarly for ɛ_1m with respect to ɛ_2m. We discuss the plausibility of this at the end of the article, whereas we now turn to the voltages induced by a trapezoidal pulse.

FIGURE 4.

The frequency dependence of the voltages induced in an alternating field, with σ_1i = 0.5 S/m, ɛ_1m = 3.0 × 10⁻¹¹ As/Vm, and d₁ = 10 nm, and with default values for the other parameters. The top plot shows |ΔΨ_org| (solid) and |ΔΨ_cell| (dashed) for E = 5 × 10⁴ V/m and θ = 0, and the bottom plot shows |ΔΨ_org| / |ΔΨ_cell|. This ratio exceeds the value of 1 for ω > 7.78 × 10⁶ s⁻¹, attaining the maximum of 3.67 at ω = 1.58 × 10⁸ s⁻¹.

Voltages induced by a trapezoidal pulse

Before focusing on specific nsPEF, it is instructive to consider the general characteristics of the voltage inducement on a nanosecond timescale. For this, we treat an onset of a direct electric field, and to keep E(t) continuous, we assume that this onset is trapezoidal with a risetime T. Such a time course of the field can be described as a sum of two ramp functions, the first one with a positive slope and starting at the time 0, and the second one with the negative slope of the same size and starting at the time T,

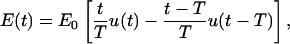(6)

where E₀ is the amplitude of the field that is reached at the end of the risetime. In the complex-frequency space, this becomes

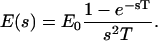(7)

In analogy with the FD study shown in Fig. 2, we assume that the field amplitude is E₀ = 5 × 10⁴ V/m, and treat the situation at θ = 0. In addition, we take T = 1 ns, which is on the order of magnitude of the shortest risetimes achievable with nsPEF generators. Proceeding as described in “Analysis in the time domain”, we insert E(s) into the expressions for ΔΨ_cell and ΔΨ_org, write all the admittivity operators as Λ = σ + ɛs, assign all the parameters their default values, and apply the inverse Laplace transform to obtain the time courses of the two induced voltages for such an onset of the field. Shown in the top panel of Fig. 5, these time courses reveal that the inducement on the cell plasma membrane is a monotonic process, whereas the inducement on an organelle membrane is transient—with the onset of the field, ΔΨ_org increases for several hundred nanoseconds, and then recedes back to zero even if the external field persists. This is consistent with the simpler, widely used steady-state consideration of a DC exposure, where the voltage induced on the cell plasma membrane is given by the static Schwan equation, ΔΨ_cell ≈ 1.5 E R cos θ, while everywhere in the cell interior the electric potential is practically constant.

The time courses of the two induced voltages also show that with default parameter values, ΔΨ_org remains below ΔΨ_cell at all times, as could be expected from the results obtained in the FD (see Fig. 2). However, if in analogy to the second FD study we set σ_1i = 0.5 S/m, ɛ_1m = 3.0 × 10⁻¹¹ As/Vm, d₁ = 10 nm, and keep the other nine parameters at their default values, the situation changes quite radically. As shown in the bottom panel of Fig. 5, ΔΨ_org now exceeds ΔΨ_cell considerably during the first tens of nanoseconds. The general properties of the two voltages—a monotonic increase of ΔΨ_cell and a transient increase of ΔΨ_org followed by a decrease to zero—of course remain unchanged.

The FD analysis described in “Voltages induced by a sinusoidal field” reveals that ΔΨ_org can only exceed ΔΨ_cell provided that either the cell membrane differs from the organelle membrane, or the cytosol differs from the organelle interior. From the results shown in Fig. 5 it now transpires that moreover, this can only occur during the first hundreds of nanoseconds after the onset of the pulse. This implies that only pulse durations shorter than this can allow for selective targeting of intracellular structures, whereas with longer pulses the cell plasma membrane is always affected to a larger extent.

For further elucidation of the effects of nsPEF, we now consider an exposure to a trapezoidal pulse with an amplitude E₀, a risetime T₁, a duration T₂, and a falltime T₃. Such a pulse can be represented as a sum of four ramp functions,

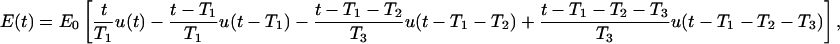(8)

or in the complex-frequency space,

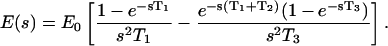(9)

We choose a trapezoidal pulse instead of a simpler rectangular pulse because this is more realistic, as on the nanosecond scale the risetime and the falltime of the pulse are not negligible with respect to the pulse duration, and in addition this allows one to study the behavior of the membrane voltage also during the risetime and the falltime.

In accordance with a typical experiment, we choose E₀ = 1.5 × 10⁷ V/m, T₂ = 10 ns for a pulse that is found to primarily affect the intracellular structures (26), and in addition we set T₁ = T₃ = 1 ns. Proceeding again along the lines described in “Analysis in the time domain” yields the time courses shown in Fig. 6, the top panel corresponding to default parameter values, and the bottom panel to values of σ_1i, ɛ_1m, and d₁ adjusted in analogy to the preceding studies. As expected, in the default case ΔΨ_org never exceeds ΔΨ_cell, whereas with adjusted parameters it does. Furthermore, the maximum value of ΔΨ_org is more than three times larger than the maximum value of ΔΨ_cell (see also the caption of Fig. 6), and consequently despite the double thickness of the organelle membrane, the electric field in it is >50% higher than in the cell membrane.

FIGURE 6.

The time courses of ΔΨ_org (solid) and ΔΨ_cell (dashed) induced by a trapezoidal pulse with an amplitude of 1.5 × 10⁷ V/m, risetime of 1 ns, amplitude duration of 10 ns, and falltime of 1 ns. The amplitude and duration are taken from Beebe et al. (26). The top panel shows the case for the default parameter values, and the bottom panel for σ_1i = 0.5 S/m, ɛ_1m = 3.0 × 10⁻¹¹ As/Vm, d₁ = 10 nm, and default values for the other parameters. In the bottom plot, the maximum value of ΔΨ_org is 25.8 V, and the maximum value of ΔΨ_cell is 8.3 V, with ΔΨ_org > ΔΨ_cell during the first 47 ns, i.e., until 35 ns after the end of the pulse (not shown).

Resting voltage on organelle membranes

It was already mentioned in the Introduction that the resting voltage normally present on the mitochondrial membrane is considerably larger than its counterpart on the cell plasma membrane. On each membrane, the voltage induced by an external electric field superimposes to the resting voltage, due to which the total voltage can be higher on a mitochondrial membrane than on the cell plasma membrane even with ΔΨ_org equal to, or slightly below ΔΨ_cell. As the membrane voltages required for electroporation by nsPEF appear to be in the range of volts (54,28), it is disputable whether a high resting voltage on an organelle membrane can alone be decisive in making this organelle the primary target of the field. Still, it could perhaps be among the reasons why mitochondria are the primary target of many observed effects of the nsPEF. This possibility has been discussed previously by Weaver (55).

Curvature of organelle membranes

Some theoretical studies suggest that the threshold value of membrane voltage required for electroporation can decrease if the membrane curvature is sufficiently high (56,8). As the organelles are significantly smaller than the cell, the typical curvatures found in organelle membranes are generally also higher than those in the cell membrane. Due to this, it is conceivable that even with ΔΨ_org somewhat lower than ΔΨ_cell, electroporation could affect an organelle membrane, but leave the cell membrane intact.

Voltage-gated channels in organelle membranes

This article is mainly concerned with the conditions that would allow for electroporation of the organelle membranes, but for completeness it should be noted that some effects caused by nsPEF could also be explained without involving electroporation. Weaver (55) proposed that the membrane voltage induced on the inner mitochondrial membrane could open the mitochondrial permeability transition pore complex. As this molecule is voltage sensitive (57,58) and involved in the induction of apoptosis (59), apoptosis could in this manner be induced also without electroporation of the mitochondrial membranes.

CONCLUSIONS

In “Voltages induced by a sinusoidal field” and “Voltages induced by a trapezoidal pulse”, we investigated the circumstances under which the voltage induced by the external field on an organelle membrane can exceed its counterpart on the cell plasma membrane. The results imply that this cannot occur if the electric properties of the organelle interior are very similar to those of the cytosol, and if the organelle membrane is very similar to cell membrane. On an organelle membrane considerably thicker than the cell membrane, as in mitochondria, the induced voltage can be higher even under these circumstances, but the electric field in the organelle membrane will remain below the electric field in the cell membrane, making electroporation of the former but not the latter unlikely.

However, if the organelle interior is more electrically conductive than the cytosol, or if the organelle membrane has a detectably lower dielectric permittivity than the cell membrane, the situation changes. For exposures to sinusoidal fields in the megahertz range, and for the first tens of nanoseconds of exposures to pulsed fields, the voltage induced on the organelle membrane can easily exceed its counterpart on the cell membrane, as illustrated in Fig. 4 and in bottom panels of Figs. 5 and 6. These findings are of course only relevant provided that the assumed differences between the organelle interior and the cytosol, or between the cell and organelle membranes are realistic. Higher ionic concentrations in the interior of some organelles could result in higher conductivity of this region with respect to the cytosol, which appears to be a realistic assumption at least in the case of potassium ions in the mitochondria. Experimental estimates obtained by dielectric spectroscopy for the mitochondria (60) and the nucleus (61,62) also corroborate that the differences between the electric conductivities of the organelle interiors and the cytosol can be considerable, and suggest that organelle membranes can also differ significantly from the cell plasma membrane in their dielectric permittivities.

Finally, as discussed in “Resting voltage on organelle membranes”, “Curvature of organelle membranes”, and “Voltage-gated channels in organelle membranes”, there are at least three additional factors that could lead to an organelle membrane being electroporated but the cell membrane left intact: high resting voltage on the organelle membrane, high curvature of the organelle, and voltage sensitivity of certain proteins in the organelle membrane. The first and the third of these factors could also contribute to the explanation why particularly mitochondria often appear to be the primary targets of nsPEF.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.