Antagonist-Induced Deadhesion of Specifically Adhered Vesicles

Abstract

By use of a model system consisting of giant vesicles adhering to flat substrates, we identified, both experimentally and theoretically, two new control mechanisms for antagonist-induced deadhesion. Adhesion is established by specific binding of surface-grafted E-selectin and vesicle-carrying oligosaccharide Lewis^X. Deadhesion is achieved by controlled titration of monoclonal antibodies against E-selectin. The first mechanism is characterized by a considerable retraction of the contact zone resulting in a loss of contact area between the vesicle and the substrate. Within the developed theoretical framework, the observed equilibrium state is understood as a balance between the spreading pressure of the vesicle and the antagonist-induced lateral pressure at the edge of the contact zone. In the second mechanism, the antibodies induce unbinding by penetrating the contact zone without significantly affecting its size. This process reveals the decomposition of the adhesion zone into microdomains of tight binding separated by strongly fluctuating sections of the membrane. Both experiment and theory show a sigmoidal decrease of the number of bound ligands as a function of the logarithm of antagonist concentration. The work presented herein also provides a new method for the determination of the receptor binding affinity of either the surface-embedded ligands or the competing antagonist molecules.

INTRODUCTION

Cell adhesion may be considered as a wetting process of a complex fluid droplet with surface bending elasticity. It is governed by the interplay of many factors, such as numerous generic interfacial forces (1,2) and membrane elasticity (3,4). However, the key to the high specificity of cell recognition relies on the topological and chemical complementarities of proteins interacting at the interface of two cells. These interactions, also called lock and key forces, can be formed by bonds between identical (homophilic) receptors embedded in opposing membranes, or between receptors and conjugate ligands exposed on the surface of the cell (5).

The mobility of at least one binding partner involved in the specific linkages is essential for the strengthening of adhesion by the formation of adhesion patches. These patches allow cells to rapidly form strong adhesion sites that can act as nucleation centers for the subsequent formation of stress fibers and muscle-like actin-myosin assemblies. Such strengthening, mediated by the actin cortex, is essential for cells subjected to strong hydrodynamic forces, as is the case for the endothelial cells lining the inner surface of blood vessels. For many processes deadhesion of whole cells or part of adhering cells is necessary. A relevant example is the transient binding of lymphocytes (T cells) to antigen-presenting dendritic cells, which is associated with the formation of adhesion domains called immunological synapses (6). Under physiological conditions a T cell has to visit many antigen-presenting cells before it is activated and starts to proliferate. This requires the repeated adhesion and complete deadhesion of the lymphocytes (7). An example of local detachments is the unbinding of the trailing end of cells crawling on surfaces, which is achieved by the uncoupling of the actin cortex from the plasma membrane (8).

Given that the presence of only 10⁴ specific adhesive molecules on the cell surface is sufficient for the normal functioning of the cell (4), the efficiency of the cell adhesion mechanism is indeed stunning. To enable such sophistication in the very noisy environment typical for the cell surrounding, several control mechanisms for cell adhesion must act together. Key parameters in the process of cell adhesion are the densities of the membrane-bound receptors (or ligands) and repelling molecules. Furthermore, the adhesion can be controlled by electrostatic forces and by antagonists competing with the ligands for binding sites on the receptor.

The density of membrane-bound receptors and ligands in the plasma membrane (and thus the adhesion strength) can be controlled in various ways. First, by depletion through internalization of receptor- (or ligand-) loaded vesicles budding from the plasma membrane (endocytosis) or, secondly, by enhancement through the fusion of vesicles carrying newly synthesized adhesion molecules within the plasma membrane (9). Lastly, the density of receptors may be influenced by proteolytic cleavage of ligands or receptor headgroups (10).

The generic forces are controlled by the glycocalix. This film contains repelling molecules that can extend up to 40 nm into the extracellular space. Because the size of typical receptors such as integrin or selectin is of the order of 10 nm, the repellers can thus exert strong steric repulsive forces between the adhering interfaces (3). An example of such a repelling molecule is the antiadhesive glycoprotein CD43 expressed at the surface of human leucocytes (11,12).

The repulsion produced by glycoprotein molecules is strongly dependent on their size (Flory gyration radius). Recently, Johnson and his collaborators have demonstrated quantitatively that polysialylation (corresponding to an increase in size) of the membrane-bound neural cell adhesion molecule (NCAM) has a large impact on the adhesive properties of cells (13). Ultimately, at physiological ionic strengths, the repulsion produced in this manner was sufficient to dominate both homophilic NCAM and cadherin attraction, and obliterate the protein-mediated intermembrane adhesion. These results support the putative role of NCAM polysialylation in the regulation of cell adhesion and intermembrane space.

Repulsion forces can also be mediated by giant macromolecules of the extracellular matrix that bind to their specific cell surface receptors. Hyaluronic acid, a highly charged giant polysaccharide, which is recognized by the cell surface receptor CD44, is an example of such a type of repelling molecule. This species, which is known to play a key role during embryonic development (14), can act as repulsive spacer between cells thus impeding their adhesion. However, if the interacting cells carry the appropriate polysaccharide receptors, such as CD44, hyaluronic acid can also act as attractive buffer and thus promote the cell adhesion (4).

Forces, both internally produced and externally exerted, are necessary for normal cell functioning. For example, leukocytes use the blood flow in their search for inflammation, and are thus submitted to large shearing forces while adhering and rolling along the blood vessel (15). Fibroblasts that structure the connective tissue, on the other hand, are able to pull strongly on their surroundings when participating in the recovery process of wounded tissue (16).

Although the biochemical and biofunctional aspects of cell adhesion have been intensively studied for many years (5,6,12,17), our knowledge of the physical basis of this extremely complex process is still rudimentary. Several important revelations in understanding the foundation of cell recognition processes emerged from studies on model systems containing the essential ingredients of adhesion. These consist of giant vesicles containing artificial or natural receptors (or ligands) that act as test (or toy) cells interacting with solid supported membranes or polymer cushions that expose the conjugate ligand (or receptor) and thus can mimic the target cell or tissue. The effect of the glycocalix is accounted for by the incorporation of lipopolymers (lipids exposing hydrophilic macromolecular chains) into the test cell. The adhesion process is evaluated by reflection interference contrast microscopy (RICM), a microinterferometric technique enabling the reconstruction of the surface profiles of adhering soft shells. By analyzing these surface profiles in terms of the theory of wetting of planar surfaces by partially wetting fluid droplets exhibiting surface (bending) elasticity, the free energy of adhesion can be estimated (18–20).

The major experimental results of the model membrane studies can be summarized as follows: adhesion inevitably leads to receptor segregation resulting in the spontaneous formation of adhesion plaques. The free energy of adhesion is determined by the (nonideal) lateral osmotic pressure exerted by the repelling molecules of the glycocalix and the unbound receptors (or ligands). The glycocalix plays a key role in the suppression of unwanted adhesion through the regulation of the surface density of the receptors and the repelling molecules. It enables the establishment of a situation near a wetting transition, thus allowing nature to optimize the density of adhesion molecules. This suggests that the adhesion strength can be controlled by modification of features such as: i), the lateral densities of the receptors and repelling molecules in the cell surface, ii), the ratio of the hydrodynamic radii of the repelling molecules to that of the receptors, and iii), the bending stiffness of the membrane. These studies have resulted in new insight into the physical basis of cell adhesion and provided experimental evidence for theoretical predictions based on the original work of Bell (21).

In a similar manner to adhesion, deadhesion is a process of extreme importance for normal cell functioning. However, deadhesion is, particularly from a physical point of view, a much less studied, and hence a less well-understood process. Nevertheless, several mechanisms for the control of deadhesion have previously been identified. In particular, the control of the local adhesion strength and inducement of deadhesion can be established through manipulation of the extracellular matrix. For example, during embryonic development, the deposition of fibronectin as adhesive sites guides cell locomotion during tissue growth. Another possibility is the generation of new blood vessels by decomposition of adhesion-mediating macromolecules (e.g., collagen) through proteolysis.

Deadhesion can also be regulated both by biomechanical and mechanical mechanisms. Owing to the results of the experiments on fibroblasts of Rees and his collaborators, it has been long known that the overall stiffness and shape of the cell has a strong impact on the deadhesion process (22). Furthermore, Crowley and Horwitz demonstrated that, also for fibroblasts, ATP rapidly destabilizes focal adhesions through two distinct, but possibly interacting mechanisms (23). The first is the phosophorylation of several major proteins by the activation of the tyrosine kinase cascade. The second mechanism is cytoskeletal contraction that generates tension. Apart from the role of the cytoskeleton, the area constraint couples the tension and the adhesion strength of the membrane of a given rigidity (24) and thus must influence deadhesion. Furthermore, controlled tension is often used in micropipette experiments to induce deadhesion and study both intramembrane interactions (25,26), and interactions between the cell membrane and the cytoskeleton (27,28).

Competitive binders (antagonists) provide a very useful tool to study the regulation of the cell morphology or the polarity of protein distributions in the plasma membranes by cell adhesion. In this connection, antibodies have been successfully applied to study the control of cell polarity by cell-cell contacts and by adhesion of the cells with extracellular matrix proteins such as laminin, collagen IV, and heparin sulfate proteoglycans (29).

In contrast with the small effect that endogenous ligands have on initiating cell attachment, they are likely to play a large role in the deadhesion process. For example, Cai and Wright propose a model for release of integrin-mediated leukocyte adhesion in which endogenous ligands such as elastase (expressed at the cell surface) are suggested to release adhesion by “eluting” the substrate-bound ligand from the integrin and cause detachment (30). They show that the elastase is capable of specific binding to the given integrins and can thus compete with the ligand. This competition was interpreted to represent a mechanism for deadhesion that is additional to the proteolytic activity of these proteins.

This work is concerned with the physical origins of the control mechanism of deadhesion provided by competitive binders (antagonists). We are aiming to model the action of antagonists (in the form of antibodies) and, in particular, their ability to induce deadhesion of vesicles that are preadhered by means of multiple ligand-receptor bonds. To achieve our goal, as a first step, we construct a simple system consisting of a vesicle specifically adhering to the substrate. Specifically, receptors of the selectin family (E-selectin) are immobilized on a solid surface (acting as target cell) whereas the conjugate ligands (sialyl-Lewis^X) are incorporated in giant vesicles acting as test cells. As a source of competition, monoclonal antibodies against E-selectin are used. After the establishment of the ligand-receptor-mediated adhesion equilibrium, antagonists are introduced into the surrounding solution. Characterization of the new thermodynamic equilibrium has shown that the antibodies used as antagonists are indeed responsible for a large impact on the adhesive properties of the vesicles.

In a second step, a theoretical framework is constructed to identify and rationalize the experimental outcomes and provide a quantitative background for the observed unbinding mechanisms. This is achieved by extending the theoretical considerations of Smith and Seifert for specific vesicle adhesion (31), where the effective adhesion strength and the average number of formed bonds is associated with the appropriate shape of a vesicle in a thermodynamic equilibrium. It will be shown, that by developing two somewhat similar three-dimensional (3D) models for two distinct actions provided by antagonists, it is possible to account for different observed stages of the vesicle unbinding process and obtain very good behavioral agreement with experiments.

MATERIALS

In this section we first provide details of the preparations for the vesicle-substrate system. To avoid repetition, the origin of the material used in the preparations is summarized in a separate section.

Giant vesicles were prepared from an equimolar mixture of DMPC (1,2-dimyristoyl-sn-glycero-3-phosphocholine) and cholesterol. To screen the nonspecific Van der Waals attraction by the glass substrate, the vesicles were doped with DMPE-PEG2000 (1,2-dimyristoyl-sn-glycero-3 hosphoethanolamine-N-polyethylene-glycol) by adding this lipid at a concentration of 1% with respect to DMPC. In addition, to allow for specific ligand-receptor-based binding of vesicles to the substrate, 8% of sialyl-Lewis^X-glycosphingolipids (32) (sLex) were reconstituted into the bilayers. The vesicles were prepared by electroswelling (33,34) in a 170 mOsm sucrose solution. To prevent suppression of adhesion due to osmotic tension, the vesicles were placed in a 210-mOsm salt buffer (100 mM NaCl, 1 mM CaCl₂, 1 mM NaN₃, 10 mM HEPES at pH of 7.2). This was sufficient to deflate the vesicles and enable the formation of a contact zone parallel to the substrate. The vesicles were deposited on the substrate from the suspension by sedimentation under gravity.

The substrate was a clean glass coverslide that was hydrophobized by immersion in a 1% toluene solution of aminosilanes (3-aminopropyltriethoxysilane) for 4 min at 60°C, which was followed by rinsing with pure toluene and drying under N₂ (35). Finally a recombinant form of the extracellular domain of human E-selectin was physabsorbed on the substrate exposing the silane layer (36). This was achieved by incubating the protein solution (maximum 5 μg/ml in the salt buffer) for 2 h at room temperature, while the whole chamber was gently mixed on a shaking platform. After rinsing with buffer, the substrate was incubated at room temperature for an additional 1 h with a buffer solution containing 3% of blotting grade blocker nonfat dry milk to prevent any direct contact of glass with the vesicle. Final careful rinsing of the slide with buffer completed the preparation.

For the competitive binding experiments, mouse anti-human E-selectin was diluted in the salt buffer at concentrations of 10–25 μg/ml and inserted into the measuring chamber with a Hamilton pipette.

All of the lipids and the cholesterol were purchased from Avanti Polar Lipids (Alabaster, AL). The aminosilanes and toluene were obtained from Fluka (Buchs, Switzerland), whereas the coverglasses originated from Merck (Darmstadt, Germany). E-selectin was made by Calbiochem (San Diego, CA), whereas the antibodies were manufactured by Chemicon (Temecula, CA). The Millipore water used for rinsing and the buffers was prepared with a system from Millipore (Molsheim, France). The fat-free milk was purchased from BioRad (Hercules, CA). Additional details of the preparation and the characterization of both the vesicles and the substrates can be found in the thesis of Lorz (20) and will be discussed elsewhere (37).

METHODS

To examine deadhesion of the vesicle, RICM has been used. This microinterferometric technique generates an interference pattern by interference of light waves reflected at the interfaces between the substrate and the buffer, and the buffer and the membrane. It allows for the reconstruction of the surface profiles of adhering bodies with ∼10 nm out of plane and ∼0.3 μm in-plane spatial resolution. Relative membrane displacements in the vertical direction can be measured with resolutions of up to 5 nm. The spatial variations of the substrate-membrane distances can be directly visualized through the variations of grayscales that can be represented in terms of 255 grayscale colors. Strongly bound parts of the membrane appear as dark regions of the interference pattern whereas weakly adhering regions separated from the substrates by ∼100 nm appear as gray areas. In combination with fast image processing thermally excited membrane fluctuations can be analyzed quantitatively to evaluate the control of adhesion by the undulation forces.

The bottom of the 900-μl measuring chamber is formed by a coverglass pressed onto a Teflon frame by a metal ring. The chamber is mounted on an inverted Axiomate 100 microscope (Zeiss, Jena, Germany), equipped with an antiflex objective (Plan Neofluar, 63× /1.25 Oil, Zeiss). The interferograms are observed with a Peltier-cooled 10-bit charge-coupled device camera (C4880-80, Hamamatsu Photonics, Hamamatsu, Japan) and the digitized images are stored directly using real-time imaging software (38).

EVALUATION OF CHANGES IN THE ADHESION ZONE

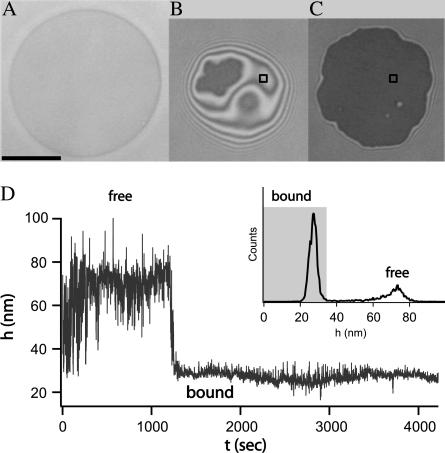
Before the formation of ligand-receptor bonds, the vesicle settles at a height governed by the effective potential acting between the membrane matrix and the substrate. Due to the passivity of the substrate and the repulsion exerted by the glycolipids reconstituted into the membrane, the minimum of this potential is sufficiently far from the substrate. Consequently, the vesicle is weakly bound and still exhibits strong undulations (39). After some time, ligand-receptor bonds begin to form. The adhesion process associated with these specific binding results in aggregation of the ligand-receptor pairs leading to two types of adhesion zones within the adhesion disk (see Fig. 1 B). In the first type, the vesicle membrane is locally trapped in patches of strong adhesion generated by receptor-ligand bonds formed while the undulations are almost totally suppressed (3). In the second type of contact, the membrane outside of the patch remains in the initial stage of weak adhesion and is subject to fluctuations (see Fig. 1 B). When the formation of patches dominates the overall effective potential, the patches of strong adhesion grow beyond the initially established contact zone between vesicle and substrate, inducing a first-order shape transition (18,19). For the vesicles whose adhesion is mediated by the sLex-E-selectin pair, such transitions occur for high coverage of the substrate and a relatively large fraction of ligands in the vesicle (37). When the equilibrium is attained, the contact zone is maximized and appears uniform within the resolution of the microscope (see Fig. 1 C).

FIGURE 1.

Different stages of the adhesion process of a single vesicle. The scale bar indicates the length of 10 μm. (A) The bright field picture of the vesicle. (B) Coexistence of a patch of strong adhesion (dark) and region of contact of the weak adhesion (bright area exhibiting interference fringes). (C) Adhesion after the shape transition induced by the growth of the patch to its maximum size associated with the aggregation of the ligand-receptor bonds. (D) Height of the membrane as a function of time for a square point that is shown in panels B and C. The inset contains the resulting histogram of heights. The bound state is defined by the peak in the distribution and is shaded in gray.

The transition from the weak to the strong adhesion state for a certain point in a vesicle can be easily seen by monitoring changes in the membrane fluctuation amplitude. This is demonstrated in Fig. 1 D where the membrane height of a given point (in the contact zone) is measured over time. The transition obviously occurs around t = 1300 s. From this graph it is possible to construct a histogram of heights (see inset of Fig. 1 D) that clearly shows a Gauss-like peak that belongs to the bound state.

Antagonist-induced unbinding

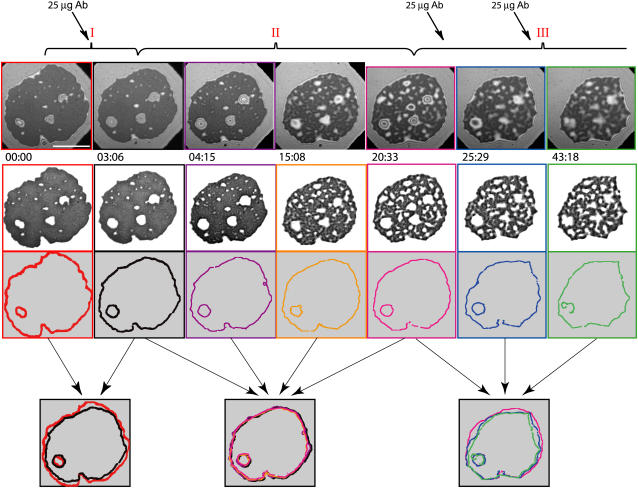
Once a steady state of adhesion is reached, small amounts of antibodies are added to the buffer solution. The mouse anti-human E-selectin is capable of blocking the sLex binding site of E-selectin, which may lead to the unbinding of the receptor-ligand bonds. Indeed, upon insertion of antibodies into the solution, three phases of unbinding of the vesicle (denoted as phases I–III) are observed.

Phase I: lateral pressure mechanism

Phase I is characterized by a decrease in size of the contact zone. This is particularly apparent in the final row of Fig. 2, where the edge of the vesicle contact zone before the antibody insertion is compared with the edge of the contact zone at the end of this phase. During this time, the contrast within the inner part of the contact zone is not altered. Instead, the entire adhesion plate still appears to be strongly bound, indicating the persistence of the ligand-receptor bonds inside this region (see the second row in Fig. 2). Because both the coverage of the substrate with E-selectin (∼3000 molecules/μm² as estimated by Lorz (20)) and the concentration of ligands in the vesicle (10 mol%), are relatively high, the contact zone must be relatively densely packed with bonds. Diffusion of molecules of the size of antibodies is thus strongly suppressed in comparison to the diffusion in the bulk solution, impeding their access to E-selectin in the contact zone. In this short initial stage (∼3 min), the action of the antibodies occurs merely at the rim of the adhesion plate, whereas the remaining part of the zone appears impermeable. Apparently, the antibodies binding to the substrate begin to exert a lateral two-dimensional (2D) pressure on the rim of the contact zone, resulting in the reduction of the excluded area of the adhesion plate. The final size of the zone is determined by the balance between the antibody pressure and the spreading pressure of the vesicle.

FIGURE 2.

Unbinding of a vesicle by antibody titration. Injections of the antibody solution are marked with thick arrows in the top part of the figure. The scale bar in the top left frame indicates the length of 10 μm. The three phases of the unbinding process are indicated with red Roman numbers. In the first row, the original RICM images taken at the times (minutes and seconds) indicated at the bottom of each image, are presented. The strong adhesion zones are extracted in the second row, whereas the rims of the contact zone are presented for the corresponding frames in the third row. The edge of the blister in the middle of the zone is shown for the purposes of facilitating the orientation. The rims for each phase are superimposed in the last row, with the thin arrows indicating the frames superimposed. Phase I is a short phase where the antibodies are acting on the rim of the contact zone merely as a lateral two-dimensional pressure. In phase II the spreading pressure of the vesicle equilibrates with the lateral antibody pressure. In this slow phase, the antibodies are penetrating the adhesion patch, and the deadhesion occurs as competitive binding of antibodies to receptors. Phase III occurs upon a further increase of antibody concentration. At this stage, both mechanisms (the receding of the rim and the penetration of antibodies into the whole adhesion zone) are in action. Details of analysis used for construction of this figure can be found in Appendix A.

Although phase I can be clearly distinguished in experiments, it is somewhat difficult, from a technical point of view, to determine exactly when it ends. The technique employed is very sensitive to membrane fluctuations exhibited by the parts of the membrane that are not specifically pinned to the substrate. However, as the initial density of bonds is relatively high, a very small number of sLex-E-selectin bonds may be replaced by antibody-E-selectin bonds before the fluctuations reach observable amplitudes (∼5 nm with this setup). Furthermore, in case of midrange density of bonds, it is to be expected that there will be a very short period of time when the antibodies penetrate the contact zone while the rim is still retreating. Ultimately, these two processes will run simultaneously, which is, within the scope of the article, identified as phase III.

Phase II: competitive binding mechanism and phase III

Phase II is a much slower regime of the deadhesion process and begins when the antibodies penetrate the contact zone. During this period (lasting ∼20 min), the vesicle and the antibodies are seeking a new equilibrium and this process is driven by the chemical potential provided by the antibodies in the bulk solution. Although it is found that the size of the total contact zone remains almost unaltered (see the overlapping edges in the last row of Fig. 2), the distribution of the bonds gradually changes from uniform to highly structured. The higher affinity of the antibodies for E-selectin causes the number of sLex-E-selectin bonds to decrease. After some time, the vesicle finds a new equilibrium and no further change in the structure of the contact zone is visible.

Further increasing the antibody concentration after the equilibrium has been achieved in phase II, induces a transition of the vesicle into phase III of the deadhesion process. At this point, the contact zone becomes highly permeable to antibodies, but the excluded area is still relatively large. Under these circumstances, both the lateral pressure mechanism that dominates phase I, and the competitive binding mechanism prevailing during phase II can act simultaneously. Considerable loss of both the size of the contact zone and the number of bound ligands can therefore be observed. The latter process can be identified by the change in contrast within the contact zone, and an increase of white area in the second row in Fig. 2. The size changes are evident from the overlapping edges from this phase (last row of Fig. 2).

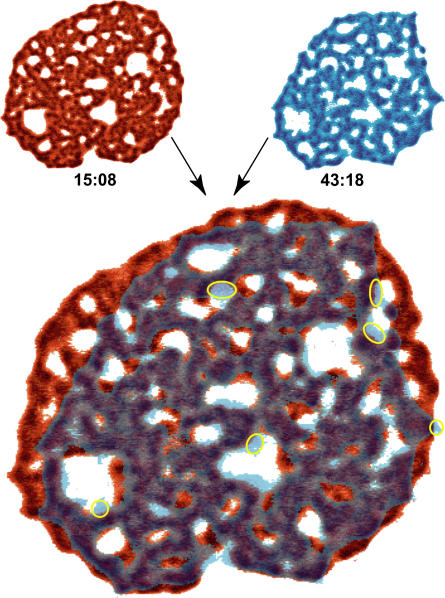
The area of strong adhesion occupying the entire contact zone remains uniform during phase I. In phase II, however, it gradually decomposes into a very large number of microdomains. After a certain time during phase II the formation of microdomains saturates and the number of newly formed microdomains is negligible in comparison to those detaching from the substrate. This is demonstrated in Fig. 3 where a highly structured contact zone from the beginning of phase II is compared to the one from phase III. Although the size of the patch has been considerably reduced over 30 min, all of the microdomains persisting into phase III can be traced in the earlier picture from phase II. At the same time, only a few microdomains (indicated in Fig. 3 with yellow circles) were formed. Interestingly, the membrane retracts only by the loss of a whole microdomain at once, which means that a microdomain must have a critical minimum size. The membrane released in the detachment of microdomains is able to fluctuate, particularly where large holes appear in the patch. This is responsible for the light blue colors in Fig. 3.

FIGURE 3.

An overlay of two pictures of the contact zone dominated by ligand-receptor interactions. The two superimposed images are shown in top left and top right corners together with their relative times when the snapshots were taken. For better visualization, the gray color scale from the original pictures has been transformed into either a red or a blue scale. The pictures were then made transparent and overlaid. Where the two pictures overlap, the gray colors emerge. The intensity of the colors reflects the strength of binding. For details see Appendix A.

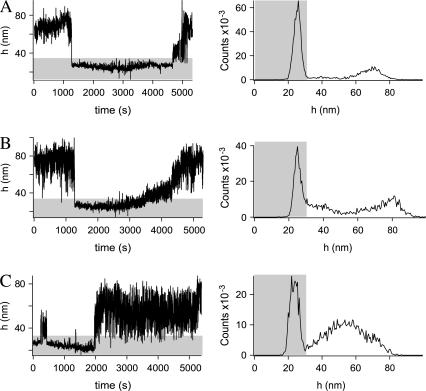
The binding and unbinding events of a surface element of the membrane can also be seen in the fluctuation diagrams (right-hand side of Fig. 4), where typical examples are presented. The unbinding is usually a prompt (Fig. 4, A and C). However, in some cases, gradual unbinding has also been observed (Fig. 4 B). Rebinding events are also recorded such as the case shown in Fig. 4 C around t = 500 s. For each fluctuation diagram, the height histogram is also presented on the left side of Fig. 4. For all cases, the bound state was long lived so that there is a clear maximum. Because all points belong to the same vesicle, the cutoff for the bound state (end of gray area) is the same for every point in Fig. 4. Details of these analyses can be found in Appendix A.

FIGURE 4.

Height of a membrane as a function of time for three different points in the contact zone of a same vesicle (left). Height histograms corresponding to the graphs on the left are given on the right, respectively. The part of the graphs shaded in gray are associated with the bound state.

If the experiment is repeated with half of the previous concentration of receptors on the substrate, somewhat different behavior is observed. In this case, as shown in Fig. 5, before the insertion of antibodies one observes an assembly of strong adhesion patches with a total area smaller than that of the contact zone. When added, the antibodies almost immediately penetrate into the patch, thus circumventing phase I. This is due to the smaller concentration of bonds within the patch resulting from the decreased coverage of the substrate by E-selectin. Furthermore, the appearance of microdomains is observed almost immediately upon insertion of antibodies, but the size of the contact zone remains virtually constant throughout the entire experiment.

FIGURE 5.

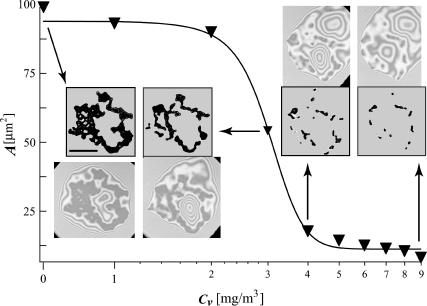
Area of the adhesion patch as a function of the concentration of antibodies. The scale bar indicates the length of 10 μm. Data points are shown as inverted triangles. The line connecting the triangles is a sigmoid fitting function. Four original pictures are presented together with the pattern of strong adhesion patches that were extracted by image processing. Every data point was processed in exactly the same way and the error associated with each one is proportional to the ratio of the surface to the circumference of the patch. The arrows connect a given point with the original picture.

By subsequent addition of small aliquots of titer (1 μg of antibodies each time) and waiting until the new equilibrium was established on each occasion, the variation of the total area of the strong adhesion patches with the number of aliquots was constructed (Fig. 5). Because the area of the patch is proportional to the number of formed bonds, and the concentration of the antagonist is proportional to the weight of inserted antibodies, the sigmoidal curve in Fig. 5 reflects the functional dependence of the number of bonds on the antibody concentration. Unfortunately, due to difficulties in determining the absolute concentration of active receptors on the substrate, it is only possible to roughly estimate the number of bonds present. The discussion of this and associated aspects will be deferred until later.

It can be seen from Fig. 5 that most of the patch area is lost after the addition of the third and fourth titers. Upon insertion of the third milligram of antibodies, the area of the patch saturates to ∼55% of its initial value, whereas after the fourth milligram the original area is reduced by 90%. Interestingly, five further aliquots are not sufficient to completely destroy the patch resulting in unbinding of the vesicle. This is attributed to the fact that the concentration of free ligand in the vicinity of the patch (and in the vesicle) is much larger than the concentration of antibodies. Hence, the rebinding events occur much more frequently and are able to compensate for the lower binding affinity. In addition, the presence of 10 μg of antibodies begins to change the osmolality of the bulk solution and hence the reduced volume of the vesicle. At this stage, the experiment must be abandoned as it is not possible to maintain constant vesicle volume, and thus, the size of the contact zone changes not because of the binding of the antibodies to the surface but rather the increased osmotic pressure difference between the inner and outer buffer solutions.

Similar experiments have been performed with fluorescently labeled soluble sLex molecules as antagonists to the membrane incorporated sLex (data not presented). However, fluorescence measurements were unable to produce reliable data because of strong bleaching and insufficient spatial resolution. In contrast, RICM data indicate that this system exhibits the same qualitative behavior as the one previously described, with the caveat that much larger concentration of the antagonizing sLex had to be used in comparison to antibody concentrations. This is to be expected as the binding constant of sLex to E-selectin is much smaller than that of the antibody to the E-selectin.

THEORETICAL CONSIDERATIONS

To better understand the observed results, two similar 3D models are developed to account for the deadhesion mechanisms dominating phase I and phase II. In particular, explicit consideration is given to the following factors: i), the enthalpy of binding of both ligands and antagonists; ii), the mobility of the ligands and the antagonists through a contribution to the mixing entropy; iii), the finite number of ligands contained in the vesicle, iv), the constant density of immobile receptors on the substrate, v), constant chemical potential of antagonists in the bulk solution, and vi), the bending energy of the vesicle shape. In this manner, the continuous approach of Seifert and Lipowsky (40) is connected with the thermodynamic approach of Bell and Dembo (41,42). The equilibrium conditions of the described ensembles are obtained by minimizing the free energy of the system in an appropriate manner. The average number of formed bonds is thus obtained as a function of the constituent concentrations and the effective binding strengths of a single antibody-receptor and ligand-receptor pair.

In both cases the vesicle surface is separated into a region parallel to the substrate forming a contact zone and a region consisting of the remaining part of the vesicle. The interactions of ligands with receptors are assumed to occur only within the contact zone. Nevertheless, the regions are able to exchange ligands and area. The antagonists are permitted to interact with the receptor only when absorbed on the substrate. The contribution to the internal energy of the system from a single bond is realized whenever a ligand or an antibody is positioned over a receptor site.

In the absence of antagonists, both models should reduce to the recently developed thermodynamic model for the equilibrium state of vesicle adhesion (31). Several results from that work are pertinent to modeling of vesicle adhesion in the presence of antagonists. In particular, in the work in question, it has been found that the magnitude of the bending energy term is usually much smaller than that of the others in the free energy, and can generally be ignored (31). The only exception is when the shape of the vesicle approaches the shape of a spherical cap for which the bending energy diverges inducing a boundary minimum in the free energy with respect to size of the contact zone. As a consequence, in the thermodynamic equilibrium, the vesicle area of contact with the substrate is maximized and determined only by the reduced volume of the vesicle.

The experimental procedure described in the previous section has shown that it is virtually impossible to completely screen the nonspecific interaction between the substrate and the vesicle. This interaction is responsible for the formation of the relatively small initial contact zone (see Fig. 1 B). The vesicle can find the thermodynamic equilibrium governed by the diverging bending energy (as in the case of the vesicles in Figs. 1 C and 2 at t = 0.00), where bond formation completely dominates the nonspecific interaction of the vesicle with the substrate. The adhesion process resulting in such adhesion plates is generally fast and uninterrupted. The final contact zone is usually uniform and densely packed with ligand-receptor pairs, and the shape of the vesicle is a spherical cap. The unbinding of such a vesicle by means of antagonists is determined by the mechanism that governs phase I and it is only later that such a vesicle can participate in phases II and III (as seen in Fig. 2).

There are often cases, however, when the vesicle appears to be in its equilibrium state without assuming the shape of the spherical cap (see, for instance, the vesicle in Fig. 5). The adhesion process associated with such a state is usually slow and stepwise, and should be expected when the probability for bond formation is reduced, either due to the low coverage or a low fraction of ligands in the vesicle. Technically, the slow equilibration leads to a relaxation of the free energy with respect to ligand density variables but not with respect to the size of the contact zone. In this constrained equilibrium, the distribution functions resulting from the minimization of the free energy are still valid, but the size of the contact zone is not determined by the bending divergence but by factors such as the nonspecific interaction potential, shape fluctuations, and the probability for bond formation. Axially symmetric shapes of vesicles in this constrained equilibrium (obtained for a fixed size of the contact zone) can be determined by the use of a continuum model (40) where the bending energy must be minimized for a chosen size of the contact zone.

The conditions for these two different equilibria in the experimental system discussed in previous sections have been explored in detail and are discussed elsewhere ((20), and B. G. Lorz, A.-S. Smith, C. Gege, and E. Sackmann, unpublished). However, it is important to emphasize that the proposed adhesion model for vesicle adhesion (31) could be applied to both the thermodynamic and the constrained equilibria. It is with this in mind that we proceed with our thermodynamic considerations.

The models for the deadhesion mechanisms dominating phase I and phase II are developed within the same framework as was undertaken for describing simple adhesion. However, for the unbinding mechanism of phase I, the size of the contact zone is determined by the equilibration of the spreading pressure of the vesicle and the lateral pressure of the antibodies. The latter is the gain in the free energy if the area of the contact zone is reduced for the area of a single site and is similar to the chemical potential in condensation process. For the unbinding mechanism of phase II, the size of the contact zone is taken to be constant and the number of formed ligand-receptor bonds is determined simultaneously with the number of antibody-receptor bonds.

The lateral pressure mechanism: phase I

Under the condition of an impermeable adhesion plate (high density of ligand-receptor bonds), the added antibodies exert lateral 2D pressure on the edge of the contact zone (see Fig. 6), without penetrating the bulk of the zone. The vesicle, however, tries to maintain the size of the contact zone by its spreading pressure. Therefore, in the presence of antibodies, the system must find a new thermodynamic equilibrium. This competition typically results in a smaller size of the vesicle contact zone. In the case that the antibody pressure is very high, the vesicle will lose the entire contact zone and detach from the substrate.

FIGURE 6.

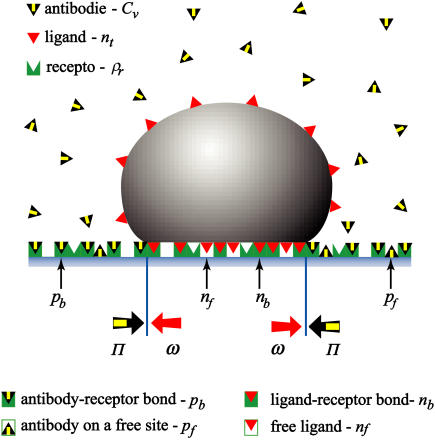
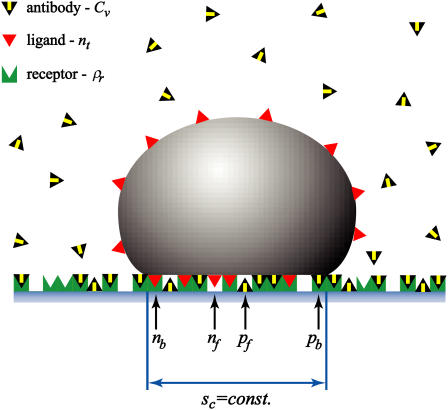
The balance between the spreading pressure of the vesicle (ω) and the lateral antibody pressure (Π) determines the size of the contact zone. Antibodies are not penetrating the contact zone and are presented with yellow-black triangles. Red triangles in the vesicle indicate ligands and give rise to the fraction n_t. The green sites in the substrate can be associated with receptors that contribute to ρ_r. Antibodies can either be specifically bound to the substrate by forming an antibody-receptor bond and contributing to p_b, or they can be nonspecifically absorbed to the sites on a substrate that are free of receptors giving rise to p_f. The contact zone s_c is depicted as the part of a vesicle at zero distance from the substrate. If, within this area, a red triangle is on top of a green site, a bond is formed that contributes to n_b. A red triangle over a white site indicates a free ligand in the contact zone and can be associated with n_f. Opposing white and gray arrows at the edge of the contact zone indicate the two balanced pressures.

For the quantitative modeling we will use the following notation:

• antibody-receptor binding energy (in units of k_BT).

• volume fraction of antibodies in the solution.

• ρ_r, fraction of the substrate surface covered by receptors.

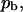• fraction of the substrate surface covered by adsorbed antibodies bound to receptors.

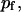• fraction of the substrate surface covered by adsorbed antibodies not bound to receptors.

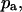• total coverage of the substrate by adsorbed antibodies,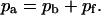

• S_t, total number of sites in the vesicle. A site has the size of the ligand.

• s_c, the fraction of the total vesicle area forming the contact zone, 0 ≤ s_c ≤ 0.5. (For a specifically adhered vesicle in the thermodynamic equilibrium, s_c = 0 if v = 1 and s_c = 0.5 only for v = 0.)

• E_a, ligand-receptor binding energy (in units of k_BT).

• n_t, total vesicle surface coverage by ligands (e.g., for n_t = 0.1, 10% of the vesicle surface is covered by ligands).

• n_b, fraction of total ligands that are in the contact zone and bound to receptors (e.g., for n_b = 0.1, 10% of all ligands in a vesicle are bound to the substrate).

• n_f, fraction of total ligands that are in the contact zone and free.

All of the variables that are expressed as fractions adopt values in the range between 0 and 1.

The spreading pressure of the vesicle

Because the 3D vesicle spreads over a 2D surface, the lateral spreading pressure is of a two-dimensional nature. The latter is defined as the work required for changing the vesicle-substrate contact area which must be determined from the model for vesicle adhesion in the absence of antibodies. Thus, it is equivalent to the effective adhesion strength resulting from binding of receptors to the substrate as defined previously (31). As this previous work contains an overview of the relevant literature as well as a thorough characterization of the behavior of the calculated spreading pressure, we will not reproduce this material in full herein. We will, however, outline the elements of the model pertinent to the unbinding of specifically adhered vesicles by ligand antagonists.

The fraction of bound ligands and free ligands in the contact zone is given by the following expressions:

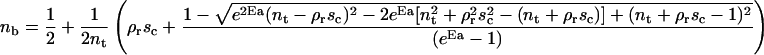(1)

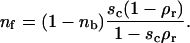(2)

These can be used to determine the vesicle spreading pressure that is, in units of k_BT/a (a is the area of a site), found to obey:

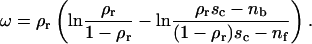(3)

Importantly, the spreading pressure always increases monotonically with decreasing size of the contact zone. The maximum is always at s_c = 0 and is given by the following expression:

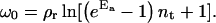(4)

It is this spreading pressure that needs to be overcome to detach a vesicle.

The lateral antibody pressure

The calculation of the 2D lateral antagonist pressure Π is analogous to determining the Langmuir absorption isotherm of particles interacting with a substrate (43). The antagonists binding to the receptors (p_b) and antagonists absorbing to the receptor-free part of the substrate (p_f) need to be in equilibrium with the very dilute antibody solution, for which the fixed chemical potential μ = ln C_v is assumed to be fixed. Minimizing the appropriate free energy (see Appendix B) results with:

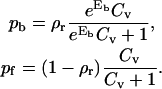(5)

It is by definition the gain in the free energy realized when the system increases its available size for a surface area of a unit site and is found to be given by the following expression:

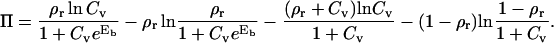(6)

Details on development of this expression, as well as the analysis of limiting cases of both the coverage of the substrate by antagonists and the antagonist spreading pressure is given in Appendix B. However, it is important to notice that the lateral pressure defined by Eq. 6 will be valid only for relatively low concentrations of the antagonists (C_v < 0.1) and completely determined by the system parameters (the antagonist-receptor binding strength, surface coverage, and the concentration of antagonists).

Determining the size of the contact zone

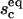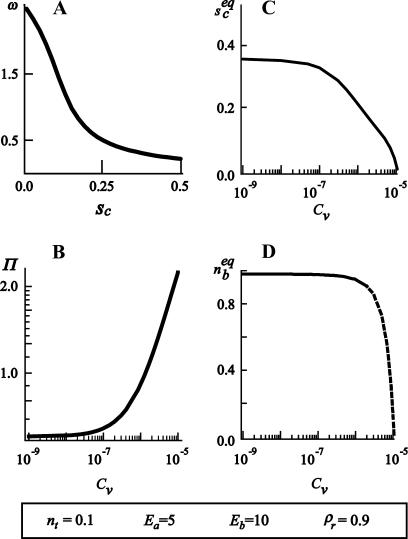
The equilibrium size of the contact zone and the fraction of bound ligands 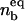in the presence of antibodies can be determined by solving ω = Π. A typical result of such a calculation is presented in Fig. 7 where 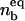and 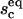are shown as functions of the antibody concentration, for given concentrations of ligands and receptors. As the initial size of the contact zone is associated with the shape of the spherical cap, the reduced volume of the vesicle determines the size of the contact zone before the insertion of antibodies.

FIGURE 7.

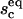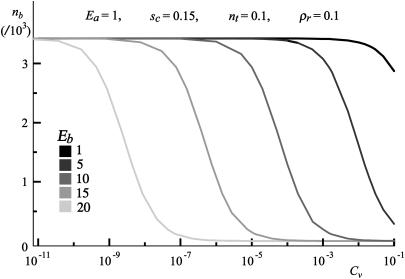
(A) The vesicle spreading pressure ω as a function of the size of the contact zone s_c. (B) Antagonist lateral pressure Π as a function of the antagonist bulk concentration C_v. (C) Equilibrium size of the contact zone and (D) equilibrium fraction of bound ligands as function of the antagonist bulk concentration C_v. Chosen binding strengths and concentrations of other ligands and receptors are indicated in the bottom of the figure. For the given parameters, there is a certain concentration (C_v ≈ 10⁻⁷) at which the size of the contact zone is significantly influenced by the presence of the antibodies. The fraction of bound ligands, however, changes at somewhat larger concentrations (C_v ≈ 10⁻⁶), indicating an increase of the density of ligand-receptor bonds in the contact zone, accompanied by an increase of the average spreading pressure, even when the zone is reduced.

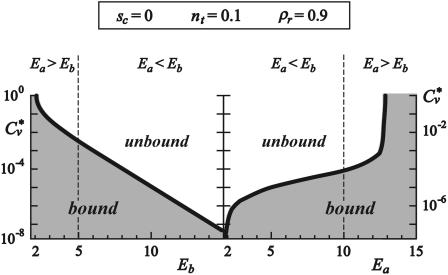
The critical concentration of antibodies C_v* necessary for the detachment of the vesicle can be determined by solving ω₀ = Π. This concentration is found to depend on the ligand-receptor and antibody-receptor binding strengths as shown in Fig. 8.

FIGURE 8.

The logarithmic plot of the critical (detachment) concentration of antibodies as a function of the antibody-receptor binding strength (left) and as a function of the ligand receptor binding strength (right). The divergence of the C_v* at both low antibody-receptor and ligand-receptor binding strengths as well as the maximum ligand-receptor binding strength for which detachment can occur is clearly visible. The parts of the diagrams with shaded backgrounds indicate the regions of parameters where the vesicle is bound to the substrate, whereas the white background signifies free vesicles. Dashed lines indicate the choice of the binding strength of the ligand-receptor pair (left) and the antagonist-receptor pair (right).

Importantly, the logarithm of the critical concentration decreases linearly with increasing antibody-receptor binding strength (left panel in Fig. 8). Moreover, it is possible to detach the vesicle even with antagonists of lower binding strengths than that characterizing the ligand-receptor pair (E_b < E_a), but that would require higher antibody concentrations. However, there is a minimum strength of antibodies that need to be available in order for detachment to be achieved.

When the detachment concentration is explored as a function of the ligand-receptor binding strength (right panel in Fig. 8), the critical concentration approaches zero very rapidly, for large differences between the two binding strengths. After this divergence at low ligand binding strengths, the logarithm of the critical concentration enters a linear regime. This linear regime ends in another divergence, this time at ligand binding strengths somewhat larger than the antibody binding strength. This result demonstrates the insensitivity of the system to the presence of the relatively weak antibodies.

The competitive binding mechanism: phase II

The penetration of antibodies into the contact zone may occur upon a spontaneous unbinding of the ligand-receptor pair, even after the spreading pressures are equilibrated. To account for this effect we have expanded the model for adhesion to allow for competitive binding within the contact zone of a constant size (see Fig. 9). The size of the contact zone (s_c) is maintained by the same mechanisms as discussed in previous sections. The ligands are still treated as a part of a finite system while the antibodies are coupled to the solution of a constant chemical potential.

FIGURE 9.

A schematic representation of the competitive binding mechanisms. The antibodies are penetrating the contact zone blocking the receptors for the ligands. The contact zone remains of constant size. The concentrations (p_f and p_b) of antibodies in the contact zone is in chemical equilibrium with the antibodies in the solution.

Minimizing of the appropriate free energy (see Appendix C for details) is a task beyond the analytical approach undertaken this far. However, it is possible to find expressions for the fraction of area occupied by antibodies in the contact in the same form as those obtained for the nonpermeable contact zone:

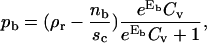(7)

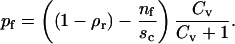The difference between Eqs. 5 and 7 is that the coverage of the surface accessible to bound and free antagonists is reduced by the presence of bound and free ligands (n_b and n_f, respectively).

The fraction of bound ligands is determined simultaneously and is presented in Fig. 10, where n_b is calculated for the case of titration with antibodies of different binding strengths, while all other parameters are kept constant. It is this n_b that must be used to determine p_b from Eq. 7.

FIGURE 10.

Fraction of bound ligands as a function of the antibody concentration for different antibody-receptor binding strengths. Other parameters are kept constant and are indicated in the graph.

It is surprising that the increase of E_b provides only a shift of the decay function of bound ligands toward smaller concentrations. This shift is linear with respect to the antibody binding strength and is equal to E_b lnC_v + const. However, an increase of more than five orders of magnitude in the concentration of antibodies is needed for the complete unbinding of ligands. Nevertheless, most of the ligand bonds are lost in a relatively short window of two orders of magnitude in the antibody concentration. When C_v → 0, the model for adhesion in the absence of antibodies, presented in Smith and Seifert (31), applies.

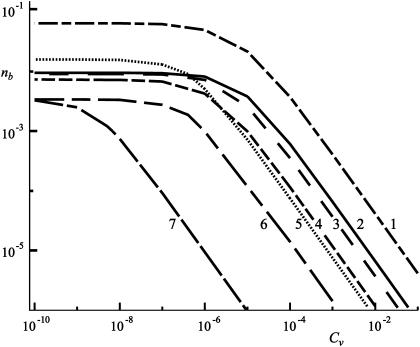
Several important properties of the decay functions can be learned from the double logarithmic plot (Fig. 11). It is easy to notice that the slope of the decay function remains almost constant despite the widely varying choice of parameters (presented for each curve in Table 1). This linear slope of the decay functions also suggests that it is not possible to completely block the receptors on the substrate from the ligands. However, this cannot be realistic as at some stage n_b will become small enough to give rise to less than one ligand bound to the substrate. Furthermore, in this limit, the thermodynamic laws on which this approach is based are expected to fail due to insufficient statistics with small numbers.

FIGURE 11.

Double logarithmic plot of the fraction of bound ligands as a function of the antibody concentration for different antibody-receptor binding strengths, for different sets of parameters. The parameters for each curve are given in Table 1 with the corresponding number.

TABLE 1.

Parameters of the curves given in Fig. 11

Curve	Ea	Eb	nt	ρr	sc
1	5	15	0.1	0.5	0.15
2	5	15	0.1	0.5	0.25
3	5	15	0.01	0.5	0.15
4	5	15	0.01	0.5	0.05
5	1	15	0.1	0.5	0.15
6	1	15	0.1	0.1	0.15
7	1	20	0.1	0.1	0.15

The number in the first column corresponds to the number indicating a curve in the graph.

The analysis of the calculated data shows that the relation 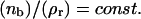is valid for the entire range of antibody concentrations and allows the prediction of the number of bound ligands if data for an analogous system are available. The scaling law with respect to the total fraction of ligands 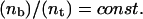in the vesicle is, however, correct only in the linear regime of Fig. 11.

DISCUSSION AND SUMMARY

We have demonstrated that the adhesion strength of soft shells mediated by specific (lock-and-key) forces can be modulated, in a dose-dependent manner, by the action of a ligand antagonist (in the form of an antibody). As the two theoretical models developed herein are able to rationalize both unbinding processes observed in our experiments, we can be reasonably confident that the main physical aspects of the problems are well accounted for. Particularly striking is the agreement between the theoretical predictions (Fig. 10) for the dependence of the number of ligand-receptor bonds on the concentration of the antibody solution, and the observed behavior of the vesicle (Fig. 5). In the latter figure, the area of the patch is presented as a function of the mass concentration of antibodies. Due to difficulties in determining the surface coverage, it is hard to determine the exact number of bonds within the patch. However, as the coverage is uniform on the micrometer length scale, the number of bonds must be proportional to the patch area on the same scale. Furthermore, as mass concentration is evidently proportional to the volume concentration of the antibodies in the solution, the excellent qualitative agreement between the theoretical approach and the presented experiments is clearly visible. In both cases, as the concentration of antibodies is increased, an initial rapid loss of bonds is followed by a much slower regime for bond detachment.

The experimental method of vesicle unbinding by antibody titration, supported by the theoretical models provides a useful technique for determining important properties of the system. First, the antagonist titration experiments are useful to visualize the formation or dissolution of adhesion microdomains. The adhesion model in the absence of antibodies should provide information concerning the ligand-receptor binding strength and the gain in the effective adhesion strength, also called spreading pressure of the vesicle (3,31). Although it is not possible to exactly define the required quantities (such as density of receptors) with this experimental setup, the utility of the approach can nevertheless be demonstrated for the vesicle in Fig. 2 by considering a relatively large range for each quantity and assuming that every receptor in the adhesion patch is, before titration, bound to a ligand. Thus, by assuming a radius of gyration of the ligand between 3.5 and 4.5 nm, with 3000–4000 receptors on 1 μm² of the substrate surface, Eq. 1 provides an estimate of the sLex-E-selectin binding strength of 2–6 k_BT. This value is of the same order of magnitude as the binding strength between P-selectin and cell-surface molecules exposing polypeptide headgroups with sLex side chains. In addition, unbinding forces of 4–5 k_BT for a single P-selectin-sLex bond were recently measured with force spectroscopy (28,44). Our result is useful in the sense that it clearly demonstrates that the theory developed herein certainly provides the correct order of magnitude for the binding strength of a single bond.

The theoretical description of vesicle deadhesion provides a method for determining several other important parameters of the system. In the case that the ligand-receptor binding strength is successfully determined, the binding strength of the inhibitor can be found. If the antibody-receptor binding strength is known, deadhesion can also be used as an alternative approach for determining the ligand binding strength and the spreading pressure of the vesicle. By choosing both a ligand and an antibody with known binding strengths, the quality of the receptor coverage could also be probed. However, the range of the above estimates for the binding strengths and the coverage in these experiments is too large to result in well-defined predictions. Though further elaboration would be clearly desirable, this work provides the foundation for systematic experimental measurements of the binding strengths of both antagonists and ligands.

Using the same estimates for the surface coverage as above, Eq. 3 provides the spreading pressure of the order of 10⁻⁵ Nm⁻¹, which is in agreement with the state of strong adhesion observed in Fig. 2. The analysis of the experimental data obtained for the vesicle from Fig. 2 by the use of an independent technique for the evaluation of the average adhesion strength (from the reconstruction of the vesicle height profile at the edge of the contact zone (39)) suggests that the spreading pressure of the vesicle in equilibrium at the beginning of phase I is less than the one evaluated from the equilibrium at the end of phase I. The theoretical model (31), clearly shows that the spreading pressure of the vesicle (e.g., average adhesion strength) is always increasing with a decreasing size of the contact zone (see Fig. 7 A). This is essential to balance an additional lateral pressure induced by titration of antibodies. As a new equilibrium is experimentally observed (end of phase I), one may conclude that at least qualitative agreement between the models and the experimental data is obtained.

The above result is interesting in the context of previous measurements of the receptor-ligand binding strength based on the observation of unbinding by pulling vesicles with magnetic tweezers. The forces measured by this technique were systematically much smaller then expected (45). Results of those experiments are consistent with the results presented herein for antibody-induced vesicle unbinding. Even low force can have large impact on the ensemble of bonds in the contact zone. Rather than providing the resistance to pulling typical for a single bond, bonds in the contact zone reorganize to increase the spreading pressure of the vesicle. In terms of antibody-induced unbinding, such reorganization results in the formation of new microdomains (see Fig. 3). This increased binding is typical for phase II, but has also been observed by the end of phase I, particularly for intermediate coverage (data not shown). Hence, the lateral pressure exhibited by antibodies, if not too strong, can actually stabilize the ligand-receptor mediated adhesion. This is simply the result of the balance between the entropy and the enthalpy of ligand-receptor binding.

Increased probability of ligand-receptor binding is also the reason why it is so hard to completely destroy the last remaining microdomains. This phenomenon manifests itself in the sigmoid tail present in both the experimental data (Fig. 5) and the theoretical model (Fig. 10). These data show that the presence of antagonists can clearly regulate the area in which the ligand-receptor binding occurs, strongly preferring formation of spatially localized multiple bonds between ligands and receptors.

This approach is not only a valuable tool in characterization of antagonist-induced unbinding of toy cells; it can also help to clarify the mechanisms of analogous processes in nature. For example, the role of elastase as a competitive binder in the process of deadhesion of polymorphonuclear leukocytes (30) can be related to the mechanisms characterized herein. Indications that the binding between the elastase and CD11b integrins in polymorphonuclear neutrophils occur have recently been suggested (46). Although, no reliable proof is yet available, it could be anticipated that the role of the elastase recognized in vitro will be related to its role in vivo. In a similar fashion, the integrin receptors of type α_Vβ₃ in endothelial cell are known to bind selectively to fibronectin coupled to the inner wall of the blood vessels. The fibronectin mediated adhesion can be counteracted by other molecules of the extracellular matrix such as hyaluronic acid. This giant polysaccharide is well known to inhibit tight adhesion by binding to the cell surface of mesenchyme cells through lectin-analog cell-surface receptors CD44. The mechanisms for this interference in vivo are expected to be closely related to these in the model systems as identified and characterized herein.

In summary, the presented method is a stepping stone in the development of a new powerful method for systematic studies of the binding strength of cell-surface receptors to their conjugate ligands in the extracellular matrix, under bio-analog conditions. Alternatively, the method provides a means with which to measure binding forces between membrane-bound antibodies and antigens. It also demonstrates the regulative role that inhibitive binding can have on a specific interaction, and identifies the physical origin of the two deadhesion control mechanisms.

It is clear that this toy model devoid of actin cortices can only provide valuable insight into the primary step of the adhesion and deadhesion process such as the nucleation and growth of receptor clusters. On the other side methods have been developed that allow the reconstitution of cortices of entangled or cross-linked actin into giant vesicles (47) to generate more realistic mechanical models of cell envelopes. Further ramifications of that system would require adding proteins involved in the control of self-assembly of focal contacts such as talin and vinculin or proteins mediating the activity of these proteins (such as GTPases of the rho family). In this case it would be relatively easy to generate still primitive but active models of cell envelopes, which would allow us to study the control mechanisms of adhesion and deadhesion processes under new and very exiting bio-analogous conditions.

This work has been sponsored by Sonderforschungsbereich under program No. 563 C4 and by the Fonds der Chemischen Industrie. A.-S. Smith thanks the Hochschul- und Wissenschaftsprogramm (HWP II) for support.

APPENDIX A: ANALYSIS OF EXPERIMENTAL DATA

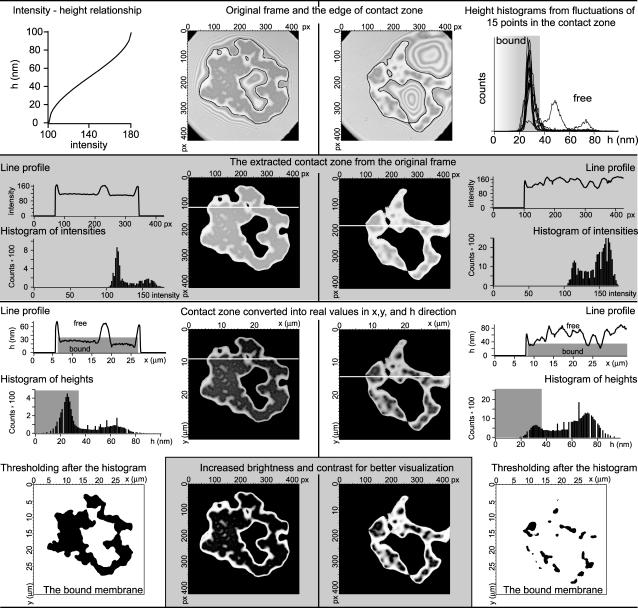
In this appendix we provide details of our data analysis. There are two important tasks, each requiring several steps, which must be accomplished to acquire relevant data. The first task is to define the contact zone in the collected pictures and translate it into real units. The second task is to determine the areas in the contact zone that are tightly bound to the substrate. The steps for both are somewhat interconnected and hence we summarize the procedure in Fig. 12.

FIGURE 12.

Schematic presentation of the data analysis procedure. Two frames, one from the beginning and one from the end of the deadhesion experiment, are analyzed in parallel. The procedure is presented in parallel for two frames. The scheme is organized in rows, alternating the white and gray background color of the row, each row representing a particular stage of the procedure. (First row) Graph where the intensity of the gray color is correlated to the height above the substrate (left). Original frames are shown with the outline of the edge of the contact zone (middle). Histogram of heights constructed from the analysis of the dependence of the height of the membrane in 15 different points in the contact zone (right). The area shaded in gray denotes the heights that are associated with the bound membrane and provides the cutoff for the bound state. (Second row) Extraction of the contact zone (the 100 nm closest to the substrate). The resulting frames are presented in the middle. On the sides, the profiles of the lines that are marked on the frames are shown. The histogram of intensities presented exactly for the resulting frames is also given. Note that the range of gray colors in these histograms is the same as the range of intensities that are transformed into heights (first row, left). (Third row) Frames resulting from the height transformation according to the graph in the first row, left. Corresponding line profiles and height distributions are given. Note that the transformation uses now all 255 colors, but it is not changing the shape of the line profile nor the histogram. Gray areas in the graph are representing the bound part of the membrane. The upper boundary of these areas corresponds to the same cutoff height (37 nm) as determined from the membrane fluctuation analysis (first row, right). (Last row, sides) Extraction of the strong adhesion by the imposition of a threshold upon the frames from the fourth row at 37 nm. (Last row, middle) For better visualization of the contact zone, the brightness and the contrast of the frames from the fourth row is performed. For details, see text.

The planar distance (x and y) are, in raw data, given in pixels. The conversion to real units is trivial by use of the scale bar. The vertical dimension (h) is given by the intensity of the gray color. The diffraction pattern is such that the interference closest to the substrate appears in the darkest color and is set to be the zero height. This is because the lipid bilayer height above the substrate is small compared to the wavelength. The simple theory that considers only light that enters the sample in the direction normal to the plane of the substrate provides a cosine law between the intensity of the gray color and the distance from zero height (48). This approach gives surprisingly good results for relative height differences <100 nm and permits precise shape reconstructions up to 800 nm. The interference pattern displays a periodic series of constructive and destructive interference that results in the height difference between an adjacent interference minimum and maximum of Δh = λ/4n = 101.9 nm (λ = 546.1 and is the wavelength of the incident light; n = 1.34 and is the refractive index of the buffer).

To determine a law that maps the intensity of the gray color to the height, first a histogram of intensities must be determined for a typical frame. Examples of such histograms can be found in the second row of Fig. 12. It is evident that only a certain interval of intensities appears in a given set of data (in the case of the presented vesicle, only intensities between 100 and 180 out of 255 appear). It is on this interval that an inverse cosine transformation must be performed to obtain the height, as presented in the top left corner in Fig. 13. If one would be determining the heights >100 nm, the periodicity of the cosine function should be taken into account. However, we restrict our discussion to the heights <100 nm where the important events in our experiments take place.

FIGURE 13.

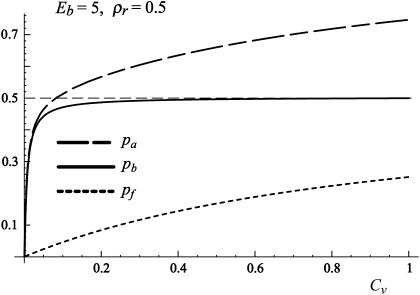
Coverage of the surface by antibodies as a function of the antibody concentration in the solution C_v. At low concentrations of antibodies in the solution p_f is considerably smaller than p_b. As the C_v increases, p_b saturates to ρ_r indicating that all the receptors on the surface are bound with antibodies.

As the contact zone is defined as the area of the vesicle that is most proximal to the substrate, we extract the contact zone by finding the first bright rim (height of 100 nm). That is a relatively simple task that can be performed by any image analysis program. Two examples of such edges are presented in the top row of Fig. 12, where they overlay frames from the beginning of the deadhesion process and from the end of the experiment, respectively. Once the edge of the contact zone is defined, the remaining information from higher layers is discarded (second row of Fig. 12).

It is now that the conversion from intensities to height can be performed (see third row in Fig. 12), and fulfill the first task. After the mapping, all 255 colors are used, and hence, stronger contrast is obtained in the contact zone. This can be clearly seen by comparing the histograms of intensities to the histograms of heights (second and third row in Fig. 12, respectively). A similar conclusion can be obtained by comparing the relevant line profiles, also presented in the second and third row of Fig. 12.

To determine which part of the membrane is strongly adhered to the substrate, the fluctuation analysis of the contact zone had to be performed. In this respect, the height fluctuations in time are measured during the adhesion and deadhesion processes for 15 points (squares of 6 × 6 pixels to decrease the influence of noise), uniformly distributed over the contact zone. Typical examples of such dependence can be seen in Figs. 1 and 3. From the dependence of height on time, it is possible to construct a histogram of heights for each point (top right corner graph in Fig. 13 is the overlay of results for all 15 points). It is clear that the bound state possesses a certain width imposed by the fluctuations. For the chosen set of data, if a given point experienced strong adhesion, a Gauss-like peak typically appears in the histogram with a maximum around 26 nm. The intensity of the peak certainly depends on the relative time that the given point has spent in the state of strong adhesion. For example, if the point has never been strongly adhered, the peak will not be evident in the histogram at all. We choose to define strong adhesion if the height of the membrane is below 37 nm (shaded gray in the histograms in Fig. 12). Although such a choice is somewhat arbitrary, it is made after realizing that all well-defined isolated peeks (analysis of only the times while the point is strongly adhered), have a maximum with the deviation of +3σ below 37 nm. This choice is consistently maintained for all analyses of the sample.

The imposition of a threshold in the histogram of heights at h = 37 nm provides the pictures in the bottom corners of Fig. 12. By counting the black pixels in these frames, it is possible to build the dependence of the strongly adhered membrane as a function of time or other relevant parameters such as the concentration of antagonist inducing the deadhesion (Fig. 5). Sometimes, for the purpose of clarity (but not for quantitative data analysis), it is possible to increase the contrast and the brightness in the pictures. In such a way, tight contacts are easy to observe by eye. Such a procedure has been used for the construction of frames in the middle of the bottom row in Fig 13, but also for the construction of the second row in Fig. 2 as well as for the entire Fig. 3. In the latter, again for visualization purpose, the gray 255 intensity scale was replaced by a red or blue 255 intensity scale, in a simple consecutive manner starting by replacing the darkest gray with the darkest red (or blue).

Discussion of errors

There will be several contributions to the errors in acquired data for the area of strong contact. The most obvious error is related to the definition of the cutoff for the height at which specific adhesion occurs. However, as long as all data are analyzed with the same cutoff, the functional dependence of the area of strong contact with time or other parameters will not be influenced. Rather a vertical shift in the data will be obtained as a first-order influence.

The size of the contact has a second order influence. The procedure of finding an edge or imposing a threshold results in an error that is proportional to the ratio of the circumference to the area of the contact. Due to the irregular shape of the contacts, large areas are generally favored. Furthermore, when the vesicle is relatively tense, the amplitudes of fluctuations of free membrane are lower, resulting in a very well-defined peak for the bound state (see the histograms of height in the third row of Fig. 12). Then, the distinction between the free and bound membrane is clear. However, such situations are usually attributed to large contact zones and large areas of strong contact. When the area of strong contacts becomes small, then the fluctuations of the free membrane increase in amplitude, often approaching the substrate without making a specific bond. As a result the shape of the peak that belongs to the bound state is blurred around the cutoff (histograms on the right side of the third row in Fig. 12).

One additional effect can be observed when comparing the line profiles for large and small areas of strong contact (left- and right-hand graphs in the third row of Fig. 12, respectively). For large contact zones, the bound part of the membrane is well below 37 nm (in profiles seen as the edge of gray areas). At small contact zones the entire profile is lifted, due to fluctuations of the free membrane to higher values and the regions of strong contact only barely penetrate below 37 nm, possibly indicating a stretching of the bonds. The provided analysis is not able to account for such fine details of the deadhesion process.

Last but not least is certainly the question of proportionality of the area to the number of formed bonds. At this stage there is no technique that would allow us to directly measure the number of formed bonds. However, extensive analysis of membrane fluctuations in the contact zone made us confident that the density of receptors on used substrates is sufficiently large and uniform so that the proportionality between the bound membrane and number of bonds is preserved, at least to the first order of magnitude.

APPENDIX B: PHASE I, THE QUANTITATIVE ANALYSIS

The free energy (in units of k_BT) of antibodies per unit surface area (area of a site) covered by receptors consists of the binding enthalpy and the mixing entropy terms for the antagonist absorbed on a receptor site and a free site:

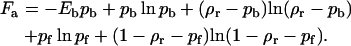(8)

Minimizing the free energy and solving dF/dp_b = dF/dp_f = μ results in p_b, and p_f given in Eq. 5. The result of such a procedure is shown in Fig. 13.

When E_b is small and ρ_r < 0.5, p_f is the dominant contribution. At large E_b, as well as at high coverage, p_f can be omitted from p_a as it is much smaller than p_b. However, it is important to note that, for fixed concentrations of both antibodies and receptors, p_a varies from zero to its maximum value in range of 0 < E_b < 20 k_BT. Further increases in binding strength do not significantly influence the number of bound antibodies on the substrate. For typical concentrations C_v < 0.1 and large antibody-receptor binding strengths, the density of antibodies on the substrate saturates (p_a → ρ_r). In this regime, antibodies occupy all of the receptors on the surface. An increase of C_v above concentrations of 0.1, leads to significant contributions of antibodies not bound to receptors but adsorbed on the surface p_f. However, such high densities of antibodies should be avoided in an experiment because they induce considerable changes in the reduced volume of the vesicle. In addition, in this limit, the description of absorption by Langmuir isotherms fails to provide accurate results.

The lateral pressure of antibodies Π is by definition the gain in the free energy when the system increases its surface area for the area of of a unit site (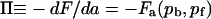). Substituting Eq. 5 and into Eq. 8 upon reorganizing results in the antibody lateral pressure given by Eq. 6.

Finding the limit of Eq. 6 when E_b → 0, one obtains that the lateral pressure becomes independent of the concentration:

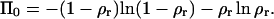(9)

In the case of a fixed concentration (left panel in Fig. 14), the shape of the curve is determined by the first two terms on the right-hand side of Eq. 6. Moreover, in the regime of large binding strengths (E_b > 10), the antibody lateral pressure can be approximated by:

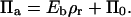(10)

FIGURE 14.

The lateral antibody pressure as a function of the antibody-receptor binding strength (left) as a function of the concentration (right). Other parameters are kept constant and used as indicated. The onset value Π₀ and the saturation value Π_s as well as the asymptotic solution Π_a are indicated with dashed lines.

On the other hand, for a fixed antibody binding strength, the lateral antibody pressure reaches saturation with increasing the concentration (right panel in Fig. 14). In the case of large binding strengths this saturation value is:

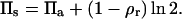(11)

Hence, in case of low antibody binding strength, it is possible that 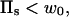and that increasing the antibody concentration does not result in the unbinding of the vesicle. However, in the regime of experimentally relevant concentrations of antibodies the lateral pressure is changing rapidly and small changes in the concentrations can induce a large impact on the size of the contact zone.

APPENDIX C: PHASE II, THE CONSTRUCTION OF THE FREE ENERGY

In a manner analogous to that used for modeling adhesion in the absence of antibodies (31), the number of conformations of antibodies and ligands over sites of the substrate in the contact zone occupied and unoccupied by receptors is found to be:

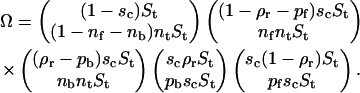(12)

It is this number of conformations that is determining the entropy of the vesicle-antagonists-substrate system. Furthermore, the binding of both the antibodies and the ligands to the receptors contributes to the internal energy. This leads to a total free energy in units of k_BT for a finite vesicle with a constant size of the contact zone:

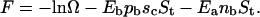(13)

For the fixed size of the contact zone (s_c) this free energy must be minimized. Henceforth, the equations dF/dp_b = dF/dp_f = lnC_v are solved simultaneously with dF/dn_b = dF/dn_f = 0, to obtain the results given by Eq. 7 and in Figs. 9 and 10.