Abstract
The absence of the PsaC subunit in the photosystem I (PSI) complex (native PSI complex) by mutagenesis or chemical manipulation yields a PSI core (P700-FX core) that also lacks subunits PsaD and PsaE and the two iron-sulfur clusters FA and FB, which constitute an integral part of PsaC. In this P700-FX core, the redox potentials (Em) of the two quinones A1A/B and the iron-sulfur cluster FX as well as the corresponding protonation patterns are investigated by evaluating the electrostatic energies from the solution of the linearized Poisson-Boltzmann equation. The B-side specific Asp-B558 changes its protonation state significantly upon isolating the P700-FX core, being mainly protonated in the native PSI complex but ionized in the P700-FX core. In the P700-FX core, Em(A1A/B) remains practically unchanged, whereas Em(FX) is upshifted by 42 mV. With these calculated Em values, the electron transfer rate from A1 to FX in the P700-FX core is estimated to be slightly faster on the A1A side than that of the wild type, which is consistent with kinetic measurements.
INTRODUCTION
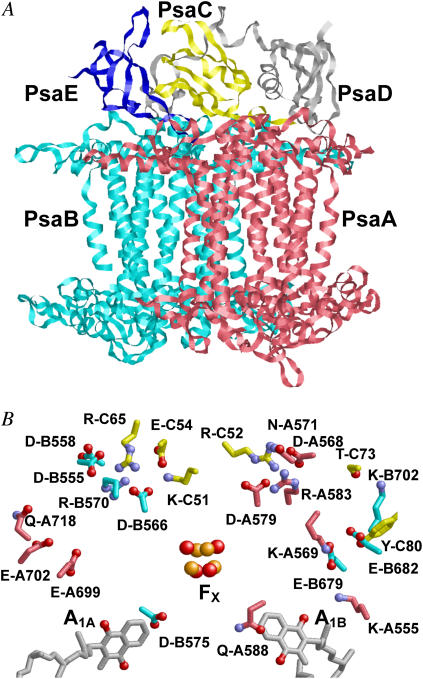
The x-ray crystal structure of Photosystem I (PSI) from Thermosynechococcus elongatus at 2.5 Å resolution (1) solved the riddle of the microscopic structure of this protein-pigment complex located in the thylakoid membrane. The central part of PSI is composed of two homologous membrane integral subunits, PsaA and PsaB (Fig. 1 A). The two homologous chains harbor as redox-active cofactors a dimer of chlorophyll a (Chla, P700), two accessory Chla, (A−1), two additional distant Chla (A0), two phylloquinones (phyllo-Q, A1), and one iron-sulfur cluster (FX). The stromal extrinsic subunit PsaC contains two additional iron-sulfur clusters (FA and FB). Similarly to bacterial photosynthetic reaction centers (RC), these six Chla and two phyllo-Q cofactors are arranged in two branches (A and B) in pseudo C2 symmetry with the rotation axis passing through P700 and FX. The axially located P700 and FX, in turn, are connected by the two chains of redox-active cofactors A−1A/B, A0A/B, and A1A/B.
FIGURE 1.
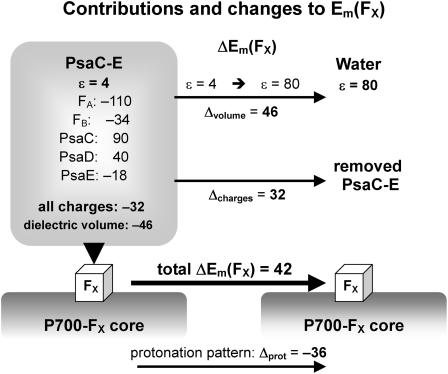
(A) Location of PsaA, PsaB, PsaC, PsaD, and PsaE subunits (displayed in pink, cyan, yellow, gray, and blue, respectively). (B) Selected residues of the interface of PsaC binding to the PsaA/PsaB heterodimer. Residues discussed in the text and Table 1 are displayed with ball and stick, in red (PsaA), blue (PsaB), and yellow (PsaC).
Subunit PsaC is largely similar to ferredoxins that contain two Fe4S4 clusters. To test the functional role of this subunit, a PSI mutant lacking subunit PsaC (P700-FX core) is studied in this work. A consequence of the P700-FX core preparation is not only the absence of PsaC, which contains the two iron-sulfur clusters FA and FB, but also the lack of PsaD and PsaE; these two subunits are in close contact with PsaC and bind to PsaA/PsaB only after PsaC is bound. A P700-FX core can be generated either chemically i), by urea treatment (urea-treated PSI) (2–5) or genetically in two ways by deleting ii), the psaC gene (psaC− PSI) (4,6), or iii), the rubA gene (rubA− PSI) (7,8). The latter leads to a P700-FX core in which FX is initially absent but can be later reconstituted. If not otherwise specified, we name all three differently generated incomplete PSI protein complexes “P700-FX cores” in this study. Despite the deletion of the subunit PsaC in the neighborhood of FX, the measured electron transfer (ET) rate from A1 to FX remains essentially unchanged (180 ns by ultraviolet-visible (UV-VIS) spectroscopy (9) or 190 ns by electron paramagnetic resonance (EPR) (10) in urea-treated PSI) relative to the native PSI complex, where the corresponding time constant was between 206 ns and 355 ns (11–16).
Here, we present the calculated Em(A1A/B) values for the P700-FX core as we presented in our previous work for the native PSI complex (17). The shift of calculated Em(FX) in the P700-FX core versus the corresponding value in the native PSI complex is also correlated with corresponding ET rates measured on P700-FX cores generated by urea treating of PSI (9,10). To investigate the electrostatic binding interaction between the PSI subunits, we present the calculated pKa values for residues in the binding interface or, if needed, we constrain the protonation probability of specific residues whose charge state was considered to be significant for PsaC binding (4,18) and monitor the resulting changes in protonation pattern. With this simple method, we obtain information on the electrostatic interaction of binding the PsaC subunit to the PsaA/PsaB heterodimer.
A key question for PSI research is the role of partial negative charges on the Em of the cofactors involved in light-induced charge separation and thus in control of functional properties. In particular, the nominal negative charge of the Fe4S4 clusters can directly contribute to the Em shift of the cofactors that precede it in the ET chain, such as A1, as recently demonstrated computationally (17) and experimentally (19,20). Selective removal of particular Fe4S4 clusters is a feasible experimental approach, which is pursued here computationally.
MATERIALS AND METHODS
Coordinates
For our computations, we used the crystal structure of trimeric PSI from T. elongatus at 2.5 Å resolution (Protein Data Bank; 1JB0) (1).
The crystal structure of the P700-FX core is yet not available. In the model of the P700-FX core, the subunits PsaC, PsaD, and PsaE were removed together with the iron-sulfur cofactors FA and FB, which are embedded in PsaC. It has been established in vitro that PsaC can be rebound to the P700-FX core without the need for ATP hydrolysis and without the need of chaperones (6,21). It has also been suggested from urea-treated PSI that the P700-FX core represents the intact PSI core and retains >90% of FX with little deterioration of the RC (2), because the binding contacts between PsaC and the PsaA/PsaB heterodimer are mainly electrostatic in nature (1,18,22). EPR data show that structural and kinetic properties of the A1 site remain identical within experimental accuracy for the P700-FX core and the native complete PSI complex (10). The structural model used for the P700-FX core in this study is, therefore, the best starting point and in part justified by experimental evidence.
For both the P700-FX core and the native PSI complex, the atomic coordinates were treated as in previous work (17). In the crystal structure, hydrogen atom positions were energetically optimized with CHARMM (23). During this procedure the positions of all nonhydrogen atoms were fixed; all titratable groups were kept in their standard protonation state, i.e., acidic groups were ionized and basic groups were protonated. The six Chla and the two phyllo-Q were kept in the oxidized neutral charge state. Analogous to the wild-type PSI, one specific crystal water (HOH-37) was also considered for the P700-FX core (17). This water molecule forms an H bond with one of the acidic oxygens of Asp-B575 that was found to change its protonation state coupled with the redox states of A1A/B as discussed later. If not otherwise stated, the results refer to computations that include this crystal water.
Atomic partial charges
Atomic partial charges of the amino acids were adopted from the all-atom CHARMM22 (24) parameter set. The charges of acidic oxygens were both increased symmetrically by +0.5 unit charges to account implicitly for the presence of the proton. Similarly, instead of removing a proton in the deprotonated state, the charges of all protons of the basic groups of arginine and lysine were diminished symmetrically by a total unit charge. For residues whose protonation states are not available in the CHARMM22 parameter set, appropriate charges were computed (25). For the cofactors, the same atomic charges as in our previous computation (17) were used. We considered FX, FA, and FB in the oxidized charge state [Fe4S4(SCH3)4]2– for the native PSI complex (26). To obtain the shift of Em(FX) between the native PSI and the P700-FX core, we considered [Fe4S4(SCH3)4]2–/3– for the oxidized/reduced state of FX (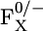 ). As in previous computations (17), a positive unit charge was located on the B-branch Chla of the P700 dimer (P700B), according to electron nuclear double resonance (ENDOR) and electron spin echo envelope modulation (ESEEM) studies (27–30).
). As in previous computations (17), a positive unit charge was located on the B-branch Chla of the P700 dimer (P700B), according to electron nuclear double resonance (ENDOR) and electron spin echo envelope modulation (ESEEM) studies (27–30).
Computation of protonation pattern and redox potential
Our computation is based on the electrostatic continuum model by solving the linearized Poisson-Boltzmann (LPB) equation with the program MEAD (31). The protonation patterns were sampled by a Monte Carlo (MC) method with our own program Karlsberg (32). The dielectric constant was set to ɛP = 4 inside the protein and ɛW = 80 for water as done in previous computations (for instance, Ishikita and Knapp (17)). All computations refer to pH 7.0 at 300 K and an ionic strength of 100 mM. The LPB equation was solved using a three-step grid-focusing procedure with 2.5 Å, 1.0 Å, and 0.3 Å resolution. The MC sampling yields the probabilities [Aox] and [Ared] of the redox states of compound A.
The Em was calculated from the Nernst equation. To minimize the statistical error in evaluating the Em, a bias potential was applied to obtain an equal amount of both redox states ([Aox] = [Ared]), yielding the value of the bias potential as the resulting Em. For convenience, the computed Em are given with mV accuracy, without implying that the last digit is significant. To obtain the absolute value of Em in the protein, we calculated the electrostatic energy difference between the two redox states of phyllo-Q in the protein and a reference model system where the experimental redox potential is known. The shift of the Em in the protein relative to the reference system was added to this experimental value. As a reference model system, we used the Em(phyllo-Q) of −463 mV versus NHE (normal hydrogen electrode) for one-electron reduction in DMF solution (33) as was done in the previous study (17).
We can calculate pKa values for titratable residues using two different pKa definitions. In a straightforward approach, a titratable residue is biased by an individual energy term to be 50% protonated, whereas the protonation states of the other titratable residues are fully relaxed at a fixed pH (pH 7 in this study). This bias energy can be used to define the pKa of this residue (Henderson-Hasselbalch pKa). This pKa describes how much energy is needed to change the protonation state of this residue in its protein environment where the protonation pattern changes locally by equilibration due to the charge change of this residue without involving changes of solvent pH. This pKa definition is, for instance, useful to describe the energetics of the adiabatic proton transfer processes between different titratable groups. The protonation dependence of the considered titratable residue obeys the Henderson-Hasselbalch equation (equivalent to the Nernst equation for a redox-active group) as a function of the bias energy.
Another approach to determine pKa values is to calculate it from the protonation pattern of all titratable residues as a function of solvent pH for a large pH range. Here, the pKa of the titratable residue under consideration can be defined as the pH value where this residue is to 50% protonated [effective pKa]. This is a more common pKa definition and corresponds to the conditions where pKa values of titratable groups in proteins are determined experimentally. When the molecular system contains only a single or several noninteracting titratable groups, the same pKa values are computed for both definitions.
In a region rich in titratable residues, it is often hard to give a specific single value for the effective pKa if one observes only a moderate protonation change over a wider pH range. In this study, we calculated pKa values as Henderson-Hasselbalch pKa at pH 7.0 as in previous studies (34,35), whereas protonation probabilities are computed by coupling solvent pH at pH 7 to all titratable residues and not by using a bias energy term. Protonation probabilities obtained in this way qualitatively relate to the pKa definition effective pKa. But, there is no quantitative correspondence between these protonation probabilities and pKa derived from the simple Henderson-Hasselbalch relation because of possible strong electrostatic coupling between different titratable residues (for further discussions about the difference between the Henderson-Hasselbalch and the effective pKa, see Supplemental discussion). Note that we do not consider possible structural changes of a protein upon pH changes. Such structural changes may occur more prominently in protein regions containing clusters of titratable residues.
Estimation of the ET rate
We estimated the ET rate from A1 to FX based on the values of Em(A1) and Em(FX) by evaluating the following empirical rate expressions (36). They describe ET processes at T = 300 K, which are downhill in energy (exergonic)
 |
(1) |
or uphill in energy (endergonic)
 |
(2) |
where R (>3.6 Å) is the edge-to-edge distance, ΔG the Em difference of the participating electron donor and acceptor groups, and λ the reorganization energy. In these rate expressions, the energy parameters (ΔG and λ) are given in units of eV and the distances (R) in units of Å. The edge-to-edge distance R of donor (A1) and acceptor group (FX) is R = 6.8 Å, identical in both A1A and A1B sides, as taken from the crystal structure (1).
RESULTS AND DISCUSSION
Role of the specific protonation pattern in the P700-FX cores
Redox states A1B0/− influencing Glu-B682
Fourier transform infrared (FTIR) spectroscopic studies indicated that one glutamate was perturbed upon formation of 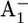 in wild-type PSI. As possible candidates, glutamates A699, A702, B679, and B682 were proposed (37). The pairs of symmetry-related glutamates Glu-A702/Glu-B682 and Glu-A699/Glu-B679 are located in equivalent positions in the A- and B-branches, respectively. In our previous study of the wild-type PSI, we found that among these glutamates only Glu-B682 showed a small but notable increase in protonation (protonation state of 0.15 H+) with the formation of
in wild-type PSI. As possible candidates, glutamates A699, A702, B679, and B682 were proposed (37). The pairs of symmetry-related glutamates Glu-A702/Glu-B682 and Glu-A699/Glu-B679 are located in equivalent positions in the A- and B-branches, respectively. In our previous study of the wild-type PSI, we found that among these glutamates only Glu-B682 showed a small but notable increase in protonation (protonation state of 0.15 H+) with the formation of 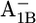 (17), whereas this residue was fully ionized in the
(17), whereas this residue was fully ionized in the 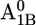 state. Concerning
state. Concerning 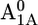 and these glutamates, the pKa calculated for Glu-B-682 is significantly higher for both redox states than those of the other three glutamates (Table 1). A comparison between the symmetry-related pairs of glutamates reveals that Glu-A699 and Glu-B679 possess similar pKa values, whereas the pKa of Glu-A702 and Glu-B682 show a significant difference. The latter indicates that the electrostatic environment of these symmetry-related glutamates belonging to the A- and B-branches is asymmetric. Related to this difference, we found an asymmetry of the corresponding protein conformations in the immediate vicinity. The backbone nitrogen of Lys-B551 is at a distance of only 2.9 Å from the acidic oxygen of Glu-A702, stabilizing its ionized state by this H bond and thus rendering Glu-A702 very acidic. The symmetry-related residue to Lys-B551 is Arg-A564. In contrast to Lys-B551 the backbone nitrogen of Arg-A564 is at a distance of 3.9 Å from the acidic oxygen of Glu-B682, which is too far to barely form an H bond. As a consequence the pKa of Glu-B682 is calculated to be significantly higher than that of Glu-A702 (Table 1), the former being close to the reference value of 4.4 in aqueous solution.
and these glutamates, the pKa calculated for Glu-B-682 is significantly higher for both redox states than those of the other three glutamates (Table 1). A comparison between the symmetry-related pairs of glutamates reveals that Glu-A699 and Glu-B679 possess similar pKa values, whereas the pKa of Glu-A702 and Glu-B682 show a significant difference. The latter indicates that the electrostatic environment of these symmetry-related glutamates belonging to the A- and B-branches is asymmetric. Related to this difference, we found an asymmetry of the corresponding protein conformations in the immediate vicinity. The backbone nitrogen of Lys-B551 is at a distance of only 2.9 Å from the acidic oxygen of Glu-A702, stabilizing its ionized state by this H bond and thus rendering Glu-A702 very acidic. The symmetry-related residue to Lys-B551 is Arg-A564. In contrast to Lys-B551 the backbone nitrogen of Arg-A564 is at a distance of 3.9 Å from the acidic oxygen of Glu-B682, which is too far to barely form an H bond. As a consequence the pKa of Glu-B682 is calculated to be significantly higher than that of Glu-A702 (Table 1), the former being close to the reference value of 4.4 in aqueous solution.
TABLE 1.
Calculated pKa values of residues for the native PSI complex and the P700-FX core in the 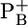 state
state
| Residues of PsaA | Redox state* | Native PSI | P700-FX core | Residues of PsaB | Redox state* | Native PSI | P700-FX core |
|---|---|---|---|---|---|---|---|
| Asp-A568 | 3.9 | 4.7 | Asp-B555 | 4.1 | 5.6 | ||
| (Asn-A571)† | Asp-B558 | 8.5 | 5.7 | ||||
| Asp-A579 | −0.3 | 2.0 | Asp-B566 | −4.8 | 3.3 | ||
| Arg-A583 | 22.3 | 13.6 | Arg-B570 | 21.3 | 15.5 | ||
| (Gln-A588)† | Asp-B575 | 5.2 | 4.7 | ||||
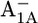 |
8.7 | 7.9 | |||||
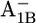 |
7.2 | 6.9 | |||||
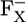 |
9.2 | 8.2 | |||||
| Glu-A699 | −2.6 | −2.4 | Glu-B679 | −4.2 | −4.3 | ||
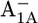 |
−2.7 | −2.4 | 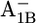 |
−3.8 | −3.9 | ||
| Glu-A702 | −1.3 | 2.6 | Glu-B682 | 4.7 | 5.2 | ||
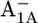 |
−1.3 | 2.8 | 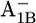 |
6.2 | 5.9 | ||
| (Gln-A718)† | Lys-B702 | 16.4 | 10.0 |
If no redox state is indicated, all redox active cofactors are in the neutral charge state except for 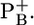
Nontitratable residue in PsaA, which is symmetry related to a titratable residue in PsaB.
In the P700-FX core environment around  Glu-B682 is slightly more ionized (protonation 0.08 H+) than in the native PSI complex. In the P700-FX core, the quartet of glutamates appears on the protein surface, stabilizing the deprotonated state. At the same time, the solvent exposure, especially of Glu-B682, shields the charge influence from A1B, thus reducing the pKa difference between the two redox states
Glu-B682 is slightly more ionized (protonation 0.08 H+) than in the native PSI complex. In the P700-FX core, the quartet of glutamates appears on the protein surface, stabilizing the deprotonated state. At the same time, the solvent exposure, especially of Glu-B682, shields the charge influence from A1B, thus reducing the pKa difference between the two redox states 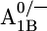 from 1.5 in the native PSI complex to 0.7 in the P700-FX core (Table 1).
from 1.5 in the native PSI complex to 0.7 in the P700-FX core (Table 1).
Asp-B575 influenced by the redox states A1A/B0/− and FX0/−
In the native PSI complex, Asp-B575 in the neighborhood of A1A changes its protonation state in response to the formation of 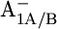 (17). The symmetry counterpart of Asp-B575 in PsaB is the nontitratable residue Gln-A588 in PsaA. This Gln-A558/Asp-B575 pair is highly conserved from cyanobacteria to higher plants. One of the acidic oxygens of Asp-B575 is H-bonded to the crystal water HOH-37 as a part of a larger water network located between the cofactors A1A/B and FX, which apparently displays a PsaA/PsaB asymmetry (1). In the P700-FX core, upon formation of
(17). The symmetry counterpart of Asp-B575 in PsaB is the nontitratable residue Gln-A588 in PsaA. This Gln-A558/Asp-B575 pair is highly conserved from cyanobacteria to higher plants. One of the acidic oxygens of Asp-B575 is H-bonded to the crystal water HOH-37 as a part of a larger water network located between the cofactors A1A/B and FX, which apparently displays a PsaA/PsaB asymmetry (1). In the P700-FX core, upon formation of 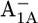 and
and 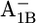 the protonation probabilities of Asp-B575 are 0.89 H+ and 0.27 H+, respectively, whereas this residue is fully ionized in the
the protonation probabilities of Asp-B575 are 0.89 H+ and 0.27 H+, respectively, whereas this residue is fully ionized in the 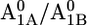 state. The similarity of the Asp-B575 protonation state between the P700-FX core and the native PSI complex (0.85 H+ for
state. The similarity of the Asp-B575 protonation state between the P700-FX core and the native PSI complex (0.85 H+ for 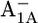 and 0.17 H+ for
and 0.17 H+ for 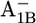 in the latter (17)) indicates that Asp-B575 is electrostatically also buried in the P700-FX core as deduced also from the crystal structure (1) for the native PSI complex. Hence, it is well shielded from the stromal surface of the PsaA/PsaB complex such that the influence of PsaC on Asp-B575 is small. As will be discussed later, the small decrease of protonation state of Asp-B575 by 0.10 H+ for
in the latter (17)) indicates that Asp-B575 is electrostatically also buried in the P700-FX core as deduced also from the crystal structure (1) for the native PSI complex. Hence, it is well shielded from the stromal surface of the PsaA/PsaB complex such that the influence of PsaC on Asp-B575 is small. As will be discussed later, the small decrease of protonation state of Asp-B575 by 0.10 H+ for 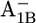 relative to the native PSI complex can partially contribute to the upshift of Em(A1B) in the P700-FX core.
relative to the native PSI complex can partially contribute to the upshift of Em(A1B) in the P700-FX core.
In this study on the P700-FX core, we additionally found that upon formation of 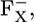 Asp-B575 is mostly protonated in both the native PSI complex and the P700-FX core (protonation states of 0.95 H+ and 0.94 H+, respectively). Indeed, the calculated pKa values for Asp-B575 are 9.4 (8.6) in the
Asp-B575 is mostly protonated in both the native PSI complex and the P700-FX core (protonation states of 0.95 H+ and 0.94 H+, respectively). Indeed, the calculated pKa values for Asp-B575 are 9.4 (8.6) in the 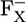 state, followed by 8.9 (8.3) in the
state, followed by 8.9 (8.3) in the 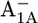 state, 7.4 (7.0) in the
state, 7.4 (7.0) in the 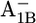 state, and 5.4 (5.1) in the neutral state (
state, and 5.4 (5.1) in the neutral state (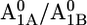 )of the native PSI complex (P700-FX core) (Table 1).
)of the native PSI complex (P700-FX core) (Table 1).
Analysis of protonation pattern changes on PsaC binding
Arg-C65
Arg-C65 participates in the H-bond network surrounding HOH-22. Its influence on the protonation pattern of titratable residues in its neighborhood is investigated by constraining it to be in the deprotonated charge state. In response to the deprotonation of Arg-C65, a dramatic change in protonation pattern is induced at Asp-B555 (0.00 H+ → 1.00 H+), Asp-B558 (0.97 H+→ 0.07 H+), and Glu-C54 (0.00 H+ → 0.23 H+) (Table 2). Arg-C65 is involved in the specificity of binding between PsaB and PsaC by forming at pH 7.0 simultaneously strong salt bridges with Asp-B555 (NArg–OAsp distance 3.0 Å) and Asp-B566 (NArg–OAsp distance 2.6 Å) (see also Table 3 of Antonkine et al. (18)). In contrast to Asp-B555, Asp-B566 is always ionized.
TABLE 2.
Changes in protonation pattern with forced deprotonation of residues Lys-C51, Arg-C52, and Arg-C65 in PsaC
| Deprotonated residue* | Affected residues | Protonation probability change |
|---|---|---|
| Lys-C51 | Glu-C54 | 0.00 → 1.00 |
| Arg-C52 | Asp-A568 | 0.00 → 1.00 |
| Arg-C65 | Asp-B555 | 0.00 → 1.00 |
| Asp-B558 | 0.97 → 0.07 | |
| Glu-C54 | 0.00 → 0.23 |
Protonation state of the residue was forced to change from 1.0 H+ to 0.0 H+ (deprotonation).
TABLE 3.
Rates kET of ET from A1 to FX in P700-FX core
| Redox potential [mV]
|
1/kET [ns]†
|
|||
|---|---|---|---|---|
| Em(A1) | Em(FX)* | Computation | Experiment | |
| A1A | −545 | −628‡ | 86¶ | 126**, 180–190†† |
| −608§ | 51¶ | |||
| A1B
|
−652
|
−628‡ | 7‖ | n.d. |
| −608§ | 6‖ | n.d. | ||
The corresponding lifetime 1/kET was estimated from the rate expressions, Eqs. (1) and (2), based on the computed redox potentials Em(A1) and Em(FX).
Calculated by adding the calculated shift of the Em(FX) between the native PSI complex and P700-FX core (42 mV) to the measured Em(FX) in the native PSI complex.
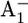 lifetime calculated with reorganization energy λ = 1.0.
lifetime calculated with reorganization energy λ = 1.0.
Based on the measured Em(FX) = −670 mV in the native PSI complex (3).
Estimated by Eq. 2.
Estimated by Eq. 1.
(5).
Lys-C51 and Arg-C52
Two double mutants, K(C51)S/R(C52)D and K(C51)S/R(C52)A, which did not prevent association of PsaC with PsaA and PsaB to the PSI complex, were originally constructed to test the influence of these two basic residues Lys-C51 and Arg-C52 on Em(FA/B) (38) (see also Golbeck (4)). On the other hand, from analysis of the crystal structure (18) it is evident that Lys-C51 forms salt bridges with Asp-B566 and Glu-C54, whereas Arg-C52 forms salt bridges with Asp-A568 and Asp-A579 (Fig. 1 B). Hence, although these central salt bridges that stabilize the association between PsaC and PsaA/PsaB are lost in those double mutants, there still exist the salt bridges between Arg-C65 and Asp-B555/Asp-B566, which may be sufficient to guarantee binding of a functional PsaC (4).
To investigate the influence of the basic residues Lys-C51 and Arg-C52 on the acidic residues serving as salt bridge partners, we force each of the two basic residues individually in the deprotonated state. Hereby, Asp-A568 becomes protonated upon deprotonation of Arg-C52, whereas all other acidic residues do not change their protonation state (including Asp-A579) and remain ionized (Table 2). This may suggest that Arg-C52 couples more strongly with Asp-A568 (NArg–OAsp distances of 2.8 Å and 3.2 Å) than with Asp-A579 (NArg–OAsp distances 2.8 Å and 3.1 Å), although the N–O distances in the two salt bridges are practically identical. The strongly ionized state for Asp-A579 is due to the proximity of Arg-A583 (closest NArg–OAsp distance 3.0 Å). The formation of salt bridges between them renders the pKa for Asp-A579/Arg-A583 extremely low/high, resulting in a pKa for Asp-A579 by 4 pH units lower than that of Asp-A568 (Table 1).
Enforced deprotonation of Lys-C51 results in protonation of the salt bridge partner Glu-C54 (Table 2), whereas no change of protonation state is observed for the other salt bridge partner, Asp-B566. This may be due to the simultaneous involvement of Asp-B566 in an intermolecular salt bridge with Lys-C51 and Arg-C65 (Fig. 1 B). In addition, Asp-B566 has an intramolecular salt bridge partner, Arg-B570 (closest NArg – OAsp distance of 2.7 Å). This strong intramolecular salt bridge stabilizes the ionized state of Asp-B566 enormously, i.e., even a simultaneous forced deprotonation of both Lys-C51 and Arg-C65 does not lead to a protonated Asp-B566.
In this study, the simultaneous deprotonation of both Lys-C51 and ArgC-52, which may mimic the K(C51)S/R(C52)A double mutant (38), results in protonation of Asp-A568 and Glu-C54. Clearly, the protonation of the former is due to the deprotonation of Arg-C52 and the latter to the deprotonation of Lys-C51. No additional changes of protonation pattern are observed compared with the corresponding changes resulting from deprotonation of Lys-C51 or of ArgC-52 alone given in Table 2. This indicates that the influence of the charge state of these residues is essentially localized at their salt bridge partners in contrast to the more delocalized H-bond network discussed above.
Protonation of Asp-B558 at the PsaC/D interface
In our computations for the native PSI complex, all aspartates are ionized except for Asp-B575 and Asp-B558. In particular, Asp-B558 is essentially protonated in native PSI for all cofactor redox states. The protonated state of Asp-B558 relates to a small cavity occupied by the crystal water HOH-22 (OAsp – Owater distance of 2.4 Å) (Fig. 1 B). Interestingly, the charge state of Asp-B558 changes dramatically from nearly protonated in the native PSI complex (0.97 H+ at pH 7 with pKa of 8.5 in the 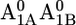 state) to nearly ionized in the P700-FX core (0.05 H+ at pH 7 with pKa of 5.7 in the
state) to nearly ionized in the P700-FX core (0.05 H+ at pH 7 with pKa of 5.7 in the 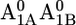 state). The calculated pKa of 5.7 for Asp-B558 in the P700-FX core is relatively close to the reference value of 4.0 in aqueous solution. This is evidently due to solvent contacts (Table 1), whereas in the native PSI complex Asp-B558 is subjected to interactions with a network of residues.
state). The calculated pKa of 5.7 for Asp-B558 in the P700-FX core is relatively close to the reference value of 4.0 in aqueous solution. This is evidently due to solvent contacts (Table 1), whereas in the native PSI complex Asp-B558 is subjected to interactions with a network of residues.
Redox potentials of A1 and FX in the P700-FX core
A1 redox potential
Em(A1A) and Em(A1B) are calculated to be −545 mV and −652 mV, respectively, in the P700-FX core (Table 3). Although these values are similar to the calculated Em(A1) in the native PSI complex (Em(A1A) = −531 mV; Em(A1B) = −686 mV (17)), the shift in Em(A1B) is slightly larger than that in Em(A1A). As a consequence, the asymmetry in the Em(A1A/B) values decreases from 155 mV (17) in the native PSI complex to 107 mV in the P700-FX core. The decrease in the difference between Em(A1A) and Em(A1B) by 48 mV relative to the native PSI complex can be assigned predominantly to an upshift of 34 mV in Em(A1B) as compared to a downshift of only 14 mV in Em(A1A). In previous work, the direct contributions of the two iron-sulfur clusters FA/FB on the Em(A1) in the native PSI complex were found to contribute to the downshift nearly symmetrically by 50 mV for Em(A1A) and by 59 mV for Em(A1B) (17). However, the apparent change of the asymmetry for the Em(A1A/B) considering the P700-FX core could be explained by a small change in protonation probability of Asp-B575. Upon removal of PsaC, the protonation of Asp-B575 remains practically unchanged for reduced 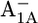 (0.85 H+ for the native PSI complex and 0.89 H+ for the P700-FX core). But, it increases protonation by 0.1 H+ for reduced
(0.85 H+ for the native PSI complex and 0.89 H+ for the P700-FX core). But, it increases protonation by 0.1 H+ for reduced 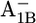 (0.17 H+ for the native PSI complex and 0.27 H+ for the P700-FX core). The residue Asp-B575 was proposed to play a crucial role in tuning the Em(A1A/B) values as revealed in the study on the native PSI complex (17). Increasing protonation of this acidic residue stabilizes the reduced state
(0.17 H+ for the native PSI complex and 0.27 H+ for the P700-FX core). The residue Asp-B575 was proposed to play a crucial role in tuning the Em(A1A/B) values as revealed in the study on the native PSI complex (17). Increasing protonation of this acidic residue stabilizes the reduced state 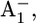 i.e., increases Em(A1).
i.e., increases Em(A1).
FX redox potential
From the optical spectrum at room temperature, the shift of Em(FX) in urea-treated PSI was measured to be +60mV, where FA/FB were removed by chemical dissociation of the subunit PsaC (3). The resulting P700-FX cores apparently have an increased solvent exposure of FX and a lack of charge interaction with the FA and FB iron-sulfur clusters. However, chemical treatment of proteins could conceivably cause modifications and structural rearrangement of the remaining subunits, particularly those near to the PsaA/PsaB interface with PsaC. Nevertheless, simply by using the atomic coordinates of the crystal structure of the native PSI complex for the remaining subunits of the P700-FX core, the calculated Em(FX) is 42 mV more positive than that for the native PSI complex, which is consistent with the experimentally measured shift of 60 mV in Em(FX) for urea-treated PSI (3). This implies that possible structural changes in the P700-FX core that are induced by urea treatment are either small or not significant for the Em(FX), which justifies the structural model for the P700-FX core used in this study.
One may argue that the shift of the Em(FX) is due to the removal of the negatively charged groups FA/FB by changing from the native PSI complex to the P700-FX core. To test this idea, we calculated the “direct contribution” of different residues/cofactors on Em(FX) in the native PSI complex with all titratable groups in standard protonation state at pH 7.0 (i.e., the acidic groups being ionized, basic groups protonated, and His neutral) (Fig. 2). Here, the negatively charged groups FA and FB are responsible for downshifts of the Em(FX) in the native PSI complex, by 110 mV and 34 mV, respectively. Due to the additivity of the direct contributions, these contributions to the Em(FX) yield a total downshift of 144 mV in the native PSI complex. Thus, elimination of atomic charges on both FA and FB from the native PSI complex should upshift the Em(FX) by 144 mV. However, in the native PSI complex, protein charges in the PsaC, PsaD, and PsaE subunits essentially neutralize the downshift of Em(FX) caused by the presence of FA/B, with an upshift of 112 mV, contributed predominantly by an upshift of 90 mV from PsaC. Thus, the total direct influence of the charges on PsaC with FA/B, PsaD, and PsaE on Em(FX) amounts to a downshift of −32 mV only. Note that all these values, especially the influence of FA/B on Em(FX), are valid only in the presence of the protein dielectric volumes from PsaC, PsaD, and PsaE whose dielectric constant was set to ɛP = 4.
FIGURE 2.
Direct influence on the shift of Em(FX) from FA, FB, and PsaC, PsaD, PsaE (PsaC-E) charges (Δcharges) and from dielectric volume (Δvolume) by changing from the native PSI to the P700-FX core. Calculated contributions and shifts (Δ) to Em(FX) are given in units of mV. Contributions to Em(FX) from specific components of the PsaC-E subunits are given in the left box that schematically represents these subunits. Changes (shifts) in Em(FX) upon removal of the PsaC-E subunits are denoted by Δ. The total shift is given as the sum of shifts from all charges, volume, and changes in the protonation pattern associated with them, i.e., ΔEm(FX) = Δcharges + Δvolume + Δprot. The direct influence from dielectric volume is obtained if for vanishing charges in the PsaC-E subunits the protein dielectric volume of PsaC-E with ɛP = 4 is removed resulting in water occupancy with ɛW = 80. The indirect influence due to associated changes in the protonation pattern of titratable residues (Δprot) upon the removal of these subunits and FA/B is given for the charges and the dielectric volume of all three removed subunits.
Removal of the subunits and cofactors from the native PSI complex is also accompanied by exposure of the resulting P700-FX core to bulk water. This effect is considered in our model by the replacement of the dielectric constant ɛP = 4 by ɛW = 80 in the volume of the removed protein and cofactors. This procedure is accompanied by generation of a new water accessible surface on the remaining PSI-RC scanned by a probe molecule of radius of 1.4 Å. Here, we obtain an upshift of Em(FX) by 46 mV due to the replacement of protein dielectric volume by the high dielectric of water in changing from the native PSI complex to a P700-FX core.
Creation of a new protein surface is often accompanied by a change of protonation pattern of nearby titratable residues. The change of protonation pattern from the native PSI complex to the P700-FX core, though it is subtle, results in a downshift of Em(FX) by 36 mV. Therefore, the total influence on the shift of Em(FX) in the P700-FX core, originating from the replacement of the protein volume of PsaC by water, yields an upshift of only 10 mV with respect to the native PSI complex. Together with the upshift of 32 mV obtained by the removal of the atomic charges from the subunits and of FA/B to generate P700-FX, Em(FX) in the P700-FX core is by 42 mV higher than that in the native PSI complex.
Although FX is not embedded in PsaC, the atomic charges of this subunit provide a significant stabilization to 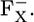 Hence, the upshift of the Em(FX) caused by PsaC implies that in addition to the negatively charged iron-sulfur clusters FA and FB, PsaC is effectively rich in positive charges originating from basic groups. Among the eight basic residues and nine acidic residues in PsaC, the FX binding niche is particularly rich in basic residues (Lys-C51, Arg-C52, and Arg-C65) rather than acidic residues (Glu-C54). These basic groups simultaneously contribute to the binding with subunits PsaA and PsaB, whose interfaces are rich in negatively charged acidic groups distributed symmetrically about the FX iron-sulfur cluster (9).
Hence, the upshift of the Em(FX) caused by PsaC implies that in addition to the negatively charged iron-sulfur clusters FA and FB, PsaC is effectively rich in positive charges originating from basic groups. Among the eight basic residues and nine acidic residues in PsaC, the FX binding niche is particularly rich in basic residues (Lys-C51, Arg-C52, and Arg-C65) rather than acidic residues (Glu-C54). These basic groups simultaneously contribute to the binding with subunits PsaA and PsaB, whose interfaces are rich in negatively charged acidic groups distributed symmetrically about the FX iron-sulfur cluster (9).
Kinetics of ET from A1 to FX in the P700-FX core
The lifetime (t1/e = 1/kET) of the reduced state 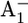 in PSI is limited by ET processes and exhibits two dominant time phases. It has been established that ET from A1 to FX is biphasic, the slower phase being 206–355 ns and the faster phase being 10–36 ns (11–16,39). Mutational studies of either Trp-A697 or Trp-B673 to Phe near A1A/A1B suggested that the former/latter originates from the forward ET from A1A/A1B to FX (5,16,40,41). In previous work (17) based on calculated Em(A1A/B), we obtained t1/e = 220–375 ns from the Em difference between A1A and FX and t1/e = 6–8 ns from the Em difference between A1B and FX, in agreement with the assignment in the mutant study (16). These estimates for the
in PSI is limited by ET processes and exhibits two dominant time phases. It has been established that ET from A1 to FX is biphasic, the slower phase being 206–355 ns and the faster phase being 10–36 ns (11–16,39). Mutational studies of either Trp-A697 or Trp-B673 to Phe near A1A/A1B suggested that the former/latter originates from the forward ET from A1A/A1B to FX (5,16,40,41). In previous work (17) based on calculated Em(A1A/B), we obtained t1/e = 220–375 ns from the Em difference between A1A and FX and t1/e = 6–8 ns from the Em difference between A1B and FX, in agreement with the assignment in the mutant study (16). These estimates for the 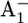 lifetime were obtained by using a reorganization energy of λ = 1.0 estimated from the kinetics of ET from A1 to FX (42).
lifetime were obtained by using a reorganization energy of λ = 1.0 estimated from the kinetics of ET from A1 to FX (42).
From kinetic studies with UV-VIS (9) or EPR (10) spectroscopy, it was revealed that the rate for the slow phase of ET from A1A to FX remained unchanged in urea-treated PSI (characteristic time of 180–190 ns). In a recent kinetic study also on urea-treated PSI by Gong et al. (5), the corresponding ET process was reexamined under the same conditions, giving rise to a slightly accelerated ET with a shorter lifetime of 126 ns.
With the same value of reorganization energy λ = 1.0 as used for the native PSI complex for ET from A1A to FX, we calculate lifetimes of 51–86 ns (Table 3) using Eqs. 1 and 2. These lifetimes are moderately shorter than the values computed for the native PSI complex (220–375 ns (17)). Hence, our calculated results show a small acceleration of ET for the P700-FX core model, consistent with the measurement by Gong et al. for the urea-prepared P700-FX core (5). The calculated rate for ET from A1A to FX is slightly larger than the measured rate. To reproduce the corresponding experimental lifetime of 126 ns (5), we can, for instance, increase Em(A1A) by 15 mV (i.e., rendering the ET reaction by 15 mV less exergonic) keeping all other conditions fixed. Such shifts in Em are smaller than 1 kBT = 26 mV and are therefore within the uncertainty limit of the measured Em, reorganization energy, or calculated Em associated with a tiny but possible protein structural change depending on P700-FX core preparation. Other factors, which we ignore in this study, such as protein dynamics may contribute to the remaining discrepancy, although the mere account of such factors without experimentally established structural-related information may result in additional artifacts. This study suggests that the upshift of Em(FX) in the P700-FX core preparation may be a key to understanding the acceleration of the ET process found for urea-treated PSI by Gong et al. (5).
It was suggested that urea treatment could be accompanied with a partial (10% (2) or 30% (10)) loss of FX with respect to the native PSI complex. With FX absent, ET cannot proceed past A1. Thus, a longer lifetime of the charge-separated state 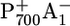 in P700-FX core is observed (10). Computationally it is possible to delete PsaC, PsaD, and PsaE from the crystal structure of the native PSI complex. Based on this simple model for the P700-FX core structure, we can reproduce the measured shift of Em(FX) (3) and, as a consequence, obtain an acceleration of ET from A1 to FX as observed in the kinetic measurements (5) for urea-treated PSI. Thus, this study demonstrates that this simple model for the P700-FX core based on the native PSI complex can essentially explain the experimental results. Furthermore, these computational results suggest that the structural essentials of the PsaA/PsaB core of the native PSI complex are conserved in the urea-treated P700-FX core as previously suggested (2).
in P700-FX core is observed (10). Computationally it is possible to delete PsaC, PsaD, and PsaE from the crystal structure of the native PSI complex. Based on this simple model for the P700-FX core structure, we can reproduce the measured shift of Em(FX) (3) and, as a consequence, obtain an acceleration of ET from A1 to FX as observed in the kinetic measurements (5) for urea-treated PSI. Thus, this study demonstrates that this simple model for the P700-FX core based on the native PSI complex can essentially explain the experimental results. Furthermore, these computational results suggest that the structural essentials of the PsaA/PsaB core of the native PSI complex are conserved in the urea-treated P700-FX core as previously suggested (2).
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
Acknowledgments
We thank Dr. Donald Bashford and Dr. Martin Karplus for providing the programs MEAD and CHARMM22, respectively. We thank Dr. Wolfram Saenger and Dr. Norbert Krauß for useful discussions.
This work was supported by the Deutsche Forschungsgemeinschaft SFB 498, Projects A3 and A5, GRK 80/2, GRK 268, and GKR 788/1, and by the U.S. National Science Foundation (MCB-MCB-0117079). H.I. was supported by the German Academic Exchange Service (DAAD).
Hiroshi Ishikita's present address is Dept. of Chemistry, The Pennsylvania State University, 104 Chemistry Building, University Park, PA 16802.
References
- 1.Jordan, P., P. Fromme, H. T. Witt, O. Klukas, W. Saenger, and N. Krauß. 2001. Three-dimensional structure of cyanobacterial photosystem I at 2.5 Å resolution. Nature. 411:909–917. [DOI] [PubMed] [Google Scholar]
- 2.Golbeck, J. H., K. G. Parrett, T. Mehari, K. L. Jones, and J. J. Brand. 1988. Isolation of the intact photosystem I reaction center core containing P700 and iron-sulfur center FX. FEBS Lett. 228:268–272. [Google Scholar]
- 3.Parrett, K. G., T. Mehari, P. G. Warren, and J. H. Golbeck. 1989. Purification and properties of the intact P-700 and FX-containing photosystem I core protein. Biochim. Biophys. Acta. 973:324–332. [DOI] [PubMed] [Google Scholar]
- 4.Golbeck, J. H. 2003. The binding of cofactors to photosystem I analyzed by spectroscopic and mutagenic methods. Annu. Rev. Biophys. Biomol. Struct. 32:237–256. [DOI] [PubMed] [Google Scholar]
- 5.Gong, X. M., R. Agalarov, K. Brettel, and C. Carmeli. 2003. Control of electron transport in photosystem I by the iron-sulfur cluster FX in response to intra- and intersubunit interactions. J. Biol. Chem. 278:19141–19150. [DOI] [PubMed] [Google Scholar]
- 6.Yu, J., L. B. Smart, Y. S. Jung, J. Golbeck, and L. McIntosh. 1995. Absence of PsaC subunit allows assembly of photosystem I core but prevents the binding of PsaD and PsaE in Synechocystis sp. PCC6803. Plant Mol. Biol. 29:331–342. [DOI] [PubMed] [Google Scholar]
- 7.Shen, G., J. Zhao, S. K. Reimer, M. L. Antonkine, Q. Cai, S. M. Weiland, J. H. Golbeck, and D. A. Bryant. 2002. Assembly of photosystem I. I. Inactivation of the rubA gene encoding a membrane-associated rubredoxin in the cyanobacterium Synechococcus sp. PCC 7002 causes a loss of photosystem I activity. J. Biol. Chem. 277:20343–20354. [DOI] [PubMed] [Google Scholar]
- 8.Shen, G., M. L. Antonkine, A. van der Est, I. R. Vassiliev, K. Brettel, R. Bittl, S. G. Zech, J. Zhao, D. Stehlik, D. A. Bryant, and J. H. Golbeck. 2002. Assembly of photosystem I. II. Rubredoxin is required for the in vivo assembly of FX in Synechococcus sp. PCC 7002 as shown by optical and EPR spectroscopy. J. Biol. Chem. 277:20355–20366. [DOI] [PubMed] [Google Scholar]
-
9.Lüneberg, J., P. Fromme, P. Jekow, and E. Schlodder. 1994. Spectroscopic characterization of PS I core complexes from thermophilic Synechococcus sp: identical reoxidation kinetics of
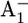 before and after removal of theiron-sulfur-clusters FA and FB. FEBS Lett. 338:197–202. [DOI] [PubMed] [Google Scholar]
before and after removal of theiron-sulfur-clusters FA and FB. FEBS Lett. 338:197–202. [DOI] [PubMed] [Google Scholar] - 10.van der Est, A., C. Bock, J. Golbeck, K. Brettel, P. Sétif, and D. Stehlik. 1994. Electron transfer from the acceptor A1 to the iron-sulfur centers in photosystem I as studied by transient EPR spectroscopy. Biochemistry. 33:11789–11797. [DOI] [PubMed] [Google Scholar]
-
11.Brettel, K. 1988. Electron transfer from
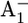 to an iron-sulfur center with t1/2 = 200 ns at room temperature in photosystem I characterization by flash absorption spectroscopy. FEBS Lett. 239:93–98. [Google Scholar]
to an iron-sulfur center with t1/2 = 200 ns at room temperature in photosystem I characterization by flash absorption spectroscopy. FEBS Lett. 239:93–98. [Google Scholar] - 12.Sétif, P., and K. Brettel. 1993. Forward electron transfer from phylloquinone A1 to iron-sulfur centers in spinach photosystem I. Biochemistry. 32:7846–7854. [DOI] [PubMed] [Google Scholar]
- 13.Leibl, W., B. Toupance, and J. Breton. 1995. Photoelectric characterization of forward electron transfer to iron-sulfur centers in photosystem I. Biochemistry. 34:10237–10244. [DOI] [PubMed] [Google Scholar]
- 14.Joliot, P., and A. Joliot. 1999. In vivo analysis of the electron transfer within photosystem I: are the two phylloquinones involved? Biochemistry. 38:11130–11136. [DOI] [PubMed] [Google Scholar]
- 15.Purton, S., D. R. Stevens, I. P. Muhiuddin, M. C. W. Evans, S. Carter, S. E. J. Rigby, and P. Heathcote. 2001. Site-directed mutagenesis of PsaA residue W693 affects phylloquinone binding and function in the photosystem I reaction center of Chlamydomonas reinhardtii. Biochemistry. 40:2167–2175. [DOI] [PubMed] [Google Scholar]
- 16.Guergova-Kuras, M., B. Boudreaux, A. Joliot, P. Joliot, and K. Redding. 2001. Evidence for two active branches for electron transfer in photosystem I. Proc. Natl. Acad. Sci. USA. 98:4437–4442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ishikita, H., and E. W. Knapp. 2003. Redox potential of quinones in both electron transfer branches of photosystem I. J. Biol. Chem. 278:52002–52011. [DOI] [PubMed] [Google Scholar]
- 18.Antonkine, M. L., P. Jordan, P. Fromme, N. Krauß, J. H. Golbeck, and D. Stehlik. 2003. Assembly of protein subunits within the stromal ridge of photosystem I. Structural changes between unbound and sequentially PS I-bound polypeptides and correlated changes of the magnetic properties of the terminal iron sulfur clusters. J. Mol. Biol. 327:671–697. [DOI] [PubMed] [Google Scholar]
- 19.Sakuragi, Y., B. Zybailov, G. Shen, D. A. Bryant, J. H. Golbeck, B. A. Diner, I. Karygina, Y. N. Pushkar, and D. Stehlik. 2005. Recruitment of a foreign quinone into the A1 site of photosystem I. Characterization of a menB rubA double deletion mutant in Synechococcus sp. PCC 7002 devoid of FX, FA, and FB and containing plastoquinone or exchanged 9,10-anthraquinone. J. Biol. Chem. 280:12371–12381. [DOI] [PubMed] [Google Scholar]
- 20.Pushkar, Y. N., I. Karyagina, D. Stehlik, S. Brown, and A. van der Est. 2005. Recruitment of a foreign quinone into the A1 site of photosystem I. Consecutive forward electron transfer from A0 to A1 to FX with anthraquinone in the A1 site as studied by transient EPR. J. Biol. Chem. 280:12382–12390. [DOI] [PubMed] [Google Scholar]
- 21.Li, N., J. Zhao, P. V. Warren, J. T. Warden, D. A. Bryant, and J. H. Golbeck. 1991. PsaD is required for the stable binding of PsaC to the photosystem I core protein of Synechococcus sp. PCC 6301. Biochemistry. 30:7863–7872. [DOI] [PubMed] [Google Scholar]
- 22.Rodday, S. M., S. S. Jun, and J. Biggins. 1993. Interaction of the FA/FB-containing subunit with the photosystem-1 core heterodimer. Photosynth. Res. 36:1–9. [DOI] [PubMed] [Google Scholar]
- 23.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy minimization and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- 24.MacKerell, A. D. Jr., D. Bashford, R. L. Bellott, R. L. Dunbrack Jr., J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- 25.Rabenstein, B., G. M. Ullmann, and E. W. Knapp. 1998. Calculation of protonation patterns in proteins with structural relaxation and molecular ensembles: application to the photosynthetic reaction center. Eur. Bophys. J. 27:626–637. [Google Scholar]
- 26.Mouesca, J., J. L. Chen, L. Noodleeman, D. Bashford, and D. A. Case. 1994. Density functional/Poisson-Boltzmann calculations of redox potentials for iron-sulfur clusters. J. Am. Chem. Soc. 116:11898–11914. [Google Scholar]
- 27.Davis, I. H., P. Heathcote, D. J. MacLachlan, and M. C. W. Evance. 1993. Modulation analysis of the electron spin echo signals of in vivo oxidised primary donor 14N chlorophyll centres in bacterial, P870 and P960, and plant Photosystem I, P700, reaction centres. Biochim. Biophys. Acta. 1143:183–189. [Google Scholar]
- 28.Rigby, S. E. J., J. H. A. Nugent, and P. J. O'Malley. 1994. ENDOR and special triple resonance studies of chlorophyll cation radicals in photosystem 2. Biochemistry. 33:10043–10050. [DOI] [PubMed] [Google Scholar]
- 29.Käss, H., and W. Lubitz. 1996. Evaluation of 2D-ESEEM data of 15N-labeled radical cations of the primary donor P700 in photosystem I and chlorophyll a. Chem. Phys. Lett. 251:193–203. [Google Scholar]
- 30.Mac, M., N. R. Bowlby, G. T. Babcock, and J. McCracken. 1998. Monomeric spin density distribution in the primary donor of photosystem I as determined by electron magnetic resonance: functional and thermodynamic implications. J. Am. Chem. Soc. 120:13215–13223. [Google Scholar]
- 31.Bashford, D., and M. Karplus. 1990. pKa's of ionizable groups in proteins: atomic detail from a continuum electrostatic model. Biochemistry. 29:10219–10225. [DOI] [PubMed] [Google Scholar]
- 32.Rabenstein, B. 1999. Karlsberg online manual. http://agknapp.chemie.fu-berlin.de/karlsberg/.
- 33.Prince, R. C., P. L. Dutton, and J. M. Bruce. 1983. Electrochemistry of ubiquinones: menaquinones and plastoquinones in aprotic solvents. FEBS Lett. 160:273–276. [Google Scholar]
- 34.Ishikita, H., and E. W. Knapp. 2005. Energetics of proton transfer pathways in reaction centers from Rhodobacter sphaeroides: the Glu-H173 activated mutants. J. Biol. Chem. 280:12446–12450. [DOI] [PubMed] [Google Scholar]
- 35.Ishikita, H., and E. W. Knapp. 2005. Redox potential of cytochrome c550 in the cyanobacterium Thermosynechococcus elongatus. FEBS Lett. 579:3190–3194. [DOI] [PubMed] [Google Scholar]
- 36.Page, C. C., C. C. Moser, X. Chen, and P. L. Dutton. 1999. Natural engineering principles of electron tunnelling in biological oxidation-reduction. Nature. 402:47–52. [DOI] [PubMed] [Google Scholar]
- 37.Hastings, G., and V. Sivakumar. 2001. A Fourier transform infrared absorption difference spectrum associated with the reduction of A1 in photosystem I: are both phylloquinones involved in electron transfer? Biochemistry. 40:3681–3689. [DOI] [PubMed] [Google Scholar]
- 38.Fischer, N., P. Sétif, and J. D. Rochaix. 1997. Targeted mutations in the psaC gene of Chlamydomonas reinhardtii: preferential reduction of FB at low temperature is not accompanied by altered electron flow from photosystem I to ferredoxin. Biochemistry. 36:93–102. [DOI] [PubMed] [Google Scholar]
- 39.Yang, F., G. Shen, W. M. Schluchter, B. L. Zybailov, A. O. Ganago, I. R. Vassiliev, D. A. Bryant, and J. H. Golbeck. 1998. Deletion of the PsaF polypeptide modifies the environment of the redox-active phylloquinone (A1). Evidence for unidirectionality of electron transfer in photosystem I. J. Phys. Chem. B. 102:8288–8299. [Google Scholar]
- 40.Xu, W., P. Chitnis, A. Valieva, A. van der Est, Y. N. Pushkar, M. Krzystyniak, C. Teutloff, S. G. Zech, R. Bittl, D. Stehlik, B. Zybailov, G. Shen, and J. H. Golbeck. 2003. Electron transfer in cyanobacterial photosystem I: I. Physiological and spectroscopic characterization of site-directed mutants in a putative electron transfer pathway from A0 through A1 to FX. J. Biol. Chem. 278:27864–27875. [DOI] [PubMed] [Google Scholar]
- 41.Xu, W., P. R. Chitnis, A. Valieva, A. van der Est, K. Brettel, M. Guergova-Kuras, Y. N. Pushkar, S. G. Zech, D. Stehlik, G. Shen, B. Zybailov, and J. H. Golbeck. 2003. Electron transfer in cyanobacterial photosystem I: II. Determination of forward electron transfer rates of site-directed mutants in a putative electron transfer pathway from A0 through A1 to FX. J. Biol. Chem. 278:27876–27887. [DOI] [PubMed] [Google Scholar]
-
42.Schlodder, E., K. Falkenberg, M. Gergeleit, and K. Brettel. 1998. Temperature dependence of forward and reverse electron transfer from
 the reduced secondary electron acceptor in photosystem I. Biochemistry. 37:9466–9476. [DOI] [PubMed] [Google Scholar]
the reduced secondary electron acceptor in photosystem I. Biochemistry. 37:9466–9476. [DOI] [PubMed] [Google Scholar] - 43.Shinkarev, V., I. Vassiliev, and J. H. Golbeck. 2000. A kinetic assessment of the sequence of electron transfer from FX to FA and further to FB in photosystem I: the value of the equilibrium constant between FX and FA. Biophys. J. 78:363–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Semenov, A. Y., I. R. Vassiliev, A. van der Est, M. D. Mamedov, B. Zybailov, G. Shen, D. Stehlik, B. A. Diner, P. R. Chitnis, and J. H. Golbeck. 2000. Recruitment of a foreign quinone into the A1 site of photosystem I. J. Biol. Chem. 275:23429–23438. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.