Dynamics of Immobilized and Native Escherichia coli Dihydrofolate Reductase by Quasielastic Neutron Scattering

Abstract

The internal dynamics of native and immobilized Escherichia coli dihydrofolate reductase (DHFR) have been examined using incoherent quasielastic neutron scattering. These results reveal no difference between the high frequency vibration mean-square displacement of the native and the immobilized E. coli DHFR. However, length-scale-dependent, picosecond dynamical changes are found. On longer length scales, the dynamics are comparable for both DHFR samples. On shorter length scales, the dynamics is dominated by local jump motions over potential barriers. The residence time for the protons to stay in a potential well is τ = 7.95 ± 1.02 ps for the native DHFR and τ = 20.36 ± 1.80 ps for the immobilized DHFR. The average height of the potential barrier to the local motions is increased in the immobilized DHFR, and may increase the activation energy for the activity reaction, decreasing the rate as observed experimentally. These results suggest that the local motions on the picosecond timescale may act as a lubricant for those associated with DHFR activity occurring on a slower millisecond timescale. Experiments indicate a significantly slower catalytic reaction rate for the immobilized E. coli DHFR. However, the immobilization of the DHFR is on the exterior of the enzyme and essentially distal to the active site, thus this phenomenon has broad implications for the action of drugs distal to the active site.

INTRODUCTION

Enzyme immobilization has expanded greatly in the last decade due to its potential applications in several fields, including use as biocatalysts, bioreactors, and biosensors, and in clinical use (1–3). Immobilization can offer several advantages, such as high concentration, the possibility of reuse, and separation of the biocatalyst from the reaction products (3,4).

Immobilization may also change enzyme properties, enhancing stability for example (5–7). Immobilization limits the global translational and rotational diffusion of dihydrofolate reductase (DHFR). A further, possible effect is modification of the internal dynamics, and this is the subject of the present investigation.

DHFR catalyzes the NADPH-dependent reduction of 7,8-dihydrofolate to 5,6,7,8-tetrahydrofolate (THF). It is an essential enzyme required for normal folate metabolism in prokaryotes and eukaryotes. Its role is to maintain necessary levels of THF needed to support the biosynthesis of purines, pyrimidines, amino acids, and thymidylate. Many compounds of pharmacological value such as methotrexate and trimethoprim work by inhibition of DHFR. DHFR is also recognized as a drug target for inhibiting DNA synthesis in rapidly proliferating cells such as cancer cells (8). As a result of its clinical and pharmacological importance, DHFR has been studied extensively with a wide range of methodologies, and there is today a considerable published literature (more than 4000 articles) on the broad subject of DHFR. The DHFR from E. coli is the most extensively studied. Since the 1950s, researchers have been studying its purification, kinetics, and structure (9–13). However, to date, only a few experimental dynamics measurements of E. coli DHFR are available.

The technique of neutron scattering is uniquely suited to measure protein dynamics, because neutron wavelengths and energies match the amplitudes and energies of macromolecular thermal fluctuations, respectively (14–18). Because of their large incoherent scattering cross-section, the motions of ¹H nuclei dominate the observations (19); the experiments provide information on collective protein dynamics as, on the timescale examined (up to ≈0.1 ns), concerted motions dominated the dynamical spectrum and the H atoms thus reflect the dynamics of the side chains and backbone atoms to which they are bound (20).

There is an overlap between the timescales of neutron scattering experiments and those of NMR. Neutron scattering experiments, however, can be performed on proteins of any size without labeling to provide total thermal averaged enzyme dynamics and time- and scale-dependent atomic fluctuation amplitudes in absolute units. NMR studies on DHFR point to an influence of nanosecond-picosecond timescale local dynamics on the much slower millisecond timescale of the catalytic activity (21,22). However, many questions about the connection between those nanosecond-picosecond motions and the catalytic mechanism of the DHFR remain unanswered.

In this work, we present an incoherent quasielastic neutron scattering study of the total thermal-averaged dynamics of native and immobilized E. coli DHFR. The neutron results combined with activity data established complex correlations between dynamics and activity. We discuss these observations in terms of the effect of transmission coefficient decreasing, or activation free energy barrier increasing, on the mechanisms for the catalyzed reaction of the DHFR. In addition, results suggest that total local thermal averaged dynamics occurring on the picosecond timescale have an influence on the much slower millisecond timescale of the catalytic activity.

MATERIALS AND METHODS

Materials

Micro-porous silica support (Sunsphere H122) was purchased from Asahi Glass (Yurakucho, Japan). Trichlorotriazine (TCT) and dry chloroform (99.9% purity, water <0.01%, HPLC grade) were purchased from Sigma-Aldrich (St. Louis, MO). Dry acetone (99.5% purity, water <0.01%) was purchased from Merck KGaA (Darmstadt, Germany). Dry triethylamine (99.6% purity, water <0.1%, HPLC grade) was purchased from BDH Laboratory Supplies (Poole, UK). Deuterium oxide (D₂0, ²H, 99.9%, NMR grade) was purchased from Minipul, Norell (Landisville, NJ). Reagents and medium components for the purification and the analysis of the activity of native and immobilized DHFR were purchased from Sigma-Aldrich, Merck, BDH Laboratory Supplies, or Becton-Dickinson (Sparks, MD). Buffers were adjusted to the appropriate pH value at the assay temperature, using a combination electrode calibrated at this temperature.

Enzyme purification

Escherichia coli cells bearing the plasmid of dihydrofolate reductase (EC 1.5.1.3) were grown in 2-liter flasks. The cells were harvested by centrifugation and disrupted by sonication. The cell lysate was centrifuged and the supernatant was applied to a methotrexate-agarose (Sigma-Aldrich) column (XK26/20; Pharmacia, Peapack, NJ) equilibrated with buffer A (20 mM Bis-Tris-propane buffer, 100 μM Ethylene-Diamine-Tetraacetic-Acid, and 5 mM β-Mercaptoethanol, pH 8). The column was washed with the same buffer solution until no more protein was detected at 280 nm in the effluent. The enzyme was then eluted using buffer A, containing 3 mM folic acid and 1 M KCl at pH 9, until no more protein was detected at 280 nm in the effluent. Fractions containing the eluted DHFR were combined, diafiltered, and concentrated by ultrafiltration (YM-10 membrane; Amicon, Millipore, Ann Arbor, MI). The concentrated enzyme was freeze-dried and stored at 4°C. The purity of the dihydrofolate reductase was determined by gel electrophoresis and specific activity determination.

Before the neutron scattering experiments, H-D exchange was carried out: the purified enzyme powder was dissolved in 50 ml of D₂O (purity 98%) and gently stirred, and then the solution freeze-dried. This procedure was repeated, and then carried out twice more with D₂O (purity 99.9%). The enzyme was dissolved for a total duration of two days in D₂O. The dried enzyme was stored at 4°C until use.

Enzyme immobilization process

DHFR was immobilized by covalently binding to Sunsphere H122, according to an adaptation of the TCT methodology (23,24). The TCT was purified in dry chloroform (25). After a drying step by evaporating the chloroform away at room temperature, TCT was dried in a vacuum desiccator. The inorganic supports were dried at 80°C for two days. To activate the dry support, 1 g was suspended in 40 ml of dry acetone. Then 260 mg of dry TCT and 196.4 μl of dry triethylamine were added to the suspension. Using a dry glass bottle, the mixture was heated at 50°C and gently stirred in an incubator for 4 h.

The mixture was cooled to room temperature, and then vacuum-filtered using a Buchner flask (Buchner, Hong Kong) and a 0.45-μm porosity solvent-resistant filter. The solid was suspended in 50 ml of dry acetone and gently stirred and then vacuum-filtered; the same procedure was repeated twice. The activated support was dried overnight in the presence of silica gel in a desiccator at 40°C.

For the coupling of DHFR, 1 g of dry activated support was mixed with 200 ml of 5 mg/ml enzyme in 0.1 M sodium phosphate buffer pH 7.0. Using a glass bottle, the mixture was gently stirred for 4 h at room temperature with a Coulter mixer (Beckman Coulter, Fullerton, CA). Then, the biocatalyst was filtrated vacuum-filtered and washed twice with 50 ml of the same buffer. The resulting immobilized enzyme was suspended with 50 ml of D₂O (purity 98%) and gently stirred. The suspension was allowed to settle, and then separated by vacuum filtration. This procedure was repeated, and then carried out twice more with pure D₂O (purity 99.9%). The immobilized enzyme was exposed to D₂O for a total duration of two days. The biocatalyst was freeze-dried and stored at 4°C until use.

For protein determination, the dried biocatalyst was treated with 0.1 M NaOH for 3 h at room temperature, the mixture centrifuged, and the amount of enzyme determined by the Bradford method (26) on the supernatant, with native DHFR as a calibration standard.

Enzyme assays

DHFR activity was measured spectrophotometrically, continuously following the decrease in absorbance that occurs at 340 nm when the cofactor NADPH and the substrate dihydrofolate (DHF) are reacted to form NADP⁺ and tetrahydrofolate (THF). A ThermoSpectronic Helios γ-spectrophotometer (ThermoSpectronic, Madison, WI), equipped with a single cell Peltier-effect cuvette holder with stirring device, was used. The standard reaction mixture (2000 μl) contained 100 mM imidazole buffer, pH 6.5, 2 mM dithiothreitol, 0.1 mM DHF, 0.1 mM NADPH, and enzyme. All assays were stirred.

Neutron scattering sample preparation

Measurements were made on two samples: free and immobilized DHFR. The sample of free dihydrofolate reductase contained 212 mg of dried purified DHFR rehydrated by adding 655 mg of pure D₂O. The immobilized dihydrofolate reductase contained 350 mg of dried biocatalyst (containing 70 mg of dried dihydrofolate reductase and 280 mg of dried activated silica support) rehydrated with 216 mg of pure D₂O using vapor exchange over pure D₂O. These quantities of DHFR and pure D₂O were selected to keep the same ratio of mass between the enzyme and the D₂O in both samples. Pure D₂O (655 mg), and 280 mg of dried activated silica support with 216 mg of pure D₂O, were used for background subtraction for the native and immobilized dihydrofolate reductase, respectively. Samples were sealed in a flat aluminum container and positioned in the neutron beam, which illuminated the full volume of all samples. The scattering of the aluminum screws was removed using a cadmium mask.

Neutron scattering measurements

The experiments were performed on the IN6 time-of-flight spectrometer at the Institute Laue Langevin (ILL, Grenoble, France) using an incident wavelength of 5.12 Å, with an elastic energy resolution of 100 μeV (full-width at half-maximum). The scattering was measured over a wave-vector range of 0.3 < Q < 2.0 Å⁻¹ at 285 K. All samples, including the vanadium and empty aluminum can, were oriented at 135° with respect to the incident neutron beam direction. The measured time-of-flight spectra were corrected, normalized, grouped, and transformed into energy transfer spectra by using the standard ILL reduction program “INX.” Correction for multiple scattering was not performed because the transmission of all samples was ∼90%, indicating that this effect can be neglected.

Quasielastic incoherent neutron scattering

An exhaustive description of quasielastic neutron scattering can be found in Bée (19). The application to protein dynamics has been reviewed in Smith (20) and Gabel et al. (17). In the case of incoherent neutron scattering, the hydrogen nuclei dominate the observation because their incoherent scattering cross-sections are very large (19). Because these protons are uniformly distributed in the protein, they allow us to probe its general dynamical properties within the time and the spatial windows of the spectrometer. Information on protein dynamics is contained in the scattering function S(Q,ω), which gives the probability of measuring neutrons scattered by the sample with an energy transfer ℏω and a momentum transfer ℏQ.

In the quasielastic incoherent approximation, the theoretical scattering function describing the internal motion in the protein can be expressed by (19)

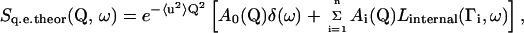(1)

where the expression within the square brackets describes the scattering function arise from diffusive motions in the absence of 〈u²〉 stands for the mean-square displacement of high frequency vibration. A₀(Q) is the elastic incoherent structure factor (EISF) and its Q-dependence provides information on the geometry of the motion.

The quasielastic component is a sum of Lorentzian functions,

(2)

where Γ_i is the half-width at half-maximum of a Lorentzian peak.

The theoretical scattering function (see Eq. 1) was fitted to the data with the standard ILL fitting program “Profit” by using the following relation (information on the Institute and programs is available on the web at http://www.ill.fr),

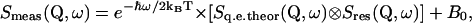(3)

in which a convolution with the spectrometer resolution function S_res(Q,ω) and a detailed balance factor e^{−ℏω/2k_BT} are applied. B₀ is the inelastic background due to the vibrational modes of lowest energy (the lattice phonons) (19). The fits were performed over the energy transfer range −0.6 to +1.5 meV. The S_meas(Q,ω) of both the immobilized and free DHFR were found to be reasonably well fitted with a single Lorentzian function (see Results, below).

RESULTS

Enzyme immobilization

The amount of immobilized enzyme, i.e., the loading of the silica support, was determined by several methods. As a first approximation, this quantity was determined by the difference between the initial activity of native DHFR added for the immobilization process and the total activity of the enzyme recovered in the first filtrate and in the washings. After an alkaline treatment, the amount of immobilized DHFR was also determined by the Bradford method (26) with native DHFR as a calibration standard. The quantification methods were in agreement and the amount of immobilized enzyme was found to be 25 mg DHFR per 100 mg support.

The enzymatic activity of the immobilized DHFR was determined using the ratio between the specific enzymatic activity of an amount of native enzyme and the same amount of immobilized enzyme. The values of residual activity of the immobilized DHFR were ∼13% with respect to its native counterpart. No increase in activity was observed with changes in assay stirring rates, or upon comminution of the silica particles, or with increased substrate concentration, indicating that the reduced activity was not caused by diffusional limitation. Furthermore, an Arrhenius plot (data not shown) showed no deviation from linearity, also indicating the absence of diffusional limitation.

Neutron scattering

Typical quasielastic neutron-scattering fitted spectra from the immobilized and native enzymes are shown in Fig. 1. Fitting with an elastic peak and one Lorentzian was found to be reasonable for the data obtained with both samples. Of particular interest is the finding that the scattering profile of the free DHFR is significantly broader than that of the immobilized species for high Q > 1.22 Å⁻¹ (Fig. 1, C and D).

FIGURE 1.

Quasielastic spectrum of native (A) and immobilized (B) dihydrofolate reductase from Escherichia coli at T = 285 K and Q = 1.73 Å⁻¹. (The plus symbol indicates data and the bold solid line is a fitted curve using Eq. 3.) The fit of the quasielastic spectra was performed for −0.6 < ℏω < 1.5 meV. The different components correspond to the elastic peak (fine solid line) and the Lorentzian line (dotted line). (C) Normalized quasielastic spectrum of native (•) and immobilized (□) dihydrofolate reductase from Escherichia coli at T = 285 K and Q = 0.74 Å⁻¹. (D) Normalized quasielastic spectrum of native (•) and immobilized (□) dihydrofolate reductase from Escherichia coli at T = 285 K and Q = 1.73 Å⁻¹.

The mean-square displacement of high frequency vibration motions 〈u²〉 is directly deduced from a linear fit of the natural logarithmic of the total scattering intensity versus Q² as shown in Eq. 1. The 〈u²〉 values are 0.23 ± 0.04 Ų and 0.19 ± 0.02 Ų for the native and the immobilized DHFR, respectively. These amplitudes are similar within error.

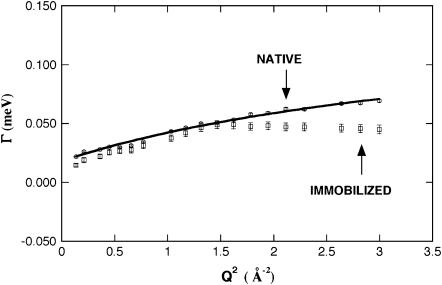
The half-width at half-maximum, Γ of the Lorentzian in Eq. 2 is given as a function of Q² in Fig. 2. Gamma versus Q² curves, at first, do not give zero intercepts in the low Q² region for either immobilized or native DHFR. Then, the Γ-values of the immobilized and native DHFR increase with Q² and asymptotically approaches a constant value Γ_∞ at large Q. The first feature indicates that the observed behavior is not free diffusion, but it is a typical characteristic of diffusion in a confined space (19), and can be approximately accounted for by the model of the model of Volino and Dianoux, where a particle diffuses in sphere of radius, r (27). The radius can be deduced from fitting the Q-dependence of the experimental EISF with the function (28,29)

(4)

Here, the p and (1–p) factors represent the fractions of protons in the protein that are considered to be immobile and mobile within the sphere of radius r, respectively. The experimental EISF is shown in Fig. 3. The EISF values of the native and the immobilized DHFR are similar to within experimental error. Using Eq. 4, we obtain radii of spheres r = 2.47 ± 0.20 Å and r = 2.59 ± 0.20 Å for the native and the immobilized DHFR, respectively. We also obtain fractions of immobile protons p = 0.61 ± 0.02 and p = 0.60 ± 0.01 for the native and the immobilized DHFR, respectively. Thus, the immobilized and native DHFR have the same values of p and r to within experimental error. An additional feature can be observed at Q∼1.5 Å⁻¹ in the native protein. This corresponds to a plateau in the EISF that the model used here does not reproduce, and has been seen also in the EISFs of other proteins in solution (28,30).

FIGURE 2.

Half-widths of the quasielastic Lorentzian function Γ as a function of Q² for the immobilized (□) and the native (○) dihydrofolate reductase from Escherichia coli at T = 285 K. The line results from the fit of Γ(Q) using Eq. 5.

FIGURE 3.

Elastic incoherent structure factor (EISF) as a function of Q for the immobilized (□) and the native (○) dihydrofolate reductase from Escherichia coli at T = 285 K. The lines result from the fit of A₀(Q) using Eq. 4.

Following Volino and Dianoux (27), the diffusion coefficient D of the mobile protons diffusing within the sphere of radius r can be estimated from Γ₀, the limit of Γ at Q = 0, with Γ₀ = 4.333 × D/r². The diffusion coefficient for the immobilized DHFR is D = 0.34 ± 0.07 10⁻⁵ cm²/s, in comparison to D = 0.47 ± 0.09 10⁻⁵ cm²/s for the native DHFR. Therefore, again, the two diffusion coefficients are the same to within experimental error.

At larger Q-values, the linewidths follows the well-known jump diffusion behavior, given by (31,32)

(5)

In the high Q-region, one observes motion on short length scales. On such scales, local jump motion of the protons becomes dominant. The residence time of a hydrogen atom on one site between jumps is τ =1/Γ_∞, where is Γ_∞ obtained from the asymptotic behavior at high Q while Γ approaches a constant value. The Γ-value at high Q of the native DHFR is still increasing over the Q-range examined, and has not yet reached the constant value. Therefore, this constant value was estimated by curve fitting using Eq. 5 and extrapolation to higher Q (Fig. 2). In contrast, the constant value Γ_∞ for the immobilized DHFR is reached over the Q-range accessed. Therefore, this constant value is directly used to calculate the residence time. The resulting residence times are τ = 7.95 ± 1.02 ps and τ = 20.36 ± 1.80 ps for the native and immobilized DHFR, respectively. Using this model, our data imply that τ is larger for the immobilized DHFR. The local jump motion is related to the local potential energy barrier imposed on a proton by its environment. The height of this potential barrier is related to the residence time by the Arrhenius relation

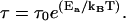(6)

In Eq. 6, τ₀ is a pre-exponential factor and E_a is the activation energy. Assuming that τ₀ is the same for the native and the immobilized DHFR, the activation energy difference between the two systems ΔE_a, is 0.54 ± 0.12 kcal/mol.

The characteristic jump distance is given by

(7)

are found to be the same to within error for the immobilized DHFR (l = 0.83 ± 0.12 Å) and the native DHFR (l = 0.61 ± 0.10 Å).

DISCUSSION

The present loading of DHFR on the Sunsphere H122, at 25 mg per 100 mg of support, is one of the highest ever observed—representing a surface coverage of ∼15% of the theoretical maximum, not including the protein hydration shell. In comparison, using a trichlorotriazine methodology to immobilize the lipase from Candida cylindracea to several supports, Moreno and Sinisterra (23) obtained loadings of between 2.7 and 12 mg per 100 mg of support.

There is an 87% decrease in activity of the immobilized DHFR, compared to the free enzyme. Activity losses of this size upon immobilization are not uncommon. Calsavara et al. (33) immobilized cellobiase in controlled pore silica by covalent binding with silane-glutaraldehyde method and lost 86% activity (33). When the immobilization of lipase from Candida cylindracea was carried out onto several supports by covalent attachment using the trichlorotriazine methodology (23), the activity losses were between 31 and 85%. Such activity losses may be due to diffusional limitation, steric hindrance, or arise because the enzyme is intrinsically less active when immobilized. Despite the very high enzyme-loading here, we found no evidence for diffusional limitation; the activity does not alter upon a change with stirring rate, and comminution of the Sunsphere H122 particles to which the enzyme is immobilized does not increase the rate. To ensure any rate decrease was not due to an increase in the apparent K_m, the immobilized enzyme was assayed with a 50% increase in both substrate concentrations; no difference was observed between these rates, or their linearity with time, and those run under normal assay conditions. This indicates that both of these sets of assay conditions were being carried out under substrate-saturating conditions. In the immobilization methodology used in this work, the activated groups of the support react with the enzyme through the amino group of lysine (23). According to the nucleotide sequences, characterizations, and three-dimensional structures, there are six lysine residues located on the outer surface of the DHFR molecule. They do not participate in the key active site hydrophobic contacts with the para-amino benzoyl glutamate of DHF and they are not located on the Adenosine binding loop, the Met-20 loop, or the βF–βG loop, which are important for the enzyme activity (13,34–36). One of the six lysine residues is close enough to the active site so that immobilization through that residue might affect access to the active site; it might thus account for a proportion, possibly up to 17%, of activity loss. This leaves the remaining activity loss, probably at least 70%, to be accounted for by an intrinsic reduction in activity of the immobilized enzyme.

In a recent hybrid quantum-classical molecular dynamics simulations approach, the overall rate (k_tot = κ × k_tst) of an enzyme reaction was expressed as a product of the equilibrium transition-state theory rate 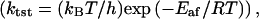which is related to thermally averaged motions that influence the activation free energy barrier, and a transmission coefficient κ, which is related to high-frequency vibrational motions that influence the dynamical recrossings of the barrier (37). Because the activation free-energy barrier is in the exponential of the overall rate, whereas the transmission coefficient is a pre-factor of this exponential, the thermally averaged motions are expected to have a larger impact on the activity than the high-frequency vibrational motions. Based on genomic analysis, kinetic measurements of multiple mutations, crystal structures, and this hybrid approach, Agarwal et al. (38) identified and characterized a network of coupled motions promoting catalysis in the enzyme DHFR (38). These promoting motions were referred to thermally averaged motions and occurred on the millisecond timescale. In addition to these motions, the authors also identified that high-frequency vibrational motions occurred on the femtosecond-to-picosecond timescale. Using this approach on a native and a mutant Escherichia coli DHFR, the calculated transmission coefficients of both enzymes were comparable (39). Although the mutation was on the exterior of the enzyme, the rate was reduced by a factor of 163 and the calculated free energy barrier was 3.4 kcal/mol higher for the mutant than for the native DHFR.

In our work, the immobilization of the DHFR through external lysine residues reduced the rate by a factor of ∼7. On the other hand, the measured mean-square displacements 〈u²〉 describing the high-frequency vibrational motions, which occurred on the femtosecond-to-picosecond timescale, are comparable for the native and for the immobilized DHFR. This result show that the contribution of high-frequency vibrational motions in DHFR is not significant to its activity, which is qualitatively consistent with the hybrid approach observations (39) and suggests that the decrease in the rate for the immobilized DHFR may be due to an increase in the free-energy barrier rather than a decrease in the transmission coefficient.

For picosecond timescale dynamics, neutron scattering results reveal the dependency of the length scale. The form of the results obtained is consistent with the restricted jump diffusion model (40). Clearly, the Γ of the restricted jump diffusion model exhibits the characters both of the diffusion within a restricted volume (here a sphere) model and the jump diffusion model tending to asymptotic values at low and high Q. At low Q, we are mainly concerned with longer length scale, i.e., with the effects of the boundaries, which force the Γ to deviate from the DQ² law (the Γ at low Q does not give zero intercepts) and to tend to a finite value, Γ₀. When the effect of confinement becomes less apparent, for example at room temperature, the Γ at low Q shows a finite Γ₀ without the plateau as it has been seen also in the Γ of other protein solutions (41). Conversely, at large Q, the nature of the local jump motions over shorter length scale predominates and, because the elementary displacements of the particles are not infinitely small, the Γ of the quasielastic component tends to the asymptotic value 1/τ.

On the longer length scale, our results imply that the fraction of immobile protons p, the diffusion coefficients D, and the radii of spheres r, in which the mobile protons diffuse, are comparable for the native and the immobilized DHFR.

On the shorter length scale, dominated by local jump motions, the calculated characteristic jump distances are similar for the native and the immobilized DHFR but their residence times, τ, change (τ = 7.95 ± 1.02 ps for the native DHFR and τ = 20.36 ± 1.8 ps for the immobilized DHFR).

According to the Arrhenius relation, the theoretical rate may be written as where E_a is the activation energy barrier for the catalyzed reaction, k_B is the Boltzmann's constant, h is the Planck's constant, R the gas constant, and T the absolute temperature. Using this theoretical rate equation, we can calculate that the activation energy difference required to reduce the rate by a factor of 7 between the native and the immobilized DHFR is 1.10 kcal/ mol. The difference in activation energy for hydrogen motion between the immobilized and the native DHFR estimated from the present work is 0.54 ± 0.12 kcal/mol. If the change in the free energy profile for average hydrogen motion probed in the present experiments were to be also present along the reaction coordinate, then an increase for the profile activation energy barrier rather than a decrease in the transmission coefficient for the reaction would result, decreasing the rate, as observed experimentally. The rate of DHFR catalysis is expected to be influenced more by motions occurring on the millisecond timescale (38). Therefore, our results suggest that local thermally averaged motions occurring on the picosecond timescale may have an influence on the much slower millisecond timescale of the catalytic activity.

CONCLUSION

We have used incoherent quasielastic neutron scattering to probe the total dynamics of the native and the immobilized E. coli DHFR. No significant change in the mean-square displacements of vibrational motions 〈u²〉 or the picosecond timescale motions on the longer length scales are seen upon enzyme immobilization. Changes in the picosecond timescale motions have been identified on shorter length scales, dominated by local-jump motions, in the immobilized DHFR as compared to the native DHFR. The average height of the potential barrier to the local motions is increased in the immobilized DHFR. The mean-square displacements of vibration motions and the thermal-averaged motions were related respectively to the transmission coefficient and the theoretical rate that influences the energy barrier as known from recent quantum-classical molecular dynamics simulations study (37–39). The results indicate that the decrease in the rate for the immobilized DHFR may be due to an increase in the energy barrier rather than a decrease in the transmission coefficient.

The local motions on the picosecond timescale may act as a lubricant for larger conformational changes, such as those associated with enzyme activity occurring on the slower millisecond timescale (16). They represent the conformational changes needed during the catalytic cycle to control access to the active site, to promote tetrahydrofolate-assisted product release and facilitate binding of the nicotinamide ring to form the Michaelis complex in DHFR (22).

It should be pointed out that the timescales referred to here are those applying at room temperature. The dynamic connection between the same molecular elements of the protein may be equally important at much slower timescales, in the case of activity at very low temperatures for example. In this context these results on the effect of local motions on catalysis are complementary to the findings that global, longer length scale, fast motions have no effect on the dynamics required for catalysis (42–44). The results presented here show that although the immobilization of the DHFR is on the exterior of the enzyme and essentially distal to the active site, experiments indicate a significant decrease in catalytic reaction rate. It is possible that the binding of ligands generally may exert a similar effect. In any event, this phenomenon has broad implications for protein engineering, drug design, and effect of pharmacaphores distal to the active site.