Exploring the Complex Folding Kinetics of RNA Hairpins: I. General Folding Kinetics Analysis

Abstract

Depending on the nucleotide sequence, the temperature, and other conditions, RNA hairpin-folding kinetics can be very complex. The complexity with a wide range of cooperative and noncooperative kinetic behaviors arises from the interplay between the formation of the loops, the disruption of the misfolded states, and the formation of the rate-limiting base stacks. With a rate constant model and a kinetic-cluster theory, we explore the broad landscape for RNA hairpin-folding kinetics. The model is validated through direct tests against several experimental measurements. The general kinetic folding mechanisms and the predicted great variety of folding kinetics are directly applicable and quantitatively testable in experiments. The results from this study suggest that 1), previous experimental findings based on the individual hairpins revealed only a small fraction of much broader and more complex RNA hairpin-folding landscapes; 2), even for structures as simple as hairpins, universal folding timescales and pathways do not exist; and 3), to treat the loop size as the sole factor to determine the hairpin-folding rate is an oversimplification.

INTRODUCTION

RNA hairpins are fundamental building blocks for complex three-dimensional RNA structures. The folding of complex RNA tertiary structures often involves the conformational change of hairpin structures (1–7). Understanding how a hairpin folds is, therefore, a prerequisite for understanding RNA tertiary structure folding. In addition, RNA functions, including splicing, translational regulation, etc., often involve the sequence-specific folding kinetics of RNA hairpins (8–10). Motivated by the significant structural and functional roles of RNA hairpins, we explore the complex sequence-dependent RNA hairpin-folding kinetics.

Since the early work of Porschke (11), there have been several experimental studies on the folding kinetics of RNA hairpin (12–16), peptide β-hairpin (17) and DNA hairpin (18–24). The early experiments focused on loop formation as the rate-limiting step. For most of the sequences studied, the folding was described by a single zipping/unzipping pathway. Moreover, depending on the loop size, most of the hairpins fold in microseconds' timescale in experiments. More recently, experiments from several groups are beginning to shed light on the complexity of RNA and DNA hairpin-folding landscapes, such as the non-Arrhenius and noncooperative kinetic behaviors (18–24). Since most of the experimental studies are limited to the kinetics specific to the sequences studied, a systematic full exploration for the sequence-dependent complexity of the folding landscape (25–27) is still missing.

Large-scale atomistic molecular dynamics simulations (28–30) enable the detailed analysis for the transition states, the kinetic intermediates, and the multiple folding pathways for the specific sequences studied. But the molecular dynamics studies are restricted to very short sequence. Monte Carlo simulations have also been used to model the RNA folding process by several authors (31–34). However, the conformational and kinetic sampling may not be complete and the method cannot give analytical results that allow for stable predictions for the long time dynamics. Recently, theoretical studies (27,35) based on statistical mechanical models were developed to study RNA folding kinetics. These statistical mechanical models are based on the master-equation (rate equation) approach (27) (see Theory and Methods, below). For short chains, the entire conformational ensemble can be exhaustively enumerated. With the complete conformational ensemble, the master equation can account for the transitions between each and every pair of the conformations and can give the information about the rate-limiting steps (36) and the population kinetics. The folding kinetics predicted from the master-equation approach is supported by the atomic simulation (29). However, the disadvantage of the master-equation approach is that it cannot give direct information about the microscopic pathways. In addition, the method is limited to short chains due to the rapid increase of the number of conformations for longer chains. More recently, aiming to study the folding mechanism at the level of microscopic pathways and to study kinetics for longer chains, we developed the kinetic-cluster model (detailed in Theory and Methods) by reducing the original large conformational ensemble into pre-equilibrated clusters (37), for which we can perform detailed microscopic kinetic analysis.

Experimental and theoretical developments suggest that the RNA hairpin-folding landscape is much more diverse and more complex than that revealed in early experiments. In this study, we develop a kinetic-cluster model for RNA hairpin folding. We go beyond the individual nucleotide sequences by focusing on the general RNA hairpin-folding scenarios as well as the specific features such as the loop and stem dependence. We first test and validate the theory through direct experimental tests for several experimentally measured duplexes and hairpins. We then employ the theory to investigate the general scenarios for RNA hairpin-folding kinetics.

THEORY AND METHODS

Transition rate model

Kinetic move set

The stability of a basepair in an RNA secondary structure (e.g., a hairpin structure) depends on the identity of the flanking basepairs and the identity of the basepair itself (38,39). This nearest-neighbor model is rationalized by the fact that RNA secondary structure is stabilized mainly by the base-stacking interactions and the hydrogen bonding—both of which are short-range local interactions and dependent primarily on the identity of adjacent basepairs (40). Adjacent basepairs form base stacks. For a given RNA sequence, we can exhaustively enumerate all the possible hairpin conformations according to the base stacks. Since a single (unstacked) basepair is not stable (38) and can quickly unfold, we define a kinetic move (equal to an elementary kinetic step for the transformation from one conformation to the other) to be the formation/disruption of a stack or a stacked basepair. Therefore, two conformations are kinetically connected if they can be interconverted through the addition or deletion of a base stack and are kinetically disconnected otherwise. Transitions between the disconnected conformations are disallowed and have rates equal to zero. Here we use the term base stack instead of basepair to define the kinetic move set because a single (unstacked) basepair is not stable. Our kinetic move model will be tested against experiments in Experimental Tests for the Rate Constant Model (see below). To compute the folding kinetics, we need a model to calculate the rate for each kinetic move.

Rate constant for a kinetic move

The transition rate for each kinetic move can be calculated from the general formula

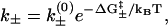(1)

with “+” for the formation and “−” for the breaking of the stack, where k_B is the Boltzmann constant, T is the temperature, and 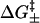is the free energy barrier of the respective transitions, and 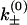is a prefactor to be determined from the experiments.

The formation of a base stack or a loop usually involves an unfavorable entropy loss ΔS due to the accompanying restriction in the torsional angles, the desolvation, etc. We assume that the transition state is at the point where the bases have been fixed to the stacked configuration but the bases have not reacted to form the stabilizing hydrogen-bonding and base-stacking interactions. The barrier for the formation of the transition state is entropic: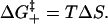

The breaking of a base stack involves an enthalpy increase ΔH due to the disruption of the hydrogen bonding and the base-stacking interactions. We assume that the transition state is at the point where the hydrogen bonding and the base-stacking interactions have been disrupted, but the torsional angles of the chain are not yet liberated from the restricted base-stack configuration. The barrier for the formation of the transition state is enthalpic: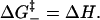

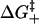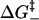Both and depend on the sequence identity of the bases involved. In our model, ΔH, ΔS, and 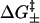are calculated from a statistical mechanical model for RNA folding (41). Assuming 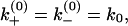from Eq. 1, we have

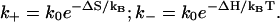(2)

The above expressions for the rate constants satisfy the detailed balance condition of 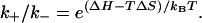If ΔS and ΔH are T-independent, k₊ would also be T-independent but k_– would be strongly dependent on T and is larger for higher T.

Rate for base-stack formation

When a base stack is formed, the increased charge density of RNA backbone would immobilize the counterions and the solvent molecules around the base stack. The reorganization of water molecules, which results in the volume contraction, increases the order of the system and yields an entropy loss (42). So the total entropic loss −ΔS (ΔS > 0) for the formation of a base stack is equal to the sum of the contributions from the loss of conformational entropy −ΔS_conf (ΔS_conf > 0) and the decrease in the entropy of hydration and counterions −ΔS′ (ΔS′ > 0) (42), which is ΔS = ΔS_conf + ΔS′. As a result, we can write the rate k₊ in Eq. 2 in the form of

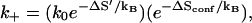so k₀ is larger than the effective diffusive prefactor

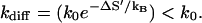The rate factor 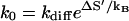is determined not only by the solvent quality (e.g., solvent viscosity) through k_diff, but also by the hydration and the electrostatic states of the nucleotide (bases) through ΔS′. Different bases can have different hydration and ion-binding states and so can have different k₀ values. For example, the GC pair and the AU pair are hydrated differently, so the GC and AU basepairs can have different k₀ values.

Rate for loop formation

According to the nearest-neighbor model, a single (unstacked) basepair is not stable (38) and has zero enthalpy (ΔH = 0). So the loop conformations closed by a single basepair are unstable and can quickly unfold (see state a in Fig. 1). As a result, because the formation of the stabilizing base stack (b → c) is much slower than the breaking of the loop (b → a),

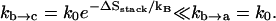So the unfolded state (a in Fig. 1 A) and the (unstable) looped state (b in Fig. 1 A) can pre-equilibrate before a stable base stack (see state c in Fig. 1 A) is formed to close the loop. Here k_{b → c} is calculated as k₊ in Eq. 2, with ΔS_stack equal to the entropy of the stack in state c and k_{b → a} is calculated as k_– in Eq. 2 with ΔH = 0 for the breaking of the unstacked basepair in state b.

FIGURE 1.

(A) A schematic free energy landscape for the loop formation. State a is the fully unfolded state that contains no basepair. State b contains a loop closed by a basepair. State c is a loop conformation stabilized by a closing base stack. Transitions b → c and c → b are rate-limited by an entropic barrier of TΔS_stack due to the formation of the closing stack and an enthalpic barrier of ΔH_stack for the breaking of the base stack, respectively. Transitions a → b and b → a are rate-limited by an entropic barrier of TΔS_loop due to the formation of the loop and an enthalpic barrier of ΔH_loop = 0 for the breaking of the single (unstacked) basepair, respectively. Here, according to the nearest-neighbor model, the single basepair in b does not make an enthalpic contribution (i.e., ΔH_loop = 0). So the disruption of state b is very fast and the relaxation between state a and the unstable state b is fast. As a result, states a and b can have sufficient time to pre-equilibrate before the loop is stabilized through the b → c transition. (B) In the kinetic-cluster model, stabilizing the pathway conformation (in the shaded free energy landscape) concomitantly stabilizes the transition state and thus speeds up the intercluster transition. This is because the free energy difference between the transition state and the pathway conformation is equal to the barrier of the kinetic move (= TΔS and ΔH for the formation and disruption of a base stack, respectively) and is independent of the free energy of the pathway conformation. Here ΔS and ΔH are the entropy and enthalpy changes associated with the formation/disruption of the base stack.

The rate for the formation of a stabilized loop can be estimated from Fig. 1 as

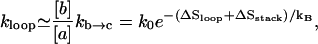(3)

where ΔS_loop is the entropy loss for the loop closure in the a → b transition, and is the relative equilibrium population between the open state a and closed state b. Eq. 3 implies that, in the present model, the rate for the formation of a stable loop is determined by not only the rate (k_{b → c}) for the formation of the closing stack but also the stability (∼[b]/[a]) of the closed loop conformation (b in Fig. 1 A).

Rate-limiting steps in RNA hairpin folding

The unfolding process involves the breaking of the native stacks, so the rate-limiting step of unfolding is to disrupt the slow-breaking native stacks. According to Eq. 2, the slow-breaking stacks are those with large enthalpy (ΔH).

On the other hand, the folding process involves the formation of the native stacks and the breaking of the nonnative base stacks, so the rate-limiting steps of folding are the formation of the slow-forming native stacks and the breaking of the possible slow-breaking nonnative base stacks. According to Eq. 2, the slow-forming native stacks are those with large ΔS and the slow-breaking nonnative stacks are those with large ΔH.

The rate constants for kinetic moves can only give rates for individual transitions in the folding process. The overall folding kinetics is determined by the collective and correlated events consisting of all the possible kinetic transitions (moves) in the folding process. To treat the statistics of the kinetic transitions, we discuss the following two theories used in this study: the master-equation method and the kinetic-cluster method.

Models for folding kinetics

Master-equation method

In the master-equation approach, the populational kinetics p_i(t) for the i^th state (i = 1, .., Ω, where Ω is the total number of chain conformations) is described as the difference between the rates for transitions entering and leaving the state,

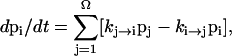where k_j→i and k_i→j are the rate constants for the respective transitions. The above master equation has an equivalent matrix form: dp/dt = M · p, where p is the fractional populational vector col (p₁, p₂, … , p_Ω), M is the rate matrix defined as M_ij = k_i→j for i ≠ j, and 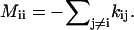Two key issues in the master-equation method are how to compute the rate constants (k_i→j and k_j→i) and how to solve the master equation.

For a given initial folding condition at t = 0, by diagonalizing the rate matrix M, we have the populational kinetics p(t) for t > 0,

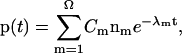(4)

where −λ_m and n_m are the m^th eigenvalue and eigenvector of the rate matrix M, and C_m is the coefficient that is dependent on the initial condition.

The eigenvalue spectrum gives the rates of the kinetic modes of the system. For a closed isolated system with the rate constants satisfying the detailed balance condition, there always exists an eigenvalue λ₁ = 0 for the equilibrium mode (43). Physically, the existence of this zero eigenvalue corresponds to the fact that as t → ∞, regardless of the initial condition of the system, the system eventually relaxes to the final equilibrium state. All other λ_m values are negative and nonzero. The smallest nonzero |λ_m| gives the rate of the slowest (rate-limiting) kinetic processes. Especially, if there only one distinctively small nonzero |λ_m| exists in the eigenvalue spectrum, the populational kinetics p(t) would be single-exponential with the rate determined by the smallest nonzero |λ_m|. The eigenvectors give the basic modes of the kinetic process and are intrinsically related to the energy landscape. In fact, from the eigenvectors we can obtain the rate-limiting steps of the kinetics (36).

The great advantage of the master-equation approach is that it is based on the complete ensemble of the conformation states and accounts for the kinetic effect of each and every interconformation transition. For a given rate constant model (see Eq. 1), the master equation can give a rigorous and exact solution for the relaxation kinetics of the system. Therefore, in this study, we will use the master-equation method to test the rate constant model against the experimental data for short sequences.

The master-equation approach has its limitations. The master-equation solution can only give ensemble-averaged macroscopic kinetics and cannot give detailed information about the microscopic pathways. Moreover, RNAs are polymers, whose number of conformations (Ω) increases rapidly with the chain length (44). So the master-equation approach is limited to short sequences whose rate matrix size is not too large. Because of these reasons (and especially for the first reason), we use the kinetic-cluster method, which, as explained in the next section, can overcome the above two difficulties.

Kinetic-cluster method

The basic idea of the kinetic-cluster method is to classify the large conformational ensemble into a much reduced system of clusters (macrostates) so that the overall kinetics can be represented by the intercluster (instead of interconformation) transitions. A great advantage here is that the microscopic kinetic rates and pathways can be examined in great detail. A number of attempts have been made to model the intercluster kinetics (45–50,53). In general, there are two types of approach. In the first type of approach, the intercluster rate is computed based on the transition state with the lowest barrier (45–52). For each pair of initial and final states, the optimized pathway is used to estimate the rate constant. In the second type of approach (53), conformations that are interconvertible through barrierless transitions are classified as a cluster, and the rate constants are calculated based on all the possible intercluster kinetic pathways. Kinetic Monte Carlo simulations have also been successfully used to obtain the intercluster rate (49,54). These and other simulations (31–34) sample the kinetic paths in a stochastic way. In our present kinetic-cluster method, a collection of pre-equilibrated conformations is classified as a cluster (macrostate). Such a cluster includes the barrierless conformational cluster defined in the previous model (53) as a special subset. So the present approach is more general. From the intercluster rate constants, we construct the reduced rate matrix. From the eigenvalues and eigenvectors of the reduced rate matrix, we can analyze the rates and pathways for the folding and unfolding kinetics.

Although both the master-equation method and the present kinetic-cluster method can predict the macroscopic kinetics, and both are based on the complete conformational ensemble, the kinetic-cluster approach has the unique advantage of providing the direct information on the microscopic pathway statistics from the intercluster transitions.

The kinetic-cluster method is based on the existence of the pre-equilibrated clusters. The pre-equilibration and cluster formation have been observed in previous experiments and computer simulations (50,53,55) and the kinetic-cluster method has been rigorously validated through extensive tests against the results from the original exact master equations (37). However, the kinetic-cluster method has its limitation. The kinetic-cluster method would fail if the system does not have well-defined discrete rate-limiting steps, in which case no pre-equilibration would occur and thus no pre-equilibrated cluster would exist.

The following is a summary for the kinetic-cluster method with applications to RNA hairpin-folding kinetics.

How to classify conformations into clusters. To simplify the illustration, we use simple unfolding kinetics to show the idea. The unfolding of a hairpin involves the breaking of the native base stacks in the native hairpin structure. If the breaking of a native base stack, say, s*, is distinctively slower than the breaking of other native stacks, then the breaking of s* is the rate-limiting step for the unfolding reaction. According to the slow-breaking s*, we can define two clusters for conformations before and after the rate-limiting stack s* is broken:

The existence of the rate-limiting stack s* implies that the transitions between conformations within a cluster are faster than transitions between conformations in different clusters. Therefore, conformations within a cluster may pre-equilibrate before entering a different cluster through intercluster transitions. As a result, each cluster can be treated as pre-equilibrated macrostate and the overall unfolding kinetics is determined by the slow intercluster transitions.

Two types of conformations: Pathway conformation and nonpathway conformations. For an intercluster transition, a conformation N_i in cluster N is transformed to a corresponding conformation U_i in cluster U through the breaking of the rate-limiting stack s*. There exist many such intercluster pathways between the clusters. We define pathway conformations as conformations (such as N_i in cluster N) that are directly connected to the other clusters through kinetic movement. They are called pathway conformations because they form the intercluster pathways. All the other conformations are called nonpathway conformations. We distinguish these two types of conformations because only the pathway conformations directly contribute to the intercluster kinetics.

Intercluster transition rates and the dominant pathways. The intercluster transition rate is given by the sum over all the possible microscopic pathways U_i ↔ N_i between pathway conformations in the respective clusters,

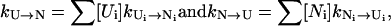(5)

where [U_i] and [N_i] are the equilibrium fractional populations of U_i and N_i in the respective clusters,

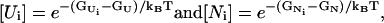(6)

where and 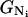are the free energies of conformations U_i and N_i, respectively, and G_U and G_N are the free energies of clusters U and N, respectively,

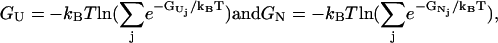(7)

where the summations in Eq. 7 are for all the (pathway and nonpathway) conformations in the respective clusters.

From the above equations for the intercluster rates, we find that the intercluster transition rates are determined by two factors: the stabilities of the pathway conformations (e.g., [U_i] and [N_i]) and the rates (e.g., 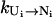and 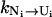) for each intercluster pathway. The interplay between these two factors leads to the following general conclusions for the intercluster kinetics:

Pathway conformations versus nonpathway conformations. For given rate constants (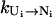), stabilizing the pathway conformations (versus the nonpathway conformations) speeds up the intercluster transition. As illustrated in Fig. 1 B, stabilizing the pathway conformation would concomitantly stabilize the transition state and thus speed up the transition. This is because the free energy difference between the transition state and the pathway conformation is determined by the barrier of the kinetic move, which is independent of the stability of the pathway conformation.

Fast versus slow pathway conformations. Some pathway conformations have large transition rate 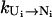and are thus called fast pathway conformations and others are the slow pathway conformations. Stabilizing the fast pathway conformations (versus the slow pathway conformations) leads to faster intercluster transitions.

Dominant pathways. The probability for the molecule to take a specific pathway, say, U_i → N_i, is determined by its fractional contribution to the total rate:

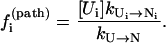(8)

We call 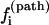the kinetic partitioning factor or pathway partitioning probability. The pathways that have the largest 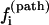are the dominant pathways. Due to the temperature and sequence-dependence of the rate constants and of the stabilities of the pathway conformations, the dominant pathways can be quite sensitive to the temperature and the sequence. Moreover, the folding and unfolding reactions can involve different rate-limiting base stacks and can thus be described by different clusters. As a result, folding and unfolding reactions can have quite different dominant pathways.

EXPERIMENTAL TESTS FOR THE RATE CONSTANT MODEL

There are two key issues of the present theory: the rate constant model and the kinetic-cluster method. Although the latter has been extensively validated (37), the former requires rigorous tests. The rate constant model includes two ingredients: 1), the definition of the kinetic move; and 2), the transition rate for a kinetic move (see Eq. 2). In this section, we aim to test the rate constant model through experimental comparisons. In addition, we can fit the prefactor k₀ in the rate constant equation (Eq. 2) from experiments.

We use the experimentally measured parameters (ΔH, ΔS) for the base stacks (56). To compute the transition rates from Eq. 2, we need to know the prefactor k₀. Due to the different energetics of the GC and AU basepairs, we assign different k₀ values for stacks with GC and AU basepairs. We determine k₀ by fitting the experimental data. Specifically, we use the relaxation rates for the (A_nU_n)₂ duplex (57) and for the (A₄GCU₄)₂ duplex (58) for AU and GC, respectively. After the prefactors are determined, we would further validate the model by applying the model to predict the relaxation rates for a wide temperature range for other hairpin-folding experiments; see Table 1.

TABLE 1.

A summary for the experiments used to test the theory

Experiment (Ref.)	Sequence	Structure	Ion condition
(57)	(AnUn)2	Duplex	0.25 M Na+
(58)	(A4GCU4)2	Duplex	1.05 M Na+
(11)	A6C6U6	Hairpin	1 M Na+
(60)	AUCCUAUT4UAGGAU	Hairpin	0.2 M Na+

It is important to note that for simple sequences such as (A_nU_n)₂, the k₀ value serves as a global scaling factor for the overall rates. So for simple sequences (A_nU_n)₂, k₀ plays no role in determining the physical nature of the kinetics, namely, the pathways, the transition states, and temperature-dependence of the rates. For all the experimentally measured sequences that we tested, the predicted shapes of the rate versus temperature curves (equal to the Arrhenius plot) agree with the experimental results. Furthermore, the k₀ parameters fitted from one experiment can give good predictions for other experiments, i.e., the fitted k₀ parameters are transferable between different experiments. These results suggest that the model, including the definition of the kinetic moves and the rate constants for the kinetic moves may be valid and reliable.

In this section, where the goal is to test the rate constant model, we use the original master equation instead of the kinetic-cluster method to remove the possibility of any error caused by the kinetic-cluster method. So the tests would be exclusively focused on the rate constant model. For each sequence tested, we consider the complete ensemble of all the possible conformations and compute the interconformation rate-matrix from Eq. 2. By diagonalizing the rate matrix, we obtain the relaxation rates from the eigenvalues of the rate matrix for different temperatures.

Duplex formation

For the duplex formation, we use the zipper model. The model assumes that all the base stacks occur contiguously in a region. We use base stacks to describe the duplex structure because stacking is the major stabilizing force. Previous approach to the duplex formation is based on a prior assumption on the two states of the transition (57). A steady-state approximation was used. In the present study, we do not make a prior assumption about the two-state of the kinetics. So the model can account for any possible kinetic intermediates. The formation of the first stack of the duplex from the single strand is a second-order chemical reaction process, while the helix growth is a first-order (linear) process. Let [A₀] and [A_N] be the concentration of the single and the fully zipped (native) duplex with N basepairs, respectively. When we use 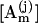to denote the concentration of the j^th state with m stacks, the rate equation can be written as

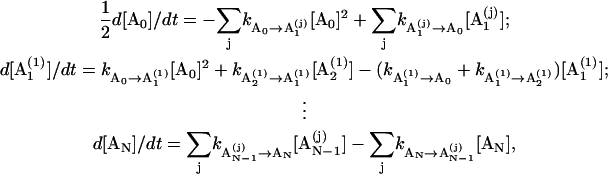where k_{a → b} denotes the a → b transition rate. Furthermore, because the temperature jump in the experiment is small (≃3 − 4°) (57), the concentration deviation from the equilibrium level is small. Therefore, we can use the following linear approximation for the concentration deviation x₀ = [A₀] – [A₀]_eq from the equilibrium value 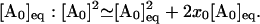With this approximation, the above equation becomes a linear master equation for the concentration deviations of A₀, A_N, and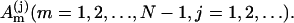

The rate for the formation of the first base stack in a contiguous helix region 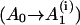is equal to 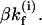Here β is the nucleation probability, i denotes the position of the base stack, and 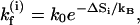where ΔS_i is entropic change for the formation of the base stack. After the first stack is formed, the growth rate (e.g., 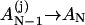) of a base stack j is equal to The breaking rate for a base stack j (e.g., 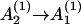) is equal to 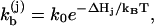where ΔH_j is enthalpic change for the formation of the base stack.

The nucleation parameter β is the probability that two bases in different strands will approach each other. The value β can be determined from the measured equilibrium constant K, which, in the zipper model, is given by

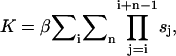where i denotes the nucleating base stack, n is the length of the helix, and 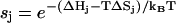is the stability of the j^th stack.

The ΔH and ΔS parameters are typically measured under 1 M NaCl condition. However, many of the experiments that we use for comparison were performed under other ionic conditions (see Table 1). For example, the measurements for the (A_nU_n)₂ kinetics is under 0.25 M Na⁺ condition (57). So we need to know the ΔH and ΔS parameters under arbitrary ionic conditions. We use the following empirical ion concentration-dependent parameters, which are reliable for ion concentrations not too low (≥mM) (59):

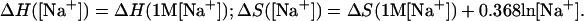The lowest nonzero eigenvalue of the above linear rate equation gives the relaxation rate and the relaxation time τ = (relaxation rate)⁻¹. Comparison between our model prediction and the (A_nU_n)₂ experimental data gives the prefactor k₀ = 6.6 × 10¹² s⁻¹ for AU stacks.

The relaxation time τ as a function of the reciprocal of temperature is shown in Fig. 2 a. The results show that the theoretical predictions are in good agreement with the experimental data for a wide temperature range and for different chain lengths. The agreement is better for longer chains. For short chains (small n), the theory-experiment difference comes from the finite size effects of the oligomers. For example, the electrostatic effect can cause nonadditivity in the base-stack stabilities (57). Moreover, the rates are overestimated for short chains due to the ignored conformations in the zipper model and the possible inaccuracy of the ion-dependence of the energy parameters used in the model.

FIGURE 2.

The temperature (T in Kelvin) dependence of the relaxation time for the duplex formation. (Symbol, experiment; line, model.) (a) (A_nU_n)₂ (from bottom to top, n = 4, 5, 6, 7) (0.25 M Na⁺). (b) (A₄GCU₄)₂ (1.05 M Na⁺). The experimental relaxation time are determined by 1/τ = 4k₁C₀ + k_–1, where k₁ and k_–1 and C₀ are from the experiment (58).

We can determine the association rate constant k₁ and the dissociation rate constant k_–1 for the two-state transition through the relaxation time τ and the equilibrium constant K,

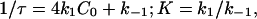where 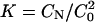is the equilibrium constant, and C_N and C₀ are the measured concentrations of the duplex and monomer, respectively. Consistent with the experimental results, our model predicts that k₁ is only weakly dependent on temperature T and the chain length n, and k_–1 decreases as temperature T decreases or duplex length n increases (data not shown).

To determine the prefactor k₀ for base stacks with the GC basepair, we study the kinetics for the duplex (A₄GCU₄)₂ (58). The duplex involves both AU and GC basepairs. Given the k₀ value for the AU pairs, we find that k₀ is equal to k₀ = 6.6 × 10¹³ s⁻¹ for the GC pair. The k₀ for the GC pair is larger than that for AU because a GC pair involves stronger bonding than an AU pair. In Fig. 2 b, we show the temperature-dependence of the relaxation rate for (A₄GCU₄)₂, and we find good agreement between theory and experiment for a wide range of temperature.

Hairpin formation

Our purpose here is to have further tests on the rate constant model through experimental comparisons for the temperature-rate dependence. We use our model to make predictions for two RNA hairpin-folding experiments (58,60) that showed quite different temperature-dependence of the relaxation rate. In Fig. 3, a and b, we show the results for sequences A₆C₆U₆ (58) at 1 M NaCl and r(AUCCUAUT₄UAGGAU) (60) at 0.2 M NaCl, respectively. We find reasonably good theory-experiment agreements.

FIGURE 3.

The temperature (T in °C) dependence of the relaxation time for hairpin disruption. (Symbol, experiment; dashed line, model.) (a) A₆C₆U₆ ((11);1 M NaCl). (b) r(AUCCUAUT₄UAGGAU) ((60); 0.2 M Na⁺).

The eigenvalues of the rate matrix in the master equation gives the relaxation rate k_r. For a two-state transition, from k_r, we can obtain the folding rate k_f and the unfolding rate k_u separately from the following two equations: k_r = k_f + k_u and K = k_f/k_u, where K is the equilibrium constant, which can be determined from our statistical thermodynamic model. At unfolding temperatures T > T_m (T_m is the folding-unfolding transition temperature), the relaxation process is predominantly an unfolding process, so 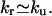At folding temperatures T < T_m, the relaxation process is mainly a folding process, so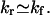

As shown in Fig. 3 a for sequence A₆C₆U₆, the value k_f increases as temperature increases, indicating a positive activation enthalpy for the folding. In our model, such positive activation enthalpy arises from the breaking of the misfolded states, which can be formed through sliding of one or more bases from the native basepair positions. Another possibility for the positive activation enthalpy of folding is for the breaking of the single-strand stacking, which is not considered in the model. In fact, neglecting the breaking of the single-strand stacking may be a reason why our predicted rate is larger than the experiment result in Fig. 3 a.

For sequence r(AUCCUAUT₄UAGGAU), the T₄ loop was treated as the RNA loop U₄. Due to the different chain stiffness, the entropy of T₄ loop may be smaller than that of U₄. As a result, the rate for loop closure may be underestimated by the model; see Fig. 3 b.

GENERAL THEORY OF HAIRPIN-FOLDING KINETICS

In this section, using the kinetic-cluster method, we present a general theory for RNA hairpin-folding kinetics. We first discuss the possible slow processes of hairpin folding and the different folding kinetics scenarios with different slow processes as the rate-limiting steps for the overall folding. We then discuss the kinetic clusters and the energy landscapes for each different scenario.

Rate-limiting steps

To fold from a fully unfolded state, the hairpin forming chain undergoes the following four types of the possible slow processes (see Fig. 4):

FIGURE 4.

The four types of possible slow folding processes: (a) loop formation, (b) formation of a rate-limiting stack, (c) direct folding, the loop is closed by a rate-limiting stack (shaded) from the fully unfolded state, and (d) detrapping through disruption of the nonnative base stack (pattern-fill).

Loop nucleation (Fig. 4 a)

The formation of the first base stack can be rate-limiting because it concurrently causes the closure of a loop, and has a rate constant of

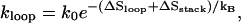(9)

where ΔS_stack and ΔS_loop are the entropic losses associated with the formation of the base stack and the corresponding loop. The process is slow if the total entropic loss (ΔS_loop + ΔS_stack) is large.

Formation of the rate-limiting stack (Fig. 4 b)

If a native base stack s* exists, whose entropy ΔS* is exceedingly larger than that of other native stacks, according to Eq. 2, the formation of s* would be exceedingly slower than the formation of other native stacks. As a result, the formation of s*, which has a rate constant of

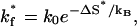(10)

is a rate-limiting step for the overall folding process.

Direct folding (Fig. 4 c)

In the loop nucleation process, if the loop is closed by a rate-limiting stack s* from the fully unfolded state, the loop closing process would be extremely slow with a rate constant of

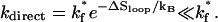(11)

The contribution from such process to the overall folding kinetics can often be ignored due to the extremely slow rate.

Detrapping (Fig. 4 d)

In the folding reaction, nonnative base stacks formed in the process need to be disrupted for the folding process to proceed. The disruption of nonnative base stacks (detrapping) has a rate constant of

(12)

where ΔH_nn is the enthalpy cost to break the nonnative base stack. The detrapping process can be slow for large ΔH_nn or low temperature T. The process can become a rate-limiting step if k_detrap is small.

Kinetic cluster

According to the above possible slow steps, we can classify the conformational ensemble into five clusters, C, I_n, I_nn, N_n, and N_nn, such that

(13)

I_n and I_nn are the conformations in cluster I without and with nonnative base stacks, respectively, and N_n and N_nn are the conformations in cluster N with and without nonnative base stacks, respectively. Fig. 5 summarizes the kinetic-cluster classifications. In Fig. 5 a, F = I + N is the cluster for all the folded and partially folded conformations and U = C + I is the cluster for all the conformations with the rate-limiting stack s* disrupted.

FIGURE 5.

Summary of the two types of kinetic-cluster classifications.

By defining the nonnative clusters I_nn and N_nn, we neglect the heterogeneity of the non-native stacks by grouping different nonnative states into the same cluster. This assumption may cause an overestimation for the folding rate due to the neglected transition time between different nonnative conformations within clusters I_nn and N_nn. The overestimation for the rate is negligible for larger k_detrap when the disruption of the nonnative stacks is fast and can become important if k_detrap is small. Nevertheless, the separation of nonnative I_nn from the nativelike I_n and nonnative N_nn from native N_n can, to the lowest-order approximation, account for the trapping effect in the folding process.

Energy landscapes

The competition between the loop nucleation (k_loop), the formation of the rate-limiting (native) stack (k_f*), and the detrapping of the nonnative stacks (k_detrap) results in a great variety of different scenarios for the energy landscapes and folding kinetics (see Fig. 6). We can classify the folding landscapes and folding kinetics into the following different scenarios; see Table 2 for a summary.

FIGURE 6.

Schematic free energy landscapes for different folding scenarios. The shaded line shows the formation of the native-like looped structures I_n from the unfolded state C. I_nn represents the non-native intermediate state. (a) Scenario 1: The rate-limiting process is the loop formation. The folding is a two-state (C → F = I + N). (b) Scenario 2: The rate-limiting process is the formation of a rate-limiting base stack. I_n and I_nn equilibrate quickly and form a pre-equilibrate macrostate (cluster) I. The folding is a two-state process U (= C + I) → N. (c) Scenario 3: Weakly noncooperative folding with a rate-limiting stack and a (or few) slow-breaking misfolded nonnative base stacks. The kinetics is multi-state (five clusters: C, I_n, I_nn, N_n, N_nn). N = N_n + N_nn (N_n and N_nn not shown). (d) Scenario 4: Strongly noncooperative folding. The disruption of an average nonnative stack is very slow and nearly every non-native state can form a kinetic trap. See also Table 2.

TABLE 2.

A summary for the different scenarios of the folding kinetics

Scenario	Energy landscape	Rate-limiting step	Cooperativity	Temperature
1	Fig. 5 a	Loop formation	Two-state C → F (= I + N)	T > Tr
2	Fig. 5 b	Formation of the rate-limiting native base stack s*	Two-state U (= C + I) → N	T > Tr
3	Fig. 5 c	Formation of s* and detrapping of the nonnative states	Multi-state C, In, Inn, Nn, Nnn	T ≤ Tr
4	Fig. 5 d	Rate-limiting steps not discrete	Glassy	T < Tr

Cooperative folding (if detrapping is fast)

The folding is cooperative (two-state) and single-exponential if the detrapping is much faster than both the loop nucleation and the formation of the rate-limiting stack:

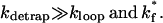(14)

If k_detrap is large, detrapping of nonnative base stacks is not a slow process. As a result, I_n and I_nn, which are separated by the slow-breaking nonnative stacks, can equilibrate quickly. As a result, they can merge to form larger pre-equilibrated cluster I. For the same reason, N_n and N_nn can be merged into a larger cluster N. The overall conformation ensemble can be classified into three clusters: C, I, and N (see Fig. 5 b). According to the competition between the loop nucleation and the formation of the rate-limiting stack, we can further distinguish two different folding scenarios:

Scenario 1: Cooperative folding through loop formation (if the formation of the native base stacks is fast). If the formation of the native base stacks is faster than the loop formation,

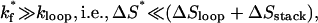(15)

no rate-limiting (native) base-stack s* exists. As a result, cluster I and N, which are separated by the possible slow-forming stacks s*, would quickly pre-equilibrate and form cluster F = I + N (see Fig. 5 a). The overall conformational ensemble is classified into two clusters, C and F, and the folding is a two-state transition: C → F corresponding to the loop formation (see Fig. 6 a). In fact, for most of the previous RNA and DNA hairpin-folding experiments (11), there is no rate-limiting (native) base stack, and the folding reaction C → F is rate-limited by the loop nucleation.

Microscopically, the transition C → F can be understood as the nonspecific formation of the loops. Once the looped conformations are formed, they can quickly interconvert to form the stable native structure through the fast breaking/formation of base stacks and the accompanying changes of the loops (e.g., through the chain sliding modes). Since the loop entropy is a logarithmic function of the loop size, which is not sensitive to the loop size change, the transitions between different looped structures within cluster F are not rate-limited by the loop changes, and are thus, fast.

Scenario 2: Cooperative folding through formation of the rate-limiting base stack (if loop formation is fast). If the slowest kinetic move is to form native base stack s*,

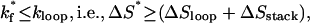(16)

then stack s* is major divider to separate different clusters and the conformational ensemble is reduced to a two-cluster system: U (= C + I) and N (see Fig. 5 b). Cluster U is the collection of conformations without the slow-forming s* (see Fig. 6 b), and the folding kinetics is two-state: U → N corresponding to the slow formation of s*.

Starting from the fully unfolded conformation C, the chain initially undergoes transition C → I to form cluster U. Because many different ways exist to form the nonspecific loops from the fully unfolded state, the C → I process is fast even if k_loop is not much larger than k_f*.

After initial fast formation of cluster U, the chain undergoes slow transition U → N to form the rate-limiting stack s*. Some conformations in U may be transiently populated at this stage because they have large (fractional) equilibrium population in U but not in the final overall conformational ensemble U + N. These conformations are kinetic intermediates. How do the emergence of the intermediate states and the two-state cooperativity compromise with each other? Since the different conformations, including the kinetic intermediates, in the cluster U have already reached equilibrium, transitions between conformations in U do not contribute to the folding time. Equivalently speaking, conformations in U act as an effective single state for the folding kinetics. Therefore, regardless of the existence of the kinetic intermediates, the resultant folding kinetics is two-state (U → N) and single-exponential.

Noncooperative folding (if detrapping is slow)

Scenario 3: Weakly noncooperative folding kinetics. If one or only a few nonnative stacks exist whose disruption rate k_detrap is slow (i.e., comparable to k_f*), the folding would be (weakly) noncooperative. For example, if one slow-disruption nonnative base stack exists, we can describe the kinetics using five clusters (C, I_n, I_nn, N_n, N_nn in Fig. 5 b; see Fig. 6 c for a schematic plot of the free energy landscape). The resultant kinetics would be multi-state and multi-exponential.

The kinetic traps would form kinetic intermediates in the folding process. These intermediates are different from the intermediates that emerged in the two-state cooperative folding process. The kinetic traps in the noncooperative kinetics prevent the formation of the pre-equilibrated cluster I (I = I_n + I_nn), while the intermediates in the cooperative kinetics are the result of the pre-equilibration of the cluster U(= C + I).

Scenario 4: Strongly noncooperative folding kinetics. The folding kinetics becomes strongly noncooperative if the detrapping from an average nonnative stack is slow: 〈k_detrap〉 ≤ k_f*, where 〈…〉 denotes the average over all the possible nonnative base stacks. See Fig. 6 d for a schematic free energy landscape. When the above condition is satisfied, on average, each individual nonnative state should be treated as a separate cluster. As a result, the use of I_n, I_nn, N_n, N_nn becomes invalid and the resultant folding kinetics is strongly multi-state (noncooperative) and strongly multiple-exponential.

Folding rate-temperature dependence

In this and the next section, we use a 21-nt sequence UAUAUCGC₇CGAUAUA as an example to illustrate the complex hairpin-folding kinetics using the kinetic-cluster theory. From the previously reported statistical thermodynamic statistical model (41), we find the folding/unfolding melting temperature T_m≃50°C for this sequence.

As shown in Fig. 7 b, from the large (ΔS, ΔH) parameters, the formation and disruption of the native base stack s* = (5,6,16,17) = (U,C,G,A) are rate-limiting for the folding and unfolding kinetics due to large ΔS = 35.5 eu and ΔH = 13.3 kcal/mol, respectively. The rate constants for the formation and disruption of s* are given by Eq. 2: 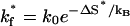=1.29×10⁶s⁻¹and which is equal to 3.19 × 10⁴ s⁻¹ at T = 37°C.

FIGURE 7.

(a) Temperature (T in °C) dependence of the relaxation rate for a hairpin-forming sequence UAUAUC- GC₇CGAUAUA. (Solid line) From the original complete conformational ensemble (master-equation method); (dashed line) from the two-cluster model (Scenario 2); and (dotted line) from the five-cluster model (Scenario 3). (b) The native structure and energy parameters of the native state. The shaded stack is the rate-limiting stack. (c) The pathway conformations U_i and N_i (i = 1, 2, … , 20) in the respective clusters U and N and the corresponding intercluster pathways and rates. U₁ → N₁ is the direct folding pathway through the loop closing by the rate-limiting stack. N₁₉ → U₁₉ is a double-breaking pathway that involves the simultaneous breaking of two stacks (one of which is the rate-limiting stack). U₄ is a nonnative pathway conformation because it contains a nonnative base stack.

Plotted in Fig. 7 a is the temperature-dependence of the relaxation rate k_r for the sequence. The predicted k_r-T relationship (Arrhenius plot) is consistent with the experimental findings for some DNA hairpins (21). The relaxation rate k_r is related to the folding rate k_f and the unfolding rate k_u through the equation k_r = k_f + k_u for a two-state transition. The kinetics is dominated by the folding reaction for T < T_m and k_r≃k_f and by the unfolding reaction for T > T_m and k_r≃k_u. The Arrhenius plot in Fig. 7 a has two characteristic temperatures: T_m≃50°C and a rollover temperature T_r≃10°CC. According to T_m and T_r, the k_r-T relationship can be classified into three regimes:

1. Unfolding at T > T_m: k_r ∼ k_u increases as T is increased because the rate for breaking the stack ∼k_b* is larger for higher T.

2. Folding at temperature T between T_r and T_m: k_r ∼ k_f increases as T decreases, indicating a negative apparent activation energy.

3. Folding at low temperature T < T_r: k_r ∼ k_f decreases as T decreases, indicating a positive activation energy.

What causes the rollover of the rate-temperature dependence plot? How to predict the rollover temperature T_r from the microscopic energetics? In this section, we explore the connections between the macroscopic Arrhenius plot and the microscopic kinetic clusters.

Since the formation of s* is the sole dominant rate-limiting step, we can classify the conformational ensemble into two clusters U and N; see Fig. 5 b. For this 21-nt sequence, there are a total of 20 hairpin conformations in cluster U to which the rate-limiting stack s* can be added through a kinetic move. These 20 conformations (U_i, i = 1, 2, …20; see Fig. 7 c) are the pathway conformations in cluster U. There are 20 corresponding intercluster pathways (see Fig. 7 c). Among the 20 pathways, U₁ (= C) → N₁ is through the direct folding and is extremely slow (see Eq. 11). The rest of the 19 pathways are fast-folding pathways (see Fig. 7 c).

The temperature-dependent competition between the stabilities of the following three types of conformations leads to the complex temperature-dependence of the folding rate: 1), the fast-folding (U₂, …, U₂₀); 2), the slow-folding (U₁) pathway conformations; and 3), the nonpathway conformations in cluster U. For the given sequence, as shown in Fig. 8 a, a decrease in temperature causes two competing effects:

1. The fast-folding pathway conformations U₂, …, U₂₀ are stabilized and the slow-folding conformation U₁ are relatively destabilized, causing a faster folding rate.

2. The nonpathway (nonnative) states in U are stabilized, causing a decrease in the total population of the pathway conformations in cluster U and hence a slower folding rate.

FIGURE 8.

(a) The populational distribution of the pathway conformations U_i → N_i for i = 1, 2, …, 20 (solid for T = 30°C and shaded for T = 90°C). The total faction population of the nonpathway conformation is listed as the state 21 in the figure. (b) The probability 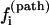for the molecule to fold along U_i → N_i (i = 1, 2, …20) (solid for T = 30°C and shaded for T = 90°C). As temperature T is increased from 30°C to 90°C, the populational distribution is shifted from the fast-folding conformation (i = 20) to the slow-folding conformation (i = 1), causing a slow folding process.

For the given sequence, the former effect dominates and thus the folding is accelerated at lower temperatures.

As the temperature is further lowered, at a critical temperature T_r, the Arrhenius plot shows a rollover behavior, i.e., the rate decreases as temperature is decreased. Two possible mechanisms for the rollover exist:

1. In the cooperative folding regime (Scenario 2), the rollover can be caused by the stabilization of the nonpathway conformations or the slow-folding pathway conformations in cluster U, which leads to a slower (instead of faster) folding rate at lower T.

2. In a noncooperative folding process (Scenarios 3 and 4), the rollover can be caused by the formation of kinetic traps. In this case, as temperature is lowered, the detrapping rate k_detrap decreases, resulting in a decrease in the overall folding rate. In this case, rollover behavior corresponds to the transition from the cooperative to the noncooperative folding kinetics and T_r is determined by the condition for Scenario 3 to occur, which is k_detrap ∼ k_f*. For the given sequence, we find T_r = 10°C.

As shown in Fig. 7 a, the two-state model cannot account for the rollover behavior. Only after we introduce the five-cluster model (C, I_n, I_nn, N_n, N_nn) in Scenario 3 can we obtain the rollover. This clearly shows that the rollover for this sequence is caused by the second mechanism above. The strongly multi-state (and glassy) folding kinetics occurs at even lower temperatures.

Folding pathways

We discuss the folding pathways for three typical temperatures below. Fig. 8 shows the plot of the kinetic pathway partitioning probability 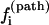defined in Eq. 8 for all the 20 U → N pathways in Fig. 7 c. The dominant pathways have the largest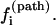

1. Cooperative folding at high temperature T = 90°C (T > T_m; Scenario 2). We find that the main folding pathways are U₁ → N₁ and U₂ → N₂, each contributing ∼14.5% and 51.6% to the total folding rate, respectively. This is because the populations of U₂ and U₁ overwhelmingly dominate the population in cluster U.

2. Cooperative folding at a lower temperature T = 30°C (T_r < T < T_m; Scenario 2). From Fig. 8 b we find the dominant folding pathway is U₂₀ → N₂₀. Approximately 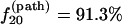of the population in U folds along this pathway. This is because of U₂₀ is the most stable fast-folding pathway conformation for T < T_m. As the temperature is increased, the population of the slow-folding (fully unfolded state) U₁ increases and that of the fast-folding state U₂₀ decreases, so the folding rate decreases.

3. Noncooperative folding at T = 10°C (T < T_r; Scenario 3). The folding kinetics can be described by the transitions between five clusters: C, I_n, I_nn, N_n, N_nn. From the unfolded state C, there are a large number of pathways to form a nonnative state in I_nn, so the chain would quickly fold to I_nn from C and I_nn becomes a kinetic trap. This is confirmed in the results of populational kinetics (data not shown). The later stage of the folding involves the detrapping from I_nn and the formation of the rate-limiting stack s*. If detrapping is faster, the chain would first detrap, then form s*. As the temperature decreases, detrapping slows down and may eventually becomes slower than the formation of s*, which is T-independent in the model. So in such low T case, the chain would first form s*, then detrap to break the nonnative stacks.

SUMMARY

The kinetic-cluster approach allows us to study the kinetic rates, rate-limiting steps, and the pathways for biologically significant RNA hairpins. The overall hairpin-folding process can be rate-limited by the formation of the loop, the formation of the slow-forming native base stack, and the disruption of the slow-breaking nonnative base stack. The competition between these different processes leads to the great wealth of different RNA hairpin-folding kinetic scenarios. The detailed folding kinetics is sequence-specific. For many sequences, there exists a temperature T_r such that for T < T_r the folding rate decreases as the temperature is decreased because of the decreased rate for breaking a misfolded nonnative base stack or the increased stability of the (misfolded) nonpathway conformations. For T > T_r, however, depending on the competition between the stabilities of the fast and the slow pathway conformations and the nonpathway conformations, as the temperature is decreased, the folding rate can either increase if the fast pathway conformations are stabilized or decrease if otherwise.

As a caveat, we note several limitations of the model. For chain length longer than 30-nt, depending on the nucleotide sequence, the chain could possibly form complex branched secondary structures. Because the branched nonhairpin structures are not considered in the hairpin-folding theory, we cannot arbitrarily generalize the conclusions found in this study to the more complex, branched RNA structures of longer chains. Another limitation is that the present model does not consider the kinetic effect of the formation and breaking of single-strand stacking (23,61). Therefore, the model may not be valid for sequences (e.g., Adenine-rich sequences) that have a high tendency to form single-strand stacking in the unfolded state. For these sequences, to break the single-strand stacking in the folding process may involve a large kinetic barrier, which is neglected in the present model. A third limitation is that the model does not account for the temperature-dependence of the rate constant (prefactor) k₀, which is dependent on the solvent viscosity and the hydration and electrostatic state of the bases. We assume that k₀ has weaker temperature-dependence than the stability factor (e.g., 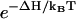). Moreover, the temperature-dependence of the (ΔH, ΔS) parameters (i.e., ΔC_p) is neglected for the base stacks.