Studying Reactive Processes with Classical Dynamics: Rebinding Dynamics in MbNO

Abstract

A new surface-crossing algorithm suitable for describing bond-breaking and bond-forming processes in molecular dynamics simulations is presented. The method is formulated for two intersecting potential energy manifolds which dissociate to different adiabatic states. During simulations, crossings are detected by monitoring an energy criterion. If fulfilled, the two manifolds are mixed over a finite number of time steps, after which the system is propagated on the second adiabat and the crossing is carried out with probability one. The algorithm is extensively tested (almost 0.5 μs of total simulation time) for the rebinding of NO to myoglobin. The unbound surface (Fe···NO) is represented using a standard force field, whereas the bound surface (Fe–NO) is described by an ab initio potential energy surface. The rebinding is found to be nonexponential in time, in agreement with experimental studies, and can be described using two time constants. Depending on the asymptotic energy separation between the manifolds, the short rebinding timescale is between 1 and 9 ps, whereas the longer timescale is about an order of magnitude larger. NO molecules which do not rebind within 1 ns are typically found in the Xenon-4 pocket, indicating the high affinity of NO to this region in the protein.

INTRODUCTION

Reactive processes are fundamental in chemistry and biology. A variety of physiologically relevant phenomena involve the formation and destruction of chemical bonds. During a typical enzymatic reaction (e.g., the Claisen rearrangement from chorismate to prephenate (1) or the conversion from dihydroxy acetone phosphate to glyceraldehyde-3-phosphate by triosephosphate isomerase (2,3)) several bonds are broken and formed. One possibility to describe a chemical reaction at atomic detail is to carry out density functional theory or ab initio calculations. Such studies are of great interest if information about the relative stability of the product and the educt state is sought. It is also possible to locate and characterize transition states which connect the two stable configurations. There are, however, reactions where the kinetics is equally important (and interesting). For such processes, mixed quantum mechanics/molecular mechanics (QM/MM) simulations can be used (4), for example to study proton transfer reactions (5–7). Such simulations are valuable, even though the timescale over which a process can be followed is limited because of the computational demands of the quantum chemical calculations. In the past, molecular dynamics (MD) simulations have been proven to provide meaningful information about structural and energetic aspects of macromolecular systems (8–10). Typical questions that have been addressed with MD simulations include, e.g., the conformational sampling of isolated proteins (protein folding/unfolding), qualitative and quantitative investigations of ligand-binding interactions, or the infrared spectroscopy of ligands in complex environments.

This work describes a new algorithm to follow the transition between two crossing potential energy surfaces (PESs) using MD simulations. For this, myoglobin (Mb) interacting with small ligands is an ideal reference system. Mb is one of the most studied biological molecules. Since the structure of Mb was first published in 1960 (11), it has been extensively studied as a model system for understanding the relationship between structure and function for proteins in general. This led to the understanding that dynamic variations in the structure were essential for function. In the case of Mb, the opening and closing of channels between pockets in the protein matrix are essential for allowing small ligand molecules such as O₂, NO, and CO to diffuse from the surrounding environment to the distal heme pocket, where binding of the ligand to the heme can occur (12,13).

Much is now known about how ligands move in the protein matrix (14). Simulations have suggested putative migration pathways (15) and these have been backed up by experimental data (16). Laser photolysis coupled with infrared spectroscopy studies have revealed information about the timescales involved in geminate recombination (17). Studies on mutants have highlighted the residues involved in controlling access to the distal pocket (18). More recently, time-resolved x-ray studies have started to provide real-time data about the events after photodissociation (19,20).

Despite these extensive studies, a detailed understanding of some of the fundamental processes occurring in Mb remains elusive. For example, the dynamics and timescales involved in the rebinding of ligands to heme after photodisociation are still not fully understood. Rebinding of CO to Mb occurs nonexponentially at low temperature but becomes exponential at room temperature with a timescale on the order of 100 ns (21). NO, on the other hand, rebinds extremely rapidly and nonexponentially at all temperatures (22). Assuming a power law dependence for the rebinding time yields a time constant of around 33 ps, whereas analyzing the data with a double exponential gave two timescales of 28 and 280 ps (22). A recent time-resolved infrared spectroscopy study on MbNO (23) has reproduced the nonexponential behavior observed by Petrich et al. (22) but found that the rebinding is even quicker, with time constants of 5.3 and 133 ps. The nonexponentiality of the rebinding kinetics has been previously explained in terms of multiple protein conformations (24) or in terms of time-dependent rebinding rates (22,25). Very recently, the latter suggestion has been investigated with femtosecond midinfrared experiments on Mb···NO (26). It has been found that rebinding occurs mainly from a metastable state B₁ with time-dependent rates, in agreement with reactive MD simulations (25). In addition to B₁, two other populations (B₀ and B₂) were identified. However, the spectroscopic signatures (B₀, B₁, and B₂) were not related to structural features. Although all experimental investigations agree on the observation of multiple timescales for the rebinding kinetics, it is interesting to note by how much the rebinding timescales depend on the experimental setup used and the model assumed to interpret the data (22,23,26). In addition to the time dependence of the rebinding process, the height of the rebinding barrier has also been investigated. Experiments suggest that the barrier is small (<1.2 kcal/mol) (22), whereas ab initio calculations have even suggested that the recombination reaction may be barrierless for NO in specific conformations (27).

To date, simulations of rebinding processes have been hindered by the fact that one cannot normally study processes which involve the formation or breaking of bonds with classical MD. This is because standard MD involves the propagation of the system on a single PES and therefore is unable to describe reactive processes. Recent work by Meuwly and co-workers (25) avoided the issue of bond formation by determining when rebinding events would occur by considering an energy criterion without actually carrying out the rebinding (the transition between the two electronic states involved) itself. The work successfully demonstrated that the height of the barrier to rebinding is dependent on the time after dissociation (25,26). This effect, mainly due to protein relaxation, was also suggested to contribute to the nonexponential rebinding rate, as mentioned above (22,25). However, this approach neglects possibilities such as subsequent escape from the bound state or the effect of the details of the bound state PES on the dynamics.

Other possibilities to avoid limitations of classical MD include the development of surface hopping methods or quantum mechanical methods. The first class includes surface-crossing algorithms, such as the method presented here, which involve deterministic (as done in this work) or stochastic switches between PESs. Quantum mechanical approaches for extended systems often use a mixed QM/MM methodology in which the reactive region is described with QM and the surrounding spectator region with classical MM. Our choice of a surface-crossing algorithm is discussed in detail below. On a more abstract level, the rebinding process has also been modeled as an N-particle random walk in one dimension (28). In addition to dynamical approaches, rebinding barriers have been investigated by a static comparison of PESs along one or more coordinates (27,29).

We have recently developed a two-dimensional ab initio PES for NO bound to hexacoordinate heme (30), spanning the Fe–ligand center of mass (CoM) distance and the Fe–N–O angle. This PES displays two minima, corresponding to Fe–NO and Fe–ON coordination modes. The Fe–NO conformation corresponds to the global minimum with a binding energy of around 21 kcal/mol, with the Fe–ON minimum as a metastable conformation with a binding energy of 8 kcal/mol. Contrary to the bound state PES, much less is known about the topology of the ⁴A interaction potential. Trajectories on the bound state of MbNO have shown that the Fe–ON conformation remains stable at 200 K and is metastable at temperatures up to 300 K (30). Once rebinding into the global minimum has occurred, no escape to the Fe–ON conformation was observed, suggesting that the Fe–ON conformation can only be prepared by excitation or by rebinding directly into this minimum. As a result, the existence of a secondary Fe–ON conformation should be taken into account in the analysis of experimental data. For this investigation, however, the existence of a—as yet unobserved—secondary minimum and the detailed topology of the Fe–NO PES is of lesser interest since the purpose of this work is to present an algorithm that allows explicitly study of a rebinding reaction.

In this work, we describe a new methodology to follow the rebinding of NO to Mb. Using two PESs to describe the interactions in the unbound and bound states, together with an algorithm which permits explicitly crossing from one state to the other, we can simulate the rebinding process of NO to Mb using classical MD. Using this approach, we investigate the dynamics of the rebinding process by carrying out extensive simulations up to 1 ns in length for individual trajectories and statistically analyze the data from a total simulation time close to 0.5 μs. Since this amount of data is required for a meaningful statistical analysis, MD simulations with classical force field are probably the only feasible approach because using QM/MM methods are still computationally too demanding.

The rest of the work is structured as follows. First, we describe the algorithm which allows the crossing from one surface to the other. This algorithm is then applied to the rebinding of NO to Mb. After briefly describing the setup of our simulations, we present the results. Finally, we discuss our observations and compare our methodology with other surface-crossing algorithms available in the literature.

METHODS

The surface-crossing algorithm

An algorithm to cross from one PES to another requires two principal components: a way of deciding when a crossing should occur and a protocol for carrying out the crossing itself.

A criterion for detecting crossings

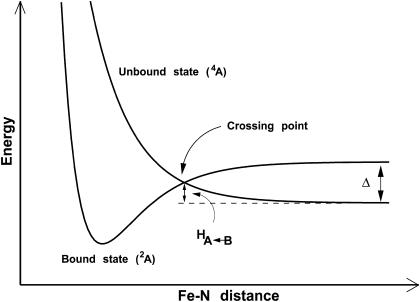
Following the approach used previously (25), an energy criterion was chosen for deciding when a crossing has occurred, namely when E_bound plus a constant Δ is less than E_unbound, i.e., E_bound + Δ ≤ E_unbound. In this expression, E_bound is the total energy of the bound energy manifold, E_unbound the energy of the unbound manifold, and Δ describes the energy difference between the bound and unbound energy surfaces, as illustrated schematically in Fig. 1. This crossing criterion implicitly assumes that the two asymptotes have identical energies (since the energy difference Δ is explicitly included in the crossing criterion). However, this is not the case, since the bound and unbound manifolds contain force field terms which are present only in the respective states. For example, the bound manifold contains a term for the bound Fe–NO interaction, whereas the unbound manifold contains Fe···N and Fe···O electrostatic and van der Waals interactions. The complete list of these terms is given in Table 1. Since some potential energy terms between the two manifolds are different, their zero of energy E₀ also differs. It was calculated to be E₀ = 11.5 ± 0.1 kcal/mol (25). This contribution needs to be taken into account when shifting the energy manifolds with respect to each other before the crossing criteria can be applied.

FIGURE 1.

Schematic of the bound and unbound potential energy surfaces for MbNO, showing the significance of Δ. Δ is the (conformationally averaged) asymptotic separation between the bound (²A) and the unbound (⁴A) state. Note that the rebinding barrier height 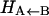is always smaller than Δ.

TABLE 1.

Contributions to the bound and unbound energy manifolds used in the energy criterion for the recrossing algorithm

Bound manifold
Bonds	Fe–N	Included in ab initio PES
Angles	Fe–N–O	Included in ab initio PES
	N–Fe–Np	Harmonic
	N–Fe–Nε	Harmonic
Unbound manifold
van der Waals	Fe···N,O
	Np···N,O
	Nε···N,O
Electrostatic	Fe···N,O,CoM
	Np···N,O,CoM
	Nε···N,O,CoM

CoM refers to the charge site at the center of mass of the NO ligand.

Δ, the asymptotic 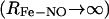difference in electronic energy between the doublet and quartet states, was previously estimated to be around 5 kcal/mol for MbCO (31). Since the bound and unbound PESs are multidimensional, the value of Δ can be expected to vary with configuration, and the meaning of Δ is that of a conformationally averaged quantity. However, since the value of Δ is only known approximately, it was chosen to be spherically symmetric. It can therefore be considered to be an empirical parameter, albeit with a clear physical interpretation. The absolute value of Δ will affect the rebinding rate and could eventually be chosen to reproduce the experimentally observed rebinding rate(s). It is important to differentiate between the asymptotic difference between the two PESs, Δ, and the more commonly used “inner barrier” 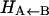, which describes the height of the rebinding barrier between the unbound state (B) and the bound state (A). Fig. 1 shows that the inner barrier 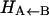is considerably smaller than the asymptotic energy separation Δ. For MbCO, the rebinding barrier 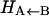has been estimated (32), measured (33), and calculated (34) to be around 4.3 kcal/mol, whereas for MbNO, 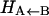is small or even zero. Initially, the value Δ = 6.3 kcal/mol has been used in this study. However, this value is only approximate and will be regarded as an adjustable parameter subsequently. At this point it is also worth noting that crossings back to the unbound surface can also occur if E_unbound < E_bound + Δ.

As described above, the choice of the value of Δ ensures that the asymptotic description of the PESs for the bound and unbound state is correct. It does not assume the presence (or absence) of a rebinding barrier, since that will be determined by the exact shape of the surfaces in multidimensional space. However, if both surfaces were one-dimensional, the height of a barrier (if any) would be completely determined by the choice of Δ.

A surface-crossing protocol

The surface-crossing algorithm works by mixing the two PESs over a short period of time, m, defined by the user, on the order of 10 fs. Once a crossing has been detected (E_bound ≤ E_unbound + Δ), the algorithm is applied. The trajectory is halted and the configuration (positions and momenta) observed m/2 fs earlier is restored. The trajectory is restarted with the appropriate velocities, and the two PESs are mixed with weights x and (1 – x) according to an equation of the form

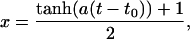(1)

where t is the current time, t₀ is the time at which the crossing occurred, and a is a constant which is determined by the mixing time chosen. This approach means that m/2 fs before the crossing, the trajectory is propagated on the pure initial state (the unbound state in the case of a rebinding process). As the trajectory approaches the crossing point, a contribution from the final state is smoothly added in. After m/2 fs the energies and forces are calculated on a 50:50 mix of the unbound and bound states. Finally, at the end of the mixing time (after m fs), the system is propagated once again on a pure surface, this time corresponding to the final state. The entire algorithm is illustrated schematically in Fig. 2.

FIGURE 2.

Schematic of the surface-crossing algorithm. The solid lines concern propagation on a pure PES (bound or unbound) whereas the dashed line represents propagation on the mixed PES. The dotted line shows the back propagation after a crossing (point 2.) has been observed. For details see text.

The precise choice of mixing time is somewhat arbitrary and has only a small effect on the resulting trajectories, which slowly diverge for different m. In this study, a mixing time of 11 fs was used. This timescale is similar to the mixing time resulting from the recently developed Coherent Switching with Decay of Mixing algorithm (35).

During the transition between the unbound and bound states, energies and forces from the newly created bonds and angles are added in. At the same time energies and forces corresponding to nonbonded interactions are removed. Changes in the parameters, when going from the unbound to the bound surface, are also taken into account in this way. In particular, this applies to the porphyrin parameters which describe the doming of the heme in the unbound state and the planar heme in the bound state. These parameters are smoothly varied during the surface mixing procedure. This algorithm was implemented in the user subroutine of the Charmm program (36).

Application to rebinding of NO to Mb

To apply this algorithm to the rebinding of NO to Mb, PESs for the bound and unbound states are required. The parameters for the protein in both states were taken from the Charmm22 force field. Parameters for the porphyrin moiety in the bound and unbound states were taken from Meuwly et al. (25). In the unbound state, the NO molecule was described using a three-point fluctuating charge model (37), whereas in the bound state a fixed charge model was used. The Fe–NO interaction in the bound state was described using a two-dimensional ab initio surface which spans the Fe–ligand CoM and Fe–N–O angle coordinates, as described above (30).

Simulation protocol

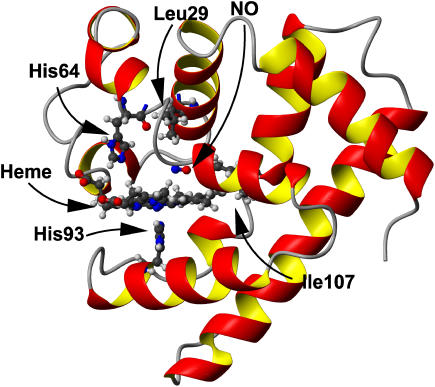
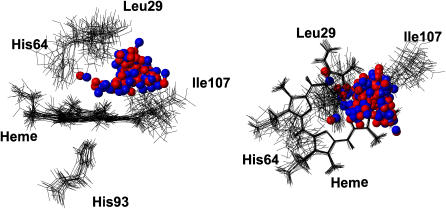
All simulations were carried out using the Charmm program (36). The computational setup follows a similar procedure to previous studies of MbNO and MbCO (25,38,39) and only a brief description is given here. Since the simulation is focused on the region surrounding the heme group, the stochastic boundary method was used to increase computational efficiency (40) (with a reaction region of radius 12 Å and a radius of the solvent sphere of 16 Å). The system contained a total of 2532 heme protein atoms, the NO ligand, and 178 water molecules, which were represented by a modified TIP3P potential (41). The nonbonded interactions were truncated at a distance of 9 Å using a shift function for the electrostatic terms and a switch algorithm for the van der Waals terms. A detailed view of the protein is shown in Fig. 3. All simulations were performed at 300 K.

FIGURE 3.

View of Mb. Residues 29, 64, 93, and 107 are shown in ball-and-stick representation, as are the heme and NO moieties. Figure prepared using MOLMOL (60).

Initial configurations for the rebinding study were generated as follows. From an equilibrated trajectory for bound MbNO, three configurations, separated by 5 ps, were taken toward the end of the 130 ps run. These three bound configurations were dissociated using the ‘sudden’ approximation (25,39,42) and propagated for 1 ns each on the unbound surface. These simulations were carried out using standard MD simulations without applying the surface-crossing protocol, i.e., no rebinding was possible during this time. From each of these unbound trajectories, snapshots were taken at 1-ps intervals between 1–5 (set A), 101–105 (set B), 501–505 (set C), and 901–905 (set D) ps after photodissociation. These snapshots served as starting configurations for studying the rebinding process using the surface-crossing algorithm described above. From each snapshot, 100 individual 5-ps trajectories were calculated using different initial velocity assignments, leading to a total of 1500 trajectories for each of the four time blocks (A–D), hence a total of 6000 dissociated trajectories.

We assessed the effect of the nonbonded cutoff by carrying out further simulations with a cutoff of 12 Å and calculating time constants for the rebinding process. The values calculated with the two different treatments of the nonbonded interactions were almost indistinguishable, showing that a nonbonded cutoff of 9 Å is sufficient for this study.

The time dependence of the rebinding process is analyzed in terms of the rebinding probability p(t). This differs from the analysis of experimental data, where the “fraction survived”, f(t), is more commonly used. The two functions are closely related, with p(t) corresponding to the time derivative of the surviving fraction: i.e., p(t) = df(t)/dt. Although the rate constants obtained from both functions are the same, their preexponential factors differ. In this work we concentrate solely on rate constants.

RESULTS

Geometric characterization of the rebinding seam

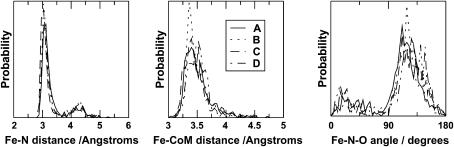
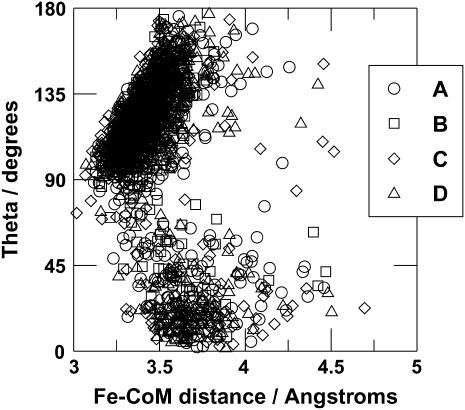
Data on the rebinding events were extracted from the trajectories and used to characterize the crossing seam. Distributions of a selection of observables from the rebinding events are illustrated in Fig. 4. It can be seen that the conformations at the crossing point are very similar for all of the time blocks (A–D). The Fe–CoM distance is typically found to be around 3.3–3.5 Å, although this corresponds to rebinding to both the Fe–NO and Fe–ON conformations. These can be distinguished in a plot of the distribution of the Fe–N distance and of the Fe–N–O angle. Rebinding into the Fe–NO conformation generally occurs at a Fe–N distance of 3.0–3.1 Å and a Fe–N–O angle larger than 90°, whereas rebinding into the Fe–ON conformation occurs at a Fe–N distance of >4 Å and a Fe–N–O angle below 90°. A two-dimensional scatter plot showing the positions of the rebinding events is given in Fig. 5. The relative proportions of rebinding into the Fe–NO and Fe–ON conformations are approximately the same for all time blocks, with 82% rebinding to form Fe–NO and the remaining 18% forming Fe–ON. Recrossing from the bound state to the unbound state is rare, but dissociation from the Fe–ON conformation was observed on 25 occasions. Overall, 1995 rebinding events were observed from the 6000 trajectories. Since the surface-crossing algorithm allows for ligand dissociation as well as ligand binding, it is possible for a single trajectory to exhibit more than one rebinding event, i.e., the number of rebinding events does not equal the number of trajectories that lead to a reaction. Multiple crossing and recrossing was found in a small number of trajectories. Thus, the number of trajectories is not equal to the number of rebinding events.

FIGURE 4.

Geometrical characterization of the rebinding points for the 5-ps trajectories. (A) Trajectories from the time block 1–5 ps; (B) trajectories from the time block 101–105 ps; (C) trajectories from the time block 501–505 ps; (D) trajectories from the time block 901–905 ps. (Left) Probability distribution function for the Fe–N distance with a dominant maximum at short separation for the Fe–NO conformation and a smaller peak corresponding to the Fe–ON state. (Middle) Fe–CoM distance; (right) the Fe–N–O angle distribution function.

FIGURE 5.

Two-dimensional scatter plot showing the position of the rebinding points projected onto the (Fe–CoM,Fe–N–O) plane. (A) Trajectories from time block 1–5 ps; (B) trajectories from time block 101–105 ps; (C) trajectories from time block 501–505 ps; (D) trajectories from time block 901–905 ps.

Trajectories from set A that did not rebind within 5 ps (911/1500) were extended to 200 ps. In the same way, trajectories that had not rebound after this time (100/911) were extended to 1 ns. After 1 ns, 77/100 trajectories remained in the dissociated state. As before, the geometrical characteristics of the crossing points were extracted from the trajectories. The distribution functions of distances (Fe–N, Fe–CoM) and angles (Fe–N–O) are all similar to those observed in the 5 ps trajectories (data not shown). The distance of the iron below the heme plane (defined as the least-squares plane of the four porphyrin N (Np) atoms) at the rebinding points was found to vary between 0.2 and 0.4 Å, with a maximum at 0.3 Å, identical to the data from the 5-ps trajectories. This compares with a relaxed Fe–heme plane distance of 0.37 Å.

Time dependence of the rebinding

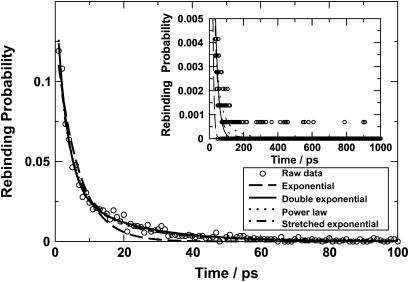
The time distribution of the 1444 rebinding events calculated from the trajectories starting from set A is plotted in Fig. 6 and fitted with various functional forms including a single exponential, a double exponential, a power law, and a stretched exponential. It is apparent that a single exponential is not sufficient to describe the distribution of rebinding times. The remaining functional forms all give a better fit to the data. The double exponential fit yielded timescales of 3.1 and 18.9 ps, whereas the power law fit yielded a time constant of 5.5 ps. The relative magnitudes of the time constants are similar to that observed in experiment (5.3 and 133 ps for a double exponential, 33 ps for a power law (23)), but the absolute values differ by a factor of between 2 and 7. This suggests that the procedure described here captures the essential physical behavior but that the conformationally and time averaged value of Δ may differ from Δ = 6.3 kcal/mol. As mentioned in the Methods section, this value is only approximate and its value is unknown.

FIGURE 6.

Time distribution of rebinding events with various fitting functions. The main graph shows the behavior up to 100 ps and the inset presents the distribution up to 1 ns. Fits with various functional forms are shown; a single exponential decay is not capable of capturing the rebinding probability as a function of time. For long times (t > 100 ps) rebinding events are observed but far fewer than for t < 100 ps (see inset).

Effect of Δ on the time distribution and assessment of errors

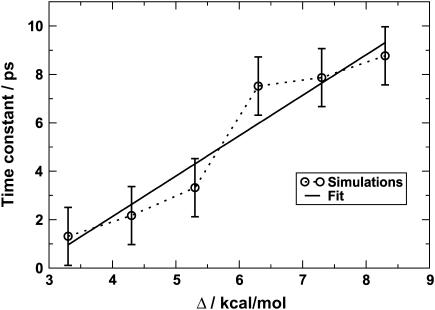
An exhaustive analysis of the rebinding times for a range of values of Δ as was done for Δ = 6.3 kcal/mol is too time consuming. Instead, a statistical approach was used to estimate the effect of varying Δ on the rebinding times. To this end, trajectories 10 ps in length were run with six values of Δ: 3.3–8.3 kcal/mol in increments of 1 kcal/mol, starting from the configurations in time block A. A simulation time of 10 ps (rather than 5 ps as was used above) was chosen to sufficiently sample the early events. Trajectories for different values of Δ were run until 150 rebinding events had been observed. This required the calculation of between 156 and 1023 trajectories for Δ = 3.3 and Δ = 8.3 kcal/mol, respectively. The large difference in the number of trajectories required to arrive at the same number of crossings reflects the fact that for larger Δ the rebinding probability decreases because the inner barrier increases with increasing Δ (see Fig. 1). Since we are interested in the fast timescale (shorter than 10 ps), the distributions were fit to single exponentials and the time constants were extracted from that. The τ_fast values are given in Table 2 and plotted in Fig. 7. An error estimate for incomplete sampling (rebinding times are estimated from 150 rebinding events instead of 593 for Δ = 6.3 kcal/mol) was obtained from the bootstrap method (43,44). Such a resampling allows the determination of error bars by calculating the distribution of the mean of subsets of data drawn at random from a larger data set. The 593 crossing events (with Δ = 6.3) observed during the initial 5-ps trajectories (see previous section) were used as the reference data set, and 20 random sets of 150 rebinding events were drawn from this. This led to error bars of ±1.2 ps (corresponding to ±1σ around the mean of the full distribution). As a first approximation, these error bars were applied to all data points. A linear fit to the distribution of time constants (τ = 1.67Δ – 4.55) suggests that a value of Δ = 5.9 kcal/mol should give a time constant τ = 5.3 ps, as suggested by experiment (23).

TABLE 2.

Effect of Δ on the calculated time constant for the rapid component of rebinding

Δ/kcal/mol	No. trajectories	τ/ps
8.3	1023	8.77
7.3	791	7.87
6.3	263	7.52
5.3	274	3.32
4.3	188	2.17
3.3	174	1.31

The second column indicates the number of 10-ps trajectories required to obtain 150 rebinding events.

FIGURE 7.

Variation of the time constant for the rapid component of rebinding as estimated from 150 rebinding events calculated over 10 ps with various values of Δ. The error bars were calculated as described in the text.

To assess the fast timescale, 1500 trajectories 10 ps in length were run using Δ = 5.9 kcal/mol. The simulation time is chosen to provide information about the fast timescale but is not expected to give a reliable value for the longer (≈50 ps) timescale. For this, much longer simulation times (such as described for Δ = 6.3 kcal/mol) would be needed. A total of 1024 rebinding events and 15 recrossings from the bound to the unbound surface were found. The distribution of rebinding events over the first 10 ps as a function of time led to a rebinding constant of 4.4 ps within the expected error bars (±1.2 ps). The trajectories in which no rebinding was observed (465) were extended to 200 ps, of which 399 did rebind. As before, the probability distribution of rebinding events as a function of time was fitted with various functional forms (data not shown). Again, a single exponential did not correctly describe the data. For a double exponential fit, the rebinding constants were found to be 3.80 and 18.01 ps. The fast rate constant now lies outside the expected error bars. These observations suggest that a simple linear relationship between Δ and the rebinding rate does not fully describe the experimental timescales.

This is not particularly surprising, since Δ is a single parameter which attempts to describe contributions to the rebinding process arising from different origins (anisotropy, protein conformation, etc.). In studies on small molecules (e.g., CN interacting with argon) (45) it was shown that the coupling Δ between the ground and first electronically excited state is coordinate dependent. Nevertheless, it is reassuring that such a simple model qualitatively reproduces the experimental observations.

Analysis of final conformations when rebinding was not observed

As described above, 77 of the 1500 trajectories started from block A with Δ = 6.3 kcal/mol did not rebind after 1 ns. It is interesting to examine the conformations of these molecules to investigate possible reasons for no rebinding being observed. These structures are shown in Fig. 8. The majority of the unbound NO ligands are found in the bottom of the Xenon-4 pocket, with a few remaining in the distal heme pocket. This suggests that the Xenon-4 pocket is a favorable site for NO after photodissociation. Movement of the ligand to the Xenon-4 pocket with localization of NO over an extended period of time was also observed in earlier simulations with the fluctuating charge model (37). These results suggest that the migration of the ligand to the Xenon-4 pocket may be involved in determining the long timescale rebinding dynamics. Due to the numerous trajectories calculated here, it was not possible to systematically analyze the movement of the ligand before rebinding occurred; however, it is likely that the molecules which rebound after 500 ps visited the Xenon-4 pocket before returning and rebinding.

FIGURE 8.

Conformations of Mb-NO after 1 ns when no rebinding was observed (77 structures). Protein structures are fitted to the porphyrin ring. For clarity, only a selection of residues from 15 structures are drawn in line representation. All 77 NO molecules are drawn in ball-and-stick.

DISCUSSION

This study discusses a simple surface-crossing algorithm entirely in the spirit of classical MD simulations, depending only on an energy criterion to decide whether or not a crossing can occur. Such an algorithm neglects “jumps” between PESs as would be possible in a quantum or semiclassical picture. Crossings occur over a fixed time interval chosen by the user. While the crossing is taking place (over 11 fs in the present case) no recrossing is allowed. To put the algorithm discussed here into perspective, alternative surface-crossing methods—mainly developed for applications to small molecules—are described in the following.

One of the first surface-crossing algorithms to successfully describe dynamics of crossing between two energy states was developed by Landau (46) and Zener (47). In this approach, the energies of two states and their coupling can be described by a Hamiltonian which, in matrix form, can be written as

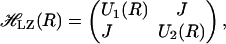(2)

where 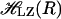is the Landau–Zener Hamiltonian along the reaction coordinate R, U₁(R), and U₂(R) are the energies of the two states and J is the coupling, corresponding to the energy difference between the two states at the crossing point, where the degeneracy is lifted. In the crossing region, within which the two states become close, the transition rate is proportional to J² and inversely proportional to the difference in gradients along the reaction coordinate on the two surfaces concerned. The final transition probability also includes the magnitude of the velocity along the reaction coordinate at the crossing point. It is worthwhile to note that J is constant and does not explicitly depend upon the configuration R.

This method is straightforward to use for model cases (48) and low-dimensional systems where the reaction coordinate is well defined (35). However, in cases with many degrees of freedom, where the reaction coordinate cannot be easily defined (e.g., rebinding processes), such an approach becomes difficult to apply. Landau–Zener theory can still be of use in understanding processes involved in the ligand photolysis reactions of heme proteins. Zhu, Widom, and Champion (49), for example, developed a multidimensional Landau–Zener description of chemical reaction dynamics and vibrational coherence to describe the photolysis of MbNO. This particular application included two quantum modes and the dissociative coordinate that describes ligand separation from the heme-iron. The energy gap function as a function of time between the ground and excited electronic states was assumed to be decreasing exponentially at a constant rate. With this model the population evolution on the different electronic states and the coherent oscillations of the nuclear coordinates, which were explicitly treated, were investigated.

Using the foundations laid by Landau and Zener, surface hopping methods have been developed. The methods developed by Tully and co-workers (50–52) are well known, in particular the method now known as “Tully's fewest switches” (51). In this intrinsically stochastic method, classical motion is simulated on a single potential energy surface at all times. Instantaneous hops between surfaces are permitted. In the fewest switches algorithm, the number of hops between the PESs is minimized, while maintaining a statistical distribution in an ensemble of trajectories that reproduce the quantum distribution over the classical states. In the mathematical formulation, there are two terms which promote transitions between the two states. First, the off-diagonal elements of the Hamiltonian, corresponding to the J in the Landau–Zener approach, and second, the nonadiabatic coupling between the two states, 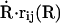, where R are the atomic coordinates and r_ij is the nonadiabatic coupling vector between the states i and j, defined as r_ij = 〈φ_i(R)|∇_Rφ_j(R)〉, where φ_i(R) is the adiabatic wave function for state i (53). In large systems, it is this latter term which is difficult to calculate. Although in principle it could be calculated with quantum mechanical calculations, such calculations would be extremely time consuming, and the resulting vector would be applicable in a consistent fashion only to surface hopping trajectories also calculated by quantum mechanical calculations. Although such calculations are—in principle—conceivable within a QM/MM framework, this goes contrary to the aim of this work, which is to develop a pure molecular mechanics approach to study reactive processes between two electronic states that may have a complicated crossing region but well-defined asymptotes. Calculating the nonadiabatic coupling vector within an MM framework raises further questions. Since the two states (bound and unbound) are described using different potential energy functions with terms which exist in one state but not in the other (for example, the Fe–NO bond), it is not clear how such a term should be calculated.

Building on the success of the methods by Tully and co-workers, Truhlar and co-workers have continued to develop surface hopping methods of increasing complexity and of higher accuracy (35,54). However, in all of these methods the determination of the nonadiabatic coupling vector, or a justifiable approximation to it, remains a central concern. For low-dimensional systems (e.g., triatomics or atom-diatom systems such as Cl–HCl) it has become possible to explicitly calculate the nonadiabatic coupling matrix elements, which were shown to depend upon the geometry (55). Recently, Neufeld (56) has proposed a statistical theory of nonadiabatic transitions which avoids using ad hoc algorithms such as Tully's fewest switches. Once again, this method requires prior knowledge of the potential energy surfaces involved and the nonadiabatic couplings between them and, as a result, cannot yet be readily applied to the system of interest here.

It was therefore decided to adopt as simple a method as possible which nevertheless retains the necessary features: an initial and a final state, a well-defined protocol with a solid physical basis for determining when a crossing should occur, and a simple mixing algorithm for crossing between the two states, each described by a high-dimensional potential energy surface. Despite these simplifications, our results indicate that the approach here is robust and captures the main physical behavior of the rebinding process as evidenced, e.g., by the observation that multiple timescales occur. It should be noted that the present algorithm will give lower estimates to reaction rates because no quantum mechanically allowed transitions (tunneling) are possible. Such processes will increase the reaction rate compared to a purely classical switching algorithm such as the one presented here.

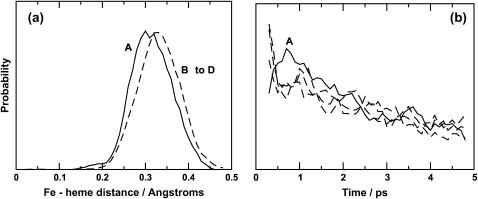
One significant strength of MD simulations is that it is possible to analyze details of the dynamics at the atomic level. Since these simulations of the rebinding of NO to heme show that the process is nonexponential in time, in agreement with experiment and previous simulations, we consider whether the results can provide insight into the rebinding mechanism itself. As described in the introduction, several mechanisms leading to nonexponential rebinding dynamics have been proposed. They include the inhomogeneous model (21) (distribution of rebinding barriers), the related multiple site model (24) (rebinding from different metastable binding sites results in the observed kinetics), and the relaxation model (22) (a time-dependent barrier modulates the rebinding process). Previous simulations (25), in which the rebinding was not carried out explicitly, found a time dependence of the recrossing probability as a function of the time after photodissociation. This was partly attributed to an increase of the distance R between Fe and the average heme plane which, in turn, is related to protein relaxation. Fig. 9 a shows the probability distributions p(R) of the Fe-heme separation at the crossing points from the simulations here starting in block A (solid line) and in blocks B to D (dashed lines). For the trajectories starting from structures immediately after photodissociation, p(R) has a shoulder around 0.20 Å and a main peak centered around 0.30 Å, whereas p(R) from the trajectories starting between 100 and 900 ps after photodissociation is shifted to larger values of R and peaks around 0.33 Å. The latter is in good agreement with results from x-ray structures where it was found that upon ligand dissociation, the iron atom moves to 0.37 Å below the plane (57). Furthermore, the rebinding probability decreases monotonically with time for blocks B, C, and D, whereas the results from time block A reveal a maximum in the rebinding probability at around 0.75 ps, followed by a decrease (see Fig. 9 b). The maximum for block A suggests that there is a period of time (several ps) over which the rebinding barrier evolves. Together with the behavior of p(R) this implies that the early processes after photodissociation are governed by heme relaxation, resulting from the displacement of the iron out of the heme plane. In addition, the observation that NO molecules are found in both the distal heme pocket and the Xenon-4 pocket at the end of the 1-ns simulations suggests that rebinding does occur from different sites within the protein, and thus supports the multiple site model for longer timescales.

FIGURE 9.

(a) Probability distribution p(R) for the Fe-heme distance defined as the distance between the iron atom and the average plane through the four pyrrole nitrogen atoms. p(R) is shown for simulations starting from block A (solid line) and from blocks B to D (dashed line) (see text for a description of the time blocks). For simulations starting from blocks B–D the maximum and average of p(R) is at 0.33 Å in good agreement with results from x-ray data. The black curve has its main peak shifted to R = 0.3 Å with a small shoulder ∼0.2 Å. (b) Rebinding probabilities over the first 5 ps from time blocks A–D (see Fig. 4). The data has been smoothed with a five-point running average.

CONCLUSIONS

We have developed and tested a conceptually simple surface-crossing algorithm to study bond-forming and bond-breaking processes suitable for high-dimensional systems using classical MD simulations. The method was applied to the rebinding of NO to Mb after photolysis, using an ab initio potential energy surface to describe the interactions between NO and the heme on the bound state (30). MbNO is a suitable system for such a test since the rebinding timescale is rapid (sub-ns) (22,23,25,26), which allows exhaustive sampling of the reactive seam and the accumulation of sufficient statistics for careful analysis. Extensive simulations (with a total time of around 450 ns) have shown that the rebinding is nonexponential, in agreement with experiment. Fitting the data with a power law or a double exponential reproduce the data equally well. Our calculated time constants from a double exponential fit are of the correct order of magnitude but somewhat too small (3.8 and 18.0 ps compared with 28 and 280 ps (22), 5.3, and 133 ps (23)), in particular for the slower component. However, the ratio between the fast and slower time constants is of similar order as found in experimental data. Given the large differences between the reported experimental data (22,23,26), our results can be considered to qualitatively agree with experimental data. Also, in deriving rebinding constants from experiment one has to assume kinetic models which may or may not describe the process correctly. The only free parameter, albeit with a clear physical interpretation, is the asymptotic separation (Δ) between the two potential energy manifolds. Varying this parameter changes the barrier for rebinding and thus the time constant. The effect of this variation was investigated in detail. A variation of Δ with the protein conformation (in particular as a function of the distance of Fe below the heme plane) could have a nonnegligible influence on the long rebinding times. In principle it would be possible to calculate the inner barrier 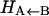for different values of Δ using umbrella sampling techniques, as was recently done for MbCO (34). However, this is outside the scope of this work. Since the rebinding times for MbCO are better known than for MbNO (see discussion above), fitting Δ to experimental data may be affected by the relatively large spread in rebinding times. Furthermore, the unbound potential energy surface (⁴A) is not yet characterized sufficiently well to justify a more advanced treatment.

Investigation of the protein and ligand conformations of structures when no rebinding was observed within 1 ns revealed that NO was mainly found in the Xenon-4 pocket, highlighting the importance of the protein cavities in controlling the access of ligands to the binding site, in particular for NO. It should also be noted that just less than 20% of the rebinding events led to formation of the Fe–ON conformation, suggesting that the presence of an Fe–ON conformation may be relevant in analyzing the data from rebinding studies.

These results suggest that the observed nonexponential rebinding dynamics of NO to Mb is governed by a time-dependent rebinding barrier at short times after dissociation, whereas at longer times a distribution of potential energy barriers due to the occupation of several locations within the protein arise. Future studies on Mb mutants (e.g., mutations of V68) will be of interest to investigate the influence of local changes around the binding site on the rebinding dynamics (58,59).