The Fe-CO Bond Energy in Myoglobin: A QM/MM Study of the Effect of Tertiary Structure

Abstract

The Fe-CO bond dissociation energy (BDE) in myoglobin (Mb) has been calculated with B3LYP quantum mechanics/molecular mechanics methods for 22 different Mb conformations, generated from molecular dynamics simulations. Our average BDE of 8.1 kcal/mol agrees well with experiment and shows that Mb weakens the Fe-CO bond by 5.8 kcal/mol; the calculations provide detailed atomistic insight into the origin of this effect. BDEs for Mb conformations with the R carbonmonoxy tertiary structure are on average 2.6 kcal/mol larger than those with the T deoxy tertiary structure, suggesting two functionally distinct allosteric states. This allostery is partly explained by the reduction in distal cavity steric crowding as Mb moves from its T to R tertiary structure.

The relationship between protein structure and function is central to biochemistry and can be usefully probed with model proteins such as myoglobin (Mb). Despite intensive experimental study, it is still unclear exactly how Mb's tertiary structure affects the geminate recombination of carbon monoxide (1,2). We are interested in examining this problem at an atomistic level by using a quantum mechanical (QM) description of the heme group with a simpler molecular mechanics (MM) treatment of the remaining Mb (QM/MM method) (2). This allows us to treat the area of interest with accurate density functional theory while including effects from the rest of the protein. As a first step we report here our results concerning the thermochemistry of CO bonding in Mb, which highlight the presence of two functionally distinct allosteric states, corresponding to the tertiary structures of unligated Mb (deoxyMb, T) and CO-ligated Mb (MbCO, R). Such allosteric states are usually associated with multimeric proteins such as hemoglobin (Hb), where they allow cooperative binding of O₂. Monomeric Mb is often considered to be nonallosteric but this view is changing (3) based partly on how lactate reduces its O₂ affinity (4), differences in MbO₂ and deoxyMb O₂ equilibration curves (5), and Mb's control of pseudoenzymatic reactions (6).

Allosteric behavior in Mb is possible because ligand binding is accompanied by structural changes as Mb relaxes between ligated (R) and unligated (T) tertiary structures. This change in structure for Mb is similar, but not identical to that observed in the α- and β-subunits of Hb (7). As CO dissociates from the heme iron, the iron atom moves ∼0.3 Å out of the porphyrin plane and the heme distorts from planarity. Concerted motion of the rest of Mb, notably the E and F α-helices (8,9), completes the transition between the T and R states. The impact of this relaxation on ligand binding is not yet fully understood.

We have explored the effect of Mb's tertiary structure on CO geminate reactivity by using QM/MM methods to calculate Fe-CO binding enthalpies. This has allowed us to probe Mb's allostery and to test our QM/MM methodology by comparing our bond energies to experiment (10). Calculating accurate metalloprotein bond energies is challenging, especially when structural relaxation accompanies ligand binding. Properties and energies of proteins vary slightly as they fluctuate between multiple conformational substates (11), within each tertiary state. We allowed for such variations and relaxation by calculating bond energies separately for Mb R and T states as averages of 11 values for different substates generated from molecular dynamics (MD) trajectory snapshots and minimized crystal structures. Previous QM/MM optimized geometries show that the Fe-CO bond is distorted ≤9° by Mb's tertiary structure and slightly stabilized by a very weak hydrogen bond between the distal histidine (His-64) and oxygen of bound CO (12,13). The energetic impact of structural relaxation upon binding was not addressed in these studies (12,13). Crystal studies reveal that relaxation from the T state to the R state enables Val-68 to move from a position where it blocks CO binding to a sterically more favorable orientation (8). Such steric crowding in the distal cavity of T state Mb is verified here and helps explain Mb's allostery.

We started with 1.15-Å resolution x-ray structures of deoxyMb and MbCO (Protein Data Bank entries 1A6N and 1A6G (14)), then removed waters of crystallization and sulfate ions. The CHARMM all-atom force field (15) was modified by additional heme group parameters and used with CHARMM v27b2 (16) to prepare both proteins and carry out MD simulations. Hydrogen atoms were added according to standard pK_A values for all amino acids except histidines. His-64 was chosen as the Nɛ-protonated tautomer, in agreement with converging opinion (12,13), and the protonation states of other histidines were assigned according to their hydrogen bonding environment. Each protein was solvated with a 9-Å layer of preequilibrated TIP3 water to create two systems of ∼10,000 atoms. Relaxation, heating to 300 K over 30 ps and equilibration until stable (∼300 ps) prepared both systems for a 100-ps production run. No constraints or restraints were applied throughout. MM minimization of each solvated crystal structure and of 10 snapshots from each MD production run, generated 11 deoxyMb and 11 MbCO structures for QM/MM BDE calculations.

The Fe-CO BDE is the energy difference between MbCO and the sum of gas phase CO and deoxyMb, if both Mbs have a similar conformation. Convergence to the same local substate for MbCO and deoxyMb is essential to obtain meaningful values, and was achieved by creating deoxyMb and MbCO “pairs” then carrying out a series of iterations, as described by Wirstam et al. (17) for O₂ binding to hemethyrin. Eleven T-state “pairs” were created by addition of CO to deoxyMbs and 11 R-state “pairs” were made by removal of bound CO from MbCO. The QM/MM calculations used the Jaguar QM program (18) and Tinker MM code (19), coupled by our QM/MM routines (2). The QM region, consisting of the heme porphine, the His-93 imidazole side chain and CO, were treated with the hybrid B3LYP functional and a flexible basis set. All other atoms made up the MM region, which was treated with the CHARMM all-atom force field (15). All results include a correction for zero-point energy (ZPE) calculated for a gas-phase model. Full computational details are in the Supplementary Material.

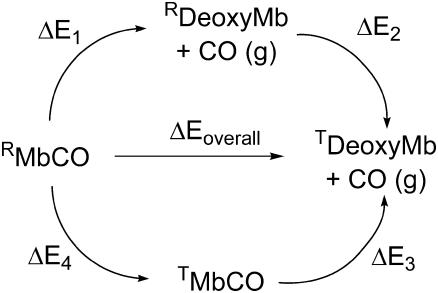
The overall BDE of Fe-CO Mb (shown as ΔE_overall in the thermodynamic cycle of Fig. 1) can be written in two different ways as a sum of two terms: ΔE_overall = ΔE₁ + ΔE₂ or ΔE₃ + ΔE₄. One contribution is the average QM/MM bond energy for the R and T states of Mb (ΔE₁ and ΔE₃, respectively). The other contribution is the relaxation energy for interconversion of R and T states in deoxyMb or MbCO (ΔE₂ or ΔE₄, respectively). These cannot be readily calculated using our method. It is, however, apparent that ΔG₂ is negative, and ΔG₄ is positive, since MbCO and deoxyMb are known to adopt R and T states, respectively. Assuming that entropic effects are small for the free energies ΔG₂ and ΔG₄, we can therefore write that ΔE₁ > ΔE_overall > ΔE₃. As a first approximation, we can take ΔE_overall as the average of ΔE₁ and ΔE₃; the difference between these values provides an estimate of the effect of the tertiary structure on the bond energy.

FIGURE 1 .

BDE thermodynamic cycle. “R”/“T” denote tertiary state and “MbCO”/“deoxyMb” indicates whether CO is bound or not to Mb.

The 11 BDEs for R state Mb range between 8.1 and 10.8 kcal/mol (see Table S1 in Supplementary Material), with an average ΔE₁ = 9.4 kcal/mol. The average for the T state is ΔE₃ = 6.9 (range 3.0–9.0 kcal/mol). This yields an estimated BDE ΔE_overall of 8.1 kcal/mol, in good agreement with the experimental value of 10.8 kcal/mol (10). The BDE for the QM region alone is 13.9 kcal/mol (1, including ZPE correction), so Mb weakens the Fe-CO bond by 5.8 kcal/mol. This weakening is greater for Mb in the T state, ΔE₁ is 2.6 kcal/mol larger than ΔE₃, showing that the two tertiary states are functionally different.

Structural analysis (Table S2 in Supplementary Material) reveals more steric hindrance in the distal cavity in the T state than in the R state. Distances between the CO oxygen and the hydrogen atoms Phe-43 C_zH, His-64 Nɛ₂H, and Val-68 Cγ₂H increase on average by 0.48, 0.53, and 0.05 Å during relaxation from the T to R. This does not, however, lead to significant changes in the tilt or bend of the Fe-CO bond (the Fe-C-O angle is ∼175° in both states), in agreement with the known rigidity of this moiety (13). Increased amplitude of the motion of the iron into the heme plane upon CO binding lowers the BDE; this average movement is 0.33 Å for the T state and 0.25 Å for the R state. The polarizing effect of the protein environment on the QM region leads to an increase of 0.4 kcal/mol on average of the Fe-CO BDE (Table S3 in Supplementary Material). These electrostatic effects weakly destabilize the bond in the R state and weakly stabilize it in the T state, but the predominant contribution to the difference in bond energies between the two conformers is steric.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.