Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1968 May;8(5):596–607. doi: 10.1016/S0006-3495(68)86510-5

Computation of Impulse Conduction in Myelinated Fibers; Theoretical Basis of the Velocity-Diameter Relation

L Goldman, James S Albus
PMCID: PMC1367402  PMID: 5699798

Abstract

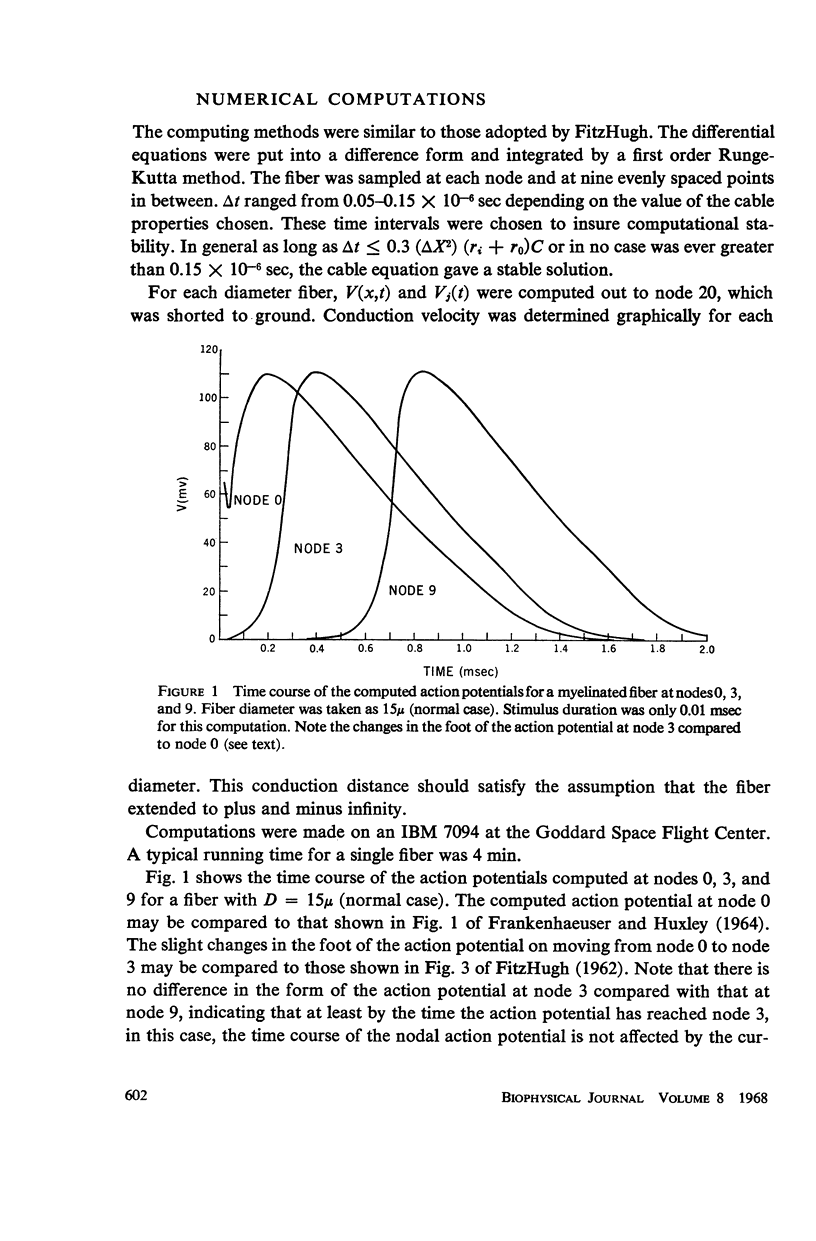
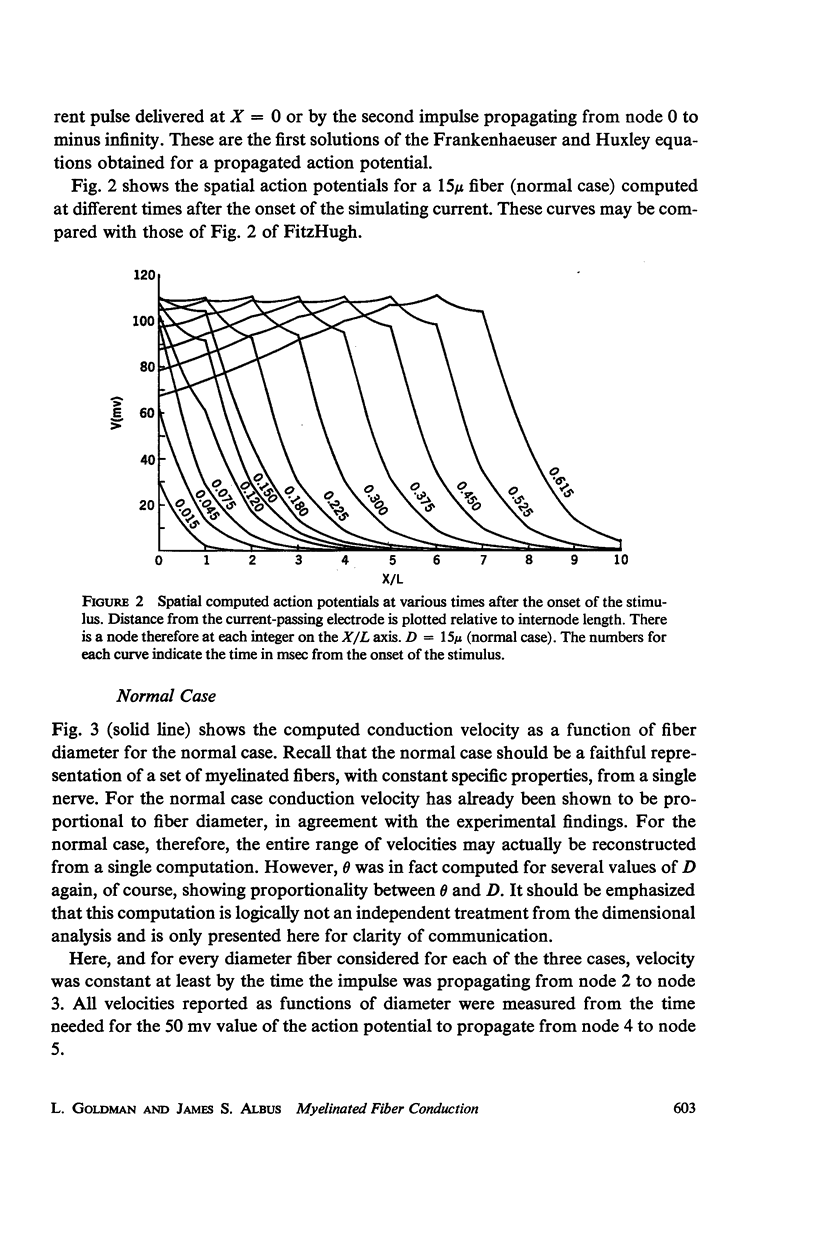
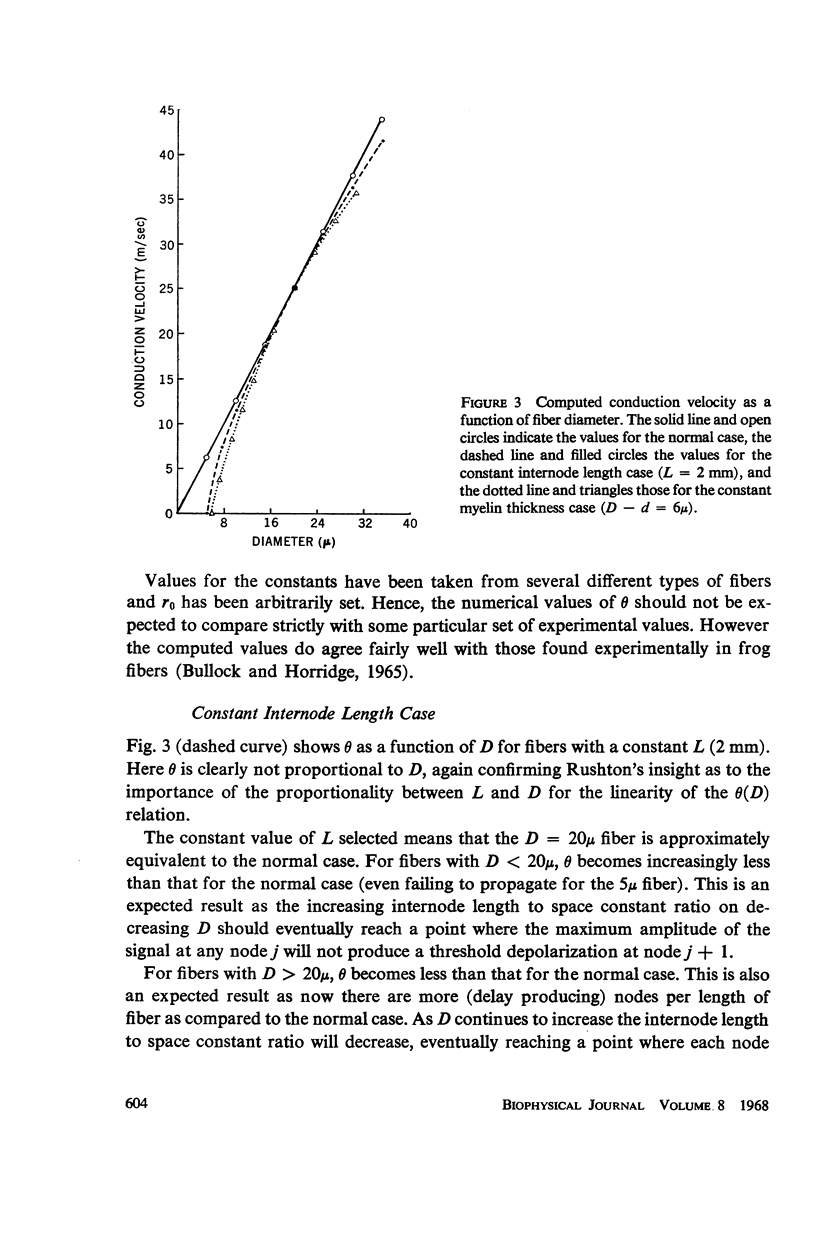
For myelinated fibers, it is experimentally well established that spike conduction velocity is proportional to fiber diameter. However no really satisfactory theoretical treatment has been proposed. To treat this problem a theoretical axon was described consisting of lengths of passive leaky cable (internode) regularly interrupted by short isopotential patches of excitable membrane (node). The nodal membrane was assumed to obey the Frankenhaeuser-Huxley equations. The explicit diameter dependencies of the various parameters were incorporated into the equations. The fiber diameter to axon diameter ratio was taken to be constant, and the internode length was taken to be proportional to the fiber diameter. Both these conditions reflect the situation that exists in real, experimental fibers. Dimensional analysis shows that these anatomical conditions are equivalent to Rushton's (1951) assumption of corresponding states. Hence, conduction velocity will be proportional to fiber diameter, in complete agreement with the experimental findings. Digital computer solutions of these equations were made in order to compute a set of actual velocities. Computations made with constant internode length or constant myelin thickness (i.e., nonconstant fiber diameter to axon diameter ratio) did not show linearity of the velocity-diameter relation.

Full text

PDF
600

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Clark J., Plonsey R. A mathematical evaluation of the core conductor model. Biophys J. 1966 Jan;6(1):95–112. doi: 10.1016/S0006-3495(66)86642-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. DODGE F. A., FRANKENHAEUSER B. Sodium currents in the myelinated nerve fibre of Xenopus laevis investigated with the voltage clamp technique. J Physiol. 1959 Oct;148:188–200. doi: 10.1113/jphysiol.1959.sp006281. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Dyck P. J., Lofgren E. P. Method of fascicular biopsy of human peripheral nerve for electrophysiologic and histologic study. Mayo Clin Proc. 1966 Nov;41(11):778–784. [PubMed] [Google Scholar]
  4. FITZHUGH R. Computation of impulse initiation and saltatory conduction in a myelinated nerve fiber. Biophys J. 1962 Jan;2:11–21. doi: 10.1016/s0006-3495(62)86837-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. FRANKENHAEUSER B., HUXLEY A. F. THE ACTION POTENTIAL IN THE MYELINATED NERVE FIBER OF XENOPUS LAEVIS AS COMPUTED ON THE BASIS OF VOLTAGE CLAMP DATA. J Physiol. 1964 Jun;171:302–315. doi: 10.1113/jphysiol.1964.sp007378. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Friede R. L., Samorajski T. Relation between the number of myelin lamellae and axon circumference in fibers of vagus and sciatic nerves of mice. J Comp Neurol. 1967 Jul;130(3):223–231. doi: 10.1002/cne.901300304. [DOI] [PubMed] [Google Scholar]
  7. GOLDMAN L. THE EFFECTS OF STRETCH ON CABLE AND SPIKE PARAMETERS OF SINGLE NERVE FIBRES; SOME IMPLICATIONS FOR THE THEORY OF IMPULSE PROPAGATION. J Physiol. 1964 Dec;175:425–444. doi: 10.1113/jphysiol.1964.sp007525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. HODGKIN A. L., HUXLEY A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952 Aug;117(4):500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Huxley A. F., Stämpfli R. Evidence for saltatory conduction in peripheral myelinated nerve fibres. J Physiol. 1949 May 15;108(3):315–339. [PMC free article] [PubMed] [Google Scholar]
  10. Pickard W. F. On the propagation of the nervous impulse down medullated and unmedullated fibers. J Theor Biol. 1966 May;11(1):30–45. doi: 10.1016/0022-5193(66)90036-1. [DOI] [PubMed] [Google Scholar]
  11. RUSHTON W. A. H. A theory of the effects of fibre size in medullated nerve. J Physiol. 1951 Sep;115(1):101–122. doi: 10.1113/jphysiol.1951.sp004655. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. TASAKI I. New measurements of the capacity and the resistance of the myelin sheath and the nodal membrane of the isolated frog nerve fiber. Am J Physiol. 1955 Jun;181(3):639–650. doi: 10.1152/ajplegacy.1955.181.3.639. [DOI] [PubMed] [Google Scholar]
  13. THOMAS P. K., YOUNG J. Z. Internode lengths in the nerves of fishes. J Anat. 1949 Oct;83(4):336-50, pl. [PMC free article] [PubMed] [Google Scholar]
  14. Vizoso A. D., Young J. Z. Internode length and fibre diameter in developing and regenerating nerves. J Anat. 1948 Apr;82(Pt 1-2):110–134.1. [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES