Abstract
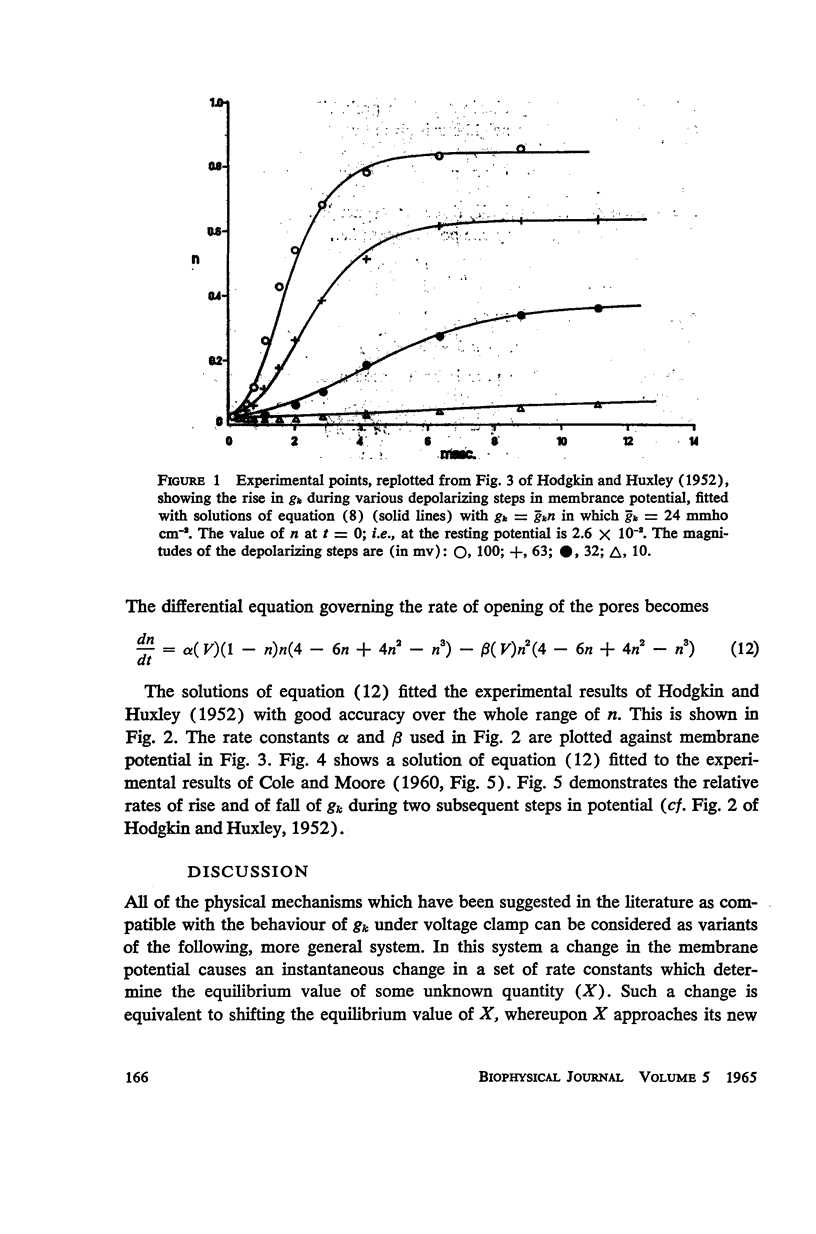
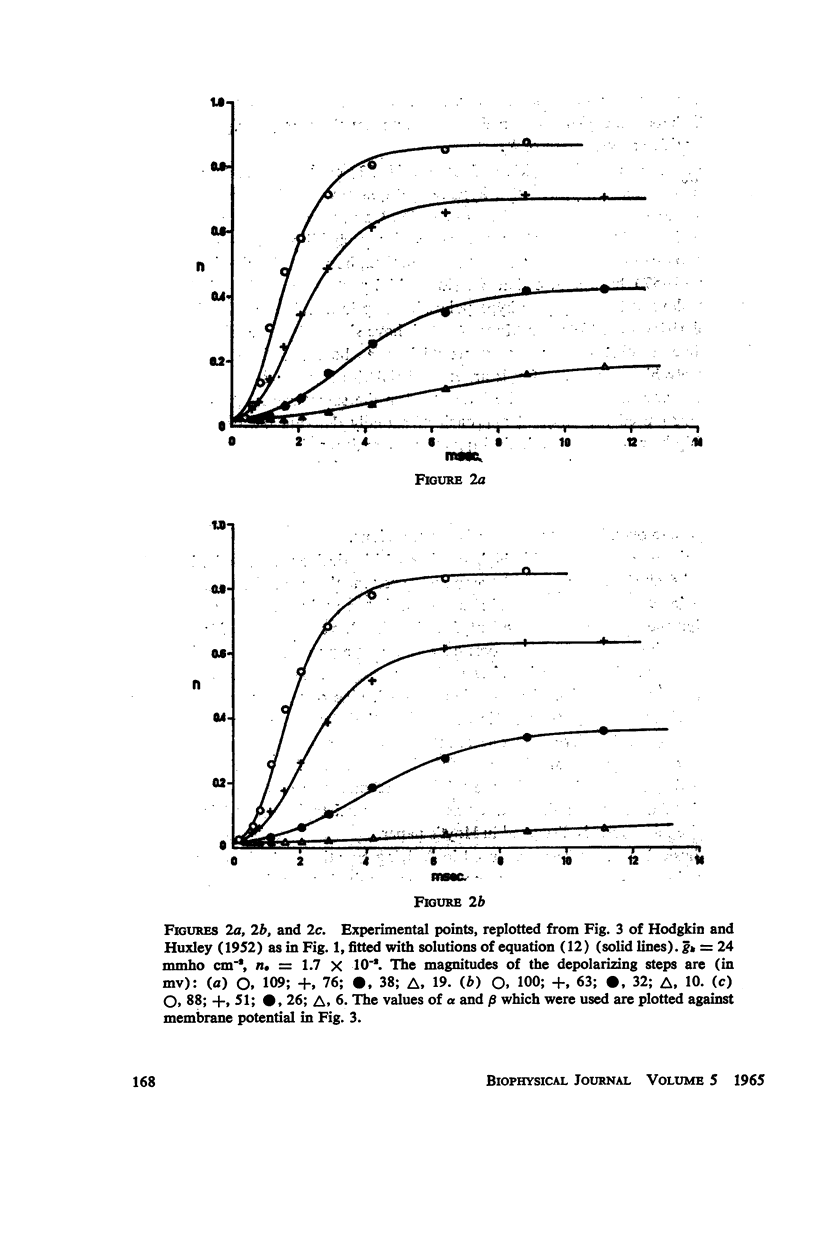
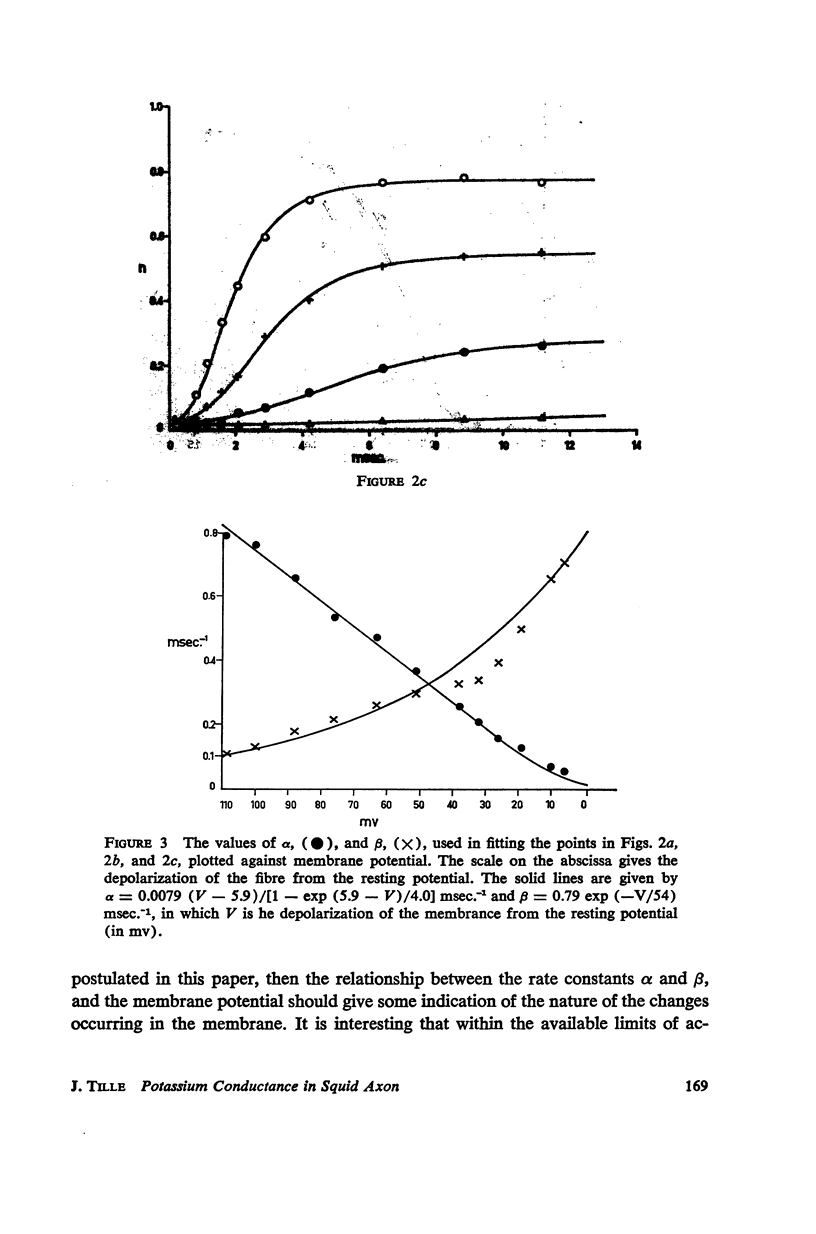
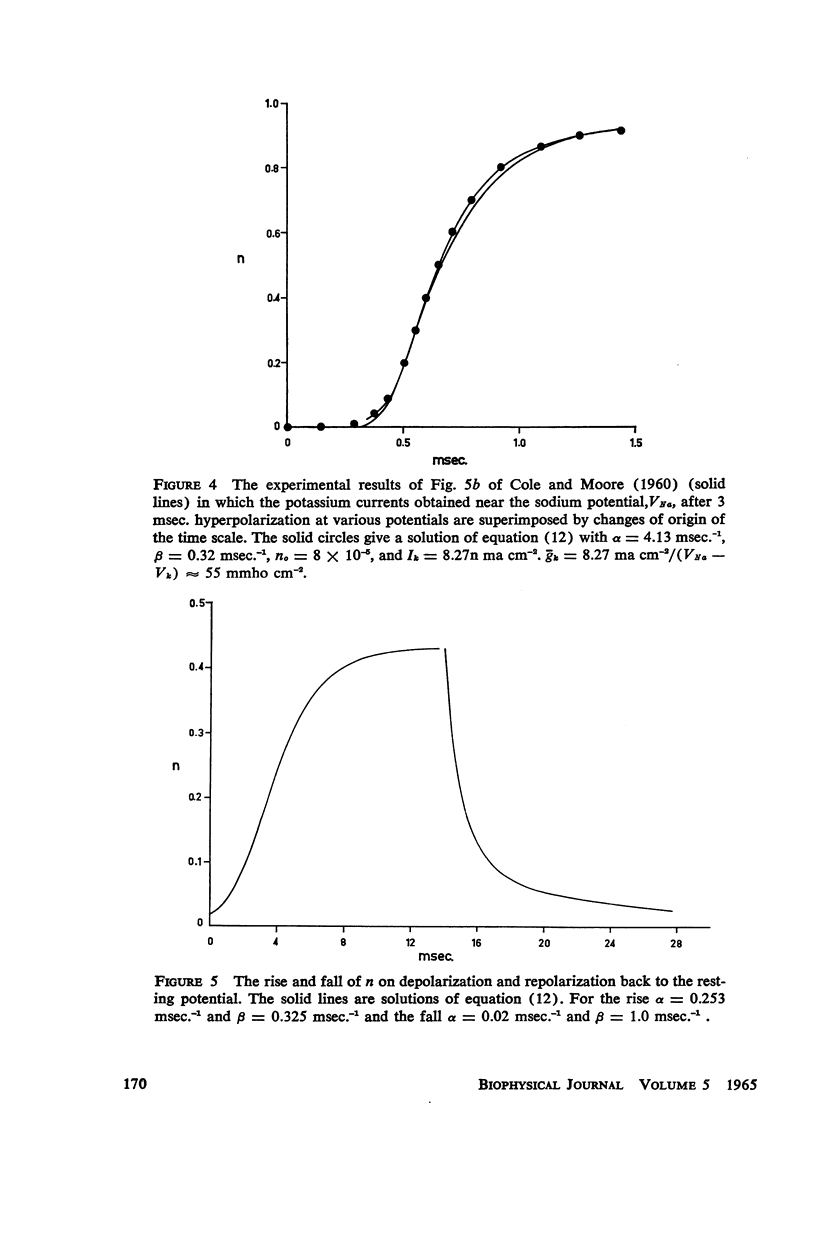
The solutions, n(t), of the differential equation dn/dt = α (1 - n) n (4 - 6n + 4n2 - n3) - βn2 (4 - 6n + 4n2 - n3) in which α and β are instantaneous functions of membrane potential, are shown to fit with good accuracy the time courses of the rise of potassium conductance during depolarizing steps in clamp potential, found experimentally by Hodgkin and Huxley and by Cole and Moore. The equation is derived by analysing the dynamic behaviour of a system consisting of a square array of interacting pores. The possible role of Ca++ ions in this system is discussed.
Full text
PDF




Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- HODGKIN A. L., HUXLEY A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952 Aug;117(4):500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HOYT R. C. THE SQUID GIANT AXON. MATHEMATICAL MODELS. Biophys J. 1963 Sep;3:399–431. doi: 10.1016/s0006-3495(63)86829-0. [DOI] [PMC free article] [PubMed] [Google Scholar]


