Structural features of cytochrome c′ folding intermediates revealed by fluorescence energy-transfer kinetics

Abstract

We employed fluorescence energy-transfer probes to investigate the polypeptide dynamics accompanying cytochrome c′ folding. Analysis of fluorescence energy-transfer kinetics from wild-type Trp-72 or Trp-32 in a crystallographically characterized (1.78 Å) Q1A/F32W/W72F mutant shows that there is structural heterogeneity in denatured cytochrome c′. Even at guanidine hydrochloride concentrations well beyond the unfolding transition, a substantial fraction of the polypeptides (≈50%) adopts compact conformations (tryptophan-to-heme distance, ≈25 Å) in both pseudo-wild-type (Q1A) and mutant proteins. A burst phase (≤5 ms) is revealed when stopped flow-triggered refolding is probed by tryptophan intensity: measurements on the Q1A protein show that ≈75% of the Trp-72 fluorescence (83% for Trp-32) is quenched within the mixing deadtime, suggesting that most of the polypeptides have collapsed.

Advances in theory and experiment continue to reveal new insights into the mechanisms of protein folding (1–17). Energy-landscape theories (2, 18–23) in particular have provided a conceptual framework for understanding this complex self-assembly process. There remains, however, a wide chasm between the information contained in theoretical models and that extracted from measurements of folding kinetics. Consequently, our experimental efforts have been aimed at developing and refining folding probes that report on the structure and heterogeneity of polypeptide ensembles.

The slow and highly heterogeneous folding kinetics of Fe^II-cytochrome (cyt) c′ from Rhodopseudomonas palustris are unusual for a four-helix bundle (24–33). Many helical bundles are fast-folding because of their highly symmetrical structures and preponderance of short-range contacts (21, 34, 35). Our investigations of cyt c′ using primarily electron-transfer triggering and heme absorption probes have indicated that either Met-15 or Met-25 binds to the unfolded ferroheme (26). Further, preliminary mutagenesis results have suggested that the faster folding phases may arise from polypeptides with Met-heme ligation (36). In the absence of misligation, Fe^III-cyt c′ refolding can be described adequately by a single kinetics phase.

Our investigations of cyt c′ have revealed the time scale required for proper heme coordination but have provided little information about polypeptide dynamics. To address this issue, we have extended our work to include use of fluorescence energy-transfer (FET) probes to gain insight into conformational changes that accompany Fe^III-cyt c′ folding. In the native protein, a single tryptophan (Trp-72; ref. 37) serves as the FET donor for our kinetics measurements; in addition, we have prepared and crystallographically characterized a position-32 mutant, Q1A/F32W/W72F, to probe distances between another site on the polypeptide chain (Trp-32) and the heme during folding.

Materials and Methods

Materials and Protein Preparation.

Guanidine hydrochloride (GuHCl, ultrapure grade, Sigma) and l-tryptophan (Fluka) were used as received. The R. palustris cyt c′ gene was cloned, and the protein was coexpressed heterologously (38) with plasmid pEC86, kindly provided by Linda Thöny-Meyer (39) in Escherichia coli [strain BL21(DE3)]. Mutant protein (Q1A/F32W/W72F) was generated by site-directed mutagenesis by using a QuikChange kit (Stratagene). DNA sequencing was performed by the California Institute of Technology DNA Sequencing Core Facility. Q1A/F32W/W72F cyt c′ was expressed and purified according to the procedures described (36). Mass spectral and protein sequence analyses were conducted by the Protein/Peptide Microanalytical Laboratory in the Beckman Institute. The purity of protein samples was assessed by SDS/PAGE gel electrophoresis and absorbance ratio (λ_280 nm:λ_398 nm, Fe^III) between 0.19 and 0.21.

Crystallization, Data Collection, and Structure Determination.

Crystals of Q1A/F32W/W72F cyt c′ were grown by the sitting-drop vapor-diffusion method. The reservoir solution consisted of 100 mM Mes, polyethylene glycol 6000, and 50 mM NaCl (pH 6.0). The protein drop was prepared by mixing 2 μl of cyt c′ solution (850 μM in 10 mM sodium phosphate buffer, pH 6.0/28 mM NaCl) with 2 μl of the reservoir solution. Crystals appeared within 2–3 days. X-ray diffraction data were collected at 100 K by using an R-Axis II imaging plate area detector and monochromatized copper-Kα radiation (1.54 Å) produced by a Rigaku (Tokyo) RU 200 rotating anode generator operated at 50 kV and 100 mA. The structure was determined at 1.78 Å by refinement of a model from isomorphous crystals (space group, P2₁2₁2₁; unit cell dimensions, 33.8 × 62.1 × 113.4 ų; two monomers per asymmetric unit) of R. palustris cyt c′ (PDB ID code ; ref. 37) against diffraction data (overall R_sym = 6.2%, overall I/σI = 24.8, completeness = 99.7%) by using DENZO (40). Rigid-body, simulated-annealing, positional, and thermal refinement with CNS (41), amid rounds of manual rebuilding, and water placement with XFIT (42) produced the final model (R_cryst = 21.1%, R_free = 26.5%, overall B factor = 34.9 Ų). The Ramachandran plot was calculated with PROCHECK (43).

Equilibrium Unfolding.

Absorption, circular dichroism, and luminescence spectra were measured on a Hewlett–Packard 8452 diode array spectrophotometer, an Aviv 62ADS spectropolarimeter (Aviv Associates, Lakewood, NJ), and a Hitachi (Tokyo) F-4500 spectrofluorimeter, respectively. Standard procedures were used to generate denaturation curves from heme absorption, circular dichroism, and tryptophan-emission changes (44). GuHCl concentrations were determined by refractive-index measurements (45).

Evaluation of the Förster Distance.

The value of the spectral overlap integral, J, for the tryptophan–heme donor–acceptor pair (46) was determined on the basis of several measurements of both tryptophan fluorescence and cyt c′ absorption at varying concentrations between 5 and 120 μM and at different GuHCl concentrations. The solution refractive index was measured to be 1.34.

Tryptophan-Fluorescence Decay Kinetics Measurements and Fitting Methods.

Tryptophan fluorescence decay kinetics at varying concentrations of GuHCl were measured by using the third harmonic of a regeneratively amplified femtosecond Ti:sapphire laser (Spectra-Physics) at 290 nm for excitation and a picosecond streak camera (Hamamatsu C5680, Ichinocho, Japan) for detection. Tryptophan emission was selected by an interference filter (λ = 355 ± 5 nm). The C5680 was used in the photon-counting mode for luminescence-decay measurements.

Analysis of FET kinetics involves the numerical inversion of a Laplace transform [I(t) = Σ_k P(k) exp(−kt)] (47–49). We have used two algorithms to invert our kinetics data with regularization methods that impose additional constraints on the properties of P(k). The simplest constraint that applies to the FET kinetics data is that P(k) ≥ 0 (∀k). We have fit kinetics data using a MATLAB (Mathworks, Natick, MA) algorithm (LSQNONNEG) that minimizes the sum of the squared deviations (χ²) between observed and calculated values of I(t), subject to a nonnegativity constraint. LSQNONNEG produces the narrowest P(k) distributions with relatively few nonzero components. Information theory suggests that the least biased solution to this inversion problem minimizes χ² and maximizes the breadth of P(k) (50). This regularization condition can be met by maximizing the Shannon-Jaynes entropy of the rate constant distribution {S = −Σ_k P(k)ln[P(k)]}, implicitly requiring that P(k) ≥ 0 (∀k) (51). Maximum-entropy fitting produces stable and reproducible numerical inversions of the kinetics data. The balance between χ² minimization and entropy maximization is determined by graphical L-curve analysis (52). The P(k) distributions from maximum-entropy fitting are broader than those obtained with LSQNNONEG fitting but exhibit comparable maxima. A simple coordinate transformation using the Förster equation (Eq. 1) recasts the P(k) results obtained by LSQNONNEG or maximum-entropy fitting as probability distributions over r (46, 53).

The value of τ_D (2.4 × 10⁻⁹ s) was obtained from luminescence-decay measurements with l-tryptophan (2–10 μM) in various solvent conditions [100 mM sodium phosphate without and with GuHCl (0.4 and 2.0 M), pH 7.0]. At tryptophan concentrations greater than 10 μM in the presence of GuHCl, additional decay components attributable to aggregation of the model complex were observed.

Stopped Flow-Triggered Folding.

The folding kinetics of Q1A and Q1A/F32W/W72F Fe^III-cyt c′ were measured with a BioLogic SFM-4S stopped-flow mixer coupled via optical fiber to a monochromator fitted with a five-stage photomultiplier tube. For fluorescence-monitored folding experiments, the excitation source was a 200-W mercury/xenon arc lamp (260 nm ≤ λ_ex ≤ 355 nm). The PMT output was recorded with a 16-bit, 20-MS/s digital oscilloscope (CompuScope 1602, Gage Applied Science, Lachine, QC, Canada). Kinetics traces were measured at 355 nm for a time period up to 5 s, typically at a sampling rate of 50 KS/s. In refolding experiments, unfolded cyt c′ (100–150 μM in 3.2 M GuHCl) was diluted 14-fold with a combination of 100 mM sodium phosphate buffer and 3.5 M GuHCl solution, pH 7.0, resulting in final protein concentrations of ≈7–10 μM and varying GuHCl concentrations (Q1A, 0.6–1.5 M; Q1A/F32W/W72F, 0.4–0.8 M). The stopped-flow mixing deadtime under these conditions was ≈5 ms. Kinetics traces could be fit adequately to single-exponential functions.

Results

Crystal Structure of Q1A/F32W/W72F cyt c′.

The structure of Q1A/F32W/W72F cyt c′ was determined at 1.78-Å resolution. The mutant protein has four antiparallel α-helices bundled in a fold that is virtually identical with that of the wild-type protein [rms deviation (RMSD) in α-carbon position = 0.44 Å] (Fig. 1 Inset) (37). The final model has good stereochemistry (RMSD_bond ≤ 0.017 Å, RMSD_angle ≤ 1.7°) with most residues (91.3%) falling in the most favored regions of the Ramachandran plot. The heme iron is five-coordinate, and the average iron-to-His-117 distance is 2.05 Å. The vacant sixth coordination site is surrounded by Leu-12, Met-15, Leu-85, three Phe residues (Phe-55, Phe-78, and Phe-82), and the methylene chain of Arg-8. There are minor perturbations in the hydrophobic heme pocket of the mutant protein, particularly in the Phe-82 and Leu-85 side chains. The replacement of Trp-72 with Phe-72 affects the hydrophobic interactions with helix 2. The introduction of Trp-32 at the top of the bundle does not perturb the surrounding structure.

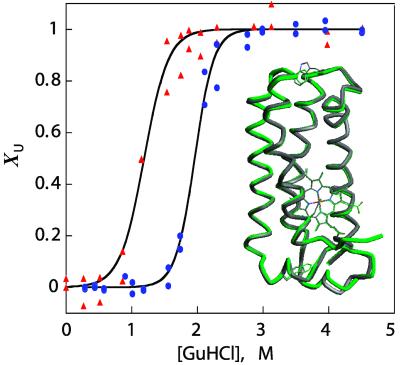
Fig 1.

Denaturation curves for Q1A (•) and Q1A/F32W/W72F (▴) cyt c′ determined by heme absorption, circular dichroism, and tryptophan fluorescence (χ_U is the fraction of unfolded protein). (Inset) Structures of two cyts c′. Backbone atoms of the R. palustris protein (PDB ID code , green) are superimposed on the corresponding atoms in the Q1A/F32W/W72F mutant (gray) with a calculated RMSD of 0.44 Å. The mutated side chains are also shown.

Equilibrium Unfolding.

GuHCl-titration curves generated from ensemble-averaged probes (far-UV circular dichroism, tryptophan fluorescence, and heme absorption) are well described by two-state equilibria. The pseudo-wild-type Q1A protein {[GuHCl]_1/2 = 1.9(1) M; ΔG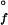 (H₂O) = −33(3) kJ⋅mol⁻¹} is more stable toward unfolding than the Q1A/F32W/W72F mutant {[GuHCl]_1/2 = 1.1(1) M; ΔG 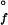(H₂O) = −16(2) kJ⋅mol⁻¹} (Fig. 1). The reduced stability of the Q1A/F32W/W72F mutant most likely is attributable to subtle changes in hydrophobic interactions accompanying the Phe ↔ Trp exchanges.

Energy-transfer partners incorporated into a single polypeptide provide site-specific conformational detail. Measurements of FET kinetics can give probability distributions of distances between a fluorescent donor (D) and acceptor (A). FET rates depend on the inverse sixth power of the DA distance (Eq. 1; refs. 46 and 53):

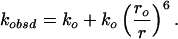A DA pair is characterized by a critical length (r_o) that defines the range of distances (r) that can be probed (0.3r_o < r < 1.5r_o) (Eq. 2),

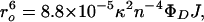where κ is the orientation factor (2/3 for random orientation), n is the refractive index of the solution, Φ_D is the donor fluorescence quantum yield, and the integral J describes the spectral overlap between the normalized donor fluorescence spectrum and the acceptor molar absorption spectrum. The 34-Å critical length (r_o) of the tryptophan–heme pair yields a 10–50-Å range of measurable distances. The Trp-72 fluorescence decay kinetics in folded pseudo-wild-type (Q1A) cyt c′ can be fit to a single exponential function with a decay time of 41 ps, corresponding to a Trp-72-to-heme separation of ≈17 Å. This value is in good agreement with the crystallographically determined distance. Fluorescence decay kinetics in the folded mutant (Q1A/F32W/W72F) are consistent with a distribution of Trp-32-to-heme distances centered at 22 Å with a full width at half-maximum of 2 Å, similar to the distance (≈25 Å) found in the crystal structure. The shorter distance determined from the FET kinetics is likely caused by favorable orientation of the tryptophan and heme transition dipoles in the folded protein.

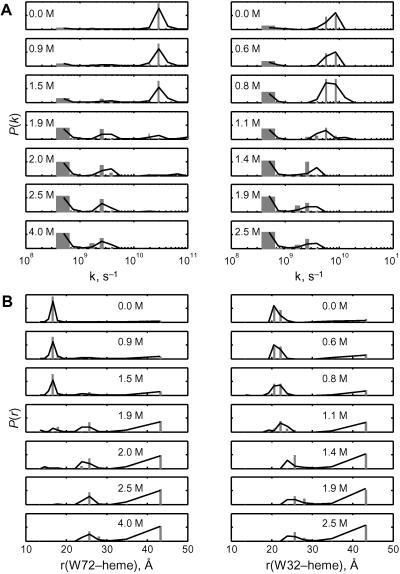
More complex behavior is evident after the addition of GuHCl. As GuHCl is added to the protein solution, the Trp-72 and Trp-32 decay kinetics become biphasic: the appearance of slow decay times (≈2.4 ns) indicates the presence of unfolded polypeptides (Fig. 2A). Additionally, the fast-decay components shift to slower rates with increasing [GuHCl], suggesting a loosening of the native structure. The FET kinetics data obtained in the presence of denaturant can be interpreted in terms of a heterogeneous collection of compact and extended conformations. The mean DA distance moves to larger values as [GuHCl] increases (Fig. 2B). At the GuHCl midpoints (Q1A, 1.9 M; Q1A/F32W/W72F, 1.1 M), substantial populations of polypeptides with intermediate DA distances (r_avg ≈ 22–25 Å) are revealed. Finally, at GuHCl concentrations above the midpoint, the short-r distribution loses all amplitude in favor of extended (r > 43 Å) and nonnative compact conformations (with mean distances of ≈25 Å). The variations in the DA distance distributions are consistent with cooperative unfolding of cyt c′, but the FET kinetics reveal structural heterogeneity that is not apparent from ensemble-averaged spectroscopic probes.

Fig 2.

Distributions of tryptophan excited-state decay rate constants [P(k)] (A) and tryptophan–heme distances [P(r)] (B) extracted from FET kinetics obtained for Q1A (Left) and Q1A/F32W/W72F (Right) cyt c′ with variations in GuHCl concentrations (bar, LSQNONNEG; line, maximum entropy) are shown.

Fe^III-cyt c′ Folding.

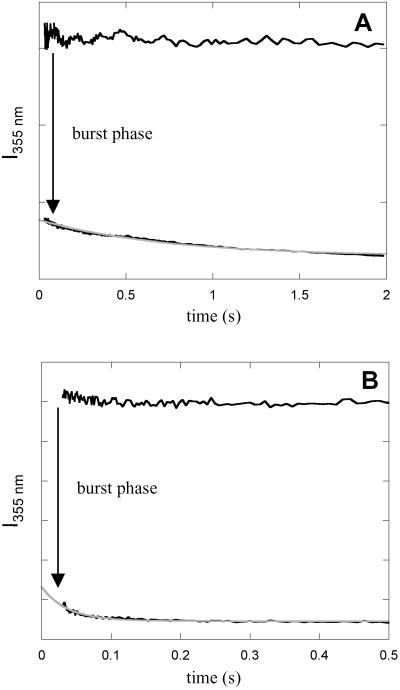
The native heme environment of Fe^III-cyt c′ forms in a single kinetics phase (≈1-s time constant) after stopped-flow dilution of GuHCl (26). In contrast, a burst phase is revealed when refolding is probed by tryptophan fluorescence intensity. The majority (≈75%) of the Trp-72 fluorescence is quenched within the mixing deadtime (≈5 ms), whereas the remaining fraction takes a few seconds. Similar behavior is observed for the Trp-32 mutant. Fluorescence measurements on the Q1A/F32W/W72F mutant show an increase in the amplitude of the burst phase (≈83%) and folding rate (20 s⁻¹) compared with the wild-type protein (Fig. 3).

Fig 3.

Folding kinetics of cyt c′ measured by tryptophan-fluorescence intensity. (A) Q1A {[GuHCl] = 1.2 M, ΔG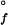 = −12 kJ⋅mol⁻¹, [cyt c′] = 10 μM}. (B) Q1A/F32W/W72F {[GuHCl] = 0.4 M, ΔG 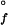= −11 kJ⋅mol⁻¹, [cyt c′] = 10 μM}. The data (black curves, logarithmically compressed to contain 100 points per decade) can be fit adequately by a single-exponential function decay [gray curves, k_f (Q1A) = 1.4 s⁻¹, k_f (Q1A/F32W/W72F) = 27 s⁻¹]. The fluorescence signals of the unfolded proteins are represented by the upper traces.

Discussion

Analysis of tryptophan-to-heme FET kinetics from two distinct residues [Trp-72 (wild type) and Trp-32 (mutant)] reveals underlying structural heterogeneity in chemically denatured cyt c′. Even at GuHCl concentrations well beyond the unfolding transition, a substantial fraction of the polypeptides (≈50%) adopts compact structures (25 Å) in both pseudo-wild-type and mutant c′ [where Trp-72 (32) is 41 (81) residues from Cys-113] (Fig. 2b). By comparison, the fraction (≈10%) of compact molecules (29 Å) in unfolded dansyl-labeled yeast cyt c [DNS(Cys-102)-cyt c, where Cys-102 is 84 residues from His-18] is significantly smaller (54). This dramatic difference in the relative composition of collapsed and extended structures in denatured c′ and c can be due to differences in their primary amino acid sequences. Sequence comparisons show that c′ has a substantially higher fraction of nonpolar residues (54.4%) than c (49.1%) (Table 1). Also, the c′ sequence contains a large number of small residues (e.g., 25 alanines), whereas c has many charged and basic residues (e.g., 16 lysines, Saccharomyces cerevisiae). It is reasonable to suggest that different protein folds and sequences will modulate the balance between compact and extended molecules.

Table 1.

Amino-acid compositions of cytochromes c′ and c (yeast)

Property	Residues	cyt c′		cyt c
		Number	Mole %	Number	Mole %
Tiny	A, C, G, S, T	47	37.6	34	31.5
Small	A, C, D, G, N, P, S, T, V	69	55.2	52	48.1
Aliphatic	I, L, V	21	16.8	15	13.9
Aromatic	F, H, W, Y	7	5.6	14	13.0
Nonpolar	A, C, F, G, I, L, M, P, V, W, Y	68	54.4	53	49.1
Polar	D, E, H, K, N, Q, R, S, T	57	45.6	55	50.9
Charged	D, E, H, K, R	37	29.6	34	31.5
Basic	H, K, R	21	16.8	23	21.3
Acidic	D, E	16	12.8	11	10.2

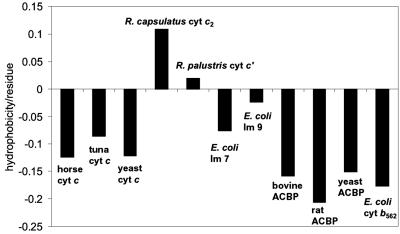
Theoretical investigations of lattice model proteins have identified two limiting folding regimes: the so-called attractive case in which a collapsed intermediate forms and the repulsive case in which folding proceeds without global collapse (7–10, 23, 55–57). When correlated with the primary amino acid sequence and overall stability, it seems that the more hydrophobic and less-optimized sequences tend to have a higher propensity to form compact structures, whereas the less-hydrophobic and strongly optimized sequences lead to repulsive interactions that disfavor compaction (7–10, 23, 57). Our results for c′ folding accord with the attractive limit; that is, because of its higher hydrophobic amino acid content, compact denatured structures are more prevalent in c′. Interestingly, by using Eisenberg's index (58), the calculated average residue hydrophobicity for c′ is also significantly greater than those of several other four-helix bundles (Fig. 4). (It is important to note that the hydrophobicity index does not take the heme into account.) The presence of a large population of compact molecules during folding could lead to topological and energetic frustration (7–9, 23, 57), explaining why the c′ folding dynamics are so different from those of other helical bundles.

Fig 4.

Comparisons of calculated average hydrophobicity values derived from Eisenberg's scale (22) for cyts c and four-helix bundles [Im (E colicin-binding immunity protein) 7, Im 9, Acyl-CoA-binding protein (ACBP), cyt c′, and cyt b₅₆₂]. The heme groups in the cyts are neglected in these calculations.

Our work on the electron transfer-triggered folding of cyt c′ shows clearly that a four-helix bundle is not necessarily a fast-folding motif and that topology alone does not dictate the folding time scale. Even in the absence of misligation (Fe^III-cyt c′), the folding dynamics are complex. The dominantly hydrophobic sequence of this four-helix bundle seems to favor the formation of nonnative compact structures. The FET measurements suggest that low concentrations of denaturant “loosen” the protein fold, leading to broader DA distributions with increased mean r values. Folding monitored by tryptophan fluorescence reveals that a substantial compaction of the polypeptide occurs in milliseconds, but several seconds are required for the heme to adopt its native environment. Assuming that the burst-phase population is homogeneous, the tryptophan fluorescence-intensity measurements suggest average DA distances of 26 and 28 Å in the Trp-32 and Trp-72 proteins, respectively. However, these intensity measurements cannot tell whether there is one collapsed intermediate or a heterogeneous distribution of compact (folded and/or nonnative) and extended structures, because only an analysis of FET kinetics during folding provides probability distributions of DA distances. The results for DNS(Cys-102)-cyt c indicate that, after folding is initiated, an equilibrium between compact (60%) and extended (40%) molecules is established rapidly (54). If this interpretation is correct, then a key difference between c′ and c is the relative population of compact structures in the burst-phase ensemble (c′, 75%; c, 40%). This behavior parallels that found under equilibrium conditions in the denatured molecules (c′, 50%; c, 10%). The striking difference in composition of the c and c′ burst intermediates is in line with results from lattice-model simulations: the hydrophobicity of the peptide and overall stability of the protein seem to be key factors in determining the population of compact nonnative structures during the search for the native fold (7–9, 23, 57).

Abbreviations

• cyt, cytochrome

• FET, fluorescence energy transfer

• GuHCl, guanidine hydrochloride

• RMSD, rms deviation