Quantifying signaling-induced reorientation of T cell receptors during immunological synapse formation

Abstract

Productive T cell recognition of antigen-presenting cells (APCs) is normally accompanied by the formation of a cell–cell contact called the “immunological synapse.” Our understanding of the steps leading up to this formation has been limited by the absence of tools for analyzing 3D surfaces and surface distributions as they change over time. Here we use a 3D fluorescence quantitation method to show that T cell receptors are recruited in bulk within the first minute after the onset of activation and with velocities ranging from 0.04 to 0.1 μm/s; a speed significantly greater than unrestricted diffusion. Our method reveals a second feature of this reorientation: a conformational change as the T cell pushes more total membrane into the interface creating a larger contact area for additional receptors. Analysis of individual T cell receptor velocities using a single-particle tracking method confirms our velocity measurement. This method should permit the quantitation of other dynamic membrane events and the associated movement of cell-surface molecules.

T cell activation occurs as a result of the recognition by the T cell receptor (TCR) of peptides displayed in the cleft of MHCs on the surface of antigen-presenting cells (APC). The affinity of the TCR for activating peptide-MHC is typically low, on the order of 5–50 μM (1, 2). However, T cells are able to recognize and respond to APCs displaying ≈10–200 peptides bound to MHC molecules (3–5). Much of the ability to respond to such low numbers of ligands may be due to the formation of an immunological synapse (6) in which distinct zones of receptor ligand pairs (supramolecular activating complexes, SMACs; ref. 7) are formed. Although many of the signaling molecules are known and their localization in the nascent synapse is a matter of great interest, the means by which they organize into these zones is not clear.

Two recent studies (8, 9) have demonstrated that generalized membrane redistribution toward the synapse occurs during the first minutes of T cell recognition. In both of these studies, the process appeared to be accelerated by costimulatory signaling through CD28 and/or LFA-1, and in one study it was shown to be sensitive to a myosin motor inhibitor (8). That this membrane reorientation correlates directly with TCR/CD3 and MHC movement has been shown by Wülfing et al. (10) and Krummel et al. (11), though the nature of the reorientation on the T cell has not been well examined.

In this study we have used a method that utilizes 3D sampling of molecular densities on T cell surfaces to quantify and track the recruitment velocities of TCRs as they move into the immunological synapse. For this approach, we used a previously described transfectant in which the CD3ζ signaling chain associated with the TCR was labeled with GFP (11). The computational method utilizes an image segmentation algorithm (12) to identify pixels in a 3D data set that contains data for GFP-labeled TCR/CD3 molecules on the surface of the T cell. Then, we used a continuum method based on “conservation of green-fluorescent-protein” and conservation of cell membrane mass to compare 3D localization at consecutive timepoints to quantify TCR motion. We verify our measurement of CD3ζ velocity by using a discrete single particle tracking (SPT) method (13, 14) that uses monovalent FAb-labeled fluorescent beads to quantify the motion of individual TCRs. Both analyses show that TCRs reorient toward the synapse shortly after recognition with a speed that corroborates previous suggestions of an active transport process rather than diffusion. The 3D continuum method also shows that recruitment to the nascent synapse involves a conformational flattening of the membrane leading edge on contact with the APC encounter in addition to active translocation of TCRs along the membrane.

Methods

Cell Culture.

D10.G4 is a Th2-type T cell clone derived from AKR/J mice and bears TCRs that recognize conalbumin peptide CA 134–146 in the context of IA^k (15). D10 CD3ζGFP transfectants are described in ref. 11. All clones were maintained by weekly restimulations with irradiated APCs and peptides or whole protein. IA^k-bearing CH27 cells were used as APCs.

Microscopy.

Imaging experiments were carried out by using a Zeiss Axiovert-100 microscope fitted with a high-speed piezo-electic z-motor, dual excitation and emission filter wheels, and a Princeton Instruments Interline camera. Hardware control was achieved by using metamorph software (Universal Imaging, Media, PA). For each experiment, T cells were plated into Nunc coverslip-wells, and loaded with 1 μM FURA-2 AM-ester (Molecular Probes) for 20 min and subsequently washed once by a media exchange. Cells were then moved to a 37°C heated stage and APCs were added. Data collection was done at 15-s intervals over a 15- to 30-min period. At each time point, we collected a differential interference contrast image, FURA340 and FURA380 images, and a 19–25 deep z-stack encompassing ≈20 μM of z depth. Measurement of the waist diameter was done using the line-function in the metamorph software package.

Continuum Method.

Segmentation.

The segmentation filter (12) converts the original array of pixel intensities into a new array called the discriminant, the elements of which describe the likelihood that a particular pixel is part of the cell membrane. For each pixel in a given z slice, we calculate the 2D discriminant array D as follows: D = −(Φ − Φ_o) (Φ_xx/(|Φ_x |+ ɛ) + Φ_yy/(|Φ_y |+ ɛ)), where ɛ (a small number) ensures a nonzero denominator, and single (double) subscripts x and y denote first (second) partial derivatives in the subscripted direction. The derivatives are calculated by using a centered 9-point quadratic fit to the data. The background Φ_o is constant for each slice and is equal to the sum of the median and the median deviation of all nonzero values of Φ for a given z section. The discriminant for each z section is binarized by using a threshold that is equal to the median of all positive values of the discriminant. The binary is refined further by retaining only those pixels that have a value of 1 and have at least two nearest neighbors (each pixel has eight neighbors) that also have a value of 1. This represents a minimum requirement for connectivity. This binary is refined again by retaining all pixels with a value of 1 that have at least three nonzero nearest neighbors. The final binary image is obtained by removing all isolated nonzero valued pixels. Connectivity to adjacent z sections is determined by retaining all pixels that have a value of 1 and at least 3 nearest nonzero neighbors in the two adjacent z sections. Individual 3D objects are obtained by nearest neighbor connectivity throughout the entire volume.

Density and velocity.

We write the number of GFPs in a subvolume δxδyδz as δN(x, y, z) = N(x, y, z)δxδyδz, where N(x, y, z) is the GFP density. Cartesian and spherical densities are related by the expression δN(x, y, z) = N(r, θ, φ) r² sinθ δrδθδφ, where the geometric center of the T cell is the origin of the coordinate system, θ = 0° is the computed center of intensity of the synapse, and θ = 180° is in the opposite direction. The measured pixel intensity represents an emitted energy per subvolume, which in turn corresponds to the molar concentration of molecules in that subvolume. The experimentally measured intensity per subvolume is δI(x, y, z) = βτδN(x, y, z)/α, where τ is the exposure time, β is an assumed constant scaling factor, and α is a normalizaton factor that accounts for bleaching and variations in the number of filtered data points from different time states. We calculate α for each time state by choosing any of the time states as a reference. We set α = 1 for this reference state. We equate Σ δN and Σ δN_ref and obtain

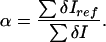Substituting the spherical representation on the right side of the expression for δN into the expression for δI and summing over all (x, y, z) that lie in the range θ − δθ/2 to θ + δθ/2, we obtain

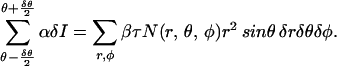The right side of the equation can be represented as N*(θ)sinθ, where N*(θ) is the angular density of GFP. We write

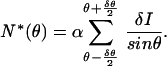We note that this angular dependent GFP density is calculated simply by using only the measured intensities within a volume of angular extent δθ, and the normalization factor α. In all of the analyses presented here, we used δθ = 3.6°.

The receptor velocity is the difference between the total and the membrane velocities. Conservation of GFP allows the velocity in the θ direction to be calculated by slicing the T cell at some angle θ and equating the rate of change of the amount of GFP in the volume contained between θ and 180°, to the flux of GFP leaving the volume. (When θ = 90°, the T cell is cut in half; when θ ≠ 90°, the cut is conical.) We write

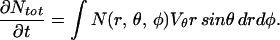We change derivatives to differences, convert to measured intensities via δI = βτδN/α, and obtain

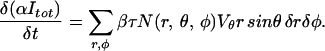δI_tot can be simplified by using the expression αδI = βτN(r, θ, φ)r² sinθ δrδθδφ. We write

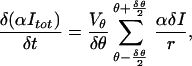where each δI has an associated value for r. Pairs of adjacent time states are used to solve for V_θ, which yields

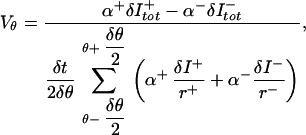where “+” and “−” denote the two time states, and the average flux is used to time-center the velocity. Membrane velocities are also obtained from this equation by invoking conservation of membrane mass: the intensity from each subvolume is set equal to 1, and the normalization factor α is computed by using the total number of extracted points, instead of the total intensity.

Labeling of TCRs by Using Submicrometer-Sized Fluorescent Beads.

H57-597 anti-TCRβ monoclonal antibodies were digested with immobilized papain (Pierce). FAb was purified from Fc fragments by Protein A absorbtion (Amersham Pharmacia), and purity was confirmed by SDS/PAGE. Anti-TCR FAbs were linked to the surface of 0.026-μm diameter red carboxylate Fluospheres (Molecular Probes) in a 1:1 average molar ratio of FAb/spheres. Nanospheres were sonicated and centrifuged to remove any agglomerates, then diluted to 9 × 10¹³ spheres per ml in 50 mM Mes, pH 6.0. A molar ratio of 1:1:60 of spheres/Fab/BSA (to block hydrophobic interactions) was allowed to equilibrate at room temperature for 15 min. FAb and BSA were then covalently linked to the surface of the spheres by the addition of 2 mM 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide, adjusting the pH to 6.5, and rotating for 2 h at room temperature in the dark. The reaction was quenched by the addition of 100 mM glycine for 30 min, and excess uncoupled protein was removed by extensive dialysis of the spheres through a 300-K molecular weight cutoff (MWCO) regenerated cellulose membrane against PBS at 4°C followed by size exclusion chromatography.

T cells were labeled with low numbers of anti-TCR nanospheres just before microscopy. Any exposed hydrophobic sites remaining on FAb/BSA-linked spheres were blocked by sonicating in the presence of 0.05% Tween 20 (Sigma). Blocked spheres were diluted 1:10 in PBS, passed through a 0.2-μm filter, and added 1:25 to cells in PBS at 4°C for 25 min. The calcium indicator dye FURA-2 AM (Molecular Probes) was simultaneously loaded into T cells at 10 μM. Cells were incubated with the nanospheres on ice for 25 min, washed once with 10 ml PBS, then resuspended in 200 μl phenol-deficient RPMI medium 1640 and allowed to attach to coverwells for microscopy at 37°C. Microscopy experiments with labeled T cells were performed as described above with peptide-pulsed CH27 cells as APCs. However, for these experiments two 3D fluorescence images were collected sequentially at each time point, for GFP followed immediately by the red emission from the nanospheres.

Single Particle Motion Analysis.

Centroids of individual nanospheres in space were determined from the maximum intensity pixel within single bead diffraction-limited spots in 3D fluorescence data. Tracking of a few beads on the same cell was typically aided by beads being well separated in 3D space (moving much smaller distances per time interval than their typical separation) and having differing fluorescence intensities, which could be used to distinguish two closely placed particles. The velocity V(i) of a particle toward the interface at time point i was determined by the simple difference equation:

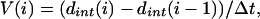where d_int(i) is the distance of the particle from the center of the T/APC interface at time i and Δt is the time step between time points i − 1 and i. To correct for gross motion of the entire T cell and changes in morphology, the velocity of the rear of the cell (V_r(i)) was subtracted. V_r(i) was calculated as

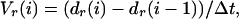where d_r is the distance from the center of the T/APC interface to a point on the rear of the cell along a vector through the cell x–y center of mass. The cell center of mass was determined from the x–y coordinates of the cell boundary identified in differential interference contrast images.

Results

TCR Motion Assessed in CD3ζ-GFP-Transfected T Cell Clones.

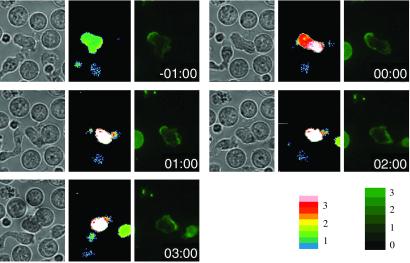
We assessed the motion of TCR/CD3 complexes by using a fusion protein of CD3ζ with GFP transfected into a T cell clone (11). A notable feature of TCRs revealed by these transfectants is that before activation, the bulk of the CD3 molecules in polarized T cells are localized predominantly in the uropod, opposite the leading edge. As shown in Fig. 1, the bulk of this receptor pool reorients rapidly after TCR mediated activation occurs, so that within 2.5 min of activation, a majority of receptors has moved to the front of the T cell, facing the synapse. In contrast, T cells that encounter APCs bearing a weak agonist rarely reorient receptors, or the receptor motion is so slow that the T cell–APC couple dissipates before any significant reorientation is observed (ref. 11 and data not shown).

Fig 1.

Initial polarization and antigen-specific repolarization of CD3ζGFP in D10 T cell clones. T cells transfected with CD3ζGFP were imaged at 15-s intervals during contact with 10 μM CA-134-146-peptide-pulsed APCs. Data show the FURA ratio overlayed with the contrast image and the GFP intensity in a mid z plane at the indicated times relative to first contact. For a movie version of this figure, see Movie 1, which is published as supporting information on the PNAS web site, www.pnas.org.

To quantify this motion directly, we used our ability to collect multiple z planes of data in short time periods. By using a high-speed piezoelectric z motor and individual frame rates of ≈50 ms, 25 fluorescence planes (z sections) were collected in sequential 1 μm z steps within ≈3 s at 15- or 20-s time-lapse intervals. Although these data are collected on a wide-field fluorescence microscope and are therefore subject to associated haze, individual membrane intensities nonetheless are mapped predominantly to individual pixels. We therefore sought a mechanism to “mine” these membrane-representative pixels and then translate the data into velocity measurements.

Image Segmentation and Continuum Analysis.

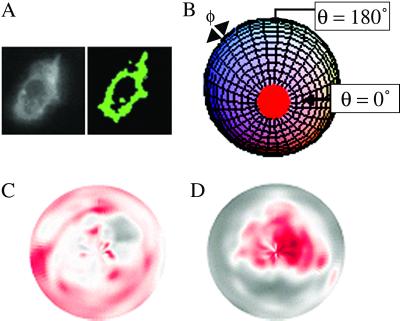
Fig. 2A shows a typical z section. Quantitative analysis begins by “segmenting” from the background the labeled pixels that comprise the cell membrane. Although this task can be accomplished easily for a single z section by the human eye, an automated segmentation method is required to process the large amount of data acquired in a time-lapse experiment. We segmented the data by using a filter (12) developed by W.C.M.. The image is viewed as a topographic map, where pixel intensity represents altitude, i.e., peaks and valleys. Pixels are identified as “membrane” if they lie along a ridge line. All of the non-black pixels in Fig. 2A Right are pixels from the Left that have been identified by the filter as membrane.

Fig 2.

3D data segmentation and normalized densities of CD3ζGFP during antigen-specific repolarization. (A) An example of segmentation showing a widefield fluorescence image (Left) and the binary map of captured pixels (Right). (B) A 2D coordinate system for viewing data. Pixel intensities were mapped to polar coordinates (θ, φ), where θ = 0° (front of the T cell) is the vector from the center of the T cell to the center of the B cell, and corresponds to the center of the polar plot. θ = 180° (the rear of the cell) corresponds to the circumference of the polar plot. φ (−180° ≤ φ ≤ 180°) is the azimuthal angle. (C and D) 2D graphical representation of time dependent TCR clustering. Black and red represent low and high intensities. A diffuse TCR distribution before flux (C) becomes a clustered distribution within 10 min of flux (D).

The membrane pixels from all of the z sections (at a particular time point) are grouped into distinct 3D objects via nearest-neighbor connectivity. Three objects are algorithmically identified in the figure. The green pixels in the figure constitute a slice of the object of interest. The filter operates on our data without any user intervention, except for the final step, where the user chooses the particular 3D object to consider, from all those that are identified. The final result of the filter for a particular time state is an object that is described by a collection of n points (x_i, y_i, z_i, I_i)|_i=1, n, where I_i is primarily composed of intensities derived from a subvolume δxδyδz that is centered at (x_i, y_i, z_i).

There are many ways to use the filtered data (x, y, z, I) to view the time-dependent 3D motion of the TCRs. Fig. 2 C and D show a semiquantitative, but visually stunning representation of receptor motion toward the synapse, in which a 3D filtered data set has been mapped into a 2D polar representation (Fig. 2B) at two times; Fig. 2Cshows that 5 min before flux there is a diffuse pattern of TCR, whereas, within 10 min after flux (Fig. 2D), most of the receptors have accumulated near the synapse.

The 3D filtered data can be used to obtain a more quantitative estimate of the time-dependent TCR densities and velocities, if we assume that the mass of the T cell membrane and the amount of GFP in a particular T cell are invariant. Conservation of GFP is a simplifying assumption and eliminates the need for applying a separate coefficient to accommodate effects caused by bleaching. We believe that GFP conservation is reasonable, because typical GFP expression and reinternalization times are long compared with data acquisition times (16) and quantification of levels using a standard bleach correction algorithm suggests that down-modulation does not occur in our systems for upwards of 10 min after the onset of calcium signaling (data not shown).

TCR Velocities.

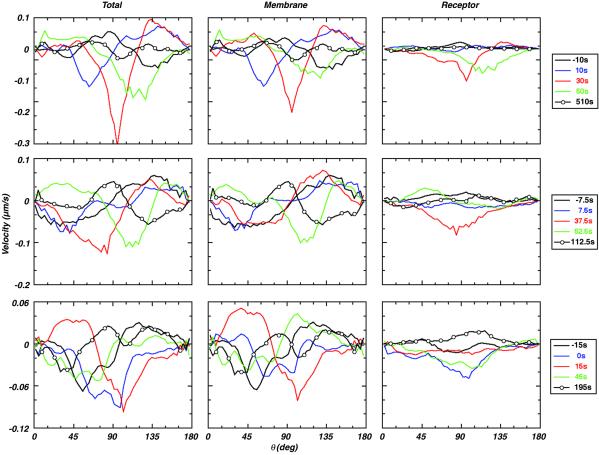
We map the data from a Cartesian to a spherical coordinate system to calculate membrane motion toward the synapse and receptor motion through the membrane. We use the filtered data from adjacent time states to calculate the average temporal and angular dependences of both velocities. A velocity at a particular angular location (θ) is obtained by equating the flux of GFP through a ring of membrane that is normal to the θ direction, to the rate of change of the amount of GFP in either volume bounded by the ring. Hence, the calculated velocity varies as a function of θ. The rows in Fig. 3 show calculated velocities for three individual cells at various pre- and postflux times. The columns show three different velocities. The “Total” velocity is calculated by using the intensities from the filtered data. Consequently, this calculated velocity is the sum of the membrane velocity because of changes in cell shape plus the actual receptor velocity through the membrane, hence, the “total” receptor velocity. The column labeled “Membrane” is calculated by assigning unit intensity to each of the filtered data points. Because this tracks only changes in membrane location, not intensity, it is an estimate of the “membrane” velocity or the motion caused by changes in overall cell shape. The “Receptor” velocity is the motion of the receptor through the membrane, which is simply the difference of the Total and Membrane velocities. Unlike the density calculations, common scaling factors cancel in this analysis, so that the absolute magnitude of the velocity can be determined.

Fig 3.

Instantaneous velocities of CD3 molecules in a developing synapse assessed by 3D quantitation. Calculated temporal and angular dependence of three different velocity measures for three T cells. The “Receptor” velocity describes movement of the receptors, with respect to the membrane motion. The “Membrane” velocity describes only the movement of cell membrane. The “Total” velocity is the sum of the Membrane and Receptor velocities. The data for the three cells show two distinct features: (i) early time velocities can be attributed to a conformational wave that transits the membrane (compare black, blue, and red Membrane and Total velocities); and (ii) preflux Receptor velocities are small, followed by a large increase in receptor motion toward the synapse between 0 and 30 s after flux. Note that negative velocities are toward the synapse.

The data shown in the figure are quite dynamic. The locations of the black, blue, and red negative peaks in the Total velocity of all three cells show a wave propagating in time from the front of the cell toward the midplane. Comparisons with the Membrane velocities show that this wave of receptor motion is due mostly to membrane motion and not the actual motion of the receptors through the membrane. This finding suggests that the membrane deforms significantly when a cell collides with a neighboring cell at the beginning of the process of synapsis.

The Receptor velocities represent CD3ζ movement with respect to the cell membrane. The figure shows that this motion is relatively small before calcium flux. However, for two of the cells there was a dramatic rise in the velocity toward the synapse ≈30-s after flux, whereas, the remaining cell showed an increase when calcium flux occurred. In all cases examined, this movement corresponds to an observed shift in the bias of receptors that is visible in the original optical data. The peak receptor velocities are clearly directional and they are at least an order of magnitude greater than diffusional velocities for this transmembrane receptor as determined by fluorescence recovery after photobleaching (FRAP; refs. 17–19).

Single Particle Tracking Analysis.

Because the data generated in the preceding figures rely on a GFP tag and the method calculates velocities for a group of receptors by using wide-field data, we sought to confirm these results for the motion of single TCRs. To achieve this, we used single particle tracking to follow single TCRs labeled with fluorescent nanospheres by using the 4D microscopy system described above. Nonmitogenic anti-TCRβ FAb fragments were conjugated to highly fluorescent beads allowing us to reassess the motion of individual receptors, and to verify that motion was occurring along the membrane and not through an internalizing route.

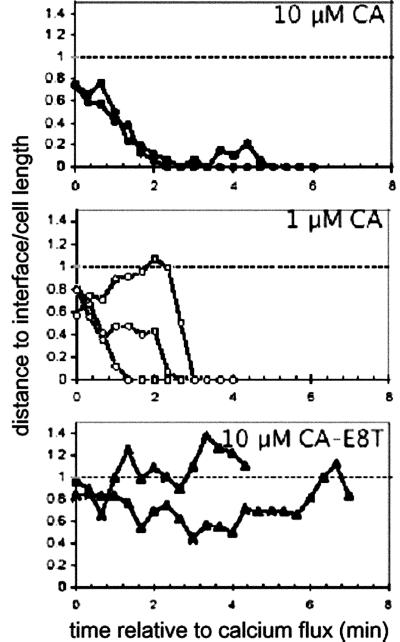
As shown in Fig. 6, which is published as supporting information on the PNAS web site, this technique demonstrated that individual TCRs were initially localized toward the uropod before activation but were rapidly shuttled toward the interface after calcium flux. On encountering an APC presenting agonist peptide, and approximately coincident with the initial rise in intracellular calcium, beads were observed to rapidly translocate to the nascent synapse, and once localized in the interface, remained there for periods exceeding the time of observation (>20 min). As shown in Fig. 4, most beads moved toward the synapse within the first 3 min when T cells engaged agonist ligand but typically remained at the rear of the T cell for the duration of T cell/APC contact when weak agonist ligands were encountered.

Fig 4.

Single particle tracking of TCR recruitment to the nascent immunological synapse. Example time-lapse positions of nanosphere-labeled TCRs. Coordinates of each nanosphere in (x, y, z) space were determined from 3D fluorescence images, and the distance from each particle to the interface was calculated by using differential interference contrast images to determine the interface location. Shown are the distances of each particle from the interface at each time point normalized by the length of the cell of individual nanospheres on single T cells responding to APCs pulsed with: •, 10 μM CA 134-146; ○, 1 μM CA 134-146; ▴, 10 μM CA 134-146-E8T. Representative movies of responses to agonist and weak-agonist recruitment are published as Movies 1–3 on the PNAS web site.

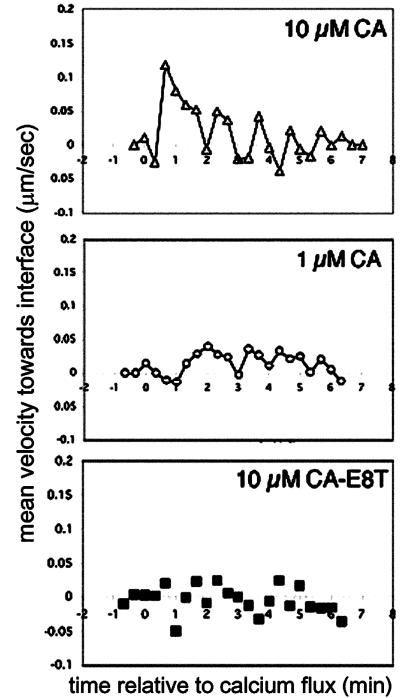
To further assess the motion of individual receptors in this system, we undertook a velocity analysis using these nanospheres. Velocities of individual particles were calculated from position changes at each time point, with motion due to bulk x-y translation of the cell subtracted. Receptor velocities rapidly increased from a basal level of <0.05 μm/s to ≈0.15 μm/s in response to 10 μM agonist-pulsed APCs (Fig. 5 Top). This spike in receptor velocity occurred for multiple TCRs observed on the same cell within a narrow window of time postinitial calcium rise, and returned to low levels coincident with the arrival of receptors in the interface. Lower concentrations of agonist delayed the mean time of onset for receptor recruitment (Fig. 5 Middle) and the maximum velocity of receptors after this onset was lower (≈0.05 μm/s) than observed at the higher peptide density. This was in contrast to APCs presenting weak agonist peptide CA-E8T, which induced only infrequent momentary bursts of increased TCR velocity with no sustained or coordinated velocity up-regulation for multiple receptors (Fig. 5 Bottom).

Fig 5.

Velocities of TCR as measured by single particle tracking. Instantaneous velocities of nanosphere-labeled TCRs as a function of time were measured by tracking position changes as a function of time. Motion of the tail of T cells was subtracted to correct for translation of the whole cell, as described in Methods. Shown are mean velocities of nanospheres (n ≥ 10) as a function of the time relative to initial intracellular calcium elevation for TCRs on T cells responding to APCs pulsed with 10 μM CA (Top), 1 μM CA (Middle), or 10 μM CA-E8T (Bottom).

Membrane Rebiasing.

The data in Fig. 3 demonstrate that cellular activation during synapse formation involves a conformational change that continues to push increased quantities of total membrane toward the APC. To quantify this effect, we measured the diameter of the contact region for cells during recognition of wild-type or weak-agonist peptides. As shown in Fig. 7, which is published as supporting information on the PNAS web site, T cells recognizing APCs in the presence of weak-agonist peptides antigen have a mean synapse waist diameter of 11.8 μm after 5 min of contact whereas those recognizing T cells presenting agonist peptide have increased this contact area to a mean of 21 μm after 5 min. This finding confirms that T cell recognition does indeed give rise to an increased contact area during recognition of the antigen-bearing APC.

Discussion

We describe here a method for quantifying 3D membrane distributions and the velocities of receptor proteins during biological processes. Before this study, the primary methods for calculating bulk molecular mobility in living cells were limited to FRAP and FLIP (fluorescence loss in photobleaching). These approaches require bleaching of dye-labeled structures followed by time-lapse recording of dye redistribution. Although the FRAP and FLIP methods are highly sensitive and appropriate for structures that are more or less stably localized within immobile cells, they are considerably more difficult to use in actively moving, 3D structures or in a time-lapse setting. Further, they are limited to events at a single locus (the bleach spot). The continuum approach described here provides a method to assesses bulk distribution and velocity measurements of molecules and structures across the entire cell.

That this analysis is able to quantify and accurately describe the behavior of moving molecules in the cell membrane was verified by using a single particle tracking approach. Bead tracking is one method for the analysis of the behavior of individual or small cohorts of molecules in living specimens (13, 14). Here the use of FAb-labeled small nanospheres can provide additional information by providing a window into the variability of velocities for individual particles. The small size (≈30 nm) size of these beads exceeds what has been suggested to be the vertical dimension of the synapse (15–20 nm) (18) and yet they are clearly brought into the synapse.

Previous studies have shown that a large portion of TCR/CD3 and MHC complexes appear at the synapse region within 10 min of contact with an APC (10, 11, 20). However, evidence obtained by conventional FRAP analysis of transmembrane CD3ζ constructs or TCR have demonstrated slow rates of diffusion of transmembrane proteins [≈0.011 μm²/s for a IL-2R-CD3ζ chimera (17) to 0.018 μm²/s for FAb-labeled TCR (18), to 0.12 μm²/s for GFP-labeled TCR on Jurkat cell surface (19)]. Based on these rates, the time required for a receptor to cover 18 μm (the approximate distance from the back of the cell to the front) is ≈1–5 h.∥ Typical fluid mosaic models of membrane flow, however, suggest that transmembrane signaling and accumulation of receptors are controlled by the relatively slow speed of diffusion for the receptors and tethering of those that reach their ligand (21, 22). Our data provides direct evidence of an active process initiated after signaling onset, thus confirming and quantifying previous work (8–11).

Three possibilities have been proposed to explain molecular movement that exceeds values predicted by random diffusion (23). Transient confinement has been proposed to limit membrane proteins below the rates of diffusion through the action of obstacle clusters such as lipid “rafts.” By limiting diffusion of enzymes and substrates within their domains, these are proposed to promote signaling (24). However, such a confinement acts to limit molecular speeds below the levels of diffusion for proteins in a fluid membrane and is thus unlikely to explain our faster-than-diffusion results. A second version of transient confinement, the so-called “membrane–skeleton fence” (25), suggests that the cytoskeleton or elements binding to it are involved in establishing zones into which proteins are confined but can diffuse within (26). Such a mechanism has potential to explain our rapid rates of motion if a “fence” were assembled in a band from the B/T interface. Coupled with tethering to ligands at the site of contact, this could also produce rapid directional movement. One argument against this mechanism derives from our data (Figs. 4 and 5) in which beads move, more or less smoothly, toward the interface. A membrane–skeleton fence might be expected to obstruct this movement but this was not observed.

A third possibility for motion is an active mechanism involving directed motion of proteins attached to the cytoskeleton. Studies using cross-linking antibodies and lectins first demonstrated a cytoskeletal requirement for receptor “capping” (27). In ≈20% of cells, we observed a rear-localized pool which never reoriented, thus suggesting that some TCR/CD3 complexes do not attach to the machinery that is responsible for the rapid reorientation. Studies of neurons have suggested that the glycine receptor may alternate between a form attached to the cytoskeleton and a form that is freely mobile (28). A similar mechanism may act here at the level of TCRs. Such a hypothesis is supported by biochemical data showing that at least a portion of the CD3ζ molecules in T cells are associated with the cytoskeleton (29). In addition, the active transport described here is inhibited by BDM, an inhibitor of myosin motors (ref. 8; W.C.M. and M.F.K., unpublished data), further indicating both a cytoskeletal connection. In any event, the data and analysis presented here demonstrates that receptor reorientation cannot be mediated by simple passive diffusion.

It remains unclear at this point how many other proteins in the membrane move in during this reorientation. Experiments using avidin-beads coated onto surface-biotinylated T cells demonstrated that these beads undergo a relatively late (≈5–10 min after activation) reorientation from the uropod into the synapse region (8). Because the tethering in this previous study was nonspecific and we have only observed forward movement in TCR associated proteins, it is possible that other types of molecules move countercurrent to what we observed here or do not translocate at all. It would be very interesting to know what other signaling molecules/receptors are also transported by these same mechanisms and which are not.

The analysis we present here also reveals that TCR redistribution toward the site of antigen receptor contact is the sum of at least two distinct types of events (see Fig. 8, which is published as supporting information on the PNAS web site). Upon recognition, a pronounced wave of membrane movement spreads from the front of the cell to the back. This rippling corresponds in time to the period in which a tight junction is formed and suggests that the cytoskeleton continues to push the cell membrane into the APC face, thus leading to an increase in the overall surface area at the interface. Increased surface contact has been observed in T cells reacting to bilayers confirming that this is a T cell intrinsic activity (18). Previous studies have demonstrated that leukocytes show a forward motion of membrane lipid flow during locomotion (30). In addition, two previous studies have assessed the T cell shape factor on activation, showing that T cells become more spherical after antigen-receptor signaling (31, 32). Our data are consistent with these results and further suggest that the interconversion from “hand mirror” to a more spherical shape occurs by an intermediate process in which the rear of the T cell continues to move toward the APC as the front of the T cell stays fixed. The TCR velocity that we measure here is thus the sum of this conformational event and a direct movement along this membrane.

It has previously been shown that the active transport mechanisms that we analyze here are the product of stimulation through both the TCR and one or more of the costimulatory receptors (CD28, LFA-1) (8, 9). Because weak TCR signals do not trigger this effect and lower concentrations of agonist peptide antigens give rise to slower speeds, we conclude that this system can convert stoichiometrically small signals into a strong cellular repolarization. Such a receptor-induced recruitment of additional receptors is likely to represent a positive feedback loop for activation, bringing more molecules into play to potentiate signals.

Abbreviations

• TCR, T cell receptor

• APC, antigen-presenting cell

• FRAP, fluorescence recovery after photobleaching