Herpes viruses hedge their bets

Abstract

Static latency is the hallmark of all herpes viruses. The varicella zoster virus, for instance, causes varicella (chickenpox), and after a latent phase of between 5 and 40 years, it can give rise to herpes zoster (shingles). This latency and the subsequent reactivation has intrigued and puzzled virologists. Although several factors have been suggested, it is unknown what triggers reactivation. However, latency can be explained with a simple evolutionary model. Here, we demonstrate that a simple, yet efficient, bet-hedging strategy might have evolved in a number of viruses, especially those belonging to the herpes virus family and most importantly in varicella zoster virus. We show that the evolution of latency can be explained by the population dynamics of infectious diseases in fluctuating host populations.

Static latency (1, 2) is a characteristic feature of all herpes viruses; whereas herpes simplex 1 and 2 and varicella zoster virus (VZV) stay latent in cells of the nervous system, and cytomegalovirus and Epstein–Barr virus establish themselves in cells of the immune system (1, 2). Their latency is static in the sense that no virus is produced and that latency seems to be actively maintained by a number of viral genes (3–7). In contrast, dynamic latency (2) involves an actively replicating virus that is kept at bay through the host's response and not because of the virus's replication strategy. The latency of the HIV is an example of dynamic latency (8). Here, our main interest is in trying to understand when and why latency evolves rather than in the molecular mechanisms involved in establishing, maintaining, and controlling latency. These are very different questions, not least because the former approach already postulates that latency is a useful strategy for the virus.

We focus on VZV because it displays the longest latency period and may thus serve as a canonical example for latent behavior. During the latent phase, VZV resides in neurons in the dorsal root and trigeminal ganglia (5, 6). It does not seem to replicate until it reactivates and the clinical symptoms of herpes zoster develop; reactivation is not normally associated with a particular inciting event (2). Waning immunity, predominantly with age, has been suggested as a factor that can trigger reactivation (2, 4), especially early reactivation (9). VZV [like herpes simplex virus (HSV) 1 and HSV2] can, however, reactivate even in the presence of cellular and humoral immune response (9, 10). Exposure to chickenpox can be ruled out as a likely cause for reactivation, as the epidemiology of shingles does not follow the periodic pattern typical for chickenpox (2, 9). It therefore seems that static latency has evolved as an active strategy of the virus (1), where the virus colonizes immunoprivileged sites and stays dormant until reactivation (1, 2, 7, 10).

Previously, research into latency has focused largely on molecular mechanisms of latency and reactivation of latent virus. Arguments for the evolution of latency have stressed the importance of latency for persistence of the viral species in small host populations (2, 11, 12), thus the search for genes that maintain and regulate viral latency. But while we observe VZV today because it has persisted throughout human history, this does not make persistence the reason for the evolution of latency. Such teleological (including “good for the species”) arguments are untenable from a modern evolutionary perspective; selection does not operate on the species or a group of viruses but on individual viral genes (13). Here, we show that the evolution of latency can be understood by considering the life history of a latent virus in a stochastic environment. We show that static latency can confer a selective advantage over other, nonlatent strains of the same virus.

Theory: An Effective Model for VZV Epidemics

Like plants in dry regions (14, 15) or investment fund managers in the city, parasites are frequently faced with unpredictably fluctuating environments (16–19). In the case of VZV (or HSV1 and HSV2), fluctuations in the effective number of susceptible hosts because of lifelong immunity upon initial infection confront the virus with a highly stochastic environment, in addition to the stochasticity intrinsic in the infection process. Normally, 90–95% of the population is immune against VZV (9), and the disease can only temporarily spread again if a new cohort of uninfected individuals has grown large enough. Such a cohort of susceptibles can disappear suddenly if a local outbreak of VZV occurs. Changes in the number of susceptible hosts are unpredictable from the point of view of the individual virus. The small size of early human populations and the corresponding random fluctuations in the number of available susceptible hosts will also have contributed to such changes.

We have condensed an epidemiological model (20) into an effective model of latent infection dynamics; each infected case can produce a certain amount of infective capacity immediately after initial infection, and it can produce some infective ability after latency. This decreases the environmental uncertainty but also creates a tradeoff for the virus because its carrier may die during the quiescent phase. However, if infected hosts survive the latent period, they can then give rise to a secondary infection (i.e., shingles) after a latency period, τ. There are two reasons for making the assumption of this underlying tradeoff between investment of infectious potential and latency that can be motivated from the epidemiology and immunology of the virus, respectively: (i) herpes zoster is caused by reactivated virus leaving cells of the nervous system that were infected during the initial bout and thus were unable to contribute to spreading the infection to other hosts; thus, we have to assume that not all of the available virus was invested into transmitting disease to other, previously unchallenged hosts (11); and (ii) latency is a costly strategy and is maintained by a host of viral genes (5, 7). Our assumption of the tradeoff is, we believe, the most parsimonious way to investigate the competition between latent and nonlatent strains of the same virus. Our model can incorporate the effects of reduced transmissibility from acute herpes-zoster cases compared with varicella cases.

We model environmental stochasticity by randomly setting the fitness of each period to either a high value or a low value, indicating, respectively, high or low availability of susceptible hosts. The delicate interplay between environmental factors and availability of susceptible individuals is summarized by randomly assigning one of two values for the effective transmission rate, r_b for “bad” (few susceptible hosts) and r_g > r_b (many susceptible hosts) for “good” conditions, to each period. The probability that a good period will occur is P, and consequently the probability that a bad period will occur is 1 − P; we have chosen these probabilities to reproduce the observed frequency of outbreaks (every 2–3 years). This qualitatively describes the otherwise rather complicated and involved population feedback process that regulates the number of susceptibles (20). The outcome of the procedure is the effective number of infections, N_t, in each period t:

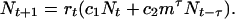Here, c₁ is the infective potential invested in infections during chickenpox while a second bout of infection during shingles has an infective potential of c₂. The probability of surviving one period is given by m, where m ≤ 1. Iterating Eq. 1 allows us to extract the geometric mean growth rate of a population with latency τ, λ_τ (the geometric mean growth rate is defined as lim_t→∞(N_t/N₀)^1/t). In the Appendix, we show how Eq. 1 can be derived from standard, discrete-time epidemiological models.

In the effective model, we implicitly assume that the number of susceptibles is controlled by a virus with arbitrary but constant latency. For reasons of clarity and computational simplicity, we will assume that the dominant strain has no latency (τ = 0). A strain with a different latency can only invade, i.e., succeed in the environment that is shaped by the presence of a nonlatent virus, if its growth rate exceeds the growth rate of the dominant strain (21–23). We assume that the only evolutionary freedom for the virus is adjusting the length of the latent period τ during which it lies dormant in the (seemingly recovered) host. We can then calculate λ_τ, i.e., the growth rate of a virus, which “waits” for τ periods after its initial infective period before it becomes effective again (the average time from the recovery from chickenpox to the appearance of shingles) as the geometric mean growth rate of N_t through Eq. 1 (18).

Results

In the nonlatent case, the geometric mean growth rate is given by λ₀ = (c₁ + c₂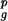)rr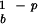. If there is a latent period, τ > 0, then the geometric mean growth rate cannot be calculated by analytical means, and we use numerical methods to establish the mean growth rate. Here, we show how the growth rate changes with the length of the latency period. The details of the model can be adjusted to describe the duration of the latent period, the infectivity, and the frequency of reactivations of different viruses. Here, we have chosen parameters that loosely try to capture the epidemiology of VZV.

Our model contains seven parameters (r_g, r_b, c₁, c₂, m, p, and τ). Three of these parameters, c₁, c₂, and τ, embody life-history decisions of the virus. We will assume that these life-history traits are independent. We are interested in whether strains that have a latent period can invade a viral population in which no latency occurs. If this is the case, then latency can evolve as an adaptation to environmental fluctuations. We therefore consider the ratio of λτ/λ₀. If this is greater than 1, then a latent virus will invade a population of a nonlatent virus; if it is less than 1, then it will become extinct.

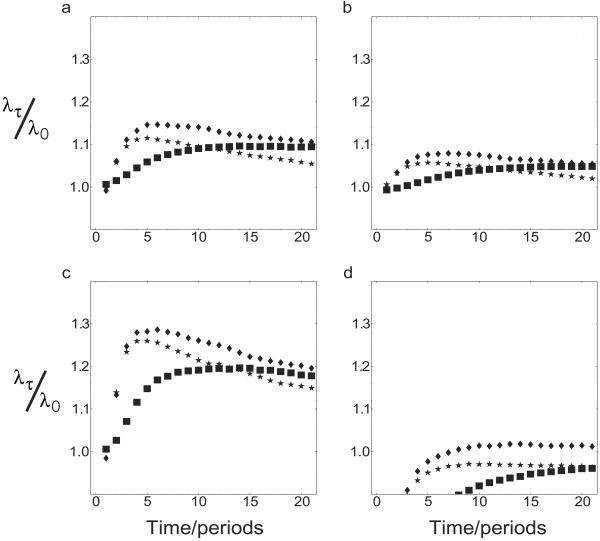
In Fig. 1, we investigate different environmental conditions. In Fig. 1a, we consider the case in which the ratio between r_g/r_b ≃ 13 was chosen to roughly reflect the observed difference between the susceptibility to chickenpox in human populations which have not been exposed to chickenpox (100%) and in which chickenpox is endemic (5–10%). The length of a time step was set to be 1 year, and the survival probability m was chosen to reproduce a possible case of average host life expectancy, 40 years, corresponding to m = 1 − 1/40 = 0.975. The infective potential invested into the primary infection was chosen to be c₁ = 0.9, and the infective potential for the second bout was c₂ = 0.1 (Fig. 1a, ♦). A choice of equal probability of good and bad years, P = 1/2, was chosen to ensure that the model reflects the observed periodicity of 2–4 years in VZV epidemics. The three different lines represent different survival probabilities, m, and different fractions, c₁, c₂. We found a maximum in λ_τ/λ₀ at τ = 5. This indicates that under conditions similar to those in recent human populations, a latent strategy confers an evolutionary advantage to the virus. It can also be seen that if the survival probability is decreased, the maximum growth rate is found for a shorter latent period (Fig. 1a, *). If the infective potential used for chickenpox, c₁, is increased while the total infective potential (c₁ + c₂) is kept constant, then the maximum growth rate is found for longer latencies (Fig. 1a, ▪).

Fig 1.

Growth rates versus latency τ. We plotted average values of λ_τ/λ₀ for three fluctuating environments. (a) r_g = 3.65, r_b = 1/r_g ≃ 0.274, and P = 0.5. Different symbols represent the cases for which (i) m = 0.975, c₁ = 0.9, and c₂ = 0.1 (⧫), (ii) m = 0.9, c₁ = 0.9, and c₂ = 0.1 (*), and (iii) m = 0.975, c₁ = 0.99, and c₂ = 0.01 (▪). (b) r_g = 2.58, r_b = 0.387, and other parameters are as described in a. (c) r_g = 6.32, r_b = 0.158, and other parameters are as described in a. (d) We have assumed the same values for r_g and r_b as described in a, but now bad periods are more likely than good periods with P = 0.4.

In Fig. 1 b and c, we changed the ratio of viral reproductive potential to illustrate how parameter choices influence the evolutionary dynamics of this system. We have chosen r_g/r_b ≃ 7 in Fig. 1b and r_g/r_b ≃ 40 in Fig. 1c. If the differences between good and bad years is less pronounced (low value of r_g/r_b), we observe that bet-hedging virus cannot invade. If the fluctuations in the environmental conditions increase, the maximum of λ_τ/λ₀ moves out to τ = 18. This behavior is confirmed in the two other cases investigated here. Fig. 1 a and c confirms that for a system where the survival probability is high and investment into direct offspring is high, it is evolutionarily advantageous to wait longer if the relative reproductive rate in the “bad” periods is low. We also find that long latency confers an advantage if bad periods are more frequent than good periods, if P < 0.5 (Fig. 1d).

We thus find that for risky environments bet-hedging (14, 21) by adopting a latent strategy confers an advantage, and latent virus can invade (21, 23) a population with a resident nonlatent virus. If good periods are sufficiently good and bad periods sufficiently bad (due to lack of available hosts), then latency makes sense; hedging one's bets by waiting for some time before becoming infectious again is now worthwhile. At the optimal length of the latency period, the virus strikes a balance between losing hosts through mortality, which imposes a costs on latency, and the benefits of latency through bet-hedging. (We have implicitly assumed that the optimal growth rate is a strategy that is evolutionary stable and cannot be invaded by other strategies. This follows from our model if one chooses the strain with the highest growth rate as the resident strain and assumes that this strain causes the sequence r_t. The geometric mean growth rate of this strain can then be normalized.) The optimal length of the latency period decreases with increasing quality of the environment (that is, availability of susceptible hosts), as bet-hedging becomes less important when the difference between good and bad periods is small. We found that the optimum value length of the latency period decreases if the cost of staying latent is too high, i.e., if hosts are more likely not to survive until the second infective stage. Then it is best not to adopt latency but to invest all infectivity into the first stage. We also found that long latent periods pay off if the effective potential of the second infective period is small compared with the first.

Discussion

Our results indicate that a strategy that combines some infectiousness in a second infective stage with a long delay can have a competitive advantage over strategies with no delay. It has previously been suggested (1, 2, 11, 12) that viral latency has evolved for the virus to persist. This seems unlikely in the case of VZV. First, the virus spreads very efficiently in respiratory secretions before the emergence of the symptoms of chickenpox, but spreads much less efficiently from shingles lesions after reactivation. Second, latency introduces a delay in the population dynamical feedback, which often leads to unstable dynamics. Such fluctuations can in fact lead to reduced persistence. Our results indicate that latency has evolved because in a fluctuating environment, it makes a virus a superior competitor to nonlatent competing strains. Therefore, in stochastic environments (which are not necessarily restricted to small populations), bet-hedging can form an evolutionary favorable strategy. Applied to VZV, this means that fluctuations in the number of susceptible hosts could have favored the evolution and maintenance of latency, not because the virus would otherwise not persist but because it outcompetes the competition.

We note that the ability of some viruses (including HSV1, HSV2, and VZV) to infect neurons already requires them to carry genes coding for all replicative functions that would normally be found in other tissues. Neuroinvasiveness (2) must therefore be seen as a costly strategy, and the evasion of the host's immune response may be sufficient to explain why this has happened. Latency, however, is a separate evolutionary problem that is best understood in its proper ecological setting of competing viruses. The small genomes of viruses (typically in the order of tens or hundreds of genes) make it unlikely that viruses have developed very refined techniques for dealing with such unpredictable environments (given the already high cost of neuroinvasiveness). Moreover, even complex forecasting techniques are not always better, and there may be little incentive for complex behavior (together with the necessary molecular apparatus) to evolve. (If we grossly extrapolate this statement to the aforementioned fund manager, then our analysis suggests that in certain situations a random number generator will outperform more sophisticated investment strategists.) Simple strategies can be very effective, and, as we have shown here, a fixed delay before reactivation may suffice. The flip-side of this is that what seems to be a very refined mechanism for reactivation may be a simple timer or even a chance event. The winning strategy matches the strategy that VZV uses and perhaps, to a lesser extent, probably also that of HSV1 and HSV2.

Of course, bet-hedging can also have a positive selective effect in a model that incorporates space explicitly (18); we expect that in a spatial context, latent virus will also outcompete nonlatent virus given sufficient demographic stochasticity in the host population. Here, we have demonstrated that the evolution of latency can already be understood theoretically without an explicit treatment of space.

The attraction of the present approach lies also in the fact that it shows that no particularly refined trigger for the reactivation of VZV in infected neurons is required to explain the evolution of latency. As long as the virus stays latent for some time before reactivation, it can prove superior to nonlatent strains in sufficiently risky environments. It therefore seems that not only do viruses play games (24), but some viruses also hedge their bets. The population biology of infectious diseases (20), and not the molecular biology of viral reactivation, may thus hold the key for an understanding of viral latency.

Abbreviations

• VZV, varicella zoster virus

• HSV, herpes simplex virus

Appendix

Our effective model, Eq. 1, relates to standard discrete-time epidemiological models (20). To illustrate this relation, we use a S − I₁ − I₂ − ⋯ − I_1+τ − R model, where S(t) represents the number of susceptible hosts at time t, and we have introduced a reservoir, I_i(t) with 1 ≤ i≤ 1 + τ, for the number of hosts at time t that were infected i time units ago. R(t) represents the number of recovered hosts at time t and Q(t) = S(t) + R(t) + Σ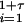I_i (t) the total population size. The full epidemiological model is given by

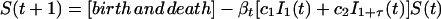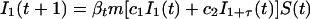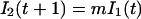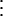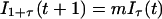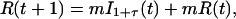where m is the probability to survive from one time step to the next, β_t is the transmission parameter at time t, and c₁ and c₂ are the rates at which new cases develop from acute (varicella) and latent (herpes zoster) cases, respectively. We have assumed that the time steps are sufficiently small so that the number of newly infected individuals is approximately given by the product of the infectivity produced, c₁I₁ + c₂I_1+τ, the number of susceptibles, S(t), and the transmission parameter, β_t. We now define the effective number of susceptibles r_t as

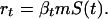The second equation of Eq. 2 can thus be rewritten as

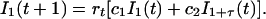The population dynamical feedback ensures that the geometric mean growth rate of I₁ equals lim_t→∞(I₁(t)/I₁(0))^1/t = 1 (23). In the case of no latency (τ = 0), the geometric mean growth of I₁ equals the geometric mean of r_t times c₁ + c₂.

Next, consider a new virus strain with a different latency that is introduced into a population that already harbors a strain that has epidemic behavior described by the system (2). We are interested in whether such a strain will decrease and eventually disappear or increase and invade the population. We therefore consider the growth of this strain of the virus when it is rare. If a strain is rare, then it will have negligible effect on the number of susceptible hosts. The number of newly infected cases resulting from the rare virus strain, I^*₁, is

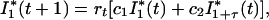where r_t is given by Eq. 3 and therefore independent of I^*_i. The value of I^*_{1 + τ}(t) follows straightforwardly from the value of I^*₁τ generations ago, i.e., I^*_{1 + τ}(t) = m^τI^*₁(t − τ). By substituting N_t = I^*₁(t), we obtain our effective epidemiological model (1).

If a strain has a growth rate that exceeds unity, it can invade the population and possibly replace the resident strain. In this way, a replacement dynamics can be constructed that only stops when a strain evolves with a growth rate that is so high so that a viral population consisting of this strain cannot be invaded by strains with different latencies.

The combined stochasticity in β_t and S(t) determines the stochastic behavior of r_t. In this article, we are not concerned with deriving details of this distribution. Instead, we assume (in an ad hoc manner) that the behavior of r_t can be caricatured in a simple manner; in particular, we assumed that r_t takes the values r_g with probability P and r_b with probability 1 − P and that the values of r_t for different times are uncorrelated. Our results hold for epidemiological models that produce such time-series behavior for r_t. This offers a conceptually simple and general framework to study the effect of unpredictability in the number of susceptibles. The simple effective model does, however, retain the essential dynamics of more complicated epidemiological models of latent viral infections.