Abstract
Fluorescent spectroscopy experiments with single-enzyme molecules yield a large volume of statistical data that can be analyzed and interpreted using stochastic models of enzyme action. Here, we present two models, each based on the mechanism that an enzyme molecule must pass through a sequence of conformational transformations to complete its catalytic turnover cycle. In the simplest model, only one path leading to the release of product is present. In contrast to this, two different catalytic paths are possible in the second considered model. If a cycle is started from an active state, immediately after the previous product release, it follows a different conformational route and is much shorter. Our numerical investigations show that both models generate non-Markovian molecular statistics. However, their memory landscapes and distributions of cycle times are significantly different. The memory landscape of the double-path model bears strong similarity to the recent experimental data for horseradish peroxidase.
Large biomolecules may act as machines that generate motoric motions or, in the case of enzymes, catalyze individual reaction events. To understand the functions of enzymes at a molecular level, experiments with single molecules are important. Such experiments have been performed for lactate dehydrogenase (1, 2), alkaline phosphatase (3, 4), β-d-galactosidase (5), cholesterol oxidase (6), horseradish peroxidase (7), staphylococcal nuclease (8), and RNA polymerase (9). Because realistic computer simulations of enzymic turnover cycles are not yet possible, interpretation of experimental data are based on phenomenological models of single-enzyme kinetics. Theoretical and experimental investigations reveal that proteins are characterized by rugged energy landscapes (10, 11). Intramolecular relaxation in proteins involves passing through a large number of metastable substates and may therefore be slow.
Conformational changes are essential for the catalytic enzyme function. They are generally used to explain allosteric regulation and the phenomena of cooperativity in enzymes with several interacting subunits. Conformational memory has been found for the enzyme wheat germ hexokinase (12, 13). Experiments on peptide binding to class II MHC proteins have further suggested that conformational memory of previous functional states is present in such macromolecules (14, 15). A strong memory effect has also been discovered in single molecules of the hairpin ribozyme (16). In the investigations of cholesterol oxidase by Lu et al. (6), slow conformational fluctuations in the equilibrium state of a single enzyme, leading to modulation of its affinity for a given substrate, were shown to explain correlations between subsequent catalytic cycles. In this case, conformational dynamics was not directly influenced by enzyme activity and played an external role with respect to its catalytic function. In contrast to this, experiments with horseradish peroxidase could be interpreted by assuming that the memory of earlier functional states was present in an enzyme molecule (17).
Processes of conformational relaxation may be intrinsically involved in a molecular turnover cycle (18–20). In this view, the binding of a substrate makes an enzyme leave its state of thermal equilibrium and initiates a sequence of conformational changes, eventually leading to a conformation where a reaction event converting substrate into product is facilitated. This is followed by another sequence of conformational transitions returning the enzyme to its equilibrium free state. Models of single-enzyme kinetics, based on this picture, have been used to study effects of mutual synchronization of turnover cycles for enzymic reactions in microvolumes (21, 22) and to analyze the experimental data on external optical synchronization of a photosensitive cytochrome P450-dependent monooxygenase system (23). However, implications of conformational relaxation for statistics of single-enzyme events have not been investigated so far.
In this paper, two molecular models with conformational relaxation are considered. In the first model, a turnover cycle is assumed to follow a fixed sequence of conformational transitions described by a continuous conformational coordinate. In the second, two different conformational paths are possible. Binding of a substrate in the activated state immediately after release of a product leads here to a catalytic cycle, the duration of which is significantly shorter than that of the normal turnover cycle involving full conformational relaxation. We show that the memory of previous functional states is characteristic for both considered models. A detailed analysis, however, reveals that their memory landscapes (as introduced in ref. 17) show important differences. Furthermore, essential differences are also found in other statistical properties of the models, such as autocorrelation functions and distributions of cycle times.
Models of Single-Enzyme Kinetics
The Michaelis–Menten (MM) Model.
According to the classical MM model (24), a substrate molecule S binds to the enzyme E at rate k1 to form the enzyme–substrate complex ES. This complex can either decay again at rate k−1 to free substrate and enzyme molecules or complete the enzymic reaction to give free product P and free enzyme E at rate k2,
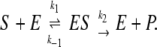 |
The substrate binding rate is proportional to the substrate concentration, k1 = αS.
Thus, only two distinct states, corresponding to the free enzyme and the enzyme–substrate complex, are present in this theoretical description. In their study of dynamical disorder, Xie et al. (6) have used the MM model where the substrate binding rate constant depended on the instantaneous conformational state of the enzyme molecule and equilibrium conformational fluctuations produced slow random variations of the rate k1. Below, the standard MM model with constant rates is chosen as a reference system.
Single-Path Model.
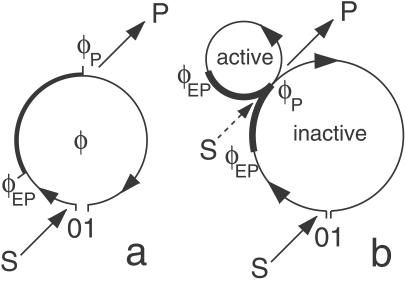
This model additionally takes into account the processes of conformational relaxation inside the enzymic turnover cycle (see Fig. 1a). The cycle starts when a substrate molecule is bound. Although a free enzyme molecule is in the state of thermal equilibrium, the initial state of the enzyme–substrate complex is far from equilibrium, and therefore relaxation to its equilibrium conformation begins. The complex passes through a series of conformational substates, until a conformation favorable for the chemical transformation of the substrate into the product is reached. In our simple model, we assume that the energy barrier is reduced so strongly in this conformational substate that the substrate–product transformation takes place without any waiting time. After that, the relaxation of the enzyme–substrate complex is continued until a conformation optimal for the release of a product molecule is achieved. Once this has occurred, a free enzyme molecule in a conformational state far from equilibrium is obtained. Thus, it starts its own conformational-relaxation process leading to the equilibrium state.
Fig 1.
Molecular models of enzyme action. (a) Single-path model. Binding of substrate S initiates a cycle that represents diffusive drift relaxation along the conformational coordinate φ. Release of product P at φ = φP is further followed by relaxation to the equilibrium conformation state of a free enzyme. (b) Double-path model. Immediately after release of product, the enzyme is in the active state, in which it may bind substrate and perform a rapid catalytic cycle. The enzymes are assumed fluorescent in the parts of their cycle marked by thick lines.
Conformational relaxation in proteins is a complex process, because it involves motion through a large number of hierarchically organized metastable substates (10). As a rough simplification, it can be modeled (see ref. 25) as diffusive drift along an effective conformational coordinate. To describe conformational-relaxation processes inside an enzymic turnover cycle, three different coordinates, corresponding to the substrate–enzyme and product–enzyme complexes and to the free enzyme, are generally needed. We shall combine them into a single conformational coordinate φ, so that the interval 0 < φ < φEP corresponds to the substrate–enzyme complex, the interval φEP < φ < φP corresponds to the product–enzyme complex, and a free enzyme is found inside the interval φP < φ < 1. Thus, the initial state of the substrate–enzyme complex is φ = 0, the product is released at φ = φP, and the free enzyme returns to its equilibrium state when φ = 1 is reached. The conformational motion inside a turnover cycle is described by a stochastic Langevin equation
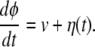 |
Although the mean speed of relaxation is generally different at its different stages, we assume for simplicity that it is always constant and equal to v. The white Gaussian noise η in this equation takes into account conformational fluctuations accompanying the relaxation process. It has intensity σ and the correlation function
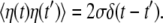 |
For small noise intensities σ, the mean time T0 = 〈tturn〉 needed to complete a cycle (the turnover time) and its relative statistical dispersion ξ = T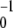 〈Δt
〈Δt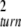 〉1/2 are approximately given by T0 = 1/v and ξ =
〉1/2 are approximately given by T0 = 1/v and ξ = 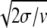 .
.
In this model, binding of a substrate is possible only from the equilibrium state of free enzyme, reached when the cycle is completed (φ = 1). Binding takes place at a rate k1 = αS, where S is the substrate concentration and α is the binding rate constant. In our example, we neglect a possibility of substrate dissociation. Moreover, we assume that product dissociation takes place instantaneously when the state φ = φP is reached.
Double-Path Model.
Investigations of peptide binding to proteins (14, 15) and recent experiments with single-enzyme molecules (7, 17) indicate that some enzymes may have more complex internal organization. Immediately after release of a product, they are found in an active state. Binding of a substrate in this state is possible and, if it has taken place, a new product molecule is formed within a short time. But if substrate binding in the active state has not occurred, the enzyme enters an inactive state. Starting from the inactive state, a turnover cycle can also be initiated, but the turnover rate is then much smaller.
In the context of conformational relaxation, this situation can be modeled by assuming that two different turnover cycles are possible inside the same enzyme molecule (Fig. 1b). Now the enzyme can perform either a rapid cycle characterized by a short mean turnover time Ts, or a slow cycle with a longer mean turnover time Tl. After having bound a substrate molecule in the ground state (φ = 0), the slow cycle is initiated, the enzyme–product complex is formed at the point φEP, and the product is released at the point φP. At this moment, cycle branching takes place. Within a short time interval after product release, the enzyme is “active”: it can bind a substrate and thus trigger a short turnover cycle. If this has not occurred, the enzyme must undergo slow conformational relaxation to its ground state (φ = 1), and only then start a new slow turnover cycle by binding substrate from this ground state.
For simplicity, we shall assume that motions inside both cycles are described by the same stochastic Langevin equation (Eq. 2), and thus are characterized by the same drift velocity v and intensity σ of intramolecular noise. The slow cycle takes the whole interval 0 < φ < 1, whereas the rapid cycle starts at φ = 0 and ends at φ = φs, where φs = Ts/Tl. Binding of the substrate from the ground state occurs at rate k1 = αS. The probability w of binding substrate from the active state, immediately after product release, depends on the substrate concentration and is given by w = 1 − exp(−aS), where a is a coefficient specifying probability of binding of a single substrate molecule within the active state. At low substrate concentrations, so that aS ≪ 1, the probability w is proportional to the substrate concentration (w ≈ aS). At high substrate concentrations it approaches unity, so that short activated cycles become dominant.
Statistical Characterization of Enzymic Cycles
The time series data derived from spectroscopic experiments with single-enzyme molecules monitors only a certain state of the enzyme. For example, in the case of cholesterol oxidase one can only distinguish the fluorescent oxidized state of the tightly bound coenzyme FAD from the nonfluorescent reduced form FADH2 (6). The reaction catalyzed by horseradish peroxidase oxidizes the nonfluorescent substrate dihydrorhodamine 6G to the fluorescent product rhodamine 6G so that the fluorescent enzyme–product complex can be observed (7). To compare the model predictions with such experimental data, we define for each model a binary variable Xt, which has the value Xt = 0, if, at time t, an enzyme is in the “fluorescent” state, and Xt = 1 if an enzyme is in the “nonfluorescent” state. For the classical MM model, the fluorescent state is chosen to correspond to the substrate–enzyme complex. For both models with conformational relaxation, we assume that an enzyme is in a fluorescent state (Xt = 0) when a product–enzyme complex has already been formed but the product has not yet dissociated (φEP < φ < φP).
By running a simulation of one of the stochastic models, a certain time series Xt is obtained. This stochastic data can be processed in different ways to obtain statistical characterization of enzymic cycles. Normalized two-time and three-time autocorrelation functions G2(τ) and G3(τ1, τ2) of such binary stochastic processes can be defined as
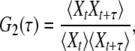 |
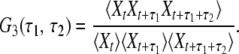 |
They can further be used to construct the memory function (17),
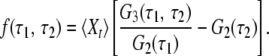 |
This memory function vanishes if the stochastic process Xt is Markovian. Indeed, for any Markov process the three-time conditional probability π3(Xt1|Xt2, Xt3) to find the system in a state Xt1 at time t1, provided it was in the states Xt2 and Xt3 at two previous moments t2 and t3 (t2 > t3), does not depend on the earlier state Xt3 and is therefore reduced to the two-time conditional probability π2(Xt1|Xt2). The memory function (Eq. 6) can be equivalently written as f(τ1, τ2) = π3(Xt+τ1+τ2 = 1|Xt+τ1 = 1, Xt = 1) − π2(Xt+τ1+τ2 = 1|Xt+τ1 = 1), and therefore it is identically zero for a Markov process that has no memory. Note that because the considered random process is statistically uniform, its moments 〈Xt〉, 〈XtXt+τ〉, and 〈XtXt+τ1XtXt+τ1+τ2〉 cannot explicitly depend on time t. Thus, 〈Xt〉 = 〈Xt+τ1〉 = 〈Xt+τ1+τ2〉 = const.
In addition to autocorrelation functions, statistical distributions of cycle times can be considered. For a binary process Xt, such cycle times are defined as intervals separating subsequent release of product molecules by the same enzyme (that is, as intervals between subsequent transitions from X = 0 to X = 1).
The autocorrelation functions (Eqs. 4 and 5) follow the definitions used in ref. 17. In the literature (see, for example, ref. 6), a different definition is also found, and according to this, the stochastic process is specified by a binary variable ξt, taking value ξt = 1 in the fluorescent state and ξt = 0 in the nonfluorescent state. Moreover, another normalization of the autocorrelation functions is used. Because ξt = 1 − Xt, the two definitions are closely related. However, under the other definition the three-time autocorrelation function of a Markov process would not factorize into a product of two two-time correlation functions, and a memory function, similar to Eq. 6, cannot be easily introduced.
Results and Discussion
The time series Xt generated by the MM model is Markovian. Its normalized two-time autocorrelation function is a simple exponential, G2(τ) = 1 + (k−1 + k2) k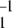 exp[−(k1 + k−1 + k2)τ]. The three-time autocorrelation function of the MM model factorizes, G3(τ1, τ2) = G3(τ1)G2(τ2), and its memory function vanishes, f(τ1, τ2) = 0. The cycle times can be defined for the MM model as time intervals T between subsequent release of the products. In the formal limit, when dissociation of a substrate–enzyme complex is negligibly small, the distribution over such cycle times is given by q(T) = k1k2(k1 − k2)−1 [exp(−k2T) − exp(−k1T)]. Generally, the distribution q(T) can be determined numerically. It increases linearly as q(T) ≈ k1k2T for small cycle times T, reaches a maximum, and then slowly decreases in the limit of large times.
exp[−(k1 + k−1 + k2)τ]. The three-time autocorrelation function of the MM model factorizes, G3(τ1, τ2) = G3(τ1)G2(τ2), and its memory function vanishes, f(τ1, τ2) = 0. The cycle times can be defined for the MM model as time intervals T between subsequent release of the products. In the formal limit, when dissociation of a substrate–enzyme complex is negligibly small, the distribution over such cycle times is given by q(T) = k1k2(k1 − k2)−1 [exp(−k2T) − exp(−k1T)]. Generally, the distribution q(T) can be determined numerically. It increases linearly as q(T) ≈ k1k2T for small cycle times T, reaches a maximum, and then slowly decreases in the limit of large times.
To numerically investigate the models with conformational relaxation, the stochastic differential equation (Eq. 2) has been discretized by dividing time into equal small steps Δt and thus replaced by a stochastic map
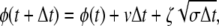 |
where ζ are independent Gaussian random numbers with 〈ζ〉 = 0 and 〈ζ2〉 = 2. Because dissociation of substrate, back transformation of product into substrate, and reverse binding of product are excluded in the considered models, the points φ = 0, φ = φEP, and φ = φP cannot be passed in the opposite direction. Should this have happened in a simulation, we replaced φ(t + Δt) yielded by the map (Eq. 7) by the values vΔt, φEP + vΔt, or φP + vΔt, respectively.
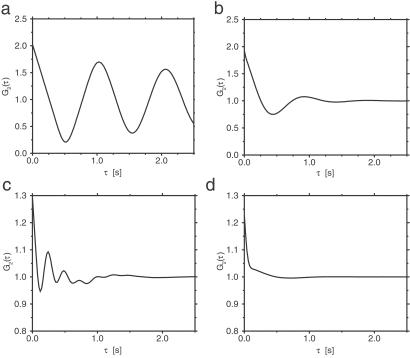
The results for the single-path conformational-relaxation model are presented first. Fig. 2 a and b shows normalized autocorrelation functions G2(τ) in this model for two different intensities of intramolecular noise. When the noise is relatively weak (corresponding to the statistical dispersion of 10% in turnover times), oscillations with the period equal to the mean turnover time are observed in the autocorrelation function (Fig. 2a). Increasing the noise intensity so that the mean statistical dispersion of turnover times becomes 40% leads to strong damping, and only the first oscillation is then discernible (Fig. 2b).
Fig 2.
Normalized autocorrelation functions G2(τ) in the single-path (a and b) and double-path (c and d) models. The parameters of the single-path model are T0 = 1 s, v = 1 s−1, φEP = 0.2, φP = 0.55, α = 25 mmol−1⋅s−1, S = 1 mmol⋅liter−1, and ξ = 0.1 (a) or ξ = 0.4 (b). The parameters of the double-path model are Tl = 1 s, Ts = 0.25 s, v = 1 s−1, φEP = 0.15, φP = 0.25, α = 25 mmol−1⋅liter⋅s−1, a = 0.925 mmol−1⋅liter, S = 1.5 mmol⋅liter−1, and ξ = 0.1 (c) or ξ = 0.4 (d).
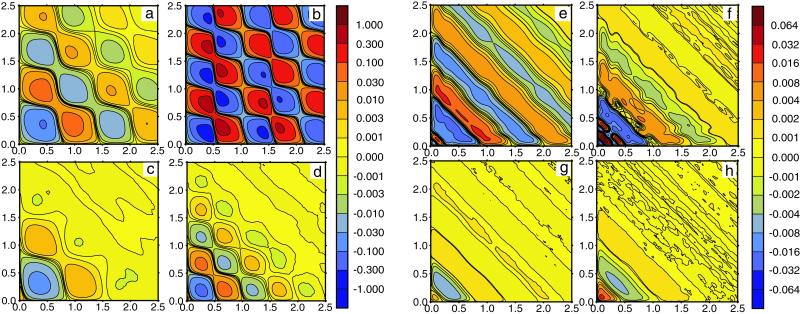
The typical memory functions f(τ1, τ2) computed for the single-path model are displayed as memory landscapes in Fig. 3 a–d. When the intensity of intramolecular noise is low (Fig. 3 a and b), a checkerboard pattern with alternating minima and maxima is observed. Increasing the noise intensity (Fig. 3 c and d) leads both to smaller amplitudes of oscillations of the memory function and to more rapid decay of such oscillations. If substrate concentration is low (Fig. 3 a and c), the enzyme spends more time waiting in the ground state until binding of a substrate molecule triggers a reaction cycle, and therefore the period of oscillations in the memory function is longer. Furthermore, the amplitude of oscillations is smaller and they are damped more strongly at low substrate concentrations, as seen by comparing Fig. 3 a and c with b and d. Because the binding of substrate is a stochastic process, it introduces an additional source of fluctuations for the single-enzyme kinetics. The contribution from such fluctuations is larger when an enzyme molecule waits for a longer time to bind a substrate.
Fig 3.
Memory landscapes of single enzymes. (a–d) Single-path model. Statistical dispersions of turnover times are ξ = 0.1 (a and b) and ξ = 0.4 (c and d); substrate concentrations are S = 0.0625 mmol⋅liter−1 (a and c) and S = 1 mmol⋅liter−1 (b and d). Other parameters are the same as in Fig. 2 a and b. (e–h) Double-path model. Statistical dispersions of turnover times are ξ = 0.1 (a and b) and ξ = 0.4 (c and d); substrate concentrations are S = 0.5 mmol⋅liter−1 (a and c) and S = 1.5 mmol⋅liter−1 (b and d). Other parameters are the same as in Fig. 2 c and d. Memory functions f(τ1, τ2) are plotted using color codes indicated by vertical bars on the right side of the panels.
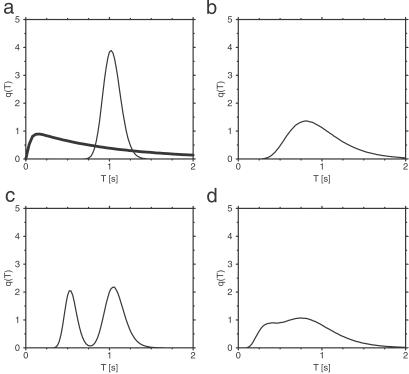
Fig. 4a shows the distribution q(T) of cycle times computed for the single-path conformational-relaxation model at a relatively low intensity of intramolecular noise. For comparison, the respective distribution for the MM model with the same mean production rate is also presented (thick curve). The two distributions are qualitatively different. In the conformational relaxation model, the distribution is roughly Gaussian, and the probabilities for having short cycles are exponentially low. In contrast to this, the distribution q(T) for the MM model is strongly asymmetric and linear for small cycle times T. This reflects the different nature of cycle times in both systems. In the MM model, the enzyme is only waiting for a transition in one of the two possible discrete states. The process is Markovian, and the probability that a transition will occur within the next short time interval does not depend on how long the enzyme has already stayed in the respective discrete state. Hence, both transitions can relatively easily occur within a short time interval. In the relaxation model, the cycle involves diffusive drift motion along a fixed conformational path. Only when such motion is completed may the next cycle start. Therefore, short cycle times will be found only if, as a statistical fluctuation, the velocity of motion along the cycle turns out to be very high, much higher than the average drift velocity. Such fluctuations are very rare, and this explains the existence of an effective gap at short cycle times in the distribution q(T). Fig. 4b displays the distribution q(T) for the single-path model with strong intramolecular noise. Although the distribution is broad, very short cycles are still only rarely found, as compared with the MM kinetics.
Fig 4.
Distributions of cycle times q(T) in the single-path (a and b) and double-path (c and d) models. The parameters of the single-path model are ξ = 0.1 (a) and ξ = 0.4 (b), and substrate concentration is S = 1 mmol⋅liter−1. The parameters of the double-path model are ξ = 0.1 (c) and ξ = 0.4 (d); substrate concentration is S = 1.5 mmol⋅liter−1. Other parameters are the same as in Fig. 2, except for φP = 0.55 and φEP = 0.2. The thick solid line in a shows distribution q(T) for the MM model with parameters k1 = 10 s−1, k−1 = 9 s−1, and k2 = 2.483 s−1.
The same numerical investigations have been repeated for the double-path conformational-relaxation model. The autocorrelation functions G2(τ) exhibit a more complex structure in this case (Fig. 2 c and d). It can be understood as a superposition of damped oscillations with the period Tl and Ts corresponding to the long and the short paths. For the same intensity of intramolecular noise, oscillations are damped more strongly in the double-path model. This is because stochastic switching between the path introduces an additional effective noise, reducing the coherence of intramolecular dynamics. Moreover, it can also be noted that the maximum at τ = 0 is much stronger for the double-path model. When intramolecular noise is strong, oscillations are no longer visible (Fig. 2d). The autocorrelation function has then a narrow peak at τ = 0 and a shoulder extending to τ ≈ 1.
The memory functions for the double-path model are displayed in Fig. 3 e–h. In contrast to the previously discussed model, the checkerboard structure is absent here, and a pattern of stripes extending perpendicular to the diagonal direction is observed instead. Generally, the amplitude of variations in the memory function is smaller in this model and the oscillations are damped more strongly. For low substrate concentration (Fig. 3 e and g), the characteristic time scale of the pattern is determined by the duration of long inactive cycles that are then prevailing. Elevating the substrate concentration (Fig. 3 f and h) leads to a pattern mainly determined by the short active cycles. When the intramolecular noise is increased (Fig. 3 g and h), the amplitude of the diagonal stripe pattern decreases and the memory landscape becomes nearly flat.
Thus, the intensity of intramolecular noise is important in determining the properties of autocorrelation and memory functions. When noise is weak, an enzyme goes like a mechanical clock through an ordered sequence of conformational states, and this is reflected in the presence of oscillations with the clock cycle period in the auto-relation functions. Strong noise destroys the ordered cyclic motion and washes out the oscillations.
The statistical distributions of cycle times for the double-path model (Fig. 4 c and d) show a bimodal structure, with the maxima corresponding to the characteristic durations of the long and the short cycles. When the intramolecular noise is low, two separate peaks are visible (Fig. 4c). At strong noises (Fig. 4d), the peaks become broad and overlap.
Our results indicate that both investigated models exhibit memory of previous activity states. Enzymes must pass through a sequence of conformations, and only when this process is completed can the next reaction event occur. Thus, an interval between two reaction events cannot be arbitrarily small. Such memory should be absent for the enzymes obeying standard MM kinetics. On the other hand, the shapes of the memory landscapes are qualitatively different for the two models. The pattern of diagonal stripes obtained for the double-path model is more closely reproducing the structure of memory landscapes based on the experimental data for horseradish peroxidase (17). This theoretical study, based on two simple models of enzyme action, reveals that effects of conformational relaxation may be essential for the analysis of single-enzyme experiments and for understanding the operation of such molecular machines. Further systematic statistical investigations of such a family of models are needed.
Acknowledgments
This work was supported by Peter und Traudl Engelhorn Stiftung zur Förderung der Biotechnologie und Gentechnik (Germany).
Abbreviations
MM, Michaelis–Menten
Appendix
In this Appendix, concentration dependences of macroscopic reaction rates for both conformational-relaxation models are analytically determined. For the MM model, the dependence of the inverse of the mean product generation rate V (per single-enzyme molecule) plotted versus the inverse of the substrate concentration S is linear and given by 1/V = (k2)−1 + (k−1 + k2)(k2α)−1(1/S). This representation is known as the Lineweaver–Burk plot of an enzymic reaction.
The mean product generation rate for the single-path model with low intramolecular noise can be found analytically. We define the probability p0 to find an enzyme in its ground free state and the probability density p(φ), so that the probability to find an enzyme inside the cycle in the interval from φ to φ + dφ is p(φ)dφ. The normalization condition implies that p0 + ∫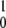 ρ(φ)dφ = 1. The cycles are initiated when, at rate αS, a free enzyme binds a substrate. Hence, we have vρ(φ = 0) = αSp0. Because the reverse reaction is absent, the rate V of product generation is, under steady state conditions, equal to the rate of substrate binding, i.e., V = αSp0. In the steady state, all cycle phases are equally probable, and the distribution ρ(φ) is flat, i.e., ρ(φ) = const. Therefore, p0 + ρ = 1 and vρ = αSp0. This yields the dependence
ρ(φ)dφ = 1. The cycles are initiated when, at rate αS, a free enzyme binds a substrate. Hence, we have vρ(φ = 0) = αSp0. Because the reverse reaction is absent, the rate V of product generation is, under steady state conditions, equal to the rate of substrate binding, i.e., V = αSp0. In the steady state, all cycle phases are equally probable, and the distribution ρ(φ) is flat, i.e., ρ(φ) = const. Therefore, p0 + ρ = 1 and vρ = αSp0. This yields the dependence
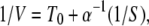 |
where T0 = 1/v is the cycle duration.
To extend this analysis to the double-path model, we note that, under steady state conditions, we should distinguish then between the probability p0 of finding an enzyme in its free ground state, and the probability densities ρl and ρs to find it inside a long and a short cycle, respectively. The normalization condition yields p0 + ρl + ρsφs = 1. The product generation rate is given by V = v(ρl + ρs). Additionally, we have two conditions vρl = αSp0 and ρs = w(S)(ρl + ρs), where the last one takes into account that a short cycle can be initiated with probability w(S) each time a product molecule has been released. Solving this set of equations, we obtain
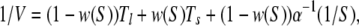 |
where w(S) = 1 − exp(−aS).
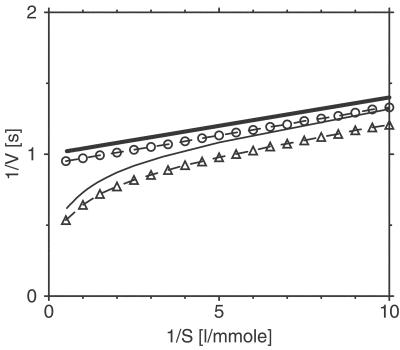
In the derivation of Eqs. 9 and 8, fluctuations of times T0, Tl, and Ts due to intramolecular noise have been neglected. The Lineweaver–Burk plots for both models with a relatively strong noise have been numerically determined from the simulation data and are shown in Fig. 5, together with the respective analytical predictions in the low-noise limit. We see that the single-path system has a linear Lineweaver–Burk plot, and therefore, based only on the macroscopic reaction properties, it cannot be distinguished from the MM model. For the double-path system, long inactivated cycles are dominant at low substrate concentrations (1/S ≫ a), as follows from Eq. 9. In this limit, w(S) ≈ 0 and the linear Lineweaver–Burk dependence with T = Tl holds approximately. As the substrate concentration is increased, the contribution from activated cycles with T = Ts grows and the reaction is enhanced. When the substrate is abundant (1/S ≪ a), we have w(S) ≈ 1 and the reaction rate is controlled by the rapid turnover cycle, so that 1/V ≈ Ts. A similar result is obtained from numerical simulations of the double-path model at strong noise (see Fig. 5b). Thus, enzymes described by a double-path conformational-relaxation model have nonlinear Lineweaver–Burk plots, similar as found for enzymes with several cooperating subunits (26, 27). Some deviations from linear Lineweaver–Burk plots in enzyme kinetics involving conformational relaxation have previously been considered (28).
Fig 5.
Lineweaver–Burk plots for the single-path (circles) and the double-path (triangles) models. The parameters of the single-path model are α = 25 mmol−1⋅liter⋅s−1, T0 = 1 s, and ξ = 0.4; the parameters of the double-path model are α = 25 mmol−1⋅liter⋅s−1, a = 1 mmol−1⋅liter, Tl = 1 s, Ts = 0.55 s, and ξ = 0.4. Thick and thin solid lines show the respective analytical predictions in the weak noise limit, given by Eqs. 8 and 9.
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Xue Q. & Yeung, E. S. (1995) Nature 373 681-683. [DOI] [PubMed] [Google Scholar]
- 2.Tan W. & Yeung, E. S. (1997) Anal. Chem. 69 4242-4248. [Google Scholar]
- 3.Craig D. B., Arriaga, E. A., Wong, J. C. Y., Lu, H. & Dovichi, N. J. (1996) J. Am. Chem. Soc. 118 5245-5253. [Google Scholar]
- 4.Chiu D. T., Wilson, C. F., Karlsson, A., Danielsson, A., Lundqvist, A., Strömberg, A., Ryttsén, F., Davidson, M., Nordholm, S., Orwar, O. & Zare, R. N. (1999) Chem. Phys. 247 133-139. [Google Scholar]
- 5.Craig D. B. & Dovichi, N. J. (1998) Can. J. Chem. 76 623-626. [Google Scholar]
- 6.Lu H. P., Xun, L. & Xie, X. S. (1998) Science 282 1877-1882. [DOI] [PubMed] [Google Scholar]
- 7.Edman L., Földes-Papp, Z., Wennmalm, S. & Rigler, R. (1999) Chem. Phys. 247 11-22. [Google Scholar]
- 8.Ha T., Ting, A. Y., Liang, J., Caldwell, W. B., Deniz, A. A., Chemla, D. S., Schultz, P. G. & Weiss, S. (1999) Proc. Natl. Acad. Sci. USA 96 893-898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Davenport R. J., Wuite, G. J. L., Landick, R. & Bustamante, C. (2000) Science 287 2497-2500. [DOI] [PubMed] [Google Scholar]
- 10.Frauenfelder H., Sligar, S. G. & Wolynes, P. G. (1991) Science 254 1598-1603. [DOI] [PubMed] [Google Scholar]
- 11.Pande V. S., Grosberg, A. Y. & Tanaka, T. (2000) Rev. Mod. Phys. 72 259-314. [Google Scholar]
- 12.Ricard J., Meunier, J.-C. & Buc, J. (1974) Eur. J. Biochem. 49 195-208. [DOI] [PubMed] [Google Scholar]
- 13.Ricard J., Buc, J. & Meunier, J.-C. (1977) Eur. J. Biochem. 80 581-592. [DOI] [PubMed] [Google Scholar]
- 14.Rabinowitz J. D., Vrjic, M., Kasson, P. M., Liang, M. N., Busch, R., Boniface, J. J., Davis, M. M. & McConnel, H. M. (1998) Immunity 9 699-709. [DOI] [PubMed] [Google Scholar]
- 15.Kasson P. M., Rabinowitz, J. D., Schmidt, L., Davis, M. M. & McConnel, H. M. (2000) Biochemistry 39 1048-1058. [DOI] [PubMed] [Google Scholar]
- 16.Zhuang X., Kim, H., Pereira, M. J. B., Babcock, H. P., Walter, N. G. & Chu, S. (2002) Science 296 1473-1476. [DOI] [PubMed] [Google Scholar]
- 17.Edman L. & Rigler, R. (2000) Proc. Natl. Acad. Sci. USA 97 8266-8271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Careri G., Fasella, P. & Gratton, E. (1975) CRC Crit. Rev. Biochem. 3 141-164. [DOI] [PubMed] [Google Scholar]
- 19.Welch G. R., (1986) The Fluctuating Enzyme (Wiley, New York).
- 20.Blumenfeld L. A. & Tikhonov, A. N., (1994) Biophysical Thermodynamics of Intracellular Processes: Molecular Machines of the Living Cell (Springer, Berlin).
- 21.Mikhailov A. S. & Hess, B. (1996) J. Phys. Chem. 100 19059-19065. [Google Scholar]
- 22.Mikhailov A. S., Stange, P. & Hess, B. (2001) in Single Molecule Spectroscopy: Nobel Conference Lectures, eds. Rigler, R., Orrit, M. & Basché, T. (Springer, Berlin), pp. 277–292.
- 23.Schienbein M. & Gruler, H. (1997) Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 56 7116-7127. [DOI] [PubMed] [Google Scholar]
- 24.Michaelis L. & Menten, M. L. (1913) Biochem. Z. 49 333-369. [Google Scholar]
- 25.Socci N. D., Onuchic, J. N. & Wolynes, P. G. (1996) J. Chem. Phys. 104 5860-5868. [Google Scholar]
- 26.Monod J., Wyman, J. & Changeaux, J.-P. (1965) J. Mol. Biol. 12 88-118. [DOI] [PubMed] [Google Scholar]
- 27.Koshland D. E., Némethy, G. & Filmer, D. (1966) Biochemistry 5 365-385. [DOI] [PubMed] [Google Scholar]
- 28.Sidorenko N. P. & Deshcherevskii, V. I. (1970) Biofizika 15 785-792. [PubMed] [Google Scholar]