Coarse-Grained Strategy for Modeling Protein Stability in Concentrated Solutions. II: Phase Behavior

Abstract

We use highly efficient transition-matrix Monte Carlo simulations to determine equilibrium unfolding curves and fluid phase boundaries for solutions of coarse-grained globular proteins. The model we analyze derives the intrinsic stability of the native state and protein-protein interactions from basic information about protein sequence using heteropolymer collapse theory. It predicts that solutions of low hydrophobicity proteins generally exhibit a single liquid phase near their midpoint temperatures for unfolding, while solutions of proteins with high sequence hydrophobicity display the type of temperature-inverted, liquid-liquid transition associated with aggregation processes of proteins and other amphiphilic molecules. The phase transition occurring in solutions of the most hydrophobic protein we study extends below the unfolding curve, creating an immiscibility gap between a dilute, mostly native phase and a concentrated, mostly denatured phase. The results are qualitatively consistent with the solution behavior of hemoglobin (HbA) and its sickle variant (HbS), and they suggest that a liquid-liquid transition resulting in significant protein denaturation should generally be expected on the phase diagram of high-hydrophobicity protein solutions. The concentration fluctuations associated with this transition could be a driving force for the nonnative aggregation that can occur below the midpoint temperature.

INTRODUCTION

Protein denaturation and the precipitation of solid phases from protein solutions pose tremendous challenges in both biological and pharmaceutical contexts. The formation of protein aggregates in vivo has been linked to a number of debilitating pathologies including Alzheimer's, Parkinson's, Huntington's, and Creutzfeldt-Jakob's diseases, as well as sickle cell anemia, Down's syndrome, and cystic fibrosis (1–3). Furthermore, the aggregation of protein drugs during processing, storage, and delivery negatively impacts both their therapeutic value and their biological safety (4–7). As a result, there is an urgent need to understand the physical basis for protein unfolding and aggregation processes.

One of the practical barriers to studying protein stability is the fact that protein unfolding and refolding events are often related to protein aggregation (8–10). Moreover, since aggregation processes follow trajectories that pass through metastable intermediate states, kinetic factors and irreversibility can significantly complicate the picture (11–15). Despite these complexities, there is vast experimental support for the idea that equilibrium fluctuations associated with two types of thermodynamic stability can play a central role in initiating and controlling the rate of protein aggregation. The most familiar type involves conformational fluctuations of individual protein molecules into nonnative structures (see, e.g., (2,8,10,16–18)). These structural fluctuations, which reflect the marginal stability of the native state (19), generally result in a net increase in the exposure of hydrophobic residues to the solvent and thus an increase in the driving force for protein self-association. Consequently, perturbations that destabilize the native fold, such as modifications to solution formulations (10) or sequence mutations (9), can also lead to increased levels of protein aggregation.

A second equilibrium effect that can have a pronounced influence on the solubility of proteins is the presence of large protein concentration fluctuations under solution conditions where liquid-liquid (L-L) phase separation is thermodynamically favored. The main idea here, which is consistent with both experimental observations and theoretical predictions (20–28), is that these fluctuations create locally concentrated quasidroplets (29) of proteins that lead to the formation of a rich variety of protein phases including crystals, fibers, amorphous aggregates, and gels. Determining the microscopic mechanisms of these nucleation events and the subsequent growth processes remains an outstanding challenge. However, from a practical viewpoint, the ability to simply predict the location of the equilibrium unfolding curve and the loci of L-L phase coexistence on the protein solution phase diagram is an important step toward forecasting and avoiding unwanted protein precipitation, even if a molecular-scale understanding of the subsequent aggregation processes is still lacking.

One prerequisite for making the aforementioned equilibrium predictions concerning protein stability is to have a model that is both tractable and rich enough to describe, at least qualitatively, the thermodynamics of protein folding/unfolding and the corresponding protein-protein interactions of the native and denatured states of proteins in solution. Unfortunately, simulating concentrated protein solutions using the detailed structural models typically employed to study the folding problem (30–34) is computationally prohibitive. Historically, this issue has been sidestepped by greatly simplifying the description of protein-protein interactions, in effect treating protein molecules as colloidal particles (22,35–42).

Although this simplification results in models that can produce insights into the physics of protein crystallization and the interactions between stable native proteins, it does so by largely neglecting the effects of protein sequence, the polymeric character of the proteins, conformational fluctuations of the molecules, and the thermodynamics of unfolding, all of which play an important role in determining protein stability. Clearly, a compromise between the detailed structural models used to study the protein folding problem and the colloidal interaction models designed to study protein crystallization is needed.

As a first step toward addressing this issue, Cheung and Truskett have recently introduced a coarse-grained modeling strategy (43) that predicts the effects of protein concentration, temperature, and elementary properties of protein sequence (e.g., number of hydrophobic and polar residues) on the native-state stability of proteins in solution. Their approach, which builds on some of the collective insights provided by other studies (see, e.g., (44–55), uses random heteropolymer collapse theory (56,57) to calculate the temperature- and species-dependent protein-protein interactions and the intrinsic thermodynamic stability of the native state. Although this type of coarse-grained strategy does not treat the geometric details of secondary and tertiary protein structure, the basic sequence information provided at the heteropolymer level allows the approach to successfully predict the qualitative experimental trends for how protein concentration affects the native-state stability of several commonly studied proteins (43). The model also suggests how these experimental trends can be understood in terms of a competition between attractive protein-protein interactions and entropic crowding effects.

In this article, we use Cheung and Truskett's model to systematically explore the interplay between native-state stability and the fluid phase boundaries of several solutions of model globular proteins with different sequence hydrophobicities. To accomplish this, we employ some very efficient transition-matrix Monte Carlo techniques that have been independently developed to study the thermodynamic properties and phase behavior of pure liquids and mixtures (58–60). The main findings of our study are as follows. Solutions of model proteins with low sequence hydrophobicity remain in a single liquid phase over a broad range of protein concentrations and temperatures. In contrast, those containing proteins with high sequence hydrophobicity exhibit the type of temperature-inverted, first-order L-L transition that is associated with aggregation processes in aqueous solutions of proteins and other amphiphilic molecules (20,21,26,28,61,62). Interestingly, the L-L transition that occurs in solutions of the most hydrophobic protein investigated in this study extends significantly below the midpoint temperature for unfolding T_m, creating an immiscibility gap between two very different types of phases—a dilute solution comprising mostly native proteins and a concentrated solution of predominantly denatured proteins.

The model's predicted trends for how protein sequence hydrophobicity affects the relative locations of the L-L demixing transition and the equilibrium unfolding curve on the phase diagram appear to be in good qualitative agreement with the experimentally observed behavior for solutions of hemoglobin (HbA) and its sickle variant (HbS) (20,26). In addition, the results suggest that a first-order L-L transition causing substantial protein denaturation should generally be expected on the phase diagram of high-hydrophobicity protein solutions. The concentration fluctuations associated with such a transition could, in principle, be an important thermodynamic driving force for the nonnative aggregation that occurs below T_m in solutions of high hydrophobicity proteins such as myoglobin (63). However, further experimental and theoretical studies will be necessary to test this idea.

Coarse-grained modeling strategy

In this section, we briefly describe the coarse-grained modeling strategy originally introduced by Cheung and Truskett (43), focusing on the model's physically salient features and underlying assumptions. The interested reader is referred to Cheung and Truskett (43) for the mathematical details and in-depth discussion of the model. The physical idea underlying this approach is that many aspects of native-state stability and the global phase diagrams of protein solutions can be predicted using a model that incorporates the intrinsic stability of an isolated native protein in aqueous solution and a basic description of the solvent-mediated protein-protein interactions involving the native or denatured states.

Intrinsic stability of a protein

There is an intrinsic free energy difference 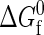associated with each unimolecular protein folding reaction. This quantity characterizes the temperature-dependent difference in free energy between the native and denatured states in the absence of protein-protein interactions. As the protein concentration approaches zero (i.e., infinite dilution), 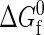completely determines the thermodynamics of protein folding. At higher protein concentrations, protein-protein interactions significantly contribute to the free energies of the native and denatured states. In the coarse-grained modeling strategy (43), 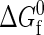is calculated by a random heteropolymer collapse theory (57). The inputs to the heteropolymer collapse theory include temperature T, the number of residues in the protein sequence N_r, the fraction of those residues that are hydrophobic Φ, and the free-energy χ(T)k_BT associated with transferring a hydrophobic residue from the protein core into an environment where it is in intimate contact with the solvent. Cheung and Truskett have adopted an approximation of χ(T)k_BT introduced by Dill et al. (57) that is essentially a parameterization of experimental transfer free energy data for a typical hydrophobic amino acid from its pure phase into water.

To compare model sequence hydrophobicities Φ with those calculated from actual proteins, one also needs to define which amino-acid residues should be considered hydrophobic. In this article, we refer to Φ-values of real proteins that are calculated assuming the following set of hydrophobic residues: Ala, Gly, Ile, Leu, Met, Phe, Pro, Trp, Tyr, and Val. Of course, there are alternative choices for the set of hydrophobic amino acids, which differ slightly from the one presented above (see, e.g., (57,64,65)), but they result in the same qualitative trends when incorporated into the coarse-grained modeling approach. As should be expected (and is shown in Fig. 1 a), the heteropolymer collapse theory predicts that moderate increases in the sequence hydrophobicity Φ of a protein results in increased intrinsic stability of the native state.

FIGURE 1.

Temperature-dependent properties of two different globular proteins in solution (number of residues N_r = 154; sequence hydrophobicity Φ = 0.4 (solid) and Φ = 0.5 (dashed)) as predicted by the coarse-grained model (43), based on heteropolymer collapse theory (57). (a) Scaled intrinsic free energy of folding 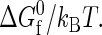(b) The ratio of the effective diameters for denatured-denatured σ_DD and native-native σ_NN interactions. (c) Scaled strength of contact attractions 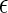_DD/k_BT between denatured proteins.

Protein-protein interactions

The heteropolymer collapse theory also predicts other structural characteristics of the proteins that allow for an estimation of the state-dependent, protein-protein interactions. These include the effective radii of gyration of the native (N) and denatured (D) states, R_N and R_D, and the corresponding fraction of the solvent-exposed residues in each state that are hydrophobic, Θ and Φ. One assumption in the coarse-grained model is that the attractive part of the protein-protein interaction is due primarily to the driving force of proteins to desolvate their hydrophobic surface residues by burying them into a hydrophobic patch on a neighboring protein. The repulsive part of the potential, on the other hand, accounts for the volume that each individual protein excludes to the centers of mass of other protein molecules in the solution.

The interprotein potentials are expected to be quantitatively different for each of the various types of protein-protein interactions (i.e., NN, ND, and DD). First, heteropolymer collapse theory correctly predicts (see Fig. 1 b) that denatured protein molecules generally exclude more volume to other proteins (R_D > R_N) than their native-state counterparts (57). Moreover, denatured proteins display a greater fractional surface hydrophobicity than folded molecules (Φ > Θ). Mean-field calculations (43) predict that the magnitudes of the average contact attractions between two proteins will scale as

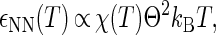(1)

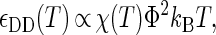(2)

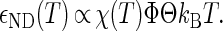(3)

Given Eqs. 1–3 and Φ > Θ, it can be expected that contact attractions involving denatured proteins will generally be stronger than those involving the native state (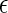_DD > 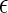_NN). Moreover, the attractive strength between proteins increases with the hydrophobic content Φ of the protein sequence, as is illustrated in Fig. 1 c. The proportionality constants that have been omitted from Eqs. 1–3 simply represent geometric factors associated with the sizes of the interacting proteins and are discussed in detail elsewhere (43).

Cheung and Truskett incorporate the interprotein exclusion diameters, σ_DD/σ_NN = R_D/R_N and σ_ND/σ_NN = (R_N + R_D)/2R_N, and the contact energies of Eqs. 1–3, all of which are derived from the heteropolymer collapse theory (43), into an effective protein-protein potential V_ij (22) that qualitatively captures many aspects of protein solution thermodynamics and phase behavior (see, e.g., (22,66)):

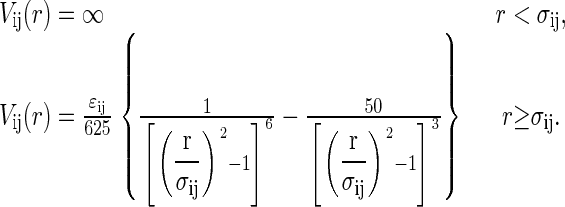(4)

In the above equation, we adopt the notation ij ∈ (NN, ND, DD).

In short, the coarse-grained model represents an effective binary mixture of native and denatured proteins (the aqueous solvent only entering through χ(T)) connected via the unimolecular protein folding reaction. The links between the intrinsic native-state stability of the proteins 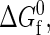the physical parameters defining the protein-protein interactions (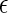_ij,σ_ij), the protein sequence (N_r,Φ), and the interactions with the aqueous solvent χ(T) are established by the heteropolymer collapse model (43,57). As in actual protein solutions, the fraction of proteins in the native state generally depends on both temperature and protein concentration. This is because temperature affects the intrinsic stability of the native state 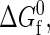and both temperature and protein concentration influence the interaction energy between proteins in solution.

Cheung and Truskett have studied how protein concentration affects the equilibrium unfolding behavior in their coarse-grained model (43) using reactive canonical Monte Carlo simulations (67,68). Here, we significantly extend their analysis to rigorously determine the liquid-state phase boundaries of concentrated solutions of proteins of varying sequence hydrophobicity. We approach this biomolecular system with the understanding that it essentially parallels that of the classic reactive phase equilibria problem for a binary solution (see, e.g., (69)). Below we explain how transition-matrix Monte Carlo simulations provide an ideal technique for simultaneously determining the thermodynamic phase boundaries and the protein folding equilibrium curves.

METHODS

Transition-matrix Monte Carlo

We use transition-matrix Monte Carlo (TMMC) simulations to study the fluid phase behavior of the coarse-grained protein model described above. Transition-matrix-based sampling methods provide a general means for precisely calculating the relative free energy of a system along a suitable order parameter path. When originally developed, the range of applicability of transition-matrix methods was largely restricted to lattice (discrete) systems (70–73). Only recently have they gained prominence as a highly efficient computational method for the thermodynamic properties of continuum systems (58–60,74–79).

An important general step in the calculation of thermodynamic properties via molecular simulation is the determination of the relevant order parameter distribution. Examples of commonly encountered order parameters include the system's energy, density, or composition. The order parameter distribution is of crucial thermodynamic importance because it provides a direct link to a system's free energy expressed as a function of that order parameter. For example, in the case of a pure fluid at some fixed temperature, knowledge of the number density probability distribution is tantamount to knowing the system's free energy, and therefore its thermodynamic properties, as a function of density (at the same specified temperature).

To calculate the order parameter probability distribution via conventional Monte Carlo, one would simply collect a histogram of order parameter values visited by the system during the course of the simulation; this constitutes a so-called visited-states approach. In contrast, in a transition-matrix approach, the calculation of the same distribution is based upon information regarding attempted transitions made by the system from one order parameter value to another. Transition statistics turn out to be more informative than visited-states statistics. Notice that precise determination of the probability distribution requires that all order parameter values be sampled sufficiently, in particular regions of low probability that are difficult to access. Because the use of transition statistics alone is unable to overcome this sampling problem, a biasing scheme is often introduced to encourage the system to sample uniformly all order parameter values. This combination is made more robust through the establishment of a feedback mechanism between the biasing scheme and the collection of transition statistics, thereby providing a self-adaptive approach to the true equilibrium distribution. The algorithm is very effective in negotiating rugged free-energy landscapes. The particular implementation of transition-matrix Monte Carlo used here was originally introduced and described in detail by Errington and Shen (60). Therefore, only a brief summary is provided in this section.

In this work, transition-matrix Monte Carlo simulations are performed in the grand-canonical ensemble. This corresponds to holding fixed the chemical potentials of each species in a system of volume V at temperature T. Under these conditions, the macrovariable or order parameter of interest is the total number of proteins in (equivalent to the concentration of) the system. In particular, it is the total protein number probability distribution that is of ultimate interest because it is directly related to the system's free energy as a function of concentration. In the case of a binary mixture (native and denatured species) where the components can react (fold/unfold), chemical equilibrium is imposed by setting the chemical potential difference between the components to zero (80), and at the same time, by specifying an overall activity difference that is equal to the intrinsic free energy of folding 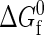(67,68,81). The latter is valid so long as the intramolecular and intermolecular degrees of freedom can be assumed to be separable. Although this type of separability is not strictly satisfied in real protein systems, it has been assumed as a workable starting point in the development of the coarse-grained model (43). As a result, the only thermodynamic parameters that need to be specified are: a single chemical potential μ; the intrinsic free energy of folding 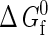; volume V; and temperature T.

Transition-matrix Monte Carlo proceeds as a conventional grand-canonical Monte Carlo simulation for multicomponent systems where the following types of trial moves are performed: displacements, insertions/deletions, and identity changes. During the course of the simulation, the unbiased acceptance probability of every trial move is accumulated in a so-called collection matrix whose purpose is to provide a convenient bookkeeping framework. Periodically, the accumulated transition statistics are used to provide an updated estimate of the total protein number distribution which, in turn, is used to bias the simulation so that all total protein number values (concentrations) are sampled uniformly. Although trial moves are ultimately accepted or rejected based on a biased acceptance criterion as in multicanonical sampling (82), unbiased acceptance probabilities continue to be accumulated. Notice that this aspect of the method allows one to introduce periodically a new, more effective biasing function without having to discard any information that has already been collected.

The total protein number (or concentration) probability distribution yielded by TMMC is unique to the chemical potential used in the simulation. However, once this probability distribution is determined, histogram reweighting can be used to determine the distribution at other chemical potential values (83). In Fig. 2 a, we provide one example of the raw calculated and reweighted distributions for a protein of hydrophobicity Φ = 0.445. Furthermore, when combined with isochoric-semigrand averaged quantities, i.e., mean values of a quantity at fixed total protein number and chemical potential difference, which are straightforward to collect in a TMMC simulation, the thermodynamic properties of the system can be calculated. Note that the isochoric-semigrand averages are independent of the chemical potential used in the simulation. In Fig. 2, b and c, examples of these averages are provided. Analysis of the data when more than one phase can exist is relatively straightforward and is described in Errington and Shen (60).

FIGURE 2.

Example of raw data and various quantities yielded by transition-matrix Monte Carlo that can be combined appropriately to determine the thermodynamic properties of the system. (a) The raw and reweighted total particle number, or concentration, probability distributions Π. (b) Semigrand average of the number of denatured proteins N_D as a function of the total number of proteins. (c) Semigrand average of the potential energy per particle u scaled by well-depth of the native-native interaction 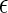_NN as a function of the total number of particles.

Simulation details

The transition-matrix Monte Carlo simulations of the coarse-grained protein model were performed in the grand-canonical ensemble. Interprotein interactions were described by Eq. 4 and were simply truncated at a distance r = 2.5 σ_ij. No long-range corrections were employed. All simulations were performed in a cubic simulation cell of minimum side length L/σ_NN = 9. Trial moves consisted of 25% protein displacements, 25% identity changes, and 50% insertions/deletions. The biasing function was updated every 100,000 Monte Carlo steps. In all cases, TMMC simulations were initiated with an empty simulation cell and restricted to sample total protein numbers between 0 and 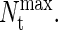The value of 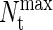was initially set to a value of 100, and then increased after each N_t value in the total protein number range was visited a minimum of 50,000 times. This process was repeated until the total concentration range of interest was sampled. We report dimensionless protein concentration as 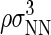= 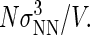Finally, a constraint was imposed to prevent the system from crystallizing, a serious problem if one is focusing exclusively on the liquid-state properties of the model. The product 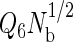is a useful order parameter for this purpose, where Q₆ is a global bond-orientational metric that can distinguish between amorphous and crystalline particle packings (84–87), and N_b is simply the total number of bonds or nearest-neighbor pairs in the system. Nearest-neighbor pairs were defined as proteins with centers of mass closer than that of the first minimum in the interprotein pair correlation function. We found that 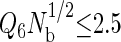prevented the system from crystallizing, allowing the simulations to visit both the relevant stable and metastable states. To assess the influence of the order parameter on the fluid-phase properties, we performed several simulations between 356 and 359 K using different order parameter values ranging from 1.5 to 2.5 for the highest hydrophobicity protein, and found that the phase coexistence properties were unaffected by the order parameter value. In the results reported in this work, we used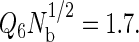

RESULTS AND DISCUSSION

Here, we apply the advanced Monte Carlo simulation methods outlined in the previous section together with Cheung and Truskett's coarse-grained model to analyze the thermodynamic behavior of concentrated protein solutions. We choose a chain length of 154 residues to both extend our previous work (43) and to study medium sized, single-domain globular proteins, which this HPC theory models well (57). In addition, we choose sequence hydrophobicities typical of those found in the protein data bank (0.40 ≤ Φ ≤ 0.50) (65). The results provide a reasonable starting point for addressing two fundamental questions that may have important practical implications for understanding protein stability:

• Do solutions of globular proteins generally exhibit the type of temperature-inverted, first-order L-L phase transition on their phase diagrams that is associated with aggregation processes in aqueous solutions of amphiphilic polymers (61,62) and the sickle variant of hemoglobin (26)?

• If so, how does protein sequence hydrophobicity affect the relative locations of the L-L phase transition and the equilibrium unfolding curve on the phase diagram?

This information may provide new insights into the connection between the intrinsic properties of protein molecules and the conditions for their solutions that can give rise to various types of insoluble protein aggregates.

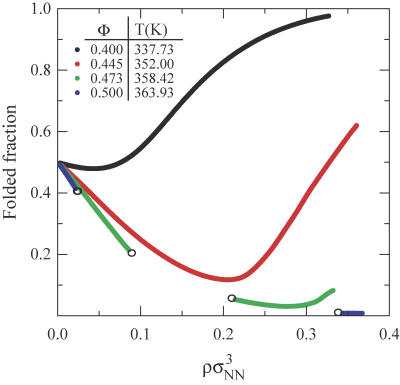
As a first step in our analysis, we study the thermodynamic consequences of concentrating solutions of four model proteins (N_r = 154, Φ = 0.40, 0.445, 0.473, and 0.50), each at their respective infinite dilution midpoint temperatures for unfolding (see Fig. 3). These hydrophobicities translate from the total integer segments and nonpolar segments (1.4 segment = 1 residue) defined by Dill (56). Recall that, at these temperatures, 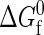for the proteins is identically zero (i.e., the fraction folded = 0.5 in the infinite dilution limit), and so there exists no intrinsic thermodynamic preference for either the native or the denatured state. In other words, any concentration-induced stabilization (i.e., increased T_m) or destabilization (i.e., decreased T_m) of the native state or, for that matter, any L-L phase separation that appears in Fig. 3 can be attributed solely to the protein-protein interactions in solution.

FIGURE 3.

Fraction of folded proteins versus protein concentration ρσ³ at their respective infinite dilution folding temperatures where 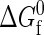= 0. The folding temperatures are listed in the plot, and the open circles indicate coexistence points for liquid-liquid phase transitions.

For the lowest hydrophobicity protein studied (Φ = 0.40), Fig. 3 shows that increasing protein concentration leads to essentially negligible destabilization of folded proteins at low concentrations, followed by an increase in native-state stability at very high concentrations. Moreover, the fraction of folded proteins changes continuously with protein concentration, indicating that the solution does not undergo a first-order L-L phase transition under these conditions. These results are in good qualitative agreement with the aqueous solution behavior of the low hydrophobicity protein ribonuclease A (Φ = 0.37), which also displays stabilization of the native state with increasing protein concentration and exhibits a high native-state solubility (88). Given these predictions, it is natural to ask what would happen if the same calculation were carried out for a solution of proteins with slightly higher sequence hydrophobicity. Fig. 3 illustrates that solutions of a higher-hydrophobicity protein (Φ = 0.445) display a pronounced concentration destabilization of the native state at low protein concentrations, followed by restabilization at higher protein concentrations. This nonmonotonic dependency is in good qualitative agreement with the experimental behavior of single-phase solutions of the higher-hydrophobicity protein metmyoglobin (Φ = 0.52) over a wide range of pH conditions (89).

The type of basic trends described above for how protein concentration and sequence hydrophobicity impact native-state stability in single-phase solutions of globular proteins have been previously analyzed in the context of Cheung and Truskett's coarse-grained model (43), and thus we only summarize the main ideas here. In short, the concentration dependencies of native-state stability can be understood in terms of a balance between destabilizing protein-protein attractions and stabilizing crowding effects. At finite concentrations, marginally stable native proteins preferentially unfold if 1), they have enough local free volume to accommodate the more expanded denatured state; and 2), they form favorable denatured-native or denatured-denatured contact attractions with neighboring proteins. As a result, one generally expects protein-protein attractions to induce some degree of protein destabilization at low protein concentrations. This expectation is consistent with experimental results that indicate that reversible formation of nonnative oligomers in solution can play a central role in inducing protein unfolding (90). Furthermore, as should be expected, and is in fact illustrated by model calculations in Fig. 1 c, protein-protein attractions are more favorable on average for higher-hydrophobicity proteins. This explains why higher-hydrophobicity proteins typically show a more pronounced protein-protein attraction-induced concentration destabilization than their lower-hydrophobicity counterparts.

On the other hand, since the denatured state is more expanded than the native configuration (see Fig. 1 b), excluded volume arguments suggest that the native state should ultimately be restabilized at sufficiently high protein concentrations, a phenomenon sometimes referred to as macromolecular crowding. The crowding effect is similar in nature to the confinement-induced stabilization of proteins that has been studied extensively by experiments (91,92) and computer simulations (49,55,93–95). Note that crowding is typically more pronounced for lower-hydrophobicity proteins because, as polymer theory predicts, these proteins tend to exhibit more expanded denatured configurations than higher-hydrophobicity proteins, all other factors being equal (96–98). In fact, as is seen in Fig. 3, crowding almost entirely masks the destabilizing effect of protein-protein attractions in model solutions of the Φ = 0.40 protein.

Interestingly, Fig. 3 also illustrates that the highest hydrophobicity proteins, Φ = 0.473 and 0.50, show a qualitatively new feature: they each exhibit a first-order L-L demixing transition when protein concentration is increased beyond a critical value that depends on both temperature and sequence hydrophobicity. This type of demixing transition is manifested as a discontinuity, i.e., an immiscibility gap, along the fraction folded versus protein concentration isotherms. The relative proportions of the two coexisting phases present in the immiscibility gap is determined by the lever rule (69).

The reason why this type of phase separation occurs in the model is easy to understand, and, in fact, it is somewhat analogous to why vapors condense upon isothermal compression if their interparticle attractions are sufficiently large relative to k_BT. In short, increasing protein concentration from infinite dilution decreases the translational entropy of proteins in solution, but increases the number of favorable protein-protein attractions. If the protein-protein attractions are sufficiently favorable, then the protein solution can minimize its free energy by phase-separating to take advantage of both effects, i.e., forming a low-concentration phase that retains high translational entropy of the proteins and a high-concentration phase that takes advantage of the favorable protein-protein interactions. Of course, the situation is far richer for protein solutions than for condensing vapors because proteins solutions can also shift their relative conformational populations of native and denatured molecules to take full advantage of the favorable protein interactions in the high-concentration phase. In particular, as is clear from Fig. 3, the highest hydrophobicity protein solutions of Φ = 0.473 and 0.50 undergo substantial protein unfolding upon phase separation to realize the highly favorable denatured-denatured protein contact interactions. Also, note that the Φ = 0.50 protein solution favors phase separation at a lower value of protein concentration than the Φ = 0.473 protein solution, which is in line with the expectation that higher hydrophobicity proteins tend to show lower solubility in aqueous solution.

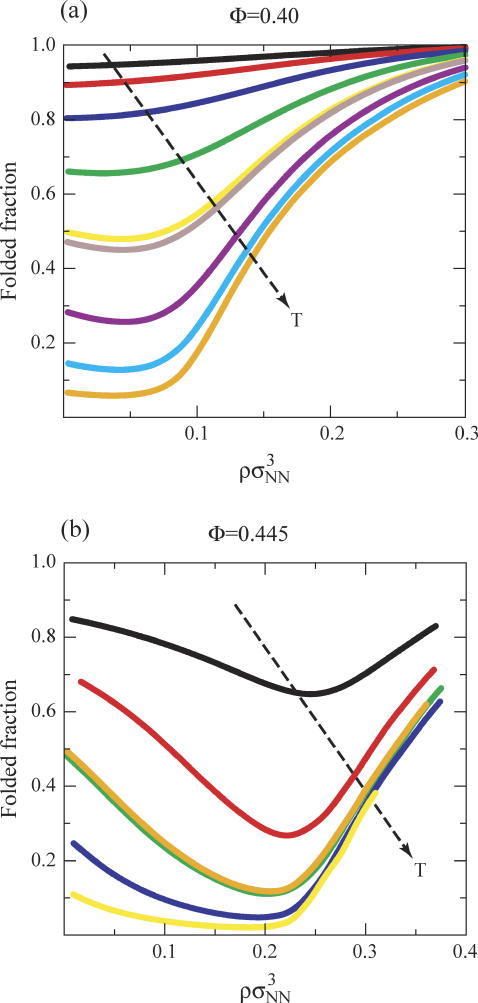
Thus far, by choosing to analyze model protein solutions at temperatures where 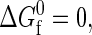we have effectively removed any effect of the intrinsic stability of the protein. In Fig. 4, we take a step back and view a more comprehensive data set for the temperature and protein-concentration dependencies of the Φ = 0.40 and Φ = 0.445 protein solutions. Notice that in both cases, the primary role of temperature is to destabilize the compact native fold relative to the more expanded denatured state. As a result, the higher temperature solutions show protein-protein attraction induced destabilization at lower protein concentrations when compared to the more stable solutions at lower temperatures. Similarly, the higher temperature solutions require higher protein concentrations than the lower temperature solutions to undergo crowding-induced restabilization. Finally, protein-protein interactions are not strong enough, in either of these two solutions, to cause L-L demixing for the range of temperatures and concentrations investigated.

FIGURE 4.

Fraction of folded proteins versus protein concentration ρσ³ for the model proteins N_r = 154, Φ = 0.40 and 0.445. The isotherm values for the Φ = 0.40 protein are 330, 332, 334, 336, 337.73, 338, 340, 342, and 344 K. The isotherm values for the Φ = 0.445 protein are 348, 350, 351.8, 352, 354, and 356 K.

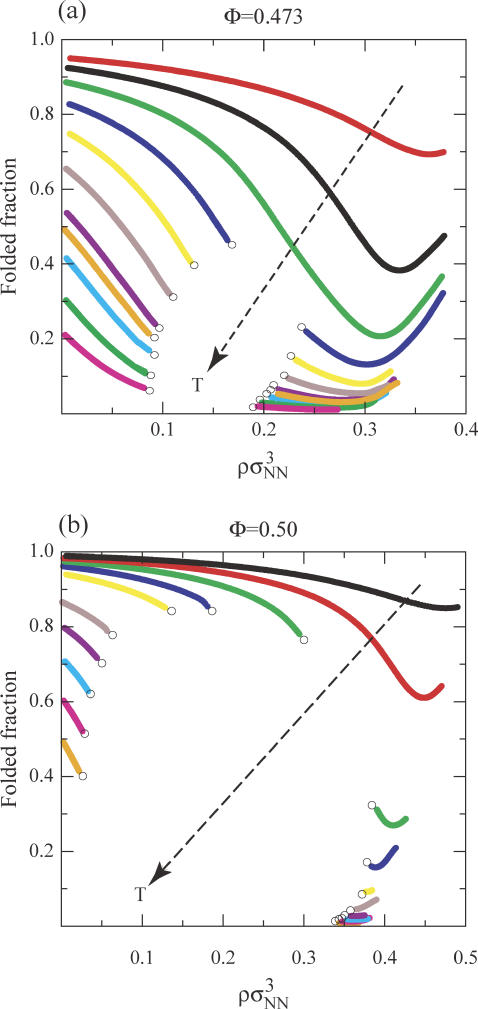
In Fig. 5, we present the temperature and protein-concentration dependencies of the fraction of native-state molecules for the Φ = 0.473 and Φ = 0.50 protein solutions. Recall that the Φ = 0.473 protein solution has weaker protein-protein attractions than the higher-hydrophobicity Φ = 0.50 solution, and, in both solutions, attractions involving native species are weaker than those involving denatured proteins. As a result, a single homogeneous phase of the Φ = 0.473 solution persists over the range of temperatures and concentrations where the native state is the majority species. However, if this solution is heated to temperatures where the denatured state is thermodynamically favored, L-L demixing readily occurs. This result is consistent with experimental observations for the polypeptides fibronectin, acylphophatase, and protein G, that indicate the formation of nonnative aggregates are related to conditions of weakened native state stability (e.g., increasing temperature (99), adding denaturants (100), and destabilizing mutations (101,102)). In contrast, for the Φ = 0.50 solution, we find that protein-protein attractions are strong enough to drive L-L phase separation even for temperatures well below T_m, where the native state is thermodynamically favored. More comprehensive representations of the L-L phase boundaries for the Φ = 0.473 and Φ = 0.50 model protein solutions are shown in Fig. 6.

FIGURE 5.

Fraction of folded proteins versus protein concentration ρσ³ for the model proteins N_r = 154, Φ = 0.473 and 0.50. The isotherm values for the Φ = 0.473 protein are 352, 353, 354, 355, 356, 357, 358, 358.43, 359, 360, and 361 K. The isotherm values for the Φ = 0.50 protein are 354, 355, 356, 357, 358, 360, 361, 362, 363, and 363.93 K. Open circles represent coexistence points for a liquid-liquid phase transition.

FIGURE 6.

Liquid-liquid coexistence curves for protein solutions in the temperature versus protein concentration ρσ³ plane for the model proteins N_r = 154, Φ = 0.473 and 0.50. The darker circles indicate the equilibrium unfolding curves, and the lighter circles bound the liquid-liquid coexistence regions. All lines act as guides to the eyes.

The predicted trends for how sequence hydrophobicity affects the relative locations of the equilibrium unfolding curve (i.e., the concentration-dependent T_m) and the L-L phase transition in Cheung and Truskett's model appear to be in good qualitative agreement with the experimentally determined behaviors of solutions of hemoglobin HbA (Φ = 0.566) and its more hydrophobic sickle variant HbS (Φ = 0.570). In particular, HbS shows a temperature-inverted, L-L transition that extends far below the equilibrium unfolding curve and coincides with physiological conditions (20,21,26,28,103). In contrast, for solutions of the less hydrophobic HbA protein, the analogous L-L transition appears to occur above the equilibrium unfolding curve, and at temperatures much higher than are physiologically relevant. For the case of the sickle variant HbS solutions, the pathological aggregation associated with the L-L transition is the polymerization and self-assembly of protein fibers (20,26,28,103). However, even when HbS is liganded to geometrically hinder this fiber formation, its solutions still apparently show an inverted L-L transition that, instead, facilitates the formation of amorphous protein aggregates (26).

As discussed earlier, the fluctuations associated with the type of first-order, L-L transitions shown in Fig. 6 create locally concentrated regions that can facilitate the precipitation of various insoluble protein structures. The fact that considerable protein unfolding occurs in the particular transitions predicted here makes it likely that the resulting protein aggregates would have a distinctly nonnative character. However, Cheung and Truskett's coarse-grained model, at least in its present form, does not contain sufficient structural detail to study the formation of these nonnative protein precipitates. In fact, in Conclusions we mention some possible extensions to the model to help address this issue. Nonetheless, the ability of the coarse-grained model to predict the relative locations of the L-L transition and the equilibrium unfolding curve on the phase diagram can still allow for some further qualitative comparisons to the solubility and aggregation behavior observed in experimental protein systems.

For example, based on the phase diagram of the solution of Φ = 0.50 protein shown in Fig. 6, one would predict that nonnative aggregation processes could readily occur in high-hydrophobicity protein solutions at temperatures far below T_m, conditions where the native state is nominally stable. As we mentioned above, this type of behavior does, in fact, occur for the sickle variant of hemoglobin HbS (Φ = 0.570) (20,21,26,28,103,104). However, substantial aggregation below T_m is also experimentally observed via spectroscopic measurements in solutions of the high-hydrophobicity protein myoglobin (Φ = 0.52) (63). In contrast, based on the lack of an L-L demixing transition for the lower hydrophobicity proteins below T_m, one would expect that low-hydrophobicity proteins could avoid the formation of insoluble nonnative aggregates under conditions where the native state is thermodynamically favored. This type of predicted behavior is also consistent with the high solubility of the low hydrophobicity protein ribonuclease A (Φ = 0.37) for temperatures below its equilibrium unfolding curve (88).

CONCLUSIONS

To summarize, we have employed robust transition-matrix Monte Carlo simulation to rigorously determine the equilibrium unfolding curves and the fluid phase boundaries of protein solutions of several model proteins with varying sequence hydrophobicity. The coarse-grained model (43) for the protein solutions derives the intrinsic stability of the native fold and the solvent-mediated, protein-protein interactions between native and denatured states from a heteropolymer collapse theory. This model was chosen because it is computationally tractable to analyze both its native-state stability and its global phase behavior. Moreover, it has already been shown to capture some of the nontrivial relationships between protein concentration and the native-state stability of several commonly studied proteins (43).

Our main findings can be summarized as follows. Solutions of proteins with low sequence hydrophobicity are predicted to exhibit a single liquid phase over a wide range of protein concentrations and temperatures. On the other hand, solutions containing proteins with high sequence hydrophobicity display the type of temperature-inverted, first-order L-L transition that is typically associated with hydrophobic aggregation processes of amphiphilic molecules in aqueous solutions. One of the most interesting results is that the L-L transition that occurs in solutions of the most hydrophobic protein that we study extends far below the equilibrium unfolding curve, creating an immiscibility gap between two very different types of phases—a dilute solution comprising mostly native proteins and a concentrated solution of predominantly denatured proteins.

The predicted trends for how sequence hydrophobicity modifies the relative locations of the L-L phase transition and the equilibrium unfolding curve appear to qualitatively agree with the observed solution behavior of hemoglobin HbA and its sickle variant HbS. Moreover, the results suggest that a first-order L-L transition resulting in significant protein denaturation should be expected to be found on the phase diagram of high-hydrophobicity protein solutions. The concentration fluctuations associated with such a transition could, in principle, be an important thermodynamic driving force for the nonnative aggregation that occurs below T_m in solutions of high hydrophobicity proteins such as myoglobin. Nonetheless, further experimental and theoretical studies will be necessary to thoroughly test this prediction.

Finally, we recognize that, although many of the predictions of this study are interesting, they derive from a highly coarse-grained equilibrium model for protein solutions. For example, this model does not capture the irreversible formation of protein aggregates that are observed experimentally (13). Although we predict that protein solutions will ultimately be restabilized due to molecular crowding, solution kinetics also play an important role in real protein environments, and may prevent this restabilization. However, using this model, we are able to study the complicated nature of the underlying driving forces for protein stability in solution.

Future studies that utilize this strategy may gain quantitative results, at the expense of computational time, by using more protein-specific collapse models that incorporate details such as amino-acid residue correlations, folding intermediates, or more information about the conformational fluctuations of the denatured state. A more rigorous treatment of protein solvation that can handle basic charge, salt, and pH effects (see, e.g., (105) and (106)) would also broaden significantly the applicability of the model. The effect of these additional solvation parameters are nontrivial and difficult to predict offhand, and we are working toward incorporating electrostatic interactions into our model. Currently, we are exploring avenues to study directionality of the effective protein-protein interactions, albeit in a coarse-grained manner. We expect the added orientational aspects to lead to richer, more featured phase diagrams, perhaps including the self-organization transitions (107) that are a central component of many biological assembly processes.