Abstract
This article focuses on the second step of the catalytic mechanism for the reduction of ribonucleotides catalyzed by the enzyme Ribonucleotide Reductase (RNR). This step corresponds to the protonation/elimination of the substrate's C-2′ hydroxyl group. Protonation is accomplished by the neighbor Cys-225, leading to the formation of one water molecule. This is a very relevant step since most of the known inhibitors of this enzyme, which are already used in the fight against certain forms of cancer, are 2′-substituted substrate analogs. Even though some theoretical studies have been performed in the past, they have modeled the enzyme with minimal gas-phase models, basically represented by a part of the side chain of the relevant amino acids, disconnected from the protein backbone. This procedure resulted in a limited accuracy in the position and/or orientation of the participating residues, which can result in erroneous energetics and even mistakes in the choice of the correct mechanism for this step. To overcome these limitations we have used a very large model, including a whole R1 model with 733 residues plus the substrate and 10 Å thick shell of water molecules, instead of the minimal gas-phase models used in previous works. The ONIOM method was employed to deal with such a large system. This model can efficiently account for the restrained mobility of the reactive residues, as well as the long-range enzyme-substrate interactions. The results gave additional information about this step, which previous small models could not provide, allowing a much clearer evaluation of the role of the enzyme. The interaction energy between the enzyme and the substrate along the reaction coordinate and the substrate steric strain energy have been obtained. The conclusion was that the barrier obtained with the present model was very similar to the one previously determined with minimal gas-phase models. Therefore, the role of the enzyme in this step was concluded to be mainly entropic, rather than energetic, by placing the substrate and the two reactive residues in a position that allows for the highly favorable concerted trimolecular reaction, and to protect the enzyme radical from the solvent.
INTRODUCTION
Ribonucleotide reductases (RNRs) are very important enzymes for all living organisms. They catalyze the conversion of ribonucleotides into deoxyribonucleotides, the monomeric precursors for DNA biosynthesis and repair (1–6). A number of RNRs of different species have been discovered, pointing out a common radical-based reaction mechanism and a protein free-radical to activate the substrate (7). Despite their central and common metabolic functions, these enzymes have very different amino acid sequences and different metallic cofactors to accomplish the same chemistry. Their division into three classes was based on the cofactor required to initiate the radical-dependent nucleotide reduction process (8–13).
The enzymatic activity was shown to be dependent upon the formation of a complex between two different homodimers named R12 and R22. The x-ray structures of each homodimer have already been determined (14). The larger dimer named R12 controls the overall enzyme activity and is composed of two identical subunits (761 residues per subunit), each one lodging one active site (for reduction of purines and pyrimidines) composed of five conserved residues: Cys-439, Cys-225, Cys-462, Glu-441, and Asn-437, and three independent allosteric sites named the specificity site (s-site), the adenine-specific site (a-site), and the hexamerization site (h-site) (15–17). The other dimer, named R22, have 375 residues in each subunit, each one containing a stable neutral tyrosyl free radical at position 122, coupled to a binuclear iron (Fe2O2) cluster required for generation and transfer of the radical (12,13). The tyrosyl radical is deeply buried by >10 Å from the surface of the protein (18), which assures its protection from the solvent. It is believed that upon substrate binding, the tyrosyl radical is transferred through a conserved hydrogen-bond pathway to Cys-439 in the active site (2,19,20), where the reaction takes place.
With information from different spectroscopic and mutagenesis experiments, the first suggestion for the mechanism of the natural substrate was made by Stubbe (1,2,5) and collaborators in 1990. This mechanism has been intensively studied in the last few decades and several studies have already updated the first proposal, based on site-directed mutagenesis experiments (21), isotopic labeling and kinetics (19), spectroscopic measurements (3), small organic model approaches (22,23), and theoretical calculations (24–28).
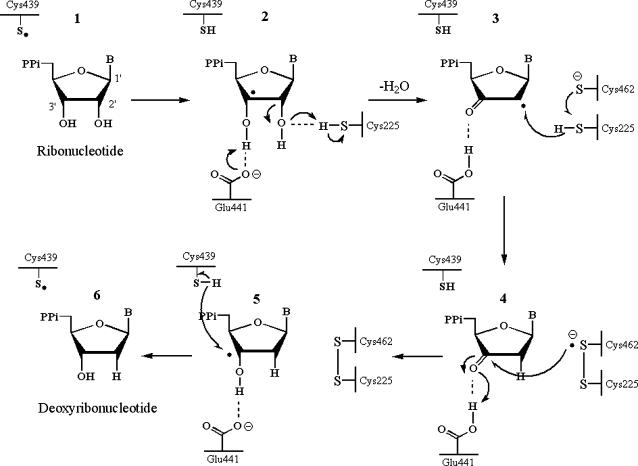
The mechanism that is currently accepted is depicted in Scheme 1. The first step involves the abstraction of the 3′-H of substrate 1 by radical Cys-439. Subsequently, the reaction involves the elimination of one water molecule from carbon C-2′ of the ribonucleotide, catalyzed by Cys-225 and Glu-441. In the third step, there is a hydrogen atom transfer from Cys-225 to carbon C-2′ of the 2′-ketyl radical 3, after previous proton transfer from Cys-462 to Cys-225. At the end of this step, a radical anionic disulfide bridge and the closed-shell ketone intermediate 4 are obtained. This intermediate has been identified during the conversion of several 2′-substituted substrate analogs, as well as with the natural substrate (24,26,29), interacting with enzyme mutants. The next step is the oxidation of the anionic disulfide bridge, with concomitant reduction of the substrate, generating 5. The spin density shifts from the sulfur atoms to the C-3′ atom of the substrate, with simultaneous proton transfer from Glu-441 to carbon C-3′. The last step is the reverse of the first step and involves a hydrogen transfer from Cys-439 to C-3′, regenerating the initial radical and resulting in the final product 6.
SCHEME 1.
Catalytic mechanism for class I ribonucleotide reductase.
As DNA replication and repair are dependent of the availability of deoxyribonucleotides, the inhibition of this enzyme became one of the most attractive targets for antitumor, antiviral, and antibacterial therapies (30–35). One of the RNR inhibitors (2′,2′-difluoro-2′-deoxycitidine) has been approved recently for the treatment of nonsmall lung cancer in Europe and pancreatic cancer in the United States (36).
This inhibitor belongs to a very important class of suicide inhibitors, the 2′-substituted substrate analogs. Despite its use in the treatment of certain forms of cancer, their general mechanism of action is still poorly understood. It is believed that they deviate from the natural pathway already at the second step (36–39).
However, detailed microscopic understanding of this step has been difficult to achieve. Therefore, its elucidation will provide a better understanding of the mechanism of the inhibitors. In the near future, this will allow the design of new inhibitors able to compete with the natural substrate in a more specific, potent, and less toxic way (40).
The proposed mechanism for some of these 2′-substituted inhibitors show that, just as it happens with the first step, the mechanistic behavior of the second step is also equivalent to the natural substrate's, although different products are obtained here (26,36,37,41). Whereas in the natural substrate the second step is characterized by elimination of the 2′-hydroxyl group by Cys-225 through protonation, with the inhibitors a similar reaction leads to elimination of a different group since the inhibitors are substituted precisely at position 2′ (37).
Until now, few theoretical studies have been devoted to the second mechanistic step (24,25), and although in some theoretical studies many active site residues were included in the computational model, the final optimized structures show that the residues move from their positions and orientation, once that they are disconnected from the protein backbone. Moreover, the long-range enzyme-substrate interactions, usually quite important for the enzyme's efficiency, were not possible to elucidate with such heavily truncated models.
The main objective of this work is to study this step of the mechanism using a much more realistic enzyme model that reflects both the steric constraints of the active site residues, and all the relevant enzyme-substrate electrostatic interactions. Therefore, included in the present enzyme model is a whole R1 monomer with 733 residues plus the substrate and a 10 Å thick shell of water molecules. Such a model allows for a much better understanding of the role of the enzyme machinery in this reactional step.
METHODS
Modeling
The overall model system used in this work was based in the crystal structure determined by Eklund et al. (18,42,43), of a R1 trimer with the bound substrate, from where one of the R1 monomers was kept and the others deleted. Afterwards a shell of water molecules with 10 Å thickness was added around the whole system.
This model is so extensive that it corresponds to the largest model of R1 that has been studied to this date by QM/MM methods. It is represented in Fig. 1 and is composed of 29,620 atoms with all hydrogens and water molecules included. Hydrogen atoms were added using InsightII 2000 (SGI, Mountain View, CA).
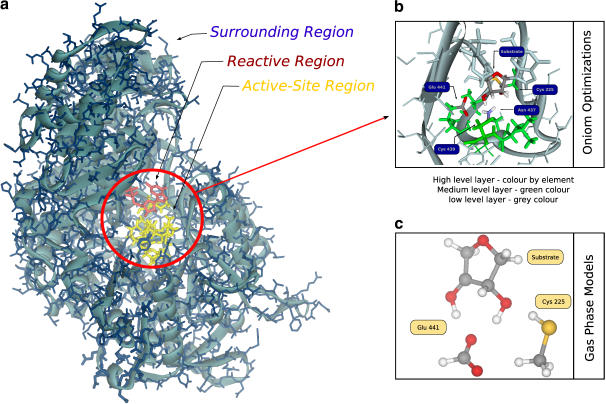
FIGURE 1.
(a) The E-S model obtained from the x-ray structure of the active site for R12 dimer of RNR with the bound substrate. The reactive region is colored red, the active site region is colored yellow and the surrounding region is colored blue. The blue background is indicative of a 10 Å layer of water molecules. (b) The division of the system in three theoretical levels for geometry optimizations. The high level layer is colored by element type, the medium level layer is colored green and the low level layer is colored blue. (c) The gas phase model. As geometry is optimized with the ribose ring and the active site residues disconnected from the protein, they can adopt the most favorable positions to the reaction without steric strain.
Multiple substrates binding modes is a common problem in proteins. This is usually due to the lack of specificity of the enzyme for a given substrate, which occurs when an enzyme binds many different substrates. Contrarily, RNR is highly specific for ribonucleotides, and the substrate fits very tightly into the three binding pockets, namely the ribose, phosphate, and base binding pockets. Therefore, the substrate is highly constrained to bind in a single, well-defined conformation, which is expected to be the one present at the crystallographic structure. However, to be on the safe side, we have checked whether there are more binding conformations with significant occupation at room temperature than the one from the x-ray structure.
For that purpose, we have analyzed the conformational space in a previous work (28) through a series of docking calculations (using the software GOLD (44)), followed by molecular mechanics geometry optimizations (using the CHARMM software (45))), and subsequent semiempirical geometry optimizations (at the Austin model, or AM1, level of theory). From these results, where a very limited number of highly similar minima were obtained, we concluded that the binding mode present at the crystallographic structure is dominant at room temperature, and we have used such structure throughout this work.
For the purpose of understanding the role of the enzyme machinery, the model was divided into three regions—namely, the reactive region, active site region, and surrounding region. The reactive region included the substrate and all functional groups from the active site residues that do participate directly in this second step, i.e., the thiol group from Cys-225 and the carboxyl group from Glu-441. The active site region includes the remaining atoms from the reactive residues, i.e., from Cys-225 and Glu-441, as well as all the residues close to the substrate (the heptapeptide Ser-436–Ile-442 plus Cys-225). The surrounding region contains the remaining atoms of the monomer plus the solvent.
The division in three regions was used to determine the enzyme-substrate interactions. Residues Cys-225 and Glu-441 were included in the reactive region, as they cannot be considered to be simply interacting electrostatically with the substrate—they both react with it, Cys-225 giving a proton and Glu-441 receiving a proton (from the 3′ hydroxyl group).
Subsequently, we have built a second model, the gas phase model, which included only the reactive region. However, in this last minimal model the geometry was optimized with no restrictions at all, i.e., with the Cys-225 and Glu-441 residues disconnected from the enzyme backbone in the gas phase. Fig. 1, a–c, illustrate the models discussed.
The reactive region reflects the intrinsic chemical reactivity of the system, as well as the geometric constraints imposed by the enzyme to the reactive residues. The active-site and surrounding regions reflect both the short- and long-range enzyme-substrate interactions, respectively. This overall model has been called the enzyme-substrate model (E-S), with corresponding energy EE-S. The energy of the reactive region was termed ER, the active site region energy was named EAS, and the surrounding region energy was named ES . The energy of the gas phase model is referred to as Egas.
Calculations
Geometry optimizations
As the system is very large, and geometry optimizations are very time-consuming, we have resorted to the method ONIOM (46–50) to deal with the system. This method allows the division of a system in several regions, each one studied with a different theoretical level. The accuracy of the method is dependent on the chosen regions and the theoretical level used in each of them.
According to the ONIOM methodology we have divided the system into three consecutive overlapping layers, designed as the high-level, medium-level, and low-level layers. (Fig. 1 b). The high-level layer includes all atoms from the substrate, but without the phosphates and the base (which were replaced by hydrogen atoms), plus all the atoms that are directly involved in the reaction, i.e., the carboxyl group from Glu-441 (carboxylate group and the neighbor β-CH2), the thiol group from Cys-225 and the amide group from Asn-437. The medium-level layer contained an extended model of the active site, including the heptapeptide Ser-436–Ile-442 plus Cys-225, thus including all the residues that are close to the substrate. The atoms described at this theoretical level are the ones that undergo more significant geometric rearrangements during the reaction. The low-level layer contains all the atoms of the enzyme plus the solvent. The atoms described at the low-level of theory do not suffer significant geometric modifications during the reduction pathway, but are still important for the correct alignment of the active site residues.
There is a subtle difference between the terms “layer” and “region”. We have used “region” to separate the reactivity of the system, i.e., as mentioned previously, the reactive region reflects the active site reactivity plus the substrate, whereas the active-site and surrounding regions reflect both the enzyme-substrate interactions and the steric constraints imposed by the enzyme to the reactive residues. Alternatively, the term “layer” has been used to characterize the set of atoms that have been computationally studied with a particular level of theory. Therefore, here, “region” is linked to reactivity and “layer” is associated with geometry optimization, e.g., Asn-37 is a nonreactive group from the active-site region but has been included in the high-level layer due to its proximity and hydrogen-bonding to the substrate and reactive amino acids.
The geometry of the high-level layer was optimized with the higher theoretical level, at the density functional theory level. The B3LYP functional was chosen, since it is known to give very good results for organic molecules. The 6-31G(d) basis set was employed, as implemented in Gaussian 03 (51,52). The inclusion of diffusion functions in the basis set for geometry optimizations was investigated before (Hertwig (53)). The conclusion was that the corrections to the geometry were very small, and corrections in energy differences (like energy barriers or energies of reaction) were negligible. Therefore, it seems inadequate from a computational point of view to include diffuse functions in geometry optimizations, considering the inherent increase in computing time that diffuse functions would cause. The medium-level layer was treated with the semiempirical Austin model (AM1) (54). For the low-level layer, a lower theoretical level was used. In this case, it corresponds to molecular mechanics, based on the CHARMM force field. Hydrogen was used as a link atom at the truncated bonds across the two regions.
To use the CHARMM force field we have divided the optimizations in two parts. In the first part, the high-level layer and medium-level layer were self-consistently optimized with the standard method of ONIOM that is included in Gaussian 03, and from which the reactants, transition state (TS), and products were obtained. Our first step in this process concerns the search for the transition state, starting from a structure similar to the transition state obtained for the same step in an earlier work using minimal models (24); once the transition state was located, the minima connected to the obtained transition state were determined through internal reaction coordinate (IRC) calculations. Although both proton transfer steps ran smoothly during the IRC calculations, the last steps could not be optimized due to convergence problems. Therefore we took the last optimized minimum from the IRC calculation and reoptimized it with a tighter SCF criterion. In all cases, we resorted to the ONIOM method and all optimizations and the stationary points were obtained with standard Gaussian convergence criteria. The transition structure was verified by vibrational frequency calculations and atomic charges and spin densities were calculated using a Mulliken population analysis (55).
After obtaining the three stationary points, we mechanically embedded them into the surrounding region. This proved to be an easy procedure because the backbone and the external side chains kept their initial x-ray positions (root-mean-square <1 Å for reactants, TS, and products). Such root-mean-square results indicate that no significant rearrangement is expected in the surrounding region since only rather small rearrangements have occurred in the much closer active-site region. Subsequently, we have constrained the coordinates of the atoms of the active-site region to their positions obtained before, and optimized the geometry of the surrounding region using the CHARMM software (56). The use of the micro interactions scheme was not implemented because the active-site region was kept frozen. The very small rearrangements in the inner active-site region obtained before justify this procedure.
Energy calculations
Higher theoretical levels were used to obtain the final energies. For this purpose, the reactive region and the active-site region were taken together and the energy of this large system was recalculated at the unrestricted density functional theory level, with the same functional (B3LYP) and the 6-31+G(d) basis set as implemented in G03. The surrounding region was kept at the MM level of theory due to its large size. This region was also replaced by a dielectric constant of 4, to check the difference between the atomistic modeling of this region and the dielectric continuum modeling used by us and others in previous works. Final energies were obtained using the ONIOM extrapolative methodology.
RESULTS
The model enzyme corresponds to the largest model of R12 ever studied with quantum mechanics/molecular mechanics hybrid methods. We started by locating the transition state for this reaction. Frequency calculations have shown only one imaginary value (954.7i cm−1) corresponding to the desired transition state. The reactants and the products of the reaction were obtained through IRC calculations, followed by further tighter optimizations. The obtained minima did correspond to the reactants and the products that are related with the reaction pathway. Fig. 2 illustrates the obtained structures.
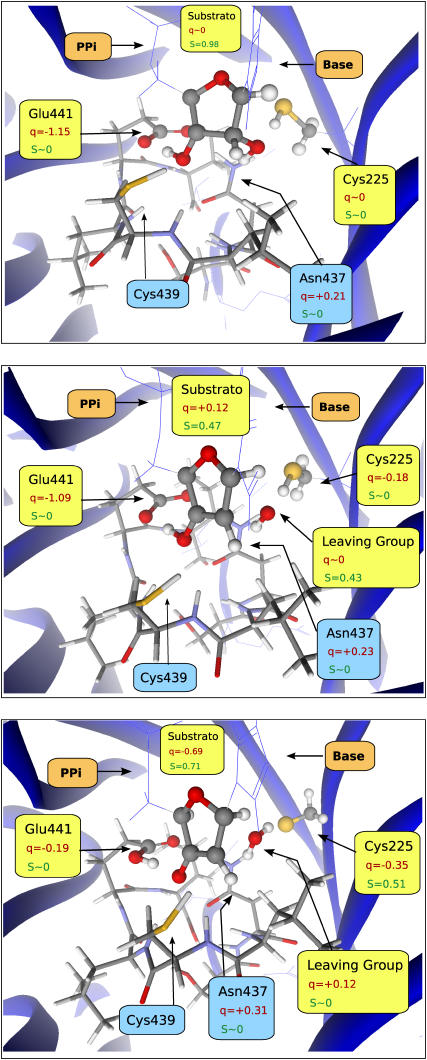
FIGURE 2.
Reactants (top), transition state (center), and products (bottom) for the reaction studied here. The reactive region is depicted in ball-and-stick representation, the active site region is depicted in stick representation, and the surrounding region is depicted in wire model and ribbons. Relevant atomic charges and spin densities are included in atomic units.
After the geometry optimization, the model kept the essential geometric features and hydrogen-bonding network observed in the crystallographic structure.
It was observed that only the reactive and active-site regions undergo significant rearrangements. The other region, the surrounding region that contains all the remaining atoms, did not undergo significant modifications during the reduction pathway. This means that the function of this last region should be primarily to preorganize the residues of the active site and to protect the radical from the solvent.
Therefore, in the next analysis, which discusses the characteristics of the optimized structures of reactants, TS, and products, we will only describe the structure of the reactive and active-site regions. The key geometric features of the reactants, transition state, and products for the active-site and reactive regions are shown in Table 1, together with the results obtained with the gas phase model.
TABLE 1.
Selected geometric parameters for the reactants, transition state, and products
| Distance
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Angle | Substrate
|
Glu-441 | Cys-225
|
||||||
| Model | C2′–O2′–HCys | C3′–O3′ | O3′-HO3′ | O2′–C2′ | C2′–C3′ | Oglu–HO3′ | SCys–HCys | HCys–O2′ | |
| Reactants | E-S | 124 | 1.35 | 1.02 | 1.45 | 1.49 | 1.59 | 1.36 | 2.07 |
| Gas phase | 115 | 1.35 | 1.00 | 1.43 | 1.50 | 1.62 | 1.36 | 2.02 | |
| TS | E-S | 143 | 1.32 | 1.06 | 2.26 | 1.37 | 1.46 | 1.47 | 1.44 |
| Gas phase | 107 | 1.28 | 1.47 | 1.93 | 1.42 | 1.05 | 1.55 | 1.36 | |
| Products | E-S | 162 | 1.27 | 1.60 | 2.88 | 1.40 | 1.02 | 2.37 | 0.99 |
| Gas phase | 45 | 1.28 | 1.51 | 5.39 | 1.39 | 1.04 | 2.74 | 0.97 | |
Distances in Ångstrom, angles in degrees, and frequencies in cm−1. The following nonstandard notations have been used: Hcys refers to the thiol proton of Cys-225, HO3′ refers to the proton of the 3′ hydroxyl group of the substrate, and Oglu refers to the oxygen of the carboxylate group of Glu-441 for which the proton is transferred.
Earlier gas-phase theoretical studies considering only truncated unconstrained side chains (24,25,57) have indicated that the lowest energy structure for the active site has each of the oxygens of Glu-441 hydrogen-bonded to a different substrate hydroxyl group (a double-hydrogen bond). However, the present model indicates that this is unfeasible at the active site of RNR. Instead, one of these oxygens makes a hydrogen bond with the 3′ hydroxyl group of the substrate, while the other makes a hydrogen bond with one of the hydrogens of the NH2 group of Asn-437. The hydrogen from the other hydroxyl group of the substrate (HO2′) remains hydrogen-bonded to the nitrogen of Asn-437 during the whole reaction (∼2.20 Å).
In the reactants, the spin density is mainly localized at carbon C-3′ of the substrate (0.98 a.u.), and the charge placed at the carboxylate group of the anionic Glu-441 (−1.15 a.u.), as expected.
Interestingly, at the transition state, the spin density is shared between the substrate (0.47 a.u.) and the leaving-hydroxyl group (0.43 a.u.). The charge is still mainly located at Glu-441 (−1.09 a.u.) as in the reactants, although slightly delocalized to Cys-225 (−0.18 a.u.) (as compared to an almost null charge in the reactants). It is interesting to note that, in the gas phase model, the proton of the 3′-hydroxyl group is already halfway between the 3′-hydroxyl and the carboxylate of Glu-441, whereas, in the E-S model, it is still bound to the 3′-hydroxyl group, being transferred only after the transition state.
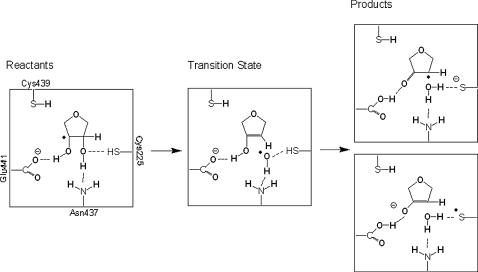
We can further notice that the leaving 2′-hydroxyl group does not have an anionic nature at the transition state. Instead, it is eliminated transiently as a radical, with a spin density of 0.43 a.u.. In the products the thiol proton is transferred to the leaving 2′-hydroxyl group, resulting in a water molecule. One of the water protons is still hydrogen-bonded to the nitrogen of Asn-437 (2.19 Å). The proton originally belonging to the 3′ hydroxyl is transferred to the carboxylate of Glu-441, and the charge and spin become delocalized between the substrate and Cys-225. Scheme 2 illustrates the obtained results. The observed delocalization in the spin and charge distributions in the products can be interpreted in terms of the keto-enolate resonance equilibrium shown in Scheme 2. Note that both the C3′-O3′ and C3′-C2′ bonds have lengths that are intermediate between typical single and double bonds (see Table 1).
SCHEME 2.
Chemical structures of the stationary points along the reaction pathway.
Subsequently, we have evaluated the interaction energy between the enzyme and the substrate. The purpose was to understand whether the enzyme was stabilizing the transition state though electrostatic interactions. The contributions from the active site region and from the surrounding region were calculated separately to distinguish between short-range stabilization and long-range stabilization.
Table 2 illustrates the energy of the reactants, transition state, and products, considering both the E-S and the gas phase models. The individual energy of each layer and the E-S model is also shown together with the resulting activation energies and reaction energies. The interaction energies as well as their contribution for the activation energies and reaction energies are displayed in Table 3.
TABLE 2.
Energies for reactants, transition state, and products of reaction, activation energies (Ea), and reaction energies (Er), divided by regions
| Model | Ea | Er | Reactants | Transition state | Products |
|---|---|---|---|---|---|
| E-S | 20.2 | 8.1 | −2.421236E+06 | −2.421216E+06 | −2.4212287E+06 |
| Gas phase | 17.1 | 12.1 | −6.339234E+05 | −6.339063E+05 | −6.339113E+05 |
| Reactive region | 16.6 | 5.3 | −6.339166E+05 | −6.339000E+05 | −6.339113E+05 |
| Active site region | −1.6 | −2.6 | −1.736733E+06 | −1.736735E+06 | −1.736736E+06 |
| Surrounding region | 0.0 | −0.1 | −5.128818E+04 | −5.128783E+04 | −5.128914E+04 |
All values are in kcal/mol.
TABLE 3.
Interaction energies
| Model | Ea | Er | Reactants | Transition state | Products |
|---|---|---|---|---|---|
| EInter R—AS | 4.9 | 6.4 | 7.015387E+02 | 7.064684E+02 | 7.079427E+02 |
| EInter (R:AS)—S | 0.3 | −0.9 | −2.316046E+02 | −2.313179E+02 | −2.325015E+02 |
| EInter Total | 5.2 | 5.5 | 4.699341E+02 | 4.751505E+02 | 4.754412E+02 |
These interaction energies are between the reactive region and the active site region (EInter R—AS), between the reactive and active site regions, and the surrounding region (EInter(R:AS)—S). The contributions for the activation energies (Ea) and reaction energies (Er) are also shown; all values in kcal/mol.
Several conclusions can be drawn from Tables 2 and 3. First, we can see that most of the contributions both for the activation and the reaction energies originate in the active site and reactive regions, which, taken together, have a value of 19.9 (16.6−1.6+4.9) and 9.1 (5.3−2.6+6.4) kcal/mol, respectively for those energies. This means that the surrounding region does not have a significant participation during the reaction pathway and its function is not to stabilize the transition state through long-range interactions. Secondly, it is clear that the major contribution to these energies arises from the reactive region, whose behavior is very similar to the small gas phase models. In fact, the barrier is increased by the enzyme machinery.
Concerning the short-range interactions, we see that, although the active-site region internal energy decreases by 1.6 kcal/mol at the transition state, and the barrier in the reactive region is decreased by 0.5 kcal/mol (compared with the gas phase model), the interaction between both regions increases by 4.9 kcal/mol. The positive contribution of the interaction energy means that this region does not stabilize the transition state through short-range specific electrostatic interactions. The overall result is that the barrier is raised by 2.8 kcal/mol in relation to the gas phase model. Therefore, at least in this reactional step, this region of the enzyme does not perform a short-range electrostatic transition-state stabilization.
The contribution for the reaction energy from the active site and reactive region is also similar to the one obtained with the gas phase model (9.1 kcal/mol, taking both regions together).
The relatively small contribution from the active-site region to the activation and reaction energies justifies the use of the ONIOM technique to optimize the geometry, and further emphasizes that the portion of the enzyme not considered in earlier works (which is even further away from the active site than the active-site region) should not have a relevant role in this reactional step.
The introduction of the surrounding region does not change this picture. As expected, the contribution from this region is even smaller, a total of 0.3 kcal/mol for the activation energy and −1.0 kcal/mol for the reaction energy, taking the internal and interaction energies together. As the main source for these energies is the long-range interaction energy, we also conclude that, at least in this reactional step, the enzyme does not significantly stabilize the transition state through long-range electrostatic interactions (−0.9 kcal/mol). These results further justify the use of a molecular-mechanics technique to deal with the surrounding region, whose contribution is the smallest in this system.
Another result that was evaluated was the difference in the results by using an explicit or implicit surrounding region. The implicit surrounding region was obtained substituting the atomistic surrounding region by a dielectric continuum with a dielectric constant of 4. This dielectric constant accounts for an average value of 3 for the protein and 80 for the buried water molecules, and was chosen because it was shown in the past to lead to good agreement with experimental data; subsequently, it was extensively used in earlier works (24,26,28,36,37,40,41). The results are shown in Table 4.
TABLE 4.
Energies for reactants, transition state, and products of reaction, activation energies (Ea) and reaction energies (Er) with explicit and implicit surrounding region
| Model | Ea | Er | Reactants | Transition state | Products |
|---|---|---|---|---|---|
| Implicit surrounding region | 20.0 | 8.0 | −2.379309E+06 | −2.379289E+06 | −2.379301E+06 |
| Explicit surrounding region | 19.9 | 9.1 | −2.369948E+06 | −2.369929E+06 | −2.369939E+06 |
| Difference | 0.1 | −1.1 |
Values for energies do not include water molecules.
The activation energy is almost equivalent using either implicit or explicit representations of the surrounding region. The energy of reaction has shown a slightly larger variation, although still quite small and not very significant. This means that the implicit surrounding region with a dielectric constant of 4 used in earlier calculations has captured the essential aspects of the enzyme reactivity. This was already expected from Tables 2 and 3, where it was shown that the surrounding region has only a negligible role in the enzyme energetics.
Another interesting property evaluated here is the steric strain energy at the active site. This energy corresponds to the difference in the activation and reaction energies calculated in the inner layer and the gas phase model, and reflects the effect of constraining the position/orientation of the substrate and the reactive active-site residues (due to their connections to the active-site backbone and their interactions with the remaining of the enzyme). The overall result (shown in Table 5 below) is that little strain is involved in the generation of the transition-state structure, compared with the gas phase model, which means that the source for the enzyme catalytic power does not come from a better E-S size/shape complementarity of the transition state relative to the reactants, which is a common enzymatic catalytic strategy. This was predictable because the transition-state geometry depends essentially on the chemical bonds being formed and broken, and is very similar in both models. Larger differences are obtained in the products, where the constraints imposed by the enzyme raise the steric-strain energy to 7.3 kcal/mol.
TABLE 5.
Steric strain energy in kcal/mol
| Steric strain energy | |
|---|---|
| R | 6.8 |
| TS | 6.3 |
| P | 1.4 |
| Ea | −0.5 |
| Er | 7.3 |
Importance of Asn-437 updated
The importance of Glu-441 and Asn-437 in the catalytic mechanism of RNR has been a subject of great discussion in the last decade (21,24,26,58,59). The results from mutagenesis experiments, UV-visible, and EPR spectroscopic measurements published by the Stubbe (31) and Sjoberg (21,57) groups have shown that several mutations on these residues decrease the rate of the reaction, or even preclude it. These observations indicate that Asn-437 and Glu-441 are determinant for the catalytic mechanism.
The importance of Glu-441 is presently well understood, as this residue acts as a base on the second step, receiving a proton from the 3′ hydroxyl group of the substrate, and in the fourth step it acts as an acid, giving back the proton to the 3′ hydroxyl oxygen. However, as Asn-437 does not react with the substrate, or with any of the active site residues, its relevance for the catalytic mechanism has remained unclear until now.
Several theoretical studies on the catalytic mechanism have already been performed (24–26,58), and although some of them have included most of the active site residues (including Asn-437), these were modeled as being disconnected from the enzyme backbone. Due to the large translational and rotational freedom of the residues in these cases, the models were not capable of reproducing effects based on the stereochemical constrains of the active site.
The presence of such constraints clearly suggests that Asn-437 has a determinant role in placing the 2′-hydroxyl group with the correct orientation relative to the thiol group of Cys-225. Moreover, it seems obvious from the model that mutations on this residue will induce an incorrect orientation of the 2′-hydroxyl group of the substrate, making more difficult, or even inhibiting, the water-elimination step. In that case, the radical will be retained at carbon C-3′ of the substrate, and will return very easily to Cys-439 by the inverse reaction of the first step (with an activation energy of only 0.6 kcal/mol (28), and a favorable reaction energy of −16.1 kcal/mol), thus regenerating the original tyrosyl radical. This should clearly be the situation in the inert mutant N437Q, where no tyrosyl radical decay was observed (21). Such behavior is related to the size of the glutamine, which occupies a larger volume in the active site, and which may compromise the correct orientation of the 2′-hydroxyl group, in this way precluding the proton transfer from Cys-225.
CONCLUSIONS
This work is devoted to the study of the second step of the catalytic mechanism of RNR. A very large high-level theoretical model was used that accounts for the geometric constraints of the substrate and active-site residues, and the interactions between the enzyme and the substrate. It was shown that the reaction occurs without significant conformational rearrangements. The overall result is that the reaction in the enzyme is very similar to the one with minimal gas phase models, and thus the enzymatic structure does not lower the activation energy of this second step through electrostatic interactions.
If we consider the reaction in water as the reference state, the picture does not change. Recalculating the activation energy of the gas phase model immersed in a dielectric continuum with a dielectric constant of 80, we obtain a lowering of the barrier of only 3.2 kcal/mol and an increase in the reaction energy of 0.1 kcal/mol. As approximately half of this energy is spent in the reorganization of the solvent (60), the real difference between the gas phase and water phase reference states resumes to 1.6 kcal/mol in the barrier and <0.1 kcal/mol in the reaction energy.
It was concluded that the enzyme does not stabilize the transition state either through short or long-range electrostatic interactions. We have been faced before with such a situation, in a similar study on the first step of this mechanism (28). It must be noted that this step is not the rate-limiting one, and therefore it is not meaningful for the enzyme to catalyze it. However, there is one aspect in which we must consider that the enzyme catalyzes this reaction. The reaction in gas phase or in solution is trimolecular, and in the enzymatic system, it is bimolecular. It is difficult to quantify such difference in terms of free energy because it will depend in the concentration of the reactants, although it is obvious that it will be significant. Warshel has estimated that the cost for the association of two biological molecules at 1 M concentration should be ∼+2.4 kcal/mol (61). In physiological environment, we should consider the concentrations of all present acidic and basic species to be able to estimate the entropic cost of generating the reactants complex (outside the enzyme active site there is a wide range of proton donors and acceptors). However, each species has its own reactivity, which makes this calculation far from trivial. Anyway, their concentrations are ≪1 M, and their reactivity is not much superior to that of a thiolate or an acetate, which just shows that the free energy cost is larger than the aforementioned +2.4 kcal/mol. Besides the cost of the encounter of the three reactants, their relative orientations do play a significant role here, which is not accounted for in the arguments introduced above. In an earlier work we have demonstrated the importance of the cooperativity between the proton donor and the proton acceptor in this reaction. Indeed, if we do not consider a coupled protonation/deprotonation, the chemical barrier rises by 13.5 kcal/mol (37). In the enzymatic system, the cooperativity is guaranteed by the preorientation of the active-site residues. This energy cost is paid off during enzyme folding, stored in the active site, and thus not obviously detectable from the enzyme alone, whose active site already has all residues in favorable positions to promote a concerted proton transfer from Cys-225 to the substrate and from the substrate to Glu-441. Even Asn-437 has a role here, as this residue was found to be crucial to place the living group in a favorable orientation relative to the thiol of Cys-225 for protonation. Therefore, the energetic gain associated to the preorientation of the proton donor and acceptor in the active site is quite large, larger than 2.4 kcal/mol. The exact value depends on the concentration of physiological proton donors and acceptors and their intrinsic reactivity, plus the entropic and energetic cost of generating the correct orientation for a coupled protonation/deprotonation in the reference state. It is not possible at present to accurately quantify these values, both of which are associated to the preorganization of the active site, although we can calculate their magnitudes. However, we can definitively say that, in this step, the source for the catalytic power of the enzyme is entropic, rather than electrostatic.
Another fundamental role for the enzyme seems to be to protect the radical from the solvent. We cannot ignore that these radical reactions would never be feasible without the enzyme machinery, as the radical intermediates would immediately be quenched by the environment.
In this article we have also compared the results obtained with an explicit or an implicit representation of the surrounding region. The results indicate good agreement between both representations, and further validate earlier studies.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org. It contains coordinates for the stationary points discussed in the text.
Supplementary Material
Acknowledgments
Fundação para a Ciência e Tecnologia (FCT, Project No. POCTI/35736/99, Portugal) and the National Foundation for Cancer Research (USA) are gratefully acknowledged for financial support. N.M.F.S.A.C. further thanks the FCT for a PhD grant.
References
- 1.Stubbe, J. 1990. Ribonucleotide reductases: amazing and confusing. J. Biol. Chem. 265:5329–5332. [PubMed] [Google Scholar]
- 2.Stubbe, J., and J. W. Kozarich. 1980. Fluoride, pyrophosphate, and base release from 2′-deoxy-2′-fluoronucleoside 5′-diphosphates by ribonucleoside-diphosphate reductase. J. Biol. Chem. 255:5511–5513. [PubMed] [Google Scholar]
- 3.Stubbe, J., and J. W. Kozarich. 1980. Inorganic pyrophosphate is released from 2′-chloro-2′-deoxyuridine 5′-diphosphate by ribonucleoside diphosphate reductase. J. Am. Chem. Soc. 102:2505–2507. [Google Scholar]
- 4.Erikson, S., and B.-M. Sjoberg. 1989. Ribonucleotide reductase. In Allosteric Enzymes. G. Herve, editor. CRC Press, Boca Raton, FL. 189–215.
- 5.Stubbe, J. 1990. Ribonucleotide reductases. Adv. Enzymol. Rel. Areas Mol. Biol. 63:349–419. [DOI] [PubMed] [Google Scholar]
- 6.Sjöberg, B.-M. 1995. Nucleic Acids and Molecular Biology. F. L. D. Eckstein, editor. Springer, Berlin. 92.
- 7.Reichard, P. 1993. From RNA to DNA: why so many ribonucleotide reductases? Science. 260:1773–1777. [DOI] [PubMed] [Google Scholar]
- 8.Hammarsten, E., P. Reichard, and E. Saluste. 1950. Pyrimidine nucleosides as precursors of pyrimidines in polynucleotides. J. Biol. Chem. 183:105–109. [Google Scholar]
- 9.Reichard, P., and B. Estborn. 1951. Utilization of deoxyribosides in the synthesis of polynucleotides. J. Biol. Chem. 188:839–846. [PubMed] [Google Scholar]
- 10.Blakley, R. L., and H. A. Barker. 1964. Cobamide stimulation of the reduction of ribotides to deoxyribotides in Lactobacillus leichmannii. Biochem. Biophys. Res. Commun. 16:391–397. [DOI] [PubMed] [Google Scholar]
- 11.Beck, W. S., and J. Hardy. 1965. Requirement of ribonucleotide reductase for cobamide coenzyme, a product of ribosomal activity. Proc. Natl. Acad. Sci. USA. 54:286–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Barlow, T. 1988. Evidence for a new ribonucleotide reductase in anaerobic E. coli. Biochem. Biophys. Res. Commun. 155:747–753. [DOI] [PubMed] [Google Scholar]
- 13.Fontecave, M., R. Eliasson, and P. Reichard. 1989. Oxygen-sensitive ribonucleoside triphosphate reductase is present in anaerobic Escherichia coli. Proc. Natl. Acad. Sci. USA. 86:2147–2151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Eriksson, M., U. Uhlin, S. Ramaswamy, M. Ekberg, K. Regnstrom, B. M. Sjoberg, and H. Eklund. 1997. Binding of allosteric effectors to ribonucleotide reductase protein R1: reduction of active-site cysteines promotes substrate binding. Structure. 5:1077–1092. [DOI] [PubMed] [Google Scholar]
- 15.Scott, C. P., O. B. Kashlan, J. D. Lear, and B. S. Cooperman. 2001. A quantitative model for allosteric control of purine reduction by murine ribonucleotide reductase. Biochemistry. 40:1651–1661. [DOI] [PubMed] [Google Scholar]
- 16.Kashlan, O. B., C. P. Scott, J. D. Lear, and B. S. Cooperman. 2002. A comprehensive model for the allosteric regulation of mammalian ribonucleotide reductase. Functional consequences of ATP- and dATP-induced oligomerization of the large subunit. Biochemistry. 41:462–474. [DOI] [PubMed] [Google Scholar]
- 17.Kashlan, O. B., and B. S. Cooperman. 2003. Comprehensive model for allosteric regulation of mammalian ribonucleotide reductase: refinements and consequences. Biochemistry. 42:1696–1706. [DOI] [PubMed] [Google Scholar]
- 18.Nordlund, P., B. M. Sjoberg, and H. Eklund. 1990. Three-dimensional structure of the free-radical protein of ribonucleotide reductase. Nature. 345:593–598. [DOI] [PubMed] [Google Scholar]
- 19.Stubbe, J. A., and W. A. van der Donk. 1998. Protein radicals in enzyme catalysis. Chem. Rev. 98:2661–2662. [DOI] [PubMed] [Google Scholar]
- 20.Rova, U., A. Adrait, S. Potsch, A. Graslund, and L. Thelander. 1999. Evidence by mutagenesis that Tyr370 of the mouse ribonucleotide reductase R2 protein is the connecting link in the intersubunit radical transfer pathway. J. Biol. Chem. 274:23746–23751. [DOI] [PubMed] [Google Scholar]
- 21.Persson, A. L., M. Eriksson, B. Katterle, S. Potsch, M. Sahlin, and B. M. Sjoberg. 1997. A new mechanism-based radical intermediate in a mutant R1 protein affecting the catalytically essential Glu441 in Escherichia coli ribonucleotide reductase. J. Biol. Chem. 272:31533–31541. [DOI] [PubMed] [Google Scholar]
- 22.Mohr, M., and H. Zipse. 1999. C-H bond activation in ribonucleotide reductases—do short, strong hydrogen bonds play a role? Chem. Eur. J. 5:3046–3054. [Google Scholar]
- 23.Lenz, R., and B. Giese. 1997. Studies on the mechanism of ribonucleotide reductases. J. Am. Chem. Soc. 119:2784–2794. [Google Scholar]
- 24.Cerqueira, N. M. F. S. A., P. A. Fernandes, M. J. Ramos, and L. A. Eriksson. 2004. New insights into a critical biological control step of the mechanism of ribonucleotide reductase. J. Mol. Struct. Theor. Chem. 709:53–65. [Google Scholar]
- 25.Siegbahn, P. E. M. 1998. Theoretical study of the substrate mechanism of ribonucleotide reductase. J. Am. Chem. Soc. 120:8417–8429. [Google Scholar]
- 26.Fernandes, P. A., L. A. Eriksson, and M. J. Ramos. 2002. The reduction of ribonucleotides catalyzed by the enzyme ribonucleotide reductase. Theor. Chem. Acc. 108:352–364. [Google Scholar]
- 27.Siegbahn, P. E. 2003. Mechanisms of metalloenzymes studied by quantum chemical methods. Q. Rev. Biophys. 36:91–145. [DOI] [PubMed] [Google Scholar]
- 28.Cerqueira, N. M. F. S. A., P. A. Fernandes, M. J. Ramos, and L. A. Eriksson. 2004. Ribonucleotide activation by enzyme ribonucleotide reductase: understanding the role of the enzyme. J. Comput. Chem. 25:2031–2037. [DOI] [PubMed] [Google Scholar]
- 29.Mao, S. S., T. P. Holler, G. X. Yu, J. M. Bollinger, S. Booker, M. I. Johnston, and J. Stubbe. 1992. A model for the role of multiple cysteine residues involved in ribonucleotide reduction—amazing and still confusing. Biochemistry. 31:9733–9743. [DOI] [PubMed] [Google Scholar]
- 30.Stubbe, J., and W. A. van der Donk. 1995. Ribonucleotide reductases: radical enzymes with suicidal tendencies. Chem. Biol. 2:793–801. [DOI] [PubMed] [Google Scholar]
- 31.Lawrence, C. C., M. Bennati, H. V. Obias, G. Bar, R. G. Griffin, and J. Stubbe. 1999. High-field EPR detection of a disulfide radical anion in the reduction of cytidine 5′-diphosphate by the E441Q R1 mutant of Escherichia coli ribonucleotide reductase. Proc. Natl. Acad. Sci. USA. 96:8979–8984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cory, J. G. 1988. Ribonucleotide reductase as a chemotherapeutic target. Adv. Enz. Regul. 27:437–455. [DOI] [PubMed] [Google Scholar]
- 33.Robins, M. J., V. Samano, W. J. Zhang, J. Balzarini, E. Declercq, R. T. Borchardt, Y. Lee, and C. S. Yuan. 1992. Nucleic-acid related compounds: 74. Synthesis and biological-activity of 2′(and 3′)-deoxy-2′(and 3′)-methylenenucleoside analogs that function as mechanism-based inhibitors of S-adenosyl-L-homocysteine hydrolase and or ribonucleotide reductase. J. Med. Chem. 35:2283–2293. [DOI] [PubMed] [Google Scholar]
- 34.Nocentini, G. 1996. Ribonucleotide reductase inhibitors: new strategies for cancer chemotherapy. Crit. Rev. Oncol. Hematol. 22:89–126. [DOI] [PubMed] [Google Scholar]
- 35.Gerfen, G. J., W. A. van der Donk, Yu, C. Farrar, R. G. Griffin, J. Stubbe, J. R. McCarthy, D. P. Matthews, and E. T. Jarvi. 1998. Characterization of a substrate derived radical detected during the inactivation of ribonucleotide reductase from Escherichia coli by 2′-fluoromethylene-2′-deoxycytidine 5′-diphosphate. J. Am. Chem. Soc. 120:3823–3835. [Google Scholar]
- 36.Pereira, S., P. A. Fernandes, and M. J. Ramos. 2004. Theoretical study of ribonucleotide reductase mechanism-based inhibition by 2′-azido-2′-deoxyribonucleoside 5-diphosphates. J. Comput. Chem. 25:227–237. [DOI] [PubMed] [Google Scholar]
- 37.Fernandes, P. A., and M. J. Ramos. 2003. Theoretical studies on the mode of inhibition of ribonucleotide reductase by 2′-substituted substrate analogues. Chem. Eur. J. 9:5916–5925. [DOI] [PubMed] [Google Scholar]
- 38.Heinemann, V., Y. Z. Xu, S. Chubb, A. Sen, L. W. Hertel, G. B. Grindey, and W. Plunkett. 1990. Inhibition of ribonucleotide reduction in CCRF-CEM cells by 2′,2′-difluorodeoxycytidine. Mol. Pharmacol. 38:567–572. [PubMed] [Google Scholar]
- 39.van der Donk, W. A., G. X. Yu, L. Perez, R. J. Sanchez, J. Stubbe, V. Samano, and M. J. Robins. 1998. Detection of a new substrate-derived radical during inactivation of ribonucleotide reductase from Escherichia coli by gemcitabine 5′-diphosphate. Biochemistry. 37:6419–6426. [DOI] [PubMed] [Google Scholar]
- 40.Cerqueira, N. M. F. S. A., P. A. Fernandes, M. J. Ramos, and L. A. Eriksson. 2005. Overview of ribonucleotide reductase inhibitors: an appealing target in anti-tumour therapy. Curr. Med. Chem. 12:1283–1294. [DOI] [PubMed] [Google Scholar]
- 41.Fernandes, P. A., and M. J. Ramos. 2003. Theoretical studies on the mechanism of inhibition of ribonucleotide reductase by (E)-2′-fluoromethylene-2′-deoxycitidine-5′-diphosphate. J. Am. Chem. Soc. 125:6311–6322. [DOI] [PubMed] [Google Scholar]
- 42.Uhlin, U., and H. Eklund. 1994. Structure of ribonucleotide reductase protein R1. Nature. 370:533–539. [DOI] [PubMed] [Google Scholar]
- 43.Uhlin, U., T. Uhlin, and H. Eklund. 1993. Crystallization and crystallographic investigations of ribonucleotide reductase protein R1 from Escherichia coli. FEBS Lett. 336:148–152. [DOI] [PubMed] [Google Scholar]
- 44.Jones, G., P. Willett, R. C. Glen, A. R. Leach, and R. Taylor. 1997. Development and validation of a genetic algorithm for flexible docking. J. Mol. Biol. 267:727–748. [DOI] [PubMed] [Google Scholar]
- 45.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- 46.Bakowies, D., and W. Thiel. 1996. Hybrid models for combined quantum mechanical and molecular mechanical approaches. J. Phys. Chem. B. 100:10580–10594. [Google Scholar]
- 47.Dapprich, S., I. Komaromi, K. S. Byun, K. Morokuma, and M. J. Frisch. 1999. A new ONIOM implementation in Gaussian 98. I. The calculation of energies, gradients, vibrational frequencies and electric field derivatives. J. Mol. Struct. Theor. Chem. 461:1–21. [Google Scholar]
- 48.Sherwood, P. 2000. Hybrid Quantum Mechanics/Molecular Mechanics Approaches. J. Grotendorst, editor. Forschungszentrum Jülich, John von Neumann Institute for Computing, Jülich, Germany. 285–305.
- 49.Svensson, M., S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber, and K. Morokuma. 1996. ONIOM: a multilayered integrated MO + MM method for geometry optimizations and single point energy predictions. A test for Diels-Alder reactions and Pt(P(t-Bu)3)2 + H2 oxidative addition. J. Phys. Chem. 100:19357–19363. [Google Scholar]
- 50.Torrent, M., T. Vreven, D. G. Musaev, K. Morokuma, O. Farkas, and H. B. Schlegel. 2002. Effects of the protein environment on the structure and energetics of active sites of metalloenzymes. ONIOM study of methane monooxygenase and ribonucleotide reductase. J. Am. Chem. Soc. 124:192–193. [DOI] [PubMed] [Google Scholar]
- 51.Frisch M. J., G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, and J. Tomasi, et al. 2003. Gaussian 03, Ver. B.04. Gaussian, Pittsburgh, PA.
- 52.Frisch, M. J., G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, and J. A. Montgomery Jr., S. D. J. C. Burant, J. M. Millam, A. D. Daniels, and K. N. Kudin, et al. 2001. Gaussian98, Vers. A.11.2. Gaussian, Pittsburgh, PA.
- 53.Hertwig, R. W., and W. J. Koch. 1997. On the parameterization of the local correlation functional: what is Becke-3-LYP? Chem. Phys. Lett. 268:345–351. [Google Scholar]
- 54.Dewar, M. J. S., E. G. Zoebisch, E. F. Healy, and J. J. P. Stewart. 1985. AM1: a new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 105:3902–3909. [Google Scholar]
- 55.Mulliken, S. 1955. Electronic population analysis on linear combination of atomic orbital-molecular orbital molecular wave functions. Int. J. Chem. Phys. 23:1833. [Google Scholar]
- 56.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- 57.Siegbahn, P. E. M., L. Eriksson, F. Himo, and M. Pavlov. 1998. Hydrogen atom transfer in ribonucleotide reductase (RNR). J. Phys. Chem. B. 102:10622–10629. [Google Scholar]
- 58.Pelmenschikov, V., K. B. Cho, and P. E. Siegbahn. 2004. Class I ribonucleotide reductase revisited: the effect of removing a proton on Glu-441. J. Comput. Chem. 25:311–321. [DOI] [PubMed] [Google Scholar]
- 59.Kasrayan, A., A. L. Persson, M. Sahlin, and B. M. Sjoberg. 2002. The conserved active site asparagine in class I ribonucleotide reductase is essential for catalysis. J. Biol. Chem. 277:5749–5755. [DOI] [PubMed] [Google Scholar]
- 60.Warshel, A. 1998. Electrostatic origin of the catalytic power of enzymes and the role of preorganized active sites. J. Biol. Chem. 273:27035–227038. [DOI] [PubMed] [Google Scholar]
- 61.Warshel, A. 1991. Computer Modeling of Chemical Reactions in Enzymes and Solutions. John Wiley & Sons, New York.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.