Automated Detection of Elementary Calcium Release Events Using the À Trous Wavelet Transform

Abstract

We developed an algorithm for the automated detection and analysis of elementary Ca²⁺ release events (ECRE) based on the two-dimensional nondecimated wavelet transform. The transform is computed with the “à trous” algorithm using the cubic B-spline as the basis function and yields a multiresolution analysis of the image. This transform allows for highly efficient noise reduction while preserving signal amplitudes. ECRE detection is performed at the wavelet levels, thus using the whole spectral information contained in the image. The algorithm was tested on synthetic data at different noise levels as well as on experimental data of ECRE. The noise dependence of the statistical properties of the algorithm (detection sensitivity and reliability) was determined from synthetic data and detection parameters were selected to optimize the detection of experimental ECRE. The wavelet-based method shows considerably higher detection sensitivity and less false-positive counts than previously employed methods. It allows a more efficient detection of elementary Ca²⁺ release events than conventional methods, in particular in the presence of elevated background noise levels. The subsequent analysis of the morphological parameters of ECRE is reliably reproduced by the analysis procedure that is applied to the median filtered raw data. Testing the algorithm more rigorously showed that event parameter histograms (amplitude, rise time, full duration at half-maximum, and full width at half-maximum) were faithfully extracted from synthetic, “in-focus” and “out-of-focus” line scan sparks. Most importantly, ECRE obtained with laser scanning confocal microscopy of chemically skinned mammalian skeletal muscle fibers could be analyzed automatically to reproducibly establish event parameter histograms. In summary, our method provides a new valuable tool for highly reliable automated detection of ECRE in muscle but can also be adapted to other preparations.

INTRODUCTION

Since their first description by Cheng et al. (1), calcium sparks have gained an enormous attention as they have been detected in a variety of cell types such as heart, skeletal, and smooth muscle (2–4) and increasing evidence of their physiological importance is at hand (5). Sparks may constitute the elementary building block of intracellular calcium signaling via ryanodine receptor Ca²⁺ release channels (RyR) that can be observed in its native environment, i.e., the intact sarcoplasmic reticulum (SR) or endoplasmic reticulum (ER). Our knowledge about the dynamics of elementary Ca²⁺ release has increased along with the extensive work dedicated to the study of ryanodine receptors with a variety of methodological approaches on distinct cell preparations (6). In contrast to lipid bilayer experiments or electrophysiological measurements on purified SR vesicles, laser scanning confocal microscopy in combination with fluorescent Ca²⁺ dyes allows only indirect observation of the RyR channel Ca²⁺ current. However, the dynamic interplay between SR, the SR Ca²⁺-ATPase (SERCA), motor proteins, and mitochondria is largely conserved. Although amphibian skeletal muscle fibers show rather stereotypical event morphologies, chemically or mechanically skinned mammalian skeletal muscle spontaneously displays a multitude of Ca²⁺ release morphologies (7). We adopt the term elementary calcium release events (ECRE), denoting the whole variety of observed release event morphologies, among them “sparks” (short-lived fluorescence elevations due to the simultaneous opening of a RyR cluster) and “embers” (long-lived, low amplitude signals probably representing the opening of a single RyR Ca²⁺ channel, e.g., Shtifman et al. (8)) as subgroups.

A central problem in ECRE imaging arises when the important kinetics of the sometimes extremely short-lived (∼10 ms) signals are analyzed in detail. For example, fast scanning of amphibian skeletal muscle cells in the XYT mode has been used by Brum et al. (9), achieving a scanning rate of 4 ms / (85 × 5.3 μm). The temporal resolution can be further enhanced with two-dimensional (XT) imaging, scanning the same line (∼80 μm) every 0.8–2 ms. The resulting uncertainty about the relative position of the line scan with respect to the center of Ca²⁺ release (“off-center” imaging) leads to the typical monotonically decreasing ECRE amplitude histograms (10,11). The effects of confocal imaging on the measured spark morphology was extensively studied by Pratusevich and Balke (10) and combined with mathematical modeling to clarify the relationship between the source strength and event histograms by Izu et al. (11). The combined effects of “off-center” imaging and the nearly Gaussian spark profile lead to a high frequency f of events with small amplitude a (f ∼ a⁻¹, (12)). However, it has been shown that erroneous modes are introduced into amplitude distributions due to the biased rejection of small amplitude events (13) particularly with nonautomated detection methods (detection “by eye”). To overcome this problem, several automated detection methods have been published (11,13,14), the most common being the algorithm of Cheng et al. (15), modified later in González et al. (16) and Ríos et al. (12). An interactive detection procedure has been presented by Sebille et al. (17), which, however, emphasizes user intervention to include or exclude events by eye detection. Generally, all of these methods identify sparks by a rise in fluorescence intensity in a previously low-pass filtered image. The approach taken by Cheng and colleagues is based on applying a double threshold to the normalized image. Let μ, σ, and κ denote the image mean intensity, an estimate of the background standard deviation and the threshold parameter, respectively. Then, a high, variable threshold (μ + κ × σ, κ ∼ 3.9) is used to identify statistically significant fluorescence elevations and a lower threshold (μ + 2 × σ) is applied to check whether the signal intensity is sufficient to distinguish a spark from small “random” fluorescence elevations. The algorithm by Izu et al. (11) starts with a thresholding operation to produce a binary image. A pixel is set to unity (“on”) if its value does exceed a threshold equal to the background intensity plus 1.4 times the standard deviation of the background fluctuations, otherwise it is set to zero (“off”). The binary image is then updated N_generation times according to the following rule: if the symmetric N_size × N_size neighborhood of a pixel (i,j) contains <N_live “on” pixels, (i,j) is set “off”, otherwise it is “on” in the next iteration. Although both of these methods prove to be reliable on images with low noise levels, their performance in terms of detection efficiency and reliability at higher noise levels is limited. In this study, we have developed a novel automated detection algorithm based on the à trous wavelet transform that shows a considerably improved detection sensitivity and better statistical properties at high and especially at low signal/noise ratios (SNR defined as background mean μ divided by mean ±SD σ). The wavelet transform is extensively studied in mathematics (18,19) as well as in a large number of applied sciences such as acoustics, fluid dynamics, and astronomy (20). The wavelet transform decomposes the signal of interest in different spectral bands by an iterative application of band-pass filters. Image noise can be estimated and reduced in each spectral band and a denoised version of the image can be reconstructed. ECRE are then detected in the wavelet transform of the denoised image. To our knowledge, it has not yet been used for the analysis of dynamic fluorescence signals from living cells.

METHODS

Data

Synthetic data sets were used to assess the performance of the algorithm. To quantify the statistical properties of our algorithm, we produced a data set representing low-noise experimental data (SNR 3.5) as well as two more data sets with considerably lower SNR (2.5 and 2.0). Synthetic images contain 512 × 2048 pixels, equal to the spatial and the temporal dimension of our experimental XT-images, respectively (87.5 μm × 4198 ms). A completely synthetic reference spark with standard parameters (rise time (RT), 8.2 ms; full duration at half-maximum (FDHM), 16.4 ms; full width at half-maximum (FWHM), 2.39 μm) was synthesized. It has a single exponential rise and decay characteristic (rise and decay time constants independent) and a Gaussian profile in space (see Fig. 5). These functions provide a good fit to real sparks (21). Images containing sparks, rescaled to fixed amplitudes, and placed at random positions were produced. Gaussian noise was added to obtain a desired SNR. We analyzed the amplitude range from ΔF/F₀ = 0.0–1.0 with an amplitude step size of 0.1 and 20 synthetic images per amplitude bin. In the amplitude region of interest where the analyzed statistical parameters rise to their maximum (ΔF/F₀ = 0.2, 0.3), 200 images per amplitude bin were used.

FIGURE 5.

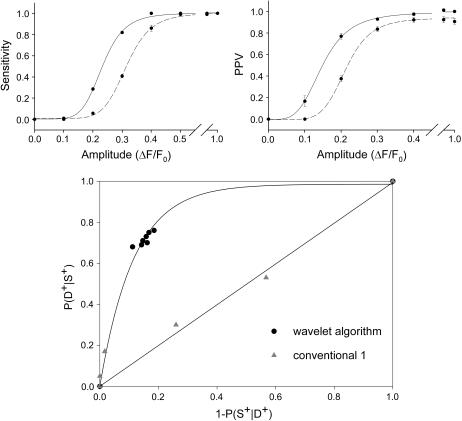
Summary of the statistical properties of both algorithms (wavelet, solid lines; conventional, dashed lines) at SNR 2.5. The parameters used were δ = 4.00, τ = 3.75 (wavelet algorithm), and κ = 3.9 (conventional algorithm). Errors are presented as mean ±SE (n = 20, amplitudes 0.2, 0.3 n = 200).

Experimental procedures

Experiments on saponin-treated, permeabilized muscle cells were carried out as described by Kirsch et al. (7). C57 SV-129 mice were sacrificed in accordance with the animal handling guidelines laid down by the local animal care committee and single muscle fibers were obtained from the extensor digitorum longus muscle. The solutions used correspond to the mammalian relaxing, internal, and Ringer solution as specified in Kirsch et al. (7).

Confocal microscopy and fluorescence imaging

The experimental data set was acquired by laser scanning confocal microscopy of Ca²⁺-fluo-4 fluorescence in saponin-skinned fibers incubated with 75 μM fluo-4 (Molecular Probes, Eugene, OR). Fibers were imaged through a w40× water immersion objective (UAPO40wW/340/1.15, Olympus, Tokyo, Japan) with a confocal laser scanning unit (FV-300, Olympus) using the 488-nm line of a 20-mW Kr/Ar-laser (Omnichrome, Melles Griot, Carlsbad, CA) on an inverted microscope (IX70, Olympus). The fluorescence signal was collected at λ > 510 nm using a long-pass filter and a photomultiplier.

Noise

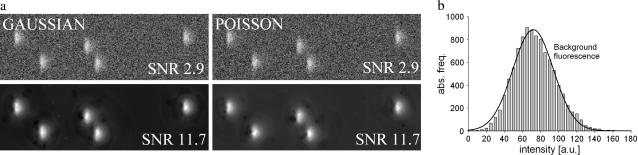
The wavelet algorithm can be used in its general form on a variety of different data sets. However, in its specific form presented here it is designed for the analysis of two-dimensional (XT) dynamic Ca²⁺ measurements with the fluorescent dye fluo-4. The background fluctuations of these images can be considered photon noise and follow a Poisson distribution. However, for the signal intensities achieved in experimental situations (as in “Experimental procedures”), a Gaussian distribution yields a good approximation of the background noise. Fig. 1 b shows a histogram of the background intensity of a typical line scan image with a Gaussian fit. Fig. 1 a shows synthetic events embedded in Gaussian (left panel) and Poisson (right panel) noise and the respective denoised images (lower panels, denoising strength δ = 4.00; definition see below). The signal/noise ratio of the denoised images is identical for both noise types. Thus, simulation and experimental observations suggest that the results obtained with Gaussian noise simulations can be applied to the experimental situation.

FIGURE 1.

Noise characteristics. (a) The same simulated ECRE were embedded in Gaussian (left) and Poisson (right) distributed noise at a signal/noise ratio (SNR) of 2.9. Denoising of the images with the wavelet-based denoising method (bottom panels) resulted in identical SNR values (11.7) for both noise types. (b) The histogram of fluorescence intensity background fluctuations of an experimental line scan shows a Poisson distribution that is well approximated by a Gaussian (black solid curve).

Another possible way to deal with Poisson noise is by using variance stabilizing transformations (22). The resulting transform has noise properties as if the noise originated from a Gaussian distribution, i.e., a Poisson distributed background can be transformed to a Gaussian distributed noise. Therefore, we follow the technique employed by Song et al. (13) and Cheng et al. (15) and embed synthetic sparks in Gaussian distributed noise, thus achieving a good approximation to experimental conditions and comparability of our results with the literature.

Image preprocessing

First, the raw image was normalized with respect to an estimate of the background fluorescence. Therefore, each image row (time axis) was divided by its mean to remove the t-tubular pattern present in line-scan images leading to a slight increase of the image SNR. Then, pixels whose value exceeded a 1.5 σ threshold above the mean were set to zero and a second run of computing the row mean ignoring zero-valued pixels was done. Finally, every pixel of the raw image was divided by its row mean value. That produced the normalized image F/F_o used during further analysis steps.

The wavelet transform

Wavelet-based techniques are computationally efficient time-frequency methods that decompose an image in a coarse representation and several “detail” levels. The coarse image preserves the large-scale structure and the mean of the image whereas the “detail” or wavelet levels complement the coarse level and thus preserve the total image information. The decomposition is achieved by filtering the signal with a set of low- and high-pass filters as specified below (18). The basis functions for the different resolution levels are all derived from one elemental function—the scaling function φ—by dilation and translation. This function satisfies the dilation equation (23)

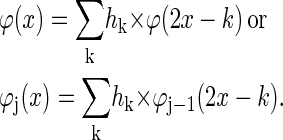(1)

Equation 1 expresses the fact that the convolution kernel φ can be constructed as a linear combination of compressed and shifted versions of itself. The h_k are the coefficients of a low-pass filter and determine the form and the properties of the resulting wavelets. The second form of Eq. 1 is used to proceed from one resolution level j-1 to the next j and φ results from iteration for j → ∞. Furthermore, φ integrates to 1. The corresponding wavelet ψ that serves as a basis for the construction of the detail levels is given by

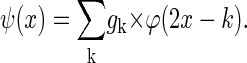(2)

The g_k are coefficients of a high-pass filter closely related to the low-pass filter (h_k) mentioned above and ψ integrates to zero (19). This leads to the important property of detail/wavelet levels to have zero mean. The resulting wavelets satisfy:

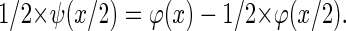(3)

Despite the multitude of possible functions fulfilling these conditions they show very different characteristics and are therefore not equally suitable for different scientific applications (24). Our algorithm is based on the two-dimensional discrete wavelet transform with the cubic B-spline as the scaling function. Cubic B-splines lead to a scaling function offering various favorable features such as quasiisotropy and smoothness. This allows a nonrecursive representation of the scaling function as a piecewise polynomial (25,26):

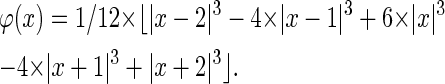(4)

The implementation of the transform was achieved by the so-called à trous (with holes) algorithm that yields a nonorthogonal transform. Its advantage lies in the fact that it is shift invariant and conserves the original image dimensions, i.e., it is nondecimated. A detailed description of the properties of the à trous and the Mallat algorithm is given in Mallat (18) and Shensa (27). Implementation of the algorithm is straightforward: in each step the image is convolved with a cubic B-spline filter with 2^i-1 zeros inserted between the B-spline filter coefficients at level i, therefore the name “with holes”. The convolution mask in one dimension is 1/16 · [1, 4, 6, 4, 1]. Thus, we get a series of smoothed images F^(k) with F⁽⁰⁾ as the normalized raw image. The wavelet coefficients at level k, W^(k), are given by:

(5)

The decomposition allows the exact reconstruction of the original signal F⁽⁰⁾ by

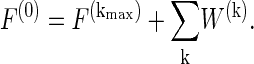(6)

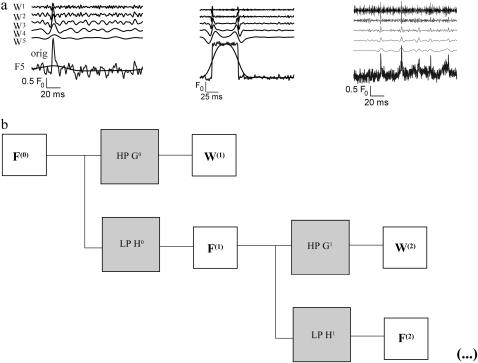
Fig. 2 a shows traces from synthetic and experimental data analyzed with the à trous wavelet transform. The left panel shows the wavelet transform of a simulated spark function with additive Gaussian noise. Underlying the original trace the smoothed signal F(5) is displayed. It has the same mean as the raw trace and follows the overall trend of the signal. Wavelet levels W(5)–W(1) follow from bottom to top. The band-pass character of the wavelet transform is clearly visible. The central panel shows the transform of the one-dimensional trace of a noisy step function and the right panel shows a trace of repetitive calcium sparks from skeletal muscle (experimental data). It should be noticed that the variance of the wavelet coefficients decreases with level k. The latter feature allows one to remove image noise and to retain significant coefficients on all wavelet levels as explained in the next section.

FIGURE 2.

(a) À trous wavelet transform of different model signals. (Left) A spark-like event; (middle) a square pulse (both synthetic with additive white Gaussian noise); (right) experimental data showing repetitive release events. The lowest trace is the raw data and the underlying smooth trace of F(5) (see text). From bottom to top follow W(5)–W(1). (b) Filter bank structure of the à trous wavelet transform. One iteration consists of one convolution of the signal with a low-pass (LP) and a high-pass (HP) filter (H and G, respectively). The low-pass filtered signal is the input for the next iteration step.

Denoising

Wavelets are a powerful tool for noise removal. Similar to Fourier transform techniques, wavelet coefficients can be removed and the image reconstructed from the remaining coefficients. We used the scheme proposed by Starck and Murtagh (20). We only want to give a brief outline of the method here. First, an initial estimate of the background noise standard deviation (σ₀) is computed from the pixel values below a 2 × σ threshold, where σ denotes the standard deviation of the image involving all pixels. Compute the wavelet transform of the image, set all the coefficients that do not exceed a 3 × σ_j threshold (σ_j being the standard deviation of the wavelet coefficients on level j) to zero but retain their original values to obtain a noise estimate. The mean ±SD σ_j for each wavelet level j is calculated as:

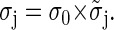(7)

The 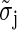are values for the standard deviation of white Gaussian noise (WGN) processed by the à trous algorithm obtained from simulations with synthetic WGN images. The noise estimate is updated from the pixels having zero coefficients at all levels, taking care to remove the background signal F(5). The procedure is repeated until convergence and yields the final estimate σ_I. A stable estimate is usually reached within few iteration steps. The image is finally reconstructed from the wavelet coefficients thresholded at δ × σ_I according to Eq. 6. The parameter δ will be referred to as the denoising parameter from now on and provides one of the two basic parameters of the algorithm determining its final sensitivity and reliability.

Detection

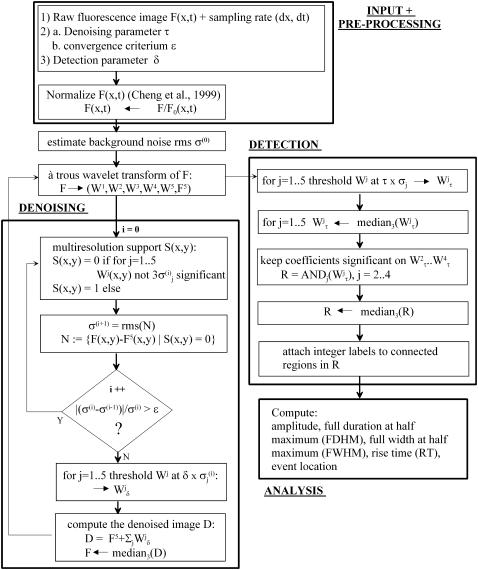
The denoised image is again transformed with the à trous algorithm and ECRE are detected on the wavelet levels W^(k) by applying a simple threshold operation. With increasing index k there appear events of increasing size and lower frequency content. Thus, events with sharp spikes such as sparks appear on high-resolution wavelet levels such as W(2) and W(3) whereas longer events with slower rise and decay characteristics such as embers tend to appear on low-resolution levels. Let τ denote the detection threshold parameter. The regions of interest are extracted as pixels with an F/F₀ value exceeding a threshold of τ times the standard deviation of the image and produces a set of binary images. This process is applied to the wavelet coefficients W^(k) (k = 2…4). For high event frequency data containing sharp rising and decaying events (spark-like) as they occur in voltage clamp experiments with amphibian skeletal muscle fibers, we used exclusively W(2) and W(3) for detection. These frequency bands contain the important coeffcients that represent spark-like events. The intersection of the binary images is median filtered to remove very small areas and yields a set of regions of interest where actual ECRE are searched for. The parameter τ is the other central parameter adjustable by the user and allows further modification of detection properties. Finally, event parameters were calculated according to their common definition on three-point averages through the event center in the median filtered raw data to yield largely undistorted estimates. Selection conditions were: amplitude ΔF/F_o ≥ 0.2, FWHM ≥ 0.6 μm, FDHM ≥ 5 ms for the conventional algorithm and ΔF/F_o ≥ 0.001, FWHM ≥ 0.1 μm for the wavelet algorithm unless otherwise indicated. The selection criteria for the conventional algorithm represent typical values used in practice (e.g., Lacampagne et al. (28)) whereas the wavelet algorithm could be run effectively without restrictions. The filter bank structure of the wavelet transform is shown in Fig. 2 b and the overall structure of the algorithm is presented as a flow chart in Fig. 3. The three main modules are input and preprocessing, denoising, and detection. The details are explained in the preceding paragraphs. The code was written in the IDL programming language (IDL research systems, Boulder, CO). The IDL source code of the important steps is given in the Appendix.

FIGURE 3.

Flow-chart diagram of the algorithm. The processing direction starts from the top (input + preprocessing) downwards to the denoising procedure. After convergence of the denoising process, the denoised image is again transformed and ECRE candidates are localized by the detection subroutine. Finally, the morphological analysis (bottom right) of the ECRE is carried out.

Statistical analysis

All data are presented as means ±SE. Data fits were done with the Sigma Plot 2000 regression tool; test sensitivities and positive predictive values were fitted to four parameter logistic functions. Statistical analysis was carried out using the software package Sigma Plot 2000 (SPSS, Chicago, IL). Student's t-tests were applied and P-values <0.05 were defined as significant.

RESULTS

Synthetic data

The algorithm was applied to three different synthetic data sets with SNR 2.0, 2.5, and 3.5, respectively. The parameters tested were δ = 4.00, 3.75, 3.50, 3.25, τ = 3.75, 3.50, 3.25, 3.00 (i.e., all combinations of δ and τ), and additionally τ = 4.00, 4.50, 5.00 at δ = 4.00 for the à trous algorithm and κ = 4.7, 4.3, 3.9, and 3.5 for the conventional algorithm. Images with a SNR varying over a range from 2.0 to 3.5 were synthesized to show the improved detection efficiency of the wavelet algorithm especially in the presence of noisy backgrounds, a major problem in certain experimental settings. The data set with the highest SNR (3.5) is in good agreement with our own experimental results obtained from mammalian skeletal muscle fibers. The statistical parameters used to quantify our results are (S denotes the event “spark occurred”, D⁺ and D⁻ denote the events “detected” and “not detected”, respectively):

1. Detection sensitivity P (D⁺|S), i.e., the probability for an event to be detected or simply the ratio of correctly located events and the total number of embedded events. To characterize curve fits, the D₅₀ value is given, defined as the event amplitude (ΔF/F₀) at 50% detection probability.

2. The positive predictive value (PPV) P (S|D⁺), i.e., the probability of an identified event to be a true one. This can be expressed as

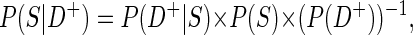(8)

by application of Bayes' law of probability. Although the positive predictive value increases when higher sensitivity values are reached, a higher overall detection probability P (D⁺) decreases P (S|D⁺). This follows from the fact that a higher overall detection probability is usually associated with low threshold parameters and less specific detection. Furthermore P (S|D⁺) increases with spark frequency P (S), a fact that should be considered when evaluating data with low event frequencies. PPV₅₀ values are defined in an analogous way to D₅₀ values.

Moreover, we show the receiver operating characteristic (ROC) of both algorithms defined as follows. The ROC is a plot of the detection sensitivity versus the false positive detection rate with the detection parameter (τ or κ) as the free parameter. We use 1 − P (S|D⁺) as a measure for the false positive detections.

As a reference, we used the algorithm of Cheng et al. (15) as the most commonly employed for spark detection, which will be referred to as the “conventional(1) algorithm”. We also compared with the algorithm by Izu et al. (11), which will be referred to as the “conventional(2) algorithm”. The latter was run with the parameters given in Izu et al. (11), N_generation = 3, N_size = 7, N_live = 12 (as defined in the Introduction).

Synthetic XT-images contained five sparks each, corresponding to 1.36 events/ (100 μm × 1 s)⁻¹, which is within the physiological range of spontaneously occurring spark frequencies in amphibian and mammalian skeletal muscle (29,7).

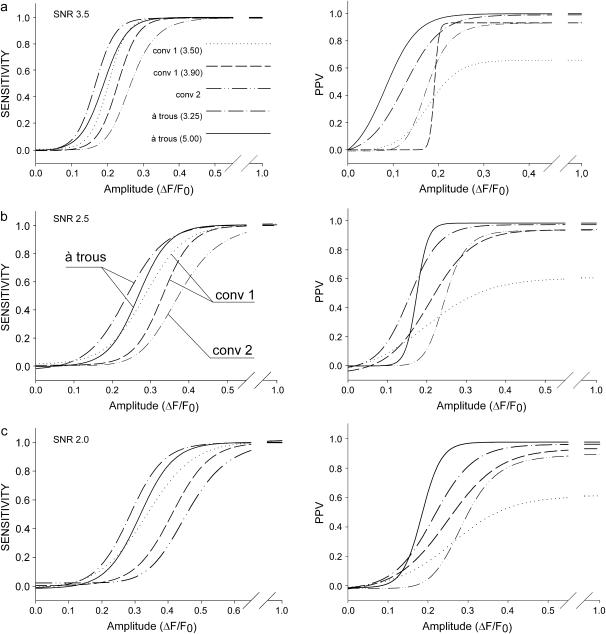
Detection sensitivity and positive predictive values (PPV) prove to be complementary test properties showing an opposite behavior with respect to the test parameters δ and τ. Fig. 4 illustrates the differences between the algorithms evaluated at δ = 4.00, τ = 3.25, and τ = 5.00 (wavelet algorithm), κ = 3.5, 3.9 (conventional(1) algorithm) and for the values given above for the conventional(2) algorithm. The curve fits for sensitivity (left column) and PPV (right column) at all noise levels ((a) SNR 3.5, (b) SNR 2.5, (c) SNR 2.0) are four parameter logistic functions. Solid and dashed-dotted lines represent the results obtained with the wavelet-based algorithm (τ = 5.00 and τ = 3.25, respectively), dashed and dotted lines represent those of the conventional algorithm(1) (κ = 3.9, 3.5, respectively) and dashed-double-dotted lines represent the conventional(2) method. These curves illustrate the general dependency of the algorithms on the threshold parameters. The results obtained with the conventional(1) algorithm at SNR 2.5, D₅₀ = 0.29, 0.33 at detection thresholds κ = 3.5, 3.9, respectively, are in good agreement with the previously published results in Cheng et al. (15): D₅₀ = 0.31, 0.34 at κ = 3.5, 3.8, respectively (compare also their Fig. 6 A and Fig. 2). In Fig. 4 it can be seen that the wavelet algorithm with a high detection threshold (solid line) shows a significantly higher sensitivity than the conventional(1) algorithm at the higher threshold (dashed line) for all SNR. Lowering the detection threshold of the conventional(1) algorithm increases its sensitivity and the curve approaches that of the wavelet algorithm. Again, at its lower threshold, the wavelet algorithm is the more sensitive algorithm again. The conventional(2) algorithm has a lower sensitivity than the other two algorithms at all SNR values tested. The important point here is that using the wavelet-based method a simultaneous improvement in both statistical parameters with respect to the conventional algorithms was achieved.

FIGURE 4.

Sensitivities (left column) and positive predictive values (PPV, right column) at (a) SNR 3.5, (b) 2.5, and (c) 2.0 for the wavelet algorithm (δ = 4.00, τ = 3.25, dashed-dotted lines; δ = 4.00, τ = 5.00, solid lines) and the conventional algorithms (κ = 3.9, dashed lines; κ = 3.5, dotted lines) are shown. The algorithm as in Cheng et al. (15) is labeled conv1 and the algorithm by Izu et al. (11) conv2. Curves shifted to the left denote improved detection properties.

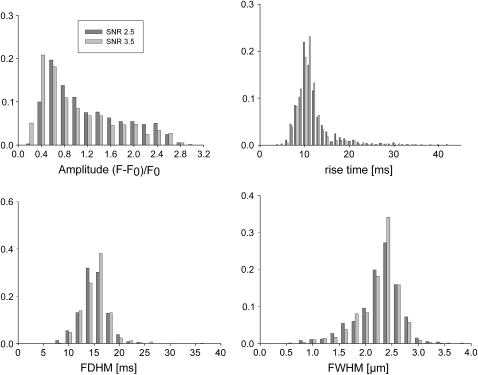
FIGURE 6.

Event parameter histograms resulting from the analysis of synthetic images in the line-scan sampling mode. The analysis of the median filtered raw data yields comparable results for both noise levels SNR 3.5 (light gray) and 2.5 (dark gray). RT (8.2 ms), FDHM (16.4 ms), and FWHM (2.39 μm) can reliably be estimated from the distribution modes. All ordinates show relative frequencies.

Another important observation deals with the positive predictive values. Until now, this value has not been used for the evaluation of the quality of ECRE detection algorithms. It has values between 0 and 1 and decreases with an increasing number of false positive detections.

Therefore, it is an important measure counterbalancing the benefits of high detection sensitivities. Even at the largest SNR tested, the PPV curve resulting from the conventional(1) algorithm at κ = 3.5 has a PPV₅₀ of 0.21 but finally does not exceed 0.66, i.e., even at large event amplitudes (F/F₀ = 2) still 34% of all detected events are false positive. This is the major reason why higher detection thresholds (typically ∼3.9) are necessary when using the conventional(1) algorithm, as detection efficiency is counterbalanced by false positive counts. At SNR 2.0 similar relationships between both techniques emerge. The wavelet algorithm (δ = 4.00, τ = 5.00) yields D₅₀ = 0.32 and PPV₅₀ = 0.19 whereas the conventional(1) algorithm at a common threshold parameter (κ = 3.9) yields D₅₀ = 0.41 and PPV₅₀ = 0.27. The conventional(2) algorithm shows PPV curves comparable to the conventional(1) algorithm at κ = 3.9, especially at higher amplitudes (ΔF/F₀ > 0.4). Therefore, the conventional(2) algorithm has an overall performance that is not superior to the conventional(1) algorithm. Fig. 5 (top panels) summarizes the differences between the wavelet and the conventional(1) algorithms using parameter values as they were applied on our experimental data set, i.e., δ = 4.00, τ = 3.75 (solid lines), and κ = 3.90 (dashed lines). Sensitivities and positive predictive values are shown for intermediate noise levels (SNR 2.5). The rising phase of the curves up to their respective maximum is shown and they clearly demonstrate the improved detection properties achieved with the wavelet method for the chosen parameter combination (D₅₀ = 0.25 and PPV₅₀ = 0.15 for the wavelet algorithm and D₅₀ of 0.33 and PPV₅₀ of 0.22 for the conventional(1) algorithm). D₅₀ and PPV₅₀ values for more parameter combinations are summarized in Table 1. Thus, in terms of detection sensitivity and reliability a major improvement with regard to both properties tested can be achieved using the à trous algorithm.

TABLE 1.

Detection statistics

δ	τ	D50	Dmax	PPV50	PPVmax
SNR 3.5
0	3.50	0.20	1	0.21	0.66
0	3.90	0.23	1	0.19	0.93
3.25	3.25	0.15	1	0.19	0.99
3.25	3.75	0.16	1	0.18	0.99
4.00	3.25	0.17	1	0.13	0.99
4.00	3.50	0.17	1	0.12	0.99
4.00	3.75	0.17	1	0.12	1
4.00	4.00	0.18	1	0.11	1
4.00	4.50	0.18	1	0.08	1
4.00	5.00	0.19	1	0.09	1
SNR 2.5
0	3.50	0.29	1	0.33	0.61
0	3.90	0.33	1	0.22	0.94
3.25	3.25	0.20	1	0.31	1
3.25	3.75	0.21	1	0.27	1
4.00	3.25	0.24	1	0.16	0.97
4.00	3.50	0.25	1	0.16	0.98
4.00	3.75	0.25	1	0.15	0.98
4.00	4.00	0.26	1	0.14	0.98
4.00	4.50	0.26	1	0.18	0.98
4.00	5.00	0.27	1	0.18	0.98
SNR 2.0
0	3.50	0.34	1	0.37	0.61
0	3.90	0.41	1	0.27	0.93
3.25	3.25	0.23	1	0.39	0.97
3.25	3.75	0.24	1	0.32	0.98
4.00	3.25	0.29	1	0.22	0.96
4.00	3.50	0.29	1	0.22	0.97
4.00	3.75	0.30	1	0.22	0.97
4.00	4.00	0.30	1	0.21	0.98
4.00	4.50	0.31	1	0.18	0.97
4.00	5.00	0.32	1	0.19	0.98

Fig. 5 (bottom panel) shows the ROC of the wavelet-based method and of the conventional(1) (conv1) algorithm. The curve is based on the values obtained at SNR 2.5 and at the crucial amplitude ΔF/F₀ = 0.3 where both algorithms show the clearest difference in detection. All τ and κ values given above were included. Furthermore, two reasonable assumptions are made: i), both algorithms do not detect any events when τ or κ tend to infinity, therefore the curve starts at the origin, and ii), when τ or κ tend to zero, both, sensitivity and false positive detection tend to 1 as events cannot be distinguished from background. The data points associated with the wavelet-based method clearly cluster in the upper left quadrant, whereas the conventional(1) method lies close to a straight line through the origin. This means that at a given probability of event detection the wavelet method provides a higher probability of true detection and must therefore be considered more efficient.

Event histograms and amplitude distortion

To test the algorithm on experimental-like data, a spark-like event with a typical morphology (e.g., Kirsch et al. (7)) found in experiments (RT: 8.2 ms, FDHM: 16.4 ms, FWHM: 2.39 μm) was synthesized. It has exponential temporal rise and decay characteristics and a Gaussian spatial profile. To simulate actual recording conditions where line-scan images contain numerous event amplitudes, artificial line-scan images were produced from the synthetic spark image (XY) via “off-center sampling”, i.e., variable scan line to spark center distance. It should be noted that this procedure influences the mean and standard deviation of the line-scan image and thus, the detectability of the other events. To account for this decrease in spatial event amplitude, which, in general, decreases the detectability of an event with increasing distance from the spark center for a given threshold level, the following technique was used: the probability density function (pdf) P for sampling the event in a distance [r, r + dr] from the event center is given by

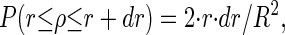(9)

R denoting the event radius and ρ the random variable radius. The pdf for the intensity I is then given by the relation

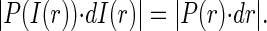(10)

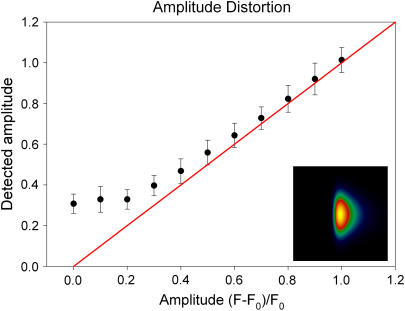
I(r) is the spatial intensity profile of the event and assuming I(r) to be Gaussian (I(r) = exp(−r²/2)), the probability density P(I(r)) is inversely proportional to the intensity I as can be shown by substituting the inverse function of I(r), r(I) in Eq. 10 and solving for P(I(r)). The result of analyzing 1000 events is shown for SNR 3.5 and 2.5 in Fig. 6. The amplitude distribution shows the typical decay expected from the true pdf with a mode introduced at amplitudes near 0.2 due to the poor detection at very small amplitudes. The other parameters are distributed with high accuracy around their actual values, also at the elevated noise level. Fig. 7 illustrates to what extent event amplitudes are distorted by the analysis procedure. The synthetic event is shown in the inset. Real amplitudes, which are below the detection threshold, have to be elevated above the threshold (by noise) to be detected, therefore the curve in Fig. 7 is almost flat for amplitudes ≤0.2. The deviation from the perfect straight line decreases with increasing amplitudes as the relative contribution of noise to the amplitude falls.

FIGURE 7.

Amplitude distortion introduced by the algorithm. Low event amplitudes are less reliably reproduced because of the additive noise. Events below the detection threshold have to be elevated above this threshold to be detected. Therefore, the curve is flat for small amplitudes. The inset shows the synthetic spark used for the analysis.

Experimental data

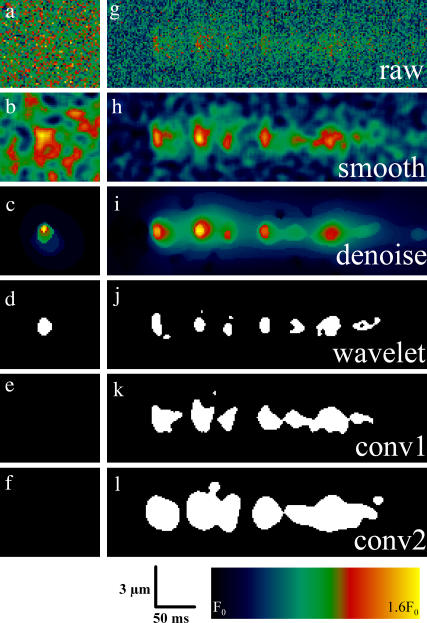
Experimental results were obtained from mouse skeletal muscle fibers chemically skinned with saponin. In these preparations, ECRE can frequently be observed (7). In Fig. 8, a single simulated event (SNR 2.5, left column), an experimentally recorded repetitive ECRE (right column), and the results after processing are shown. Fig. 8, a and g, shows the normalized raw images. Below, panels b and h show the results obtained from a simple “smoothing” operation with a median filter of size 3 × 3 pixels and subsequent boxcar averaging of size 5 × 5 pixels, a typical preprocessing filter applied to raw data (similar procedures can be found in Song et al. (13) and Cheng et al. (15)). The wavelet denoised images can be seen in Fig. 8, c and i, showing a more homogenously suppressed background signal and therefore, a clearer separation between signal and background. The SNR of the normalized raw image was close to 5 and the SNR of the smoothed image nearly 21. The wavelet-based denoising scheme improved the SNR to a value of 68. It should also be noted, that the accentuation of the repetitive release event from the background is clearly seen even though, with a maximum ΔF/F₀ of 0.63, it is far from being a high-amplitude event. To achieve the same SNR with a boxcar or a binomial filter, the sharp rise characteristics of a Ca²⁺ spark would be irretrievably lost.

FIGURE 8.

Direct comparison of denoising and detection properties of the wavelet-based method (c–d), the conventional method 1 (b, e, h, k), and the conventional method 2 (f, l). The analysis was carried out on a simulated event (left column) and raw fluorescence data containing a spontaneous repetitive Ca²⁺ release event (right column). (b, h) The same data after “standard” preprocessing (3 × 3 median and 5 × 5 boxcar filter). (c,i) Wavelet denoised raw data. (d, f, j–l) Output of the detection procedures of the respective algorithms. The single release events appear clearly separated after the wavelet procedure whereas some of them appear clustered after the conventional method. However, they still merge on lower resolution levels as can be seen from the underlying signal elevation in panel i.

The fact that high frequencies are preserved by the wavelet algorithm contributes to the improved detection of ECRE as seen in panels d–f and j–l. The simulated event was only detected by the wavelet-based method whereas the two other algorithms (conv1, κ = 3.8 and conv2) gave negative results. The experimental event was segmented in a different way by the three algorithms. The wavelet algorithm yields seven clearly separated release events. The result of the conventional(1) algorithm (Fig. 8 k) shows the last four events of panel j as a single connected region. The event would thus be classified as a single, long event and the repetitive nature of these events might thus remain undetected. A similar condition is encountered with the conventional(2) algorithm by Izu et al. (11), an even stronger tendency to fuse closely located regions of interest is observed (l). A subsequent separation of these events would require another segmentation process by the analysis procedure. However, the small regions attached to the events in Fig. 8, j and k, are not counted as individual events in the analysis procedure, because their morphological characteristics do not fulfill spark selection criteria. Fig. 8 i shows another important feature of many ECRE. Repetitive events often occur on top of a common region of elevated pixel values. From a multiresolution point of view, one can say that repetitive events merge on a low resolution level. This offers a new, objective possibility for the automated detection and analysis of repetitive ECRE, a release mode frequently found in experimental recordings that may offer new insights in the gating of RyR clusters.

High ECRE densities

Under certain experimental conditions like voltage-clamped amphibian muscle fibers (16), high ECRE frequencies can be observed. We tested our algorithm on a simulated data set containing high event densities. Fig. 9 shows such a normalized test image. The events are typically closely spaced together and have most of their wavelet coefficients in the high frequency range W(1)–W(3). Because W(1) contains also noise associated coefficients, we restricted the detection procedure to wavelet levels W(2) and W(3) of the denoised image. The results obtained with this modified detection procedure and the conventional(1) algorithm are shown in Fig. 9. The detected events are indicated by a black dot in the peak region. The left and right panels show the result obtained with the modified wavelet detection method (δ = 4.00, τ = 3.75) and the conv1 algorithm (κ = 3.5), respectively. It is clearly seen that the adapted wavelet algorithm effectively separates even highly clustered events and is therefore also suited for the detection of ECRE in the case of high event frequencies.

FIGURE 9.

Simulated line-scan image with high ECRE frequency as it occurs in voltage-clamped amphibian fibers. Events are spark-like and the detection is therefore restricted to wavelet levels W(2) and W(3). The result is almost identical to the conventional(1) algorithm.

DISCUSSION

We developed an improved method for the automated detection of ECRE. The novel method is based on the wavelet transform, a technique closely related to classical Fourier analysis. The wavelet transform was used in two ways. First, it was used as an efficient denoising tool and second, the denoised image was again transformed to detect ECRE across the wavelet levels. The method yields high signal/noise ratios, preserving the steep rising phase of spark-like events. This is possible because the high-frequency information is not completely discarded as in other filter methods such as binomial or boxcar filters. The detection procedure leads to considerably improved detection properties when compared with conventional methods. In particular, detection sensitivity as well as detection reliability are both improved simultaneously with respect to the conventional method of ECRE detection. Interestingly, the difference between both methods is even more pronounced at higher noise levels. Therefore, we conclude, that the novel algorithm is especially useful when low SNR fluorescence measurements have to be evaluated quantitatively. The improvement achieved by the wavelet-based method has important implications for the interpretation of line-scan images that we illustrate with the following example. Imagine an experiment including two conditions A and B under which Ca²⁺ sparks are recorded. Under condition A, an average spark frequency (sparks per image) of 5 (1.36 / (100 μm × 1 s)⁻¹) is produced and under condition B, a 20% decrease of event frequency to 4 (1.088 / (100 μm × 1 s)⁻¹) shall occur. These conditions were realized at SNR 2.5 with the line-scan sampling technique described above and analyzed with the conventional algorithm (κ = 3.9) and the wavelet algorithm (δ = 4.00 and τ = 3.75). Very small events (ΔF/F₀ < 0.2) cannot be detected by both algorithms; therefore, both underestimate the true event frequency. In our setting, the conventional algorithm performed even slightly better than in Cheng et al. (15) where a SNR of ∼3 was reported. This may be partly due to the fact that our synthetic spark has a wider peak region than the averaged spark of Cheng et al. (15). For condition A, the conventional method yields a mean frequency (sparks per image) of 〈f〉_c = 3.94 (±0.97) and the wavelet algorithm 〈f〉_w = 3.75 (±0.98). The difference would not be significant (p = 0.17) using Student's t-test. Analysis of condition B yields 〈f〉_c = 3.26 (±0.79) and 〈f〉_w = 3.35 (±0.74), which would also not be significant (p = 0.40). However, the difference between conditions A and B is highly significant using either of the two methods. This result suggests a similar capability of both methods to identify correctly both experimental conditions. However, the rate of false positive detections is a crucial point here. Although the wavelet algorithm stays well below 1% false detections (condition A, 0.008; condition B, 0.003), the conventional algorithm has 7.3% erroneously detected sparks under condition A and 14.4% false positive detections under condition B. This unacceptably high rate of errors not only results in a very biased estimation of spark frequencies, it also introduces a distortion of the event parameters. This suggests a careful interpretation of low amplitude ECRE such as lone embers (30) with amplitudes around ΔF/F₀ ∼ 0.3. This is especially important when absolute fluorescence values are being processed, e.g., when release flux estimates are calculated from fluorescence images. When the results of both methods are corrected for the erroneous detections, both still yield a statistically significant difference between groups A and B. However, in contrast to the conventional method the results of the wavelet algorithm do not change in a significant way after the correction. We therefore conclude that our novel algorithm is a valuable tool for the automated detection of ECRE. Its accuracy is still good at high noise levels and low event frequencies. Experimental conditions that lead to a reduction in spark frequency (31,32) should benefit to a large extent from the improved algorithm as they are especially vulnerable to the above demonstrated effects of false detections. Moreover, the detection of small amplitude events is facilitated because a low amplitude threshold does not need to be included in our detection procedure. In contrast, previously used algorithms applied low amplitude cutoffs as high as ΔF/F₀ = 0.4 (28). Although the iterative scheme of our method leads to an increase in computation time, this is generally not a problem as event analysis has yet to be performed in real time. The qualitative improvements more than outweigh this minor constraint. An interesting implication of our study is the fact that different classes of ECRE might allow a more specific detection due to their frequency content. Right now, we detect all ECRE in permeabilized muscle cells in the same frequency bands (i.e., wavelet levels). The study of high event density data (Fig. 9) with an adapted detection method and observations on the wavelet transform of slow events (as discussed in “The wavelet transform” section and Fig. 2 a) suggest extensions of the method. A wavelet-oriented approach allows the use of detection criteria in the wavelet space. These are inherently different from criteria established in the data space (space/time) and offer the possibility to adapt the detection method to the nature of the data. Finally it should be emphasized that the algorithm based on the à trous wavelet transform may also prove to be most useful for the analysis of other biophysical recordings with similar features, e.g., dynamic fluorescence data from neurons or nonexcitable cells.

APPENDIX: IDL CODE

; NORMALIZE IMAGE (see Cheng et al. (15))

n_image = NormIm(image)

image = n_image

; DENOISING

delta = 4.

den = Denoise(image,delta)

image = den

; DETECTION

tau = 3.75

det = Detect(image,tau)

; ANALYSIS computes location, amplitude,

; FDHM, FWHM, RT:

Analyse, n_image, image, det

function Denoise, ima, k

 ; n-dimensional vector t contains standard deviations of

 ; the wavelet coefficients W1..Wn of a Gaussian (N(0,1))

 ; distributed random variable

 commonvar, t

 y = ima & nx = (size(ima))[1] & ny = (size(ima))[2]

 ; initialize standard deviation (SD)

 sigma0 = 0.0

 sigma1 = stddev(y)

 eps = 0.001 ; convergence criterium

 count = 0 ; init. iteration counter

 z = MRA(y) ; compute the à trous transform of y

 ; z = fltarr(6,nx,ny) W1..W5 -> z(0..4,*,*)

 ; F5 -> z(5,*,*)

 r = fltarr(nx,ny) & n = r

 d1 = r & d2 = r & d3 = r & d4 = r & d5 = r

 supp = bytarr(nx,ny)

 ; produce 2D images, W1..W5 -> d1..d5, F5 -> r

 r(*,*) = z(5,*,*)

 d1(*,*) = z(0,*,*) & d2(*,*) = z(1,*,*) & d3(*,*) = z(2,*,*)

 d4(*,*) = z(3,*,*) & d5(*,*) = z(4,*,*)

while (abs(sigma1-sigma0)/sigma1 gt eps) do begin

 ; compute SD of noise stimate from the

 ; multiresolution support supp

 m = 0.

 sd = 0.

 sum = 0.

 sq_sum = 0.

 ; threshold wavelet levels d1..d5

 T_d1 = (abs(d1) gt 3.*t(0)*sigma1)

 T_d2 = (abs(d2) gt 3.*t(1)*sigma1)

 T_d3 = (abs(d3) gt 3.*t(2)*sigma1)

 T_d4 = (abs(d4) gt 3.*t(3)*sigma1)

 T_d5 = (abs(d5) gt 3.*t(4)*sigma1)

 supp = T_d1 + T_d2 + T_d3 + T_d4 + T_d5

 if (min(supp) eq 0) then begin

 for i=0, nx-1 do begin

 for j=0, ny-1 do begin

 if (supp(i,j) eq 0) then begin

 n(i,j) = y(i,j) − r(i,j)

 sum += n(i,j)

 sq_sum += (n(i,j)^2)

 m ++

 endif

 endfor

 endfor

 sd = sqrt(1./(m-1)*(sq_sum-(1./m)*sum^2))

 sigma0 = sigma1

 sigma1 = sd

 count ++

 endif else begin

 GOTO, stop_it

 endelse

 endwhile

 stop_it:

 ; reconstruct the image with the final SD estimate

 T_d1 = (abs(d1) gt k*t(0)*sigma1)

 T_d2 = (abs(d2) gt k*t(1)*sigma1)

 T_d3 = (abs(d3) gt k*t(2)*sigma1)

 T_d4 = (abs(d4) gt k*t(3)*sigma1)

 T_d5 = (abs(d5) gt k*t(4)*sigma1)

 y = d1*T_d1 + d2*T_d2 + d3*T_d3 + d4*T_d4 + d5*T_d5 + r

 y = median(y,3) ; suppress small areas

return, y

end

function Detect, ima, k

 y = ima

 z = MRA(y) ; see Denoise

 eps=.001

 nx = (size(ima))[1] & ny = (size(ima))[2]

 x = fltarr(5,nx,ny) & f5 = fltarr(nx,ny)

 im = f5 & x_bin = f5 & xr = f5

 f5(*,*) = z(5,*,*)

 for i=1, 4 do begin

 im(*,*) = z(i,*,*)

 ; threshold wavelet levels W2..W5

 im1 = median(y*(im gt k*stddev(im)),3)>eps

 x(i,*,*) = im1

 endfor

 ; logical AND operation over thresholded W2..W5

 x_bin(*,*) = (x(4,*,*) AND x(3,*,*) AND x(2,*,*) AND x(1,*,*)) gt 0

; attach integer labels to regions of interest

xr = label_region(median(x_bin,3))

return, xr

end