Properties of linkage disequilibrium (LD) maps

Abstract

A linkage disequilibrium map is expressed in linkage disequilibrium (LD) units (LDU) discriminating blocks of conserved LD that have additive distances and locations monotonic with physical (kb) and genetic (cM) maps. There is remarkable agreement between LDU steps and sites of meiotic recombination in the one body of data informative for crossing over, and good agreement with another method that defines blocks without assigning an LD location to each marker. The map may be constructed from haplotypes or diplotypes, and efficiency estimated from the empirical variance of LD is substantially greater for the ρ metric based on evolutionary theory than for the absolute correlation r, and for the LD map compared with its physical counterpart. The empirical variance is nearly three times as great for the worst alternative (r and kb map) as for the most efficient approach (ρ and LD map). According to the empirical variances, blocks are best defined by zero distance between included markers. Because block size is algorithm-dependent and highly variable, the number of markers required for positional cloning is minimized by uniform spacing on the LD map, which is estimated to have ≈1 LDU per locus, but with much variation among regions. No alternative representation of linkage disequilibrium (some of which are loosely called maps) has these properties, suggesting that LD maps are optimal for positional cloning of genes determining disease susceptibility.

The human linkage map began half a century ago (1, 2), revealing that two or more genetic entities may be confounded in a single clinical entity (3). Differential diagnosis through linkage became the cornerstone of medical genetics, driving techniques that mapped many genes and led to the Human Genome Project. Linkage disequilibrium (LD), the association between alleles of closely linked genes, has a much shorter history. It began in evolutionary theory (4) but was soon used to localize the effect on disease susceptibility (or other trait) of a sequence not previously annotated (positional cloning). Novel ideas generated a new vocabulary. A haplotype specifies markers on one member of a pair of homologous chromosomes (5). A diplotype is a set of haplotype pairs with the same genotype to which a vector of probabilities may be assigned, summing to 1 for each diplotype (6). In this vector, the probability corresponding to the ith haplotype (perhaps conditional on family or other information) is the chance that a haplotype drawn at random from that individual be i. For example, the diplotype with genotype Aa Bb is the union of AB/ab and Ab/aB, and its probability vector corresponds to the four possible haplotypes. A phased diplotype is a unique pair of haplotypes identified by somatic cell hybridization or inferred by family study, the other elements of the probability vector being 0 (or, loosely, very small). An LD map is constructed from a physical map with additive units (LDU) for use in positional cloning by enhancing the resolution of the linkage map, for identifying sequences predisposing to recombination, and for discriminating other processes and events in population history (7). A haplotype map is at best an LD map with haplotype annotation. Many questions remain unanswered about the optimal construction of LD maps, discrimination of high-LD blocks and low-LD steps, measurement of interpopulational differences, and application to positional cloning. Here we address the first two questions by diplotype analysis.

Materials and Methods

We analyzed two bodies of recently published data on which current ideas of LD blocks are based. Jeffreys et al. (8) selected a 216-kb segment of the class II region of the MHC in 6p21.3. They typed 296 single-nucleotide polymorphisms (SNPs) in a panel of 50 unrelated north-European British semen donors. The three largest LD blocks coincided with regions of low meiotic recombination, separated by peaks of recombination frequency with a standard deviation of only 300 bp. Daly et al. (9) typed 103 SNPs in 617 kb on chromosome 5q31. By latent variable analysis, they delimited 11 LD blocks of tens to hundreds of kb in 129 parent–child trios from a European-derived population. We sampled only parents for diplotypes. These small, densely mapped regions are useful to determine the operating characteristics of LD mapping, with results so simple that application to whole chromosomes now requires only that the sequence be finished and that SNPs be typed at high resolution whether for haplotypes or diplotypes.

We used samples of diplotypes between pairs of markers to fit the Malecot equation and construct LD maps by the interval method (7). These and other options are available in ldmap, which performed the analyses reported here (http://cedar.genetics.soton.ac.uk/public_html/). This approach to LD map construction is an extension of the Malecot model for the decline of association with distance d with expected value ρ = (1 − L)Me^−ɛd + L, where M is 1 for monophyletic origin and <1 otherwise, L describes residual association at large distance, and ɛd equals the product of recombination and time (10). This equation includes both expected decline of LD after a bottleneck and expected increase through drift and mutation. Because L is the asymptote, it is not observed in a small region, and the block structure revealed by a high density of SNPs distorts a direct estimate of L. Instead of direct estimation, L may be predicted as the K_ρ-weighted mean absolute value of a standard normal deviate with information K_ρ = n[Q(1 − R)/R(1 − Q)] for n diplotypes of two loci with allele frequencies Q < R, 1 − Q (7). Corresponding to the test of LD by χ = ρ²K_ρ, the empirical variance based on the composite likelihood is V = ∑K_ρ(ρ̂ −ρ)²/(m − k), where ρ̂ is an empirical estimate of ρ, m is the number of marker pairs, and k is the number of parameters estimated by minimizing the weighted sum of squares. Taking L at its predicted value, we test the hypothesis that M = 1 by χ = Δ/(m − 2)V, where Δ is the excess in the weighted sums of squares under the subhypothesis with only ɛ estimated and V is the empirical variance when M and ɛ are both estimated. The argument has been generalized to any measure ψ of pairwise LD (10). Although composite likelihood violates the independence assumption, it does not favor one choice of ψ over another (11).

LD map construction depends on obtaining an estimate ɛ_i for the ith interval between adjacent pairs of k SNPs (i = 1, . . . , k − 1). Pairwise association data between all SNPs which span the interval being estimated provide some information about ɛ_i, although information is negligible at large distance. The LD map is constructed iteratively with a map location in LDU = ∑ɛ_id_i, where d_i is the ith distance in kb between adjacent SNPs (7). After convergence to ɛ ∼ 1, each ɛ_i is multiplied by this estimate of ɛ, thereby scaling the LD map so that 1 LDU corresponds to the “swept radius” 1/ɛ to which LD useful for positional cloning extends (10). The composite likelihood and M and L estimates are unchanged by this scaling, which assures that the expected value of ρ conforms to (1 − L)Me^−D + L, where D is distance in LDU. Estimates of ɛ_i recover LD blocks and give useful estimates of distance in the LD map, but they do not have the optimality of maximum likelihood.

Results

To establish benchmarks, we tested subhypotheses of the Malecot model on the physical maps used by the authors (8, 9). The values of L are significantly greater than predicted from the information weight, contrary to experience with SNPs at much lower resolution (10). Obviously the three parameters of the Malecot model cannot accurately describe block structure in the physical map. Both sequences are short, the sample sizes are relatively small, and the blocks are too prominent to estimate L directly. The values of M are significantly <1, suggesting that the frequency of the rarest haplotype was not 0 after the last major bottleneck (Table 1).

Table 1.

Tests of M = 1 for physical map

Data	ɛ	M	L	df	∑Kρ(ρ̂ − ρ)2	χ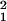
6p21.3	0.1214	(1)	(0.190)	43,657	54,457	3,998
	0.0195	0.510	(0.190)	43,656	49,888
5q31	0.0047	(1)	(0.079)	5,252	27,097	92
	0.0041	0.917	(0.079)	5,251	26,628

Parameters fixed by hypothesis are in parentheses.

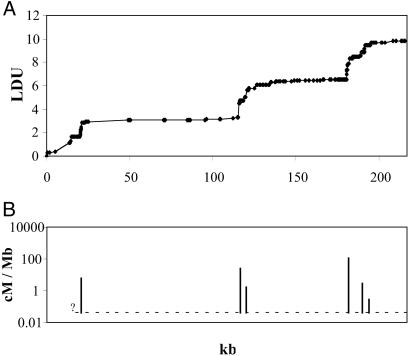
Block structure is evident in both samples, corresponding well but not perfectly with the different algorithms used by the authors (Figs. 1 and 2). The three major steps in 6p21.3 coincide with hot spots of meiotic recombination. The density of SNPs within steps is not high enough to localize LD cold spots with the same precision as the corresponding recombination hot spots, which were estimated to span <2 kb (8). If the LD cold spot turns out to be wider, there are at least three possible explanations (7). First, the LD mapping algorithm may not have the necessary precision. Second, there may be multiple recombination hot spots within a small region. Third, the location of current hot spots may be affected by mutations, insertions, and deletions in recombinogenic sequences and may therefore be more variable in LD than in current recombination.

Fig 1.

Graph of the LD map of 6p21.3 (A) and meiotic recombination (B) reported by Jeffreys et al. (8), oriented from pter to qter. The dotted line is a rough estimate of recombination within the major blocks defined by recombination hot spots as centimorgan (cM)/Mb = 0.04. Such low levels make definition of the small steps arbitrary and, therefore, of doubtful utility for positional cloning.

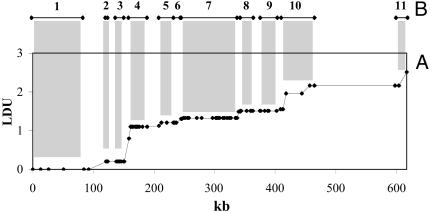
Fig 2.

Graph of the LD map of 5q31 (A) and comparison with the 11 blocks (B) inferred from latent variables by Daly et al. (9). This is a more typical region, not selected by recombination hot spots. It illustrates the high frequency of small steps (e.g., between blocks 2 and 3, 5 and 6, and 8 and 9) and, therefore, the subjectivity of block definition. It remains to be established whether splitting or lumping is more favorable to positional cloning, or irrelevant.

The ρ metric is unique in being a probability based on evolutionary theory and applicable to random or selected samples (12). As expected, ρ fits association data considerably better than alternative metrics, whether each is weighted by its information on the null hypothesis that ρ = 0 or the alternative hypothesis H₁ of the Malecot model (10). However, previous trials were at low resolution and might not apply to the samples analyzed here. We therefore compare ρ with r, the absolute value of the correlation with information n on the null hypothesis (10). The necessary and sufficient condition for ρ = 1 is that one of the haplotype frequencies be 0, consistent with absence in founders. On the contrary, r = 1 only if the two off-diagonal frequencies are 0, a coincidence unlikely to characterize founders. As expected, estimates of M are much less for r than for ρ, the parameters are inconsistent (Table 2), and the residual (error) variance is much greater whether distance is measured in kb or LDU (Table 3). Use of metrics other than ρ introduces extraneous variation in measurement of LD, requiring a larger sample to achieve the same power in positional cloning. Only part of the variance is due to sampling and inversely proportional to sample size, whereas ρ and LDU reduce the evolutionary variance that is independent of sample size. Therefore the cost of an inefficient metric is systematically underestimated in Table 3: Even larger sample sizes would be required and might not be sufficient to compete with the optimal metric. Evolutionary variance and error in the model usually inflate V, requiring its incorporation in tests of significance. The 6p21.3 region is exceptional in reducing V below 1, reflecting correlation of the ɛ_i at high density. This will be increasingly observed in LD maps at high resolution.

Table 2.

Comparison of ρ and r for distance in kb and LDU

Data	Metric	Map length	ɛ	M	L	df	∑Kψ(ψ̂ − ψ)2
6p21.3	ρ	215.65 kb	0.0195	0.510	0.190	43,656	49,888
	r	215.65 kb	0.0257	0.175	0.114	43,656	58,260
	ρ	9.84 LDU	1	0.865	0.190	43,361	37,757
	r	12.69 LDU	1	0.322	0.114	43,361	50,312
5q31	ρ	616.67 kb	0.0041	0.917	0.079	5,251	26,628
	r	616.67 kb	0.0038	0.488	0.055	5,251	56,240
	ρ	2.51 LDU	1	0.916	0.079	5,149	16,612
	r	2.62 LDU	1	0.515	0.055	5,149	47,481

L = predicted value.

Table 3.

Empirical variance, sample size, and efficiency for ρ and r

Data	Metric	Empirical variance		Sample size		Efficiency
		kb	LDU	kb	LDU	kb	LDU
6p21.3	ρ	1.143	0.871	1.31N	N	0.76	1.00
	r	1.334	1.160	1.53N	1.33N	0.65	0.75
5q31	ρ	5.071	3.226	1.57N	N	0.64	1.00
	r	10.710	9.221	3.32N	2.86N	0.30	0.35
Total	ρ	6.214	4.097	1.52N	N	0.66	1.00
	r	12.045	10.382	2.94N	2.53N	0.34	0.39

^*Lower bound cN to the number required for same power as ρ metric with LD map (c = 1), where N is the sample size for LDU with ρ metric.

As a final test of the LD maps, we varied the minimal value of ɛ_i from 0 to 0.001. The variance increases at high values. Setting the minimum to 0 gives the best results (Table 4). The estimate of L agrees with its predicted value for 5q31, but not for 6p21.3. The latter greatly enriches the number of SNPs around intense recombination hot spots, and so neighboring blocks are confounded with L. There is agreement between recombination hot spots (8) and the LD cold spots indicated in Fig. 1. Agreement with the less well defined blocks in 5q31 is more approximate (Fig. 2), but cannot be evaluated in the absence of recombination evidence and a justification of the latent variable used to define steps (9). Every author so far has used a different criterion to define blocks. The optimal definition depends on unknown utility to complement information in LD maps, which reveal block structure but do not specify block definition.

Table 4.

Goodness of fit of minimal ɛ_i for LD map

Data	Minimal ɛi	LDU	M	∑Kρ(ρ̂ − ρ)2
6p21.3	0	9.84	0.865	37,757
	0.0001	9.86	0.868	37,763
	0.001	9.63	0.861	37,828
5q31	0	2.51	0.916	16,612
	0.0001	2.52	0.918	16,646
	0.001	2.55	0.926	17,096

The standard error of LD map length if the observations were not autocorrelated and the Malecot model for the physical map were exact would be SE(ɛ)Σd_i, where the standard error SE (ɛ) incorporates the empirical variance. This is an underestimate when the assumptions are incorrect, and so we shall not rely on it. The lengths of the 6p21.3 and 5q31 regions are 9.84 and 2.51 LDU, respectively. Altogether, 12.35 LDU and 832.32 kb are spanned. If the genomic length is 3 × 10⁶ kb, the corresponding length in LDU is 44,514. On such fragmentary evidence there is ≈1 LDU per locus, but with much variation among regions. The 6p21.3 region was chosen with the knowledge that it contains the TAP2 recombination hot spot (13), but the estimated genetic length of 0.22 cM agrees closely with the predicted value for a segment of 216 kb with 0.89 cM/Mb on the male map (8). The estimated time back to founders if θ = 0.0022 is t = 9.84 LDU/0.0022 = 4,473 generations or roughly 100,000 years, in good agreement with a bottleneck caused by migration out of Africa at about that time.

Discussion

The data of Jeffreys et al. (8) are unique in providing independent evidence of recombination hot spots that coincide with steps between blocks. This may well be true generally and depend on specific sequences enhancing recombination. However, chance and selective sweeps may also create blocks separated by steps. Expansion of a young haplotype gives little opportunity for diversification by mutation or recombination compared with older haplotypes that would be replaced in a complete sweep, destroying evidence that a block was created by recent selection or drift rather than low recombination (14). In the absence of a rationale for precise definition, at least five schools compete for attention. Splitters declare a block when ɛ exceeds a small threshold, whereas lumpers set the threshold higher. Steppers prefer large blocks punctuated by steps that may span several markers. Blockers look within steps for small blocks even if only between adjacent markers. Monophysites prefer equal numbers of markers per LDU regardless of block definition. These contending schools cannot be expected to choose the same markers to scan the genome or a candidate region.

Elsewhere, the efficiency of ρ to fit the Malecot model has been demonstrated by comparison with six other metrics in eight bodies of data (10). This does not exhaust the unlimited number of metrics that can be used, among which ρ is unique in being a probability that is a simple function of the haplotype frequencies for two diallelic loci, founded on an evolutionary theory that allows LD to increase or decrease by recombination and mutation (10). In random samples, ρ is numerically equal to 0 ≤ D′ ≤ 1, defined (but not as a probability) by Devlin and Risch (15). In case-control samples D′ diverges from ρ and is inefficient (15), whereas ρ is efficient for all values of the enrichment factor ω defined as c/f, where c is the ratio of cases to controls and f is the ratio of affected to normal in the general population (12). Allowing for ω, ρ approaches the δ metric as ω increases (11). The general formula is ρ = |D|/min[QR, Q(1 − R), (1 − Q)R, (1 − Q)(1 − R)], where allele frequencies Q and R and covariance D in random samples are estimated from the enrichment factor ω, which equals 1 in random samples and exceeds 1 in case-control samples. Then D′ in the sense of Devlin and Risch is the value ρ would take for ω = 1, which is not appropriate for case-control samples. Originally, D′ was defined as a two-valued function (16–18), and its continued use is ambiguous. Multiallelic measures of LD have also been proposed, without theoretical support (19).

Because alternatives to ρ have no theoretical appeal and have been shown to fit the Malecot model less well for the kb map, we have examined only one alternative to ρ for constructing an LD map. The evidence presented in Table 3 demonstrates the advantage of ρ over the absolute value of the correlation r to construct an LD map and of LDU to represent variation of LD with physical location. A recent paper (20) compared D′ in the Devlin and Risch sense (equal to ρ in a random sample) with r (denoted by Δ) and concluded that the latter is less affected by sample size and high allele frequencies. This inference was based on the sampling variance, neglecting evolutionary variance. The sampling variance of r under H₀ is the reciprocal of sample size, and r under H₁ is relatively free of confounding with allele frequencies. On the contrary, its larger evolutionary variance is notoriously sensitive to allele frequencies (15, 18, 19). Use of r stems from a theory that assumed no LD in founders (21), whereas application to real populations allows LD to increase by drift or decrease by recombination after a bottleneck in founders (10). The relevant theory was derived in terms of the probability ρ, and so far has not been extended to r. Both measures are biased by the asymptote with predicted value L_p, which is smaller for r than for ρ. This bias is removed in the Malecot model for multiple pairs, and the low efficiency of r is then apparent. Consideration of each LD pair in isolation from flanking markers does not give a sound basis either for LD mapping or positional cloning, and should be avoided in any extension to haplotypes.

The superiority of ρ does not generalize to positional cloning of an oligogene, where the gene frequency Q of a causal SNP is unknown and the constraint of Q less than or equal to the frequency R of a predictive SNP cannot be enforced or ρ estimated directly. Whatever statistic is used for positional cloning, equal spacing of predictive SNPs on the LD map should be more efficient than either equal representation of arbitrarily defined blocks of unequal size or equal spacing on the physical map to which markers are primarily annotated, and so optimal construction of both maps is essential. In the absence of additive LD units, diagrams to indicate blocks and intervening steps are not maps in the postmedieval sense and do not provide either efficient choice of markers or a scale on which genes for disease susceptibility may be localized (22, 23).

We have not touched on the many problems of positional cloning by multiple haplotypes (18, 24, 25). The arbitrary choice of an arbitrary number and types of markers has discouraged use of haplotypes, for which no optimal statistic has been identified. A popular paradigm suggests a candidate region by linkage or functional assay, narrows the region by LD, and confirms this evidence by some unspecified analysis of haplotypes. Whatever form this extension takes, it will benefit from a reliable map in LD units.

Abbreviations

• LD, linkage disequilibrium

• LDU, LD unit

• SNP, single-nucleotide polymorphism

• cM, centimorgan