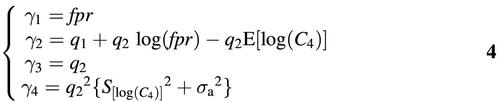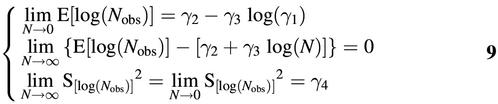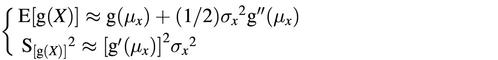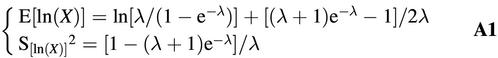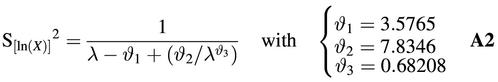Stochastic processes defining sensitivity and variability of internally calibrated quantitative NASBA-based viral load assays

Abstract

For quantitative assessment of virus particles in patient plasma samples various assays are commercially available. Typical performance characteristics for such assays are sensitivity, precision and the range of linearity. In order to assess these properties it is common practice to divide the range of inputs into subranges in order to apply different statistical models to evaluate these properties separately. We developed a general statistical model for internally calibrated amplification based viral load assays that combines these statistical properties in one powerful analysis. Based on the model an unambiguous definition of the lower limit of the linear range can be given. The proposed method of analysis was illustrated by a successful application to data generated by the NucliSens EasyQ HIV-1 assay.

INTRODUCTION

Viral load assays based on amplification technology are used all over the world for screening and monitoring purposes. Proficiency studies and quality assurance programs are tools to monitor the quality of the assay systems themselves as well as of the laboratory staff that use them in practice. Important items include assay variability, detectability and the lower limit of the linear range. Typically, in assay design and development as well as in proficiency testing, data obtained by testing a series of concentrations are analyzed using a variety of statistical techniques to assess these properties (see for example 1). These techniques include different sorts of analysis of variance models to assess quantitative properties and probit or logistic regression to assess sensitivity. In order to apply these models, the dynamic range tested has to be divided (more or less arbitrarily) into subgroups to ensure that the heterogeneity of variances within these subgroups is not too great, whereas it is known that the assay variability, defined as the standard deviation of the logarithm of the quantitation result, depends on the viral load tested. It would be beneficial to develop a single mathematical/statistical model that covers all properties. The current paper aims to develop such a model. Although many details of the current studies are applicable to both NASBA-based and PCR-based viral load assays, the focus is on the former.

One of the commercially available internally calibrated NASBA-based viral load monitoring systems is the NucliSens product line. The list of applications is long and includes both RNA and DNA targets (see for example 2). Important targets in the quantitative field are HIV-1 RNA (3–6) and HBV DNA (7). The NASBA amplification technology was successfully combined with homogeneous detection using molecular beacons (2,6,8–10). These oligonucleotides are designed such that they can generate a fluorescence signal only when they are bound to a nucleic acid strand with a complementary sequence, in this case an amplicon. As the concentrations of amplicons increase continuously during the NASBA process, the time-dependency of the fluorescence signals provides information on the underlying kinetics of the NASBA-driven RNA formation (6,8–10).

The NucliSens product line is, amongst others, characterized by the feature of internal calibration. A fixed amount of artificial RNA or DNA, referred to as the calibrator, is added to the sample prior to the assay. This calibrator is co-extracted and co-amplified together with the endogenous viral nucleic acid. The calibrator differs from the endogenous nucleic acid by a short sequence. The use of specific molecular beacons with specific fluorophores allows simultaneous specific detection of both amplification processes. Quantitation is based on the assessment of the relative RNA growth rates during the transcriptional phase of the amplification (10).

In a previous paper we presented the results of modeling studies on the relation between the input concentrations and transcription rates (10) and we presented a mathematical model describing the fluorescence curves as a function of time and several relevant parameters. In the current paper we wish to go a step further and to include stochastic elements that play an important role in molecular diagnostics. As such, a general mathematical model is obtained that describes several performance characteristics in a single model. The procedures will be illustrated using data generated with the NucliSens EasyQ HIV-1 assay. This assay is also used as leading example in the theoretical sections.

THEORY

Overview of the assay and some definitions

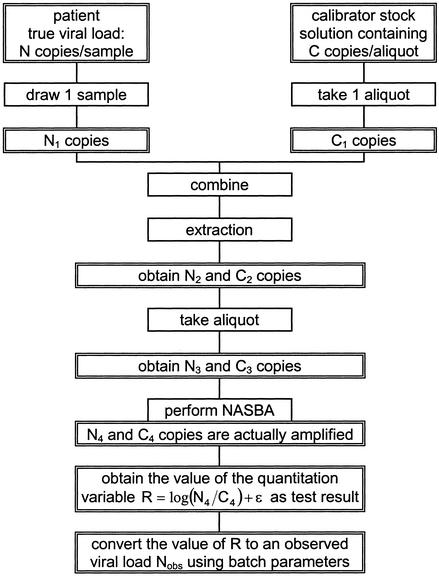
Consider a patient with a given load of endogenous viral RNA [referred to as wild-type (WT) RNA]. From this patient a blood plasma sample is taken. Let the expectation of the number of WT copies in this particular volume of plasma be N. For a random sample drawn from the patient, it should be realized that the actual number of copies present is a random variable. Let the plasma sample contain N₁ copies. Then calibrator RNA is added to this patient sample. In the NucliSens assays, this calibrator is added in dry form as a so-called accusphere. These accuspheres are produced by freeze-drying small aliquots from a large pool of a solution of the calibrator RNA. The concentration of calibrator RNA in this pool is such that, on average, a single accusphere contains C copies. Similar as for the patient sample, the actual number of copies in a single accusphere is a random variable. Let an individual accusphere contain C₁ copies. Both WT and calibrator RNA are simultaneously subjected to the extraction. The numbers of copies present in the extract are N₂ and C₂. From this extract a fraction is used for the amplification, containing N₃ and C₃ copies, respectively. These copies enter the amplification, but not all copies are amplified to yield a detectable number of amplicons. Let the number of copies that actually contribute to the total signal be N₄ and C₄. The response to be obtained in the NASBA-based assay is determined by the ratio of the amplified copy numbers (N₄ / C₄), and is expressed on a logarithmic scale (base 10). More precisely, the response variable obtained reflects the logarithm of the transcription rate ratio, which is proportional to the input ratio N₄ / C₄ (10). The observed value is converted to a viral load (to be referred to as N_obs) by using the so-called batch parameters. Obviously, random error due to the NASBA assay is added to the total variation of the response variable. Figure 1 gives a schematic representation of all individual steps.

Figure 1.

Schematic overview over the model.

Model building

For the construction of a mathematical model, the following considerations and assumptions are relevant. (i) The values of N and C are known and fixed. (ii) The variables N₁, N₂, N₃, N₄, C₁, C₂, C₃, C₄, ε, R and N_obs are random variables. (iii) The variables N₁ and C₁ follow Poisson distributions. (iv) Given the realizations of N₁ and C₁, the values N₂ and C₂ follow binomial distributions, with a p-value determined by the extraction efficiency (to be referred to as r). (v) Given the realizations of N₂ and C₂, the values N₃ and C₃ follow binomial distributions, with a p-value equal to the fraction taken (to be referred to as f). (vi) Given the realizations of N₃ and C₃, the values N₄ and C₄ follow binomial distributions, with a p-value equal to the probability that an individual molecule is amplified to yield a detectable number of amplicons (to be referred to as p). (vii) The value of log(N₄ / C₄) is to be assessed by the NASBA-based assay. (viii) The NASBA assay itself (amplification and detection) induces a random variation ε that is normally distributed with expectation 0 and variance σ_a². (ix) The quantity log(N₄ / C₄) + ε is the final response variable, to be referred to as R. (x) The conversion of R to log(N_obs) is done by a linear transformation using a fixed set of numbers referred to as the batch parameters. A test result is classified as positive if two conditions are fulfilled simultaneously: (i) a WT signal is detected and (ii) the observed value of N_obs exceeds the threshold N_lim. In the other cases the estimated viral load is below the limit of detection (‘negative’).

Probability distributions of the relevant random variables

The variables N₁ and C₁ are considered to follow Poisson distributions as it seems reasonable to assume that the three basic probabilistic conditions for Poisson variables are fulfilled. First, the expectation of the number of molecules in the sample is proportional to the sample volume. Second, two subsequent samplings from the same pool are stochastically independent and identically distributed. Third, if the volume of the sample is small enough, the probability that two molecules are present in the same sample approaches 0. Therefore, N₁ ∼ Poi(N) and C₁ ∼ Poi(C), with the symbol ∼ to indicate a probability distribution.

As summarized above, given the realization of the random variable N₁, the variable N₂ follows a binomial probability distribution with parameter r. General stochastic theory then shows that N₂ ∼ Poi(rN). Similarly, it follows for the other steps in the scheme:

The response variable

The response variable R is defined as

R = log(N₄ / C₄) + ε with ε ∼ N(0,σ_a²)2

with log the logarithm with base 10 and N reflecting a normal distribution. Note that R is defined only if the realizations of N₄ and C₄ both exceed 0. This notion has some important implications, as will be shown below. The total variability in this variable is defined by the variability in N₄, C₄ and ε. The observed value of R is converted to a logarithmic viral load [log(N_obs)] by a linear transformation (10). To this end, batch parameters are used. For reasons of convenience, this transformation is written as

log(N_obs) = q₁ + q₂R3

with q₁ and q₂ reflecting the batch parameters (the exact formal definition of the batch parameters is slightly different, but here only the linear relation is of importance). As described previously (10), it is not possible to directly assess the ratio N₄ / C₄; the quantitation variable merely reflects the logarithm of some multiple of the N₄ / C₄ ratio, but batch parameters can be used to convert this to an observed viral load.

The batch parameters are assessed once and are then kept fixed. Therefore, in discussions on random errors they are not important.

Probabilistic aspects of the response variable

The variable R is the response variable used for quantitation. If the realization of N₄ = 0, then a test result without detectable WT signal is obtained, which is classified as ‘negative’. In this case R is not computed at all. If there is a detectable WT response, it means that the realization of N₄ > 0 and in that case the value of R can be computed. If the estimated viral load is below the lower limit of detection, the result is classified as ‘negative’, otherwise it is classified as ‘positive’ and a quantitation result is presented. In order to assess the variance of R, use has to be made of the probability distribution of the logarithm of N₄ under the restriction that the realization of N₄ > 0. Some details of the properties of the logarithm of such a truncated Poisson variable can be found in the Appendix (equations A1 and A2).

A realization of 0 for the variable C₄ implies the absence of a calibrator signal. Therefore, similar considerations are required for the probability distribution of C₄ as described for N₄. However, as the value of Poisson parameter fprC (see equation 1) is considered to be fixed for a given batch, there is no need to use explicit equations for the expectation and variance of log(C₄), as will become clear from the derivations presented below.

From equations 2 and 3 it follows that the random variable log(N_obs) can be written as the sum of three independent random variables: log(N₄), log(C₄) and ε. Therefore,

E[log(N_obs)] = q₁ + q₂{E[log(N₄)] – E[log(C₄)] + E[ε]}

S_[log(Nobs)]² = q₂²S_[R]² = q₂²{S_[log(N4)]² + S_[log(C4)]² + S_[ε]²}

with E[.] the expectation and S_[.]² the variance of the random variable indicated. In order to write these in manageable forms, define

and it follows using the Appendix equations

E[log(N_obs)] = γ₂ + γ₃{log(N) + {[(γ₁N + 1)e^–γ₁N – 1] / [2γ₁Nln(10)]} – log(1 – e^–γ₁N)}5

S_[log(Nobs)]² = (γ₃ / ln10)² / [γ₁N – ϑ₁ + ϑ₂ / (γ₁N)^ϑ₃] + γ₄6

As noted above, it is possible to express E[log(C₄)] and S_[log(C4)]² in terms of fpr and C using the Appendix equations, but given a value for fprC these two are constants and are incorporated in γ₂ and γ₄. Nevertheless, it is important to note that C is so high that Pr(C₄ = 0) can be ignored. In other words, e^–fprC can be set to 0 (see equation 1) and E[log(C₄)] can be approximated by log(fprC). Therefore, it follows

γ₂ = q₁ – q₂log(C)7

independent of the product fpr.

Numerical analysis of equation 5 shows that, in approximation,

E[log(N_obs)] = γ₂ + γ₃log(N) if γ₁N = 1.97978

This result is important in defining the lower limit of the linear range of the assay, and will be rounded to γ₁N = 2.

It is interesting to note the following limits that can be derived:

Equation 5 shows that the relationship between the input and the output, that is between log(N) and E[log(N_obs)], is non-linear in nature. For high values of N, equation 9 shows that E[log(N_obs)] can be approximated by γ₂ + γ₃log(N). The difference between these two is given primarily by the entity log(1 – e^–γ₁N) – [(γ₁N + 1)e^–γ₁N – 1] / [2γ₁Nln(10)], which reaches its maximum of 0.041 for γ₁N approximately 4. For very low inputs, with N approaching 0, equation 9 shows that the expectation of log(N_obs) is well-defined and it approaches a value in which γ₁ plays an important role.

A test result is classified as ‘positive’ if two conditions are fulfilled: a WT signal is detected (N₄ > 0) and the quantitation result exceeds a pre-set lower limit (N_obs > N_lim). More precisely, the probability that a result is positive is the product of the probability Pr(N₄ > 0) and the conditional probability Pr(N_obs > N_lim | N₄ > 0). Using the Normal approximation it follows:

Pr(pos) = (1 – e^–γ₁N)[1 – Φ({log(N_lim) – E[log(N_obs)]} / √{S_[log(Nobs)]²})]10

with E[log(N_obs)] and S_[log(Nobs)]² according to equations 5 and 6 and Φ(.) reflecting the cumulative standard normal probability distribution function.

Data analysis using the current models: maximum likelihood

Consider an experiment in which samples with viral loads over a considerable range are subjected to the NucliSens EasyQ HIV-1 assay. These samples yield either a quantitation result, or are classified as below the limit of detection (‘negative’). The values of the parameters given in equation 4 can be assessed by using maximum likelihood techniques. The contribution to the total log likelihood of a test result classifying as below the limit of detection at a given level of N is given by the probability that a test result is obtained that is not classified as positive, and is computed using a cumulative probability distribution function as (see equation 10):

L_neg = ln{1 – (1 – e^–γ₁N)[1 – Φ({log(N_lim) – E[log(N_obs)]} / √{S_[log(Nobs)]²})]}11

For a positive, quantifiable result, the contribution to the total log likelihood is based on the probability density function under the restriction that N₄ > 0 in combination with the probability Pr(N₄ > 0). Let x_i(N) be the realization of log(N_obs) for observation i at a given value of N, and the contribution of this particular data point to the total log likelihood can be expressed as

L_pos = ln{(1 – e^–γ₁N)(1 / √{S_[log(Nobs)]²})φ({x_i(N) – E[log(N_obs)]} / √{S_[log(Nobs)]²})}12

In equations 11 and 12 the entities E[log(N_obs)] and S_[log(Nobs)]² are computed according to equations 5 and 6, and φ(x) = [1 / √(2π)]exp[–(1 / 2)x²]. For each individual observed test result the contribution to the log likelihood is computed by equation 11 or 12, and all contributions are summated. Numerical techniques can then be used to assess the values of the parameters γ₁ through γ₄ such that the total log likelihood is maximized.

MATERIALS AND METHODS

Dilution series of the so-called VQA stock of HIV-1 RNA (Virology Quality Assurance) (1) were subjected to the NucliSens EasyQ HIV-1 assay, the details of which are described elsewhere (6,8). All results were obtained using a single batch. For the current study magnetic extraction was used as front-end (7), in which the extract can be concentrated into a smaller volume than in the current NucliSens Extractor (11).

RESULTS

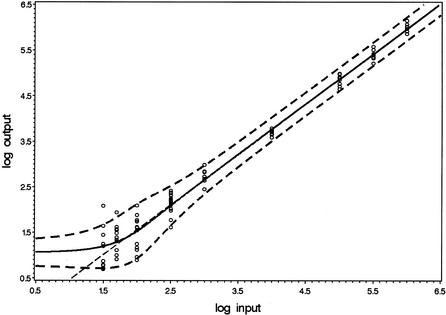
Dilution series of WT HIV-1 RNA with nominal concentrations ranging from 10 to 10⁶ copies per input were subjected to the NucliSens EasyQ HIV-1 assay. Figure 2 presents the observed quantitative results. Test results classifying as ‘below limit of detection’ are not presented. Using maximum likelihood techniques, the parameters of the model were assessed. For the current data, the optimal parameter values were γ₁ = 0.0295, γ₂ = –0.629, γ₃ = 1.10 and γ₄ = 0.0163. The figure includes the predicted values of E[log(N_obs)] according to equation 5 as well as the intervals E[log(N_obs)] ± 2√{S_[log(Nobs)]²} (equations 5 and 6). Finally, the straight line with intercept γ₂ and slope γ₃ is included. According to equation 9, the expectation E[log(N_obs)] approaches this line for high values of N. The figure shows that this approximation is reasonable for all inputs exceeding the point where the curve of E[log(N_obs)] crosses this straight line. According to equation 8, this intersection is approximately at γ₁N = 2, hence at N = 67. Figure 2 shows that this intersection point can be used as a definition for the lower end of the linear range. For the current data, lim_N→0 E[log(N_obs)] = 1.05 logs.

Figure 2.

Model concerning quantitative results. The circles present the individual observations. The solid line presents the modeled values of E[log(N_obs)]. The dashed lines are at a distance of two times the predicted SD. The intercept and slope of the straight dashed line are given by γ₂ and γ₃.

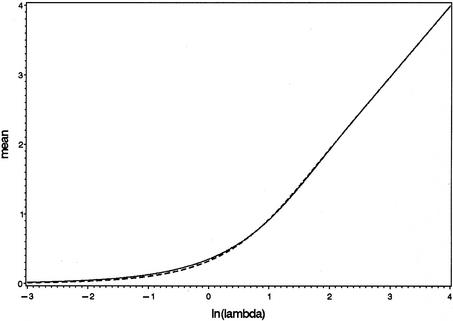
The bend in the curve corresponding to E[log(N_obs)] in Figure 2 is due to stochastic properties of the logarithm of a Poisson distributed variable (compare Figure 2 with Figure 4 in the Appendix). Recall that the predicted values for the expectation and variance of log(N_obs) are valid only for results of which a detectable WT signal is detected in the first place, and this probability rapidly decreases with decreasing values of the input. At very low inputs, with fprN values clearly <1, it follows that the actual values that N₄ can reasonably attain are only 0 and 1; the probability Pr(N₄ > 1) is very low if fprN << 1 (see equation 1). Therefore, at these inputs, the mere detection of a WT signal implies that the actual realization of N₄ can hardly be anything else but 1. At this level of fprN values, information on the actual value of N is lost.

Figure 4.

Approximation of the mean of the logarithm of a truncated Poisson variable with equation A1 (dashed line). The solid line reflects the simulation results.

The model also allows predictions on the variability as a function of the input (equation 6). The assay variability is predicted to stabilize for high WT inputs at a value of √γ₄ = 0.128 logs. The maximal predicted variability is obtained at an input of 92 copies, and equals √0.0899 = 0.30 logs. At an input of 400 copies, the predicted standard deviation is 0.20 logs. Equation 9 (last part) shows that the predicted standard deviations for very low and very high inputs are asymptotically the same, which is also reflected in Figure 2. At very high inputs, the variability in log(N₄) is so small compared with the variability in log(C₄) + ε that it can be ignored. At very low inputs, the probability Pr(N₄ > 1) can be ignored, and the probability distribution of N₄ under the restriction that it is positive (otherwise R is not defined) is a degenerated probability distribution with zero variance, leading to the same result.

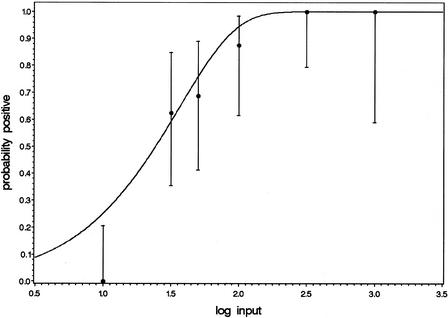
Finally, given the parameter values, the predicted probability of obtaining a positive test result can be computed as a function of the input using equation 10. The observed and predicted hit rates are presented in Figure 3. The concentration yielding a hit rate of 95% is estimated to be 103 copies/input, whereas a 50% hit rate is obtained at an input of 24 copies. Figure 3 also includes the two-sided 95% confidence intervals that can be computed for the individual observed hit rates using the binomial probability distribution. The observed hit rate at 10 copies/input is rather low compared with the predicted hit rates, but for the remaining part the model adequately describes the data.

Figure 3.

Model concerning hit rates. The dots represent the observed fractions of positive test results, with the two-sided 95% confidence intervals based on the binomial probability distribution. The number of observations varied with the inputs tested.

DISCUSSION

In the current paper the stochastic processes involved in molecular diagnostics are studied from a mathematical point of view. The study shows that a single statistical model can be used to study linearity, variability and detectability. The lower limit of the linear range can be assessed using clear and unambiguous definitions, and is not hampered by issues like heterogeneity of variances over the linear range or low hit rates. Input concentrations corresponding to pre-set hit rates can be estimated, which is important with respect to the sensitivity of the assay. In addition, it is possible to estimate the assay variability as a function of the input, which is amongst others important in assessing the limit of quantitation.

As is the case for every model, the equations presented here are approximations of reality. For example, it is assumed that the variance component due to the assay itself (σ_a²) does not depend on the input. At very high inputs this is not entirely true, as the calibrator signal is hardly detectable and therefore the contribution of the calibrator to the variability may be higher than in other ranges. A similar notion might be valid for the low inputs, where the WT signal is on the edge of being detectable. Another approximation is the use of the Normal probability distribution to assess hit rates (equation 10) and in the maximum likelihood techniques (equations 11 and 12). Finally, the current equations assume that fpr (γ₁) can be considered to be a constant, whereas it is more realistic to assume that there is a random component to this as well. This parameter makes its appearance in lots of positions in the equations, thereby making detailed mathematical analyses assuming a stochastic nature for fpr very complex. Further studies are required to expand the models to include this source of variation.

The data analyzed in the current paper were obtained using a single batch over several experimental runs. As such, the standard deviation contains both the inter- and intrarun variability. Studies have shown that the interrun variability is so small that it can safely be ignored (T. A. M. Oosterlaken and P. A. van de Wiel, unpublished results). If this were not the case, then the models should be expanded to include indicators for the experimental runs involved.

The NucliSens assay is an internally calibrated assay. Changes in extraction efficiency should not affect the quantitation. That this is actually achieved is reflected by equation 7 which shows that the location of the straight line describing the linear range of the assay is not affected by the actual value of the product fpr.

The predicted hit rate at the lowest input is clearly higher than the observed hit rate. This is probably due to the following considerations, which are very difficult to include in mathematical models. An assay should be sensitive, implying that a high hit rate at low concentrations is a beneficial property. On the other hand, the incidence of false-positive results should be low. The positive predictive value, which is the probability that the sample tested does actually contain the analyte given that the assay result is positive, should be very high. Therefore the threshold to be used to decide whether or not a WT signal is actually present is chosen higher than theoretically minimally required. As such, WT signals just above the background will be dismissed as just noise.

A test result is classified as being below the limit of detection (‘negative’) if no WT signal is detected or if the estimated viral load, in the presence of a detectable WT signal, is below a threshold. The equations on the variance and expectation of log(N_obs) describe the complete distribution of the test results under the restriction that a WT signal is observed (that is, N₄ > 0). This means that, at low viral loads, only a part of the distribution will be visible, whereas the results below the limit of detection with a detectable signal can be treated as left-censored observations. The models show that high quantitation results cannot be obtained at very low inputs, as both E[log(N_obs)] and S_[log(Nobs)]² stabilize with N approaching 0.

The product fpr (γ₁) plays an important role in the equations. It makes its appearance at a crucial position in the equation on detectability (equation 10). The factor 1 – e^–γ₁N describes the probability that at least one WT copy enters the amplification that contributes to the total signal [Pr(N₄ > 0)], and represents an upper bound for the probability of obtaining a positive test result as a function of the input. The other factor in equation 10 gives the probability that a positive result is obtained under the condition that a molecule enters the amplification in the first place. The lower limit of the linear range is given by 2 / γ₁ (equation 8), hence a high value of the product fpr implies a lower limit at a low input. Closely related to this is the level at which E[log(N_obs)] stabilizes for low inputs. Once again, a higher value of fpr (γ₁) implies a further extension of the linear range to lower inputs (see equation 9). If sensitivity of the assay is to be improved or, analogously, the linear range is to be extended to lower inputs, then the efforts should focus on increasing the value of the product fpr. In more practical terms this means that f (the fraction of the eluate used), r (the extraction recovery) or p (probability that a single molecule yields a detectable signal) should be increased. The strategy behind the development of magnetic extraction is, amongst others, to increase the value of f, the fraction of the eluate used, whereas the technique is under development to further increase the recovery r. Increasing the value of p would require further optimization of the amplification module and/or the quality of the enzymes. Note that the value of N stands for the expectation of the total number of WT copies entering the assay (see Fig. 1); the sample volume is not part of the equations. As such, as has indeed been shown experimentally (12), increasing the sample volume will have a direct impact on sensitivity if this is to be expressed in terms of copies/ml but not when it is expressed as copies/input. On the other hand, the use of high plasma volumes might also lead to increased concentrations of plasma components that can interfere with the amplification, hence reducing p.

The input concentration corresponding to a hit rate of 95% is often used as a definition of the limit of detection (LOD). Interestingly, the models imply that the lower end of the linear range is by definition below this LOD. After all, according to equation 8 the lower end is at an input such that γ₁N = 2. At this input equation 10 predicts that Pr(pos) ≤ 1 – e^–γ₁N = 1 – e^–2 ≈ 0.86. The quantitative linear range is often defined as the concentration range for which there is a linear relation between the logarithm of the input and E[log(N_obs)] and for which the probability of obtaining a positive test result >95%. This can further be extended to include a minimal assay standard deviation. The results of the current study indicate that with respect to the first two items, the 95% detectability requirement is sufficient.

As illustrated in the current paper, it is possible to apply the model to experimental data. For the first time, it is possible to draw conclusions on accuracy, precision and sensitivity based on a single analysis. There is no need to distinguish, on arbitrary grounds, an input range for which the variability is assumed to be constant. Also, as has been reported elsewhere (J.J.A.M. Weusten, P.A.W.M. Wouters and M.C.A. van Zuijlen, submitted for publication), effective use is made of the available information in the data set when it comes to sensitivity analyses, whereas the standard probit-analyses only use the dichotomous result ‘positive’ or ‘negative’.

In conclusion, a mathematical model was developed that enables simultaneous analysis of linearity, variability and detectability. It is believed that models like these can be helpful in developing and optimizing viral load diagnostics, as well as in statistical data analysis. In addition, they can contribute to the scientific knowledge of these systems. Further studies are required to refine the models.

APPENDIX

Truncated Poisson probabilities

Let X be a random variable obtained from a Poisson distribution with parameter λ under the restriction that its realization is positive. In this case, the probability distribution function is Pr(X = x) = (e^–λλ^x) / [(1 – e^–λ)x!]. Straightforward calculus now shows that the expectation µ_x = λ / (1 – e^–λ) and the variance σ_x² = λ[1 – (λ + 1)e^–λ] / (1 – e^–λ)². General statistical theory reveals that approximations for the expectation and variance of some function g(.) of the random variable X can be computed (see for example 13):

implying for the logarithmic transformation g(x) = ln(x):

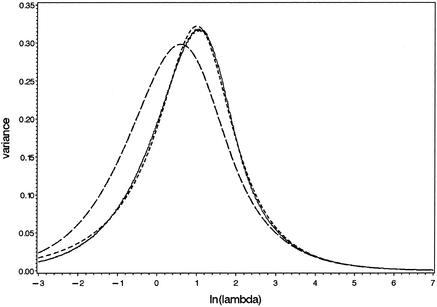
Large-scale computer simulations were performed to study the validity of these equations. To this end, values were chosen for the Poisson parameter λ by taking values for ln(λ) between –3 and +7 with increments of 0.01. For each λ, a total of 10⁵ observations were drawn from truncated Poisson distributions, and the mean and variance of the logs of these random values were computed. The summary statistics so obtained as well as the approximations according to equation A1 are presented in Figures 4 and 5. It is clear that the approximation for the mean is fairly accurate, but the approximation for the variance fails. Therefore, an alternative equation was searched for. There was no need to define a firm theoretical basis; any equation that is manageable and yields a reasonably good approximation would suffice. Empirical study of the observed curve suggests to use the equation as given in equation A2, in which the actual values of the parameters were optimized by using non-linear regression procedures. The quality of this approximation is also presented in Figure 5. This equation is used in the current paper.

Figure 5.

Approximation of the variance of the logarithm of a truncated Poisson variable with equations A1 (long dashes) and A2 (short dashes). The solid line reflects the simulation results.