C5′- and C3′-sugar radicals produced via photo-excitation of one-electron oxidized adenine in 2′-deoxyadenosine and its derivatives

Abstract

We report that photo-excitation of one-electron-oxidized adenine [A(-H)•] in dAdo and its 2′-deoxyribonucleotides leads to formation of deoxyribose sugar radicals in remarkably high yields. Illumination of A(-H)• in dAdo, 3′-dAMP and 5′-dAMP in aqueous glasses at 143 K leads to 80-100% conversion to sugar radicals at C5′ and C3′. The position of the phosphate in 5′- and 3′-dAMP is observed to deactivate radical formation at the site of substitution. In addition, the pH has a crucial influence on the site of sugar radical formation; e.g. at pH ∼5, photo-excitation of A(-H)• in dAdo at 143 K produces mainly C5′• whereas only C3′• is observed at high pH ∼12. ¹³C substitution at C5′ in dAdo yields ¹³C anisotropic couplings of (28, 28, 84) G whose isotropic component 46.7 G identifies formation of the near planar C5′•. A β-¹³C 16 G isotropic coupling from C3′• is also found. These results are found to be in accord with theoretically calculated ¹³C couplings at C5′ [DFT, B3LYP, 6-31(G) level] for C5′• and C3′•. Calculations using time-dependent density functional theory [TD-DFT B3LYP, 6-31G(d)] confirm that transitions in the near UV and visible induce hole transfer from the base radical to the sugar group leading to sugar radical formation.

INTRODUCTION

In recent work on heavy ion irradiated (Ar⁺¹⁸) DNA, a substantial increase in the extent of sugar radical formation, over that for gamma radiation, was reported (1,2). It was proposed that formation of sugar-phosphate backbone radicals occurred predominantly in the core of the Argon ion-beam track in which a high energy density creates multiple ionizations and excited states. This led us to propose that excited state cation radicals could be precursors to neutral sugar radicals (1,2). Subsequent studies to test this hypothesis found that photo-excitation of the guanine cation radical (G•⁺) resulted in direct formation of sugar radicals in both double-stranded DNA (dsDNA) and in model systems (3,4).

In these model systems (2′-deoxyribonucleosides/tides) it was found that photo-excitation of G•⁺ (3,4), results in near complete conversion (∼80–95%) of the G•⁺ to various sugar radicals C1′•, C3′• and C5′• at low temperatures ∼143 K. Investigation of the effect of pH on the visible light illumination of the one-electron-oxidized guanine moiety in 2′-dG in aqueous glasses found that only the protonated guanine cation radical moiety, i.e. G•⁺, results in sugar radicals whereas the corresponding neutral radical [G(-H)•] did not lead to sugar radical production (4). G•⁺ in 2′-dG has a pK_a = 3.9 and is deprotonated at N1 at pH 7 (5). However, in dsDNA, base pairing of guanine with cytosine induces a shift in the deprotonation equilibrium towards G•⁺ thereby increasing its abundance relative to G(-H)• (6–12). In accord with this, photo-excitation of G•⁺ in hydrated dsDNA, is found to result in formation of significant amounts (∼50%) of C1′• (3,4). Time-dependent density functional theory (TD-DFT) calculations indicate that specific excited states of G•⁺ in 2′-dG show considerable hole delocalization into the deoxyribose sugar, in accord with our proposed mechanism of action, viz. deprotonation from the sugar moiety of the excited molecular cationic radical to produce a neutral sugar radical (4).

For illumination of G•⁺ in 2′-deoxyribonucleotides, a phosphate group at C3′ discourages formation of C3′•, a phosphate at C5′ discouraged formation of C5′• (4). This effect explains results found for dsDNA, in which illumination of G•⁺ either at 77 K (3) or at 143 K produced only C1′• (4). Theoretical calculations suggest the rationale for this observation as they show that hydroxyl groups tend to stabilize free radicals on adjacent carbons and phosphate substitution increases the C-H bond energy at the site of substitution (13,14).

In this work, using adenine based 2′-deoxyribonucleosides and 2′-deoxyribonucleotides, we show that one-electron oxidation of the adenine moiety produces the adenine cation radical, A•⁺, which owing to its high acidity, pK_a ∼1 (5,6,10,15), readily deprotonates to form the corresponding neutral adenine radical [A(-H)•]. We find that this species, A(-H)•, undergoes the same photo-conversion to sugar radicals as does G•⁺. We employ ¹³C isotopic substitution at C5′ in 2′-deoxyadenosine ([5′-¹³C]dAdo) to identify positively C5′• and to confirm the identity of C3′•, both produced via photo-excitation of A(-H)•. As expected, a β-¹³C-coupling is present in C3′• and an axially symmetric anisotropic α-¹³C coupling is present in C5′•. The β-¹³C-coupling observed in C3′• is, to the best of our knowledge, the first such coupling reported in a condensed phase from ESR studies. The nature of the ¹³C5′ couplings in C5′•, C4′• and C3′• are explored using DFT theoretical calculations.

MATERIALS AND METHODS

Model compound sample preparation

2′-Deoxyadenosine (dAdo), 2′-deoxyadenosine 3′-monophosphate (3′-dAMP), 2′-deoxyadenosine 5′-monophosphate (5′-dAMP) and lithium chloride (99% anhydrous; SigmaUltra) were obtained from Sigma Chemical Company (St Louis, MO). Potassium persulfate (crystal) was obtained from Mallinckrodt, Inc. (Paris, KY). Deuterium oxide (D₂O) (99.9 atom % D) was purchased from Aldrich Chemical Company Inc. (Milwaukee, WI). 5′-¹³C-2′-deoxyadenosine ([5′-¹³C]dAdo) (Scheme 1) with 98% isotopic purity was obtained from Omicron Biochemicals, Inc. (South Bend, IN). All chemicals were used without further purification.

Scheme 1.

Isotopically substituted compound used.

Glassy samples of nucleoside or nucleotide are prepared by dissolving ∼3 mg of the compound in 1 ml of 7 M LiCl in D₂O in the presence of 3-5 mg K₂S₂O₈ (3,4). If required, the pH was adjusted by adding microliter amounts of 1 M NaOH in D₂O or concentrated HCl under ice-cooled conditions. The solutions were then thoroughly bubbled with nitrogen and the glasses prepared by cooling to 77 K, as reported earlier (3,4). All samples are stored at 77 K.

γ-Irradiation

Glassy samples were γ-irradiated (⁶⁰Co) with an absorbed dose of 2.5 kGy.

Annealing and illumination of samples

To carry out the temperature-dependent annealing of the samples, a variable temperature assembly was used. A copper–constantan thermocouple was used to monitor temperatures (3,4,9). The glassy samples (7 M LiCl) were annealed to 150-155 K for 10-15 min (3,4), resulting in loss of (light yellow) Cl₂•⁻ and the concomitant formation of only one-electron oxidized adenine base radicals as evidenced by their ESR spectra (Supplementary Figure S1). We find no sugar radical formation by direct attack of Cl₂•⁻ on the sugar moiety.

The glassy samples of nucleosides or nucleotides, containing the [A(-H)•] were then photo-excited at 143 K with a 250 W tungsten lamp. An Argon-ion laser (488 nm, 800 mW) was also employed for comparison. Comparison of the sugar radical yields obtained by the Argon-ion laser at 77 K with that by the 250 W tungsten lamp at 77 K shows that the laser was about 10 times as effective owing to its greater fluence. From this we estimate the intensity of the tungsten lamp on the sample to be only ∼60 mW (Supplementary Figure S2). For the study of wavelength dependence (shown in the Supplementary Figure S3) we employed both the 250 W tungsten lamp and a 200 W high-pressure Xe lamp, Oriel Corporation. In this later study various filters were employed, specifically band-pass filters (340-370, 380-480 nm) and a cut-off filter (≤540 nm). No significant wavelength dependence was observed (vide infra). During photo-excitation, we cannot significantly increase the temperature beyond 150 K because the glass softens and radicals are lost.

Electron spin resonance

After γ-irradiation at 77 K, annealing to 150-155 K and illumination at 143 K, samples were immediately immersed in liquid nitrogen, and an ESR spectrum was recorded at 77 K and 40 dB (20 µW) (1-4,9). Fremy's salt (with g = 2.0056, A_N = 13.09 G) was used for field calibration similar to our previous works (1-4,9).

Analysis of ESR spectra

Least square fittings of benchmark spectra (Figure 1) were employed to determine the fractional composition of radicals (Scheme 2) in experimental spectra using programs (ESRPLAY, ESRADSUB) written in our laboratory. The fraction that a particular benchmark spectrum contributes to an overall spectrum is based on double integrated areas, which are directly proportional to the number of spins of each radical species (moles of each radical).

Figure 1.

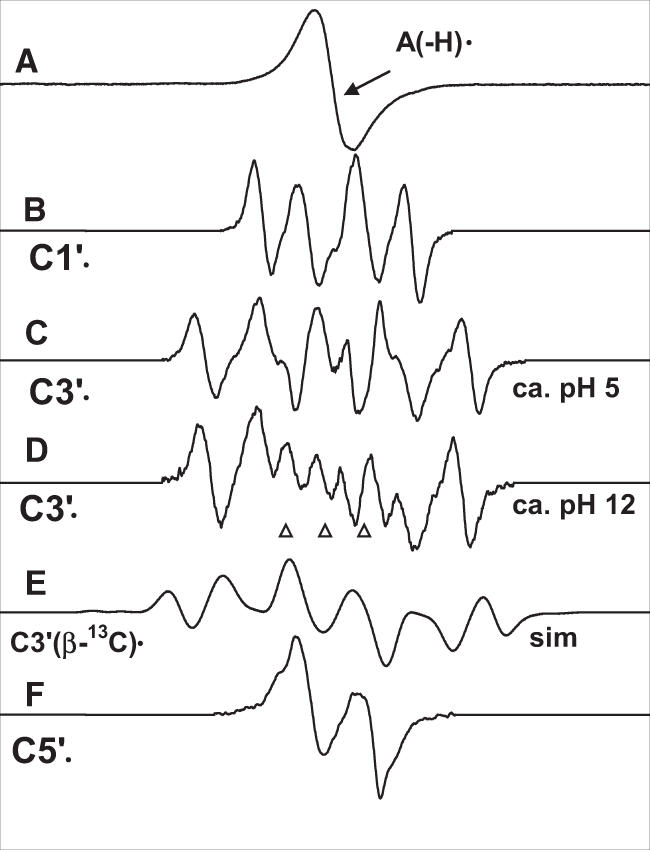
Benchmark spectra used for computer analysis. (A) A(-H)•, produced from dAdo. (B) C1′•, produced from G•⁺ in 3′-dGMP (4). (C) C3′•, produced from A(-H)• in 5′-dAMP at native pH (∼5) of 7 M LiCl glass. (D) C3′•, produced from A(-H)• in dAdo at pH ∼12. (E) Simulated spectrum for C3′• using three β-hydrogen couplings and a single β-¹³C isotropic hyperfine coupling (see text). (F) C5′•, produced from A(-H)• in 3′-dAMP (for details see Table 1). pHs are approximate. The three reference markers in this and in subsequent figures are Fremy's salt resonances (The central marker is at g = 2.0056 and each of three markers is separated from the adjacent one by 13.09 G).

Scheme 2.

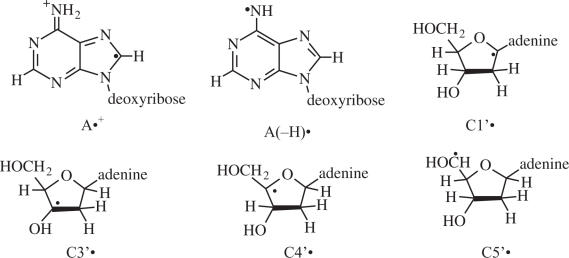
Radicals studied in this work.

The benchmark spectrum used for A(-H)• is that obtained from dAdo before photo-excitation. This spectrum shown in Figure 1A agrees well with those of the same radical reported in the literature (16-20). The benchmark spectrum used for C1′• (Figure 1B) is derived from 3′-dGMP via photo-excitation of G•⁺ (4). Two benchmark spectra (Figure 1C and D) are employed for C3′• because the hyperfine coupling constants vary slightly with pH (Table 1). Figure 1E shows the simulated C3′• spectrum using the three β-hydrogen couplings, 21 G, 28 G, 40.5 G and a single β-¹³C isotropic hyperfine coupling of 16 G (vide infra), an isotropic g = 2.0032, and 8 G line-width. For C5′•, the spectrum obtained via photo-excitation of one-electron oxidized adenine base-radical in 3′-dAMP at the native pH of 7 M LiCl glass (pH ∼5) was used with 5% of the spectrum for C1′• (Figure 1B) subtracted. All subtractions are based on the spectrum intensities determined from double integration of the first derivative spectra.

Table 1.

Hyperfine couplings and g-values for deoxyribose radicals^a

Compoundb	Hyperfine coupling constants (G)	g-Value (apparent)c
C1′•d
dAdo, 3′-dAMP	15.5 (1βH), 35(1βH)	2.0029
C3′•
dAdo, 5′-dAMP	21 (1βH), 28 (1βH), 40.5 (1βH)	2.0032
dAdo (pH ca. 12)	18.6 (1βH), 28 (1βH), 38 (1βH)	2.0032
C5′•
dAdo, 3′-dAMP, 5′-dAMP	∼21 (1αH)	2.0023

^a,bValues are for radicals at 77 K, formed by illumination at 143 K and at native pH (∼5), unless otherwise stated.

^cThe apparent g-value (experimental center of spectrum) is reported.

^dThese hyperfine couplings are identical to those found for C1′• in 3-dGMP (4).

As in our previous work (4) with glassy samples, a sharp singlet ‘spike’ from irradiated quartz at g = 2.0006 was subtracted from all spectra before analysis.

TD-DFT calculations

TD-DFT calculations were performed to determine the energy and the nature of the molecular orbitals in geometry optimized dA(-H)• in dAdo. Geometry optimization was performed using B3LYP functionals with the 6-31G(d) basis set provided in the Gaussian 03 program package (21-29). Calculations using the 6-31G(d) basis set were performed to determine the nature of the first 16 electronic transitions.

RESULTS

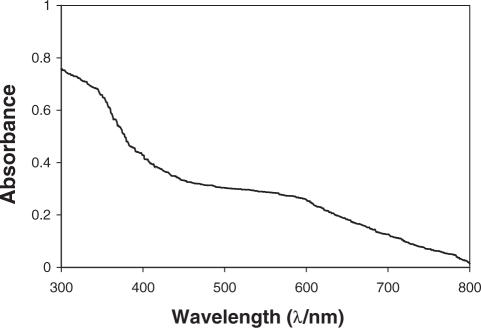
The UV-visible spectrum of A(-H)• in dAdo, taken at 77 K in a 7 M LiCl glass, is shown in Figure 2. This spectrum is very similar to that reported in the literature for A(-H)• in dAdo, in aqueous solution at room temperature (5). This result shows that Cl₂•⁻, via one-electron oxidation (Supplementary Figure S1) at adenine moiety produces A•⁺ [pK_a ∼1 (5,6,10,15)]—a strong Brønsted acid, which readily deprotonates even at 77 K, from the exocyclic nitrogen to form the corresponding neutral adenine radical [A(-H)•]. In fact, this deprotonation occurs in the solid state even at 4 K (30). Therefore, for the pH range studied here (pH 5–12), we assume that the one-electron oxidized adenine radical exists in its de-protonated state as A(-H)•.

Figure 2.

The UV-vis absorption spectrum of A(-H)• produced by Cl₂•⁻ oxidation of dAdo, at 77 K in 7 M LiCl glass/D₂O. This absorption imparts a purple color to the sample.

Wavelength dependence of radical formation

The 2′-deoxyadenosine nucleosides/tides investigated here show no observable wavelength dependence for the conversion of A(-H)• to sugar radicals at wavelengths from 310 to 700 nm (Supplementary Figure S3). This observation is consistent with our previous work in which no wavelength dependence was found for the conversion of photo-excited G•⁺ to the sugar radicals in model systems (4).

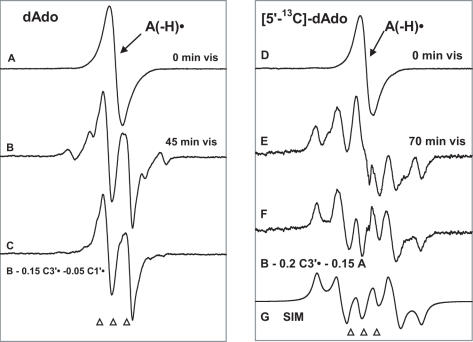
dAdo and [5′-¹³C]dAdo

Figure 3 shows the effect of visible illumination on A(-H)• in dAdo (Figure 3A–C, left panel) and in [5′-¹³C]dAdo (Figure 3D–G, right panel) at the native pH of 7 M LiCl glass (∼5). In Figure 3A, the ESR spectrum of A(-H)• in dAdo, formed via oxidation by Cl₂•⁻, is shown. It is noteworthy that the ESR spectra from A(-H)• for all the compounds used, at the two pHs (∼5 and 12) used, are identical and agree with the spectrum of A(-H)• reported in the literature (16–20). Hence this spectrum in Figure 3A has been used as benchmark spectrum for A(-H)• (Figure 1A). Figure 3B shows the ESR spectrum found after visible illumination at 143 K for 45 min. Comparison of the spectrum in Figure 3B with that in Figure 3A shows that there is almost complete conversion of A(-H)• to sugar radicals. The outer line components originate mainly with a sextet (Figure 1C) that has been assigned to C3′• (3,4). Subtraction of C3′• spectrum (Figure 1C) as 15% and C1′• spectrum (Figure 1B) as 5% from that in Figure 3B results in the spectrum shown in Figure 3C. A similar ‘doublet’ spectrum was earlier assigned to C5′• (in guanine 2′-deoxy ribonucleosides/tides) (4); this assignment to C5′• is strongly supported by experiments using ¹³C substitution at C5 (vide infra). Relative yields of the various sugar radicals formed via photo-excitation of A(-H)• are C5′• 80%, C3′• 15% and C1′• 5%. Upon photo-excitation at 77 K for 200 min, the extent of conversion of A(-H)• in dAdo to the sugar radicals was significantly less, i.e. only 40% at 77K versus 100% at 143 K (Supplementary Figure S4) while the relative yields of sugar radicals were similar C5′• 65%, C3′• 25% and C1′• 10%. Because of the higher yields, throughout this work, the photo-excitation studies were carried out at 143 K.

Figure 3.

(A) ESR spectrum of A(-H)• formed by oxidation of dAdo in 7 M LiCl glass/D₂O with Cl₂•⁻. (B) Spectrum after illumination with visible light for 45 min at 143 K, containing contributions from 80% C5′•, 15% C3′• and 5% C1′•. (C) Spectrum found after subtraction of C1′• and C3′• components (Figure 1B and C) from spectrum (B). This doublet is attributed to C5′•. (D) ESR spectrum from A(-H)• in [5′-¹³C]dAdo in 7 M LiCl glass/D₂O. (E) Spectrum after illumination for 70 min with visible light at 143 K. This spectrum is made up of 80% C5′• and 20% C3′•; both radicals possess substantial ¹³C couplings (Table 2 and Scheme 3). (F) Spectrum obtained after subtraction of simulated C3′• spectrum (20%) (Figure 1E) and of A(-H)• spectrum (15%) (Figure 1A) from (D). This spectrum is assigned to C5′• (see text). (G) Simulation of spectrum in (F) using the parameters given in the text and in Table 2 and Scheme 3. All spectra were recorded at 77 K.

Since the C4′• may give also give rise to a doublet ESR spectrum in an amorphous state (18–20,31) we chose to verify our assignment of the doublet to C5′• by performing experiments with [5′-¹³C]dAdo (Figure 3D–G). A compelling rationale for performing these experiments are theoretical calculations on dAdo (DFT, B3LYP functionals, 6-31G(d) basis set, full optimization) which indicate that the ¹³C hyperfine couplings for C4′• and C5′• should differ dramatically. For C5′•, the ¹³C couplings for a C5′ atom are predicted to be quite large and anisotropic, with axial symmetry, as expected for a planar radical in which high spin density is localized largely in a p-orbital on an atom with a nuclear spin of 1/2 (Table 2 and Scheme 3). Specifically, in C5′•, A (¹³C₅) is predicted to be (15.8, 16.2, 90.0) G (Scheme 3) with A_isotropic = 40.7 G. On the other hand, for C4′•, the ¹³C-couplings for a C5′ atom are predicted to be small and nearly isotropic. Specifically, for C4′•, A(¹³C₅) is predicted to be (−10.1, −9.7, −7.6) G. Thus, the ¹³C₅ substitution permits us to distinguish easily between C4′• and C5′•.

Table 2.

Hyperfine coupling constants for sugar radicals in [5′-¹³C]dAdo (Gauss)

Radical	Coupling/site	Experimentala		Theoretical
		Aiso	Atotal	Aiso	Atotal
C3′•	β-(5′-13C)	16	—	10.3	(9.3, 9.6, 12.0)
C4′•	α-(5′-13C)	—	—	−9.1	(−10.1, −9.7, −7.6)
C5′• (planar)	(5′-13C)	46.7	(28, 28, 84)	40.7	(15.8, 16.2, 90.0)
	α-(5′-H)	−21	(−28, −21, −12)	−24.7	(−37.3, −25.7, −11.0)
C5′• (nonplanar)	(5′-13C)	—	—	72.96	(49.7, 50.1, 119.1)
	α-(5′-H)			−7.26	(−18.6, −8.9, 5.7)

^aCalculations for hyperfine couplings at DFT[b3lyp, 6-31G(d)] and were all first fully optimized at 6-31G(d) except for the planar conformation of C5′ which was optimized with the radical site held planar.

Scheme 3.

Hyperfine coupling of ¹³C5′ for C4′• and C5′• in dAdo.

Illumination of A(-H)• in [5′-¹³C]dAdo at 143 K results in the spectrum shown in Figure 3E. Using dAdo with ¹²C as a guide, subtracting 20% of the intensity of the C3′• benchmark spectrum (Figure 1E) and 15% of the intensity of the spectrum of A(-H)• (Figure 1A) from the full intensity of spectrum in Figure 3E results in spectrum in Figure 3F. The resulting multiplet spectrum with 105 G breadth is consistent with a C5′• radical with a ¹³C (nuclear spin = 1/2) coupling at C5′. Figure 3G presents an anisotropic computer simulation of this spectrum using A(¹³C) = (28, 28, 84) G and A(H) = (−28, −12, −21) G, with g-value = (2.0038, 2.0035, 2.0023) and anisotropic (6,4,6) G line-width. The simulation in 3G matches the experimental spectrum in Figure 3F very well and confirms that the major coupling is a large anisotropic hyperfine interaction with the ¹³C at C5′ (Table 2 and Scheme 3). This, in turn, confirms that the original doublet observed for dAdo (Figure 3C) that originates from C5′•. This assignment is supported by TD-DFT calculations of the ¹³C5′ hyperfine couplings in C5′• for planar and non-planar sites which favor the near planar conformation (Table 2). The isotropic component of the ¹³C coupling (46.7 G) as well as the 5′-αH coupling (−21 G) in C5′• are consistent with a close to planar radical site (32) (Table 2 and Scheme 3).

Effect of phosphate substitution (3′-dAMP and 5′-dAMP)

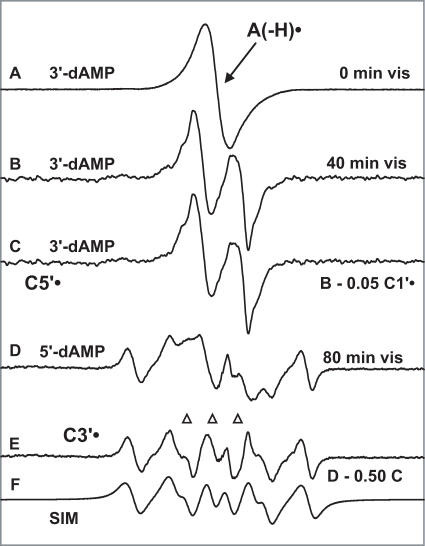
Figure 4 shows the effect of visible illumination on A(-H)• in 3′-dAMP and 5′-dAMP. In Figure 4A, the ESR spectrum of A(-H)• in 3′-dAMP, prepared via oxidation by Cl₂•⁻, is shown. The spectra observed for A(-H)• from 3′-dAMP (Figure 4A) and 5′-dAMP (data not shown) were identical and they match exactly with the spectrum of A(-H)• shown in Figure 1A. In Figure 4B, the ESR spectrum obtained after 40 min of visible light illumination, at 143 K, of A(-H)• in 3′-dAMP is shown. In 3′-dAMP, the formation of C3′• is depressed (relative to dAdo), as expected, because of the presence of a phosphate group instead of an -OH at C3′ (13,14). Subtraction of 5% of the C1′• benchmark spectrum (Figure 1B) from that in Figure 4B results in spectrum Figure 4C. This spectrum an ∼21 G doublet, is used as a benchmark spectrum for C5′• (Figure 1E). This spectrum matches very well with the doublet obtained from dAdo samples and shown in Figure 3C.

Figure 4.

(A) ESR Spectrum from A (-H)• in 3′-dAMP in 7 M LiCl glass/D₂O. (B) After illumination of A(-H)• in 3′-dAMP for 40 min C5′• (∼95%) and C1′• (∼5%) are present. (C) Spectrum of C5′•, found by subtraction of 5% of the C1′• benchmark spectrum (Figure 1B) from the spectrum shown in (B). (D) Spectrum after illumination of A(-H)• in 5′-dAMP in 7 M LiCl glass/D₂O for 80 min. (E) Spectrum of C3′•, found by subtraction of 50% of the C5′• benchmark spectrum (Figure 1E) from the spectrum shown in (D). (F) Computer simulation of the C3′• spectrum using the ESR parameters given in the text. All illuminations are with visible light at 143 K and all spectra were recorded at 77 K.

In Figure 4D, the spectrum obtained after 80 min visible illumination of A(-H)•, at 143 K, in 5′-dAMP at the native pH of 7 M LiCl (∼5) is shown. Subtraction of the C5′• spectrum (Figure 1E) as 50% of total intensity from that in Figure 4D results in spectrum Figure 4E. This spectrum is assigned to C3′•. A simulation of the C3• spectrum, using three isotropic hyperfine coupling constants 21 G, (1βH), 28 G (1βH), 40.5 G (1βH), with g_iso = 2.0032 and 6.5 G line-width is shown in Figure 4F; this simulation matches the experimental spectrum in Figure 4E nicely. This C3′• spectrum is used as a benchmark spectrum for C3′• at pH ∼5 (Figure 1C).

A significant aspect of these experiments is that a phosphate substituent at either the C5′- or C3′-site results in reduced radical formation at the site, relative to dAdo. In 3′-dAMP, the ESR spectrum is dominated by C5′• (Figure 4B and C) and no C3′• formation is observed in contrast to results for dAdo in which we find C3′• (compare Figure 3B with Figure 4B). In 5′-dAMP, C5′• does form, but at a reduced fraction (50%) relative to that in dAdo (80%) (compare Figure 3B with Figure 4D). These observed decreases in radical formation are consistent with calculations which show that phosphate group substitution at the sugar in a model nucleotide destabilizes the corresponding radical (13,14). However, the fact that still C5′• forms in 5′-dAMP indicates that that factors other than thermodynamic stability alone play a role in determining radical formation in 5′-dAMP.

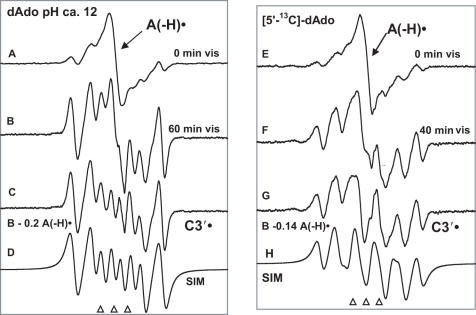
dAdo and [5′-¹³C]dAdo at high pH

In Figure 5, the results of photo-excitation at 143 K of A(-H)• in dAdo (Figure 5A-D, left panel) and in [5′-¹³C]dAdo (Figure 5E–H, right panel) glassy samples at pH ∼12 are shown. In Figure 5A, we show the ESR spectrum obtained via oxidation of dAdo by Cl₂•⁻. Analysis of this spectrum using the benchmark spectra in Figure 1 indicates that it is a composite from ∼50% A(-H)•, [the central singlet, indicated by arrow (Figure 1A)] and ∼25% C3′• (Figure 1D). The remaining ∼25% originates with a broad, poorly defined underlying singlet which is not yet identified. In Figure 5B, we present the spectrum obtained after 60 min of visible light illumination at 143 K. A substantial increase in the intensity of line components from C3′• is evident. Subtraction of the A(-H)• spectrum shown in Figure 1A, (∼20% of total intensity) from the spectrum in Figure 5B yields the spectrum in Figure 5C which is assigned to C3′•. In Figure 5D, a simulated spectrum using the hyperfine coupling constants [18.6 G (1βH), 28 G (1βH), 38 G (1βH)] with g_iso = 2.0032 and 7.0 G line-width is shown; this simulation nicely matches the experimental one in Figure 5C. The hyperfine couplings used in the simulation are very near to those found for the same radical in a single crystal of 5′-dGMP [16.7 G (1βH), 27.5 G (1βH), 38.2 G (1βH)] (33).

Figure 5.

Spectra obtained for identically prepared samples of dAdo (A–D) and [5′-¹³C]dAdo (E–H) in 7 M LiCl glasses. (A) ESR spectrum found after oxidation of dAdo by Cl₂•⁻ consisting of A(-H)•(50%) (the central singlet, Figure 1A) and C3′• (25%) (Figure 1D). (B) After illumination of the sample in A with visible light for 60 min at 143 K, the A(-H)• signal is lost by ∼80% and the C3′• signal is increased. (C) Spectrum assigned to C3′• obtained by subtraction of the A(-H)• signal (20%) from spectrum (B). (D) Simulation of the spectrum in (C) for C3′• using the parameters given in the text. (E) ESR spectrum recorded after oxidation of [5′-¹³C]dAdo by Cl₂•⁻ consisting of A(-H)• and C3′•. (F) After illumination of the sample in E for 40 min at 143 K. (G) C3′• spectrum showing a 16 G β-¹³C coupling found by subtraction of the A(-H)• signal from spectrum (F). (H) Simulation of the spectrum in G using parameters given in the text. All spectra were recorded at 77 K.

The spectra resulting from studies employing identically prepared samples of [5′-¹³C]dAdo are shown in Figure 5E–H. In Figure 5E, the ESR spectrum, obtained via oxidation by Cl₂•⁻ is shown. Analysis of this spectrum indicates it is a composite of the spectra of A(-H)• (40%) [the central singlet, indicated by arrow (Figure 1A)], C3′• (30%), and 30% underlying broad resonance comparable with the results observed in the spectrum mentioned in Figure 5A. In Figure 5F, the spectrum obtained after 40 min of visible light illumination at 143 K is shown. Subtraction of the A(-H)• spectrum shown in Figure 1A, as ∼14% of the intensity of the original spectrum, yields the spectrum in Figure 5G which is assigned to C3′•. The breadth of this spectrum is 16 G larger than that in 5C as a result of a 16 G β-hyperfine coupling arising from the ¹³C carbon at the C5′ position. A simulated spectrum using three β-hydrogen isotropic couplings, A(1H) = 19.5 G, A(1H) = 25.5 G, A(1H) = 38 G, a single β-¹³C isotropic hyperfine coupling of 16 G, an isotropic g = 2.0032, and 8 G line-width is shown in Figure 5H. The simulated spectrum matches the experimental spectrum in Figure 5G reasonably well, although, a small background signal is apparent in the experiment.

TD-DFT calculations

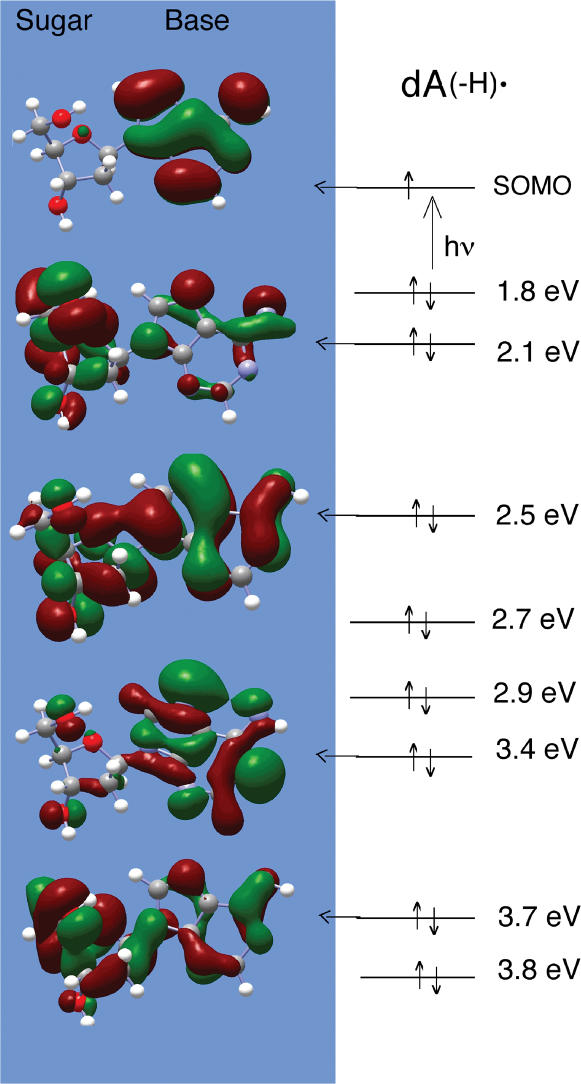
In previous work with DNA and guanine nucleosides and nucleotides we proposed that, on photo-excitation of G•⁺, a variety of sugar radicals are produced by hole delocalization into the sugar moiety of the nucleoside/tide (4). Subsequent fast deprotonation from the sugar then results in formation of neutral sugar radicals at the sites of highest hole localization. This was supported by TD-DFT calculations for G•⁺ in 2′-dG (4). To aid in our understanding of this mechanism in adenine nucleosides, we have performed TD-DFT calculations of the excited states and transition energies of A(-H)• in dAdo using B3LYP functionals and a 6-31G(d) basis set (21–29). The A(-H)• structure was geometry optimized [B3LYP, 6–31G(d)] and the first 16 transition states calculated by TD-DFT [6-31G(d)] and the first 10 transitions are reported in Table 3.

Table 3.

TD-DFT b3lyp 6-31G(d) calculated electronic transitions for A(-H)• in dAdo

Transition	ΔE(eV)	λ (nm)	fa	Transition (density)	Delocalization into sugarb
1	1.79	694	0.0000	65β→66β (0.87)c	0
2	2.11	588	0.0014	62β→66β (0.84)	3
3	2.50	496	0.0376	64β→66β (0.94)	2
4	2.69	461	0.0154	63β→66β (0.9)	0
5	2.90	428	0.0000	60β→66β (0.95)	3
6	3.38	367	0.004	61β→66β (0.9)	0.5
7	3.70	335	0.0018	59β→66β (0.82)	3
8	3.84	323	0.0041	58β→66β (0.76)	1.5
9	3.98	311	0.0017	57β→66β (0.74)	3.5
10d	4.23	293	0.0717	66α→67α (0.67)	0
				55β→66β (0.47)	3

^aOscillator strength.

^bEstimate of degree of hole delocalization from the base onto the sugar suggested by the dominant initial MO (57β through 65β) in the transition: 0, nearly all remains on the adenine base; 1, shared between base and sugar ring favoring base; 2, equally shared between base and sugar ring; 3, shared between base and sugar ring favoring sugar; 4, nearly all transferred to the sugar ring.

^c65β→66β represents the transition between the 65th MO and the SOMO (66th MO) in A(-H)• in dAdo. β refers to the orbital for the beta electron spin. The numbers in parentheses are the 1-particle RhoCI excited state density for that transition. Only the major contributor(s) to each state is(are) given.

^dThe LUMO is 67α and this transition is dominated by SOMO→LUMO transition. The energy of 4.2 eV is not in the experimental range.

The first 9 transitions are in the UVA-visible region. The 10th transition at 4.2 eV is the first to involve the SOMO and LUMO in a transition and is out of the experimental energy range employed. The first 9 calculated transitions are inner shell (MOs 57-65) to SOMO (MO 66) transitions none of which involve the LUMO. Many of the inner shell filled MOs have substantial contributions from atomic orbitals on the sugar ring and singly excited states thus transfer the hole, in part, from the adenine ring to the sugar ring. In Figure 6, we show five molecular orbitals for A(-H)• in dAdo [computed by DFT (6-31G^*, B3LYP) and visualized via Gaussview] that illustrate hole distribution between sugar and base moieties. As expected, the SOMO for A(-H)• indicates the hole is localized on the adenine base. The overall features calculated for A(-H)• in dAdo are very similar to those determined earlier for G•⁺ in 2′-dG (4).

Figure 6.

Molecular orbitals and transition energies for A(-H)• in dAdo. MOs were computed by DFT [6-31G(d), B3LYP], transition energies by TDDFT. The SOMO shows the expected MO for A(-H)• with the hole localized on the adenine base. A number of inner shell MOs which dominate transitions are shown and are visualized via Gaussview. Excitation from inner MOs shown to the SOMO would in a number of cases transfer a significant portion of the hole from the adenine base to the sugar ring. The SOMO to LUMO transition is at higher energies (4.2 eV) (Table 3).

The differences in the distribution of the hole for different MOs would suggest that there would be a significant wavelength dependence on sugar radical formation; however, we have not found such an effect in nucleosides or nucleotides. The high density of states throughout the region with hole transfer to the sugar likely mitigates a wavelength dependence.

It has been reported that TD-DFT calculations have the tendency to underestimate energies of charge transfer excited states, i.e. DA→D⁺A⁻ because the coulombic energy of charge separation to form the D⁺A⁻ charge transfer excited state is not fully accounted for (34–37). In our work, inner MO transitions do not create a full charge transfer state and the initial DFT ordering (i.e. 55β to 66β) is largely maintained in the predicted transition energy ordering (Table 3) suggesting only modest effects if any. Thus this calculational limitation has no substantial effect on the overall semi-quantitative model presented.

DISCUSSION

Mechanism of sugar radical formation via photo-excitation of A(-H)•

Our proposed mechanism for photoconversion of A(-H)• to neutral sugar radical(s) is photo-induced delocalization of the hole from the base into the sugar, followed by deprotonation from the sugar moiety (Scheme 4). This results in positive charge on the sugar moiety and concomitant negative charge on the base (Figure 6). Since the pK_a of (the no longer oxidized) adenine is ∼10, protonation of the adenine base is expected. It is not clear whether deprotonation at the sugar moiety precedes, follows or is concerted with protonation of the base.

Scheme 4.

Schematic representation of the mechanism of sugar radical formation in dAdo using C5′• formation as an example.

Table 4 summarizes the yields of the sugar radicals obtained from the adenine containing compounds investigated. There is no convincing evidence for production of C2′• or C4′• via photo-excitation of A(-H)•, which is consistent with our previous work on G•⁺ (4). We also find that there are indications of only small amounts of C1′• (Table 4).

Table 4.

Sugar radicals formed on photo-excitation of A(-H)•^a,^b,^c

Compound	Percent convertedd	C1′•e	C3′•e	C5′•e
dAdo	100	5	15	80
5′-dAMP	100	—	50	50
3′-dAMP	100	5	—	95
dAdo (pH 12)	80	—	100	—

^aPercentage expressed to ±5% relative error.

^bAll glassy samples are at the native pH of 7 M LiCl (∼5) unless stated otherwise in table.

^cSamples were illuminated at 143 K and spectra recorded at 77 K.

^dPercentage of dA(-H)• that converts to sugar radicals. The total spectral intensities before and after illumination were the same, within experimental uncertainties.

^eEach calculated as percentage of total sugar radical concentration; these sum to 100%.

Theoretical calculations of the C–H bond energies for the adenosine deoxyribose moiety in dAdo give the following relative energies in kcal: C1′(0.0 kcal) < C5′(2.5 kcal) < C4′(3.5) < C3′(3.7) < C2′(7.1) (38). The relatively large C2′–H bond energy of 101.4 kcal/mol likely explains why C2′• is not observed. However, bond energy arguments fail to account for the relative amounts of C1′•, C3′• and C5′• produced in dAdo as well as the lack of production of C4′•. If the relative bond energies cited were the principal factors underlying radical formation, C1′• would be the predominant radical formed, which is not the case. For 3′-dAMP, the lack of production of C3′• and for 5′-dAMP the lowered extent of formation of C5′• relative to dAdo, is in agreement with the radical stabilities predicted by calculations on model compounds (13,14). However, even for nucleotides, the calculations indicate that C1′• is the most stable sugar radical (38). The lack of C1′• production in the nucleotides again suggests the relevance of other than thermodynamic factors. Thus, while bond energies must have some impact on radical formation (through sugar deprotonation), other factors, such as the effect of hole localization on the sugar and the availability of proton acceptor sites, must also be involved.

The site of deprotonation from the sugar moiety is likely to be related to the distribution of the hole on the sugar moiety because the associated positive charge will both polarize and weaken C–H bonds, thereby facilitating proton loss. The likely proton acceptor sites are nearby water molecules, Cl⁻ or heteroatoms on the molecule involved.

Role of base protonation in sugar radical production

In our previous work involving photo-excitation of G•⁺ in 2′-dG, photolysis of the N1 deprotonated G•⁺ (pH > 8) did not result in sugar radical formation (4). In contrast, we show in this work that deprotonation of A•⁺ at the exocyclic nitrogen does not hinder photo-conversion of the electron-loss radical to sugar radicals. If the base is required to be protonated for sugar radical formation, as was found for G•⁺ (4), then reprotonation of the adenine base in the excited state would precede deprotonation from the sugar.

Identification C5′• and the β-¹³C coupling in C3′•

The 21 G doublet found in the ESR spectra of adenine nucleosides/tides is attributed to C5′• and this assignment is verified by ¹³C substitution at C5′ in dAdo. The C5′• ESR spectrum found for [5′-¹³C]dAdo (Figure 3E and F) shows the ESR spectra and anisotropic couplings expected for C5′•. DFT calculations confirm this assignment and suggest the radical site is nearly planar. Single crystal ESR investigations of C5′• in dAdo•H₂O reports one anisotropic C5′ hydrogen hyperfine coupling with A_iso varying from 15 to 18 G (39–41) and a small (6 G) coupling to a C4′ hydrogen (39). In our earlier work, via photo-excitation of G•⁺ in 2′-dG we also isolated the C5′• spectrum as an ∼19 G doublet (4). The reason for the variation in the hyperfine splitting of C5′• in various environments, single crystals and glassy samples, is unclear; however, calculations (Table 2) clearly predict that only slight changes in the planarity of the radical site with environment can readily account for the small differences in the overall doublet splitting observed.

The β-¹³C₅ coupling of ∼16 G combined with our DFT calculations clearly identifies C3′• in our dAdo samples.

Absence of C4′•

C4′• radicals were not observed either in our previous study of guanine nucleosides/tides in which G•⁺ was photo-excited (4) or in this current work with adenine nucleosides/tides. We note that a recent study of product yields in X-ray irradiated, crystalline, double-stranded oligonucleotide samples, where direct ionization and hole formation at the sugar moiety is expected, found that the products identified yielded no evidence for C4′• as an intermediate (42). As mentioned earlier, theoretical calculations show that C4′• is energetically as stable as C1′• and C3′• (38). Thus, we could expect C4′• to be formed based on bond energies (38). It is well known that C4′• readily undergoes beta-phosphate elimination (15,43–46). However, beta-phosphate elimination would yield subsequent radical species which are not observed in this study. Furthermore, beta-phosphate elimination could not explain the absence of C4′• in dAdo, in which no phosphate group is present. Our results here and obtained from our previous work (4), have led us to conclude that the photo-excitation process at 143 K does not produce an observable C4′•. We note, however, that it is, of course, possible that a transitory C4′• is formed which rapidly converts to another sugar radical such as C5′•.

TD-DFT calculations

The TD-DFT calculations performed provide two important insights into the photoexcitation process in A(-H)•. The first is that the transition(s) responsible for sugar radical formation is(are) inner orbital to SOMO excitations rather than the more familiar SOMO to LUMO transition. Second, the transitions in the visible region transfer a hole to the sugar moiety, providing a driving force for deprotonation from the sugar and concomitant sugar radical formation. These calculations are, thus, supportive of the proposed mechanism through which photoexcitation of A(-H)• leads to production of neutral sugar radicals.

We note that direct abstraction of a hydrogen atom by the DNA base radical from the sugar moiety in the excited state might be considered a possible alternative mechanism for sugar radical formation. We have no evidence for this mechanism and some evidence, i.e. the absence of a large primary deuterium isotope effect on C5′• formation via photo-excitation of G•⁺ in 2′-dG (4), that argues against it.

IMPLICATIONS OF THIS WORK

1. Our work shows that photo-excitation of G•⁺ in model compounds or dsDNA (4) and of A(-H)• leads to specific sugar radicals via inner orbital to SOMO transitions followed by deprotonation from the sugar moiety. We thus have a technique for selective formation of electronic states (holes) and resulting specific sugar radicals in DNA and model structures.

2. In dsDNA, hole transfer from A to G would strongly inhibit sugar radical formation via excited A(-H)•. However, sugar radical formation on excitation of A(-H)• would likely be important in ssDNA where the lack of base stacking would isolate holes on A.

3. We note that a series of investigations of hole transfer through DNA employ continuous visible illumination (43,47–53). The work reported herein as well as our previous efforts (3,4) may have implications for these studies, since excitations of holes on guanine or adenine results in sugar radical formation.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.