Deterministic Model of Dermal Wound Invasion Incorporating Receptor-Mediated Signal Transduction and Spatial Gradient Sensing

Abstract

During dermal wound healing, platelet-derived growth factor (PDGF) serves as both a chemoattractant and mitogen for fibroblasts, potently stimulating their invasion of the fibrin clot over a period of several days. A mathematical model of this process is presented, which accurately accounts for the sensitivity of PDGF gradient sensing through PDGF receptor/phosphoinositide 3-kinase-mediated signal transduction. Analysis of the model suggests that PDGF receptor-mediated endocytosis and degradation of PDGF allows a constant PDGF concentration profile to be maintained at the leading front of the fibroblast density profile as it propagates, at a constant rate, into the clot. Thus, the constant PDGF gradient can span the optimal concentration range for asymmetric phosphoinositide 3-kinase signaling and fibroblast chemotaxis, with near-maximal invasion rates elicited over a relatively broad range of PDGF secretion rates. A somewhat surprising finding was that extremely sharp PDGF gradients do not necessarily stimulate faster progression through the clot, because maintaining such a gradient through PDGF consumption is a potentially rate-limiting process.

INTRODUCTION

Wound healing requires the concerted efforts of multiple cell types (1,2). Of these cells, dermal fibroblasts are responsible for reproducing, remodeling, and later contracting the extracellular matrix (ECM) to rebuild and condense the regenerated tissue, but first they must invade the provisional matrix of the fibrin clot. The fibroblast response, through a combination of directed migration (taxis) and proliferation, develops over several days thereafter, forming fibroblast-dense granulation tissue that gradually penetrates the clot. The progression of wound invasion and closure is controlled by soluble factors released in the clot and by the ECM, and overactive cell proliferation and matrix deposition results in pathologically abnormal healing, or fibrosis (3,4). Fibroblast invasion, as a rate-limiting process in wound healing, is thus a critical factor in the efficiency and fidelity of tissue repair.

The first step in the wound-healing cascade is the aggregation and activation of blood platelets, which release platelet-derived growth factor (PDGF) in the clot. PDGF acts as a potent chemoattractant for fibroblasts (5–7) and also stimulates their proliferation, thus increasing the density of fibroblasts as they migrate into the fibrin clot. Other important stimuli released by platelets include transforming growth factor β, which eventually stimulates fibroblasts to produce collagen and fibronectin ECM, and insulin-like growth factor-1, which enhances fibroblast proliferation (8–12). Another early event, typically elicited in the first 24 h postwounding (13), is the recruitment and activation of neutrophils and macrophages, mediators of innate immunity. Activated macrophages secrete PDGF, transforming growth factor β, and other growth factors, reinforcing or replacing platelet-derived signals aimed at fibroblasts. Although it is clear that many factors influence fibroblast responses, PDGF is unique in its ability to accelerate fibroblast invasion (6,10,14).

How are fibroblast responses elicited by PDGF transduced inside the cell? PDGF receptors belong to the well-studied receptor tyrosine kinase class of signal transducers; as with other receptor tyrosine kinases, ligand-induced dimerization of PDGF receptors activates their intrinsic kinase activity, leading to receptor transphosphorylation on selected intracellular tyrosine residues and recruitment of cytosolic signaling proteins (15–17). Of particular importance in PDGF signaling is the phosphoinositide (PI) 3-kinase pathway (18,19), due to its particularly strong activation by the PDGF receptor (20,21) and its roles in multiple functional responses (22). PI 3-kinases catalyze phosphorylation of phosphatidylinositols, producing specific 3′ PI lipid second messengers in the plasma membrane. This pathway leads to modulation of the cytoskeleton, in a localized manner that is biased by chemoattractant gradients, and is required for PDGF-stimulated motility and chemotaxis (23–27).

We have recently characterized the kinetics, dose responsiveness, and spatial regulation of PDGF receptor-mediated PI 3-kinase signaling, culminating in an experimentally validated, mechanistic model of PDGF gradient sensing (28–32). Compared with the chemotactic responses of the model cell systems, Dictyostelium discoideum and neutrophils, we found that PDGF gradient sensing in fibroblasts exhibits less sensitivity in general and a greater dependence on the midpoint concentration of the gradient. Optimal gradient sensing is observed in a relatively narrow range of PDGF concentrations that yield near maximal PI 3-kinase recruitment without saturating PDGF receptor occupancy. From the standpoint of wound healing, this insight at the single-cell level has led us to question how a suitable gradient might be maintained throughout the clot as the fibroblast population invades, a question I aim to address here through analysis of an invasion model focused on PDGF-stimulated responses.

Spatially directed cell migration and wound invasion have been described and analyzed extensively using mathematical models. Migration of a cell population in a chemoattractant field has long been treated as a macroscopic transport process, with cell dispersion and chemotaxis modeled by analogy to molecular diffusion and convective mass transfer, respectively (33–36). Another important modification was the recognition that chemoattraction is receptor-mediated and thus saturable, which lent some molecular/mechanistic basis to the modeling of eukaryotic cell movement ((37), and references therein); however, even recently this important aspect has not been adopted in most models. Elegant, phenomenological models focusing specifically on cellular dynamics during wound healing have described ECM and growth factor effects on fibroblast migration, proliferation, and/or collagen production, and have illustrated the importance of fibroblast taxis in the invasion process (38–44). None of these models faithfully accounts for receptor dynamics and intracellular processes, however, to include ligand binding as well as receptor activation, regulation, and signaling, and in most cases it is neither practical nor prudent to do so. With our recent analyses, we may now connect the dots between the PDGF concentration profile and PI 3-kinase-mediated fibroblast migration signaling.

Incorporating an accurate description of PDGF gradient sensing in a simplified model of wound invasion, I show that a constant PDGF gradient and chemotactic signaling can be maintained at the leading front of the fibroblast population through induced, receptor-mediated endocytosis and consumption of PDGF. This effect is directly coupled to the level of receptor activation and thus intracellular signaling to proliferation and migration responses, forming an integrated control mechanism for chemotaxis in tissues.

MODEL FORMULATION

Single-cell level: coarse-grained model of PI 3-kinase signaling

Cell migration is assumed here to depend on PI 3-kinase signaling, which we have quantitatively characterized. In developing the model at the intracellular level (Fig. 1 a), all variables are defined as dimensionless quantities. Across the characteristic length of a cell, defined as ɛ, the PDGF gradient is assumed to be nearly constant, giving the local ligand concentration u at any relative cellular position ξ (0 ≤ ξ ≤ 1, with ξ = 0 and ξ = 1 defining the trailing and leading edges, respectively):

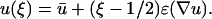(1)

For gradients in more than one spatial dimension, u(ξ) is treated as a vector with orthogonal components. Note that, in this article, averaging over cell orientations relative to the gradient is implicit. The local receptor activation at quasi-steady state, r, is related to the local ligand concentration by the expression,

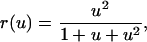(2)

which accurately reflects the degree of cooperativity observed in the dose response of PDGF receptor phosphorylation (28). The quasi-steady-state approximation is appropriate given the separation of timescales between the receptor- and cell population-level dynamics (minutes versus hours). Although the phenomenological form of Eq. 2 was offered previously (32), it is shown in Appendix A to be a more than adequate approximation of a mechanistic model incorporating receptor binding, dimerization, and trafficking. From Eq. 2, the average receptor activation in the cell is obtained by integration, with the suitable approximation

(3)

Equation 3 is derived in Appendix B.

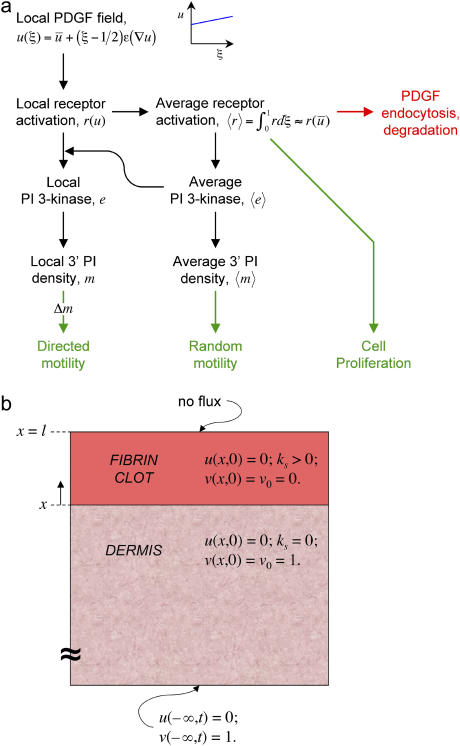
FIGURE 1.

Model schematic. (a) Single-cell model. The dimensionless PDGF concentration u controls activation of cell surface receptors locally; activated receptors bind the PI 3-kinase enzyme, drawing upon a homogeneous cytosolic pool, yielding a local increase in the density of 3′ PI lipid messengers in the plasma membrane. Random migration and chemotaxis are assumed to depend on the average 3′ PI density and the asymmetry in the 3′ PI profile, respectively, and are coupled in a consistent way to fibroblast proliferation and receptor-mediated PDGF clearance. (b) Macroscopic model. The PDGF concentration u and fibroblast density v evolve as a function of time and location in two tissue domains: a finite clot, where PDGF is produced by platelets and macrophages (normalized rate k_s), and an adjoining, semi-infinite dermis, where the fibroblasts are initially found at a constant, resting density (v = 1). A one-dimensional patch wound with clot thickness l is depicted here.

Cell motility signaling is mediated by an intracellular second messenger, m (3′ PIs), produced by an activated enzyme, e (PI 3-kinase), which is activated by receptor-mediated binding at the plasma membrane. Both are expressed as scaled variables. The equations governing enzyme activation are as derived previously (32). The fractional enzyme activation, e, is assumed to be at all locations in pseudo-equilibrium with a common pool of cytosolic enzyme molecules, with relatively fast enzyme diffusion in the cytosol:

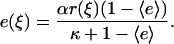(4)

The two constant parameters here are the receptor/PI 3-kinase expression ratio, α, and normalized dissociation constant, κ. The average enzyme binding, 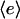, also satisfies the equilibrium relationship, allowing one to solve for it:

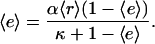(5)

The steady-state messenger density profile, m(ξ), is subject to production by locally activated and cytosolic PI 3-kinase and consumption characterized by a first-order rate constant (28,30). It is scaled such that its average value, 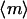, is 1 when 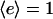; in the absence of stimulation, with all PI 3-kinase in the cytosol (e = 0), the basal value of m is defined as m₀. Hence, the balance on m is given by

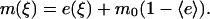(6)

The potential blurring of the messenger gradient via its lateral diffusion in the cell membrane is not considered here, although a suitable approximation of this effect may be incorporated readily (results not shown).

Cell population level: phenomenological model of fibroblast invasion

The following equations apply to the wounded region, which includes both the fibrin clot and the neighboring dermis (Fig. 1 b). It is assumed that conditions are such that there is a natural separation of timescales between platelet and macrophage activation and the fibroblast invasion process described by the model, and between invasion and the ultimate contraction and resolution of the wound. At the tissue level, cells at a given location experience an average PDGF concentration 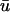; in light of the approximation in Eq. 3, the distinctions between u and 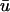, and between r and 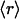, are dropped from this point forward. The dimensionless fibroblast density, v, is scaled such that v = 1 in the dermis initially. PDGF is secreted only in the clot, at a constant, normalized rate k_s (in general, k_s could depend on time and location in the wound), and the ligand is degraded spontaneously and through receptor-mediated endocytosis by fibroblasts:

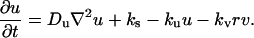(7)

Cells proliferate at a normalized net rate R_p, and they invade the clot through random migration (dispersion coefficient D_v) and chemotaxis:

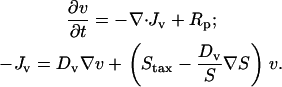(8)

The general form of the cell migration flux vector, J_v, which includes the variation of random migration speed with chemoattractant concentration (chemokinesis), is from the derivation by Alt (34). S is the average cell migration speed, and the chemotactic flux is given by S_taxv, where the chemotactic cell speed S_tax depends on the extracellular PDGF gradient experienced by cells at that location (see below). Note that when higher chemoattractant concentrations yield faster random migration, chemokinesis and chemotaxis are in opposition with respect to migration in the direction of the chemoattractant gradient.

Although cell migration signaling is the focus of this model, fibroblast proliferation and survival are arguably just as important in the fibroblast invasion process. An appropriate phenomenological expression is assumed here, without regard to specific pathways for now:

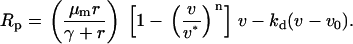(9)

The parameters γ, v*, and k_d account for saturability of proliferation signaling, contact inhibition, and survival threshold, respectively. The resting fibroblast density, v₀, is taken as 1 in the dermis and 0 in the clot.

The final piece of the wound invasion model is to specify the relationship between intracellular signaling and the flux of the fibroblast population introduced in Eq. 8. Random migration and chemotaxis are coupled to the average concentration and concentration gradient of the messenger inside the cell, respectively (see also Appendix B); the difference in m between the front and rear portions of the cell, Δm (technically, a vector), determines the fraction of the cell speed that contributes to directed motion, akin to a tug-of-war. Dimensionless quantities are thus defined:

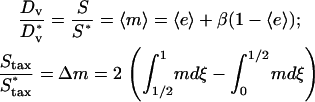(10)

Random and directed components of fibroblast migration are thus related in a consistent way to PDGF receptor-mediated PI 3-kinase activation. In that regard, it is noteworthy that the same dependence was assigned for the dispersion coefficient D_v and overall cell speed S. D_v is proportional to S²P, where P is the persistence time, and so the ratio of D_v/S is proportional to the average run length SP. Consistent with Eq. 10, experiments with fibroblasts in culture have shown that this quantity is insensitive to perturbations, at least in certain situations; S and P are affected in a reciprocal manner (45). D_v and S are related to 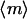simply by proportionality constants; a more complicated dependence could be imposed if warranted. With Eq. 10, the migration flux in Eq. 8 may now be written as

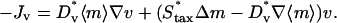(11)

Model implementation

Definitions and base values of all model parameters are summarized in Table 1, and justification for certain parameter values is offered in Appendix C. Finite-element model calculations were performed using FEMLAB (COMSOL, Burlington, MA). Initial and boundary conditions were as follows (Fig. 1 b). In both the clot and dermis, u = 0 initially. It was assumed that PDGF is only produced in the clot, that cell quiescence is only supported in the dermis (v(0) = v₀ = 1 in the dermis, 0 in the clot), and that there is no flux of PDGF or cells (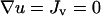) normal to the top surface of the “skin”. Concentrations and fluxes were matched across the clot-dermis interface. The dermis was extended to a sufficient size (well beyond what is plotted in the figures), with a characteristic length scale several times greater than (D_u/k_u)^1/2, and therefore it was specified that u = 0, v = 1 at the outer boundary of the dermis.

TABLE 1.

Model parameters and order-of-magnitude, base-case values

Parameter	Definition	Base value
ɛ†	Characteristic cell dimension	0.03 mm
α	Maximum receptor/PI 3-kinase ratio	10
κ	Dimensionless KD, PI 3-kinase recruitment	0.1
m0	Dimensionless 3′ PI density, unstimulated	0.1
ks	Normalized PDGF secretion rate in the clot	1 h−1
Du	PDGF diffusion coefficient in tissue	0.01 mm2/h*
ku	Rate constant, spontaneous PDGF degradation	0.1 h−1
kv	Rate constant, fibroblast-mediated PDGF depletion	1 h−1*
μm	Rate constant, maximal fibroblast growth	0.05 h−1
γ	Dimensionless saturation constant, fibroblast growth	0.1
v*	Dimensionless, contact-inhibited fibroblast density	10
n	Contact inhibition sensitivity parameter	3
kd	Rate constant, fibroblast death	0.01 h−1
v0	Dimensionless resting cell density, clot (dermis)	1 (0)
Dv*	Maximum fibroblast dispersion coefficient	3 × 10−4 mm2/h*
Stax*†	Maximum chemotactic cell speed	0.1 mm/h*

^*The values of these parameters are discussed in Appendix C.

^†The product of these two parameters may be lumped as one in this model.

RESULTS

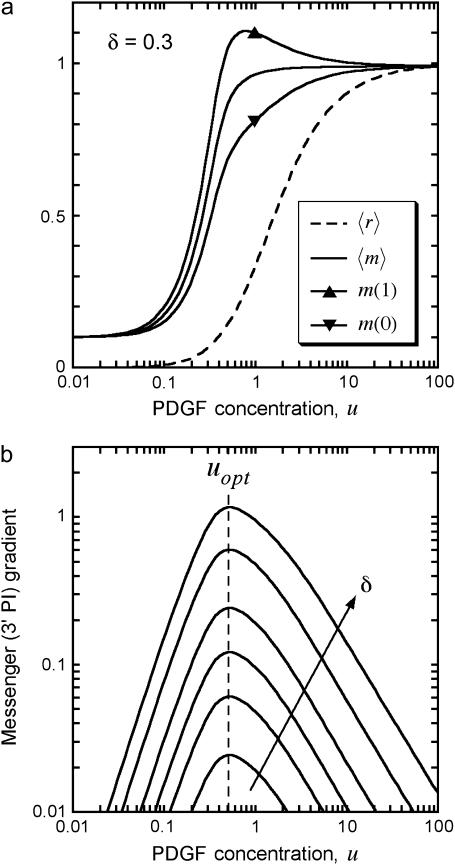
PDGF gradient sensing and fibroblast chemotaxis is optimized in a specific range of PDGF concentrations

A key feature of the model, based on quantitative experiments (28,30,32), is saturable activation of the PI 3-kinase enzyme (Eqs. 4 and 5). This means that near-maximal enzyme recruitment can be achieved with submaximal receptor activation, requiring that α > 1 and α ≫ κ; order-of-magnitude values of α = 10, κ = 0.1 are consistent with the dose responses of PDGF receptor and PI 3-kinase activation in mouse fibroblasts. Thus, there is an intermediate regime of PDGF concentrations that yield near-maximal enzyme recruitment and random fibroblast migration (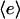, , 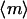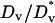≈ 1) yet also elicit the greatest contrast in signaling between the front and rear of a cell in a PDGF gradient (Fig. 2 a). The PDGF concentration that gives optimal gradient sensing and chemotaxis, u_opt, is insensitive to the relative steepness of the gradient, defined as 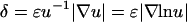. For the values of α and κ chosen, u_opt ≈ 0.5, and u ∼ 0.2–2 yield at least half-maximal gradient sensing (Fig. 2 b). At much lower PDGF concentrations, enzyme activation is low; at much higher concentrations, enzyme activation is maximal, but receptor saturation precludes gradient perception.

FIGURE 2.

PDGF gradient sensing is optimized at intermediate PDGF concentrations. Analysis of the single-cell model (Eqs. 2–6) is presented, assuming α = 10, κ = 0.1, m₀ = 0.1. (a) Average receptor activation and 3′ PI messenger level, and messenger levels at the front (ξ = 1) and back (ξ = 0) of the cell, for PDGF gradients of varying midpoint PDGF concentration and a 30% gradient across the cell. (b) The difference between front and rear messenger levels [m(1) – m(0) = e(1) – e(0)] is plotted as a function of midpoint PDGF concentration with relative gradient δ = 0.02, 0.05, 0.1, 0.2, 0.5, or 1. The curves peak at u = u_opt ≈ 0.5.

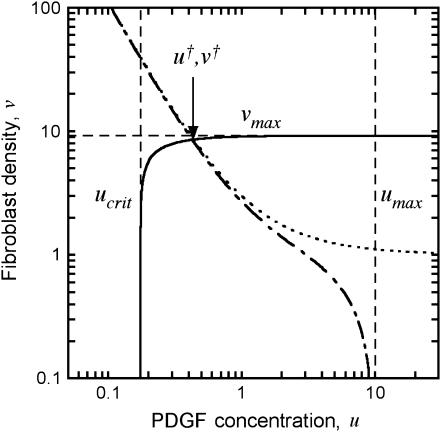
Reconciliation of fibroblast proliferation and fibroblast-mediated PDGF consumption defines the dynamic range of PDGF concentration in the clot

The other pivotal feature of the model is the coupling between receptor activation and cell density-dependent PDGF consumption through receptor-mediated endocytosis, which results in a trade-off between cell proliferation and PDGF depletion. This trade-off is best assessed through an analysis of steady-state nullclines associated with the PDGF and fibroblast conservation equations in the clot, assuming no spatial gradients (Fig. 3). Equations 7–9 thus reduce to

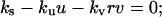(12)

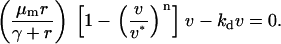(13)

Equations 12 and 13 have a trivial solution, with v = 0, u = k_s/k_u = u_max; Eq. 13 dictates that the cells can only proliferate when the PDGF concentration exceeds a critical value u_crit, satisfied by 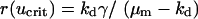, and it follows that the trivial solution is only stable when 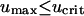. When u_max exceeds u_crit, there exists an asymptotically stable nontrivial solution (u^†,v^†), with v^† > 0, u^† < u_max. One concludes that the dynamic range of PDGF concentration in the clot, where v = 0 initially, is bounded by u^† and u_max. Hence, the PDGF dynamic range is defined as

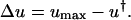(14)

Aspects of the proliferation term, Eq. 9, determine the sensitivity of the solution (u^†,v^†) to the PDGF rate constants, k_s, k_u, and k_v. With a threshold receptor activation that must be met for survival in the clot, and contact-inhibited growth at high cell density, one finds regimes in which only one of u^† or v^† is sensitive to these rate constants. When PDGF is limiting for cell growth, the PDGF concentration is maintained near its critical value, with u^† ≈ u_crit. Conversely, when PDGF production is in excess, the cell density is maximal, with v^† ≈ v_max = 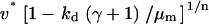. In the intermediate or “cusp” regime, one finds that u^† ∼ u_crit and v^† ∼ v_max (Fig. 3).

FIGURE 3.

Dynamic range of the PDGF concentration profile in the clot. The steady-state nullclines, in the absence of spatial gradients, describe conditions where PDGF synthesis and consumption are balanced (Eq. 12; dot-dashed curve, base-case parameters; dotted curve, consumption by fibroblasts only, with k_u = 0) or where there is zero net fibroblast growth (Eq. 13, solid curve). The intersection of these curves, (u^†,v^†), satisfies both criteria, bounding the PDGF concentration profile between u^† and u_max = k_s/k_u.

The analysis outlined here suggests how chemotaxis of the invading fibroblasts may be sensitive to PDGF concentration yet robustly maintained throughout the clot. As long as u^† ∼ u_opt or less, and u_max ≫ u_opt, the fibroblasts will experience a suitable gradient for chemotaxis. Further, the sharpness of the gradient will be maximized when Δu is large and the cell density is high; the aforementioned cusp region of PDGF production best satisfies these criteria.

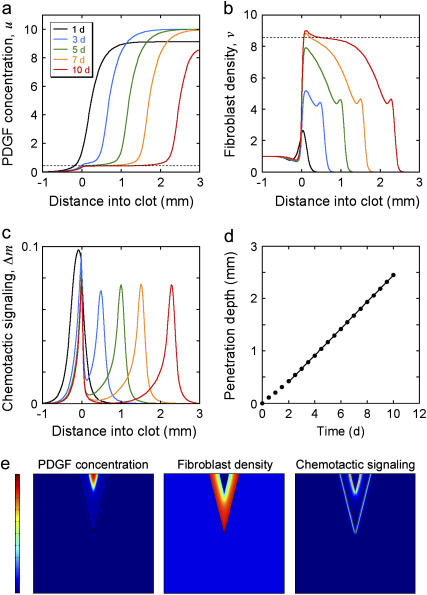
Fibroblast-mediated PDGF consumption allows for the maintenance of a constant PDGF gradient that propagates in tandem with the invading fibroblast front

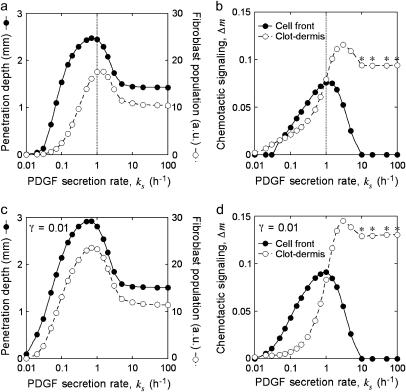
Model calculations were performed for a “patch” wound, with gradients in only one dimension, assuming a clot thickness l = 3 mm (Fig. 1 b; Fig. 4, a–d). At time t = 0, there is no PDGF in either the clot or dermis, and fibroblasts reside only in the dermis at a constant density v = 1; thereafter, PDGF is produced at a constant rate throughout the clot, and fibroblasts are allowed to move from the dermis into the clot. The calculated PDGF and fibroblast density profiles at various times, with base-case parameter values (Table 1), are shown in Fig. 4, a and b. The PDGF concentration profile that develops over several days shows that defining its dynamic range in terms of u_max and u^† (Eq. 14) is a good approximation (Fig. 4 a); for the base case, u_max = 10, corresponding to a low nanomolar PDGF concentration (see Appendix C). The cell density profile develops two maxima for this set of parameter values, at the clot-dermis interface and at the leading fibroblast front (Fig. 4 b). These maxima coincide spatially with sharp peaks in chemotactic signaling, Δm, brought about by the contrasts in PDGF production (clot-dermis) and fibroblast density (leading front) (Fig. 4 c). After ∼3 days, the shapes of the cell front and PDGF concentration profiles remain roughly the same as they move through the clot, and the penetration depth of the fibroblast front (defined here as the maximum distance into the clot where v = 0.5) increases linearly with time (Fig. 4 d). These features of the PDGF concentration and fibroblast density profiles were reproduced in a two-dimensional “slash” wound model (Fig. 4 e and Movie 1 in the Supplementary Material), with nearly identical Δm peak values and fibroblast penetration rate. In the following sections, it is demonstrated that the Δm peak at the leading front and the overall rate of fibroblast invasion stem from the PDGF dynamic range, Δu, and its relation to u_opt, as analyzed in Figs. 2 and 3.

FIGURE 4.

Progression of wound invasion. (a–d) Model calculations were performed assuming base-case parameters and a one-dimensional patch clot with thickness l = 3 mm. Profiles of PDGF concentration u ((a) dashed line, u = u^† = 0.424), fibroblast density v ((b) dashed line: v = v^† = 8.53), and chemotactic signaling Δm (c) at the indicated times in days are shown. (d) The fibroblast penetration depth, defined here as the maximum distance into the clot at which v = 0.5, increases linearly with time after a transient of ∼2 days. (e) Model calculations assuming a two-dimensional slash clot. The V-shaped clot has a depth of 10 mm and a width of 5 mm at the top; the dimensions of the tissue portion shown are 20 × 20 mm. Profiles of PDGF concentration (scale, 0–10), fibroblast density (scale, 0–10), and chemotactic signaling (scale, 0–0.1) are shown at t = 7 days. The magnitude of the latter incorporates both x- and y-components of the Δm vector, according to .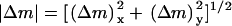

Fibroblast invasiveness is driven by chemotactic signaling at the leading fibroblast front and is optimized across a reasonably broad range of PDGF secretion rates

When the normalized rate of PDGF secretion, k_s, is either too low (v^† ≪ v_max or u_max < u_opt) or too high (u^† ≫ 1), it is reasoned that fibroblast chemotaxis and thus the rate of wound invasion should suffer. From a series of model calculations, it was confirmed that the fibroblast penetration depth at t = 10 days is indeed reduced when the PDGF secretion rate, k_s, is increased or decreased significantly (Fig. 5 a). Also shown on this plot is the total cell population size in the clot (), also at t = 10 days, another indicator of the quality of response. In the limit of very low k_s, such that u_max < u_crit, there is a net cell death in the clot, and the fibroblast population cannot propagate into the wound. As k_s is increased above the critical value, there is a sharp increase in penetration depth, corresponding with an increase in the PDGF dynamic range, Δu. At intermediate PDGF secretion rates, the system is surprisingly robust, with an order-of-magnitude span of k_s values (0.2–2 h⁻¹) that support fibroblast invasion velocities >80% of the maximum. As the secretion rate is increased even further, sufficient for receptor saturation (u^† ≫ 1; r ≈ 1), fibroblast invasiveness is reduced to a plateau level. In that limit, it is noted that Eqs. 8–11 reduce to the generalized form of Fisher's equation (46):

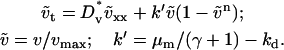(15)

In this case, it is well known that the cell density profile will assume a constant shape that propagates at a velocity of 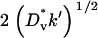, in close agreement with the fibroblast invasion rate reached at high k_s (assessed as in Fig. 4 d; results not shown).

FIGURE 5.

Sensitivity of fibroblast invasiveness to PDGF secretion rate. Calculations were performed as in Fig. 4, a–d, after adjustments to the normalized PDGF secretion rate, k_s. The dimensionless saturation constant for fibroblast proliferation was set at the base-case value (0.1, a and b; the vertical lines signify the base-case value of k_s, 1 h⁻¹) or 10-fold lower (c and d). Fibroblast penetration depth (determined as in Fig. 4 d) and population size (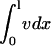) were assessed at t = 10 days (a and c). The peak values in chemotactic signaling, Δm, at the leading fibroblast front and clot-dermis interface at t = 7 days are shown for the same parameter values (b and d). The asterisks signify that the peak at the clot-dermis interface is progressively moved rearward into the dermis as k_s gets large.

Of the two peaks in chemotactic signaling, Δm, the one formed at the leading fibroblast front drives invasion of the fibroblast population, whereas the other at the clot-dermis interface serves a different, potentially important role: preventing the fibroblast profile from dispersing back into the dermis. Fibroblast invasiveness, as judged by penetration depth and population size in the clot, therefore correlates well with the Δm peak at the fibroblast front and not with the peak at the dermal interface as k_s is varied (Fig. 5 b). With either very low or very high k_s, there is no discernible Δm peak at the leading front.

As one might predict, the robustness of fibroblast invasiveness as a function of PDGF secretion rate is enhanced when the threshold for fibroblast proliferation signaling is lowered (Fig. 5, c and d). With a 10-fold reduction in the value of γ (Eq. 9), the peak in fibroblast penetration depth is broadened modestly, but it is the width of the fibroblast population size peak that more significantly reflects the support of fibroblast proliferation at lower values of k_s (compare Fig. 5, a and c). As reasoned from the analysis presented in Fig. 3, the reduction in γ tends to increase the steady cell density v^† and reduce the minimum PDGF concentration needed for cell stasis in the clot, u_crit; both effects contribute to enhance the PDGF gradient steepness and thus chemotactic signaling at the leading fibroblast front, particularly in the low k_s regime (compare Fig. 5, b and d).

Large PDGF gradients promote fibroblast invasion but can also suppress the invasion rate

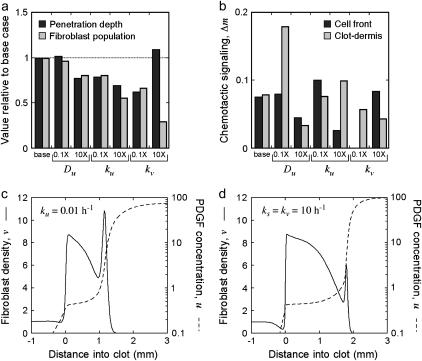
The other parameters that directly affect the PDGF profile are D_u, k_u, and k_v, which were shifted from their base values by one log in each direction to assess their impact on fibroblast invasiveness (Fig. 6 a) and the magnitudes of the two chemotactic signaling peaks (Fig. 6 b). Reducing the value of D_u, the PDGF dispersion coefficient, has little effect on the leading Δm peak or fibroblast penetration depth; the base D_u value is already sufficiently low, such that the steepness of the PDGF gradient at the leading fibroblast front mirrors that of the fibroblast density profile (the Δm peak at the dermal interface is sharpened considerably, however). In contrast, a 10-fold increase in D_u is sufficient to smear out the PDGF concentration profile and modestly reduce fibroblast invasiveness. The effects of changes in the value of k_v, the receptor-mediated PDGF consumption rate constant, are similarly predictable. Reducing the k_v value by 10-fold leaves the PDGF concentration profile in the saturated regime, ablating the leading Δm peak and reducing invasiveness, whereas an increase in k_v yields offsetting effects on the PDGF gradient; Δu is widened (by reducing u^†, such that u^† ≈ u_crit, and leaving u_max unchanged), but at the expense of the cell density that can be supported. Finally, shifting the value of k_u, the rate constant characterizing background PDGF degradation, yielded the most surprising results. Increasing its value by 10-fold inhibits invasiveness, which is easy enough to explain based on a correspondingly lower u_max, but decreasing its value also results in reduced fibroblast penetration. This was contrary to expectation, because decreasing k_u has little effect on the PDGF concentration trailing the invading fibroblast front, u^† (Fig. 3), while u_max and thus Δu are increased; indeed, a higher Δm value is observed at the leading front.

FIGURE 6.

Sensitivity of fibroblast invasiveness to other PDGF rate constant values. Calculations were performed as in Fig. 5 after adjustments to rate constants in the PDGF balance, Eq. 7. See accompanying descriptions in the text. (a) Fibroblast penetration depth and population size at t = 10 days, normalized by the base-case values, after a 10-fold reduction or increase in the indicated parameter values. (b) Peak values in chemotactic signaling, Δm, at the leading fibroblast front and clot-dermis interface at t = 7 days were determined for the same parameter values as in a. (c and d) Fibroblast density and PDGF concentration profiles at t = 7 days for the case of a 10-fold reduction in k_u (c) or 10-fold increases in both k_s and k_v (d); these parameter shifts yield the same u_max and nearly identical u^† values.

How is the correlation between chemotactic signaling and invasiveness broken? The decrease in k_u affects the cell density profile dramatically, with a large spike in cell density at the leading front (Fig. 6 c), and random migration of this peak rearward proved to be the mitigating factor with respect to the overall specific cell flux 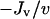. This is forced in the model by the saturation of receptor activation and thus the rate of fibroblast-mediated PDGF consumption at high PDGF concentrations, which limits the fibroblasts' ability to maintain the extremely sharp PDGF gradient as they move. The analysis in Fig. 3 indicated that a similar PDGF concentration profile is achieved by increasing both k_s and k_v by 10-fold. In this case, the leading fibroblast density peak is less pronounced and shows improved invasiveness, as the larger value of k_v better equips the cells for maintenance of the large PDGF gradient (Fig. 6 d). Still, the enhancement in penetration depth, 13% greater than the base case, was deemed modest relative to the near twofold increase in chemotactic signaling at the leading front (results not shown).

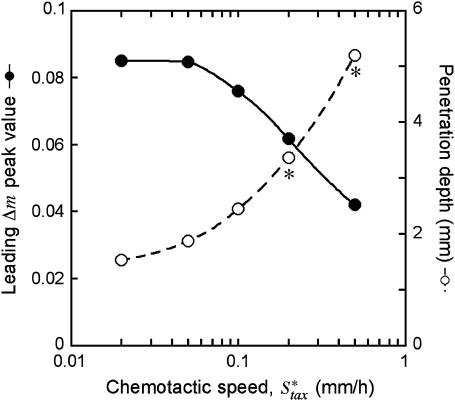
To further test the limitations on fibroblast invasion rate, the maximum chemotactic cell speed (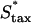) was varied, applying a different form of pressure on the cells to move faster (Fig. 7). Here, the problem of balancing PDGF consumption and fibroblast invasion rates is solved by broadening the fibroblast density and PDGF concentration profiles as 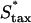is increased, yielding a reduction in the leading Δm peak value. As one might predict, the penetration depth increases linearly with the product of Δm(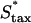) (results not shown).

FIGURE 7.

Variation of fibroblast invasiveness with maximum chemotactic cell speed. The peak value in chemotactic signaling (Δm) at the leading fibroblast front is a decreasing function of the maximum chemotactic cell speed, 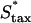. The penetration depth at t = 10 days, evaluated as in Fig. 5, a and c, increases linearly with the change in the product of Δm(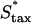). Above the base-case 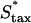value of 0.1 mm/h, the fibroblasts reach the exterior boundary of the 3 mm clot by 10 days, and so the comparable penetration depth was estimated by extrapolation of the constant propagation velocity regime (values denoted by asterisks).

DISCUSSION

The impetus of this work was not to provide accurate estimates of fibroblast density profiles or invasion rates during wound healing, as it is fully acknowledged that the PDGF-centric model presented here is a gross simplification of the actual fibroblast response. Certainly the role of the ECM, coupled with fibroblast-mediated ECM alignment and remodeling as considered in other modeling efforts (39,40,47), is at best macroscopically lumped in the cell migration and proliferation parameters, as are the effects of the many other molecular and physical factors at play. Rather, the goal was to explain the robustness of fibroblast invasiveness over relatively large length scales, across which the PDGF concentration profile might span several logs, given the characterized sensitivity of PDGF gradient sensing. In this sense, the major conclusions are expected to be sufficiently general.

Model analysis suggests that a constant PDGF gradient, suitable for stimulating fibroblast chemotaxis, can be maintained through PDGF receptor activation-dependent consumption of PDGF. The model is based on receptor-mediated endocytosis and intracellular proteolysis of PDGF, which is estimated to be significant based on the density of cells in tissue and the low concentrations at which growth factors are effective. In principle, the cells might also utilize a pathway linking receptor-mediated signaling to secretion or activation of an extracellular protease, as considered in models of ECM-driven haptotaxis (38,44,48). Thus, the PDGF gradient seen by the leading cohort of invading fibroblasts spans concentrations defined by the presence versus absence of cells, and near-optimal fibroblast invasion is stimulated across a reasonably broad range of PDGF secretion rates. Reconciliation of the trade-offs presented by the rates of cell proliferation, receptor-mediated PDGF consumption, and cell chemotaxis ultimately defines and in some cases limits fibroblast invasiveness.

Given that receptor-mediated consumption of PDGF is cell density-dependent, the sensitivity of the fibroblast proliferation term to PDGF concentration turns out to be an important consideration for chemotaxis (as explored in Figs. 3 and 5). By reducing the saturation constant γ, proliferation in the clot becomes insensitive to PDGF, effectively decoupling proliferation and chemotaxis and allowing greater flexibility in how the fibroblast population responds. A priori, one can expect then that adding to the model factors that influence fibroblast proliferation but not chemotaxis (e.g., insulin-like growth factor-1, certain components of the clot ECM) will produce the same effect.

Aside from adding more spatiotemporally varying regulatory factors, how might this invasion model be refined? As implemented in certain studies (40,49–53), a hybrid model wherein discrete fibroblasts respond stochastically to continuous external variables may be constructed. Heterogeneity among individual cells, with respect to expression levels of receptors, PI 3-kinase, and any other cell-associated molecules, for example, may then be considered. In the context of the model, such heterogeneity would affect each cell's contribution to PDGF consumption as well as its responsiveness to the gradient, perhaps leading to invasion of a select fibroblast subpopulation. From our perspective, a more significant refinement would be to replace the hypothetical, phenomenological model of cell movement control (Eqs. 10 and 11) with a more mechanistic description. Clearly, the difficult task of relating, through quantitative experiment and analysis, 1), signal transduction through PI 3-kinase and/or other pathways, 2), cell polarity and cytoskeletal dynamics, and 3), cell migration characteristics needs to be undertaken if we wish to better understand chemotactic invasion processes.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX A: PDGF RECEPTOR ACTIVATION AT QUASI-STEADY STATE

A kinetic model is presented here, starting from our previous PDGF receptor dimerization mechanism and model (28), with the addition of slower processes such as receptor synthesis, basal receptor turnover, and intracellular receptor trafficking. Treatment of those additional effects follows the recent model of human growth hormone receptor activation (54). It is subsequently shown how this reasonably detailed model may be approximated by the scaled, steady-state receptor activation function (Eq. 2), with no additional parameters. The kinetic balances are:

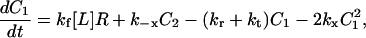(16)

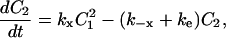(17)

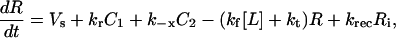(18)

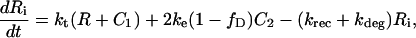(19)

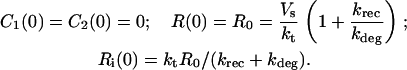(20)

C₁, C₂, R, and R_i are the numbers of 1:1 ligand-receptor complexes, active PDGF receptor dimers, empty PDGF receptors, and internalized receptors available for recycling, respectively. It is assumed that a constant fraction f_D of receptors internalized as dimers are marked for degradation and thus not included in R_i (one might find it reasonable to further assume f_D = 1, but I wish to derive a more general case). [L] is the extracellular concentration of PDGF, assumed to be constant or changing slowly, and V_s is the rate of new PDGF receptor synthesis. R₀ is defined as the number of PDGF receptors on the cell surface in the absence of PDGF. Other rate constant definitions are given in the sources cited above.

Combining Eqs. 16–20 reveals the following steady-state balance on receptor species:

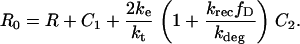(21)

Equation 17 gives the relationship between C₂ and C₁ at steady state:

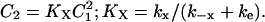(22)

Together with Eq. 16 and after some simplification, one obtains the dimer fraction, 2C₂/R₀, at steady state:

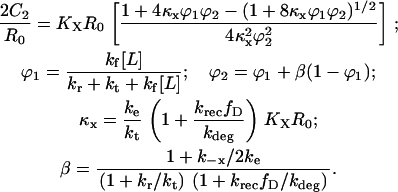(23)

Normalizing 2C₂ by its saturation value, 2C_2,max (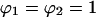), gives the fractional receptor activation, r:

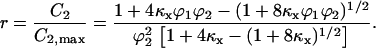(24)

In dimensionless form, with [L] scaled by (k_r + k_t)/k_f ≈ K_D,L, Eq. 24 contains only two adjustable parameters, κ_x and β, yet it was found that one can simplify this expression even further. Order-of-magnitude estimates, based on parameters reported previously (28) and analysis presented in Appendix C, place κ_x ∼100 and β no greater than ∼0.01. It is readily shown that Eq. 24, with β = 0, is equivalent to the solution obtained with the a priori assumption of pseudo-equilibrium for 1:1 complex formation (C₁ = [L]R/K_D,L), as justified previously (28). With β ≪ 1, it was found that Eq. 24 is closely approximated by Eq. 2, with u defined as [L]/L*, where L* is whichever value of [L] gives r = 1/3.

APPENDIX B: DERIVATION OF AVERAGE RECEPTOR ACTIVATION AND SECOND MESSENGER METRICS

Expressions are derived here for 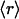, the average receptor activation level, 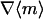, the gradient of average 3′ PI level across various cells, and Δm, the asymmetry in 3′ PI density within a single cell (chemotactic driving force) (Eq. 10). Given a linear PDGF gradient on the length scale of a cell, u(ξ) (Eq. 1), and the local receptor activation function r(u) from Eq. 2, the mean receptor activation is as follows:

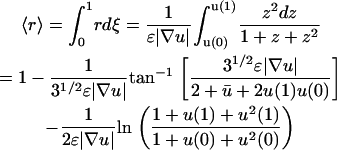(25)

Performing a series expansion, with appropriate simplification,

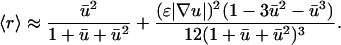(26)

Analysis of Eqs. 25 and 26 reveals that the second term in Eq. 26 may safely be neglected, and so it is reasonable to further approximate that

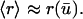(27)

The distinction between u and 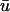may now be dropped. With Eq. 27, one applies the chain rule to obtain

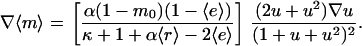(28)

Under the same conditions for which Eq. 25 simplifies to Eq. 27,

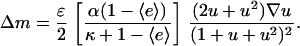(29)

Or, in terms of the relative gradient (percent difference) across the cell, ,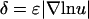

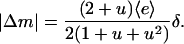(30)

Note that Eqs. 29 and 30 are equivalent to the result that one obtains assuming a linear messenger profile inside the cell (i.e., Δm ≈ [m(1) – m(0)]/2 = [e(1) – e(0)]/2).

APPENDIX C: PARAMETER ESTIMATES

PDGF diffusion

The diffusion coefficient of PDGF (24 kDa) in solution is ∼10⁻⁶ cm²/s (∼0.3 mm²/h), but proteins are far less mobile in tissues (55,56). The base-case value of D_u used in the model (0.01 mm²/h) is ∼30 times lower than for diffusion in aqueous solution.

Fibroblast-mediated PDGF depletion

To derive the magnitude of the rate constant k_v, one needs to estimate the PDGF concentration, fibroblast density, and receptor activation level that give, in dimensionless terms, u = 1, v = 1, and r = 1, respectively. The first of these is derived from the steady-state receptor activation model (Eq. 24, with β ≈ 0). From our previous analysis of PDGF receptor activation in NIH 3T3 fibroblasts, the parameter grouping k_eK_XR₀ is estimated as ≈0.21 min⁻¹, and K_D,L ≈ 1.5 nM (28). The grouping R₀/V_s is the characteristic time required to synthesize all of the cell's initial surface receptors. A reasonable range, based on EGF receptor synthesis in fibroblasts, is R₀/V_s ≈ 300–1000 min (57,58). Together with f_D ≈ 1, it is estimated that κ_x ≈ 60–200. Noting that r = 1/3 when u = [L]/L* ≈ 1, it is estimated that L* ∼ 0.1–0.2 nM. A modest fibroblast density in dermal tissue is taken as ∼10⁵ cells/ml (<1 vol %). Considering the influence of receptor downregulation by ligand-induced endocytosis, perhaps balanced by induction of PDGF receptor synthesis at the level of transcription (28,59–61), the maximum number of activated PDGF receptors at steady state is considered to be in the range of 10⁴–10⁵/cell. Together with an endocytic rate constant for activated PDGF receptors ≈0.2 min⁻¹ (28) and the range of L* estimated above, one obtains a range of 0.1–2 h⁻¹ for k_v, from which a value of 1 h⁻¹ was deemed reasonable. It should be noted that another model of dermal wound healing assumed a lower fibroblast density in the dermis (∼10⁴/ml) but in essence the same contact-inhibited density as inferred here (∼10⁶/ml) (39).

Cell migration parameters

The characteristic value of the cell dispersion coefficient, 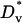, (3 × 10⁻⁴ mm²/h = 5 μm²/min) is based on quantitative cell tracking measurements of fibroblasts migrating on ECM in two and three dimensions (45,62–64). Maximum fibroblast speeds in those experiments, under random migration conditions, is ∼0.5 μm/min (0.03 mm/h). The base-case estimate of the maximum chemotactic cell speed, 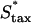, is conservatively taken as ∼3 times this value (0.1 mm/h) to reflect enhancement in net cell translocation rate when membrane protrusion and other motility processes are spatially asymmetric.