Statistical Validation Based on Parametric Receiver Operating Characteristic Analysis of Continuous Classification Data

Abstract

Rationale and Objectives

The accuracy of diagnostic test and imaging segmentation is important in clinical practice because it has a direct impact on therapeutic planning. Statistical validations of classification accuracy was conducted based on parametric receiver operating characteristic analysis, illustrated on three radiologic examples.

Materials and Methods

Two parametric models were developed for diagnostic or imaging data. Example 1: A semiautomated fractional segmentation algorithm was applied to magnetic resonance imaging of nine cases of brain tumors. The tumor and background pixel data were assumed to have bi-beta distributions. Fractional segmentation was validated against an estimated composite pixel-wise gold standard based on multi-reader manual segmentations. Example 2: The predictive value of 100 cases of spiral computed tomography of ureteral stone sizes, distributed as bi-normal after a nonlinear transformation, under two treatment options received. Example 3: One hundred eighty cases had prostate-specific antigen levels measured in a prospective clinical trial. Radical prostatectomy was performed in all to provide a binary gold standard of local and advanced cancer stages. Prostate-specific antigen level was transformed and modeled by bi-normal distributions. In all examples, areas under the receiver operating characteristic curves were computed.

Results

The areas under the receiver operating characteristic curves were: Example 1: Fractional segmentation of magnetic resonance imaging of brain tumors: meningiomas (0.924–0.984); astrocytomas (0.786–0.986); and other low-grade gliomas (0.896–0.983). Example 3: Ureteral stone size for treatment planning (0.813). Example 2: Prostate-specific antigen for staging prostate cancer (0.768).

Conclusion

All clinical examples yielded fair to excellent accuracy. The validation metric area under the receiver operating characteristic curves may be generalized to evaluating the performances of several continuous classifiers related to imaging.

The accuracy of diagnostic test and imaging segmentation is important in clinical practice because it has a direct impact on therapeutic planning. Recently, continuous classification tools are more frequently used in practice, each of which yields continuous rather than ordinal rating data, and methods for evaluation have been developed (1–4). For example, with the availability of three-dimensional (3D) imaging acquisitions and reconstructions, volumetric data are increasingly available. Another example is the use of cancer markers such as CA125, which is important for cancer detection and staging.

In contrast, traditional diagnostic tests were often based on an ordinal rating scale. For example, a five-point scale might be adopted for observer performance evaluations, where 1 = definitely normal, 2 = probably normal, 3 = probably abnormal, 4 = probably abnormal, and 5 = definitely abnormal. A discrete subjective rating method was used in a multi-modal (magnetic resonance [MR], computed tomography [CT], and ultrasound) comparative ovarian cancer technology assessment study (5,6), in one of a series of prospective multicenter Radiologic Diagnostic Oncology Group clinical trials sponsored by the funded by the National Institutes of Health in the 1990s. The advantages of the continuous diagnostic over ordinal scale are that detailed information is preserved, they are more natural with the advancements in measurement tools and computing methods, and enable more objective interpretations. Ordinal rating data will not be the focus of this article. Instead, we will evaluate the performances of continuous classifiers only.

To conduct a validation analysis based on continuous classifiers, the most important component in the validation framework is a binary gold standard, which is the classification truth for each observation in terms of two mutually exclusive classes, eg, tumor versus non-tumor, diseased versus non-diseased. For simplicity, we assume a two-class truth by labeling the control class as C₀ and disease class as C₁. A popular method for assessing the overall classification accuracy is a receiver operating characteristic (ROC) curve (7,8). It is a function of sensitivity versus (1-specificity) at all possible decision threshold. We have previously developed several methods, including nonparametric, semi-parametric, and parametric, for estimating and comparing ROC curves derived from continuous data (1–4).

In this article, we evaluate and validate the accuracy of several continuous diagnostic classifiers including semiautomated brain MRI segmentation (9), spiral CT of ureteral stone size (10), and prostate-specific antigen (PSA) for cancer staging (11). We conduct secondary analyses to validate their classification accuracy, illustrated on these examples. The connection between these three clinical examples is that the diagnostic and classification systems all generate continuous, rather than categorical, data. In addition, we develop statistical methods to estimate the unknown gold standard and to apply an appropriate transformation of non-normality data that are frequently observed.

MATERIALS AND METHODS

Example 1: Magnetic Resonance Imaging of Brain Tumors

Imaging protocol

A total of nine patients were selected from a neurosurgical database of 260 brain tumor patients, of which three had meningiomas (M), three astrocytomas (A), and three other low-grade gliomas (G) (9). The imaging protocol consisted of the following parameters: patient heads were imaged in the sagittal planes with a 1.5T MRI system (Signa, GE Medical Systems, Milwaukee, WI), with a postcontrast 3D sagittal spoiled gradient recalled acquisition with contiguous slices (flip angle, 45°); repetition time, 35 ms; echo time, 7 ms; field of view, 240 mm; slice-thickness,1.5 mm; 256 × 256 × 124 matrix).

Fractional segmentation

Instead of applying binary manual segmentation, Warfield et al (12) have proposed an automated segmentation algorithm that yields voxel-wise continuous probabilistic measures indicative of the tumor class. The automated fractional segmentation was applied only to a single, randomly selected two-dimensional MR image containing the tumor. The relative signal intensity was modeled as a normal mixture of the two classes based on an initial semi-automated binary segmentation.

Binary gold standard

Using the same randomly selected slice, an interactive segmentation tool (MRX, GE Medical Systems, Schenectady, NY) was used and executed on an Ultra 10 Workstation (Sun Microsystems, Mountain View, CA). The structures were contoured by three independent imaging readers, blinded to the semiautomated fractional segmentation results. An anatomic object was defined by a closed contour, and the computer program labeled every voxel of the enclosed volume. Of the gold standard, the background and brain tumor pixels defined the C₀ and C₁ classes, respectively.

Example 2. Spiral Computed Tomography of Uretral Stones

Imaging protocol

A total of 100 unenhanced spiral CT scans were obtained to evaluate flank pain in patients with obstructing ureteral stones documented by means of chart review (10). A standard protocol was used (280 mA; 12 kVp; pitch, 1.0–1.6). The imaging thickness was 5 mm, with images reconstructed at 5-mm increments.

Ureteral stone size

Two radiologists initially reviewed the CT scans independently and blindly to derive several imaging features, one of which was the size of the ureteral stone measured in millimeter, using a caliper on CT images. This size variable was treated as the classifier to predict treatment options.

Binary gold standard

The actual treatment received by each subject was considered as the gold standard, either spontaneous passage (class C₀) or surgical intervention (class C₁).

Example 3. Prostate Specific Antigen for Prostate Cancer Staging

Prostate cancer biopsy and PSA

In a subset of patients enrolled in a multicenter prospective Radiologic Diagnostic Oncology Prostate Cancer Staging Clinical Trial (11), magnetic resonance imaging was performed in 213 patients with prostate cancer after excluding the missing data in the baseline biopsy, 180 cases were included here. Results of the PSA were treated as the main diagnostic variable.

Binary gold standard

Radical prostatectomy was performed in all patients to provide the gold standard, which was based on histopathology to separate patients further into local (periprostatic invasion of tumor and spread of diseased to the seminal vesicles and lymph nodes) versus advanced (stages A and B) disease. Of the gold standard, the local and advanced stages were regarded as classes C₀ and C₁, respectively.

Statistical Methods

Mixture modeling of distributions

Depending on the types of data, different types of mixture distributions for the two populations were chosen, we now focus on two parametric models, named the bi-beta and bi-normal models. In Example 1 on brain tumor segmentations, because the semi-automated fractional segmentation yielded pixel-wise probability of the tumor class, the range of the data is restricted to [0, 1]. A convenient model for such probabilistic data is a mixture of two beta distributions, here called the bi-beta model. Characteristics of the beta distribution are found in classical literature on statistical distribution theory (13). Specifically, the distribution of the fractional segmentation in class C₀ was assumed to be F(x) ~ Beta(α₀,β₀), while the distribution of the fractional segmentation probabilities in class C₁ was assumed to be G(y) ~ Beta(α₁, β₁). The ROC parameters were the four shape parameters in these beta distributions. For simplicity, we assumed pixel-wise independence, and more complicated models that incorporate spatial homogeneity will be developed for validation in the future.

In Examples 2 and 3, the diagnostic classifiers were PSA and ureteral stone size (in mm), respectively, thus both outcome variables take on positive values rather than probabilistic values as in Example 1. We applied a nonlinear normality Box-Cox transformation algorithm (see Appendix A.1) (2–4,14). After such a parametric transformation, a mixture of two normal distributions can be assumed, known as the bi-normal model in the literature (1,15,16). We assume here that the measurements in class C₀ have a standard normal distribution, while the measurements C₁ of the diseased class have a normal distributions. The bi-normal model in the literature is a slight variation in terms of parametrization of these two ROC parameters.

Composite gold standard estimate from multiple manual segmentations

In Example 1, for the purpose of validation, it is necessary to derive a composite binary gold standard by combining multiple manual segmentations by three independent image readers. We have applied our recently developed, Simultaneous Truth and Performance Level Estimation (STAPLE) program (outlined in Appendix A.2.) (17–19), an automated expectation-maximization (EM) algorithm (20) for estimating the composite gold standard. For each pixel, a maximum likelihood estimate of the composite gold standard of tumor or background class was optimally determined over all image readers’ results. This algorithm has a major advantage over ad hoc combination methods such as a pixel-wise or voxel-wise voting scheme across all readers. Instead, it considers a higher weight for readers with estimated better quality in segmentation (17,18).

Normality transformation

As mentioned in both Examples 2 and 3, the classification data may not be suitable for the bi-normal model without any transformation. We applied a nonlinear Box-Cox (14) normality transformation to the continuous and positively valued classification data (see Appendix A.1.).

Receiver operating characteristic analysis

Statistical validations were carried out using ROC analysis. In the radiology literature, Metz et al (1) have provided a maximum-likelihood solution for estimating ROC parameters, with algorithms implemented with software available from the Kurt Rossmann Laboratories for Radiologic Image Research, Department of Radiology, at the University of Chicago (Chicago, IL). Conventionally, and as in these popular programs, a bi-normal model is often used, with two ROC parameters, a standardized difference in the means, and the ratio of the standard deviations of the distributions of the diseased and control classes. These are simple functions of the two sets of (mean, standard deviation) parameters of these classes. As an extension, we specified the four shape parameters in the bi-beta model as the ROC parameters.

Once these parameters are estimated by maximizing the likelihood function, at a pre-specified cutoff threshold value, the true positive fraction (or sensitivity) and the true negative fraction (or specificity) = 1 − (false positive fraction) are estimated.

An ROC curve consists of all (1-specificity, sensitivity)-pair by varying all possible threshold values (see notations and assumptions for ROC analysis given in Appendix A.3). In Example 1, stratified ROC analyses were performed in each tumor case and type against the estimated composite voxel-wise gold standard using the STAPLE program (17–19) based on an EM algorithm (20). Over all thresholds γ (γ ⊆ [0,1]), the four bi-beta ROC parameters were estimated via matching moments (see details in Appendix A.4).

In Examples 2 and 3, after estimated Box-Cox transformations, the bi-normal ROC parameters were estimated by maximizing the likelihood function over all possible thresholds γ ⊆ ℜ (see details in Appendix A.5).

An invariance property of the ROC curve states that with any monotone transformation such as the nonlinear Box-Cox transformation considered here, the underlying ROC curve, as well as the resulting area under the curve (AUC), remain the same (3). However, the parametric assumptions may not be appropriate and the estimated AUC biased if, for example, skewed data are fitted with a bi-normal model, therefore leading to unsatisfactory goodness-of-fit (16).

Numerical Simulation of the Receiver Operating Characteristic Parameters and the Resulting Area Under the Curve

Bi-beta model

We assessed the relationship between possible underlying parameters and the resulting ROC curves via either numerical integration or exact computations. We considered hypothetical scenarios of the mixture distributions having equal variances or unequal variances in the resulting samples in the two classes. As the mean of a two-parameter Beta(α,β) distribution is α/(α + β) and the variance is αβ/{(α + β)²(α + β+1)}, we set one of the two shape parameters of the distribution as 1 for simplicity. By varying the value of the other parameter, we achieved different underlying mixtures. The ROC parameters considered were as follows:

(α₀, β₀,α₁, β₁) = {(1,1,1,1);(1,1.5,1.5,1);(1,2,2,1); (1,2.5,2.5,1);(1,3,3,1); (1,9,9,1)} with equal variances, and = {(1,2,1.5,1); (1,1.5,3,1); (1,9,3,1); (1,2,9,1)} with unequal variances. In this model, the population means had various combinations from 10%–90% in fractions. Similarly, the population variances were flexibly varied.

Bi-normal model

In this model, the distribution under class C₀ is standard normal, while the population means of class C₁ was expressed as α. By considering small population standard deviations close to 1, the location-shift in these the distribution of C₁ ranged from 0.25–2.5. Similar simulation studies for the bi-normal model have been carried out previously (3). The parameters considered were (α,β) = {(0.25,1); (0.5,1); (0.75,1); (1,1); (1.25,1); (1.5,1); (1.75,1); (2,1); (2.25,1); (2.5,1)} with equal variances, and = {(0.25,1.5); (0.5,1.5); (0.75,1.5); (1,1.5); (1.25,1.5); (1.5,1.5); (1.75,1.5); (2,1.5); (2.25,1.5); (2.5,1.5)} with unequal variances.

RESULTS

Example 1: Magnetic Resonance Imaging of Brain Tumors

Estimated Binary Gold Standard

In Figure 1, we present the manual segmentation results of a meningioma case according to an index summary of all three imaging readers’ performances (Fig 1, left panel). The estimated composite gold standard is also provided (Fig 1, right panel).

Figure 1.

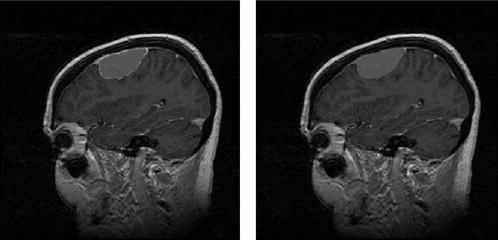
Three segmenters’ manual segmentation results (left) and the estimated composite binary pixel-wise ground truth (right) for Example 1 on MRI brain segmentations of meningiomas, astrocytomas, and gliomas.

Receiver operating characteristic analysis

Table 1 presents the estimated bi-beta ROC parameters for all cases, with the corresponding resulting AUCs for these cases. High accuracy values were achieved using the semi-automated segmentation algorithm for all cases. The AUCs for the meningiomas were 0.924, 0.968, and 0.984 for meningiomas, 0.786, 0.926, and 0.986 for astrocytomas, and 0.896, 0.916, and 0.983 for other mixed low-grade gliomas. The ROC curves in Figure 2 showed case-to-case variations of segmentation accuracies, which were the smallest for meningiomas but were the largest for astrocytomas.

Table 1.

The Bi-Beta ROC Parameters and AUCs for Example 1

Tumor Type	${\widehat{\alpha }}_0$	${\widehat{\beta }}_0$	${\widehat{\alpha }}_1$	${\widehat{\beta }}_1$	AUC
Meningioma	0.029	0.885	0.269	0.041	0.984
	0.032	1.523	0.130	0.023	0.968
	0.172	0.783	1.184	0.339	0.924
Astrocytoma	3.208	5.504	1.379	0.794	0.786
	0.250	1.130	1.010	0.304	0.926
	0.177	2.679	0.217	0.009	0.986
Glioma	0.004	0.339	0.109	0.016	0.983
	0.106	0.573	1.169	0.411	0.916
	0.351	1.190	1.131	0.404	0.896

Figure 2.

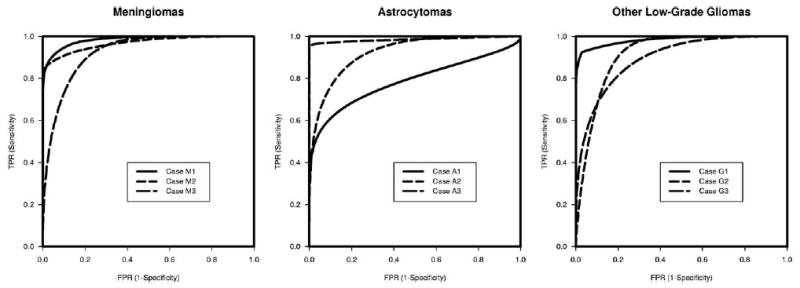
Bi-beta ROC curves for Example 1 on MRI brain segmentations of meningiomas (left), astrocytomas (center), and gliomas (right).

Example 2. Spiral Computed Tomography of Ureteral Stones

Box-Cox transformation

The estimated Box-Cox transformation coefficient was $\widehat{\lambda }=0.11$. The test of normality showed that the P values were .05 and <.001 before this transformation, in comparison to .92 and .94 after the transformation, for the distributions of the ureteral stone sizes in the spontaneous passage and the interventional samples, respectively.

Receiver operating characteristic analysis

The estimated ROC parameters were $(\widehat{\alpha },\widehat{\beta })=(1.17,0.85)$, with a resulting AUC of 0.813, which was fairly high. See Figure 3 for both the unsmooth nonparametric empirical and the smooth parametric bi-normal ROC curves. The parametric curve followed closely to the empirical curve.

Figure 3.

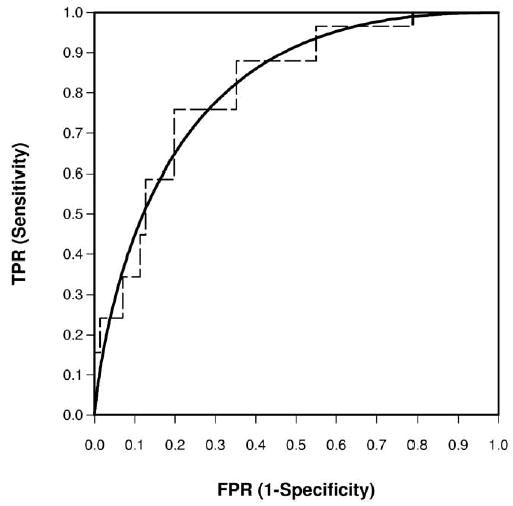
Empirical and bi-normal ROC curve for Example 2 on CT of ureteral stone sizes for predicting treatment outcomes.

Example 3. Prostate Specific Antigen for Prostate Cancer Staging

Box-Cox transformation

The estimated Box-Cox transformation coefficient $\widehat{\lambda }=0.33$. The test of normality showed that the P values were .003 and <.001 before this transformation, in comparison to .06 and .10 after the transformation, for the PSA values in the local and the advanced prostate cancer stage samples, respectively.

Receiver operating characteristic analysis

The estimated ROC parameters were $(\widehat{\alpha },\widehat{\beta })=(1.20,1.30)$, with an AUC of 0.768, suggesting fair to moderate accuracy. See Figure 4 for the ROC curve.

Figure 4.

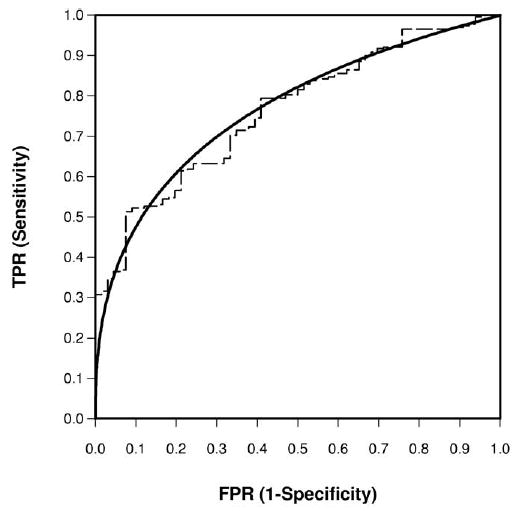
Empirical and bi-normal ROC curve for Example 3 on PSA for prostate cancer staging.

Numerical Simulation of the Receiver Operating Characteristic Parameters and the Resulting Area Under the Curve

Bi-beta model

Table 2 presents the corresponding AUC for the specified bi-beta model parameters.

Table 2.

Bi-Beta ROC Parameters and the Resulting AUCs in a Simulated Study

Variances	${\widehat{\alpha }}_0$	${\widehat{\beta }}_0$	${\widehat{\alpha }}_1$	${\widehat{\beta }}_1$	AUC
Equal	1	1	1	1	0.500
	1	1.5	1.5	1	0.706
	1	2	2	1	0.834
	1	2.5	2.5	1	0.908
	1	3	3	1	0.950
	1	9	9	1	1.000
Unequal	1	3	1.5	1	0.847
	1	1.5	3	1	0.847
	1	9	3	1	0.995
	1	3	9	1	0.995

Bi-normal model

Table 3 presents the corresponding AUC for the specified bi-beta model parameters.

Table 3.

Bi-Normal ROC Parameters and the Resulting AUCs in a Simulated Study

Variances	$\widehat{\alpha }$	$\widehat{\beta }$	AUC
Equal	0.25	1	0.570
	0.50	1	0.638
	0.75	1	0.702
	1.00	1	0.760
	1.25	1	0.811
	1.50	1	0.856
	1.75	1	0.892
	2.00	1	0.921
	2.25	1	0.944
	2.50	1	0.961
Unequal	0.25	1.5	0.555
	0.50	1.5	0.609
	0.75	1.5	0.661
	1.00	1.5	0.710
	1.25	1.5	0.756
	1.50	1.5	0.797
	1.75	1.5	0.834
	2.00	1.5	0.866
	2.25	1.5	0.894
	2.50	1.5	0.917

DISCUSSION

In this article, we have presented both parametric bi-beta and bi-normal models for validating continuous diagnostic or imaging classification results. In the first example, we focus on the performance of a semi-automated fractional segmentation, which gave probabilistic interpretation of the presence of tumor in all pixels in an MR image. The hidden pixel-wise gold standard was estimated using our recently developed EM-algorithm, STAPLE. In the next two examples, we examined cancer marker PSA and CT of ureteral stone size data derived from individual patients. A nonlinear transformation model was applied to these data, enabling a bi-normal parametric model.

To interpret the AUC values, an area of 1 represents a perfect classifier, and 0.5 represents a classifier that has the same accuracy as flipping an unbiased coin. Subjectively, a rough guide is that fair-to-excellent accuracy is achieved when AUC ≥0.7. In a classical article on AUC by Hanley and McNeil (34), the authors gave the sample size necessary in a table for testing various differences between the two correlated AUCs, when one is minimally 0.7.

In all of these clinical examples, we observed satisfactory accuracy, as evidenced by fairly to high AUC values. In Example 1, the estimated AUCs were between 0.786 and 0.986, although the ROC curves in Figure 2 were variable. Thus, the semi-automated segmentation algorithm was moderately to highly accurate, as compared with the composite gold standard derived from three manual segmentations using STAPLE. However, the accuracy was rather case-dependent. The AUCs were reasonably high, at 0.813 and 0.768, for ureteral stone size and for PSA, respectively.

There are several advantages of our proposed ROC validation methodology. The unknown gold standard can be estimated via the STAPLE algorithm. The bi-beta and bi-normal parametric modeling are quite flexible for modeling the distributions of fractional data and positive-valued diagnostic data, respectively. The means and variances of the underlying mixture distributions may be characterized by simple functions of the parameters in these models. In particular, under the bi-normal model, a goodness-of-fit test of normality to assess modeling fitting was conducted using the z-test, with P values reported. These methods are natural extensions of existing methods, such as the bi-logistic or bi-gamma models, found in the literature (21,22).

As a limitation, in the first clinical example, only three radiologist segmentations were used in the brain tumor example. We have previously conducted a digital phantom experiment consisting of one set covering approximately 11% of a 256 × 256 pixel image (18). We assumed three segmenters, one yielding results equal to the ground truth, and one set equal to the ground truth shifted left 10 columns, and set equal to the ground truth shifted right 10 columns. After 11 iterations, STAPLE discovered that one of the segmenters’ result was identical to the ground truth, and the remaining two were slightly incorrect. A comparison between the STAPLE result and other measures, such as those based on a voting rule or using the median of the segmenters, will be investigated in the future.

However, all parametric models should be used with caution. If parametric assumptions are not met, then violations of the corresponding assumptions could lead to poor fitting and inferences. Alternative methods such as nonparametric smoothing methods may be considered, which may be much more computer intensive and less straightforward (23,24).

Statistical validation of classification accuracy may be conducted using several other metrics (16,25), particularly when spatial information is also important in dealing with 2-dimensional imaging pixel or 3D voxel data. For comparing two sets of segmentation results, existing validation metrics other than area under the ROC curve, for example, entropy-based mutual information (26), Jaccard (27) and Dice (28) similarity coefficient, and Hausdorff distance measure (29,30). We have already investigated such metrics in separate articles (19,31).

In summary, we have conducted parametric evaluations of two types of continuous classification data using ROC analysis, with application to three clinical examples. The proposed method may be adapted to several validation tasks in radiologic research, as illustrated in our clinical examples.

A.1. A Box-Cox Normality Transformation

The Box-Cox transformation (14), from a positive-valued measurement X to a real-valued measurement X′, has the form X′ = (X^λ − 1).λ when λ ≠ 0, and = log(X) when λ = 0. The transformation parameter, λ, is estimated by a maximum likelihood method via nonlinear optimization (2). Subsequently, a test of normality may be performed using the z-test (32) under each binary gold standard class to ensure the bi-normal assumption.

Here we now include an S-Plus (http://www.insightful.com) function to estimate the optimal Box-Cox transformation coefficient (l in the following program codes) after entering the x- and y- sample data under classes C₀ and C₁, respectively.

It can be shown that we may maximize the profile log likelihood, a function of λ, conditioned on other ROC parameters (33):

$$\begin{array}{l}\text{arg}\_\text{max}l(\lambda |x_1,\cdots ,x_m,y_1,\cdots ,y_n)=\text{arg}\_\text{max}[-mlog(s_{x\text{'}})\\ -nlog(s_{y\text{'}})+(\lambda -1)\left\{\sum _{i=1}^{m}log(x{\text{'}}_i)+\sum _{j=1}^{n}log(y{\text{'}}_i)\right\}+c]\end{array}$$ (1)

where c is a constant free of the parameters. Because a nonlinear optimization routine is used, we include the S-Plus codes using a built-in a nonlinear minimization function:

bclik<−function(lambda){

m <− length(x); n<− length(y); xlog<− log(x); ylog<− log(y)

if (l = = 0){xnew<-xlog;ynew<-ylog}; else {xnew<− (x^l−1)/l; ynew<− (y^l−1)/l}

m×log(stdev(xnew))+n×log(stdev(ynew))-l-1)×(sum(xlog)+sum(ylog))}nlmin(bclik,0)

A.2. Expectation-Maximization Algorithm for Estimating a Composite Gold Standard

Denote the hidden voxel-wise gold standard by T, and a set of manual segmentations by r = 1,…,R segmenters. For simplicity, assume that their conditionally independent manual segmentations on the same image with a total of l = 1,…,N voxels, yielded binary decisions (eg, tumor versus background; diseased versus non-diseased) B_lr.

Characterize the r-th segmenter’s performance quality by his true specificity (Q_0r) and and sensitivity (Q_1r), respectively. The conditional independence assumes that (B_lr|T_l,Q_0r,Q_1r)⊥(B_lr′|T_l,Q_0r′,Q_1r) for any pair of segmenters, r ≠ r′.

To estimate all of the T_l’s, the maximum likelihood estimate is $\widehat{\text{T}}=\text{arg}\underset{\text{T}}{max}\text{P}(\text{B}|\text{T},{\text{Q}}_0,{\text{Q}}_1)$, for all voxels. However, segmentor-specific quality, Q_0r and Q_1rare unknown. We have developed a software (STAPLE) to iteratively estimate the voxel-wise gold standard using an EM-algorithm (17–20). This algorithm is briefly outlined as follows, with k = 1,…K iterations till convergence:

The expectation (E) step

In the (k−1)-th iteration, let

$$\begin{array}{l}{u}^{(k-1)}=\prod _{r:B_{1r}=1}{\widehat{Q}}_{1r}^{(k-1)}\prod _{r:B_{1r}=0}(1-{\widehat{Q}}_{1r}^{(k-1)})\mathrm{\hspace{0.17em} }\text{and\hspace{0.28em}}{\nu }^{(k-1)}\\ =\prod _{r:B_{1r}=0}{\widehat{Q}}_{0r}^{(k-1)}\prod _{r:B_{1r}=1}(1-{\widehat{Q}}_{0r}^{(k-1)})\end{array}$$ (2)

Define a weight variable, a common notation in an EM-algorithm, for iteration (k−1):

$$w_l^{(k-1)}=f(T_l=1|B_l,{\widehat{Q}}_{0r}^{(k-1)},{\widehat{Q}}_{1r}^{(k-1)})=\frac{u^{(k-1)}\overline{\pi }}{u^{(k-1)}\overline{\pi }+{\nu }^{(k-1)}\pi },$$ (3)

where π = P(T=0) and $\overline{\pi }=1-\pi =P(T=1)$. At k = 0, the initial segmentation quality parameters may be estimated using the median rating or a voting rule as the initial gold standard over R segmenters.

The maximization (M) step

At the k-th iterative step, we maximize the log-likelihood, such that

$$\begin{array}{l}({\widehat{Q}}_0^{(k)},{\widehat{Q}}_1^{(k)})=arg\mathrm{\hspace{0.17em} }{\text{max}}_{(Q_0,Q_1)}\\ \times \mathrm{\hspace{0.17em} }E\left[\text{log}\{f(B|T,Q_0,Q_1)f(T)\}|f(T|B,{\widehat{Q}}_0^{(k-1)},{\widehat{Q}}_1^{(k-1)})\right]\end{array}$$ (4)

and that for the r-th segmenter,

$$\begin{array}{l}({\widehat{Q}}_{0r}^{(k)},{\widehat{Q}}_{1r}^{(k)})=\text{arg\hspace{0.28em}}{\text{max}}_{(Q_0,Q_1)}\mathrm{\hspace{0.17em} }\sum _{l:B_{1r}=0}\{{\overline{w}}_l^{(k-1)}\text{log}{Q}_{0r}\\ +\mathrm{\hspace{0.17em} }{w}_l^{(k-1)}\text{log}(1-Q_{1r})\}+\sum _{l:B_{1r}=1}\{{\overline{w}}_l^{(k-1)}(1-\text{log}{Q}_{0r})\\ +\mathrm{\hspace{0.17em} }{w}_l^{(k-1)}\text{log}{Q}_{1r}\}\end{array}$$ (5)

where $w_l^{(k-1)}$ is the weight variable defined earlier for iteration (k−1), and ${\overline{w}}_l^{(k-1)}=1-w_l^{(k-1)}$.

The maximum likelihood estimates of the segmentation quality parameters are:

$$\begin{array}{l}{Q}_{0r}^{(k)}=\frac{\sum _{l:B_{1r}=0}{\overline{w}}_l^{(k-1)}}{\sum _{l:B_{1r}=0}{\overline{w}}_l^{(k-1)}+\sum _{l:B_{1r}=1}{\overline{w}}_l^{(k-1)}}\mathrm{\hspace{0.17em} }\text{and\hspace{0.28em}}{Q}_{1r}^{(k)}\\ =\frac{\sum _{l:B_{1r}=1}{w}_l^{(k-1)}}{\sum _{l:B_{1r}=1}{w}_l^{(k-1)}+\sum _{l:B_{1r}=0}{w}_l^{(k-1)}}.\end{array}$$ (6)

In our experience, typically only K <20 iterations were required to achieve convergence in several segmentation applications.

A.3. Mixture Modeling in Receiver Operating Characteristic Analysis

For simplicity, independence is assumed in space or over all individuals, both for classes C₀ and C₁. We label the measurements of C₀ as X_i(I = 1,…,m individuals or pixels), and the measurements of C₁ as Y_j (j = 1,…,n individuals or pixels).

At each possible threshold γ, the underlying cumulative distributional function (c.d.f.) under class C₀ is F(γ), with a survival function, and a probability density function (p.d.f.) f(γ). Similarly, at the same threshold γ, the underlying c.d.f. under class C₁ is G(γ), with a survival function, a p.d.f. g(γ).

Each point along the ROC curve, given γ, is the false positive rate $(\text{FPR})=1\text{-specificity}=\overline{F}(\gamma )$ and true positive rate $(\text{TPR})=\text{sensitivity}=\overline{G}(\gamma )$. When the threshold takes on all possible values (ie, γ ⊆ [0, 1] for fractional data and γ ⊆ ℜ for real-valued data), an ROC curve is formed in the space [0,1] × [0,1].

A.4. A Bi-Beta Receiver Operating Characteristic Curve

Assume F(x) ~ Beta(α₀,β₀) and G(y) ~Beta (α₁,β₁). The estimates of the four beta shape parameters are obtained by matching the mean and variances of the beta distributions with what are found in each sample, separately from the nondiseased and from the diseased sample data (I do not understand how exactly this is done). This moment approach is much simpler than solving iteratively for the maximum likelihood estimates, and works well for a large number of pixel data typically encountered in image processing, which we will present with simulations in a separate article.

From the sample data in class C₀, let the mean of be and the standard deviation be s_x; similarly, from the sample data in class C₁, let the mean and standard deviations be &ymacr; and the standard deviation be s_y, respectively, then the estimates of the parameters in the bi-beta model are: ${\widehat{\alpha }}_0=\overline{x}\{\overline{x}(1-\overline{x})s_x^2-1\},{\widehat{\beta }}_0=(1-\overline{x})\{\overline{x}(1-\overline{x})s_x^2-1\}$; similarly, ${\widehat{\alpha }}_1=\overline{y}\{\overline{y}(1-\overline{y})s_y^2-1\}$ and ${\widehat{\beta }}_1=(1-\overline{y})\{\overline{y}(1-\overline{y})s_y^2-1\}$.

The definition of the area under the ROC curve (AUC) (34) is $AUC=P(X<Y)={\int }_{\gamma }\overline{G}(\gamma )d\overline{F}(\gamma )$, which is approximated by numerical integration using S-Plus or other software packages under the bi-beta model.

A.5. A Bi-Normal Receiver Operating Characteristic Curve

Based on a bi-normal model for Examples 2 and 3, after the Box-Cox transformation, assume F(x) ~ N(0,1) and G(y) ~ N(α,β), the maximum likelihood estimates of the parameters may also be derived from the sample means and standard deviations, $\overline{x},{\text{s}}_{\text{x}},\overline{y}$, and s_y. The estimated parameters are: $\widehat{\alpha }=(\overline{y}-\overline{x})/s_x\mathrm{\hspace{0.17em} }and\mathrm{\hspace{0.17em} }\widehat{\beta }=s_y/s_x$.

In the bi-normal model, the AUC is an explicit function of the ROC parameters $AUC=\mathrm{\Phi }\left(\frac{\alpha }{\sqrt{1+{\beta }^2}}\right)$, where Φ is the cumulative probability function of a standard normal distribution (35). The standard error for making inferences based on AUC may be found in the literature (2).