The solitary wave of asexual evolution

Abstract

Using a previously undescribed approach, we develop an analytic model that predicts whether an asexual population accumulates advantageous or deleterious mutations over time and the rate at which either process occurs. The model considers a large number of linked identical loci, or nucleotide sites; assumes that the selection coefficient per site is much less than the mutation rate per genome; and includes back and compensating mutations. Using analysis and Monte Carlo simulations, we demonstrate the accuracy of our results over almost the entire range of population sizes. Two limiting cases of our results, when either deleterious or advantageous mutations can be neglected, correspond to the Fisher–Muller effect and Muller's ratchet, respectively. By comparing predictions of our model (no recombination) to those of simple single-locus models (strong recombination), we show that the accumulation of advantageous mutations is slowed by linkage over a broad, finite range of population size. This supports the view of Fisher and Muller, who argued in the 1930s that progressive evolution of organisms is slowed because loci at which beneficial mutations can occur are often linked together on the same chromosome. These results follow from our main finding, that distribution of sequences over the mutation number evolves as a traveling wave whose speed and width depend on population size and other parameters. The model explains a logarithmic dependence of steady-state fitness on the population size reported recently for an RNA virus.

The scope of evolutionary biology ranges from understanding the origin and extinction of species to predicting the accumulation of drug- or antibody-resistant mutations in a population of microbes during an infection of an individual. Viruses like HIV in which persistent infection of individuals lasts for large numbers of viral generations provide a valuable opportunity to test evolutionary theory by comparing model predictions to a wealth of readily obtained data. In addition, evolutionary models can be used to infer important properties of viral populations.

The forces that produce and maintain genetic variation in a population are thought to be known. These include the “systematic pressures” (1) of mutation, natural selection, and migration. If these were the only forces operating, the fate of the population could be modeled deterministically. However, all evolution occurs in finite-size populations, which is the source of the other major evolutionary factor: random genetic drift. Drift adds a stochastic element to evolution, resulting from the chance sampling of individuals from one generation to the next and from the fact that not all possible genetic variants can be present in a finite population. For given levels of systematic pressure, evolution will be mostly deterministic if the population size is large enough but will be mostly neutral and dominated by drift (2) when the population size is small. Between these two limits there exists a large intermediate region, in which both selection and stochastic effects are critically important (3).

The roles of the principal factors in evolution are well studied by using models restricted to one or two nucleotide sites (loci). The linkage between loci in a chromosome and the associated interdependence of loci is another major factor of evolution presenting a serious mathematical challenge. Seventy years ago, Fisher (4) and Muller (5) suggested that the fixation of advantageous genotypes is slowed down by linkage. They argued further that recombination associated with sex can decouple the fates of genetic variants (alleles) at different loci. Later, Hill and Robertson (6) showed that selection of an allele at one locus increases genetic drift at a second linked locus, decreasing the effectiveness of selection at both loci. Recent analytic (7) and simulation-based (8) work supports this view. Felsenstein (9) argued that the views of Fisher (4), Muller (5), and Hill and Robertson (6) are essentially the same. Quantitative studies of this effect either consider two or three loci, use pseudorandom simulation, or make drastic simplifying assumptions.

A second major effect of linkage is Muller's ratchet (9), which is the steady accumulation of deleterious mutations via genetic drift. Simply put, when drift and mutation operate, the best-fit genotype in the population will eventually be lost, despite the action of selection; then the next best-fit genotype will be lost, and so on. The loss of the fittest genotypes will be irreparable unless some other process recreates individuals of comparable fitness. One such process is recombination. Thus, Muller's ratchet has figured prominently in discussions of the evolution of sex (10–14). Back mutations at mutated loci can, in principle, also counteract Muller's ratchet, but when such loci are sparse in a genome, back mutations are rare. It is known experimentally that the loss of fitness due to a mutation at one locus can be compensated by mutations at other loci (15). Interaction such as this between loci, or epistasis, has been shown to be an efficient deterrent of Muller's ratchet (16–18).

Prior analytic studies of Muller's ratchet have considered one of two possible extremes. In the one limit, when a population is very small, all individuals are of the same genotype nearly all of the time, and events of fixation of new alleles are well-separated in time (19–21). In the opposite limit, when a population is very large, the distribution of genomes over the number of deleterious mutations has to be considered. The main idea of the approach used in this case is that the distribution is nearly always close to an equilibrium distribution (22). After the best-fit genotype is lost from population, this equilibrium is regained rapidly. The average time to loss of the best-fit genotype has been calculated by using diffusion theory (23–26).

In the present work, we consider a model of multilocus evolution that does not include recombination but does include advantageous, deleterious, and compensating mutations. We predict the rate of either decline or advance in fitness for arbitrary values of the parameters and compare these results to the well-studied case of very strong recombination. When either the frequency of mutant alleles or the population size is sufficiently large, deleterious mutations can be neglected, and advantageous mutants accumulate. In this case, our results represent an accurate prediction for the Fisher–Muller effect. In the opposite limit, in which advantageous mutations are not important and deleterious mutation accumulate, our results give the rate of Muller's ratchet. In contrast to previous studies of the Fisher–Muller effect (7, 13, 27), we do not consider fixation events of single advantageous mutants. Instead, we count together as a group all of the sequences with the same number of uncompensated deleterious mutations (22) and study the time dependence of the size of each group. We treat all of the groups deterministically, with the exception of the smallest, best-fit group (28, 29). In contrast to previous studies of Muller's ratchet, our framework does not depend on the population being either genetically uniform or close to the infinite-population equilibrium. As a result, our findings are valid over a very broad range of population parameters and can be used to predict the overall evolution rate for a variety of experimental populations. We show how the model can be applied to data from vesicular stomatitis virus passed in cell culture (30, 31). Detailed mathematical derivations are published in Mathematical Appendix as supporting information on the PNAS web site, www.pnas.org. We present the principal results below.

The Multilocus Model of Asexual Populations

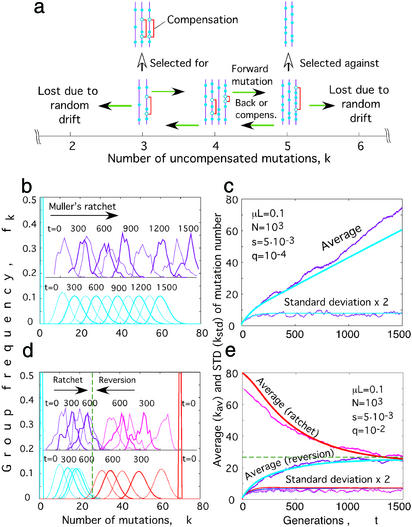
The model (Fig. 1a) considers a haploid population containing a fixed number of DNA or genomic RNA sequences (genomes), N, each comprising L nonconserved nucleotide sites (loci). There is no recombination. Each locus can be in one of two states (alleles): better fit (defined as wild type) or less fit (mutant). We model Wright–Fisher reproduction (1, 4). Each generation, every sequence in the population is replaced by its progeny, the average number of which is proportional to the fitness of the sequence. We assume that the population size is constant through time. Each mutant allele a sequence carries decreases its log fitness by a small amount s (the selection coefficient). The actual number of progeny of a sequence varies randomly around the average value, according to the Poisson distribution, restricted by the condition that the total number of sequences remains constant. Mutations occur after progeny are generated at average rate μ per locus per generation. If the locus is in the wild-type state, the mutation is deleterious to fitness (forward) with fitness cost s, and if the locus is in the mutant state, the mutation is advantageous (back).

Figure 1.

(a) A model for genetic evolution of many linked loci in a haploid population. Sequences are grouped according to the number of uncompensated mutant loci per sequence, k. Filled circles show mutant (less-fit) loci. Open circles connected by brackets show compensated mutations. Green arrows show events of forward, back, and compensating mutations. (b–e) Two numerically obtained examples of evolution of a population at a low (b and c) and moderate (d and e) density of mutant/compensating loci per mutant locus, q. Parameter values are shown in c and e, respectively. (b and d) The frequency of sequences with k mutant loci at different times (shown on the curves). Ragged curves obtained by pseudorandom simulation correspond to Muller's ratchet (purple), initial value k = 1 and to its reversion (magenta), initial k = 70. The smooth curves (cyan for the ratchet and red for reversion) were obtained numerically by using the semideterministic approximation (Eqs. 2, 6, and 8–10 in Mathematical Appendix). (c and e) Corresponding time dependence for the average and the standard deviation of k (wave width). Dashed lines in d and e show the steady-state value of k_av.

In real biological systems, log fitness may be nonadditive over loci, because different regions of RNA and proteins representing the genomic sequences interact with each other in various ways. We include this effect (epistasis, or coselection) as follows. For each locus that is in the less-fit state, there is a fraction q of all loci at which a mutation can occur to fully compensate the deleterious effect of the mutation at the locus (21) (within q, we include a back mutation at the same locus). If the first locus is in the better-fit state, forward mutations at these other loci decrease fitness, and back mutations increase it, as if in the absence of epistasis. In this model of epistasis, all sequences with the same number of uncompensated mutant loci, k, have the same fitness, exp(-sk), and we count them together as one group (Fig. 1a). This model implies that: (i) whether a locus is in the wild-type or the mutant state or is compensating depends on the state of other loci; (ii) a sequence with maximum fitness 1 is not unique; (iii) the number of locus differences between a sequence and a best-fit sequence is, generally, not equal to k. The existence of compensatory mutations is well established experimentally for a number of viruses and bacteria (15, 32–36), although the degree of compensation is often not 100%. A compensatory mutation, for example, can restore the proper folding of a protein (or RNA) or the local binding between two protein (or RNA) regions impaired by a mutation at the first locus.

The choice of an appropriate mathematical method depends on the range of model parameters (s, μL, q, N) and the average number of the uncompensated mutations per sequence, k_av. For RNA viruses, the typical mutation rate per locus, μ, is in the range ∼10⁻⁴ to 10⁻⁵, and the number of loci under consideration (i.e., of nonconserved nucleotides) is L ∼ 10²–10³. The parameter relevant to this work is the effective mutation rate per genome, μL. For a number of RNA viruses, the total mutation rate per genome has been estimated to be between 0.1 and 1 (37). However, these estimates extrapolate from rates measured at a few loci to the entire genome and do not take into account that many mutations will be lethal or very strongly deleterious. For long-term evolution considered here, only substitutions with small s are relevant, so that we can safely assume that μL < 0.1. [In HIV, we have estimated that nucleotides with s ∼ 0.01 occupy 10–20% of the genome and exhibit typically two, not four, as assumed in ref. 37, variants per nucleotide (38, 39). Assuming that other RNA viruses are similar in this respect, these two observations lower an effective genomic rate, as compared with estimates in ref. 37, by the factors of 0.16 and 1/3, respectively. Excluding deletions and insertions included in ref. 37, and taking into account that μL is defined per virus replication cycle, not per RNA replication cycle, yields additional factors, 1/1.4 and 2, respectively.] We note that our Monte Carlo results show that predictions of the model are accurate even when μL is not much less than one.

The relevant range of the selection coefficient, s, which generally varies widely among nucleotides, depends on the time scale of interest. Here we focus on long time scales, on the order of 10² to 10³ generations, and assume that s is much less than the effective mutation rate per genome, μL. Although the range of q is unknown, we estimate it as being between its minimum value, 1/L ∼ 10⁻³, and 10⁻² (see Fig. 4). We are interested in the entire range of population sizes, N ≫ 10, and a broad range of k_av, 0 < qk_av < 0.5.

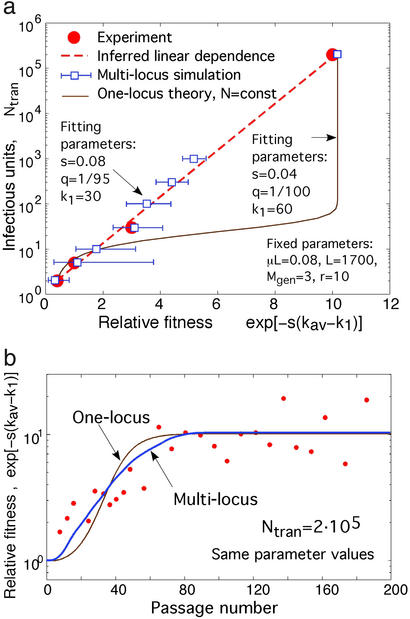
Figure 4.

Fit of theory to experimental data for vesicular stomatitis virus. The red circles are data points (30, 31). Open blue squares and the thick blue line are the best-fit values obtained from pseudorandom simulation of the model in Fig. 1a generalized for the experimental setup described in the text. Thin brown lines show the best-fit values for the one-locus model (20, 44) of a well-mixed population of a constant size, N_tran. (a) Relation between N_tran and the critical fitness determined, as in the experiment, as the average value that did not change between passages 0 and 20. The red dashed line shows an inferred linear dependence (30). At N_tran < 10³, fitness was averaged over 30 simulation runs. Blue bars show the standard deviation predicted for the average over six experiments (31). (b) Dependence of the average fitness on the passage number at a large value of N_tran. Data points (and the largest-N point in a) are from Fig. 1d in ref. 30. The thick blue line was obtained in a single run of pseudorandom simulation of a population of a constant size N_tran; the groups k containing >100 sequences were treated deterministically (Eq. 2). The values of the fitting parameters and of the fixed parameters estimated from independent data are shown. Overlapping virus generations in the experiment are modeled with M_gen = 3 nonoverlapping generations per passage. The amount of virus in a plaque is assumed to expand by a factor of r = 10 per generation (larger values of r yield similar results). k₁ is the number of uncompensated mutant loci in the reference variant. The efficient value of μL per virus replication cycle is explained in the text.

Semideterministic Approximation and Solitary Wave

The main idea of our mathematical treatment, which applies if s ≪ μL, was based on observing the distribution of sequences over k through time in Monte Carlo simulations (ragged curves in Fig. 1 b and d). We observed that, unless the population size N was very small, (i) a typical distribution contains many groups of sequences indexed by k, and (ii) most groups contain a large number of sequences. Thus, changes in the distribution may be treated nearly deterministically. The relevant evolutionary factors affecting very large groups are mutation and selection but not drift. The frequencies of these groups obey a deterministic equation (Eqs. 1 or 2; Mathematical Appendix). In contrast, the groups at the edges of distribution are small and subject to random drift that may cause these groups to be lost from a population (Fig. 1a). Based on a standard one-locus diffusion model, we implemented a cutoff condition determining when an edge group is regarded to be lost (Eqs. 3–10). The more important of the two edges is the left edge, which contains the best-fit sequences present in a population.

Using this semideterministic approach, which takes much less computer time than pseudorandom simulation, we calculated numerically the time dependence of the average frequency of sequences with k loci in the mutant (less-fit) state for various sets of parameters. We assumed that all of the sequences initially have the same number of mutant loci. Two characteristic examples are shown in Fig. 1 b and c, and d and e. The average distribution over k, after a transition time, assumes a quasistable profile that moves like a solitary wave either to the left or to the right in successive generations, depending on the parameter values and the initial value of k. Gessler (40) also found a stable distribution profile by using pseudorandom simulations. If back and compensating mutations are absent, i.e., q = 0, the wave moves at a constant speed to the right (the population becomes less-fit), the effect of Muller's ratchet (Fig. 1 b and c). In contrast to the prediction of neutral models (41), the average rate of accumulation of mutations, dk_av/dt, is not equal to the neutral mutation rate. Instead, it is less than this and depends on the population size and other parameters. In contrast to the prediction of one-locus models including selection (3), the accumulation rate does not increase rapidly in time but rather remains constant.

If back or compensating mutations are present, the wave can move either to the right (ratchet) or to the left (reversion), slowing down gradually as it approaches a steady-state point (Fig. 1 d and e). At sufficiently large N, a steady state is reached at k_av close to zero (see below), so that only reversion can be observed (except for extremely small initial values of k_av). Although a distribution obtained by pseudorandom simulation fluctuates around the average obtained in the semideterministic approach (Fig. 1 b and d), the accumulation rates over long time scales obtained by the two methods are similar (similar slopes in Fig. 1 c and e).

On an intuitive level, the formation of a quasistable wave moving to the right (Muller's ratchet) can be understood from combined action of three factors. Forward mutations work to move the wave to the right, selection acts to expand its tail to the left, and random drift checks this expansion by destroying sequences at the left edge. A fourth factor, back/compensating mutations, can restore the lost sequences at the left edge and reverse the direction of the wave (reversion).

To extend the analysis beyond numeric calculations and simulation, we developed an analytic method (Mathematical Appendix) that confirms the above results and derives the ratchet or reversion rate for arbitrary values of the model parameters for the case when s is much less than μL. Under this assumption, the distribution of sequences over k can be shown to be broad. The logarithm of the average distribution changes only slightly between adjacent discrete values of k and generations t and can be approximated by a function continuous in these variables. In this approach, which can be verified analytically (Validity of Approximations, Mathematical Appendix), the semideterministic equation (Eq. 11) has a continuous set of solutions, each in the form of a solitary traveling wave (Eqs. 12 and 13). A wave with a width (standard deviation) larger than the critical value (μL/s)^1/2 moves to the left (reversion of deleterious mutations). A wave with a smaller width moves to the right (Muller's ratchet). The specific value of the width and, therefore, of the wave speed and direction is determined by the stochastic cutoff at the left edge. The cutoff in this approach is reduced to the requirement that a group becomes empty when the frequency of sequences in it drops below ∼1/(μLN) (Eq. 19). In the absence of the cutoff, as we found out from the numerical calculation, a wave is not stable and is increasing its width with time.

Wave Speed vs. Population Size and Mutant Frequency

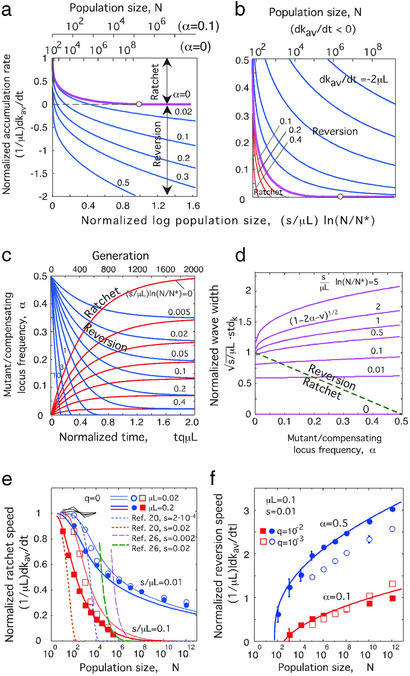
The accumulation rate in units of the mutation rate, which we denote v, can be expressed (Eq. 20) in terms of two composite parameters, the average density of mutant/compensating loci, α = qk_av, and the normalized log population size, (s/μL)ln(N/N*), where N* is the characteristic population size proportional to the standard deviation of k (Eq. 21). In Fig. 2 a and b, we present this expression graphically, by plotting either v or α as a function of the normalized log population size, shown on the lower axis, when the other parameter, α and v, respectively, is fixed. The upper axis shows the corresponding values for N at a set of typical values of model parameters. We observe that: (i) The ratchet and reversion rates change slowly, logarithmically with population size (Fig. 2a). (ii) Muller's ratchet exists in a broad range of population sizes, which shrinks as α increases (Fig. 2a). At α = 0, the ratchet speed becomes 0 at N = N*exp(μL/s) (Eq. 29). The authors (24–26) who studied the case α = 0 obtained a finite, albeit small, ratchet speed at this point in N. The reason for the difference between this and our result is that the continuous approximation in k we use here breaks down when both v and α become small (Approximation 3, Mathematical Appendix). (iii) If the population size is less than N*exp(μL/s), the population has a steady state at some value of α (Fig. 2b; Eq. 31), at which neither the ratchet nor reversion occurs. The existence of the steady state in this interval of N is also evident from the time dependence of α (Fig. 2c; Eqs. 20 and 22). (iv) A wave shrinks as it moves to the right (as α increases) and expands as it moves to the left (α decreases), although at moderate population sizes, this happens rather slowly (Fig. 2d; Eqs. 20 and 22).

Figure 2.

(a and b) Analytic relationship between the average accumulation rate of mutations, dk_av/dt, the frequency of mutant and compensating loci in a sequence, α, and the log-normalized population size, (s/μL)ln(N/N*), in the case s ≪ μL (Eq. 20). The scales on the upper abscissa are for values of N alone, with the main parameters fixed at μL = 0.1, s = 0.01, and the values of α or dk_av/dt shown at the axes. (a) Dependence of dk_av/dt on log-normalized N at fixed values of α shown on the curves. The scale for the values of N at fixed parameters on the top was calculated, for α = 0.1, by using Eqs. 15, 19, 20, and 21; and, for α = 0, Eqs. 16, 17, 20, and 47. (b) Dependence of α on N calculated at fixed values of dk_av/dt shown on the curves in units of μL. The open circles in a and b show the point ln(N/N*) = μL/s at which both the accumulation rate and the value of α are 0. Blue, purple, and red curves in b correspond to reversion, steady-state, and Muller's ratchet, respectively. N* is estimated from Eqs, 15 and 21 with ξ ≈ 1. (c) Time dependence of α (Eqs. 20 and 22) at fixed values of the log-normalized N shown on the curves. Blue and red curves correspond to reversion (initial α = 0.5) and ratchet (initial α = 0), respectively. The upper abscissa shows the scale for time alone at μL = 0.1, q = 0.01. (d) Dependence of the width of the distribution in k (std_k) on α at fixed values of log-normalized N (shown on the curves; Eqs. 15 and 20). (e and f) Examples of predicted accumulation rate with the specific values of parameters shown in the figure. (e) The Muller's ratchet speed vs. N in the absence of back and compensating mutations (q = 0, right moving wave). (f) The dependence of reversion speed on N (finite q, left-moving wave). Symbols show results of pseudorandom simulation averaged over 5–10 runs. The time interval was 1,000–5,000 generations (e) and the time in which the wave travels one-fourth of the distance to the steady state value of k (f). For N > 10⁴, the edge groups that contained <100 sequences per group at a given time were simulated stochastically, and the remaining groups were treated deterministically. The solid lines are obtained analytically [Eqs. 20 and 47 (e) and Eqs. 20 and 21 (f)]. Short broken lines show the left-hand side of Eq. 15 obtained from simulation, thus testing Eq. 15, which relates the width and the speed of the wave. Dotted and dashed curves show previous results for small N (20) and for large N at s/μL = 0.1 (26).

To verify the accuracy of our entire approach at s ≪ μL, we calculated the ratchet and reversion rate as a function of N for several representative sets of parameter values (Fig. 2 e and f). The comparison with the results of pseudorandom simulation shows that the analytic approach is, indeed, accurate over a broad interval of N. We also show, for comparison, analytic results from the literature (20, 26) obtained for either very small or very large N (Fig. 2e). At intermediate N, these models are clearly at variance with simulation results.

Tsimring and colleagues (28, 29) used essentially the same initial approach and a very similar population model to predict a solitary wave that is stable due to a cutoff at the left edge. Our work confirms this qualitative conclusion. However, our results for the accumulation rate and the wave shape (Fig. 2 and Mathematical Appendix) differ from those obtained by these authors. The reason for the difference is their approximation of the distribution of mutant frequency with its expansion in the first and second derivatives in k. As we show in Mathematical Appendix, one is allowed to expand the logarithm of the distribution but not the distribution itself, because it changes sharply in k at its far left slope. The resulting equation for the distribution density (Eq. 11), in contrast to what these authors assumed, does not have a form of the linear diffusion equation.

Transition to One-Locus Model

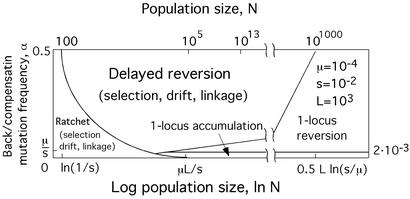
The overall direction of evolution and the dominant evolutionary forces over the entire range of N and α are illustrated schematically in Fig. 3. In two of three regions that correspond to Muller's ratchet and delayed reversion, the factors of mutation, random drift, selection, and linkage are all equally important. The reversion rate is approximately constant over a wide time interval (Fig. 1e or 3c) and depends on population size. Reversion is slowed due to linkage, as compared with the one-locus result that applies in the limit of strong recombination, in a broad finite interval of population sizes N, such that ln(1/s) < ln N ≪ k ln(σ/q) (Eqs. 33–35). In the third region, which is located at large N and small α (Fig. 3), linkage is not very important, and the reversion rate assumes the value obtained from the one-locus theory (3). Better-fit variants in this region accumulate with time, not quasilinearly but either exponentially or, in the stochastic case, in step-like fashion. The transition between the multilocus and the one-locus theory results takes place when the left edge of the “wave” hits the wall at k = 0 (Approximation 5, Mathematical Appendix).

Figure 3.

Overall direction and dominant factors of evolution. Parameter values for this example (shown in the figure) are representative for RNA viruses. The schematic diagram is based on the analytic results (Eqs. 20, 21, 33, and the following text, which are published as supporting information on the PNAS web site).

Generally, a one locus two-allele theory can be used either in the limit of strong recombination or when only two genetic variants are present in population at any time. The transition to the one-locus theory in the limit of large N predicted by the above model is intuitively expected: at very large N, every genetic variant preexists in a population, and frequent mutations break down linkage disequilibrium. This may happen at population sizes that are unrealistically large from a biological point of view (Fig. 3). In agreement with this, models assuming infinite population size do not generally find any advantage of recombination for progressive evolution (9, 13). Our results for the reversion rate differ from an approximate estimate by Maynard Smith (10), which predicts that linkage delays reversion at arbitrarily large N (after Eq. 34).

Comparison with Experiment

It has been observed that RNA viruses often accumulate mutations approximately linearly over limited but fairly long time intervals. This effect has been observed in persistent HIV infection (42) and along transmission chains of various viruses (see ref. 43 and references therein). Our results show that linear dependence does not necessarily imply selectively neutral evolution. Note that the predicted linearity is neither exact nor universal, because the wave slows down when approaching a steady state, and because there are random fluctuations on top of the linear dependence (Fig. 1 c and e).

Predictions of our model are also consistent with the results of in vitro studies of vesicular stomatitis virus by Novella et al. (30, 31). In these experiments, a fixed amount of virus, N infectious units, was passed many times between cell cultures. At each passage, it was allowed to grow into N separate plaques that were mixed for the next transfer. The average fitness of the virus mixture was measured at different passages by using a competition assay with a reference virus variant. The authors found that the average log fitness either increased or decreased with passage number, depending on N and on the fitness of the initial virus strain. The critical value of fitness that did not, on average, change with passage exhibited a linear dependence on log N (Fig. 4a). Novella et al. also measured the dependence of the reference variant fitness on the passage number at a large value of N (Fig. 4b). Using three fitting parameters and estimating other parameters from independent data (legend to Fig. 4), we fit predictions of our model to both dependencies (Fig. 4 a and b). Because the best-fit value of s for these experiments is on the order of μL, we could not use the semideterministic approach and used simulation. We show, for comparison, results of fitting (Mathematical Appendix) of the one-locus model (20, 44), which predicts an N-shaped dependence between critical fitness and log N (Fig. 4). Thus, our model both predicts a linear dependence in log N and gives a better fit to experimental results. Still, more data points are needed to make sure that the observed dependence is indeed linear over the entire range of log N.

To conclude, we have developed an approach to predict the overall rate of genetic evolution and have applied it to a simple population model with weak selection and a large number of linked loci. The general expression for the accumulation rate of mutations we obtained is valid over a very broad range of population sizes and other parameters. These results can be applied to a broad variety of experimental populations of viruses and bacteria. The approach is quite flexible, and we are working to generalize it to include the factors we left out in this study, such as recombination (important for some viruses such as HIV) and variation of selection coefficient among nucleotides.