Chemosensing in Escherichia coli: Two regimes of two-state receptors

Abstract

The chemotaxis network in Escherichia coli is remarkable for its sensitivity to small relative changes in the concentrations of multiple chemical signals. We present a model for signal integration by mixed clusters of interacting two-state chemoreceptors. Our model results compare favorably to the results obtained by Sourjik and Berg with in vivo fluorescence resonance energy transfer. Importantly, we identify two distinct regimes of behavior, depending on the relative energies of the two states of the receptors. In regime I, coupling of receptors leads to high sensitivity, while in regime II, coupling of receptors leads to high cooperativity, i.e., high Hill coefficient. For homogeneous receptors, we predict an observable transition between regime I and regime II with increasing receptor methylation or amidation.

The chemotaxis network in Escherichia coli is the best studied signal-transduction network of any living organism. The function of the network is to allow E. coli to swim toward attractants, such as amino acids or sugars, and away from repellents. The cells perform chemotaxis by detecting temporal changes in their chemical environment and transducing this information into a decision to swim straight or change direction (tumble). The chemotaxis system is remarkable for its high sensitivity to small relative changes in chemical concentrations and for the ability of cells to retain sensitivity over a wide range of ambient chemoeffector levels (1). The latter property relies on an adaptation system in which receptors are methylated/demethylated by CheR/CheB at four specific residues (modification sites) (2, 3). Adaptation in chemotaxis is precise, i.e., cells return precisely to the same rate of tumbles if chemoeffector levels stop changing. The adaptation system is also robust in that precise adaptation occurs for a range of levels of chemotaxis proteins (4). Another remarkable property of the system is its ability to integrate signals from different chemical cues, allowing chemotaxis toward any of multiple attractants (5).

In E. coli, there are five chemotaxis receptors: two high-abundance receptors, Tar and Tsr, and three low-abundance receptors Tap, Trg, and Aer. These receptors are highly similar in their cytoplasmic signaling domains, with differences primarily in the periplasmic ligand-binding domains. All five chemoreceptors associate as homodimers. In living cells, these homodimers are observed to cluster near one or both poles of the cell (6). In vitro crystallographic studies of cytoplasmic domains of the receptors reveal a complex of three homodimers (a “trimer of dimers”) (7). In vivo crosslinking studies demonstrate that trimers of dimers can be composed of mixtures of homodimers of different types (8, 9). Clustering of trimers of dimers is mediated by the linker protein CheW and by the kinase CheA (6, 8), both of which are essential for phosphorylation of the response regulator CheY (10). In its phosphorylated form, CheY interacts with the flagellar motors to induce tumbling (11).

Recently, Sourjik and Berg (12–14) introduced a new tool to study signaling in chemotaxis: in vivo fluorescence resonance energy transfer (FRET). They constructed fluorescent protein fusions to CheY and to its phosphatase CheZ, thereby creating a FRET pair that they used to monitor the stimulus-dependent activity of the receptor–kinase complex (Fig. 1a). Receptors were engineered with specific patterns of glutamates (E) and glutamines (Q) at the modification sites. Higher numbers of glutamines favor increased CheA kinase activity. In the absence of the adaptation system (cheRcheB strains), the glutamates and glutamines are not modified. In the presence of the adaptation system, glutamates are methylated and demethylated by CheR and CheB, respectively, and glutamines are also deamidated to glutamates by CheB. Adaptation compensates for the effects of ligand binding on CheA kinase activity; for example, a net increase in methylation (CheA kinase enhancement) follows addition of attractant (CheA kinase inhibition). Sourjik and Berg observed that the inhibition constant K_i of the response to the attractant α-methylaspartate (MeAsp) varied over almost five orders of magnitude depending on the modification states of the Tar and Tsr receptors (12). Moreover, in strains expressing both Tar and Tsr receptors, the higher the fraction of a given receptor, the lower was the K_i and the higher the cooperativity of the response to its ligand (see Fig. 3a). Cells expressing only Tsr receptors showed an extremely cooperative (i.e., steep) response to serine, with a Hill coefficient of ≈10.

Fig. 1.

Response of receptor activity to step of attractant. (a) Response measured by FRET by Sourjik and Berg (12) to quantified steps of the attractant MeAsp. (b) Response of the mixed-cluster MWC model with equal contributions from 14, 15, and 16 receptor clusters, with binomial distributions of receptors at a Tar:Tsr ratio of 1:2, to steps of MeAsp. In all cases, we set K_a^off = 0.02 mM, K_a^on = 0.5 mM, K_s^off = 100 mM. All energies in thermal energy units k_BT. The experimental strains, and our corresponding choices of offset energies ɛ_a, ɛ_s, are as follows: •, wild-type, 0, 0; ▾, cheR mutant, 0.2, 0.2; ▵, cheRcheB mutants–Tar {EEEE}, 1.0, –1.5; ◇, Tar {QEEE}, 0.0, –1.5; □, Tar {QEQE}, −0.6, −1.5; ▿, Tar {QEQQ}, −1.1, −1.5. All lines are to guide the eye.

Fig. 3.

Effect of receptor homogeneity on response to attractant. (a) Response measured by FRET to steps of MeAsp in ref. 14. Nonadapting cheRcheB mutant strains were constructed with Tar receptor expression at zero (◇), one (•), two (▪), and six (▴) times wild-type levels. (b) Dose–response curves for the mixed-cluster MWC model to steps of MeAsp. Response curves are shown for Tar:Tsr ratios 0:1 (◇), 1:2 (•), 1:1 (▪), and 3:1 (▴) with all parameters the same as in Fig. 1b. All lines are to guide the eye.

The signaling properties of the chemotaxis network have been the subject of numerous modeling studies. Notably, Barkai and Leibler (15) were able to account for the adaptation properties of the network by using a two-activity-state model for receptor complexes (16). In one state, a receptor is both active as a kinase and susceptible to demethylation by CheB; in the other state, the receptor is inactive and not susceptible to demethylation. This direct coupling between kinase activity and rate of demethylation provides a mechanism for integral feedback (17) and leads to precise and robust adaptation. However, this elegant model for adaptation does not directly account for the sensitivity or signal-integration properties of the network. To account for enhanced sensitivity, several studies have invoked interactions among receptors (18–24). In particular, Bray et al. (18) proposed a model of “conformational spread” among receptors. Along these lines, and in light of the in vivo FRET results, Shimizu et al. (22) reported an Ising-type lattice model for receptors, and Sourjik and Berg (14) studied the related allosteric model of Monod, Wyman, and Changeux (MWC) (25). However, these studies were limited to receptors of a single type. To study a mixed array of receptors, Mello and Tu (21) used a mean-field version of an Ising-type model, later generalized by Mello et al. (24) to include stochastic simulations. They achieved excellent agreement with the FRET data but at the cost of a very large number of parameters. Moreover, different parameter sets had to be used for wild-type and nonadapting cells (21). The model of Albert et al. (23) also produced excellent agreement with the FRET data but relied on dynamic receptor-complex formation, which is not supported by experiment (26).

FRET Studies Suggest Two Regimes of Receptor Response

In Fig. 1a, we reproduce kinase-activity dose–response curves to steps of MeAsp measured by using in vivo FRET by Sourjik and Berg (12). The two curves at the lower left have approximately the same inhibition constant K_i ≈ 3 μM for half-maximal activity. However, what is not seen in Fig. 1a because the response curves are normalized is that the initial activity in the absence of attractant is ≈16 times higher for wild-type cells than for cheR mutant cells. In cheR mutant cells, the receptors are presumably mostly demethylated. The remaining curves, for engineered cheRcheB mutant cells, show two distinct declines in kinase activity. For the first decline, the value of K_i1 increases (and the amplitude decreases) with increasing glutamine content of the Tar receptors, whereas for the second decline, the value of K_i2 remains approximately constant. Also, for these four cheRcheB curves, the initial activity, in the absence of attractant, is higher than for wild-type, and changes by a factor of <1.5 among the four.

Overall, the six dose–response curves suggest two regimes of receptor response. Encompassed in the first regime are the wild-type and cheR cells, which have low initial activity and a single low K_i. The second regime includes the four cheRcheB cells, which have high initial activity, a high and variable K_i1, and a distinct and even higher K_i2. One should note that, for the cheRcheB cells, the receptors do not undergo methylation/demethylation, so that the Tar receptors remain as engineered (e.g., EEEE and QEEE), whereas the other receptors, mainly Tsr receptors, remain “wild type, ” i.e., QEQE.

In what follows, we show that a model of coupled two-state receptors (25) can account for the full range of FRET data (12–14), including receptors of multiple types both with and without a functioning adaptation system. An essential observation is that there are two regimes of behavior of two-state receptors and that both regimes are present in the FRET data. Interestingly, in one regime, receptor coupling leads to enhanced sensitivity to ligand (lower apparent K_i), whereas, in the other regime, receptor coupling leads to an increased Hill coefficient. Homogeneous receptors are predicted to display a transition between these two regimes as a function of increasing receptor methylation or glutamine content, which favors the active state of receptors.

Model

Two Regimes of a Single Two-State Receptor.

To explain precise adaptation in chemotaxis, Barkai and Leibler (15) used a two-activity-state model for receptor complexes (16). Presumably, the two activity states correspond to two distinct configurations of each receptor homodimer, one leading to high kinase activity (on) and one leading to low or zero kinase activity (off).

We consider a model receptor with two activity states implying a total of four free-energy states (Fig. 2b Inset): (i) on without ligand bound E_on, (ii) on with ligand bound E_on –log([L]/ K_d^on), (iii) off without ligand bound E_off, and (iv) off with ligand bound E_off –log([L]/ K_d^off), where [L] is the ligand concentration and K_d^onand K_d^off are the dissociation constants in the on and off states (27) (all energies are in units of the thermal energy k_BT). The terms proportional to log([L]) represent the loss of ligand volume entropy upon binding to the receptor. Within this model, the probability for a receptor to be on at equilibrium is the sum of Boltzmann factors for the two on states, with and without ligand, divided by the sum of the Boltzmann factors for all four states

.

Fig. 2.

Two regimes of a two-state receptor. Representative energy-level diagrams for a single two-state receptor as a function of ligand concentration. The four possible states of the receptor are shown in Inset. Red curves (on) and blue curves (off) correspond to active and inactive configurations of the receptor, and the superscripts refer to no ligand bound (0) and ligand bound (L). Dotted lines, energy levels of the unbound receptor; solid curves, ligand-bound receptor; arrows, ligand concentrations when lowest free-energy states cross. (a) Regime I : In the absence of a ligand, the on-state free energy is above the off-state free energy; crossing occurs at [L] = K_d^off. (b) Regime II: In the absence of a ligand, the on-state free energy is below the off-state free energy; crossing occurs at [L] = K_d^off exp(E_off − E_on).

For attractants, we assume that the binding of ligand favors the off state, i.e., K_d^off ≪ K_d^on.

Eq. 1 predicts two regimes of behavior depending on the relative energies E_on and E_off. As shown schematically in Fig. 2, regime I occurs when E_on > E_off, and regime II occurs when E_on < E_off (a crossover regime occurs when E_on ≈ E_off). In regime I, in the absence of ligand, the off state predominates, so most receptors are already off (p_on ≪ 1). Adding a ligand causes p_on to decrease further. Specifically, p_on is reduced to approximately half-maximum when the denominator of Eq. 1 doubles, i.e., when 1 + [L]/ K_d^off = 2, or, equivalently, when the off state with a ligand becomes copredominant with the off state without a ligand. Thus the K_i for half-maximal activity in regime I is constant and is set by the dissociation constant in the off state, [L] = K_i = K_d^off.

In contrast, in regime II in the absence of a ligand, the on state predominates, so most receptors are on (p_on ≈ 1). In this case, to reduce p_on to half-maximum requires that the off state with ligand becomes copredominant with the on state without a ligand. Half-maximum p_on corresponds to setting exp(−E_off) [L]/ K_d^off equal to exp(−E_on) in the denominator of Eq. 1. Compared to regime I, the result is a larger ligand concentration [L] for half-maximal activity, K_i ≈ K_d^off exp(E_off –E_on), which increases as E_on decreases.

This simple two-activity-state model accounts qualitatively for a number of features of the response curves in Fig. 1a. The very low activity of the cheR mutant is natural if the receptors in this strain are in regime I. Similarly, the approximately constant value of K_i for the cheR and wild-type cells is expected if both are in regime I. For the engineered cheRcheB cells, the high and nearly constant initial kinase activities correspond to regime II. Moreover, the increase of the K_i1 values follows automatically from Fig. 2 (or Eq. 1) if the replacement of glutamates (E) by glutamines (Q) lowers the on-state energy of the Tar receptors (3, 28).

However, the two-state model for a single receptor does not account for many other features of the data, including the high sensitivity to ligand (28), the integration of multiple chemical signals, or the increase of cooperativity with receptor homogeneity (Fig. 3a; ref. 14). To account for these features, we must consider interactions among receptors.

Two Regimes of Coupled Two-State Receptors.

We first consider the MWC model (25), in which n identical two-state receptors are so strongly coupled that all n receptors are either off or on together. The probability for the cluster of n receptors to be on at equilibrium is

If the individual receptors are in regime I (E_on > E_off), the K_i for half-maximal activity is given by the concentration at which (1 + [L]/ K_d^off)ⁿ = 2, which means K_i ≈ (log 2/n) K_d^off. In other words, the apparent K_i of a cluster of n receptors is smaller than the dissociation constant K_d^off of a single receptor by a factor ≈n. Therefore, the larger the cluster, the smaller is the apparent K_i. In contrast, if the individual receptors are in regime II (E_on < E_off), the K_i for half-maximal activity is K_d^off exp[(E_off –E_on)], the same as for a single receptor, but now the cooperativity of the transition, i.e., the Hill coefficient, is equal to n because

Thus, the coupling of n identical receptors leads to qualitatively different effects in the two regimes: In regime I, the sensitivity to ligand is increased by a factor of n, with the Hill coefficient remaining equal to 1, whereas in regime II, the sensitivity to ligand is unchanged, but the Hill coefficient (cooperativity) increases to n. (In the next section, we will show how these results are modified if the receptors are not identical.)

Thus, the model for identical receptors helps explain both the observed high sensitivity to ligand (cheR and wild-type cells in Fig. 1a) and the observed high cooperativity for homogeneous receptors (Fig. 2a) as consequences of receptor-receptor coupling in regimes I and II, respectively. The model further indicates how the wild-type strain can achieve simultaneous low K_i and high kinase activity. If adaptation tunes the receptors in wild-type cells to the crossover regime, E_on ≈ E_off, then K_i ≈ K_d^off (high sensitivity) and p_on ≈ 1/2 (high activity), consistent with the wild-type dose–response curve shown in Fig. 1a.

Mixed Clusters of Two-State Receptors.

To compare theory to experiment in detail, we must take into account the presence of receptors of different types. We study a variant of the MWC model in which clusters are composed of random mixtures of receptors of two types, Tar and Tsr (details in supporting information, which is published on the PNAS web site). Receptors of each type are characterized by an offset energy ε_r = E_{r, on} − E_{r, off} and by dissociation constants K_r^on and K_r^off for MeAsp, where r = a, s for Tar, Tsr receptors ( K_s^on is taken to be arbitrarily large). In terms of the offset energies, ε_r > 0 corresponds to regime I, and ε_r < 0 corresponds to regime II. Methylation of glutamates, or replacement of glutamates by glutamines, affects receptors only by decreasing ε_r, i.e., favoring the on state. As in the usual MWC model, all receptors in a cluster are assumed to be off or on together.

Results

Response of Mixed Clusters of Two-State Receptors.

In Fig. 1b, we show dose–response curves to MeAsp for equally weighted 14, 15, and 16 receptor clusters with an average Tar:Tsr ratio of 1:2, which is nominally the in vivo ratio, for different values of ε_a and ε_s, but no other changes of parameters. The curves reproduce well a number of features of the experimental data. The “cheR” curve is in regime I and has low initial activity (0.05) and high sensitivity (K_i1 ≈ 3.5 μM). The wild-type curve is in the crossover regime and achieves both high initial activity (0.5) and high sensitivity (K_i1 ≈ 5.4 μM). For the cheR curve, the value of K_i1 is ≈5 times smaller than K_a^off = 0.02 mM; this 5-fold increase of sensitivity to MeAsp corresponds to the average number of Tar receptors in the clusters. The remaining “cheRcheB” curves, which have high initial activity (≈1), are generated for a series of offset energies ε_a for the engineered Tar receptors, with a single offset energy ε_s for the Tsr{QEQE} receptors. For these cheRcheB curves, the effect of mixed clusters becomes apparent. First, there are two comparable declines in activity, at K_i1 and K_i2, corresponding to MeAsp saturation of the Tar and Tsr receptors, respectively. Second, the value of K_i1 is always larger than K_a^off and increases with Tar glutamine content (decreasing ε_a). The large initial activity and large and increasing value of K_i1 are characteristic of receptors in regime II but occur even for Tar{EEEE} receptors that have offset energies in regime I (ε_a = 1.0). The explanation is that, in a cluster, the Tar{EEEE} receptors (≈1/3) are likely outnumbered by the Tsr{QEQE} receptors (≈2/3) that are biased to be on (ε_s = −1.5), resulting in the cluster as a whole being strongly in regime II. Third, the plateaus in activity between K_i1 and K_i2 reflect a competition between Tar receptors, which are saturated with MeAsp and individually favor being off, and Tsr receptors, which have little MeAsp bound (K_s^off = 100 mM) and which individually favor being on. The heights of plateaus increase with the number of Tar glutamines because the associated decrease of Tar offset energies ε_a translates directly into higher cluster activities.

Neither the data in Fig. 1a nor the mixed-cluster-model results in Fig. 1b show enhanced Hill coefficients, even for the cheRcheB curves. In the theoretical model, a single cluster in regime II has a Hill coefficient determined by the number of receptors that bind a ligand, i.e., for MeAsp, the Hill coefficient is given by the number of Tar receptors. However, clusters of different sizes and different numbers of Tar and Tsr receptors are inhibited at different ligand concentrations. The resulting spread in K_i values results in an ensemble Hill coefficient close to 1. According to this analysis, the Hill coefficient should increase with increasing receptor homogeneity. Such an increase is observed in Fig. 3b, where theoretical dose–response curves are shown for increasingly homogeneous clusters of Tar receptors. Indeed, an identical effect was observed experimentally by Sourjik and Berg (14), who found the Hill coefficient to increase to ≈4 with increasing homogeneity of Tar{QEQE} receptors (Fig. 3a).

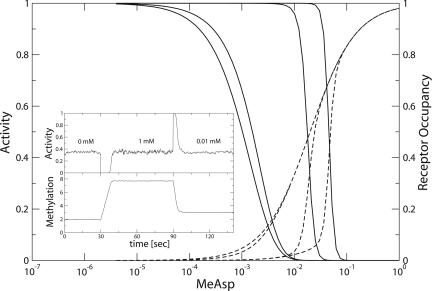
One prediction of our model is that for homogeneous receptors, there will be a transition between regime I and regime II behavior with increasing receptor methylation or glutamine content. In Fig. 4, we show theoretical results for homogeneous clusters of Tar receptors. Note in regime I the enhanced sensitivity, K_i/ K_a^off ≈ 0.05 for the Tar{EEEE} curve, and in regime II, the high Hill coefficient is ≈9 for the Tar{QEQQ} curve. The Hill coefficient for the Tar{QEQQ} receptors remains high despite our use of three different cluster sizes (14, 15, and 16) because K_i is the same for all cluster sizes of homogeneous receptors in regime II (see Eq. 2). In Fig. 4, we also show the fraction of receptors with bound MeAsp. In regime I, binding of a ligand to a small fraction of receptors results in a large decline in activity. In contrast, in regime II, ligand binding and loss of activity are exactly correlated, and both are highly cooperative.

Fig. 4.

Transition from regime I to regime II for homogeneous receptors. Response of homogeneous clusters of Tar receptors to steps of MeAsp within the MWC model. Dose–response curves (solid) and receptor-occupancy curves (dashed) are shown for Tar receptor methylation states EEEE, QEEE, QEQE, and QEQQ (left to right), where the Tar-receptor parameters and cluster sizes are those used in Fig. 1b. (Inset Upper) Adaptation of averaged activity is shown of a cluster Tar receptors exposed to two steps of MeAsp from 0 mM up to 1 mM at t = 30 s and then down to 0.01 mM at t = 90 s. (Inset Lower) Average methylation level of receptors. Averages are taken over 100 independent clusters of six Tar receptors. Details of the Barkai-Leibler-type adaptation model (15) are given in supporting information.

Free-Energy Model for Scaling of Wild-Type Response Data.

Sourjik and Berg made the striking observation that the dose–response curves for wild-type cells, adapted at different ambient concentrations of MeAsp, could be collapsed onto a single curve (figure 3c in ref. 12). They proposed that the response to the addition of MeAsp might be solely a function of change in receptor occupancy, and they inferred occupancy versus total MeAsp from a particular nonadapting mutant. Our model suggests an alternative interpretation, namely that the response to MeAsp is solely a function of change in receptor free energy. Specifically, in our model, the only effect of adding MeAsp is to lower the free energy of receptor off states relative to on states. Assuming that adaptation always returns this free-energy difference to some fixed value, then the response to the addition of MeAsp should depend solely on the induced change in free-energy difference. In Fig. 5, we show a collapse of Sourjik and Berg’s data by using this free-energy difference as a scaling variable (details in supporting information). The data collapse is roughly as good as the collapse found initially by Sourjik and Berg and, importantly, includes the response for adaptation at zero ambient MeAsp, which their approach could not.

Fig. 5.

Free-energy scaling of wild-type response. Response measured by FRET to steps of MeAsp in ref. 12 for wild-type adapted cells. (Left) Data are shown for addition (Lower) and subsequent removal (Upper) of MeAsp (with curves to guide the eye) for cells adapted at various ambient MeAsp concentrations (see Inset, units are in mM). (Right) Response curves are rescaled according to a free-energy model as described in supporting information. The parameters are the same as in Fig. 1b, K_a^off = 0.02 mM, K_a^on = 0.5 mM, K_s^off = 100 mM.

Precision of Adaptation and Assistance Neighborhoods.

In Fig. 4 Inset, we show adaptation results for model Tar receptors (details in Table 1, which is published as supporting information on the PNAS web site). Similar to the model of Barkai and Leibler (15), we assume that the demethylation rate is proportional to receptor activity and that the methylation rate is proportional to receptor “inactivity.” An important difference from previous adaptation models is that we assume that CheB and CheR act on groups of receptors (assistance neighborhoods). Our use of assistance neighborhoods follows the recent observation by Li and Hazelbauer (29) that single CheR and CheB proteins have a range of, respectively, seven and five receptors in their immediate vicinity. Methylation/demethylation is assumed to be equally likely for each available modification site within the assistance neighborhood. This model for methylation/demethylation is consistent with the assumption, essential for precise adaptation, that CheB and CheR function at saturation, i.e., at rates independent of the number of methyl groups. The use of assistance neighborhoods increases the precision of adaptation compared to single-receptor models by effectively increasing the ladder of methylation levels from 8, for a single receptor homodimer, to 48 for an assistance neighborhood of 6 receptors. This increase of methylation levels allows CheB and CheR to function at saturation without encountering fully demethylated or fully methylated conditions. Indeed, the “assistance neighborhood” model does lead to precise adaptation (Fig. 4 Inset). For homogeneous Tar clusters, the range of adaptation is limited by K_a^on = 0.5 mM, because above this concentration, the Tar receptors become saturated and stop responding. However, the range of adaptation increases for mixed clusters because the Tsr receptors with K_s^off = 100 mM continue to respond to MeAsp.

Discussion

The chemosensing system of E. coli is notable for its exquisite sensitivity, over a wide range of concentrations, to small relative changes in multiple attractants and repellents. Quantification of these properties has been greatly enhanced recently by the in vivo FRET studies of Sourjik and Berg (Figs. 1a and 3a; refs. 12–14). These studies suggested to us two regimes of receptor behavior: one regime characterized by low to moderate kinase activity and a low, constant K_i (high sensitivity) and the other regime characterized by high kinase activity and a high K_i, which increased with receptor glutamine content (nominally equivalent to increased receptor methylation). We showed that similar regimes occur automatically in the model for two-state receptors (16) used by Barkai and Leibler (15) to account for precise adaptation. The first regime occurs when the receptor’s kinase-active state is higher in energy than the inactive state in the absence of ligand (E_on > E_off), and the second regime occurs in the opposite case (Fig. 2). Interestingly, the effects of receptor-receptor coupling (20) differ markedly between these two regimes (Fig. 4). In regime I, coupling leads to enhanced sensitivity, whereas in regime II, coupling leads to high cooperativity (i.e., high Hill coefficient).

Most of the in vivo FRET studies used cells expressing multiple types of receptors, and there is strong evidence from crosslinking studies (8) that homodimers of receptors form well mixed arrays. We therefore studied a variant of the MWC model in which clusters are composed of random mixtures of two-state receptors of two types, Tar and Tsr. This mixed-cluster MWC model reproduced the central features of the experimental dose–response curves (Fig. 1), including the variable activity and low, constant K_i in regime I, and the high activity and high, glutamine-dependent K_i1, variable plateau heights, and constant K_i2 in regime II. Within our model, the sole effect of receptor modification is to shift the receptor offset energy, ε = E_on − E_off. For example, the series of cheRcheB-mutant curves in Fig. 1b depends only on shifts of ε_a for the Tar receptors. Our model also reproduced the increase of cooperativity (Hill coefficient) with receptor homogeneity (Fig. 3). Importantly, the MWC model predicts that homogeneous receptor clusters will display a transition from regime I to regime II behavior with increasing receptor methylation or glutamine content (Fig. 4). This transition has been observed experimentally in vitro by Li and Weis (30) for engineered Tsr receptors, and in vivo by Sourjik and Berg (unpublished results) in cells expressing engineered Tar receptors without Tsr receptors.

Similar models for coupled two-state receptors have been described in refs. 15, 19–21, 23–25, and Sourjik and Berg (14) used the MWC model to model homogeneous receptors. What is previously undescribed in our approach is that we used the two regimes of receptor activity to explain the FRET data for mixtures of receptors without recourse to a large number of parameters. Specifically, we used fixed K_ds for each type of receptor, with methylation affecting only receptor offset energies. In this regard, our work follows the elegant Ising-model study of Shimizu et al. (22). However, their choice of K_a^on and offset energies precluded consideration of regime II, which is essential to understanding the behavior of cheRcheB mutants (Figs. 1 and 3).

Finally, we generalized our mixed-cluster MWC model to include adaptation within the framework proposed by Barkai and Leibler (15). Namely, methylation and demethylation rates respond to receptor activity to return receptors to a fixed free-energy difference between on and off configurations. Following the logic of this model, we showed that wild-type dose–response curves can be scaled according to free-energy changes induced by addition or removal of attractant (Fig. 5). We suggest that, in wild-type cells, adaptation tunes all receptor clusters to a total free-energy difference near zero. In this crossover range between regimes I and II, receptor clustering leads to increased sensitivity to ligand while maintaining a high signaling activity of receptors.

Signaling by receptors that modulates their kinase and/or phosphatase activities is ubiquitous in bacteria (31). As in chemotaxis, the responses of these receptors to a ligand will depend on the relative on- and off-state free energies. Moreover, there is no such thing as “the affinity” of a two-state receptor for a particular ligand, because each of the two states has its own ligand-binding affinity, K_d^on and K_d^off and the total response involves an interplay of the two. Our estimated ratio K_a^on/K_a^off = 25 for MeAsp binding to Tar is larger than found by biochemical assays for l-aspartate binding to Tar, including approximate ratios 2 (32), 7 (3), and 10 (33). Although the origin of this variability is not clear, K_d values may depend on the presence and stoichiometry of the receptor-binding proteins CheW and CheA and on physiological conditions (34). Our estimated in vivo values for K_a^on and K_a^off compare favorably with in vivo values obtained from fits to the adaptation-time data of Berg and Tedesco (35) (see supporting information). The best way to measure in vivo K_d values may be to combine systematic activity studies of cells expressing a single receptor type with scaling analysis as in Fig. 5.

Coupling of receptors may also prove to be a general mechanism for enhancing sensitivity to weak signals. Although our results highlight the importance of receptor-receptor coupling in the chemotaxis system and suggest an effective cluster size of ≈15 receptors, little is known about possible domains or structures larger than trimers of dimers formed by chemotaxis receptors.

Abbreviations

FRET

fluorescence resonance energy transfer

MeAsp

α-methylaspartate

MWC

Monod, Wyman, and Changeux