Nanomechanics of the subtectorial space caused by electromechanics of cochlear outer hair cells

Abstract

The stereocilia of the cochlear inner hair cells (IHCs) transduce vibrations into the sensory receptor current. Until now, mechanisms for deflecting these stereocilia have not been identified experimentally. Here, we identify a mechanism by using the electromechanical properties of the soma of the outer hair cell to produce an intracochlear, mechanical force stimulus. It is known that the soma of this cell generates mechanical force in response to a change of its transmembrane potential. In the present experiments, the force was induced by intracochlear electrical stimulation at frequencies that covered the entire functionally relevant range of 50 kHz. Vibration responses were measured in the transverse direction with a laser Doppler vibrometer. For frequencies up to ≈3 kHz in the first three turns of the guinea-pig cochlea, the apical surface of the IHC and the opposing surface of the tectorial membrane were found to vibrate with similar amplitudes but opposite phases. At high frequencies, there was little relative motion between these surfaces in the transverse direction. The counterphasic motion up to ≈3 kHz results in a pulsatile motion of the fluid surrounding the stereocilia of the IHCs. Based on physical principles of fluid flow between narrowly spaced elastic plates, we show that radial fluid motion is amplified relative to transverse membrane motion and that the radial motion is capable of bending the stereocilia. In conclusion, for frequencies up to at least 3 kHz, there appears to be direct fluid coupling between outer hair cells and IHCs.

A major focus of sensory science is the elucidation of mechanisms by which stimuli are transduced into neural responses. Hearing has proved to be the most enigmatic of the sensory modalities to understand. The sensory cells of the receptor organ, the cochlea, remain only partially accessible to our experimental tools. The main, and to date intractable, experimental problem is gaining access to the top or apical surface of the hair cells in the sensory epithelium, the organ of Corti (Fig. 1A), while maintaining the cochlea in its pristine physiological condition. The mechanoelectrical transducers are located at this surface, in a bundle of microvilli, popularly called stereocilia. The adequate stimulus for the transducers is bending of the stereocilia (1). Despite their crucial role in sound processing, mechanisms of stereociliary bending in situ remain unknown.

Fig. 1.

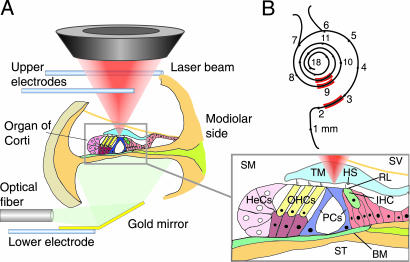
Recording locations in the organ of Corti. (A) The organ vibrates as a result of electromechanical force produced by the OHCs, for which the stimulus is an extracellular electric field produced between the two upper electrodes placed in scala vestibuli (SV) and the lower electrode in scala tympani (ST). The lower electrode also served as a mirror for illumination. Velocity was measured with a laser Doppler vibrometer (not shown); its laser beam (red cone) is shown focused on the lower surface of the TM. Velocity was measured at different radial positions along this surface and at the opposing locations on the RL of the OHCs, IHC, and pillar cells (PCs), and also on the Hensen’s cells (HeCs) and BM. The yellow line shown diagonally below SV depicts Reissner’s membrane, which was left (visually) intact to enable the apical surface of the cells to be bathed in the endolymphatic fluid of scala media (SM). HS, Hensen’s stripe. (B) Measurement regions (red) along the cochlea, with distances indicated from the basal end of the BM.

Based on geometrical considerations (2–4), stereociliary bending has long been believed to result from shear motion between the overlying tectorial membrane (TM) and the apical surface of the hair cell. According to this model, the shear motion arises when transverse motion of the basilar membrane (BM) is transformed into differential radial motion of the TM and the reticular lamina (RL), the structure formed by the apical surfaces of the hair cells and supporting cells (Fig. 1A). However, recent experiments emphasize the inadequacy of this static model for high-frequency stimuli, such as those contained in speech. These experiments have shown that the organ of Corti is a viscoelastic material (5) and that the RL does not vibrate as the rigid structure (6–18), assumed by the static model. Moreover, the static model does not allow for fluid–structure interactions in the narrow region between the TM and RL, known as the subtectorial space, nor in general within the organ of Corti (14). Also, interaction between inner hair cells (IHCs) and outer hair cells (OHCs), other than via the classical route of the BM, has been suggested based on auditory-nerve recordings (19–21) and modeling (22–23).

We investigated dynamics of the subtectorial space by measuring the vibration of its boundaries in response to electromechanical force produced by the OHCs. The soma of these cells are electromotile (24), responding to a change of transmembrane potential (25) over the entire range of functionally relevant frequencies (26–28). There is compelling evidence that somatic electromechanical force is responsible for the exquisite frequency selectivity of the auditory periphery (29). The mechanisms by which this force act on the stereocilia of the IHCs, the true sensors of sound-induced vibration in the cochlea, remain unknown. Using intracochlear electrical stimulation, we have been able to offer a perspective for understanding underlying mechanisms.

Results

Counterphasic Motion of TM and IHC Up to 3 kHz.

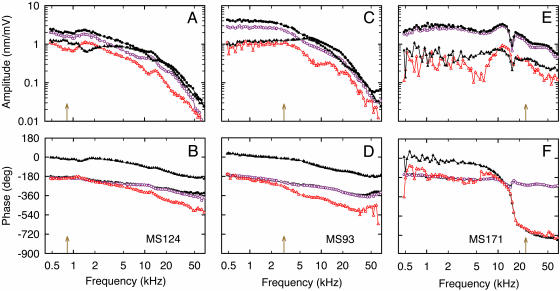
The most salient feature, found in all preparations with intact TM, was that up to stimulus frequencies of at least 3 kHz the lower surface of the TM vibrated in phase with the RL of the OHCs, which in turn vibrated ≈180° out of phase with the RL of the IHC (Fig. 2B, D, and F). In other words, as the OHC contracts pulling its apical surface in the direction of scala tympani, the RL rotates about the apex of the pillar cells, causing the apical surface of the IHC to move in the direction of scala vestibuli (Fig. 3A, blue dashed-dotted line). However, the lower surface of the TM moves in phase with the apical surfaces of the OHCs and, therefore, in the opposite direction to the motion of the IHC. That is, for OHC contraction, the depth of the subtectorial space at the IHC is decreased relative to its resting position and vice versa for OHC elongation. This depth modulation implies a “pulsating” mode of fluid motion in the subtectorial space. Movie 1, which is published as supporting information on the PNAS web site, shows this vibration pattern.

Fig. 2.

Displacement amplitudes (A, C, and E) and phases (B, D, and F) of the lower surface of the TM (colored symbols) and the opposing RL (black symbols) for three preparations at 13 mm (A and B), 9 mm (C and D), and 2.5 mm (E and F) from the basal end of the BM. Displacement is referred to the voltage in scala vestibuli relative to that in scala tympani; phase is positive for motion toward scala vestibuli. Arrows denote CFs calculated from the neuronal tonotopic map in Tsuji and Liberman (32): 0.8, 3, and 24 kHz. Data symbols, circles for second-row OHCs (closed black, RL; opened purple, TM) and triangles for IHCs (closed black, RL; opened red, TM). The measurement order for each experiment was random. Notice that up to at least 3 kHz the TM at both radial positions vibrates in phase with the RL of the OHC, which in turn vibrates 180° out of phase with the RL of the IHC. This counterphasic motion of TM and RL at the IHCs implies pulsating fluid motion in the subtectorial space. Also notice that for frequencies near in vivo CF in the first cochlear turn (F), the TM and RL vibrate in phase at the IHC; that is, there is no evidence here of pulsating fluid motion. MS identifies the preparation.

Fig. 3.

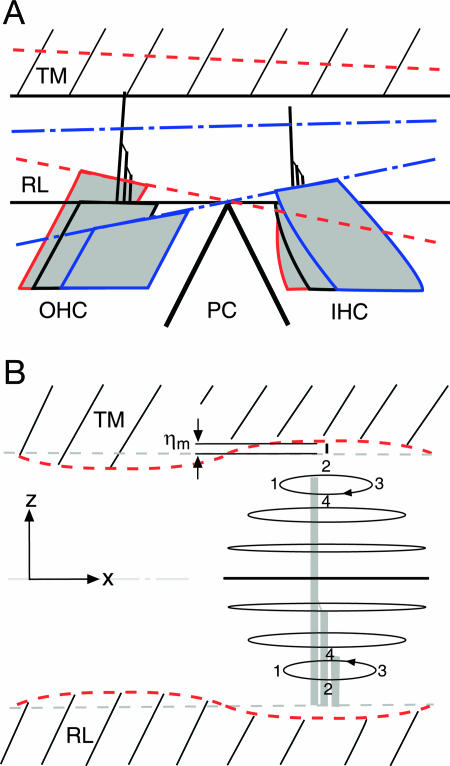
Dynamics of the subtectorial space in response to the somatic electromechanical action of the OHCs for stimulus frequencies up to at least 3 kHz. (A) Phase relations of the RL and TM. Blue dashed-dotted lines: OHC contraction causes anticlockwise rotation of the RL about the apex of the pillar cells (PC), reducing the depth of the subtectorial space at the IHC. Red dashed lines: OHC elongation increases the depth of the subtectorial space at the IHC. (B) Elliptical fluid–particle trajectories resulting from counterphasic sinusoidal motion of the RL and TM at the IHC. The numerals 1–4 track the phases of the trajectories. The radial component of the displacement (x direction) is a parabolic function of vertical position in the space, whereas the transversal component (z direction) decreases cubically from the value (η_m) at the RL and TM, to zero at the midline (Supporting Text). The radial amplitude is at least an order of magnitude greater than the transverse amplitude, indicative of a pulsating fluid mode. The cartoon is not scaled: the measured value of η_m was 1–10 nm, whereas the depth of the subtectorial space is 4–8 μm for the first to third cochlear turns, respectively. The three gray vertical rectangles depict the IHC stereocilia.

In-Phase Motion of TM and IHC near Characteristic Frequency (CF) in the First Cochlear Turn.

Although an almost counterphasic motion of the IHC and overlying TM was found for frequencies in the region of the CF in the second cochlear turn (Fig. 2D), and in the third turn where CF <3 kHz (Fig. 2B), the two surfaces were found to move in phase at CF in the first cochlear turn (Fig. 2F). That is, here there was no evidence of a pulsating mode. On average, IHC phase relative to TM phase at CF for the first, second, and third turns was, respectively, 11 ± 29° (n = 6), 258 ± 42° (n = 26), and 191 ± 42° (n = 16). In-phase motion at CF was never found in the other cochlear turns and always existed in the first turn where, on average, it began at 13.9 ± 1.2 kHz (n = 6). Further details of the in-phase motion of the TM and IHC are given in Supporting Text, which is published as supporting information on the PNAS web site.

Filter Shapes at the OHC.

The vibration responses of OHCs from the second and third turns exhibit a low-pass characteristic, whereas those from the first turn present a resonance followed by an antiresonance. This dichotomy of responses was a general feature. Specifically, the OHC responses in the second and third turns, with their 180° phase roll-off (Fig. 2 B and D) and high-frequency asymptotic slope of −12 decibels (dB)/octave (oct) (Fig. 2 A and C), can be described as those of a second-order nonresonant low-pass filter, with the two corner frequencies^† located at 3.9 ± 1.4 kHz (n = 22) and 27 ± 14 kHz (n = 22) for the second turn and at 4.0 ± 1.7 kHz (n = 16) and 36 ± 15 kHz (n = 16) for the third turn. The same type of filter responses was obtained in the absence of the TM and with clamped BM (18), but for all three cochlear turns. Other features are also similar to those in that report: (i) 180° phase difference between IHC and OHCs and (ii) positive low-frequency amplitude slope for IHCs, evident, for example, in Fig. 2C up to 7 kHz. However, in contrast to that report (18), the first-turn recordings always exhibited high-frequency resonance and antiresonance. We attribute this high-frequency behavior to the presence of the TM and free-swinging BM in the present preparation. The frequencies of the resonant maximum were approximately equal for all four radial recording positions, as they were for the antiresonance. Both frequencies were located below CF, at −0.97 ± 0.12 oct (n = 6) and −0.55 ± 0.09 oct (n = 6), respectively. The frequency of the resonant maximum coincided with the frequency at which the IHC and its overlying TM began to move in phase. Moreover, as this frequency is approached from below, the phase lead of the IHC relative to the OHC, amounting to ≈180° at low frequencies, decreases to become zero (modulo 360°) at this frequency. At higher frequencies, IHC phase lags OHC phase, asymptotically by ≈90° (modulo 360°) (109 ± 14°, n = 6, evaluated at 1 oct above CF). In the absence of the TM and with clamped BM, there was never evidence of either resonance or antiresonance in the vibration responses (18).

For all cochlear turns, the phase responses of the RL and opposing TM at the OHC location superimposed for all frequencies up to at least 20 kHz (Fig. 2 B, D, and F). Superposition was also found for their amplitude responses (Fig. 2 A, C, and E), the largest differences being typically 5 dB (e.g., Fig. 1A, below 20 kHz). Superposition of the responses from these two structures is consistent with electron microscopical observations that the longest OHC stereocilia are firmly embedded in the overlying TM (30). This finding, together with our requirement that the longest stereocilia remain in the same focal plane as the protofibrils in the lower surface of the TM (see Materials and Methods), contributes to our confidence in the viability of the preparation.

Pharmacological Block of Somatic Electromotility.

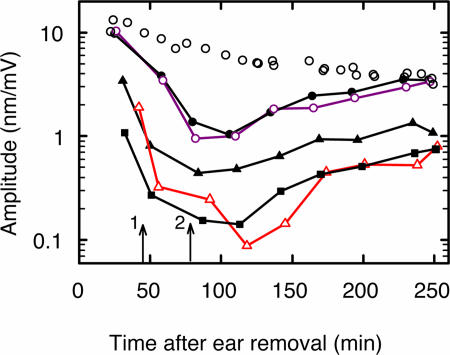
Nonspecific electrically induced motion of the organ of Corti was also tested pharmacologically with a chloride-channel blocker, anthracene-9-carboxylic acid (9-AC) (31), which is known to block the somatic electromotility of OHCs (18). Within ≈7 min (including 5-min perfusion time), 2.5 mM 9-AC began to cause amplitude attenuation; within ≈40 min the total reduction amounted to 20 dB, independent of frequency (±2 dB) up to ≈50 kHz. An example is illustrated in Fig. 4. All experiments (n = 5) unequivocally demonstrated that the electrically induced vibrations derive from the electromechanical action of the OHCs and not from nonspecific stimuli, such as electrophoretic fluid drag or surface charges.

Fig. 4.

Effect of 9-AC on electrically evoked displacement at 0.8 kHz in the third turn of the cochlea. 9-AC was applied at the time indicated by the arrow marked 1; wash out began at the arrow marked 2. RL: black circles (second-row OHC) and triangles (IHC). TM: colored circles (second-row OHC) and triangles (IHC). BM: black squares. BM recording location was at the intersection with the BM of a normal vector from the RL of the IHC. Because such pharmacological experiments required longer time than normal, the uppermost data points (open black circles) represent control data from a cochlea (at the RL of a second-row OHC), which was not perfused with 9-AC. This compound reduced the amplitude within 7 min (including ≈5-min perfusion time); there was no effect on the phase response (data not illustrated). Amplitudes returned asymptotically to the values expected for an experiment of this long duration.

Discussion

Squeezing and Extension of the Subtectorial Space.

The most salient feature of the present data is that for all three cochlear turns, the RL at the IHC and the overlying TM exhibited similar vibration amplitudes but opposite phases for stimulus frequencies up to ≈3 kHz. Counterphasic motion gradually disappeared at higher frequencies. Importantly, 3 kHz is ≈2 oct above the CF for the third turn, approximately equal to CF for the second turn, and situated on the low-frequency tail of neural tuning curves for the first cochlear turn (32). In other words, although the counterphasic motion does not appear to be tonotopically organized, its contribution to stereocilia deflection is frequency-dependent by virtue of the CF for the given cochlear location.

Counterphasic motion of RL and TM at the IHC implies squeezing and extension of the subtectorial space. Although this possibility has been considered theoretically by others (33–35), we have now experimentally demonstrated its existence. The to-date most complete theoretical description of fluid–structure interaction at the IHC stereocilia actually predicts modulation of the subtectorial space (35). In their model, Steele and Puria (35) require the TM to be sufficiently stiff so that pressure changes within the inner sulcus cannot be accommodated by transversal displacement of the TM overlying the inner sulcus. In support of their assumption, we found a progressive attenuation of TM vibration with distance into the inner sulcus, which below 2 kHz amounted to ≈12 dB per 20-μm distance from the IHC region, such that vibration was below background noise by ≈40 μm (data not illustrated).

Because the counterphasic vibration mode derives from the somatic electromechanical force produced by the OHCs, which in turn is driven by a change of transmembrane potential (25), for acoustic stimulation in vivo we expect that the mode will be evident at sound pressure levels (SPLs) below those producing saturation of the OHC receptor current. Clearly, because receptor current depends nonlinearly on stereocilia displacement (36), this mode should nonlinearly depend on SPL. Moreover, it will add (vectorially) in a frequency-dependent manner to the classical shearing mode of IHC stereocilia deflection. The relative contribution from the two modes in vivo can only be ascertained after the appropriate vibration-measurement technology is available. In any case, our data suggest that its greater contribution will be to frequencies below ≈3 kHz. It might be added that theoretical considerations (23) have suggested that relative radial motion between the TM and RL, which to date is supposed to be responsible for the shear mode, is small at frequencies well below CF compared with radial motion at CF, so that the squeezing mode might be the dominant mode of IHC stimulation well below CF in the basal turn. Indeed, the measured amplitudes are not only consistent with electromechanical data from isolated cells (28) and mechanical impedance data from the organ of Corti (5), but they are of the same order of magnitude as those for in vivo BM motion, as calibrated by the OHC ac receptor potential (Supporting Text).

Absence of Endocochlear Potential (EP).

It is important to emphasize that our recordings were made in a preparation without an EP. Assuming that the normal EP is ≈80 mV and that it is approximately zero within 30 min postmortem (37), and that the resting membrane potential is about −70 mV (38, 39), the loss of EP will reduce the electromotive drive by ≈50% (assuming that there is not an unfavorable shift of the operating point of OHC electromotility). Near CF, in vivo BM motion in response to acoustic stimuli is reduced by at least 30 dB after EP loss (40). Obviously, recordings at the RL or TM under these conditions are not available, so that it is not possible to decide how EP loss alone might influence our data. Recent data from an in vitro preparation (41), in which an artificially induced transepithelial dc potential was varied, indicates an increase in the acoustic-induced vibration amplitude of the RL by a factor of only two or three when increasing the potential from 0 to 80 mV in scala vestibuli relative to scala tympani. Reissner’s membrane was not intact in their preparation (41). Clearly, whether the presence of an EP would affect the phase difference between RL and TM at the IHC is also unknown. However, given the small effects on amplitudes reported by Chan and Hudspeth (41), it is unlikely that our phase data would be significantly affected in the presence of a transepithelial voltage. In conclusion, we suspect that restoration of EP would have little effect on vibration responses in our in vitro preparation. Because Reissner’s membrane was intact in our preparation, the next major experimental improvement would be to conduct experiments in vivo. Unfortunately, this is not yet technically feasible.

Resonant Motion in the First Cochlear Turn.

As a second salient feature, the frequency responses in the second and third turns were similar to those reported for a preparation in which the TM was absent and the BM was mechanically clamped (18). By contrast, the frequency responses reported here for the first cochlear turn exhibited resonance and antiresonance below in vivo CF, at −0.97 and −0.55 oct, respectively. Importantly, a BM antiresonance just below CF has been reported for bipolar electrical stimulation in vivo (42), suggesting that it is not an anomaly of our in vitro preparation. Piezoelectric resonance of OHCs (18, 43) might be a component of this response. However, because antiresonance was never found in the absence of the TM (18), the most parsimonious explanation is a resonance of TM motion in the radial direction, as originally proposed by Zwislocki (44), and found experimentally (7, 11, 16). Specifically, we propose that at the antiresonance frequency, the electromechanical force generated by the OHC, directed in the transverse direction, resonantly excites TM motion in the radial direction, leaving little energy for transverse motion of the RL or lower surface of the TM.

The positions of the resonance and antiresonance, relative to CF of the in vivo cochlea, are readily explained by empirical and model data. First, it is well known that the maximum of the BM response to low-intensity acoustic stimulation shifts to lower frequencies postmortem, by somewhere between 0.5 and 1 oct for the first cochlear turn of the guinea-pig cochlea (45). Therefore, the resonant frequency measured here presumably represents the CF of the postmortem cochlea, which is supported by the following cochlear mechanical model. Referring to Zwislocki (23), antiresonance between two resonant peaks is a hallmark of two elastically coupled series resonators. Zwislocki (23) has proposed a cochlear mechanical model in which one resonator consists of the inertially loaded viscoelastic BM, the other is the radially moved mass of the TM viscoelastically coupled to the spiral limbus, and the elastic coupling between the two resonators derives from the bending compliance of the OHC stereocilia. According to this model, the first resonance is caused primarily by the BM impedance, as concluded at the beginning of this paragraph from empirical data, whereas the antiresonance is caused by the parallel resonance formed by the TM mass and stereocilia compliance, as introduced in the previous paragraph. That the antiresonance was not observed in the other two cochlear turns is possibly related to the observation (23) that damping appears to increase with distance from the base of the cochlea. A resonant peak after the antiresonance was not always readily discernable in our data, but theoretically its amplitude critically depends on damping (23), which might be larger in the postmortem cochlea.

Functional Significance for Deflection of IHC Stereocilia.

The functional significance of squeezing and extension of the subtectorial space, found up to frequencies of at least 3 kHz, can be interpreted by extending known physical principles for oscillation of a fluid layer between two elastic plates (46). In essence, elastic transverse antiphase vibration of the two plates, in our case, the RL at the IHC and the opposing TM surface, is coupled into radially directed motion of the intervening fluid layer, the subtectorial space (Fig. 3B). The motion is inertial for sufficiently high frequencies (46). However, in our case the motion is probably viscous, because the stimulus frequency is low enough for the viscous boundary-layer thickness [calculated as (2μ/ρω)^1/2, where μ is fluid dynamic viscosity, ρ is fluid density, and ω is radial frequency] to be of the order of the depth of the subtectorial space (denoted here by 2δ). Therefore, we extended the earlier nonviscous analysis (46) to the case of viscous flow (Supporting Text). The fluid particle trajectories are elliptical for both inertial and viscous flow (Fig. 3B). However, instead of the radial component being independent of vertical position in the subtectorial space, as it is for inertial flow, it now depends on position. When the product of wavenumber magnitude, |k|, and δ is much less than unity, this dependence is parabolic, with zero radial motion at the TM and RL, as required for the nonslip boundary condition of viscous flow (47). For |kδ| ≪ 1, the dominant mode is for the wavenumber:

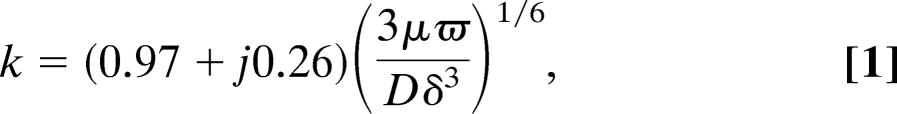where D is the flexural rigidty of the RL and TM (assumed equal). D can be readily calculated from impedance measurements (5); it has the value of 0.1 nN m. Substitution into Eq. 1 of these D values, together with δ = 2–4 μm, respectively, for the first to third cochlear turns indicates that this so-called shallow-fluid or long-wave condition (|kδ| ≪ 1) is satisfied for all frequencies for which counterphasic motion was observed between TM and RL at the IHC (<3 kHz): at 3 kHz, |kδ| = 0.13–0.18 for δ = 2–4 μm. As a check on this value, it is important to note that the corresponding range of wavelengths (λ = 2π/Re[k]) is 101–144 μm for δ = 2–4 μm. This range is consistent with the experimental observation that there was little phase difference radially along the TM from the IHC to OHCs; the distance between second-row OHCs and IHCs is ≈50 μm in the third turn and as little as 40 μm in the first turn. In other words, this long-wave motion resembles a “space clamp” with each point along the TM (or RL) moving approximately in-phase radially, with temporal frequency equal to that of the stimulus.

The condition |kδ| ≪ 1 has an extremely important consequence: The maximum amplitude of the radial fluid motion (1.5 η_m/|k|δ, where η_m is TM and RL displacement amplitude) is, for δ = 2–4 μm and stimulus frequencies up to 3 kHz, at least an order of magnitude larger than η_m. For example, at 3 kHz at the OHCs, this amplification factor ranges from 8 to 12, for δ ranging from 8 to 4 μm, respectively. Moreover, the amplitude of the transverse fluid component decreases monotonically as a cubic function from the TM and RL to zero at the middle of the subtectorial space. In other words, fluid motion is mainly radial and is, therefore, describable as pulsatile.

The presence of viscosity means, of course, that the wave is attenuated from its source at the OHCs to its target at the IHC, by a factor exp(−Im[k]x), where x is the distance between OHC and IHC; for x = 50 μm, this amounts to a factor of 0.44–0.56 for δ = 2–4 μm. These values compare with the experimental results (Fig. 2 A, C, and E), and the observation that attenuation is larger in the first turn (Fig. 2E) than in the third turn (Fig. 3A). There is also attenuation from the center of the subtectorial space to the TM and RL (Fig. 3B). However, the parabolic profile means that the attenuation in the middle third of the space, where the tip links between the longest and middle IHC stereocilia might be located, as judged from the relative heights of the stereocilia (48), is only a factor of 0.9. In other words, despite fluid viscosity, the pulsatile fluid motion resulting from the counterphasic motion of the TM and RL at the IHC has the potential of amplifying the fluid stimulus to the IHC stereocilia. This possibility is important given that the narrow subtectorial space is probably the largest source of damping in the cochlea.

Clearly, whether this amplification process is capable of deflecting IHC stereocilia and whether it is excitatory or inhibitory depends on fluid–structure interactions at the stereocilia. Using published values of stereocilia stiffness (49) and an analysis (50) based on the view that viscous fluid drag is the adequate stimulus for deflection of IHC stereocilia (50–52),^‡ we find that when the longest stereocilium extends over most of the subtectorial space (95%), deflection of its tip for stimulus frequencies >300 Hz is of the same order of magnitude (±6 dB) as fluid displacement in the radial direction. This finding concurs with the in vitro observation (9) that for intracochlear electrical stimulation, IHC and OHC stereocilia, as well as OHC somatic electromotility, have similar amplitudes for stimulus frequencies in this range. Moreover, according to our analysis, low-frequency somatic contraction of the OHC causes deflection of IHC stereocilia in the excitatory direction, that is, laterally in the direction of the longest stereocilium (Fig. 3B), and vice versa for somatic elongation. In other words, in this experimental configuration, the displacement of the IHC and OHC stereocilia are of the same polarity at low frequencies. This result is consistent with the in vitro observation (9) that there is little phase difference between these stereocilia in response to low-frequency electrical stimulation. As frequency is increased, the analysis suggests that above ≈1 kHz, deflection of the IHC stereocilia tends to lead OHC electromotility by ≈90°.

Hensen’s Stripe.

Finally, it has not escaped our attention that Hensen’s stripe (Fig. 1A), a wedge-shaped ridge running longitudinally along the lower surface of the TM in the region of the IHC stereocilia (53), might enhance the stimulatory action of the counterphasic motion of the RL and TM, as has been proposed (33, 35) for the classical shearing mode of TM and RL motion.

Conclusion

By exposing and untangling electrically induced vibration responses at the two surfaces bounding the subtectorial space, we have discovered a functionally relevant deflection mode for IHC stereocilia. This mode allows direct mechanical coupling of OHC electromechanical transduction to IHC mechanoelectrical transduction for frequencies up to ≈3 kHz. At higher frequencies, the electromechanical action of the OHC soma is probably solely via the BM, which induces the classical shearing motion between RL and TM.

Materials and Methods

The success of these experiments derived from two experimental breakthroughs, one surgical and the other technical. Today, it is still not possible to measure the vibration of the RL and the lower surface of the TM in vivo, even with the currently most sensitive technique of laser interferometry. There are two principal impediments: (i) geometrical constraints of a coiled cochlea and (ii) technical limitations associated with the low optical reflectivity of the functionally relevant vibrating surfaces and reflections from structures behind and in front of the surface on which the laser beam of the interferometer is focused. Details are given in Supporting Text.

Preparation.

We were able to address these problems by developing a temporal-bone preparation of the guinea-pig cochlea, in which Reissner’s membrane was left intact to enable the apical surface of the cells to be bathed in endolymphatic fluid, which was achieved by dissecting out an entire turn of the cochlea. The BM was free to vibrate. The surgical procedure was successful in the first, second, and third turns of the cochlea (Fig. 1B), at positions that corresponded to CF of the in vivo cochlea of 24, 3.0, and 0.8 kHz, respectively, as calculated from the neuronal tonotopic map of Tsuji and Liberman (32). The BM length in the excised first and second turns was 7–8 mm, beginning respectively at 0 and 4 mm from the basal end; in the third turn the excised length was 5 mm, beginning 10 mm from the basal end. The apical extremity of the excised cochlea was open; the basal extremity was open in the second and third turns, but closed in the first turn.

Because the condition of the TM is extremely sensitive to its ionic environment (54, 55), the best monitor of TM patency and adequate separation of perilymph and endolymph was that the tips of the longest stereocilia remained in the same focal plane as the protofibrils in the lower surface of the TM. This condition was preserved up to at least 90 min postmortem for all cochlear turns, suggesting that the ionic environment of the TM was endolymphatic for this period. At longer times postmortem, the TM began to retract medially, as it also did if Reissner’s membrane was damaged, presumably because of mixing of the perilymph from scala vestibuli with endolymph.

Vibration experiments typically began 20 min postmortem. Experiments without pharmacological manipulation were completed within 60 min postmortem for the first cochlear turn and 90 min postmortem for the other turns. Pharmacological experiments were performed up to 250 min postmortem. Care and maintenance of the animals were in accordance with institutional and state guidelines.

Velocity Measurement.

The second ingredient for a successful experiment was the confocality of the laser Doppler vibrometer (LDV), used to measure velocity (Supporting Text). The LDV system was inherently confocal (56), with a focal depth of ±1.8 μm, measured at 10 dB below peak light intensity. Because the depth of the subtectorial space (4–8 μm from first to third turn, respectively) was greater than the focal depth of this LDV system and measured displacement amplitudes were at least three orders of magnitude smaller (<1–10 nm), we were confident in being able to selectively measure the transverse velocities of the lower surface of the TM and its opposing point on the RL.

Glossary

Abbreviations:

BM

basilar membrane

CF

characteristic frequency

dB

decibel

EP

endocochlear potential

IHC

inner hair cell

9-AC

anthracene-9-carboxylic acid

oct

octave

OHC

outer hair cell

RL

reticular lamina

TM

tectorial membrane.