On the origin and highly likely completeness of single-domain protein structures

Abstract

The size and origin of the protein fold universe is of fundamental and practical importance. Analyzing randomly generated, compact sticky homopolypeptide conformations constructed in generic simplified and all-atom protein models, all have similar folds in the library of solved structures, the Protein Data Bank, and conversely, all compact, single-domain protein structures in the Protein Data Bank have structural analogues in the compact model set. Thus, both sets are highly likely complete, with the protein fold universe arising from compact conformations of hydrogen-bonded, secondary structures. Because side chains are represented by their C^β atoms, these results also suggest that the observed protein folds are insensitive to the details of side-chain packing. Sequence specificity enters both in fine-tuning the structure and thermodynamically stabilizing a given fold with respect to the set of alternatives. Scanning the models against a three-dimensional active-site library, close geometric matches are frequently found. Thus, the presence of active-site-like geometries also seems to be a consequence of the packing of compact, secondary structural elements. These results have significant implications for the evolution of protein structure and function.

Protein structures represent very interesting systems in that they result from both physical chemical principles (1) and the evolutionary selection for protein function (2). Focusing on the tertiary structures adopted by protein domains (roughly defined as independent folding units) (3), a number of key questions must be addressed. How large is the protein fold universe (4–6)? Is it essentially infinite, or is there a limited repertoire of single-domain topologies such that at some point, the library of solved protein structures in the Protein Data Bank (PDB) (7) would be sufficiently complete that the likelihood of finding a new fold is minimal? If the number of folds is finite, how complete is the current PDB library (6, 8, 9)? That is, how likely is it that a given protein, whose structure is currently unknown, will have an already-solved structural analogue? The answer to these questions is not only of intrinsic interest, but has practical applications to structural genomics target selection strategies (5, 10). More generally, can the set of protein folds and its degree of completeness be understood on the basis of general physical chemical principles, or is it very dependent on the details of protein stereochemistry and evolutionary history (11)?

In recent work that builds on the other studies (8, 12, 13), we suggested that the library of single-domain proteins already found in the PDB is essentially complete in the sense that single-domain PDB structures provide a set of structures from which any other single-domain protein can be modeled (9, 14). By using sensitive structural alignment algorithms that assess the structural similarity of two protein structures, even when proteins belonging to different secondary structure classes are compared (e.g., comparing α-proteins to α/β and β-proteins), protein structures in the PDB can be found with very similar topology; i.e., the arrangement of their secondary structural elements (α-helices and/or β-strands) is similar (9). Moreover, protein structure space is extremely dense in that there are many apparently nonhomologous structures that give acceptable structural alignments to an arbitrary selected single-domain protein. However, the structural alignment usually has unaligned regions or gaps. Starting from these alignments, state-of-the-art refinement algorithms can build full-length models that are of biological utility [with an average root-mean-square deviation (rmsd) to native of 2.3 Å for the backbone atoms] (14). Furthermore, incorrectly folded models generated by structure prediction algorithms also have structural analogues in the PDB, an observation again consistent with PDB completeness (15). Nevertheless, one might argue that comparing PDB structures against themselves as well as with structures generated using knowledge-based potentials extracted from the PDB (which retain some features of native proteins), although suggestive that the PDB is complete, does not establish that the universe of single-domain protein structures is complete; nor even if true, does it establish the reason for such completeness.

Here, we address these issues and show the surprising result that the highly likely completeness of the PDB results from the requirement of having compact arrangements of hydrogen-bonded (H-bonded), secondary structure elements and nothing more. By studying compact homopolypeptide conformations having a typical distribution of secondary structures, we further show that the resulting library of computer-generated compact structures is found in the current PDB, and, conversely, the generated library of compact structures is complete, i.e., all compact, single-domain proteins in the PDB have a structural analogue in a rather small set of computer-generated models. These studies go significantly beyond previous work, where relatively small supersecondary structural elements are generated assuming that the protein is a homopolymer confined to a semiflexible tube that mimics H-bonding (16), to show that by using a simpler, physics-based force field, the complex topologies of single-domain proteins result. Furthermore, if we scan the set of randomly generated, compact structures against a three-dimensional active-site template library (17), close geometric matches for a considerable number of known active sites can be found. The possible implications of these results for both protein design and evolution are discussed below.

Results

We consider a homopolypeptide chain (termed a “sticky” homopolypeptide below) with a very minimal potential consisting of H-bonding, excluded volume, and a uniform, pairwise attractive potential between side chains. For the atomic model, folding is purely ab initio with no bias to any preselected secondary structure (18); however, its H-bond potential is biased to helices; thus, it is limited to the study of helical proteins. In contrast, the H-bond scheme in the reduced model works equally well for all protein secondary-structural classes. Furthermore, to enable all secondary-structure classes to be explored, the reduced model employs a local bias toward the assigned secondary structure (which is not obligatory), where the length and location of each biased secondary structure element is randomly selected based on PDB statistics. The actual distribution can be found in Fig. 5, which is published as supporting information on the PNAS web site. Each secondary structural element is followed by a loop, and in α/β proteins, the order of α-helices and β-strands is randomly chosen, each with 50% probability.

Global Folds of Compact Homopolypeptides with Protein-Like Secondary Structures Are All in the PDB.

Collapsed, low-energy conformations of 100- and 200-residue-long, sticky homopolypeptides were generated for the reduced protein model, whereas, because of computational cost, only 100-residue homopolypeptides were considered in the detailed atomic model (18). For each chain length in the reduced protein model, a set of chains with 150 different secondary-structure assignments is simulated (50 α-, 50 α/β-, and 50 β-proteins). For the atomic model, because its H-bond scheme does not work well for β-strands, mainly α-proteins result. For both protein representations, the topologies of the generated computer models for the set of compact, homopolypeptide chains are highly divergent. Typically, the population of the largest cluster is <5% of the total number of structures, and there is minimal energetic separation between different clusters. In contrast, in a typical structure prediction on a real protein sequence, the largest cluster population is ≈50% (19).

We selected pairs of structurally related proteins by their TM-score, a metric of structural similarity, identified by the structural alignment program TM-ALIGN (15). Compared with the conventional rmsd between a pair of structures, the TM-score is more sensitive to the similarity in global topology of the compared structures. It is normalized so that its magnitude is independent of protein size, with a value of 0.30 and a standard deviation of 0.01, for the best structural alignment of an average pair of randomly related structures (15, 20) and a value of 1.0 for two identical protein structures.

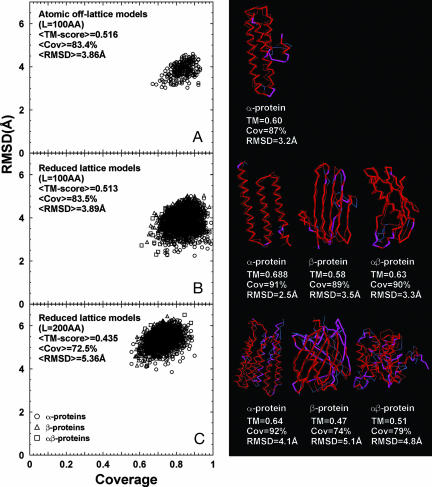
Fig. 1A and B shows the rmsd vs. coverage plot for 100-residue-long chains of the atomic and reduced protein models, respectively, where each point represents a computer model matched with the PDB structure of the highest TM-score. TM-scores on the order of 0.45 (with a z-score of ≈15) are indicative of highly significant structural similarity. In all cases, the randomly generated compact structures have related folds in the PDB. The atomic models have an average rmsd of 3.9 Å with its closest structural neighbor from the PDB, 83% average coverage, and an average TM-score of 0.52 (z-score of 22). For the 100-residue-long reduced models, these numbers are 3.9 Å, 83%, and 0.51 (z-score of 21), respectively. Thus, there is no difference in average results between the atomic and reduced protein models, indicative of their robustness and invariance to model details. This similarity further indicates that the helix-length distribution in the atomic model, in particular, and most likely in general, is dictated by the balance between compactness and H-bonding. In Fig. 1 Right, we show representative examples of structures belonging to the different secondary structural classes of proteins compared with the closest PDB structure. It is evident that protein structures of quite complex topology are generated and that all have close structural matches in the PDB.

Fig. 1.

Rmsd vs. alignment coverage of computer-generated models matched with the closest representative structure in the PDB. (Left) For each homopolypeptide with a given secondary structure pattern, 14 models (Top 1, 10, 25, 50, 75, 100, 125, 150, 175, and 200 clusters) are selected; for each, only the match of the highest TM-score identified by TM-ALIGN is presented. (A) The 100-aa (AA) atomic, off-lattice models. (B) The 100-AA reduced lattice models. (C) The 200-AA reduced lattice models. (Right) Corresponding representative examples of the structural alignments in different categories are shown. Thick backbones are from models; thin backbones are from PDB structures. Red indicates residue pairs whose distance is <5 Å; those separated by >5 Å are shown in magenta (model) and blue (PDB structure), respectively.

However, because proteins containing 100 residues are relatively small, the fact that the set of compact, sticky homopolypeptide structures can be found in the PDB, although suggestive, does not convincingly demonstrate that for longer sequences with more complicated topologies, such structures also will be found in the PDB. Thus, we considered 200-residue proteins in the reduced protein model. Again, the results are highly significant: the average coverage is 73%, with an average rmsd of 5.4 Å and a significant TM-score of 0.44 (z-score of 14). As demonstrated in the examples in Fig. 1C Right, even for proteins with very complex topologies, there are corresponding structural analogues in the PDB. As the chain length increases, on average, the corresponding structural alignments to PDB structures contain a larger number of gaps, especially for β-proteins; nevertheless, the global topology is matched, with the majority of the core region aligned. Based on our previous work, rather high-quality comparative models could be built from these alignments (14), even if one secondary-structural element is missed as can sometimes happen in the most extreme cases. It is precisely in this sense that all compact homopolypeptide structures are in the PDB. This essential point is discussed in further detail below and in Supporting Materials and Methods and Figs. 6 and 7, which are published as supporting information on the PNAS web site. Thus, the results summarized in Fig. 1 strongly suggest that the requirements to generate the complex topologies found in the PDB are inherently geometric and just involve the packing of compact structures containing H-bonded, secondary-structure elements.

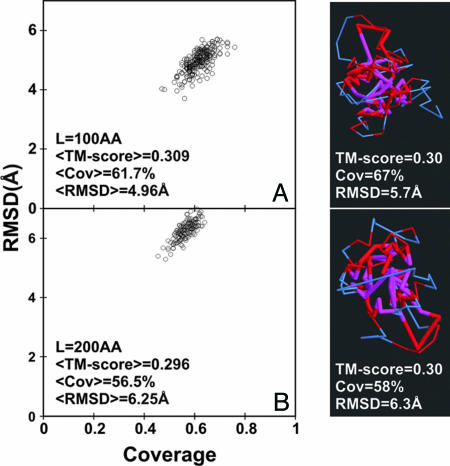
Is presence of H-bonded, secondary structures necessary to reproduce the set of single-domain protein structures found in the PDB at a reasonable level of accuracy, or is compactness alone sufficient? To examine this issue, we generated an ensemble of compact, freely jointed chains (FJC) (21) that lack both regular secondary structure and H-bonds, but that retain C^α atom-excluded volume interactions. We then performed the identical analysis as in Fig. 1. The results are summarized in Fig. 2 and are qualitatively different (see also Fig. 8, which is published as supporting information on the PNAS web site). For the resulting ensemble of compact FJC models that are 100 and 200 AA residues in length, the average TM-score is ≈0.30. This value is just the average TM-score of structural alignments between two randomly related structures. As shown in the typical examples of Fig. 2, the structures very poorly resemble real proteins both at the level of the global fold as well as in their local chain geometry. Thus, compactness alone does not recover protein-like topologies, nor does it generate appreciable secondary structure (22).

Fig. 2.

Rmsd vs. alignment coverage for the compact freely jointed chain models matched by TM-ALIGN to the closest representative PDB structure. (A) The 100-aa (AA) chains. (B) The 200 AA chains. For each chain, 20 independent Monte Carlo simulations are generated, which have excluded volume interactions (C^α–C^α distance > 3 Å) and a bias to the radius of gyration (G) of an average protein of length L, i.e., G ≈ 2.2L^0.38. For each independent simulation, up to 14 clusters chosen as in Fig. 1 are used in the structure comparison. Red indicates residue pairs whose distance is <5 Å; those separated by >5 Å are shown in magenta (model) and blue (PDB structure), respectively.

All Single-Domain PDB Structures <150 Residues Are in the Library of Compact Homopolypeptide Global Folds, Implying both Are Complete.

Thus far, we have shown that all of the generated compact, sticky homopolypeptide structures are found in the PDB. Next, we demonstrate the converse that for a representative set of nonhomologous proteins in the PDB between 41 and 150 residues in length, the “PDB150 set,” all single-domain protein structures are found in the library of computer-generated, compact homopolypeptide structures. After clustering all PDB structures at the level of 30% sequence identity, the resulting PDB150 set contains 913 representative single-domain proteins, of which there are 213 α-proteins, 116 β-proteins, 580 α/β-proteins, and 4 proteins with little if any secondary structure. Here, we exclude proteins having irregular, extended structures by using a radius of gyration (G) cutoff, i.e., G <1.5G₀, where G₀ (= 2.2L^0.38) denotes the average value of radius of gyration for a protein of length L (23). Nevertheless, a significant number of PDB structures with dangling tails remain after filtration, thereby making structure comparison with the compact, homopolypeptide library a somewhat more difficult test.

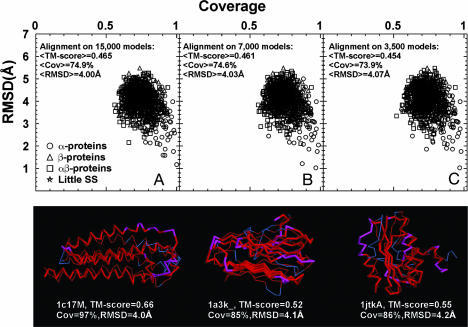
As shown in Fig. 3A, if we use the set of 15,000 clustered structures generated for the 200-residue, compact, sticky homopolypeptide chains (150 proteins, each with a distinct, randomly selected pattern of secondary structure times the top 100 clusters), then the resulting library of generated compact structures is complete with respect to the PDB. In fact, single-domain proteins in the current PDB structural repertoire can be matched to the compact structure fold library with an average rmsd of 4 Å, 75% coverage, and TM-score = 0.47 (z-score of 17).

Fig. 3.

Relationship of the library of compact, sticky homopolypeptide structures to PDB structures between 41 and 150 residues in length. (Upper) Rmsd vs. coverage for 913 representative, compact PDB structures between 41 and 150 residues to protein models in the 200-residue-long, compact, sticky homopolypeptide structural library comprised of 15,000 (A), 7,000 (B), and 3,500 (C) structures, respectively. (Lower) Structural alignments of representative α-protein (PDB ID code 1c17 chain M; 142 residues), β-protein (PDB ID code 1a3k; 137 residues), and α/β-protein (PDB ID code 1a3k chain A; 131 residues) PDB structures to the compact sticky homopolypeptide structures are shown. The thick (thin) backbones represent computer models (PDB structures). Red indicates residue pairs whose distance is <5 Å.

To demonstrate that the resulting set of structures is buildable (that is, continuous chains with physically reasonable C^α virtual bonds could be constructed from the structures), we selected the 10 worst PDB-compact homopolypeptide matches on the basis of their TM-score whose value is ≈0.37; not surprisingly, many have dangling tails that are responsible for this relatively low TM-score. As described in Table 1 and Figs. 9–11, which are published as supporting information on the PNAS web site, these alignments cover ≈2/3 of the core of the protein. Full-length models can be built by using the protein structure prediction program TASSER (19, 35); the average TM-score after TASSER modeling improved to 0.62 (z-score of 32). In all but one case (again because of a dangling tail), TASSER also improved the quality of the core regions. It is in this sense that structural space is complete: The compact homopolypeptide models are buildable, and the global topology of all proteins in the PDB can be recovered by using straightforward modeling techniques to add the unaligned residues that mainly occur in the loops. The final model sometimes contains minor modifications in the core.

In Fig. 3B, we reduce the size of the compact homopolypeptide library to 7,000 structures by reclustering the set of 15,000 models, a similar size to the PDB library used in Fig. 1. Now, the average rmsd is 4 Å, with 75% average coverage and a TM-score of 0.46 (z-score of 16). In Fig. 3C, we again reduce the number of models by half to 3,500 distinct structures by reclustering the 7,000 models using a smaller TM-score cutoff. Here, the average rmsd is 4.1 Å, the average coverage is 74%, and the average TM-score is 0.45 (z-score of 15). Thus, even when the structure library is reduced by half, the set of representative homopolypeptide conformations is still a complete representation of the PDB. Moreover, as indicated by the trend shown in Fig. 3, the space covered by such structures is very dense with many compact, sticky homopolypeptide structures that give acceptable structural alignments to PDB structures. In Fig. 3 Lower, we show structure alignments of representative PDB structures for the three different secondary structure classes to members of the compact, 15,000-member sticky homopolypeptide structural library. This library and the set of alignments to the PDB150 set are included in Supporting Materials and Methods.

The fact that the library of compact sticky homopolypeptide structures (that have not been subject to any evolutionary selection) is complete with respect to the PDB as well as the converse argues that both are highly likely to be complete. That is, they fully represent the set of topological arrangements of secondary-structural elements that single-domain proteins may adopt. Furthermore, structures of acceptable quality can be built by using the structural alignment as the starting conformation. This probable completeness is the result of the packing of H-bonded, secondary structure in compact proteins. This finding also explains why misfolded decoys generated by protein structure prediction algorithms are found in the PDB, because they too are just compact structures containing H-bonded, secondary-structural elements.

How can it be that such an apparently small number of compact structures is complete for single-domain protein structures, especially because we only consider 150 distinct secondary structure patterns (a number arbitrarily chosen for reasons of computational cost)? The reason is that a given structure can be the source of many different structural alignments, all of which can yield buildable, full-length protein models. The set of compact structures with randomly selected protein-like secondary structures can be thought of as a set of “basis vectors” or building blocks that span the space of single-domain folds. Because structural alignments sample an exponentially large number of possibilities (24), given a reasonable set, the ability to cover the PDB converges rather rapidly as a function of the number of disparate protein structures, a picture confirmed by Fig. 3.

Nonlocal Substructures Bearing a Close Relationship to Active-Site Geometries Are Found in the Compact, Sticky Homopolypeptide Structure Library.

Given the global similarity between single-domain proteins and the set of compact sticky homopolypeptide structures, we next examine the corresponding relationship between nonlocal substructures (local in space, but not local in sequence). Because of their biological relevance, we explored the extent to which the geometry of functionally important, nonlocal substructures is also a consequence of the packing of compact, secondary-structural elements. We first scanned 750 sticky homopolypeptide structures (150 proteins with distinct secondary structure times the top five clusters for the 200 AA models) and the same number of native structures (a nonredundant set at a 40% sequence identity cutoff), with a library of sequence-independent, active-site templates, the Automated Functional Template (AFT) library (17). Each AFT contains three to five functional residues and is comprised of the functional residues C^α and C^β atoms and the C^α atoms of the adjacent residues. The C^β atoms partially account for the orientation of the active-site side chains. To eliminate the direct influence of evolution that would lead to trivial results, before native structures were scanned, all enzymes sharing the first two EC digits with that of the AFT under analysis were excluded.

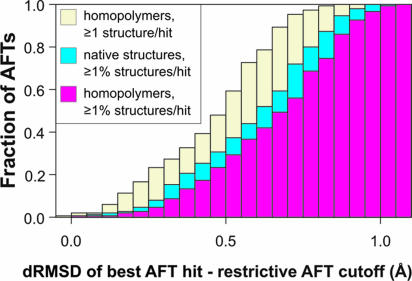
As shown in Fig. 4, in both sets, we find substructures whose geometries are very close to those of active sites, even though we remove from consideration those native structures corresponding to enzymes functionally related to the AFT under analysis. For instance, with a tolerance of 0.5 Å in the distance rmsd (drmsd) from the restrictive cutoff (the maximum drmsd observed between a true positive hit and the corresponding AFT) (17), we detected matches for 23% of the AFTs in at least 1% of the homopolypeptide structures and matches for 31% of the AFTs in at least 1% of the native structures (see Fig. 12, which is published as supporting information on the PNAS web site). Both distributions are remarkably similar, bearing in mind that the AFTs are directly derived from very specific arrangements of functional residues in native enzyme active sites. Thus, the existence of active-site-like geometries also seems to be a consequence of the packing of compact, secondary-structural elements. They occur at a remarkably high frequency, even under conditions where there is no selection pressure to adopt such geometries. Furthermore, if we require matches with a tolerance of a 0.5-Å drmsd in at least one of 3,500 sticky homopolypeptide structures (the same set shown in Fig. 3C, which is complete with respect to the PDB), then we observe that the set is 48% complete with respect to our active-site library.

Fig. 4.

Fraction of the 150 active-site functional templates, AFTs that hit at least 1% of 750 sticky homopolypeptide structures (magenta histogram), at least 1% of 750 native structures (blue histogram), or at least one of 3,500 compact sticky homopolypeptide structures (yellow histogram) at a given drmsd interval from the corresponding restrictive cutoff.

These results have a number of interesting implications: First, although the idea of designing new functions by finding backbone geometries that match known active sites and then inserting the functionally important residues has been successfully used in a number of cases (25–27), the blue curve in Fig. 4, which corresponds to structures in the PDB library, suggests that this finding could be a general design paradigm for enzymes. However, its generality must be demonstrated. Second, our results suggest that there is nothing particularly special about active-site geometries. What is special is the fact that when specific constellations of residues adopt this geometry, then a particular enzymatic function results. Third, the fact that active-site geometries occur with such relatively high frequency in our library of compact, sticky homopolypeptides (where no evolutionary pressure whatsoever has been exerted to select for them) suggests that in the very early stages of protein evolution, the probability that they could be discovered by chance is remarkably high. Evolution then could act to optimize enzymatic efficiency.

Conclusions

Our results strongly suggest that the observed repertoire of single-domain protein tertiary structures found in the PDB is the result of geometric effects due to the packing of compact, H-bonded, secondary structural elements and is not the result of evolutionary selection nor the intimate details of side-chain packing. Furthermore, the results are robust and independent of the particular model that is used (detailed atomic, off-lattice model vs. reduced, on-lattice model). Although the set of compact, sticky homopolypeptides generates reasonable tertiary structures, they are definitely not biological proteins in that they do not have a unique native state. This state requires a protein sequence (with a reasonable distribution of hydrophobic residues to induce collapse and hydrophilic residues to make the protein water-soluble) whose minimum free energy structure has an energy gap from other alternative folds. It is here that thermodynamics enters and where evolution has selected sets of sequences that satisfy this requirement. The global fold of the protein also is fine-tuned by the sequence-specific details including side chain packing. Thus, the assumptions of fold-recognition algorithms (28, 29) are consistent with nature in that fold and sequence are decoupled: there likely is a limited library of allowed structures consistent with the general physical chemical principles of compactness and H-bonding, and the “goal” of evolutionary selection is to find sequences compatible with such structures and that are energetically stabilized with respect to the sea of alternative folds. It is likely that the evolution of sequences and structures that resulted in the modern “protein universe” operated on a large, but limited, set of structures. Certainly, possible folds were unequally sequestered by evolution; the uneven usage of folds and sequences is well established (2, 30). However, in all likelihood, the limited repertoire of starting structural possibilities, established in this work, seriously impacted the course of evolution of the protein universe; it also has significant implications for protein design.

By studying the completeness of a library of compact homopolypeptides that contain a protein-like distribution of H-bonded, secondary-structural elements, we have demonstrated that the resulting set of computer-generated, compact structures can be found in the PDB and, conversely, for single-domain proteins in the PDB, even when a very small set of secondary structural elements are used (here, 150 different sequential arrangements), the resulting library is likely complete at the level of low-to-moderate resolution structures. That is, they contain the majority, if not all, of the core secondary structure elements of all compact, single-domain proteins and that structures of biological utility can be generated with simple modeling procedures that use one of these compact homopolypeptide’s structures as the starting template. This finding suggests that both the PDB and the compact homopolypeptide structural libraries are complete. Furthermore, it is highly likely that a necessary and sufficient condition for this completeness is the packing of compact, H-bonded secondary-structural elements. Although this conclusion might seem trivial, it is commonly believed that the complex folds adopted by proteins are the result of the fine tuning of the details of side-chain packing and are specially selected for during the course of evolution. This work suggests the contrary: the library of folds that are adopted is because of relatively simple and robust considerations of the packing of compact, H-bonded secondary-structural elements. In essence, single-domain proteins are in the small chain limit: they have a relatively small number of secondary-structural elements whose random packing yields a set of structures that span the space of protein folds. When the chains are completely flexible (i.e., lacking in secondary structure) and their number of degrees of freedom is on the order of the number of residues, this is not the case, and the resulting compact structure fold space is not complete.

Because our results suggest that the PDB has already explored the universe of compact single-domain protein folds, the target selection strategy of structural genomics (10, 31) might need to be revisited to focus either on multiple domain and multimeric proteins, where the PDB is most likely not yet complete (32), and/or on the selection of single-domain protein sequence families whose folds cannot be assigned by using state-of-the-art structure-prediction tools (33–35). Finally, we note that just as the likely completeness of the PDB at the level of global folds arises from geometric factors, the set of compact, sticky homopolypeptides contains the approximate geometry of many active sites in enzymes. Together, these results suggest a simple first-order picture of the origin and probable completeness of the folds in the PDB that is inherently geometric and that arises from the general physical chemical principles of the packing of H-bonded, secondary-structural elements in compact structures, with a remarkable richness of detail that follows from these few, simple assumptions.

Methods

Protein Models.

To assess the generality of the results, we used two protein models with different protein representations, force fields, and conformational search schemes that are based on replica exchange Monte Carlo sampling (18, 19, 36). If the results turn out to be insensitive to protein representation and conformational search scheme, then this finding is suggestive that the conclusions are robust and insensitive to details. If not, one would have to be cautious in interpreting how well the simulations mimic the universe of single-domain protein structures. In practice, we employ both an atomic model that is off-lattice (i.e., the atoms are in continuous space) with a full heavy-atom representation of the backbone and a reduced protein representation where the protein backbone is represented by its C^α atoms that are confined to a high coordination number lattice (19). Both models represent each side chain by a C^β atom. Although isosteric to polyalanine, these are generic protein representations that depict the most minimal geometric features shared by all proteins and should allow us to examine the most general features underlying the origin of the set of protein folds. Additional methodological details are in Supporting Materials and Methods.

Structure Generation and Analysis.

Folding starts from a set of randomly generated, expanded states. The resulting compact structures were clustered based on their mutual structural similarity and ordered according to their population using the SPICKER structure clustering algorithm (37). The top 5, 10th, and then every 25th structure to the 200th structure was compared with a template library of 6,967 proteins that cover the PDB at a 50% pairwise sequence identity cutoff. The structural similarity of each pair of native and homopolypeptide structures was assessed by using a recently developed structural alignment algorithm, TM-ALIGN (15), which uses the TM-score (20) as the metric of structural similarity. We also report the corresponding rmsd and coverage, the fraction of aligned residues, from the best structural alignment. Additional details are in Supporting Materials and Methods and also Table 2, which is published as supporting information on the PNAS web site.

Abbreviations

AFT

Automated Functional Template

PDB

Protein Data Bank

rmsd

rms deviation

drmsd

distance rmsd.