An optimal brain can be composed of conflicting agents

Abstract

Many behaviors have been attributed to internal conflict within the animal and human mind. However, internal conflict has not been reconciled with evolutionary principles, in that it appears maladaptive relative to a seamless decision-making process. We study this problem through a mathematical analysis of decision-making structures. We find that, under natural physiological limitations, an optimal decision-making system can involve “selfish” agents that are in conflict with one another, even though the system is designed for a single purpose. It follows that conflict can emerge within a collective even when natural selection acts on the level of the collective only.

Internal conflict is manifested in a broad array of animal behaviors. For example, when a rat is offered both food and an electric shock at the end of an alley, it oscillates at a certain distance from them, given certain parameters of food and shock (1). Researchers have attributed this oscillation to wavering between approach and avoidance (1). Additionally, in separate groups of rats, one group facing food only and one group facing shock only, the tendencies to approach and to avoid were measured by the force exerted on a harness (2). Results suggested that, in the combined setup, these tendencies opposed each other effectively at the point of wavering (2). Hence researchers believe that conflicting tendencies can co-occur at a dynamic equilibrium (1, 2).

Simultaneous, contradictory tendencies also appear in the form of ambivalence (3). For example, when a female stickleback transgresses into a male’s territory, the male often exhibits both incipient attack and courtship movements simultaneously (3). In a more pathological case, herring gulls attempt to both peck and incubate red-painted eggs introduced into their nests (3). The redness seems to elicit attack, whereas the shape seems to elicit brooding (3). These behaviors indicate independent and potentially conflicting behavior programs. Ambivalence, as well as oscillation, has been observed in various species of birds, fish, and mammals (3, 4).

Further evidence for internal conflict comes from displacement activities. When evenly matched male herring gulls are involved in a dispute at the boundary of their territories, they often pull the grass aggressively (3). It is thought that they are caught between a fight and a flight response and that, somehow, the collision between these incompatible drives triggers a nest-building-related activity (3). Other animals in similar situations exhibit a host of displacement activities including preening, beak wiping, drinking, eating, and self-grooming (3, 5, 6).

In humans, internal conflict is rife and perplexing. Consider the disulfiram pill: Its sole purpose is to make a person sick if s/he drinks alcohol, yet some alcoholics knowingly choose to take it. It appears that the pill serves as a threat on the self, and thus reflects full-blown internal conflict. A more subtle conflict emerges in the delay of gratification (7). When children are offered to either wait for a preferred candy or accept an inferior one immediately, they sometimes cover their eyes or look away from the immediate one (7). Furthermore, they can be taught to suppress impatience by manipulation of thought (7, 8). Brain-imaging studies have shown that such behaviors result from competition between neural systems (9). Indeed, conflict has been a main tenet in psychology (10–15), and massive evidence on it has been accumulated (7–16).

The evidence as a whole establishes the importance of internal conflict as an organizing concept and demonstrates its applicability across the animal kingdom. However, the existence of conflict seems at odds with the Darwinian view. We often take the individual to be an approximate unit of selection and, accordingly, expect the different parts of an individual, whether physical or mental, to work together as a team for a common goal. It is therefore surprising that those different parts would not only pursue different goals but actually come to contradict and frustrate each other. This mode of operation appears maladaptive in comparison with a more seamless decision-making system that could have possibly evolved. We are therefore left with an important class of observations that has not been reconciled with evolution.

In trying to address this problem, Trivers (17) and Haig (18) relied on the idea that the gene rather than the individual is the unit of selection (19). Accordingly, different genes within the same individual may have different goals, and their goals may be in conflict (17, 18) [such as in transposons (19) and imprinting (20)]. But whereas genetic conflict is important, it does not apply easily to the macroscopic behavioral evidence mentioned above. For example, it would necessitate “genes for approaching food” and “genes for avoiding shock” that benefit differentially from these two activities.

Here we show that internal conflict can emerge even in the absence of gene-level selection. Namely, conflict can emerge within a collective even when natural selection acts on the level of the collective only. We contend that this phenomenon is a natural consequence of physiological limitations, and that internal conflict can emerge even in an optimal collective subject to those limitations.

Three conceptual pieces will be used to derive this result. They are as follows: (i) the idea that behavior results from computation and is subject to computational limitations, (ii) the idea that conflict can be defined rigorously in terms of utility functions, and (iii) the idea that utility functions can be assigned to parts of a computational system based on information-theoretic considerations. These issues will be discussed in turn below. Later in this article we will give a verbal summary of the model and result, and we will end with a discussion of biological implications. Detailed analysis can be found in the Supporting Appendix, which is published as supporting information on the PNAS web site.

A Computational View of Behavior

We take the point of view that behavior results from computation (21). Behavior is dictated by a mechanism that matches the state of the organism and its environment with an appropriate response (22) (e.g., the presence of a predator is matched with a flight response; the presence of food and hunger is matched with approach). Therefore, one can model behavior as a mathematical function that maps states, E, to behavioral responses, R:

If behavior results from computation, it is subject to computational constraints. The brain is limited in the number and density of neurons and synapses, the speed of signal transduction, the space reserved for wiring, etc. (23). Thus, like any other resource, the computational resource is limited (24, 25). The theory of bounded rationality has speculated that such a limitation may lead to conflict (26). More concretely, we hypothesize that the fittest computationally limited system [i.e., the boundedly optimal system (27)] can manifest internal conflict and test this hypothesis within a rigorous, mathematical framework.

A Game-Theoretic Definition of Conflict

Notably, conflict has never been defined for the purpose above and, as a central element in this work, we provide a game-theoretic definition of it. Informally, we say that agent i is in conflict with agent j if there exists a parsimonious utility function that describes the behavior of i, and if, according to that utility function, i could have achieved a higher utility if j behaved differently than it (j) did in some play of the game.

This definition covers the range of phenomena referred to as conflict in the scientific literature. For example, as applied to the Prisoner’s Dilemma game [PD (28)], it states that conflict exists unless both players cooperate, in accordance with intuition. It also includes “mutual conflict” as a case where i benefits from a change in j and vice versa, as in the Nash equilibrium of the PD.

However, here we focus on agents that are analogous to parts of an organism’s mind or, more generally, parts of a biological collective. Applying the term “utility” to such agents departs from its usual application to individual organisms (49), and we use it to denote the existence of a goal that an agent pursues and that defines the agent’s behavior. Thus, the attribution of internal conflict to Miller & Brown’s rat implies the existence of two agents: one whose goal is to satisfy hunger and another whose goal is to avoid danger. According to the definition, one could have achieved its goal if the other behaved differently. Likewise in the case of the disulfiram pill, one agent purposely takes the pill, whereas another seeks drink, and each could achieve its goal only at the expense of the other.

Formally, let agents i ∈ {1, …, N} be parts of a computational system. Let S be the state of the world, let Ô_i be i’s output (or “action”), and let λ_i¯(S,Ô_i) be the consequence to i from its action given some implicit assumption about the behavior of the rest of the world. Say that there exists a function U_i maximized by Ô_i as follows:

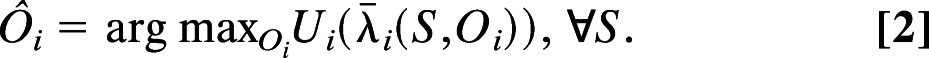Then i acts as if to maximize utility, given by the function U_i.

Now let λ_i(S,Ô_i, …, Ô_N) be the actual consequence to agent i from the combined action of all agents (λ_i need not be identical to λ_i¯). Following the notation of ref. 29, let Ô_−i = {Ô₁, …, Ô_i−1, Ô_i+1, …, Ô_N} (e.g., if Ô = {Ô₁, …, Ô_N} then Ô = {Ô_−i, Ô_i}). We say that i is in conflict with j if and only if:

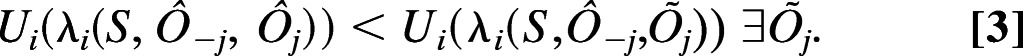Recall that the Nash equilibrium is defined as a situation where each agent does not benefit from a change in its own action, all else being equal (30). Here we defined that conflict exists unless each agent does not benefit from a change in any other agent’s action, all else being equal. Thus, our definition of conflict is a certain inverse of the Nash equilibrium concept. (To obtain the exact definition of the Nash equilibrium from Eq. 3, replace j with i, < with ≥, and ∃ with ∀.)

Utility Under Occam’s Razor

When selfish goals are assigned to agents a priori, the possibility of conflict can be taken for granted, as it has been taken in the foundation of game theory. However, here we start with a system that serves one goal and ask whether conflicting agents emerge in it a posteriori. To answer this question in accord with the definition of conflict, we must know these agents’ utilities, which are not available in advance and have to be inferred. This requirement raises yet another question: How can we infer an agent’s utility from its behavior alone (without even knowing in advance that it has any preferences, as required by the principle of revealed preference in economics)?

Our method is based on information theory. It requires that the behavior of an agent be described in the most parsimonious way. If the utility function U_i provides the most parsimonious description for the behavior of agent i, then U_i is thus qualified. To measure parsimony, we use its precise measure common in computer science, namely the number of information bits in the description (31; and see Supporting Appendix). A fundamental result in complexity theory shows that this measure retains its meaning regardless of the descriptive formalism (31).

Parsimony has predictive power, and it is very generally desirable (31). It is also known in philosophy as Occam’s razor, by which “entities should not be multiplied beyond necessity (ref. 31, p. 317).” In regard to the descriptions of agents, it will allow us to establish the following: Unbeknownst to an agent, its actions may promote the goal of the collective, given the actions of the other agents and the computational limitations. Yet it does not necessarily follow that the agent’s goal aligns with that of the collective or of any other agent by extension. One must first assign agent utilities in accord with the requirement of parsimony, and then see whether or not they satisfy the definition of conflict.

Note that the principle of revealed preference in economics assumes a priori the existence of preference and of a set of alternatives that can be compared pairwise. Here we move beyond these assumptions by inferring goals and hence utilities from information-theoretic considerations alone. This approach can be useful in general, by setting a criterion for the interpretation of behavior. (Although we will satisfy this criterion here in a mathematically precise way, it can be useful also on an intuitive level.)

Demonstrating Meaningful Internal Conflict

To qualify internal conflict, we required that the description of an agent based on a conflicting utility function be its most parsimonious description. However, for that conflict to be meaningful (“true conflict”), another requirement is necessary. Namely, the task of the collective clearly must not be to simulate conflict between its parts. To exclude such simulated conflict, the most parsimonious description of the task must not involve conflict a priori. With this requirement, the definition of the problem is complete.

Hence, let σ̂ be the system that maximizes fitness, P (σ̂), among all systems σ′ whose complexity, L(σ′) satisfies a certain computational limitation, l:

(The functions P and L must be reasonable, as in our model; see Supporting Appendix.) Through a rigorous mathematical analysis of decision-making structures, we now show that true conflict can emerge in σ̂.

Summary of the Model

Our model (described in detail in the Supporting Appendix) examines the generic problem of finding shortest paths, widely studied in computer science. It can be illustrated with the following analogy, but later we will discuss its biological application.

Imagine a robot that walks on a set of islands connected by bridges. An experimenter places the robot on one island, places a flag on another island, and observes the robot’s behavior. After the experimenter repeats this procedure many times with different pairs of islands, it appears that the robot always takes the shortest path to the flag.

Saying that the robot takes the shortest path to the flag is a parsimonious way of describing its behavior. We can now make predictions based on it. If the robot and/or the flag are placed on islands where they have not been placed before, we may guess the behavior of the robot even though we have not observed it yet in that circumstance.

According to this description of the robot’s behavior, the robot has a “goal”: to reach the flag as quickly as possible. There is a measurable quantity that is reduced consistently and efficiently by its behavior (distance to the flag), hence “cost” (distance from the flag) is minimized, and “utility” (proximity to the flag) is maximized. This utility-based description of its behavior is a parsimonious and useful description. (It also matches the concept of utility in economics by defining a complete and transitive preference ordering on the robot’s locations with respect to the flag.)

Let each island have an index number. At each point in time, the robot’s decision-making mechanism gets as input the index number of the island that it is currently standing on as well as the index of the island that the flag is on, and gives as output the index of the island to step onto next. Other mechanisms carry out this next step accordingly. Now, imagine that the situation remains exactly as in the above, except that the experimenter is not aware of the physical existence of the islands and the bridges. The experimenter can only control the inputs (which are just numbers) and record the outputs (also numbers) of the robot’s decision-making mechanism. Despite his/her blindness to the physical landscape, if the experimenter is resourceful, s/he would be able to deduce a model equivalent to that landscape, i.e., a graph (a mathematical construct consisting of nodes connected by directed edges, where nodes and edges correspond to islands and bridges respectively), that would describe the behavior of the robot and make predictions about its future behavior just as before. The utility-based description of the robot will also be valid as before.

We now use the above setup for two purposes. First, we let the task of finding shortest paths between any pair of origin and target nodes on a certain graph be our robot’s computational task. Second, we show that the best decision-making system consists of agents whose behaviors can be described most parsimoniously by assuming that the agents solve shortest-path problems on their own respective graphs, according to the inference of the blind experimenter described above. It follows that each agent has its own parsimonious utility function. The measurement of parsimony is explained in detail in the Supporting Appendix, and we mention here only that it becomes independent of descriptive formalism (asymptotically in the size of the graph, which is the reason we use large graphs in the formal proof).

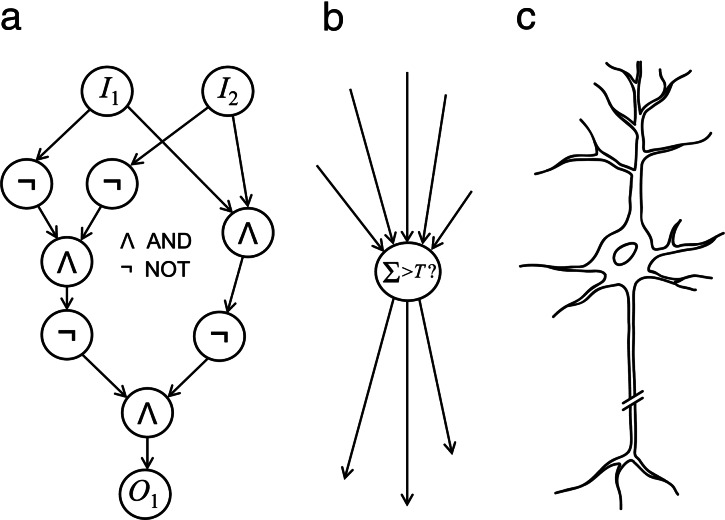
The computational architecture we consider for the construction of the robot’s decision-making mechanism is that of circuits, widely studied in theoretical computer science (e.g., 32, 33). A circuit is an acyclic interconnection of input terminals, elementary computational units called “gates,” and output terminals, by means of wires (Fig. 1a). The input terminals receive signals from the environment, and the gates receive signals from the input terminals or from other gates. Each gate computes a function of the signals on the wires directed into it and places the result on each of the wires directed out of it (including, as a special case, a linear threshold function). As a result, signals are produced on the output terminals that represent the circuit’s response to the environment.

Fig. 1.

Gates and circuits. (a) As an example of simple gates, consider the AND and NOT gates, which receive Boolean inputs. AND produces on its output wire/s “1” if both its inputs are “1,” and “0” otherwise; NOT produces “1” if its single input is “0,” and “0” if that input is “1.” By wiring together three AND gates and four NOT gates as shown, a very simple circuit can be built to compute the exclusive OR (XOR) function, which produces “1” (at the output O₁) if its two inputs, I₁ and I₂, are unequal and “0” otherwise. If AND and NOT gates (or gates from any other “complete basis,” as defined in the Supporting Appendix) are given in sufficient numbers, circuits could be built to compute any Boolean function of any numbers of inputs and outputs. This complexity is achieved through the interconnection of many simple units, as in the brain. (b) As an example of a larger gate, consider the threshold gate, which produces “1” if the weighted sum of its inputs exceeds a certain threshold value, T, and “0” otherwise. This particular gate is analogous to the single neuron (c): In both of the cases of this gate and the neuron, when the addition of stimuli from all dendrites or inputs surpasses a certain threshold value, a current is transmitted along the axon tree or output wires. Thus, circuits made of threshold gates simulate multilayered feed-forward neural networks.

Clearly, circuits are analogous to multilayered feed-forward neural networks. Each gate is analogous to a neural soma, its input wires to dendrites, and its output wires to the axon tree; the circuit’s input and output terminals are analogous to sensory and motor neurons respectively (Fig. 1 a–c). We assume that a single gate is simple relative to the circuit as a whole, and that many gates are needed for the circuit’s construction, in accordance with real neurons and brains.

We further restrict the architecture of the circuit for mathematical tractability in either of two ways: first, by considering circuits where only one wire comes out of each gate (a strong restriction), and next, by limiting the extent of merging and diverging of paths in the circuit (sequences of interconnected gates) instead (a weak restriction); these limitations are described in detail in the Supporting Appendix. We conjecture that a result similar to the one to be described holds also in an unrestricted space of circuits, although this conjecture may not be provable with presently known techniques.

Finally, we place a computational limitation on the number of gates (weighted by their sizes; Supporting Appendix). Because of this limitation, we must account for possible mistakes and illegal moves. We define that, whenever the output of the decision-making circuit labels a node that can be reached in one step, the robot will identify that node and step onto it. Otherwise, (if the move is illegal) the robot will stay in place. We also define that the best circuit is the one that takes the largest number of correct steps (i.e., steps that are consistent with a shortest path from origin to target).

It is now possible to prove the following theorem. For some graphs, the best possible circuit for finding shortest paths among all architecturally restricted circuits with up to a certain number of gates (weighted by size) is made of a number of subcircuits (agents), each of which seeks shortest paths on its own graph and maximizes its own parsimonious utility function and, these agents are in conflict with one another. Conflict emerges when the circuit produces a certain illegal move. This move has the property that each agent would have benefited if any other agent had behaved differently, thereby legalizing the move in a manner favorable to the focal agent. Thus, one agent’s maximization of its utility prevents the maximization of utility by others, and, by definition, all agents are in mutual conflict (Supporting Appendix and Figs. 3–5, which are published as supporting information on the PNAS web site).

Finally, we replace the robot with an organism and let nodes in the graph represent states of the organism and its environment [states in E (Eq. 1)]. For example, some nodes may represent the state of being idle and having a food item at hand. The decision-making mechanism (the CNS) is aware of the current state and, based on it, chooses an action that will lead the organism to another state (e.g., commence approach). This state-based approach accords with McNamara and Houston’s (22) model of fitness maximization, although here the organism uses a deterministic rather than stochastic strategy. At any period, the organism pursues a target state that is appropriate for it under current conditions and life history strategy. Thus, the organism’s task is to choose the most efficient sequence of steps from any origin to any target state that the environment and life history prescribe. Similarly to ref. 22, the organism must follow this optimal path to avoid fitness costs. In this fitness-maximizing pursuit, the same circuitry mentioned in the previous paragraph is used and leads to conflict.

Discussion

Now the graphs that are navigated by the agents are analogous to the various demands of life, such as food, sex, and protection. In nature, these demands can often, but not always, be addressed separately; and both these effects are captured in the model. When the demands do not interact, decision is easy; but when they do interact, the best tradeoff between them is hard to calculate. In such cases, if there had been no computational limitation, the organism always would have pursued the best tradeoff between the conflicting demands. This mode of operation would have given it the appearance of a unitary decision-maker. But, importantly, it turns out that under a computational limitation, the best decision-making system is one that is made of multiple agents, each caring for one aspect of homeostasis and for that aspect alone, without “sympathy” for the other agents or for the global task.

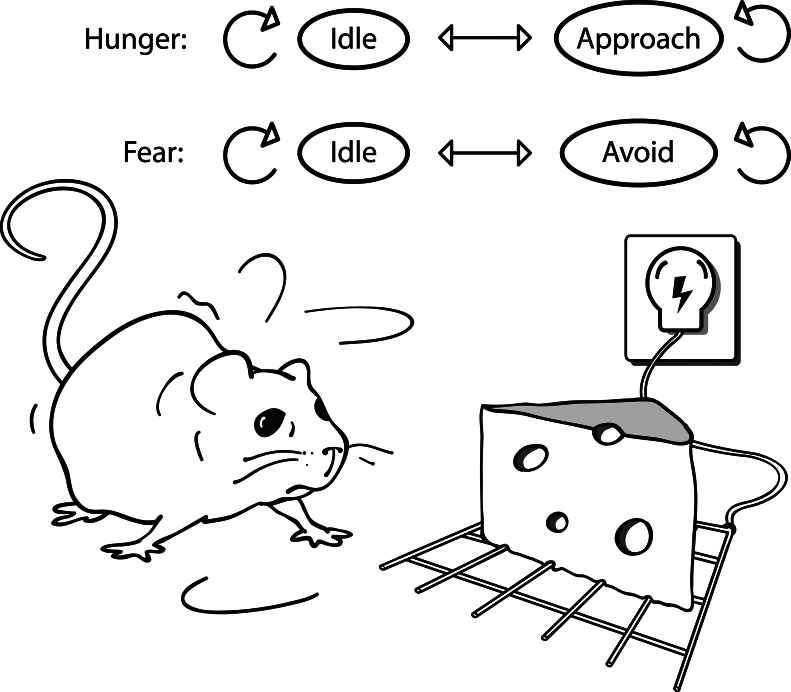
This result illuminates the behaviors abovementioned. As applied to Miller & Brown’s rat, it suggests a “hunger agent” and a “fear agent” that act independently and reach a resolution not by calculating the best tradeoff but by pitting one force against another. In the model (Supporting Appendix), conflict leads to indecision, as is observed in the rat (Fig. 2). With a change of interpretation, the model is also reminiscent of the sticklebacks and herring gulls, where the conflicted, illegal move corresponds to simultaneous attack and courtship or pecking and incubating. The more elaborate forms of conflict, where agents engage in extensive strategic interaction, demand further study; however, they too must satisfy the general definition of conflict. We have now shown that this definition can be satisfied even within an optimized entity under physiological constraints. That is, the division of the mind into independent and sometimes conflicting agents can be advantageous. This result is consistent with evidence of modularity in brain structure (34–36), although it demonstrates not only the emergence of agents in general but also the emergence of agents with personal goals that can be in true conflict with one another.

Fig. 2.

Internal conflict in Miller & Brown’s rat. A “hunger agent” attempts to approach food when food is identified and idles otherwise, and a “fear agent” attempts to avoid danger when danger is identified and idles otherwise. The agents usually move freely within each pair of states. However, when food and danger are in the same location, the simultaneous initiation of approach and avoidance is “illegal.” The definition of conflict is satisfied in that if any one agent idled, the other agent could have obtained its goal. Elements in this example resemble ones in the formal proof of conflict (Supporting Appendix). Whereas here only four states are shown, the formal proof allows for many behavioral states, a technical requirement for proving description parsimony.

In evolutionary terms, instead of arguing hypothetically that internal conflict is a remnant of past evolution (i.e., that it results from sliding off an adaptive peak in a changing fitness landscape), one can now make the stronger argument that even if natural selection were allowed to run its course and produce the fittest possible organism, there could still be conflict inside it. The only requirement is a physical limitation on the computational resource, which appears to be ubiquitous in nature. Importantly, this does not contradict the possibility that there could be conflict also because of evolutionary as well as learning constraints. Indeed, in some sense, there is a connection between the various constraints, once we can look at the evolutionary process itself as a “learning” process limited in time (37), and, therefore, in the structural and behavioral complexity achieved.

It follows that, in many cases, the observation of conflict may not indicate conflict between units of selection (such as organisms or genes) as is normally conceived but rather conflict within a unit of selection. Gene regulatory networks, dynamic physiological systems, nervous systems, and even social insect colonies can all be seen as collective decision-making systems and thus provide many opportunities to test this point. Consider the social insects: To a first approximation, their phenotypes are selected on the level of the colony (38). Yet when honeybees build a comb, they appear to “steal” each other’s materials (S. C. Pratt, personal communications). In leaf cutter ants, certain workers manage trash heaps where potentially pathogen-infected waste is thrown. If these workers try to get back into the nest, the other workers fight them back and thus prevent infection of the colony’s fungus garden (39). These observations are more readily explained by internal conflict than by genetic conflict. Consider also dynamic physiological systems: Most hormones are secreted in antagonistic pairs (40); thus insulin and glucagon determine the set point of blood sugar level by promoting opposing catabolic and anabolic reactions simultaneously, a contradiction which entails an energetic cost and may reflect rudimentary conflict. Further along this line, Zahavi (41) has made the radical claim that some chemical signals within a multicellular organism such as NO and CO are purposely noxious, i.e., that the harm they cause is a part of the message sent. Although this is perplexing, effects of this sort may, in theory, be possible.

As regards the organismal scale, internal conflict demands special attention, because it has been a focus across the behavioral and social sciences. For example, numerous forms of self-control have been discussed in economics (e.g., refs. 42 and 43), psychology (e.g., refs. 8, 13, and 44), and philosophy (e.g., ref. 45), and have been attributed to divided interests within a single individual (e.g., ref. 43). Thus Minsky (46) viewed the mind as a society of conflicting agents, a view which has culminated in the application of game theory to the interactions between the agents of the mind (43, 47, 48). So far, however, proponents of this view have taken the existence of agents with different and sometimes contradictory goals as an assumption, much like it is taken to be in classical (nonteam) game theory. This assumption has left out the question of why such agents should exist in the first place within a single unit of selection, given the apparent contradiction with evolutionary principles. We have helped to close that gap by showing that the best computational system under a limitation can involve agents that are in conflict with each other and can be seen as somewhat selfish, even though the system is designed for a single purpose and does not represent different parties in advance. Thus a certain interaction can appear to be both a team game on one level and, at the same time, a game between selfish agents on another level. In evolutionary terms, conflict can emerge not only when selection operates on the level of the single agent but also when it operates purely on the level of the collective. Importantly, this phenomenon reverses the classic question of the evolution of cooperation (28). Instead of showing how cooperation can emerge among agents with selfish goals, we showed how conflict can emerge within a collective that has one goal. Although we have provided a proof of principle to this effect, the various mechanisms by which such conflict could emerge call for further study and exploration.