Lignin Radicals in the Plant Cell Wall Probed by Kerr-Gated Resonance Raman Spectroscopy

Abstract

Lignin radicals are crucial intermediates for lignin biosynthesis in the cell wall of vascular plants. In this work they were for the first time, to our knowledge, selectively observed in wood cell walls by laser-based Kerr-gated resonance Raman spectroscopy, and the observations were supported by density functional theory prediction of their vibrational properties. For dry wood cells a lignin radical Raman band is observed at 1570 cm⁻¹ irrespective of species. For wet beech cells they were generated in situ and observed at 1606 cm⁻¹. DFT/B3LYP/6-31+G(d) modeling results support that in beech they are formed from syringyl (S) phenolic moieties and in spruce from guaiacyl (G) phenolic moieties. The observed lignin radical band is predicted as G is ∼1597 cm⁻¹ and S is ∼1599 cm⁻¹, respectively, and is assigned the (Wilson notation) ν_8a phenyl ring mode. The RR band probes lignin radical properties, e.g., spin density distribution, and these respond to charge polarization or hydrogen bonding to proximate water molecules. These observations can be crucial for an understanding of the factors that control cell wall structure during biosynthesis of vascular plants and demonstrate the unique potential of RR spectroscopy of lignin radicals.

INTRODUCTION

The cell wall of vascular plants is a highly ordered and layered arrangement of cellulose, hemicellulose, and lignin. Lignin is the second most abundant biopolymer and is found throughout the cell wall. It is derived from three hydroxycinnamyl alcohols, which in varying proportions are polymerized within the cell wall layers. The structure of lignin is exceedingly complex and is often described by tentative structures. Research in structural aspects of lignin is still ongoing, addressing, for example, the nature of synthesis control (1–5).

The properties of lignin radicals are crucial for lignin structure. In the final step of lignin biosynthesis, lignin monomer radicals add to a growing lignin polymer, which itself contains reactive radical sites (6,7). The biodegradation of lignin also involves free radical mechanisms (8–10). Despite their importance lignin radicals are today sparsely explored, and structural studies by electron paramagnetic resonance are often limited by the absence of signal fine structure (11–13).

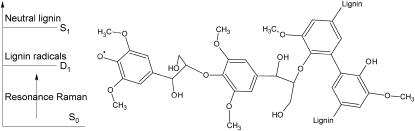
Structural studies of cell wall lignin radicals by, e.g., NMR or vibrational spectroscopy are usually limited by the very low concentration of radicals rendering weak signals that are either undetectable or swamped by signals from neutral lignin. Resonance Raman (RR) spectroscopy is, however, a powerful tool for gaining structural information and is for lignin radicals in principle enabled by their generic ultraviolet (UV)-vis band at ∼520 nm (14). The radicals are generated by various oxidants, the selectivity of which determines whether other types of oxidation products are also generated (15,16). Thus the enzyme laccase was chosen in this work as a catalyst of selective lignin oxidation producing persistent radicals. When an appropriate laser excitation wavelength is chosen in resonance with the first allowed electronic transition of the radicals (see Fig. 1) their Raman bands may be enhanced several orders of magnitude relative to those of neutral lignin.

FIGURE 1.

Simple model of lignin fragment with a reactive radical site and neutral sites. The electronic state energy diagram illustrates that the radical is selectively probed by resonance excitation due to its low-lying electronic excited D₁ state.

The phenolic moieties in the lignin polymer constitute those sites which can be oxidized into lignin phenoxyl radicals by the lignin biosynthetic system. In the absence of any studies of the vibrations of these radicals, the parent phenoxyl radical and its derivatives provide a basis for interpreting vibrational properties of the structurally related lignin radicals and specifically their RR bands.

Since the first pioneering investigations (see, e.g., Beck and Brus (17), Tripathi and Schuler (18), and Tripathi and Schuler (19)), phenoxyl radicals have been the subject of many investigations based on RR measurements in solution (see Spanget-Larsen (20) for a short but comprehensive review). The lowest energy-allowed electronic transition of the radicals is excited at ∼400–430 nm to obtain several orders of magnitude resonance enhancement of Raman bands, and the spectra are typically recorded in the microsecond range before the radical has suffered substantial decay. The most characteristic bands are caused by two phenyl ring modes dominated by CO· vibration (Wilson notation: ν7a) or by CC vibration (ν8a) and medium intensity bands by CH bending modes (ν9a, ν18a). For the phenoxyl radical in aqueous solution these are found at 1505 cm⁻¹, 1552 cm⁻¹, and 1157 cm⁻¹, 990 cm⁻¹, respectively, and the RR spectrum is dominated by the very strong 1505 cm⁻¹ CO· vibration band (21). Parasubstitution of the phenoxyl radical with electron donating groups increases the frequency of the phenyl ring modes where the CC vibration is most affected, reaching a value of 1613 cm⁻¹ for the p-benzosemiquinone radical (21) and 1620 cm⁻¹ for its anion (22). A more pronounced change is, however, that RR intensity is redistributed between normal modes, and the CC vibration band becomes increasingly dominant relative to the CO· vibration band with increasing electron donation ability of the substituent. Thus for the p-methoxyphenoxyl radical the two bands are of equal strength, and for the p-benzosemiquinone radical (and its anion) the CC vibration band dominates. However, redistribution of Raman intensity between normal modes of the same structure also occurs as a function of excitation energy when coupling to excited states other than the lowest energy state becomes important. This generic phenomenon has been noted for, e.g., the p-benzosemiquinone radical anion and adds considerable complexity to the behavior and interpretation of RR spectra (23,24).

For lignin phenoxyl radicals, redistribution of RR intensity between normal modes as a function of substitution may also arise. The C1 position (where C4 is the benzene ring carbon atom bonded to the Phe-O atom) is, however, always bonded to a carbon, which is part of several possible linkage types—constructed from saturated bonds—to other lignin phenyl rings. The influence of these linkages on the phenyl ring is not expected to vary significantly from one type to another. A significant influence does, however, arise from the C3 and/or C5 position, where the substitution of no methoxyl, a single methoxyl, or two methoxyl groups defines the three lignin moiety types, namely, p-hydroxy-phenyl, guaiacyl (G), and syringyl (S) moieties, respectively. In analogy to parasubstituted phenoxyl radicals, these three types thus differ by the degree of electron donation from the substituents to the phenyl ring.

Here we report for the first time to our knowledge an RR study of enzyme-produced cell wall lignin radicals. A recent important technical development has removed a serious obstacle of exploiting the RR effect in the study of lignin radicals. A Kerr gate, which provides a 4 ps time domain window centered on the excitation pulse, rejects most of the intense lignin fluorescence, which would otherwise swamp Raman signals (25). The lignin radicals were part of the macromolecular structure of the wood cell wall, and time-resolved techniques were not required due to their high stability in this environment.

The observations are discussed in relation to studies on the phenoxyl radical and its derivatives, as well as in light of theoretical prediction of Raman active vibrational modes of lignin phenol and phenoxyl radical model structures by density functional theory (DFT). We demonstrate the unique potential of this laser-based technique in providing structural information on lignin radicals and hence new insights into the synthesis and degradation of lignin.

EXPERIMENTAL

Materials

Wood cells (softwood, Picea abies; hardwood, Fagus sylvatica) were obtained from Sunds Defibrator (Sundsvall, Sweden) (thermomechanical pulp). Laccase (Trametes villosa) was obtained from Novozymes A/S (Bagsvaerd, Denmark). The enzyme catalyzes the selective oxidation of lignin while reducing oxygen-producing water.

Lignin radical production

Typically 1 g (dry weight) of fibers was suspended under stirring in 25 mL buffer, i.e., a 4% (w/v) suspension, and after 30 min the enzyme activity was added from an enzyme solution with activity 670 units/mL. From this instant the lignin radical production was initiated due to the presence of oxygen and the catalytic effect of the enzyme. Enzyme activity was determined by use of syringaldazine, where 1 unit corresponds to syringaldazine oxidation of 1 μmol/min at pH 5.5, T = 30°C.

Samples of: 1), lignin radicals in the dry (beech or spruce) wood cell wall were produced by a 1-h treatment at 40°C of a 4% (w/v) fiber cell suspension with laccase, after which the cells were rinsed and dried at 40°C, and 2), lignin radicals in the wet (beech) wood cell wall by the same treatment but examined in situ (at room temperature) during laccase oxidation. Control samples were produced under identical conditions but with no enzyme activity added. Enzyme activity applied per gram dry material was 0, 0.3, 3, 30, and 300 units.

Finally, reduced samples (with no radicals) were also produced by subjecting the dried fibers, previously treated with and without laccase, to a 0.1-M ascorbic acid reductive treatment for 2 h in a 5% (w/v) pulp suspension. All suspensions were buffered by 0.1 M KO-Ac at pH 4.5.

Kerr-gated RR spectroscopy

For Kerr-gated RR spectroscopy, samples in a spinning NMR glass tube were moved in a vertical cycle. The excitation wavelengths were 400 and 500 nm (300 μm spot diameter, 5–10 mW average power, 1 kHz repetition). The ∼4-ps time domain gating window was centered coincident with the excitation pulse.

The Raman Kerr-gated collection system is based on a high throughput 4 ps optical Kerr shutter described in detail in our earlier publications (25,26). The Kerr gate consists of two crossed polarizers and a Kerr medium (2-mm optical cell filled with CS₂). In the closed state, light collected from the sample is effectively blocked by two polarizers in crossed orientation. Coincident in time with the Raman scattered light from the sample, a short, 1-ps gating pulse at 800 nm that bypasses the polarizers creates a transient anisotropy within the Kerr medium. The gating beam is polarized at 45° and its intensity is set to induce, in effect, a transient half wave plate that rotates the polarization of the light from the sample and allows it to be transmitted through the cross-polarizer for the duration of the induced anisotropy. The remaining part of the signal, i.e., the main body of fluorescence arriving at later times, is effectively blocked.

The laser apparatus is based on a regenerative amplifier system followed by a two pass linear amplifier (SuperSpitfire, Spectra Physics/Positive Light, Newbury, UK) providing 800 nm, 1 ps, 2 mJ fundamental pulses at 1-kHz repetition rate. A 500-μJ pulse at 800 nm was used to drive the Kerr gate. The remainder of the fundamental was frequency doubled and used to drive a home-built optical parametric amplifier to generate a tunable probe beam or directly used as a Raman probe.

The Raman signal was obtained by averaging five cycles of each 200-s acquisition time. The spectra in the raw form, I(k), still contained a degree of unrejected fluorescence. A background-corrected spectrum, I_C(k) = I(k) − P(k), was obtained by fitting the raw spectrum, I(k), over definite wave number (k) intervals, where all samples had negligible Raman signals, to a fourth-order polynomial P(k). Assuming the polynomial P(k) to be a reasonable model of the broad fluorescence background, the I_C(k) spectrum is thus a fluorescence-free Raman spectrum. All spectra were corrected in this way. Wave number scale was calibrated against Raman bands of a t-Stilbene crystalline sample.

UV-vis spectroscopy

The enzyme catalyzed development of a UV-vis lignin radical band was followed in situ by a Cintra 40 UV-vis spectrometer, equipped with an integrating sphere. The sample—wetted by enzyme solution—was contained in an airtight cup with a glass window. Results are reported in terms of the Kubelka-Munk remission function F(R) = (1 − R)²/2R = K/S, where K is the absorption coefficient and S is the scattering coefficient.

DFT calculations

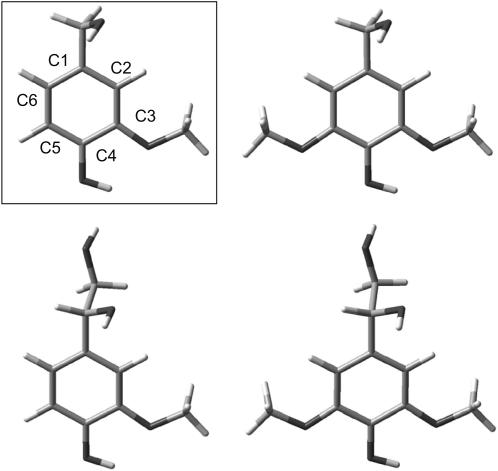
Lignin phenolic moieties and their phenoxyl radical states were modeled by phenol (or phenoxyl radical) substituted at C1 by CH₂OH and substituted at C3 by OCH₃ (Guaiacyl model) or at both C3 and C5 by OCH₃ (Syringyl model) (see Fig. 2). To obtain a manageable computational time the whole of the lignin structure, to which the phenolic moieties are covalently bonded, is thus modeled by the CH₂OH substitution. The flexible conformation of this group is defined by the two dihedral angles φ1(C2C1-CO) and φ2(C1C-OH).

FIGURE 2.

Guaiacyl (left side) and Syringyl (right side) lignin phenolic model structures. The structures shown in the top represent one specific out of several B3LYP/6-31+G(d) optimized conformations of the CH₂OH alcohol group. The extended structures, containing an additional alcohol group, are shown in the bottom (at a slightly tilted angle). An analogous set of lignin phenoxyl radical model structures was obtained by removing the phenolic H atom.

For each model several different optimized conformers were distinguished by their φ1, φ2 values. These were first located by relaxed scanning of φ1, φ2 using the fast semiempirical PM3 method and were then at the higher B3LYP/6-31+G(d) level subjected to full unconstrained structure optimization for obtaining vibrational modes, frequencies, infrared (IR), and (nonresonant) Raman intensities, using the keyword “freq=raman” at this level of theory. Normal mode wave numbers, IR absorption, and Raman intensities, were then obtained as the average ± SD obtained from the set of two to four different conformers. All calculation was performed using the Gaussian03 software package (27), and normal mode vibrations were visualized and qualitatively assigned using the GaussView software.

To examine whether the CH₂OH substitution was sufficient for modeling the influence of attached lignin, the minimum energy (B3LYP/6-31+G(d)) CH₂OH conformation was chosen and a new enlarged C1-C₂H₃(OH)₂ substituted structure generated by replacing an H atom by an additional CH₂OH group. No conformational search was performed, and this structure was subjected to full unconstrained geometry optimization using the same input keywords to obtain its vibrational properties.

Two frequency-scaling factors to be used for the neutral phenols and their phenoxyl radical analogues were derived for the lower frequencies (k < 1700 cm⁻¹) by linear least squares fit using the experimental phenol (gas phase: 26 normal modes, see Bist et al. (28)) and phenoxyl radical (argon matrix, 21 normal modes; see Spanget-Larsen et al. (20)) values, respectively. Calculated values were obtained from B3LYP/6-31+G(d) frequencies of geometry-optimized phenol and phenoxyl radical using the same input parameters as for the lignin models. This approach was preferred, as published B3LYP scaling factors are derived from molecule sets with overall little similarity to the structures considered in this work and are furthermore not derived for the 6-31+G(d) basis set (29,30).

RESULTS

The preresonantly enhanced Raman band at 1600 cm⁻¹, which originates from the phenyl rings of neutral lignin, dominates the absolute RR spectra obtained in this work (31–33). As for the parent phenol, lignin phenolic as well as nonphenolic structures are characterized by a relatively high S₀ → S₁ transition energy (UV-vis absorption band maximum at ∼270–280 nm) causing the preresonance enhancement (1). The lignin radical UV-vis band at ∼520 nm promises a selective resonance enhancement of Raman bands originating from lignin radicals when exciting at 500 nm.

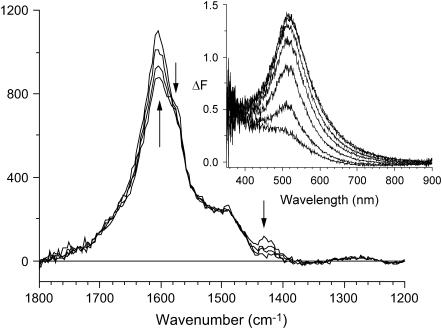
The in situ enzymatic generation of this UV-vis band (inset), as well as RR spectral changes, is depicted in Fig. 3. The UV-vis band converged after 40 min due to oxygen depletion in the airtight sample cup. For all enzyme doses, applied in an open system, the ΔF band kept rising for at least an additional hour before converging. This band is also present after drying the pulp at 40°C (results not shown). Control samples displayed no spectral changes caused by treatment without the enzyme.

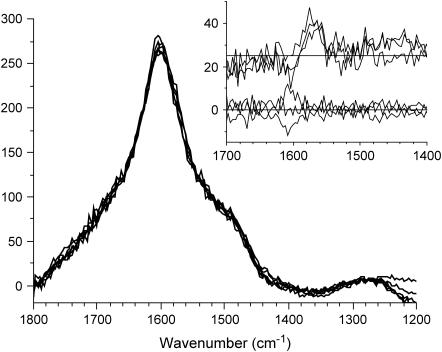
FIGURE 3.

RR spectra (λ_ex = 500 nm) of beech cells recorded 13, 31, 49, and 78 min (acquisition midpoint) after enzyme addition (300 units/g) to the wet sample. Arrows indicate position and direction of temporal changes. The y axis is in arbitrary units. (Inset) The ΔF spectra are recorded 5, 10, 15, 20, 30, and 40 min after enzyme addition. ΔF = F − F₀, where F₀ is recorded 90 s after enzyme addition.

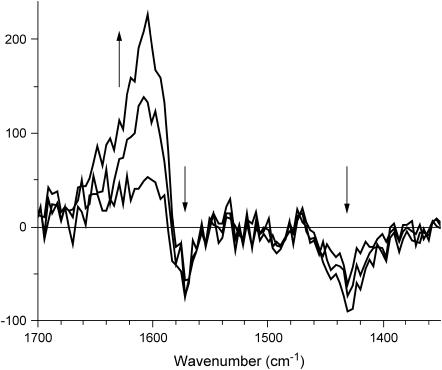
The dominant lignin Raman band at 1600 cm⁻¹ can be subtracted from the spectrum by obtaining difference spectra allowing for a more sound estimation of spectral differences caused by the generation of lignin radicals. Temporal RR difference spectra, relative to the initially acquired spectrum (Fig. 4), show an increasing radical population in the wet cell wall during enzyme treatment causing a positive RR signal, ΔI₁, at 1606 cm⁻¹ and depressions ΔI₂ and ΔI₃ at 1430 and 1570 cm⁻¹, respectively. The temporal behavior of the band intensities differs where the depression bands appear to converge faster than the positive signal.

FIGURE 4.

RR difference spectra ΔI = I − I_ref, obtained from the spectra depicted in Fig. 3, relative to the initial acquisition I_ref.

For the dry cell wall (Fig. 5), where difference spectra are obtained relative to the control sample average spectrum, the ΔI₁ band is found at 1570 ± 2 cm⁻¹ for both beech and spruce and for all applied enzyme doses. It is thus downshifted by 32 ± 3 cm⁻¹ and 37 ± 3 cm⁻¹ relative to the neutral lignin band of beech (∼1602 cm⁻¹) and spruce (∼1607 cm⁻¹), respectively.

FIGURE 5.

RR spectra (λ_ex = 500 nm) of three control and three enzyme-treated (300 units/g) beech cell dried samples normalized by integration from 1470 to 1740 cm⁻¹. The inset shows their difference spectra ΔI = I − I_ref. I_ref is the average of the three beech control (normalized) spectra. The three spectra of enzyme-treated samples are displaced for clarity.

These RR spectral changes are observed only for λ_ex = 500 nm, whereas for λ_ex = 400 nm no difference could be observed. Crucially, a subsequent ascorbic acid treatment removed the spectral difference, confirming its cause as being due to lignin radicals (result not shown).

The B3LYP/6-31+G(d) calculations gave frequency-scaling factors of 0.9784 and 0.9858 for phenol and phenoxyl radical, respectively. For the scaled low range frequencies (<1700 cm⁻¹), a root mean square (RMS) deviation of 9 cm⁻¹ (phenol) and 17 cm⁻¹ (phenoxyl radical) relative to published experimental frequencies (20,28) are observed. The analogous B3LYP/cc-pVTZ calculation on the phenoxyl radical (20) gives—as derived by the authors of this work—the scaling factor 0.9876 and an RMS deviation of 16 cm⁻¹ for the low range frequencies. In the following any references to the “highest frequency” modes refer only to modes for which k < 1700 cm⁻¹, i.e., CH and OH stretching modes are not considered.

Theoretical prediction of phenoxyl radical properties is not straightforward. Thus calculated values of the phenoxyl radical C–O· distance span a range of 1.22–1.38 Å, where the highest level ab initio theories predict values in the lower end, e.g., 1.228 Å for the CASSCF/6-311G(2d,p) method (34–36).

This work predicts a value of 1.260 Å and the scaled wave numbers of the highest frequency modes, involving aromatic C–C and C–O stretches, are for phenol predicted as (observed/calculated in cm⁻¹): 1603/1611.8, 1610/1622.2, and for phenoxyl radical as 1481/1472.5 (ν_7a, CO· str), 1515/1534.7 (ν_19b, CC str, CH bend), 1550/1572.8 (ν_8a, CC str). Larger basis sets do not give significantly better results (20).

Calculated normal mode properties for lignin phenol and phenoxyl radical models are shown in Tables 1 and 2. For the aromatic range (∼1520–1630 cm⁻¹) all normal modes—three for the phenols and two for their phenoxyl radicals—are shown, whereas for lower frequencies only the dominant Raman modes (intensity >6 A⁴/amu) are shown.

TABLE 1.

B3LYP/6-31+G(d) vibrational properties of lignin phenolic models

Lignin phenolics Approximate assignment	S phenolic model (four conformers)				G phenolic model (three conformers)
	k/cm−1	k/cm−1	Raman	IR	k/cm−1	k/cm−1	Raman	IR
R-CC str CCC bend	793.2 ± 1.1	804.0	16.4 ± 1.3	26 ± 3	792.3 ± 0.4	806.2	17.3 ± 1.1	27 ± 2
Me-CO str CCC bend	1059.0 ± 0.9	1056.3	9.9 ± 0.7	16 ± 3	–	–	–	–
R-CH bend CCC bend	1153 ± 5	1149.8	11.5 ± 1.2	68 ± 31	–	–	–	–
R-OH bend Me-CH wag	–	–	–	–	1186 ± 5	1184.7	11 ± 3	51 ± 6
R-OH bend Me-CH wag	–	–	–	–	1209.5 ± 0.4	1208.3	6.7 ± 0.8	54.3 ± 28
R str Me-CO str Phe-CO str	1339 ± 3	1337.4	29 ± 6	96 ± 44	1283 ± 4	1281.2	23 ± 3	226 ± 39
1 × Me-CH wag	1480.5 ± 0.2	1480.5	15.5 ± 0.2	8.0 ± 0.3	1480.7 ± 0.3	1480.7	13.8 ± 0.0	8.8 ± 0.2
1 × Me-CH wag	1482.3 ± 0.2	1482.7	14.2 ± 0.2	8.5 ± 0.2	1493.0 ± 0.4	1492.6	7.6 ± 1.4	41 ± 6
2 × Me-CH wag R-CC str	1492.4 ± 0.3	1492.2	6.8 ± 1.6	37 ± 4	–	–	–	–
2 × Me-CH wag	1493.5 ± 0.1	1492.7	7.5 ± 1.2	28 ± 9	–	–	–	–
Phe-CO str R-CC str	1525.3 ± 1.5	1523.2	1.3 ± 0.2	122 ± 3	1523.5 ± 1.5	1520.8	2.7 ± 0.8	158 ± 8
R-CC str CCC bend R-CH bend	1610 ± 3	1606.7	88 ± 4	3 ± 3	–	–	–	–
R-CC str R-CH bend R-OH bend	–	–	–	–	1618 ± 3	1616.5	20 ± 7	25 ± 9
R-CC str R-CH bend R-OH bend	1626.1 ± 1.6	1625.0	4.7 ± 0.3	134 ± 4	1623.5 ± 1.6	1622.0	51 ± 8	23.3 ± 0.6

For each type of model (G versus S), the leftmost column shows the scaled calculated wave numbers (including mean ± SD due to different CH₂OH conformers) and the next column to its right shows the scaled calculated wave numbers for the enlarged CH₃(OH)₂ model. The two following columns show Raman intensity (units, A⁴/amu) and IR absorption (units, KM/mol), both including ± SD due to different CH₂OH conformers. Half-filled rows indicate that a specific normal mode for one model type, e.g., G, has vibrations qualitatively dissimilar to any normal mode of the other model type.

TABLE 2.

B3LYP/6-31+G(d) vibrational properties of lignin phenoxyl radical models

Lignin phenoxyl radicals Approximate assignment	S phenoxyl radical model (two conformers)				G phenoxyl radical model (three conformers)
	k/cm−1	k/cm−1	Raman	IR	k/cm−1	k/cm−1	Raman	IR
R-CC str CCC bend	804.9 ± 0.2	812.7	16 ± 2	3 ± 3	797 ± 5	814.9	12 ± 3	5 ± 3
Me-CO str CCC bend	1046 ± 4	1046.1	8 ± 3	21 ± 22	1027.2 ± 0.5	1027.2	8.0 ± 1.3	48 ± 17
R-CH bend CCC bend	1156 ± 7	1160.7	9 ± 4	25 ± 24	1165 ± 7	1161.7	15 ± 4	53 ± 45
R-CC str Me-CO str	1342 ± 3	1340.5	12.2 ± 1.5	48 ± 23	1309 ± 4	1305.5	10.4 ± 0.7	95 ± 55
R-CC str R-CH bend	1396 ± 2	1392.8	22 ± 18	46 ± 61	1415 ± 3	1414.9	8 ± 3	54 ± 25
Me-CH wag R-CH bend R-CC str	–	–	–	–	1452 ± 4	1448.8	12.4 ± 0.9	99 ± 25
Me-CH wag CO· str R-CC str	–	–	–	–	1477 ± 3	1476.5	25 ± 5	16 ± 10
1 × Me-CH wag	1494.1 ± 0.2	1494.6	19 ± 4	7 ± 2	1495.3 ± 0.2	1495.3	14.3 ± 0.5	10.4 ± 0.8
1 × Me-CH wag	1494.4 ± 0.2	1494.7	10.3 ± 1.8	12.9 ± 0.6	1496.3 ± 1.3	1494.5	12 ± 12	29 ± 6
2 × Me-CH wag	1501.3 ± 0.7	1500.5	9 ± 3	23 ± 2	–	–	–	–
2 × Me-CH wag R-CC str	1505.1 ± 1.3	1503.8	7.7 ± 1.2	4 ± 3	–	–	–	–
CO· str R-CC str CCC bend (∼ν7a)	1526.0 ± 0.6	1526.1	32 ± 9	65 ± 6	1521 ± 2	1519.0	76 ± 3	67 ± 6
R-CC str CCC bend R-CH bend (∼ν8a)	1599 ± 4	1595.5	100 ± 3	188 ± 12	1597 ± 8	1591.4	72 ± 6	132 ± 11

The data is arranged as for Table 1.

The influence of the CH₂OH conformation on these frequencies is generally small since the normal modes depicted in the tables are localized on the phenyl ring and its (other) substituents. The influence on Raman intensities and IR absorbance is relatively higher, but semiquantitative comparisons can still be made.

Two features qualitatively distinguish G from S phenol moieties (Table 1). A Raman active ring-CC and CO stretch mode placed at 1339 cm⁻¹ for the S moiety downshifts considerably to 1283 cm⁻¹ for the G moiety. This S → G substitution also leads to significant redistribution of both IR absorption and Raman intensity between the two highest frequency modes. For the G moiety both modes have significant Raman intensity with the highest frequency mode at 1624 cm⁻¹ having more than twice the strength of the close-lying 1618 cm⁻¹ mode. For the S moiety, however, the highest frequency mode has weak Raman intensity and the 1610 cm⁻¹ mode is very dominant.

As opposed to the phenols the phenoxyl radical models have a high frequency mode dominated by the ring-CO· stretch (G, 1521 cm⁻¹; S, 1526 cm⁻¹), which is positioned below the highest frequency mode (G, 1597 cm⁻¹; S, 1599 cm⁻¹), and the two high frequency modes have both considerable IR absorption and Raman intensity (Table 2). The G → S substitution leads to significant redistribution of only the Raman intensity between these modes. The G moiety normal modes have comparable Raman intensity, whereas for the S moiety the highest frequency mode clearly dominates. Thus G → S induced redistribution of Raman intensity is from the ring-CO· stretch mode to the ring-CC stretch dominated mode.

DISCUSSION

The resonance condition obtained for λ_ex = 500 nm enables the selective probing of the molecular nature of lignin radicals. Fig. 3 depicts the temporal change of the RR spectrum, which arises when an enzyme solution is applied to the wood cell sample. These changes consist of RR signal losses and gains.

The RR signal losses or depression bands (Fig. 4) originate from those (reduced) lignin structures, which are oxidized, and thus provide information on these. It is well known that only phenolic moieties can be oxidized by the enzyme, and for thermodynamic reasons the lowest redox potential moieties, i.e., with maximum possible methoxyl substitution, are preferentially oxidized. An apparent ∼33 cm⁻¹ downshift of ΔI₃ relative to the neutral lignin band, which is the dominant RR band in the spectra shown in Fig. 3, apparently confirms this since increasing methoxyl substitution is expected to lower the strong phenyl ring mode frequencies (37).

The calculated B3LYP/6-31+G(d) vibrational properties of the lignin phenolic models (see Table 1) provide a means of examining this claim. A fraction of the normal modes was found to exhibit vibrations clearly localized to the phenyl ring and the C4-OH, C3, and C5 substituents. These modes were identified also in the extended structures. The fact that their calculated wave numbers differ little between the lignin phenolic models and the extended analogs (see Table 1) shows that the phenolic models appropriately model vibrational properties localized to the substituted phenyl rings. The same observation is made for the phenoxyl radical models (see Table 2).

The claim that ring mode frequencies are lowered presupposes qualitatively similar vibrations. It is thus meaningful only for the highest frequency mode (G, 1624 cm⁻¹, S, 1626 cm⁻¹), the frequency of which is practically unaffected by the G → S substitution. This substitution does, however, significantly reduce the Raman intensity of the highest frequency mode such that the S 1610 cm⁻¹ mode is dominant. Assuming that the calculated activities are valid for the preresonance condition, the part of the observed lignin Raman band due to phenolic moieties has contributions at ∼1620–1624 cm⁻¹ due to G structures and predominantly at ∼1610 cm⁻¹ due to S structures. As for phenol these calculated absolute values may be slightly overestimated. Thus the vibrational character of some phenyl ring modes differ qualitatively due to substitution, and for lignin phenolic moieties the DFT calculations suggest an apparent downshift of ∼10–14 cm⁻¹ of the contribution from S moieties to the observed ∼1600 cm⁻¹ Raman band relative to G moieties. This downshift is thus not due to frequency lowering of phenyl ring modes but to a different distribution of Raman intensity.

Since the relatively strong lignin radical band is placed on the high frequency side of ΔI₃, where it dominates over the depression, the actual position of the ΔI₃ band can be at higher wave numbers ∼1580–1590 cm⁻¹. Although some uncertainty thus arises due to band overlap, the RR spectral changes suggest that the oxidized lignin phenol structures have a maximum contribution to the lignin Raman band positioned 10–20 cm⁻¹ lower than the overall ∼1600 cm⁻¹ lignin Raman band. This observation thus suggests, with good support from the DFT calculations, that S phenolic moieties are predominantly oxidized.

The ΔI₂ band at 1430 cm⁻¹ is positioned close to several reported weaker lignin Raman bands. For near infrared (NIR) excitation a medium strong band is generally observed at 1453 cm⁻¹ (31). A Raman band for phenolic lignin model compounds obtained by resonant UV excitation is found close (±20 cm⁻¹) to this position for all three methoxyl ring substitution types (38). It is, however, relatively weak compared to other lignin model bands observed in the 1100–1550 cm⁻¹ region. The DFT results shown in Table 1 do not suggest Raman active modes, which can account for the ΔI₂ band. However, a vibrational mode with low intensity (not shown in the table) was identified at G, 1441.4 cm⁻¹ (Raman = 2.9, IR = 31) and S, 1441.2 cm⁻¹ (Raman = 6.0, IR = 98), reporting only average values. The vibrations of this mode are similar for the S and G structures and are assigned a combination of R-CC str, Me-CH wag, R-OH bend, and R-CH bend. For the extended structures the analogous mode was also localized to the phenyl ring part and found at 1440.5 cm⁻¹ (G) and 1438.7 cm⁻¹ (S).

It is conceivable that the preresonance effect selectively enhances the (nonresonant) activity of this mode. Thus UV-RR spectra of G and S lignin phenol model structures display relatively strong bands at 920–930 cm⁻¹ (G) and 960–980 cm⁻¹ (S) (38), whereas the DFT results of this work predict only weak Raman modes close to these ranges. For the G phenol model a vibrational mode at 928 cm⁻¹ (Raman = 2.3) is assigned to R-CH bend, R-CCC bend, and Me-CO str, and for the S phenol model a vibrational mode at 950 cm⁻¹ is assigned R-CCC bend (Raman = 4.6). These two modes are the only feasible assignments of the UV-RR bands, the second one (S) of which cannot be due to the two Syringyl R-CH bend modes, which are predicted to occur at the lower frequencies 813 cm⁻¹ and 829 cm⁻¹, respectively. Based on these considerations we tentatively assign the ΔI₂ band to the calculated 1441 cm⁻¹ mode of S phenol structures.

The positive ΔI₁ band provides direct information on lignin radicals. However, there are to the best of the authors' knowledge no vibrational assignments of lignin radicals available in the literature. As noted in the introduction, for phenoxyl radicals at least one of the two vibrational modes, ν_7a and ν_8a, is especially strongly coupled to the first (allowed) excited electronic state, which typically causes a UV-vis band at ∼400–430 nm (39–43). These are dominated by aromatic ring CC (ν_8a) and CO· (ν_7a) vibrations and are for the parent unsubstituted phenoxyl radical observed at ν_7a ∼ 1481–1505 cm⁻¹ and ν_8a ∼ 1550 cm⁻¹ (20,21). The ν_7a frequency interval indicates sensitivity to the environment, where 1505 cm⁻¹ is for aqueous solution and 1481 cm⁻¹ is obtained in low dielectric constant media (Argon).

The DFT results (Table 2) confirm previous RR observations that increased electron donation from substituents to the phenyl ring increases these frequencies. Thus the calculated ν_7a frequency increases from 1472.5 cm⁻¹ (phenoxyl radical) to (G) 1521 cm⁻¹ and (S) 1526 cm⁻¹, i.e., by 48 cm⁻¹ and 53 cm⁻¹, respectively, and the ν_8a from 1572.8 cm⁻¹ to (G) 1597 cm⁻¹ and (S) 1599 cm⁻¹, i.e., by 24 cm⁻¹ and 26 cm⁻¹, respectively. The results indicate that the ν_8a frequency is relatively sensitive to extension of the structures, which results in a lowering by ∼5 cm⁻¹. The DFT results predict ν_7a mode frequencies for the lignin model phenoxyl radicals which—even when considering the possible deviation from real frequencies—are far too low to be assigned the observed (dry environment) lignin radical band at 1570 cm⁻¹. Recalling that the ν_8a frequencies by analogy with the phenoxyl radical may be overestimated, and that an additional frequency reduction is expected by extending the model structures, the DFT results provide a conclusive assignment of the lignin radical band to the ν_8a vibrational mode.

The near identity of calculated S and G ν_8a frequency values supports the fact that the lignin radical band is observed at the same frequency for the dry state of both spruce and beech wood (results not shown). The calculated Raman intensities suggest a lignin radical (nonresonance) Raman spectrum dominated by both vibrational modes. The observation of a single band (Figs. 4 and 5) strongly suggests a selective resonance enhancement of the ν_8a vibrational mode by the lignin radical UV-vis band (Fig. 3, inset).

The UV-vis band shape, with no vibronic structure and a tail extending beyond the red end of the spectrum, may suggest that low energy charge transfer (CT) transitions, with the radical as acceptor and proximate neutral lignin as donor, are coupled to this vibrational mode. This is consistent with the fact that it is not the ν_7a mode, which is the most strongly coupled to the transition, as is observed for most substituted phenoxyl radicals, but instead the ν_8a mode. A relatively delocalized spin distributes bond length reorganizations upon CT over the whole aromatic ring and not mainly on the localized C-O·bond. Hence, the ν_8a mode would be predominantly resonantly enhanced.

This redistribution of RR intensity from the ν_7a to the ν_8a mode has, however, also been observed for parasubstituted phenoxyl radicals, when the electron donation ability of the substituent is sufficiently large (21), and the DFT results indicate that the non-RR intensity follows this trend as the G → S substitution implies increased electron donation ability. Thus conclusive evidence of the nature (e.g., localized versus CT transition) of the lignin radical UV-vis band remains to be found.

From Figs. 4 and 5 it is observed that a position shift of the lignin radical RR band by ∼36 cm⁻¹ from 1570 to 1606 cm⁻¹ results when the (beech) wood cell wall is transferred from a dry to a wet environment. This result is of immediate significance for biological environmental effects on lignin radical properties and therefore on the lignin biosynthetic process.

The environmental dependence of the properties of the parent phenoxyl radical has been observed recently (44–46) and was modeled by DFT/B3LYP/6-31+G(d,p) combined with a continuum model and explicit (hydrogen bonding) water molecules (47). In this work the (theoretical) transfer of the phenoxyl radical from vacuum to aqueous solution resulted in significant redistribution of spin density from the oxygen atom to the C4 position. The corresponding structural changes (relative to the vacuum structure) were identified as elongation of the CO· bond by ∼0.01 Å from 1.260 to 1.271 Å and small contraction of up to 0.003 Å of several CC bonds. No frequency calculations were performed.

These results qualitatively explain the observed frequency shift of ∼36 cm⁻¹ as due to increased double bond character of the lignin radical phenyl ring CC bonds, the vibrations of which dominate the ν_8a modes. Thus lignin radical properties, e.g., spin density distribution and frequencies of the ν_7a and ν_8a modes, depend on the environment and specifically on hydrogen bonding effects. The RR bands of high frequency normal modes thus probe the spin density distribution of lignin radicals and its environmental dependence. Environmental perturbations of the spin density distribution should affect the distribution of interunit bond types, and thus the resulting covalent structure of lignin.

CONCLUSION

The use of Kerr gating has enabled the observation of a lignin radical RR band and two lignin RR suppression bands corresponding to the (original) reduced structures. The lignin radicals are not randomly distributed over the lignin moieties but clearly located at moieties with a different RR (doublet) spectrum as compared to the averaged lignin spectrum. DFT calculations on lignin phenol and phenoxyl radical structures suggested that lignin radicals were formed from Syringyl (beech) and Guaiacyl (spruce) phenolic structures. The RR band was conclusively assigned the Wilson mode ν_8a. The exact nature of the lignin radical UV-vis band providing the resonance enhancement of the ν_8a mode is not known.

The solvation dependency of the radical band position is a clear indication of charge polarization or hydrogen bonding of the phenoxyl radical C-O· to proximate water molecules. For the lignin biosynthesis these solvational effects may thus be site directing or site selective with respect to molecular structure on two levels. On the smallest scale level they perturb the spin density distribution (and vibrational properties) of lignin radical moieties and can thus affect the outcome (bond type) of the radical-radical coupling process. On a larger scale they may both partially control the possible sites where lignin monomers can add to the growing polymer, and they may suppress radical decay and hence stabilize the growth process.

These effects can also play an important role for the antioxidant nature of lignin and the resultant resistance of the polymer toward oxidative degradation. They should generally be present in all chemical reactions where lignin radicals appear as transient species. Thus RR spectroscopy combined with fluorescence rejection techniques promise a unique means of studying lignin radical properties and hence lignin biosynthesis or degradation.