Systematic Analysis of Conservation Relations in Escherichia coli Genome-Scale Metabolic Network Reveals Novel Growth Media

Abstract

A biochemical species is called producible in a constraints-based metabolic model if a feasible steady-state flux configuration exists that sustains its nonzero concentration during growth. Extreme semipositive conservation relations (ESCRs) are the simplest semipositive linear combinations of species concentrations that are invariant to all metabolic flux configurations. In this article, we outline a fundamental relationship between the ESCRs of a metabolic network and the producibility of a biochemical species under a nutrient media. We exploit this relationship in an algorithm that systematically enumerates all minimal nutrient sets that render an objective species weakly producible (i.e., producible in the absence of thermodynamic constraints) through a simple traversal of ESCRs. We apply our results to a recent genome scale model of Escherichia coli metabolism, in which we traverse the 51 anhydrous ESCRs of the metabolic network to determine all 928 minimal aqueous nutrient media that render biomass weakly producible. Applying irreversibility constraints, we find 287 of these 928 nutrient sets to be thermodynamically feasible. We also find that an additional 365 of these nutrient sets are thermodynamically feasible in the presence of oxygen. Since biomass producibility is commonly used as a surrogate for growth in genome scale metabolic models, our results represent testable hypotheses of alternate growth media derived from in silico analysis of the E. coli genome scale metabolic network.

INTRODUCTION

The metabolic network is the biochemical machinery with which a cell transforms a limited set of nutrients in its environment into the multitude of molecules required for growth and survival. The advent of sequencing technology and genomic annotation has allowed genome scale metabolic models to be built for many microbial organisms, as well as human red blood cells and mitochondria (5,9,14,19–21,23,27).

Current approaches to the study of genome scale metabolic models employ an analysis of feasible and optimal behaviors subject to structural, quasi-steady state, thermodynamic, and capacity constraints (18). Structural constraints arise from the stoichiometry matrix, whose columns encode the inputs and outputs of each reaction in the metabolic network. Quasi steady-state constraints follow from the timescale separation between rapid metabolic reactions and slower environmental and cellular regulatory changes. Thermodynamic (or irreversibility) constraints arise from directionality restrictions on reaction fluxes. Capacity constraints are derived from the availability of nutrients, enzyme activities, and gene/protein expression data. All of the above constraints restrict feasible flux configurations through the network to a polyhedral set (18).

The conservation relations of a metabolic network are linear combinations of species concentrations that remain invariant to all flux configurations through the network (6,24,25). In their vector representation, the conservation relations of a metabolic network form the left null space of the stoichiometry matrix. As a result, they provide an alternative and equivalent encoding of the structural constraints imposed by network stoichiometry upon the system dynamics. Semipositive conservation relations have been of particular interest because they are associated with the conservation of chemical moieties, atomic elements, and mass (6,16,24,25). The set of semipositive conservation relations associated with a stoichiometry matrix is a polyhedral cone, which can be generated by a unique set of extreme rays, also called extreme semipositive conservation relations (ESCRs). ESCRs have the special property of being the simplest semipositive conservation relations obeyed by the system, i.e., there exists no semipositive conservation relations obeyed by the network that employ a strict subset of the species contributing to an ESCR. ESCRs are closely associated with the distributions of the largest chemical subunits whose structure is preserved by all reactions in a metabolic network (24). ESCRs have also been shown to correspond to biologically meaningful metabolite pools (6,16,24).

Metabolite producibility is an in silico property that captures the feasibility of a given species attaining nonzero steady-state concentration in the cell during growth (13). In the context of the standard set of constraints afforded to genome-scale metabolic models, this property corresponds to the existence of a thermodynamically feasible flux configuration that compensates for the growth-mediated dilution of a species at steady state. This property can be determined computationally through the solution of a linear program that implements stoichiometric, steady-state, and thermodynamic constraints.

In this article, we employ a classic theorem of alternatives from linear programming theory to demonstrate the duality between producibility in the absence of thermodynamic constraints (which we also term weak producibility) and the existence of certain ESCRs. Specifically, we show that a species is weakly producible if and only if every ESCR to which it contributes also contains a species in the nutrient media. This relationship allows the weak producibility of an arbitrary metabolite in a given nutrient media to be determined through the evaluation of a simple criterion on the ESCRs. We exploit this principle in an algorithm that identifies all minimal nutrient media that render an arbitrary metabolite weakly producible with respect to a given metabolic network.

We apply our algorithm to the ESCRs of the Escherichia coli iJR904 metabolic network to determine minimal nutrient sets for biomass production (20). Though current algorithms and computing resources do not permit computation of the full set of ESCRs for this network, we are able to obtain all of the anhydrous (or non-water-containing) ESCRs of E. coli iJR904. Employing a corollary of our main theoretical result, we use these 51 anhydrous ESCRs to compute all 928 minimal aqueous (or water-containing) nutrient sets that render biomass weakly producible. Each aqueous nutrient set generated by our analysis is minimal in the sense that any of its water-containing subsets fail to render biomass producible. We find 287 of these nutrient media sets to be feasible when testing producibility in the context of thermodynamic constraints. Further analysis reveals that 365 additional nutrient sets become thermodynamically feasible in the presence of oxygen. Our results represent theoretical predictions regarding alternate growth media for E. coli derived from in silico network analysis.

THEORY

Mathematical preliminaries

In this section, we first state a theorem of alternatives from linear programming known as Farkas' Lemma and then formulate and prove a variation of it, which we will apply to infer producibility and conservation properties of metabolic networks.

In what follows, is the set of all n-dimensional vectors with real and positive components, R^m×n is the set of all m × n matrices with real entries, and I is the identity matrix. If x ∈ Rⁿ, then x_i denotes its i^th component and the inequality x ≥ 0 is interpreted component-wise, i.e., x_i ≥ 0, i = 1, …, n, while the inequality x > 0 is interpreted as x ≥ 0, x ≠ 0. For m, n ∈ N, m, n ≥ 1, let M = {1, …, m} and N = {1, …, n}. If x ∈ Rⁿ and U ⊆ N, then x_U ∈ R^|U| refers to the vector formed by taking components with indices in set U. If A ∈ R^m×n and U ⊆ N, then A_U denotes the submatrix of A containing the columns with indices in the set U. Given i ∈ N, A_i denotes the i^th column of A. N(A) stands for the null space of A. Given a set of vectors E ⊂ R^m, we refer to the set K formed by taking positive combinations of vectors in E as the conic hull of E. We also refer to the set K as a polyhedral cone. A ray is the conic hull of a single vector. The ray r ⊂ K is extreme with respect to K if and only if it does not belong to the conic hull of E\r.

Lemma 1

See Farkas (7). Given A ∈ R^m×n and b ∈ Rⁿ, exactly one of the following two sets is empty (nonempty):

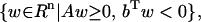(1)

(2)

Lemma 2

Given A ∈ R^m×n and arbitrary i = 1, … , m, exactly one of the following two sets is empty (nonempty):

(3)

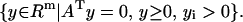(4)

Proof. The proof is given in Appendix 1.

Producibility in flux balance analysis models of metabolism

We represent a mass-balanced metabolic network of n chemical reactions involving m metabolites in a stoichiometry matrix S ∈ R^m×n. Each entry S_ij specifies the stoichiometric coefficient for metabolite i in reaction j, which is negative for substrates and positive for products. We represent the flux distribution through the reactions of the network by v ∈ Rⁿ, where a component v_j corresponds to the flux of reaction complex passing through reaction j. The concentrations of species in the system at time t are denoted by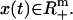

In flux balance analysis models of metabolism, S includes a reaction that consumes intracellular metabolites like amino acids, nucleotides, and lipid precursors to form a pseudo-species called biomass. This pseudo-species, which is indexed as row b in the stoichiometry matrix, represents a bulk combination of cellular macromolecules (i.e., proteins, DNA, lipid polymers) and comprises the large majority of cellular biomass.

In addition to the reactions in the stoichiometry matrix, a set of exchange fluxes u ∈ R^|U|, U ⊂ M, bring nutrient species x_k, k ∈ U across the system boundary. Each species also undergoes dilution due to expansion of cellular volume during growth, which occurs at a rate proportional to the growth rate λ > 0. Finally, thermodynamic constraints restrict a subset of reactions T ⊆ N to be irreversible. Under these assumptions, the rate of change in time of species concentrations is given by

(5)

where the variables λ, u, and v can be assumed to have implicit dependencies on x and time.

During balanced growth in a chemostat, culture contents reach a steady state (i.e., when 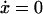), corresponding to some constant concentration vector 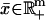and constant growth rate These additional constraints force steady-state flux configurations and to obey the relation

(6)

The feasibility of a nonzero concentration of species i at steady state (i.e., 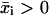) corresponds to the existence of steady-state flux configurations 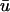and 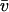that obeys the constraints in Eq. 6 and renders the i^th component of the left-hand side of Eq. 6 strictly positive. A metabolite for which such a configuration exists is called producible. Formally, this can be written as follows.

Definition 1: producible species

Species i ∈ M, is called producible by the metabolic network S with irreversible reactions T ⊂ N and nutrient media U ⊂ M, if the following set is nonempty,

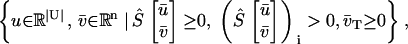(7)

where

(8)

Producibility thus corresponds to the existence of a thermodynamically feasible steady-state flux configuration that results in the net production of species i through the metabolic network S with irreversible reactions T and nutrient media U. We also introduce the notion of producibility in the absence of thermodynamic constraints (i.e., in a fully reversible network), which we refer to as weak producibility.

Definition 2: weakly producible species

Species i ∈ M, is called weakly producible if it is producible in the absence of irreversibility constraints, i.e., T = Ø in Definition 1.

Clearly, weak producibility is a necessary condition for producibility. We refer to a nutrient media U that renders i (weakly) producible as a (weak) nutrient set for i.

Duality of producibility and conservation

Vectors g ∈ R^m from the left null space of S (i.e., g for which g^TS = 0) are called conservation relations. They correspond to linear combinations of species concentrations that are held invariant by all flux configurations v through the network S. The set of semipositive conservation relations

(9)

is a polyhedral cone. Vectors in G are associated with the conservation of moieties such as carbon and mass (6).

Employing Lemma 2, we observe that the nonemptiness of the set in Eq. 7 with T = Ø,

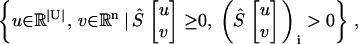(10)

is equivalent to the emptiness of the set

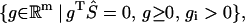(11)

which, using Fong and Palsson (8) and Forster et al. (9), can be written as

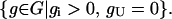(12)

The set in Eq. 12 is the set of all semipositive conservation relations containing species i and none of the species in the nutrient media U. The duality of sets in Eqs. 10 and 12, and Definition 2, lead to the following proposition.

Proposition 1

For arbitrary i ∈ M and stoichiometry matrix S, species i is weakly producible under nutrient media U if and only if all semipositive conservation relations g positive in component i are positive in at least one component from the set U.

Since G is a polyhedral cone, it may be expressed as the conic hull of a unique set of extreme rays, E, also called ESCRs (6,24,25). Using the following Lemma we will show that the existence of a conservation relation that is positive in an arbitrary species i and zero in components corresponding to nutrient media U can be simply checked through a condition on the ESCRs. We use the notation P_U(E) to denote the set of extreme rays with positive components in at least one member of the set U, i.e.,

(13)

From Eq. 13, it follows immediately that P_{U ∪ W}(E) = P_U(E) ∪ P_W(E) and P_U(P_W(E)) = P_U(E) ∩ P_W(E).

Lemma 3

The set {g ∈ G | g_i > 0, g_U = 0} is empty if and only if P_i(E) ⊆ P_U(E).

Proof. The proof is given in Appendix 1.

Lemma 3 and Proposition 1 lead to the main result of this article, Theorem 1.

Theorem 1

For arbitrary i ∈ M and stoichiometry matrix S, species i is weakly producible under nutrient media U if and only if each ESCR positive in component i is positive in at least one component in set U, i.e., P_i(E) ⊆ P_U(E).

Theorem 1 states that the weak producibility of a species in a given nutrient media can be evaluated via a simple condition on the ESCRs. Theorem 1 thus draws a direct relationship between the composition of ESCRs and the substrate-product connectivity of sets of species in the metabolic network. The following intuitive restatement of Theorem 1 arises from the correspondence between ESCRs and maximal conserved moiety pools (6,11,24): a species is weakly producible if and only if every maximal conserved moiety pool to which it contributes is supplied by at least one nutrient species.

As an aside, we note here a direct analogy between weak nutrient sets and cut sets in a metabolic network (15). As defined by Klamt and Gilles (15), a cut set C ⊂ N for a reaction j ∈ N is a set of reactions whose knockout renders flux through j infeasible at steady state. A necessary and sufficient condition for C to be a cut set for j is that C is a hitting set for all j-containing elementary modes (i.e., C intersects the nonzero components of every j-containing elementary modes). Applying the same terminology, we can restate Theorem 1 as follows: U is a weak nutrient set for i if and only if U is a hitting set for all of the i-containing ESCRs.

We also offer the following important corollaries of Theorem 1.

Corollary 1: weak nutrient equivalence

For arbitrary nutrient media U ⊂ M and species i, j, k ∈ M for which P_j(P_i(E)) = P_k(P_i(E)), i is weakly producible under nutrient media U ∪ {j} if and only if it is weakly producible under nutrient media U ∪ {k}.

Proof. The proof can be found in Appendix 1.

Corollary 1 states that species that contribute to identical sets of i-containing ESCRs are equivalent as nutrients for i in a fully reversible network. As a result, j and k can be swapped in a nutrient media without affecting the weak producibility of i.

Corollary 2: weak producibility in W-containing media

Given stoichiometry matrix S, nutrient media U, W ⊂ M, a species i ∈ M is weakly producible under nutrient media W ∪ U if and only if , where corresponds to the ESCRs of [I_w S].

Proof. The proof can be found in Appendix 1.

Corollary 2 states that the ESCRs of [I_W S] can be used to determine weak producibility for all W-containing nutrient media. It is simple to show that represents the non-W containing ESCRs of S, i.e., a partial set of ESCRs of S. As a result, Corollary 2 allows one to obtain weak producibility results from the computation of a partial set of ESCRs for S. This corollary is useful for the analysis of genome scale metabolic networks, for which the full set of ESCRs is difficult or impossible to compute.

METHODS

Algorithm for determination of minimal weak nutrient sets

Applying Theorem 1 to the ESCRs of a metabolic network, we can identify minimal sets of nutrients compatible with the weak producibility of an arbitrary species in a given metabolic network. A weak nutrient set U ⊆ M is minimal for species i with respect to metabolic network S if there does not exist a nutrient media U′ ⊂ U that renders i weakly producible under S. According to Theorem 1, weak producibility of i is ensured by the choice of a nutrient media U for which P_i(E) ⊆ P_U(E). Given the set E, corresponding to the ESCRs of S, a minimal weak nutrient set for i may be generated via a straightforward recursive algorithm F = MinNutrient(i, E) that traverses through the i-containing ESCRs in E (Appendix 2, Algorithm 1). We also allow an optional argument Z ⊆ M to MinNutrient (i,E), whose specification limits the search for nutrient sets to subsets of Z, e.g., extracellular species. Again, given the analogy between minimal weak nutrient sets and minimal cut sets outlined above, this algorithm can be understood to enumerate all of the minimal hitting sets for the collection of i-containing ESCRs. In this manner, our MinNutrient algorithm can be considered a recursive-depth/first-search alternative to the iterative-breadth/first-search minimal cut set algorithm formulated by Klamt and Gilles (15).

Genome scale metabolic model

In this study, we use the iJR904 genome scale metabolic model, which contains 762 species and 932 reactions (20). These reactions are compiled into a 762 × 932 stoichiometry matrix S. Full names of species referenced in this study and their corresponding abbreviations are listed in Table 1.

TABLE 1.

Metabolite abbreviations used in this study

Species	Abbrev.	Species	Abbrev.	Species	Abbrev.
12ppd-S*	(S)-propane 1,2-diol	fum*	Fumarate	met-L	L-methionine
15dap†	1,5-Diaminopentane	g6p	D-glucose 6-phosphate	mnl*	D-mannitol
26dap-M†	Meso-2,6-diaminoheptanediote	gal*	D-galactose	na1‡	Sodium
2ddglcn*	2-Dehydro-3-deoxy-D-gluconate	galct-D*	D-galactarate	nac†	Nicotinate
3hcinnm*	3-Hydroxycinnamic acid	galctn-D*	D-galactonate	nad	NAD
3hpppn*	3-(3-Hydroxy-phenyl)propionate	galt*	Galactitol	nh4	Ammoniun
4abut†	4-Aminobutanoate	galur*	D-galacturonate	nmn	NMN
ac*	Acetate	gam†	D-glucosamine	no2	Nitrite
acac*	Acetoacetate	gbbtn‡	γ-Butyrobetaine	no3	Nitrate
acald*	Acetaldehyde	glc-D*	D-glucose	o2‡	O2
acgam†	N-acetyl-D-glucosamine	glcn*	D-gluconate	ocdca*	Octadecanoate (n-C18:0)
acmana†	N-acetyl-D-mannosamine	glcr*	D-glucarate	om†	Omithine
acnam†	N-acetylneuraminate	glcur*	D-glucuronate	phe-L†	L-phenylalanine
ade†	Adenine	gln-L†	L-glutamine	pi	Phosphate
adn†	Adenosine	glu-L†	L-glutamate	pnto-R†	(R)-pantothenate
akg*	2-Oxoglutarate	gly†	Glycine	pppn*	Phenylpropanoate
ala-D†	D-alanine	glyald*	D-glyceraldehyde	pro-L†	L-proline
ala-L†	L-alanine	glyb‡	Glycine betaine	ptrc†	Putrescine
alltn†	Allantoin	glyc3p	Glycerol 3-phosphate	pyr*	Pyruvate
amp‡	AMP	glyc*	Glycerol	rib-D*	D-ribose
arab-L*	L-arabinose	glyclt*	Glycolate	rmn*	L-rhamnose
arg-L†	L-arginine	gsn†	Guanosine	sbt-D*	D-sorbitol
asn-L†	L-asparagine	gua†	Guanine	ser-D†	D-serine
asp-L†	L-aspartate	h2o	H2O	ser-L†	L-serine
but*	Butyrate (n-C4:0)	h‡	H+	so4	Sulfate
cbl1	Cob(I)alamin	hdca*	Hexadecanoate (n-C16:0)	spmd†	Spermidine
chol‡	Choline	his-L†	L-histidine	succ*	Succinate
cit*	Citrate	hxan†	Hypoxanthine	sucr*	Sucrose
co2*	CO2	idon-L*	L-idonate	tartr-L*	L-tartrate
cm‡	L-carnitine	ile-L†	L-isoleucine	taur	Taurine
csn†	Cytosine+C68	indole†	Indole	thm	Thiamin
cynt†	Cyanate	ins†	Inosine	thr-L†	L-threonine
cys-L	L-cysteine	k‡	K+	thymd†	Thymidine
cytd†	Cytidine	lac-D*	D-lactate	tma‡	Trimethylamine
dad-2†	Deoxyadenosine	lac-L*	L-lactate	tmao‡	Trimethylamine N-oxide
dcyt†	Deoxycytidine	lcts*	Lactose	tre*	Trehalose
dgsn†	Deoxyguanosine	leu-L†	L-leucine	trp-L†	L-tryptophan
dha*	Dihydroxyacetone	lys-L†	L-lysine	tsul	Thiosulfate
din†	Deoxyinosine	mal-L*	L-malate	ttdca*	Tetradecanoate (n-C14:0)
dms‡	Dimethyl sulfide	malt*	Maltose	tyr-L†	L-tyrosine
dmso‡	Dimethyl sulfoxide	malthx*	Maltohexaose	ura†	Uracil
duri†	Deoxyuridine	maltpt*	Maltopentaose	urea†	Urea
etch*	Ethanol	malttr*	Maltotriose	uri†	Uridine
fe2‡	Fe2+	maltttr*	Maltotetraose	val-L†	L-valine
for*	Formate	man6p	D-mannose 6-phosphate	xan†	Xanthine
fru*	D-fructose	man*	D-mannose	xstn†	Xanthosine
fuc-L*	L-fucose	melib*	Melibiose	xyl-D*	D-xylose
fuc1p-L‡	L-fucose 1-phosphate	met-D‡	D-methionine

Adapted from the E. coli iJR904 model annotation of Reed et al. (20).

^*Belongs to Class 1.

^†Belongs to Class 2.

^‡Belongs to Class 3 in Figs. 1 and 2.

Extreme ray algorithm

We calculate ESCRs via a modified form of the algorithm previously outlined in Schilling et al. (22) and Bell and Palsson (1) for the calculation of extreme pathways. The procedure R = extreme(A), implemented as a MatLab script (The MathWorks, Natick, MA), returns the extreme rays R of the cone N(A) ∩ R^m for an input matrix A ∈ R^n×m. The algorithm proceeds by computing extreme rays for a series of cones, beginning with 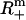and the Euclidean basis in Successive cones are formed by intersecting the current cone with the hyperplane orthogonal to the next pivot row of A, which is chosen according to a local optimization strategy described in Bell and Palsson (1). We compute , corresponding to the anhydrous ESCRs of S, by calling extreme([I_w S]^T), where w is the index of the row of the S corresponding to water.

Identifying minimal weak aqueous nutrient sets for biomass

Biomass production serves as a model for growth in flux balance analysis of metabolism (2,4,5,8,12). This process is modeled as flux through a reaction that consumes 49 species and produces biomass, which is represented as a pseudo-species in the network corresponding to row b ∈ M of S. Note that since biomass is involved in a single reaction, the existence of a nonzero biomass flux and the producibility of biomass is equivalent with respect to the system formulation in Eq. 6.

We employ 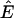, the set of anhydrous ESCRs of S, to generate minimal weak aqueous nutrient sets for the weak producibility of biomass. Naturally, we limit candidate nutrient sets to subsets of extracellular species, whose indices are represented by the set X ⊂ M. In this case, 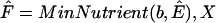outputs the family of minimal weak nutrient sets for biomass with respect to metabolic network [I_w S]. Each nutrient set to [I_w S] is equivalent to a nutrient set U ∪ {w} for S. The nutrient set U ∪ {w} is not necessarily minimal for biomass with respect to S, since removal of water from this set may still render biomass producible under S. However, since water cannot be removed from any biologically feasible growth media, these nutrient sets are physiologically minimal. We refer to each U ∪ {w} as a minimal weak aqueous nutrient set for biomass.

We also perform an alternate computation that allows for compact presentation of minimal nutrient set results. In this computation, we group extracellular species into equivalence classes according to membership in biomass containing ESCRs, i.e., species j and k for which . We then form the set Q ⊂ X by choosing one species from each equivalence class. According to Corollary 1, if species j and k contribute to the same b-containing ESCRs, then the producibility of b is invariant to the replacement of j with k in the media. This means any species belonging to a minimal weak nutrient set in can be swapped with any other species from its corresponding equivalence class. Each nutrient set in can thus be interpreted as a conjunction of species equivalence classes (i.e., Class 1, Class 2, and Class 3), each of which can be expanded to represent multiple nutrient sets in 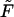(i.e., Class 1 = species 1 or species 2). Expressed in this manner, 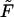provides a compact but equivalent representation of .

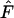Producibility test

We test the producibility of a metabolite i in the context of nutrient media U and irreversible reactions T by solving the optimization problem

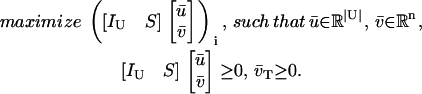(14)

A nonzero optimum in Eq. 14 corresponds to the nonemptiness of the set in Eq. 7. We can also test the producibility of a metabolite i in the context of one or more reaction knockouts C ⊂ N by applying the additional constraints to Eq. 14) We solve the linear program in Eq. 14 using the semidefinite programming package SeDuMi (http://sedumi.mcmaster.ca/).

RESULTS

Escherichia coli iJR904 is associated with only 51 anhydrous ESCRs

Computation of minimal weak nutrient sets via the MinNutrient algorithm requires knowledge of the ESCRs of a metabolic network. However, a metabolic network of the size of E. coli iJR904 can potentially be associated with thousands of millions of ESCRs, which are buried in a search space whose size is orders-of-magnitude higher. Indeed, the full set of ESCRs is not obtainable for E. coli iJR904 given current algorithms and computing resources.

We do not, however, need to know all of the ESCRs of a metabolic network to compute minimal weak nutrient sets: Corollary 2 states that predicting weak producibility in a W-containing nutrient media only requires knowledge of non-W-containing ESCRs, where W is a subset of species indices. Using this result, we can apply the MinNutrient algorithm (Algorithm 1) to the set of non-W-containing ESCRs to compute all W-containing nutrient sets for an objective species.

Water stands out in the E. coli iJR904 (and most other metabolic networks) due to its promiscuity in the network, which suggests it may contribute to a large number of ESCRs. (This may be counterintuitive to those who interpret ESCRs as having strict correspondence to maximally conserved moiety pools, since water is a simple molecule that can belong to only a limited set of moiety pools. However, as pointed out by Schuster and Hilgetag (24), the mapping of ESCRs to maximally conserved moieties is not 1:1, and in many cases the distribution of a maximally conserved moiety pool can lie in-between multiple ESCRs. Indeed, a separate calculation identifies at least 32 water-containing ESCRs in the E. coli iJR904 metabolic network.) Furthermore, water is a necessary solvent in nutrient media and in biological systems, and thus it is reasonable to assume that any minimal nutrient media supporting growth in E. coli is aqueous. Finally, inclusion of extracellular water in the nutrient media renders only nine species weakly producible (including intracellular water, intracellular/extracellular oxygen, intracellular/extracellular proton, and intracellular hydrogen peroxide), when testing weak producibility via solution of the linear program in Eq. 14. According to Theorem 1, this means that non-water-containing ESCRs in the E. coli iJR904 network have positive components in 753 of the 762 species in the system, and can thus yield informative weak producibility results for many nutrient media combinations. Motivated by the above observations, we compute the non-water-containing (i.e., anhydrous) ESCRs with the goal of determining minimal weak aqueous nutrient sets for biomass.

Successfully completing the above computation, we find that E. coli iJR904 is associated with only 51 anhydrous ESCRs. These ESCRs are provided as Supplementary Material, Table 1. As predicted by Theorem 1, these 51 vectors span 753 positive species directions, which correspond to all species that fail to be weakly producible in a water-only media. As asserted by Corollary 2, we are able to apply a simple criterion to these anhydrous ESCRs to determine weak producibility in all aqueous nutrient media. Indeed, all such predictions are corroborated through an independent computation of weak producibility via solution of the optimization problem in Eq. 14.

The small number of anhydrous ESCRs for a model of this size is remarkable. Though a full discussion of this result is beyond the scope of this article, we note two implications of this finding: Firstly, given the intuitive association of ESCRs with maximal conserved moiety pools, it suggests that E. coli iJR904 metabolic model is associated with a remarkably small number of anhydrous metabolic pools. Results alluding to a similar conclusion have been obtained by Nikolaev et al. (16), who apply an optimization approach to determine the properties of conserved pools in E. coli. Secondly, if the full set of ESCRs E is large, our results suggest that most ESCRs associated with the E. coli genome scale metabolic network involve water. However, we note that, according to Corollary 2, this potentially large set of water-containing ESCRs is functionally irrelevant, unless one is analyzing weak producibility in a physiologically infeasible anhydrous nutrient media. We defer further discussion of this and related results to another study.

Biomass is weakly producible under 928 minimal aqueous nutrient sets

Application of Corollary 2 shows that biomass is rendered weakly producible by an aqueous nutrient media U if and only if every biomass-containing anhydrous ESCR contains a species in U. We find 17 biomass-containing anhydrous ESCRs in 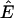. Grouping of the 142 (nonwater) extracellular species with respect to membership in these 17 ESCRs results in 11 equivalence classes, each containing between 1 and 56 species. The membership pattern of species equivalence classes among the biomass-containing anhydrous ESCRs is depicted in Fig. 1.

FIGURE 1.

The 17 biomass-containing anhydrous ESCRs associated with the iJR904 E. coli metabolic model induce 11 equivalence classes among the 143 extracellular species. Each species equivalence class corresponds to a row and each biomass, containing anhydrous ESCRs, to a column in the above plot. A square in position ij maps each species in equivalence class i to biomass-containing anhydrous ESCRs j. Equivalence classes with large numbers of species are represented by labels: Class 1 corresponds to 56 carbon sources (e.g., D-glucose, citrate, ethanol, lactose, L-tartrate), Class 2 corresponds to 54 nitrogen/carbon sources (e.g., most amino acids, nucleotides, and nucleotide precursors), and Class 3 represents 16 species that do not share anhydrous ESCRs with biomass (e.g., Fe²⁺, K⁺, D-methionine, trimethylamine, water, and proton). The full inventory of these species equivalence classes and legend of species abbreviations are given in Table 1.

Each equivalence class can be associated, with a given anhydrous chemical moiety that all members of that class share with biomass. By inspection, Class 1 contains 56 central carbon sources (i.e., citrate, pyruvate, fructose, L-lactose, D-glucose), while Class 2 corresponds to 54 nitrogen/carbon sources, including amino acids, purines, pyrimidines, and nucleotides among its members. Class 3, on the other hand, corresponds to species that do not share any anhydrous ESCRs with biomass. Among the 16 species in this class are extracellular proton and oxygen, which do not contribute to any anhydrous ESCRs since they are producible in a water-only media. Class 3 also includes metal ions such as sodium, iron, and potassium and larger molecules such as γ-butyrobetaine and AMP. The remaining eight species equivalence classes are small and represented in Figs. 1 and 2 as disjunctions of their members.

FIGURE 2.

There are 928 minimal weak aqueous nutrient sets for biomass in the E. coli iJR904 genome scale metabolic model. Two-hundred-and-eighty-seven of these nutrient sets permit growth when thermodynamic constraints are considered. Minimal weak aqueous nutrient sets are expressed in this figure as conjunctions of 11 equivalence classes of species that contribute to the same biomass-containing anhydrous ESCRs. Each conjunction represented by column j in this figure corresponds to a family of minimal weak aqueous nutrient sets, each formed by choosing one species from each equivalence class i that has a black box in entry ij. Each entry in the bottom row of the figure indicates how many total minimal weak aqueous nutrient sets are contributed by the conjunction in column j. Class 1 and Class 2 correspond to central carbon sources and nitrogen/carbon sources, respectively. Class 3 contains species that do not share anhydrous ESCRs with biomass. Please refer to Table 1 for full inventory of the species in equivalence Classes 1–3 and a legend of species abbreviations.

To compute the family of all possible minimal weak aqueous nutrient sets , we apply Algorithm 1 to . These results are represented in compact form as 10 conjunctions of the 11 species equivalence classes mentioned above (e.g., Conjunction 1 is (met-L[e] or cys-L[e]) and (nad[e] or nmn[e]) in Fig. 2. Each of these conjunctions corresponds to a family of nutrient sets (e.g., Conjunction 1 can be expanded to {met-L[e], nad[e]}, {met-L[e], nmn[e]}, {cys-L[e], nad[e]}, and {cys-L[e], nmn[e]}. In sum, contains 928 unique minimal weak aqueous nutrient sets for biomass (Supplementary Material, Table 2). These nutrient sets involve 126 of 143 extracellular species of E. coli iJR904 and nine of the 11 species equivalence classes described above.

Inspection of Figs. 1 and 2 shows how minimal weak aqueous nutrient sets are constructed from biomass-containing ESCRs. For example, NAD (nad[e]) and sulfate (so4[e]) is a minimal weak nutrient set because nad[e] contributes to ESCRs 1, 6–9, and 14–17 while sulfate (so4[e]) corresponds to ESCRs 2–5 and 10–13 in Fig. 1. Together they span all 17 biomass-containing ESCRs. L-methionine contributes to ESCRs 2–17 in Fig. 1. Combining L-methionine with any species that contributes to ESCRs 1 in Fig. 1 will form a minimal weak aqueous nutrient set for biomass; this role is fulfilled by phosphate (pi[e]), mannose-6 phosphate (man6p[e]), and nad, among others.

The composition of each minimal weak aqueous nutrient set in Fig. 2 is remarkably simple and biochemically intuitive. Detailed inspection shows a close correspondence between the composition of individual nutrient sets and the anhydrous elemental composition of biomass; namely, each nutrient set consists of a carbon, nitrogen, phosphorus, and sulfur source. Although, in many cases, multiple species provide the same atomic element in a given nutrient set, the criterion of minimality ensures that each species in each nutrient set is uniquely responsible for supplying at least one anhydrous moiety pool. For example, all nutrient sets in have one of the following species as the sole phosphorus source: phosphate, glucose-6-phosphate, mannose-6-phosphate, cob(I)alamin, NAD, or NMN. In all nutrient sets, the species L-methionine, L-cysteine, sulfate, and taurine serve as the sole sulfur sources. The tasks of providing carbon and nitrogen are usually shared among multiple species. For example, in column-1 nutrient sets, carbon and nitrogen are provided by both the sulfur source and phosphorus source. In column 7, nutrient sets carbon is provided by both Class 2 species and the phosphorus source. The only nutrient sets in which a separate atomic element is provided by each species in the set are the sets represented by column 10, in which Class 1 species provide carbon; nitrate/nitrite/ammonia provide nitrogen; sulfate or taurine provide sulfur; and phosphate provides phosphorus.

Thiosulfate and all 16 species from Class 3 do not contribute to a single minimal weak aqueous nutrient set. Since species in Class 3 do not share a single anhydrous ESCR with biomass, they are clearly dispensable with respect to the weak producibility of biomass in any aqueous nutrient media. Thiosulfate, however, shares four anhydrous ESCRs with biomass (ESCRs 3, 5, 11, and 13 in Fig. 1), yet also appears to be dispensable. Closer analysis of ESCR membership patterns show that the only other extracellular species that contribute to ESCRs 3, 5, 11, and 13 are sulfate, taurine, L-methionine, L-cysteine, and thiamine. However, these species are also the unique contributors to ESCRs 2, 4, 10, and 12, and thus at least one of them must be present in every minimal weak aqueous nutrient set for biomass. As a result, every minimal weak aqueous nutrient set for biomass is guaranteed to span ESCRs 3, 5, 11, and 13 without containing thiosulfate, making this species dispensable for the weak producibility of biomass.

Minimal weak aqueous nutrient sets (287 of 928) are thermodynamically feasible

Although weak nutrient sets are stoichiometrically compatible with the production of a species, they are not necessarily thermodynamically feasible. Irreversibility constraints restrict the direction in which moieties may flow between extracellular nutrients and intracellular species. The absence of such constraints permits behaviors like carbon fixation and oxygen synthesis, which are thermodynamically infeasible in a nonphotosynthetic organism like E. coli.

Producibility calculations via Eq. 14 show that 287 of 928 (30.9%) aqueous minimal weak nutrient sets render biomass producible in the context of thermodynamic constraints (Supplementary Material, Table 2). These thermodynamically feasible nutrient sets employ 102 of the 126 of the extracellular species that comprise nutrient sets in . These nutrient sets correspond to predictions of novel minimal media for E. coli under the FBA model of growth.

The thermodynamical infeasibility of many minimal weak aqueous nutrient sets can be attributed to the impotence of individual nutrients as carbon, nitrogen, or sulfur sources. Formally, we use the term “impotent nutrient” to refer to nutrient species that are contained only in thermodynamically infeasible sets of . Given this definition, there are a total of 24 impotent nutrients resulting from our analysis (Supplementary Material, Table 3). Six-hundred-and-two of 641 thermodynamically infeasible nutrient sets contain one or more such impotent nutrients. One-hundred-thirty-eight of the latter sets contain two impotent nutrients and 16 contain three impotent nutrients.

The most notable examples of impotent nutrients are taurine and cob(I)alamin. All 457 taurine-containing minimal weak nutrient sets and all 118 cobalamin-containing minimal weak nutrient sets fail to be thermodynamically feasible. A majority (517 of 641) of thermodynamically infeasible minimal weak nutrient sets contain either taurine or cob(I)alamin. The remaining 22 impotent nutrients each contribute to 10 or less minimal weak nutrient sets. These species include carbon sources like carbon dioxide, formate, and nitrogen sources like spermidine, L-methionine, uridine, and urea. One-hundred-and-ninety-seven of 641 thermodynamically infeasible minimal weak nutrient sets contain one or more of these species.

Many impotent nutrients are dead-end species inside the cell (i.e., aside from transport reactions, they only serve as a reaction product). Such is the case for urea, L-histidine, and L-methionine. Other impotent nutrients are not dead ends but lie in a metabolic cul-de-sac; they contain a moiety that cannot be broken down without violating irreversibility constraints of one or more reactions. For example, cob(I)alamin is a 62-carbon molecule that is formed from cobinamide and α-ribazole, through a multistep pathway that involves irreversible reactions. In the context of thermodynamic constraints, cob(I)alamin can only be converted to adenosylcobalamin, which cannot be further degraded, and thus cannot be used as a carbon source (Fig. 3). Similarly, L-lysine can only be converted to 1,5-diaminopentane, which is a dead-end species. Ironically, the impotence of carbon dioxide, a classic metabolic dead-end in nonphotosynthetic organisms, is less trivial to justify from network analysis. Carbon dioxide acts as a substrate to five carboxylation reactions that produce species that are not dead-ends (e.g., isocitrate, dethiobiotin). Although these reactions merely add carboxyl moieties to existing carbon compounds in the network, it cannot be readily proven that these reactions cannot contribute to de novo synthesis of carbon-containing species from CO₂. Our producibility calculations via Eq. 14 provide numerical evidence that any such flux configuration is thermodynamically infeasible.

FIGURE 3.

(a) All cobalamin-containing minimal weak aqueous nutrient sets are thermodynamically infeasible due to the inability of E. coli iJR904 to break down the cobalamin moiety. This results from the irreversibility of reaction ADOCBLS, which mediates the biosynthesis of adenosylcobalamin (adocbl) from N1-(α-D-ribosyl)-5,6-dimethylbenzimidazole (rdmbzi) and adenosine-GDP-cobinamide (agdpcbi). Additional metabolite abbreviations: ppi, pyrophosphate; gmp, guanosine monophosphate. (b) Taurine-containing, minimal weak aqueous-nutrient sets fail to render biomass producible in the presence of irreversibility constraints. Taurine acts as a sulfur donor by undergoing oxygen-dependent degradation to sulfite (so3) via reaction TAUDO. In the absence of thermodynamic constraints, oxygen is producible by E. coli iJR904 and this reaction is active. Oxygen fails to be producible in all minimal weak aqueous nutrient sets when thermodynamic constraints are considered, rendering the utilization of taurine as a sulfur source infeasible. Addition of oxygen renders 323 of 457 taurine-containing nutrient sets thermodynamically feasible. Networks visualized using Pajek (http://vlado.fmf.uni-lj.si/pub/networks/pajek/).

Thirty-nine of the thermodynamically infeasible nutrient sets in do not associate with a single impotent nutrient. These sets belong to one of two groups:

1. Sets containing nitrite or ammonium and one of the following species—butyrate, succinate, glycolate, octadecanoate, tetradecanoate, hexadecanoate, acetaldehyde, acetoacetate, ethanol, L-lactate, (S)-propane-1,2-diol, or acetate.

2. Sets containing phosphate and one of the following species—putrescine, 4-aminobutanoate, L-valine, l-arginine, L-isoleucine, glycine, phenylalanine, tyrosine, threonine, adenine, cytosine, xanthine, or hypoxanthine.

Addition of oxygen renders 365 additional nutrient sets thermodynamically feasible

The thermodynamical infeasibility of many nutrient sets in can be tied to the absence of oxygen. For example, taurine is the sole sulfur source in the 457 nutrient sets in which it is present; however, its conversion to sulfite requires the presence of oxygen. Oxygen can be synthesized via reverse respiration from carbon dioxide and water in the absence of thermodynamic constraints. As expected, the presence of thermodynamic constraints renders de novo oxygen synthesis infeasible. This appears to prevent the liberation of sulfur from taurine-containing nutrient sets and its subsequent incorporation into biomass (Fig. 3). Similar oxygen requirements underlie the conversion of the infeasible nutrients phenylpropanoate, 3-hydroxycinnamic acid, and 3-(3-hydroxy-phenyl)propionate species to 2-oxopent-4-enoate and fumarate or succinate. In the absence of oxygen, this pathway is inactive, thus preventing the utilization of these species as carbon sources in the network.

Given the above observations, we examine whether biomass is rendered producible when oxygen is added to nutrient sets. Indeed, the addition of oxygen has a profound effect on many thermodynamically infeasible nutrient sets in : 365 of 641 are rendered feasible in the presence of oxygen. These include 323 of 457 taurine-containing minimal weak nutrient sets. The remaining taurine-containing minimal weak nutrient sets fail to render biomass producible because they contain a thermodynamically infeasible carbon source like cob(I)alamin, carbon dioxide, or thiamine. Additional nutrient sets made feasible by the presence of oxygen include 18 of 18 minimal weak nutrient sets containing phenylpropanoate, 3-(3-hydroxy-phenyl)propionate, or 3-hydroxycinnamic acid. As noted above, these species undergo oxygen-dependent conversion to 2-oxopent-4-enoate and succinate or fumarate. Analysis of in silico reaction knockouts shows this pathway to be necessary for the utilization of these species as carbon sources by the network in the presence of oxygen. Other nutrient sets in made feasible by the presence of oxygen include eight of 10 L-proline containing nutrient sets. This effect is inhibited by the knockout of the ubiquinone-8 proton pump, the ubiquinol-8 mediated oxidation of FADH₂ to FAD, and the FAD-mediated conversion of L-proline into 1-pyrroline-5-carboxylate. Its utilization is not inhibited by the knockout of any other reactions in the network involving oxygen, aside from the oxygen transport reaction. From this analysis, it appears that the utilization of L-proline in the presence of oxygen is dependent on FAD formation.

Consistency with in vivo nutrient media

The ASAP database (10) documents in vivo growth of E. coli in 125 nutrient media, which have been mapped to the iJR904 model by Covert et al. (2). Minimal aqueous nutrient sets for biomass generated by our analysis are simpler than these nutrient media, which contain metal ions and electrolytes such as sodium, potassium, chloride, magnesium, and calcium. These ions play essential physiological roles in the cell by contributing to electrochemical and osmotic gradients and by acting as enzyme cofactors. Some of the metal ions are not included in the iJR904 annotation (e.g., magnesium, calcium, chloride). The remaining ions (potassium, sodium) that are part of the annotation are not incorporated into biomass as defined by the iJR904 model. As a result, potassium and sodium do not share any anhydrous ESCRs with biomass, and are dispensable in any aqueous nutrient media for E. coli iJR904. This gap between in vivo and in silico behavior lies in the limited definition of survival and growth, which in the current model currently only depends on the production of biomass (see Discussion).

In addition to the salts mentioned above, ASAP nutrient media contain oxygen, sulfate, phosphate, proton, water, and a carbon and/or nitrogen source. Sixty-eight of these nutrient media (Biolog plate PM1 and PM2; Biolog, Hayward, CA) contain ammonia as a nitrogen source and vary in their carbon source, chosen from a set of 68 species that includes 36 species from Class 1 and 29 species from Class 2, glucose-6-phosphate, L-methionine, and L-carnitine. The remaining 57 of the 125 nutrient sets (Biolog plate PM3) contain succinate as a carbon source and contain one or two nitrogen sources chosen from a set of 43 species that includes 39 species from Class 2, nitrate, nitrite, ammonia, L-methionine, and L-cysteine. Twenty-two ASAP nutrient media contain one or more species that are infeasible as nutrients to iJR904 in the presence of thermodynamic constraints (Supplementary Material, Table 3). These species include uracil and uridine, due to the irreversible synthesis of their pyrimidine base; L-proline, L-leucine, L-histidine, L-methionine, and L-lysine, which are only substrates for transport reactions; and the biomass reaction, thymidine, which cannot be degraded further than thiamine, and formate, which can only be degraded to CO₂. One of the ASAP nutrients, L-carnitine, is infeasible as a nutrient even in the fully reversible network, since its carbons and nitrogens belong to a separate carrier pool in the iJR904 network. These inconsistencies point to the need for additional annotation of reactions in the E. coli network and possible reformulation of thermodynamic constraints.

Many of the feasible ASAP nutrient sets are not minimal by our analysis. Some ASAP nutrient sets fail to be minimal because they contain two nitrogen sources (e.g., alanine and aspartate). However, the majority of ASAP nutrient sets are not minimal by our analysis because they contain a species that provides both carbon and nitrogen (e.g., a species in Class 2), in addition to succinate or ammonia. As a result, either succinate or ammonia serves as redundant providers of carbon or nitrogen, respectively, in these nutrient sets. Growth of E. coli under these nutrient sets with succinate and ammonia removed would determine whether these predicted minimal nutrient sets are physiologically viable.

DISCUSSION

Extensions of approach

Pool maps and producibility

Given the common physical interpretation of ESCRs as maximal conserved moiety pools, Theorem 1 can be understood to link weak producibility to the flow of conserved moieties between nutrients and species in the network. Thermodynamic constraints can be understood in this context as directional restrictions on this flow. As a result, a species may not be producible even if each maximal conserved moiety pool to which it contributes is supplied by a nutrient in the media. This implies that thermodynamic constraints have a fragmenting effect on maximal conserved moiety pools, which render a given nutrient capable of supplying only a subset of the species in the pools to which it contributes.

This intuition may be potentially exploited to formulate a path-based criterion for producibility through the analysis of pool maps, which are described in Famili and Palsson (6). Each pool map corresponds to a subset of the metabolic network that includes only species associated with a given ESCR. In a pool map, each forward reaction induces a directed edge that implies the transfer of the respective moiety between each substrate and product pair. The existence of a directed path from a nutrient to a species in a pool map may contribute to a necessary and sufficient criteria for producibility similar to that expressed in Theorem 1. We are currently investigating this approach in further detail.

Augmentation of minimal weak aqueous nutrient sets

In our analysis, we find that a large number of thermodynamically infeasible minimal weak aqueous nutrient sets render biomass producible in the presence of oxygen. This observation shows that many minimal weak nutrient sets that fail to be thermodynamically feasible may nevertheless comprise subsets of larger (thermodynamically feasible) minimal nutrient sets. Intuitively, additional nutrient requirements arise from the fragmenting effect of thermodynamic constraints on maximal conserved moiety pools. This requires the presence of multiple nutrients to supply all of the species in a given maximal conserved moiety pool, resulting in more complex minimal nutrient sets for the (strong) producibility of a species. Although we have chosen to only examine the addition of oxygen, the augmentation of nutrient sets with other species may also render them thermodynamically feasible. However, a brute force search through all such possible augmentations will clearly suffer from combinatorial explosion.

Direct incorporation of thermodynamic constraints

Theorem 1 defines a novel relationship between the ESCRs of a metabolic network and producibility in the absence of thermodynamic constraints: a species is weakly producible if and only if each ESCRs to which that species contributes contains at least one nutrient in the media. Although the condition stated in Theorem 1 is necessary and sufficient for weak producibility, it is only a necessary condition for producibility.

An analog of Theorem 1 directly applicable to networks with thermodynamic constraints arises from the analysis of the following polyhedral cone,

(15)

where T ⊂ N represents the set of irreversible reactions in the metabolic network S. The criterion stated in Theorem 1 applied to the extreme rays of G_s, which we refer to as extreme semipositive subconservation relations (ESSR), provides a necessary and sufficient condition for producibility (Supplementary Material). Unfortunately, the application of this theorem is extremely limited, since the ESSR associated with a metabolic network even outnumber the ESCRs. Their calculation (or even a calculation of a subset of ESSR, i.e., anhydrous ESSR) is intractable for a model of the size of S, given current approaches and computing resources.

Applicability to other organisms

The method outlined in this article generates minimal weak W-containing nutrient sets for any metabolic network for which non-W-containing ESCRs are computable. In particular, this study employs the non-water-containing ESCRs of the E. coli iJR904 network to enumerate minimal weak aqueous nutrient sets. Preliminary results show that computation of anhydrous ESCRs may also be possible for other metabolic networks; for example, we are able to complete this computation for the Saccharomyces cerevisiae genome scale metabolic model (unpublished data). The surprising tractability of the anhydrous ESCRs computation is by itself a potentially interesting topic of study, since it suggests that most ESCRs associated with genome scale metabolic networks involve water.

In general, however, the computation of anhydrous ESCRs is not guaranteed to be tractable. Indeed, less complete networks can potentially have many more ESCRs than a well-characterized model such as E. coli iJR904, given the higher rank of the left null space of the stoichiometry matrix and larger number of dead-end metabolites. This may render even anhydrous ESCR computation difficult or impossible, given current algorithms and computing resources. If this is the case, then our approach is flexible by allowing results to be obtained from the non-W-containing ESCRs of a metabolic network, where W ⊆ M represents any other subset of species in the network. If these non-W-containing ESCRs are obtainable, then our approach will yield all minimal W-containing weak nutrient sets consistent with the model stoichiometry. Although such results would provide only a partial characterization of minimal weak nutrient sets, they could still provide useful insight into the capabilities of the model in a given subset of potential environments.

Incorporating alternative models of growth and survival

In this study, we infer novel growth media for E. coli iJR904 by determining minimal nutrient sets that render biomass producible. These results rely on a particular in silico model of growth and survival that is based solely on biomass production, the latter which is in turn based on a strict definition of biomass composition encoded in the biomass reaction. This model of growth underlies flux balance analyses of E. coli metabolism, where it has shown significant correlation with in vivo behavior (8). Nevertheless, the ability to produce biomass, as defined in this model, may be neither necessary nor sufficient for growth or survival of E. coli. Alternative models of growth, based on different biomass compositions, consideration of essential metabolites outside of biomass, and quantitative criteria may yield significantly different minimal nutrient set results. Although a full discussion of all such alternative models of growth and survival is outside of the scope of this article, we will highlight several examples in this section and discuss their impact on minimal nutrient sets.

Alternative biomass compositions

The biomass reaction employed in the E. coli iJR904 genome-scale metabolic model is based on a particular in vivo measurement of E. coli biomass composition (20). It is quite feasible, however, that alternative biomass compositions (e.g., alternative sets of lipid components, alternative membrane lipid ratios) may be compatible with growth and survival. According to Theorem 1, the composition of the resulting weak nutrient sets under this new biomass reaction will depend strictly on ESCR sparsity patterns in the modified network. An implication of this result is that the feasibility of a nutrient set as an in silico growth media is independent of the exact ratios of lipid composition, but is sensitive to the addition/removal of lipid components to/from the biomass reaction.

For example, the addition of a species to the left-hand side of the biomass reaction can (but is not guaranteed) to result in both new biomass-containing ESCRs and new species that share ESCRs with biomass. The size of nutrient sets will thus be maintained or will increase with this perturbation, since minimal nutrient sets that already contribute to the new biomass-containing ESCRs will remain feasible, while the remaining nutrient sets will become feasible only when combined with a minimal set of species that intersects every new biomass-containing ESCRs. Note that some of the new nutrient sets produced through this augmentation process may fail to be minimal, while other old minimal weak nutrient sets may be mapped to the same new augmented minimal weak nutrient sets. As a result, the total number of minimal weak nutrient sets may increase, decrease, or stay the same as a result of this perturbation. Conversely, removal of a species from the left-hand side of the biomass reaction may result in fewer species sharing ESCRs with biomass, which may render certain species unnecessary for the producibility of biomass and render nutrient sets containing those species nonminimal. This will result in maintenance or reduction in the size of individual minimal weak nutrient sets. However, like in the previous example, the total number of minimal weak nutrient sets may increase, decrease, or stay the same.

It can be shown that simple alteration of biomass ratios, implemented as the positive rescaling of stoichiometric coefficients on the left-hand side of the biomass reaction, will not change the sparsity patterns of biomass-containing ESCRs. According to Theorem 1, such a change will have no effect on the composition of minimal weak nutrient sets for biomass. Similarly, it can be shown that such a rescaling will have no effect on the sparsity patterns of ESSR, which determine strong producibility (see above). This implies that a nutrient media in a system with positively rescaled biomass coefficients will render biomass producible if and only if it renders biomass producible in the original system.

Quantitative models of survival

In FBA, growth is equated to biomass production, and survival is equated to nonzero growth. This renders in silico survival dependent strictly on qualitative aspects of the model (i.e., network structure, which species compose the nutrient set), although insensitive to positive scaling of biomass coefficients and capacity constraints (i.e., upper bounds) on fluxes. In reality, the survival of a microbe requires maintenance of homeostasis, which may be exquisitely sensitive to actual rates of nutrient inflow and maximum throughput of metabolic reactions. An in silico growth/survival model could capture this requirement via quantitative homeostatic constraints that restrict cell density or intracellular species concentrations to a given range. Survival in such a model would be quite sensitive to the values of capacity constraints on fluxes as well as particular values of biomass coefficients. Although determination of minimal nutrient sets for such a growth/survival model would require a more involved analysis of the feasible flux polyhedron than what has been offered here, our method would provide useful starting points for any such approach.

Incorporating regulation

Constraint-based metabolic model formulations, such as those offered in this article, do not address the impact of genetic and feedback regulation on metabolic network dynamics. The lack of adequate flux constraints allows these models to exhibit some physiologically infeasible behaviors, such as lactose transport in the presence of intracellular glucose. A nutrient set, whose ability to render biomass producible depends on such a physiologically infeasible pathway, will clearly be inadequate as a growth media in vivo. Computation of biologically feasible nutrient sets thus may require incorporation of regulation into the constraint-based metabolic modeling framework.

Regulatory flux balance analysis (rFBA) is a major approach for genome-scale modeling of metabolic regulation (3). This approach simulates genetic and enzymatic regulation of metabolism through a discrete time trajectory of flux configurations that optimize biomass production subject to a sequence of flux constraints. These regulatory flux constraints represent the impact of genetic and feedback regulation on metabolism. Each set of constraints is computed as a piecewise function of the previous iteration's flux optimum and a Boolean gene regulatory network state. Although this approach has found success, there are several limitations to the ability of rFBA to capture the feasible or optimal behaviors of a regulated metabolic network (2). Firstly, rFBA uses metabolic fluxes as surrogates for intracellular species concentrations, which are the true effectors of genetic and feedback regulation. Secondly, rFBA applies the unrealistic assumption that metabolic networks reach a new optimum flux configuration immediately after each gene regulatory change. Finally, it can be shown that rFBA arbitrarily restricts itself to one of many possible trajectories through flux space, even under the instantaneous optimality assumption. This occurs because the optimal flux configuration chosen at each time step by rFBA is usually only one point in a high-dimensional polyhedral set of equivalent optima. Alternative optima may produce a different set of regulatory constraints in the next time step and result in a drastically different trajectory.

The constraint-based metabolic model formulation with which we test producibility can potentially provide an alternative to rFBA for modeling metabolic regulation on the genome-scale. Unlike FBA and rFBA, our formulation explicitly models growth-mediated dilution of the metabolome. As a result, each steady-state flux configuration and growth rate is mapped to a unique steady-state species concentration. Regulatory constraints could be implemented in this framework in the form of regulatory rules that specify feasible/infeasible combinations of steady-state flux configurations and species concentrations. As in rFBA, these regulatory rules would impose constraints that implement the logic of genetic regulation and enzymatic feedback (i.e., reaction i is “on” only if species j is present at nonzero concentration); however, unlike rFBA, these constraints would explicitly capture the regulatory coupling of flux values to steady-state species concentrations. Furthermore, this framework would allow direct querying of feasible and optimal behaviors in the context of regulation, rather than requiring the simulation of an arbitrary trajectory in steady-state space under the assumption of instantaneous optimality. This framework may, however, pose computational challenges, arising from the potential nonconvexity of the feasible flux region induced by these regulatory constraints. This would require new methods for calculating minimal nutrient sets, as well as a reformulation of most standard genome-scale metabolic analyses (e.g., biomass optimization, minimization of metabolic adjustment, network pathway analysis) (17,18,26). We are currently investigating potential approaches in this direction.

CONCLUSIONS

In this article we have applied a theorem of alternatives from linear programming to draw a novel relationship between the ESCRs of a metabolic network and producibility in the absence of irreversibility constraints. This result makes explicit how ESCRs delineate nonfeasible behaviors of the metabolic network, and also formalizes how producibility captures the connectivity of species via conserved moiety pools.

Using this principle, we have outlined a simple algorithm that traverses the ESCRs of a metabolic network to generate all minimal nutrient sets that are compatible with the weak producibility of a given species. Our approach is applicable even when all of the ESCRs of a metabolic network are not known, as is often the case for genome-scale metabolic networks. We have applied our method to the analysis of anhydrous ESCRs in E. coli iJR904, computing all minimal aqueous nutrient sets that render biomass weakly producible. Though nutrient sets generated by our analysis are not guaranteed to be thermodynamically feasible, we find that a significant number of these minimal weak aqueous nutrient sets permit in silico growth/survival under the biomass model when thermodynamic constraints are considered.

Employing the genome scale metabolic model iJR904 and the biomass model of growth, our approach generates testable hypotheses regarding E. coli minimal nutrient media. Further experiments suggested by our results may yield insight into the consistency of the E. coli metabolic network annotation with in vivo data and facilitate iterative model building and refinement.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX 1: PROOFS

Proof of Lemma 2

Let eⁱ, i = 1, … , m, denote the basis of the Euclidean R^m. Then (Aw)_i > 0 is equivalent to (– e^iTA)w < 0, and by Lemma (with b = – A^Teⁱ), the nonemptiness of the set in Eq. 3 is equivalent to the emptiness of the set

(16)

Therefore, to prove Lemma 2, it is sufficient to show that the sets in Eqs. 4 and 16 are both either empty or nonempty, for arbitrary i = 1, …, m. Let us first assume the set in Eq. 16 is nonempty and let z be an arbitrary element in this set. If we let y = z + eⁱ, then A^Ty = 0 by the definition of the set in Eq. 16. Also, since z ≥ 0, it follows that y = z + eⁱ ≥ 0. Finally, y_i = z_i + 1 > 0, from which we conclude that y belongs to the set in Eq. 4, which is therefore nonempty.

Conversely, let us assume that the set in Eq. 4 is nonempty and let y be an arbitrary element in this set. Since y_i ≠ 0, we can define z = y/y_i – eⁱ. Then A^T(z + eⁱ) = A^Ty/y_i = 0 and z ≥ 0 since y ≥ 0, y_i > 0, and (y/y_i – eⁱ)_i = 0. We conclude that the set in Eq. 4 is nonempty and the Lemma is proved.

Proof of Lemma 3

Let p = |E| and E = {r¹, … , r^p}. Then, for any g ∈ G, we have

(17)

For necessity, let us assume P_IE) ⊆ P_U(E). This is equivalent to

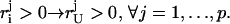(18)

For g ∈ G with g_i > 0, from Eq. 17 it follows that there exists k ∈ 1, … , p so that α_k > 0 and 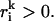From Eq. 18, it follows that which by Eq. 17 implies g_U > 0, and the set {g ∈ G | g_i > 0, g_U = 0} is empty.

For sufficiency, we provide a proof by contradiction. Let us assume that {g ∈ G | g_i > 0, g_U = 0} is empty and P_i(G) ⊊ P_U(G). This means that there exists k = 1, … , p so that and Then, if we take α_k = 1 and α_j = 0, j = 1, …, p, j ≠ k in (17), then we find a g ∈ G with g_i > 0 and g_U = 0, which means that {g ∈ G | g_i > 0, g_U = 0} is nonempty. This contradicts the assumption and the Lemma is proved.

Proof of Corollary 1

We start by noting that the equivalence

(19)

holds for any sets A and B.

Species i is weakly producible under U ∪ {j} if and only if P_i(E) ⊂ P_{U ∪ {j}}(E). Using Eq. 19, this is equivalent to P_i(E) = P_{U ∪ {j}}(E) ∩ P_i(E) = P_U(P_i(E)) ∪ P_j(P_i(E)) = P_U(P_i(E)) ∪ P_k(P_i(E)) = P_{U ∪ {k}}(E) ∩ P_i(E). Using Eq. 19 again, this means that P_i(E) ⊂ P_{U ∪ {j}}(E), which means that species i is producible under U ∪ {j}.

Proof of Corollary 2

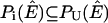if and only if species i is weakly producible under stoichiometry matrix [I_w S] and nutrient media U. This means that there exists a flux configuration for which

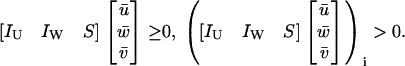(20)

However, this is equivalent to the existence of a flux configuration and , for which

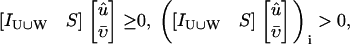(21)

which is equivalent to i being weakly producible under stoichiometry matrix S and nutrient media U ∪ W.

APPENDIX 2: ALGORITHM 1

F = MinNutrient(i, E[, Z])

/* Traverse species sharing ESCRs with i */

F = Ø

J = set of species j [in Z] for which P_i(E) ∩ P_j(E) ≠ Ø

for all j ∈ J do

if P_i(E)\P_j(E) = Ø then

add {j} to F

else

F′ = MinNutrient(i, P_i(E)\P_j(E)[, Z])

for all U′ ∈ F′ do

add U′ ∪ {j} to F

end for

end if

end for

/* Prune nonminimal nutrient sets */

for all U ∈ F do

remove U from F if there exists U′ ∈ F for which U′ ⊂ U

end for

return F.