Structural Transitions of Confined Model Proteins: Molecular Dynamics Simulation and Experimental Validation

Abstract

Proteins fold in a confined space not only in vivo, i.e., folding assisted by molecular chaperons and chaperonins in a crowded cellular medium, but also in vitro as in production of recombinant proteins. Despite extensive work on protein folding in bulk, little is known about how and to what extent the thermodynamics and kinetics of protein folding are altered by confinement. In this work, we use a Gō-like off-lattice model to investigate the folding and stability of an all β-sheet protein in spherical cages of different sizes and surface hydrophobicity. We find whereas extreme confinement inhibits correct folding, a hydrophilic cage stabilizes the protein due to restriction of the unfolded configurations. In a hydrophobic cage, however, strong attraction from the cage surface destabilizes the confined protein because of competition between self-aggregation and adsorption of hydrophobic residues. We show that the kinetics of protein collapse and folding is strongly correlated with both the cage size and the surface hydrophobicity. It is demonstrated that a cage of moderate size and hydrophobicity optimizes both the folding yield and kinetics of structural transitions. To support the simulation results, we have also investigated the refolding of hen-egg lysozyme in the presence of cetyltrimethylammoniumbromide (CTAB) surfactants that provide an effective confinement of the proteins by micellization. The influence of the surfactant hydrophobicity on the structural and biological activity of the protein is determined with circular dichroism spectrum, fluorescence emission spectrum, and biological activity assay. It is shown that, as predicted by coarse-grained simulations, CTAB micelles facilitate the collapse of denatured lysozyme, whereas the addition of β-cyclodextrin-grafted-PNIPAAm, a weakly hydrophobic stripper, dissociates CTAB micelles and promotes the conformational rearrangement and thereby gives an improved recovery of lysozyme activity.

INTRODUCTION

A grand challenge in protein science and biotechnology is to understand how proteins attain specific native structures in living cells. The problem is affiliated with several debilitating human diseases such as Alzheimer's and Parkinson's that are characterized by accumulation of toxic protein aggregates (1–5). It is also of concern in industrial production of enzymes and therapeutic proteins using DNA recombinant techniques (6–8). Whereas the three-dimensional structure of a native protein is primarily determined by its amino-acid sequence (9), the thermodynamics and kinetics of protein folding critically depend on the solution condition or the local environment. For example, protein folding in vitro is often hampered by aggregation and misfolding of denatured proteins. In vivo, however, newly synthesized polypeptide chains are able to rapidly fold into their native states in a crowded cellular medium, thereby avoiding aggregation and degradation (10).

Protein folding in vivo is assisted by molecular chaperones and chaperonins that interact with and stabilize newly synthesized polypeptides (11–15). A relatively well-understood example is protein folding in the cavity of the GroEL-GroES complex, a barrel-shaped bacteria chaperonin where a nascent polypeptide can be encapsulated and undergoes productive structural transitions (16). Although the precise mechanism by which a chaperonin assists protein folding remains uncovered, recent theoretical investigations have indubitably revealed that a chaperonin-like cavity favors the compact structure of the native protein, thereby accelerating the folding rate (17–23). Both the stability and folding kinetics of an encapsulated protein are strongly correlated with the geometry and degree of confinement (20,23). It has been shown that in an inert or a hydrophilic cage as provided by a chaperonin, a protein becomes most stable, and the rate of folding is also maximized when the cavity size is ∼1.6 times the gyration radius of the native protein (23). The confinement has little effect if the protein is too small. Conversely, it may prohibit folding if the encaged protein is exceedingly larger than the cage size (24,25).

A protein may adopt, in addition to its native and random-coil-like denatured states, a number of collapsed globular states and sometimes misfolded states (26,27). Only in its native state is the protein biologically active. Previous studies suggest that confinement affects the mechanism of structural transitions by altering the pathways leading a protein from a random-coil state to various collapsed globular states or to the native state (24,25). The changes in the thermodynamics and kinetics of protein folding are primarily due to the restriction of the configurational space for denatured states (17,23).Whereas much progress has been made regarding the effect of confinement on folding and collapse of denatured proteins, it remains unclear how the specific protein-surface interactions, in particular surface energy, affect the kinetics and thermodynamics of structural transitions for confined proteins. A recent lattice model simulation work reveals that the kinetics of protein folding in a chaperonin-like cage depends critically on the hydrophobicity of the confining surface in addition to the accessible volume (28). More recent off-lattice simulations suggest that a weakly hydrophobic environment accelerates protein folding via transient binding of the intermediate states to the cage surface (29). However, to our knowledge no experimental validation of the simulation results has been reported and little is yet known on the interplay between the confinement and surface energy, and on their specific effects in collapse and folding of confined proteins.

In this work, we use Langevin dynamics to investigate the structural transitions of an all β-sheet protein confined in spherical cages of various sizes and hydrophobicity. The effects of confinement on protein stability, folding kinetics, and yield are systematically studied by using the order parameters affiliated with protein size and configuration. The protein folding maps are generated to illustrate the kinetic pathways of the structural transitions in the bulk and under confinement. Although the Gō-like coarse-grained model is probably unable to capture the atomic details of protein folding and collapse, it should be sufficient to address the generic features concerning how confinement affects the thermodynamics and kinetics of structural transitions, in particular from denatured configurations to collapsed globular states and to the native state. Similar minimalist models have been successfully used to study protein folding in dilute solutions(30,31) and in crowded cellular media (32), competition between protein folding and aggregation(33,34), and more recently folding of proteins under confinement (23–25,29,35).

The main results from the coarse-grained simulations are validated with experiments on the refolding of hen-egg lysozyme assisted by cetyltrimethylammoniumbromide (CTAB) surfactants and β-cyclodextrin-grafted-PNIPAAm, an artificial chaperone system originally proposed by Rozema and Gellman (36–38). In experiments, the proteins are confined in the micelles of CTAB surfactants (capturer) and the structural transitions are assisted with the addition of β-cyclodextrin-grafted-PNIPAAm (the stripper) (39). The secondary and tertiary structures and biological activity of lysozyme are determined with circular dichroism (CD) spectrum, fluorescence emission spectrum, and activity measurements, respectively. The experimental results illustrate how the surface hydrophobicity of the confinement affects the protein folding and collapse, conformational rearrangement, and, most importantly, the refolding yield as indicated by the recovery of lysozyme activity.

EXPERIMENTS

Materials

The chemicals used in this study were hen-egg white lysozyme (Sigma, St. Louis, MO), reduced and oxidized glutathione (GSH and GSSG, Roche, Basel, Switzerland), dithiothreitol (DTT, Gibco BRL, Gaithersburg MD), N-isopropylacrylamide (NIPAAm, Acros, Geel, Belgium), β-cyclodextrin (β-CD, Acros), cerium ammonium nitrate (Alfa, Ward Hill, MA), and Micrococcus lysodeikicus (Sigma). Other chemicals, unless stated otherwise, are analytical pure grade and purchased from standard suppliers.

Procedures

β-CD-grafted-PNIPAAm was prepared and purified according to Lu et al. (39). In denaturation of lysozyme, a specified amount of native lysozyme was dissolved in a denaturing buffer of pH 8.6, 0.1 M Tris-HCl containing 8 M urea, 30 mM DTT, and 1 mM EDTA. After mixing, the solution was incubated at 37°C for 3 h and stored at 4°C. Refolding of lysozyme follows a two-step dilution method. In the first step, a denatured lysozyme of 50 mg/ml was mixed with 0.1M Tris-HCl at pH 8.2, containing 20 mM CTAB to give a specific molar ratio of CTAB to lysozyme. The mixture was incubated at room temperature for 30 min. In the second step, the mixture was diluted by 0.1 M, pH 8.2 Tris-HCl containing 0.4 mM GSSG and 4mM GSH, and β-CD-g-PNIPAAm or β-CD of specified concentration. The mixture was incubated at specified temperature for 24 h before being subjected to activity assay.

Structural analysis

The analysis of protein secondary structure was based on CD spectrum determined by a Jasco-715 (Tokyo, Japan). The calibration factor of the instrument was adjusted using aqueous solutions of D-1-camphorsulfonic acid. The CD spectra were taken at least five times. For all measurements, a sample containing buffer and specified concentration of CTAB was used as a reference. The protein tertiary structure was monitored by fluorescence spectra using a Hitachi (Tokyo, Japan) F-2500 fluorescence spectrophotometer with a quartz cuvette of 1 cm light path. Both excitation and emission slits were set at 10 nm. Fluorescence spectra were measured by exciting the protein solution at 280 nm and recording the emission spectra within 220–500 nm.

PROTEIN MODEL AND SIMULATION METHODS

Gō-like minimalist model

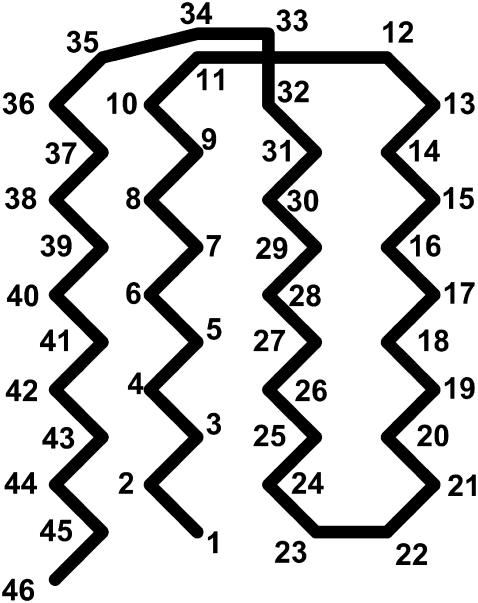
We consider an off-lattice model of an all β-sheet protein that was first introduced by Honeycutt and Thirumalai (HT) (40). Similar coarse-grained models have been extensively used in molecular simulations of protein folding(30,31) and aggregation(34,41). The HT model consists of 46 amino-acid residues, distinguishing themselves in three forms: hydrophobic (B), hydrophilic (L), and neutral (N). All residues are treated as spherical beads of equal size, tangentially connected in a sequence: B₉N₃(LB)₄N₃B₉N₃(LB)₅L. The side chains of the amino-acid residues are not explicitly considered. Fig. 1 shows the native structure of the model protein obtained from a simulated annealing method.

FIGURE 1.

Illustration of the native state of the Gō-like model. The numbers denote the bead in sequence and the native contacts are listed in Table 1.

As in previous studies (34,40,42,43), the Hamiltonian of the model protein includes the bond energy, the excluded-volume effects, and the long-range van der Waals attractions. The bond energy is related to fluctuations of bond lengths, bond angles, and dihedral angles. Specifically, the bond fluctuation is described by a harmonic potential

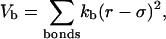(1)

where r is the center-to-center distance between two nearest-neighboring amino-acid residues, σ is the equilibrium bond length, and 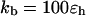is the bond spring constant. For a tangentially connected chain, the equilibrium bond length is the same as the bead diameter. Throughout this work, 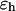and 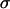are treated as the units of energy and length, respectively.

The bending potential specifies the energy associated with fluctuation of the bond angles; it is also expressed in a harmonic form

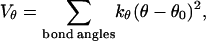(2)

where θ denotes a bond angle, θ₀ = 105° is the equilibrium bond angle, and 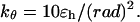The dihedral potential is described by

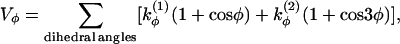(3)

where 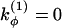and 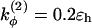if more than one of the four beads in defining the dihedral angle φ are neutral (N), and 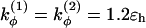otherwise. The dihedral potential exhibits a minimum at trans or gauche configurations. These energy minima are responsible for the formation of β-turns in the native structure of the model protein (34).

The “nonbonded” pair interaction includes the excluded-volume effect and the long-range van der Waals attraction. It applies to amino-acid residues separated by at least two peptide bonds via a Lennard-Jones (LJ)-like potential:

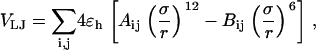(4)

where 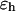stands for a unit energy, and the dimensionless parameters 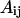and 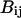depend on the identities of the interacting beads. To facilitate direct comparison with results from previous single-chain simulations, we adopt 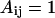and 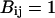for interactions between BB pairs, 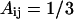and 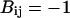for LB and LL pairs, an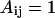d and 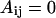for BN, LN, and NN pairs.

Despite its simplicity, the model protein exhibits a high degree of frustration, i.e., it may fold into a series of compacted but nonnative structures that are mutually inaccessible by regular molecular simulations. To avoid the frustrated conformations, we use a modified HT model (27) that retains only the hydrophobic interactions between native contacts, i.e., we consider only nonbonded pairs with a center-to-center distance below 1.167 σ in the native structure. Table 1 gives 47 pairs of amino-acid monomers that are defined as the native contacts, most involving hydrophobic residues buried in the protein core.

TABLE 1.

Indices of native contacts in the Gō-like model of an all β-sheet protein

Native contacts
(1, 24)	(1, 45)
(2, 24)	(2, 43)	(2, 45)
(3, 20)	(3, 24)	(3, 26)	(3, 43)
(4, 26)	(4, 41)	(4, 43)
(5, 18)	(5, 26)	(5, 28)	(5, 41)
(6, 28)	(6, 39)	(6, 41)
(7, 16)	(7, 28)	(7, 30)	(7, 39)
(8, 30)
(9, 14)	(9, 30)	(9, 32)	(9, 37)
(14, 32)
(16, 28)	(16, 29)	(16, 30)
(18, 26)	(18, 27)	(18, 28)
(20, 24)	(20, 25)
(24, 25)
(25, 43)
(26, 41)	(26, 43)
(27, 41)
(28, 39)	(28, 41)
(29, 39)
(30, 39)
(31, 37)

Cage potential

As in previous works (23,24,29), a spherical cage is used to represent the effect of confinement on the thermodynamics and kinetics of protein folding. The interior surface consists of uniformly distributed spherical beads with a number density 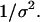The interaction between each bead and a segment of the model protein is described by a modified Lennard-Jones (LJ) potential

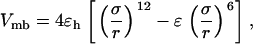(5)

where the dimensionless parameter ɛ defines the degree of hydrophobicity. For a hydrophobic segment, the parameter ɛ is positive, representing a surface attraction. For a hydrophilic or a neutral segment, 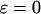regardless of the cage hydrophobicity; in that case, the surface potential is purely repulsive. Summation of 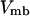over all surface beads gives the total confining potential

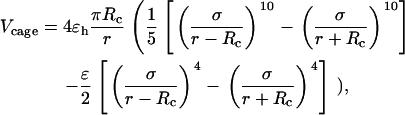(6)

where 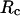is the cage radius, and r is the radial distance from the center.

Simulation method

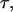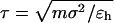We use the Langevin dynamics and velocity-Verlet algorithm to exam structural transitions of the model protein in spherical cages of different sizes and degrees of hydrophobicity. For direct comparison with previous simulations (42,43), we set the friction coefficient γ = 0.05. The protein configuration is updated at a time step of 0.005 where and 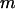is the mass of an amino-acid residue.

Three key properties are calculated during the course of simulations: the total potential energy (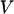), the protein radius of gyration (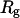), and the structure overlap function (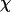). The total potential energy includes contributions from the bond energy, the long-range van der Waals interactions, and the external potential:

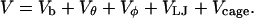(7)

The radius of gyration is defined as

(8)

where 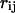is the center-to-center distance between a pair of spherical beads i and j, and 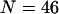is the total number of residues in the model protein. The structure overlap function is defined as

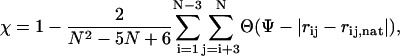(9)

where 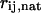is the distance between residues 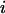and in the native structure, 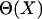is the Heaviside step function, and 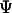stands for the deviation of an instantaneous configuration from the native structure due to thermal fluctuations. As in an earlier study, the parameter 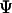is set to 0.2 in all simulations (42).

Whereas the structural transition of the confined protein exhibits sharp changes in both the total potential energy and the gyration radius, folding into a correct structure is revealed only by the structure overlap function, which provides a direct measure of the similarity between an instantaneous configuration and the native structure. To probe the structure and energy fluctuations, we also compute the heat capacity (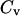) and fluctuation of the structural overlap function ():

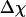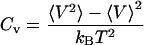(10)

(11)

The heat capacity and structure-fluctuation function exhibit maxima at the conditions of structural transitions, i.e., when the protein collapses or folds into its native structure.

Protein stability

Protein stability refers to its tolerance of the environmental conditions at which the protein preserves its unique folded structure and biological functionality. We consider the stability of the model protein in a spherical cage by simulating the protein size and structure correlation function at different temperatures. At each temperature, the protein relaxes from its native conformation over a period of at least 7500 steps, and additional 2500 steps are performed to calculate the ensemble averages. Because of the changes in protein size and structure, protein denaturation is characterized by sharp increases in the radius of gyration and in the structural overlap function.

Following Klimov and Thirumalai (44,45), we define the protein “foldability” as the relative deviation of the folding temperature 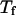from the collapse temperature :

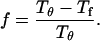(12)

Typically, the value of 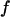falls between 0 and 1. It has been argued that a small value of 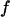means a fast (or easy) folding of a denatured protein because in this case, the native state has a deep energy minimum that synchronizes protein collapse and folding. (30,44,45)

Kinetics of structural transitions

At a fixed temperature, the protein-folding yield and the kinetics of structural transitions are calculated by running at least 30 parallel simulations with different initial configurations randomly generated at a high temperature (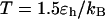). The folding yield is defined as the fraction of the parallel simulations that reach the native state over 10,000 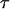steps. The folding kinetics is described by a time-dependent function that specifies the fraction of unfolded proteins in the parallel simulations:

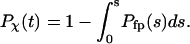(13)

In Eq.(13), 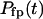is the distribution of the first-passage folding time

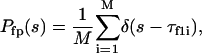(14)

where M is the number of parallel simulations and 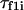denotes the first-passage time for the ith trajectory (simulation), i.e., the time when the protein arrive at its native state for the first time, and 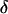is the Dirac-delta function. The protein is assumed in its native state if 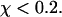For all cases considered in this work, 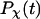can be fitted with the phenomenological equation

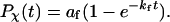(15)

The exponential constant 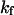specifies the rate of transition from the unfolded state to the native state. A large value of 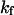corresponds to a rapid folding of the protein.

Similarly, the kinetics of protein collapse is described by the fraction of the parallel simulations where the protein is in a random-coil-like state,

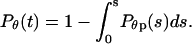(16)

Here 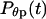is the distribution of the first-passage collapse time,

(17)

where 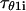denotes the first-passage time for the ith trajectory, i.e., the time when the protein has 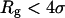for the first time. 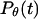can also be fitted with the exponential form

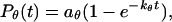(18)

where 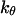reflects the transition rate from a unfolded to a collapsed state.

RESULTS AND DISCUSSION

Simulation of protein stability in a dilute solution

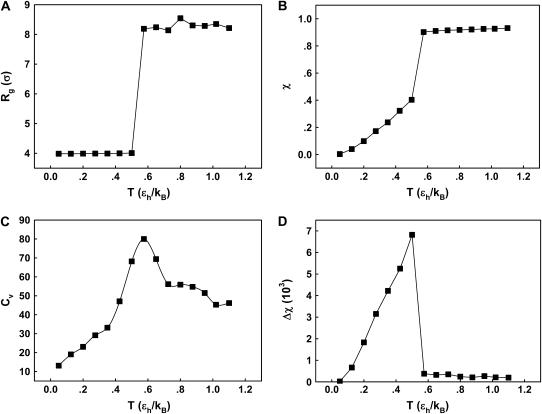
We first consider the properties of the model protein in a dilute solution for calibrating the simulation protocols, and more importantly, for providing a useful reference to assess the effect of confinement on the folding behavior. Fig. 2 shows the protein radius of gyration (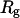), the structure overlap function (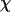), the heat capacity (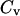), and the structure fluctuation (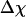) as temperature (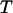) increases from zero to above the melting point. At the collapse temperature (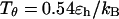), the radius of gyration jumps from that corresponding to a compact globular state at low temperature to that of a random-coil-like structure at high temperature. Similarly, at the folding temperature (), the structure overlap function shows a sharp increase due to the disappearance of the native configuration. Fig. 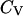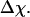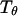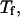2, C and D, present the heat capacity and the structure fluctuation function These two variables exhibit peaks at and respectively, corresponding to conditions where the system shows maximum fluctuations in the potential energy and in the structure. Because we use fewer native contacts, the folding temperature is slightly lower than that obtained by Shea et al. (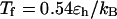) (26).

FIGURE 2.

Thermodynamics properties of the Gō-like protein in a dilute solution. Protein folding is characterized by a reduction of the protein radius of gyration (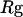) and by the structure overlap function (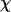). The collapse temperature is determined from 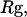corresponding to a maximum heat capacity; the folding temperature is determined from 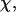corresponding to a maximum in the structural fluctuation 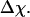(A) 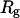versus T. (B) 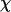versus T. (C) 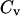versus T. (D) 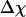versus T.

Protein stability in a hydrophilic cage

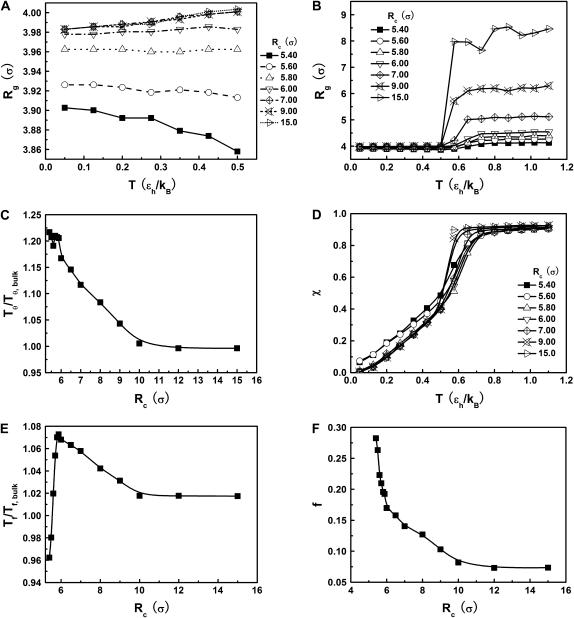
Fig. 3 presents the radii of gyration and structure overlap functions of the model protein in hydrophilic cages of different sizes. As in the bulk case, the confined protein denatures in two steps: first disappearance of its native structure and then expansion into a random-coil-like structure. Fig. 3 A shows that in the collapsed state, the protein size changes little with temperature or the degree of confinement. In the denatured state, however, the gyration radius is directly correlated with the cage size (Fig. 3 B), i.e., the smaller the cage, the smaller the protein size. As shown in Fig. 3 C, the relative collapse temperature (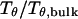) falls monotonically to its bulk value as the cage grows, indicating that a small cage protects protein stability by restriction of denatured configurations. A similar conclusion has been reached for a α/β model protein confined in spherical cages (24).

FIGURE 3.

Structural transitions in hydrophilic cages. (A) Effect of the cage radius, designated as 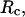on the protein gyration radius, 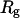(partially). (B) Effect of the cage radius, designated as 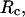on the protein gyration radius, 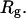(C) The relative collapse temperature 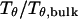versus 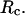(D) Effect of the cage radius, 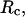on the structural overlap function, 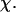(E) The relative folding temperature 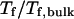versus 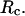(F) Foldability of the model protein 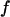versus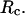

Fig. 3 D indicates that the structure overlap function is relatively insensitive to the cage size except when it is very small. In that case, the confined protein exhibits a structure that is noticeably different from its native configuration even at a very low temperature. As a result, it prohibits correct folding due to the spatial limitation. As the cage radius 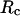increases from 5.40 to 15.0 σ (Fig. 3 E), we find that the relative folding temperature (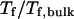) varies nonmonotonically: it first increases sharply with the cage size, reaches a maximum around 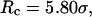and approaches its bulk value at 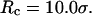The maximum folding temperature at 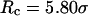suggests that the protein is most stable when it is confined in a cage of moderate size. The nonmonotonic dependence of 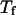on 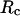indicates that although restriction of the denatured conformations favors the native state, an extreme confinement leads to overcompacted structures and inhibits correct folding. For the protein confined in an extremely small cage, opposite trends are observed in the collapse and folding temperatures, implying that a pure hydrophilic cage stabilizes compact structures without distinguishing the native and collapsed states.

Fig. 3 F shows the foldability of the model protein, defined as 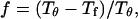in the hydrophilic cages of different sizes. As mentioned earlier, the value of reflects the cooperativity of protein folding and collapse, i.e., the smaller 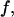the easier the protein folds. Because 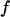falls monotonically as the cage radius increases, it appears that a small cage makes the protein folding more difficult. We will discuss later the kinetics of protein folding in detail.

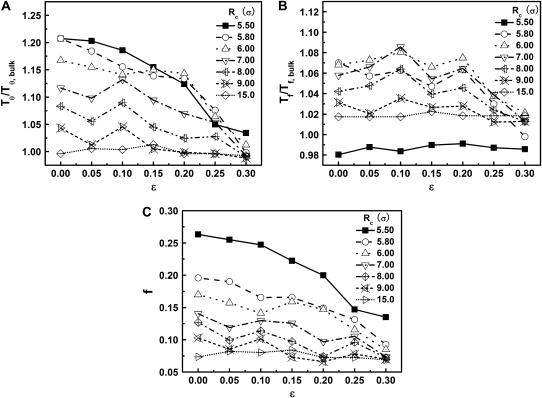
Effect of surface hydrophobicity

The hydrophobicity of the cage surface can be tuned by changing the parameter ɛ in the external potential (Eq. 6). As shown in Fig. 4 A, we find that except in a large cage (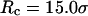) where the confinement has little effect on protein stability, the relative collapse temperatures (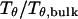) falls as the interior surface of the cage becomes more hydrophobic. The decline of the collapse temperature suggests that a hydrophobic surface disfavors the stability of the confined protein by promoting the interactions between the hydrophobic residues and the cage surface. Fig. 4 B shows the variation of the relative folding temperature (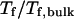) with the hydrophobicity parameter ɛ. In a small cage (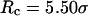), the protein folds incorrectly and the folding temperature is independent of the surface hydrophobicity. For the protein in cages with 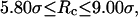the folding temperature (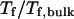) changes little with the surface hydrophobicity when 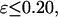but it sharply decreases as the hydrophobicity parameter is further increases (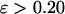). It appears that a weakly hydrophobic environment has little effect on the hydrophobic interactions of a native protein, but a strongly hydrophobic environment may destroy the protein internal structure.

FIGURE 4.

Effect of surface energy on stability of the confined protein. (A) Relative collapsing temperature (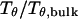) at different surface energy and cage size. (B) Relative folding temperature (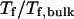) at different surface energy and cage size. (C) Foldability of the model protein 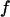at different surface energy and cage size.

Fig. 4 C shows the foldability of the model protein. It indicates that 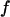falls as the cage size or surface hydrophobicity increases, suggesting that a hydrophobic surface assists folding. Apparently, protein foldability depends not only on its amino-acid sequence but also on its local solution environment.

Kinetics

Protein folding in bulk or under hydrophilic confinement

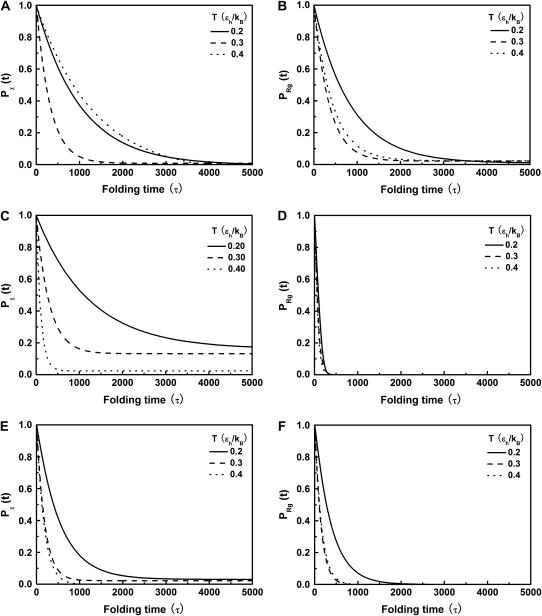
Fig. 5, A and B, present, respectively, the folding and collapse kinetics of the model protein in a dilute solution as represented by the fraction of the protein (among 30 parallel simulations) in the unfolded state, 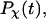and that in the random-coil-like state, 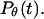Conversely, Fig. 5, C–F, show similar results for the protein folding and collapse in two hydrophilic cages with 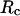= 5.88 σ and 9 σ, respectively. Table 2 gives the kinetic constants for the protein collapse and folding fitted with Eqs. 15 and 18.

FIGURE 5.

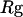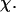
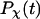Collapse and folding kinetics monitored by and is the fraction of unfolded proteins among 30 parallel simulations and is the fraction of uncollapsed proteins. The kinetic data are correlated using 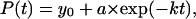which gives the folding yield 1−y₀ and the kinetic parameter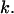 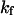and 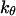represent folding and collapsing kinetic constants, respectively. (A) Collapsing kinetics in bulk solution. (B) Folding kinetics in bulk solution. (C) Collapsing kinetics at 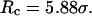(D) Folding kinetics at 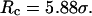(E) Collapsing kinetics at R_c = 900 σ. (F) Folding kinetics at R_c = 900 σ.

TABLE 2.

Kinetic parameters for collapse and folding of the model protein

		In bulk			In cage of 5.88 σ			In cage of 9.00 σ
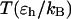	0.2	0.3	0.4	0.2	0.3	0.4	0.2	0.3	0.4
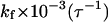	0.981	3.177	0.752	0.818	3.340	9.708	1.877	5.420	5.824
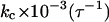	1.185	2.882	2.341	20.50	15.20	18.32	2.663	7.240	6.590

As shown in Fig. 5, A and B, we find that the protein folds slowly in a dilute solution at both low and high temperatures (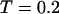 and 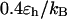), but relatively fast at an intermediate temperature (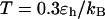). By contrast, it collapses fast at intermediate and high temperatures ( 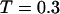and 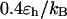) but slow at the low temperature. The similarity of the collapse rates at 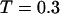and 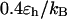suggests that the slow folding rate at high temperature is probably caused by structural fluctuations. The rapid folding and collapse at 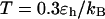reflect a subtle balance of the structure and size changes during the process of structural transitions. In this case, the kinetic parameters for the collapse and folding processes are close to each other (see Table 2), suggesting synchronized structure and size transitions.

Fig. 5, C and D, show, respectively, the fractions of unfolded and random-coil-like proteins confined in a spherical cage of radius 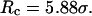At low temperatures ( 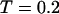and 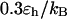), the folding rates are slightly lower than those in the bulk, indicating that a small cage hinders protein folding even though it improves the stability (Fig. 3 D). At 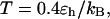however, the folding rate of the confined protein is significantly higher than that in bulk. As discussed later, the drastic improvement of folding kinetics at high temperature is caused by the more efficient folding pathways due to the confinement. In all cases, the collapse rate of the confined protein is nearly one order of magnitude faster than that in bulk. The rapid collapse of the confined protein is probably responsible for slow folding at low temperatures because it destroys the cooperativity of the size and structure transitions. As discussed later (Fig. 8), the rapid collapse increases the population of partially folded intermediates and thereby reduces the folding rate.

FIGURE 8.

Folding maps of model protein under different conditions. (A) in bulk, 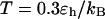; (B) in a hydrophilic cage,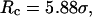 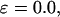and 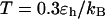; (C) in a weakly hydrophobic cage,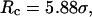 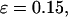and 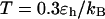; and (D) in a strongly hydrophobic cage,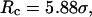 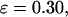and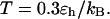

Fig. 5, E and F, present the kinetic curves for the folding and collapse of the model protein in a spherical cage with radius 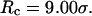Even though this large cage has little effect on the protein stability (Fig. 3, B and D), significant enhancements are observed for both kinetics of folding and collapse. Similar observations have been reported in a previous work (25). At low temperatures (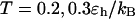), the folding rate is significantly higher than the corresponding values in bulk and that in a smaller cage (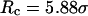). At high temperature (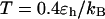), however, the folding rate is faster than that in bulk but slower than that in the smaller cage (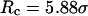). At all temperatures, the collapse rate is between that in the bulk and that in the smaller cage (see also Table 2).

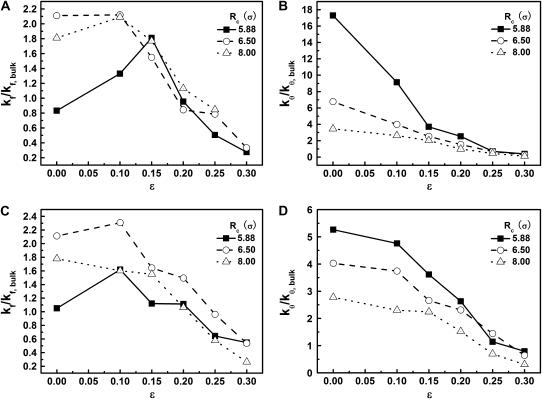
Effect of cage size and surface hydrophobicity on protein folding and collapse

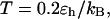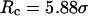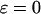We now consider the effect on surface hydrophobicity on folding kinetics. Fig. 6, A and B, show the relative kinetic constants versus the degrees of hydrophobicity for folding and collapse of the model protein in three different cages. In all cases, the temperature is fixed at far below the folding temperatures. For the protein in a small hydrophilic cage, (i.e., and ), the kinetic constant for protein folding is smaller than that in bulk, but the collapse kinetic constant is ∼17 times its bulk value. The folding rate shows a maximum at approximately 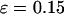for the protein in the cage with ; both hydrophilic and strongly hydrophobic surfaces reduce the folding rate. 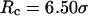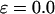Conversely, in larger hydrophilic cages ( and ), the kinetics constants for both folding and collapse are significantly higher than those in bulk. When ɛ is small (<0.1), the folding rate is relatively insensitive to the degree of hydrophobicity. As ɛ is further increased (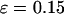), however, the folding rate quickly falls below the bulk value. Fig. 6 B shows that in all cases, the collapse kinetic constant monotonically declines with the degree of hydrophobicity.

FIGURE 6.

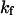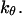Effect of cage size and surface energy on kinetic constants. and (A) 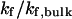versus surface energy at (B) 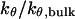versus surface energy at 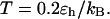(C) 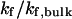versus surface energy at 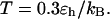(D) 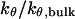versus surface energy at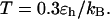

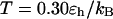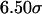Fig. 6, C and D, show the folding and collapse kinetic constants at a higher temperature (). In small cages ( and ), the kinetics of protein folding exhibits a maximum when the cage surface is weakly hydrophobic (i.e., 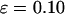). But in a larger pore, 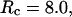the rate of folding declines almost monotonically with the surface hydrophobicity. As for the low temperature case, the kinetics constant for protein collapse falls as the surface hydrophobicity increases.

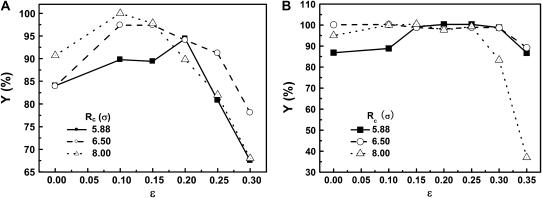
Effect of confinement and surface hydrophobicity on folding yield

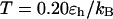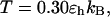Fig. 7, A and B, present the folding yields versus the surface hydrophobicity at and respectively. At 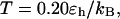the folding yield first increases with the degree of hydrophobicity ɛ, reaches a maximum when the surface is weakly hydrophobic, and decreases upon further increase of the surface hydrophobicity. The maximum folding yield depends on both cage size and surface hydrophobicity. At 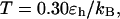the folding yield is higher than that at 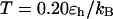except when the protein is confined in a very large and hydrophobic cage (i.e.,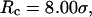 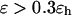). The folding yield declines sharply in strongly hydrophobic cages, probably due to the strong adsorption of hydrophobic residues on the cage surface.

FIGURE 7.

Effect of cage size and surface energy on folding yield. (A) 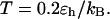(B)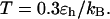

Protein folding maps

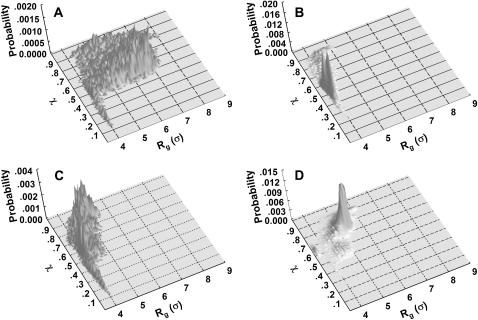
To provide further insights into the kinetics of structural transitions, we have also calculated the folding maps, i.e., the probability of the protein configuration in terms of the two order parameters χ and 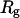during the entire folding process. Fig. 8 shows four folding maps corresponding to that in bulk and those in a small cage (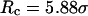) at 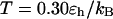and three different levels of surface hydrophobicity. Fig. 8 A shows that in bulk, the protein has high probability in the region with χ between 0.50 ∼ 0.70 and 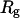between 5.0 and 7.0 σ, indicating that the protein first collapses into a global-like structure before the formation of the native state. Another important feature of this folding map is the broad distribution of the folding intermediates introduced by neglecting the long-range interactions in the Gō-like model.

Fig. 8 B indicates that when the protein is confined in a small hydrophilic cage, the folding intermediates are restricted in the region with χ between 0.45 ∼ 0.60 and 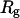comparable to that of the native form. The narrow distribution of 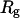explains why the confinement can significantly accelerate the kinetics of protein collapse. In this case, the folding intermediates are concentrated in a small region, suggesting a suppression of the intermediate states. Although the close confinement favors protein collapse, it also introduces energy barriers to conformation transitions, which slow down the kinetics of folding and reduce the folding yield.

Fig. 8 C shows that introduction of the surface hydrophobicity broadens the distribution of intermediates, thereby decreasing the collapse rate. This contradicts that the foldability can be significantly enhanced in a weakly hydrophobic environment. The folding map can be approximately divided into two areas: 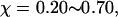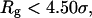where the protein is in a near-native structure and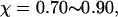 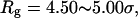where the protein is in a collapsed state.

Fig. 8 D shows the protein folding map in a small cage with strong hydrophobicity. The attraction from the cage surface leads to accumulation of intermediate states with 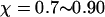and 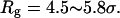Localization of the protein conformation in the high values of χ hinders not only the collapse but also the folding of the model protein. That explains the low folding yield and slow kinetics of structural transitions as shown in Figs. 6 and 7.

EXPERIMENTAL OBSERVATIONS

CTAB micelle facilitates the collapse of denatured lysozyme

To investigate the effect of confinement and surface hydrophobicity on protein folding experimentally, we employ a so-called “artificial chaperone” system where local confinement of protein is achieved by addition of surfactant molecules (36–38) . In our experiments, denatured lysozyme molecules are first captured by CTAB in the form of protein-CTAB complexes. β-CD-grafted-PNIPAAm, a stripper that strongly binds to the “capturer”, is then added to dissociate the complex and thereby triggers the protein refolding. Encapsulation of the protein with the CTAB micelles provides a hydrophobic confinement facilitating protein collapse as elucidated in Fig. 6, B and D. Conversely, formation of CTAB micelles around the proteins effectively inhibits the hydrophobic interactions between protein molecules that cause protein aggregation and thereby results in an improved refolding yield in comparison to that without surfactant molecules. The major function of a stripper, such as β-CD or β-CD-grafted-PNIPAAm, is to dissociate CTAB micelles and facilitate the refolding of the collapsed lysozyme in the presence of redox chemicals that catalyze the formation of intramolecular disulfur bridges. Compared to the conventional stripper (β-CD) that has a hydrophilic outer surface, β-CD-grafted-PNIPAAm is weakly hydrophobic due to the existence of PNIPAAm at the outer surface of β-CD. This thus provides hydrophobic sites in the refolding solution and will, as implied by the simulation results shown in Figs.7 and 8, enhance the structural rearrangement of the collapsed lysozyme.

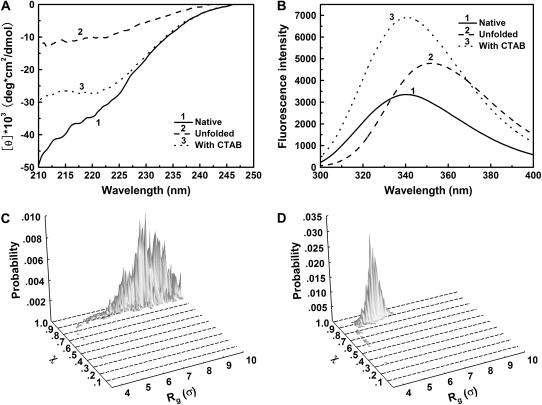
The denatured lysozyme of 0.4 mg/mL was prepared at pH 8.2, in 0.1 M Tris-HCl containing 0.4 mM GSSG, 5 M urea, and 1.36 mM CTAB (molar ratio of CTAB to lysozyme is 50:1). The critical micellization concentration of CTAB was 0.092 mM in this refolding buffer (46). After incubation at room temperature for 2 h, the lysozyme solution was subjected to CD spectrum and fluorescence intensity spectrum measurements. Fig. 9 A shows that the secondary structure of denatured lysozyme increases in the presence of CTAB micelles, indicating that the CTAB micelle leads to the partial formation of protein structure and enhances the collapse of denatured lysozyme. Fig. 9 B shows the fluorescence spectra of the native and denatured protein. The fluorescence intensity of the confined lysozyme is significantly higher than that of native lysozyme. This indicates that the confined lysozyme remains in a denatured state and has a different tertiary structure compared to its native conformation.

FIGURE 9.

Secondary and tertiary structures from experiments for confined lysozyme and from molecular simulations based on the Gō-like minimalist model. (A) Circular dichroism spectra of lysozyme in the presence of CTAB micelles; (B) Fluorescence emission spectra of lysozyme in CTAB micelles; (C) Configurational distribution of the denatured model protein in diluted solution; and (D) Configurational distribution of the denatured model protein in a spherical cage of 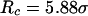and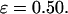

Fig. 9, C and D, give the simulation results on the conformational distribution of the model protein at a denatured condition with and without a strongly hydrophobic confinement, respectively. In consistent with the experimental observations as shown in Fig. 9 A, the hydrophobic confinement results in the reduction of 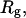indicating the collapse of the model protein. The 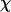value of the collapsed protein, however, is relatively high, and increases with the surface hydrophobicity. In agreement with the experimental results as shown in Fig. 9 B, the simulations indicate that a strong hydrophobic cage does not enhance protein folding.

β-CD-grafted-PNIPAAm dissociates CTAB micelles and facilitates the structural rearrangement of collapsed lysozyme

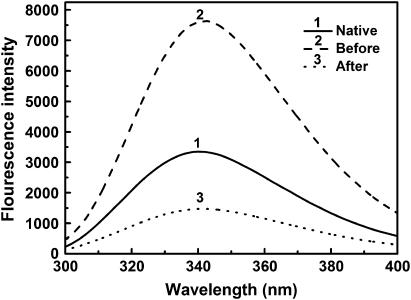
Denatured lysozyme, 50 mg/mL, was diluted by CTAB solution of 20 mM such that the molar ratio of CTAB to lysozyme was 50:1. After 30 min mixing, refolding buffer with β-CD-grafted-PNIPAAm was added into the protein solution, giving a final concentration of 0.1 mg/mL for lysozyme, and 0.70 mM for β-CD-grafted-PNIPAAm. The fluorescence emission spectrum and activity before and after adding β-CD-grafted-PNIPAAm were determined.

Fig. 10 shows that the addition of β-CD-grafted-PNIPAAm leads to a considerable reduction of the fluorescence intensity of lysozyme compared to that obtained in the presence of CTAB. This indicates that β-CD-grafted-PNIPAAm dissociates CTAB micelles and triggers the formation of the protein tertiary structure. The fluorescence intensity of the lysozyme in the presence of β-CD-grafted-PNIPAAm is lower than that of the native state due to the formation protein-β-CD-grafted-PNIPAAm complex, as being identified in our previous study of lysozyme refolding assisted by PNIPAAm (47).

FIGURE 10.

Fluorescence emission spectra of lysozyme before and after stripping with β-CD-grafted-PNIPAAm.

Fig. 11 gives the refolding of lysozyme at different temperatures using β-CD or β-CD-grafted-PNIPAAm as stripper, respectively. The terminal concentration was 0.1 mg/ml for lysozyme and 1.4 mM mg/ml for β-CD or 0.70 mM for β-CD-grafted-PNIPAAm. When β-CD-grafted-PNIPAAm is used as the stripper, the refolding yield increases with temperature and reaches 100% at 40°C. However, the refolding yield reaches a maximum at 20°C and declines against temperature if β-CD is used as the stripper. Once CTAB is stripped by β-CD-grafted-PNIPAAm, the collapsed lysozyme molecules are exposed to a weakly hydrophobic environment provided by the PNIPAAm segments, thus, as predicted by simulations as shown in Figs. 7 and 8, facilitating the conformational rearrangement and resulting in a higher refolding yield.

FIGURE 11.

Refolding yield of lysozyme obtained by using different strippers.

The above experimental results suggest that formation of CTAB micelles induces the collapse of denatured lysozyme molecules. The collapse of denatured structure is also evidenced by the enrichment of the secondary structure as shown in Fig. 9 A. However, the CTAB micelle, an effective hydrophobic cage for the encapsulated protein, does not facilitate the structural rearrangement into the folded state. Indeed, Fig. 9 B shows that the tertiary structure of the collapsed lysozyme is substantially different from that of the native conformation. We thus conclude that CTAB micelles function as the capturer in the so-called “artificial chaperone” system, resembling GroEL in vivo that captures unfolded or partially folded protein from the crowded cellular environment by its strong hydrophobic cage and thus inhibits the formation of protein aggregates (36–38). The structural rearrangement of the entrapped protein is accomplished with the assistance of ATP and GroES that changes both the conformation and the surface properties of GroEL, i.e., binding of ATP and GroES changes the hydrophobicity of GroEL cage from strong hydrophobic to hydrophilic or weakly hydrophophic (48,49). According to the simulation results shown in Figs. 7 and 8, the change of surface hydrophobicity facilitates the conformation rearrangements and protein folding. Similarly, Brinker et al. showed that enclosure of nonnative protein in the GroEL cage is essential for folding to proceed unimpaired by aggregation, and the folding under confinement can be significantly faster than that in the free solution (49). More recently, Shea and co-workers indicated that a cage of moderate hydrophobicity provides the maximum folding rate of the confined protein (29).

To assist the correct folding of the entrapped proteins, the CTAB micelles must be dissociated because, as discussed early, the interior surface, which is strongly hydrophobic, hinders the structural rearrangement (Fig. 9 D). For that purpose, a stripper, such as β-CD, is added into the refolding buffer to dissociate the CTAB micelles and facilitate the structural rearrangement of the collapsed protein. The use of β-CD-grafted-PNIPAAm as a stripper, which is weakly hydrophobic due to the existence of a PNIPAAm section, leads to an improved refolding yield in comparison with that obtained using β-CD, particularly at high temperature (Fig. 11). The improved yield is because the exposure of PNIPAAm to the solution environment provides hydrophobic sites that favor the conformational change of the collapsed protein, similar to that occurred in a weakly hydrophobic cage (Figs. 7 and 8). On the other hand, PNIPAAm also interacts with the protein via hydrophobic interaction (47) and thus inhibits the hydrophobic interaction between protein molecules that leads to the aggregation.

CONCLUSION

We have investigated the effect of confinement and surface hydrophobicity on the structural transitions of a model protein using Langevin dynamics. It is shown that without surface attraction, the confined protein favors compact configurations, but extreme confinement destroys the native structure. To distinguish protein folding from collapse, we adopt two order parameters, the radius of gyration and the structural overlap function, to represent the variations of the protein size and conformation during the folding process, respectively. Whereas both folding and collapse can be characterized by sharp changes in the radius of gyration, proper folding manifests itself in small deviations from the native structure. We find that the cage size and surface hydrophobicity have stronger influence on protein collapse than on folding. Whereas the protein stability is enhanced by decreasing the cage size, the native structure can be destroyed by increasing the surface hydrophobicity, especially at high surface energy. On the other hand, the foldability of the confined protein decreases with the cage size or the surface hydrophobicity, suggesting that the folding becomes more difficult when the protein is confined in a small hydrophilic cage.

The confinement may drastically accelerate the kinetics of both collapse and folding transitions. In a spherical cage of moderate size, a hydrophobic surface reduces the rate of protein collapse. However, rapid folding can be achieved in a hydrophobic cage of moderate size and hydrophobicity. Only in a small cage does a weakly hydrophobic cage accelerate the folding kinetics. The protein folding yield is maximized in cages with moderate size and hydrophobicity. By examining the folding maps in terms of the size and structure order parameters, we also find that the pathways of protein folding in a cage are very different from those in bulk. Although the confinement increases the probability of collapsed states, the surface attraction makes the configurational distribution more dispersed. As protein folding in bulk, the cooperativity of protein collapse and folding leads to a higher folding yield and faster kinetics.

To validate the simulation results, we have also conducted protein refolding experiments using lysozyme as the model protein and an artificial chaperone consisting of CTAB as the capturer and β-CD-grafted-PNIPAAm as the stripper. It is shown that the addition of CTAB micelles facilitates the protein collapse, i.e., the formation of protein secondary structure, However, CTAB surfactants do not attribute to the structural rearrangement that is essential to form the correct tertiary structure. The use of β-CD-grafted-PNIPAAm as a stripper contributes to a weakly hydrophobic solution environment and thus enhances the structural rearrangement. This leads to an improved recovery of lysozyme activity in comparison to that obtained by using β-CD as the stripper. The effect of surface hydrophobicity and two-step folding mechanism agrees well with the simulation results.

In conclusion, the simulation presented in this study can qualitatively reproduce the effects of the size and surface property of a confinement on the stability of entrapped protein as well as on the folding and collapse of the entrapped protein in vivo and in vitro. Both equilibrium and kinetics of protein folding can be assisted by confinement in a space of moderate size and hydrophobicity. Although the simulation results are obtained from an oversimplified coarse-grained model, the experimental validation based on a real protein indicates that the simulation results appear applicable to protein folding in general. Moreover, the molecular view in terms of collapse and rearrangement provides insight into the folding process and is helpful for the related research such as the development of new in vitro refolding methods for recombinant proteins.